Design and Mechanical Sensitivity Analysis of a MEMS Tuning Fork Gyroscope with an Anchored Leverage Mechanism
Abstract
1. Introduction
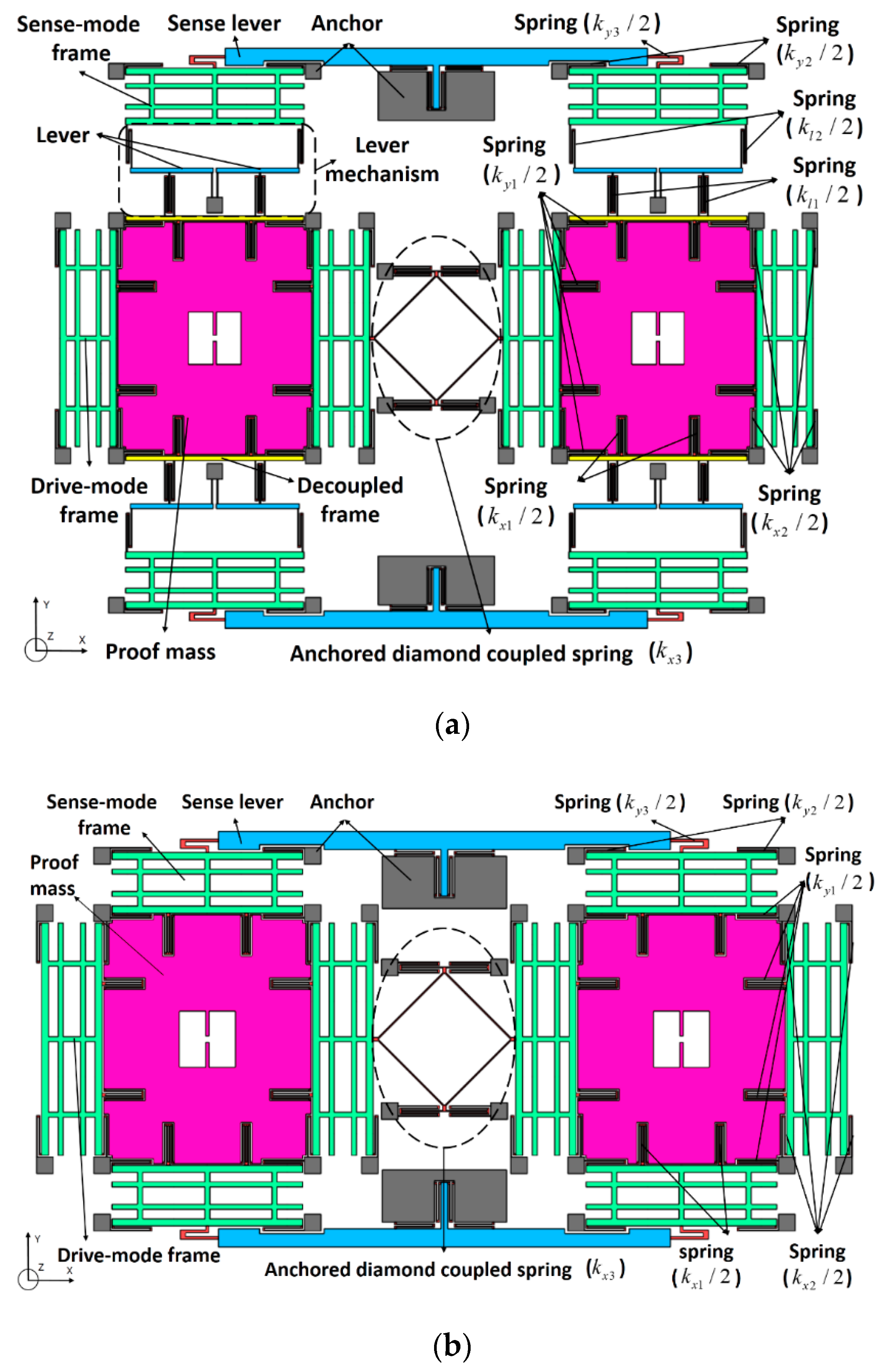
2. Architecture Design
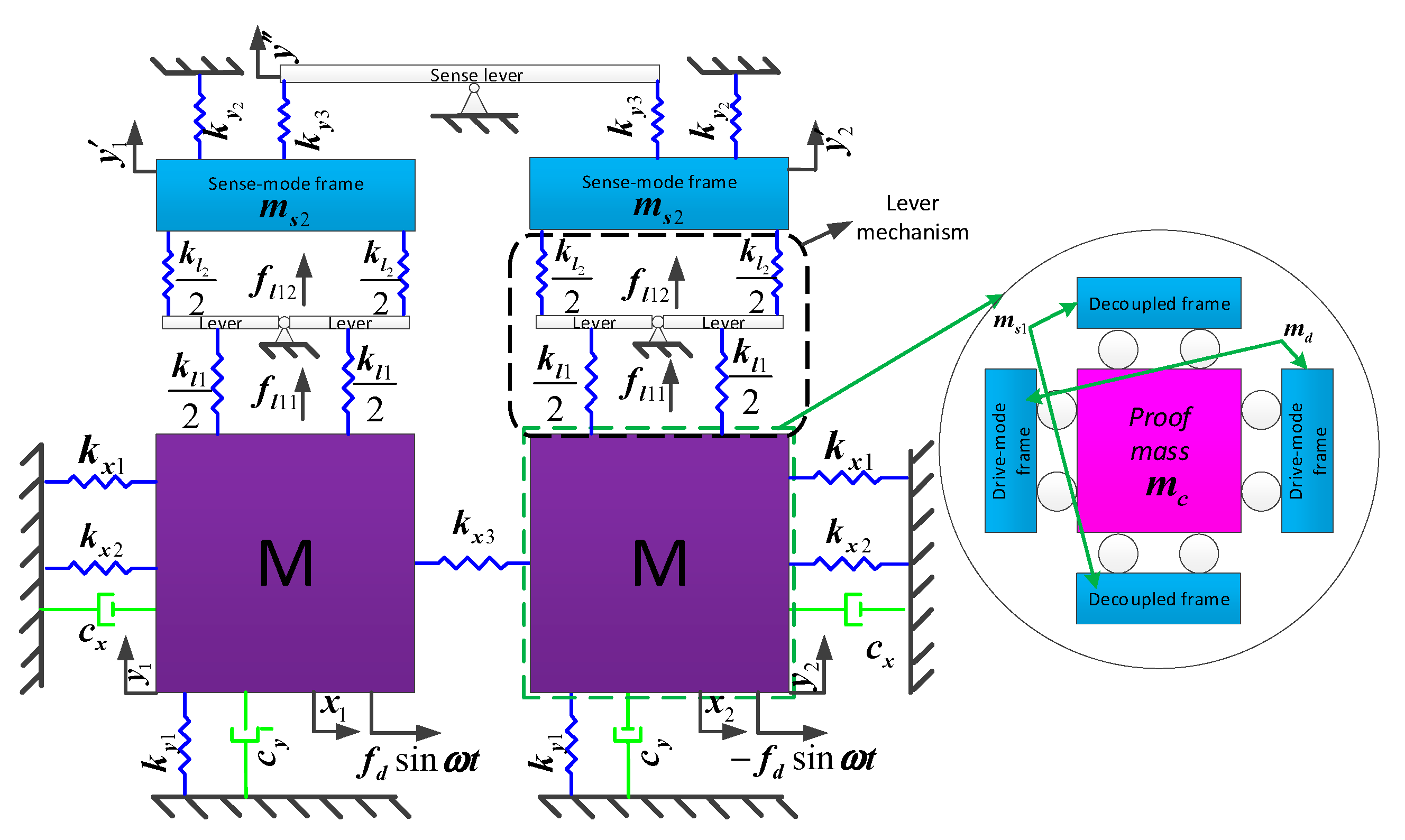
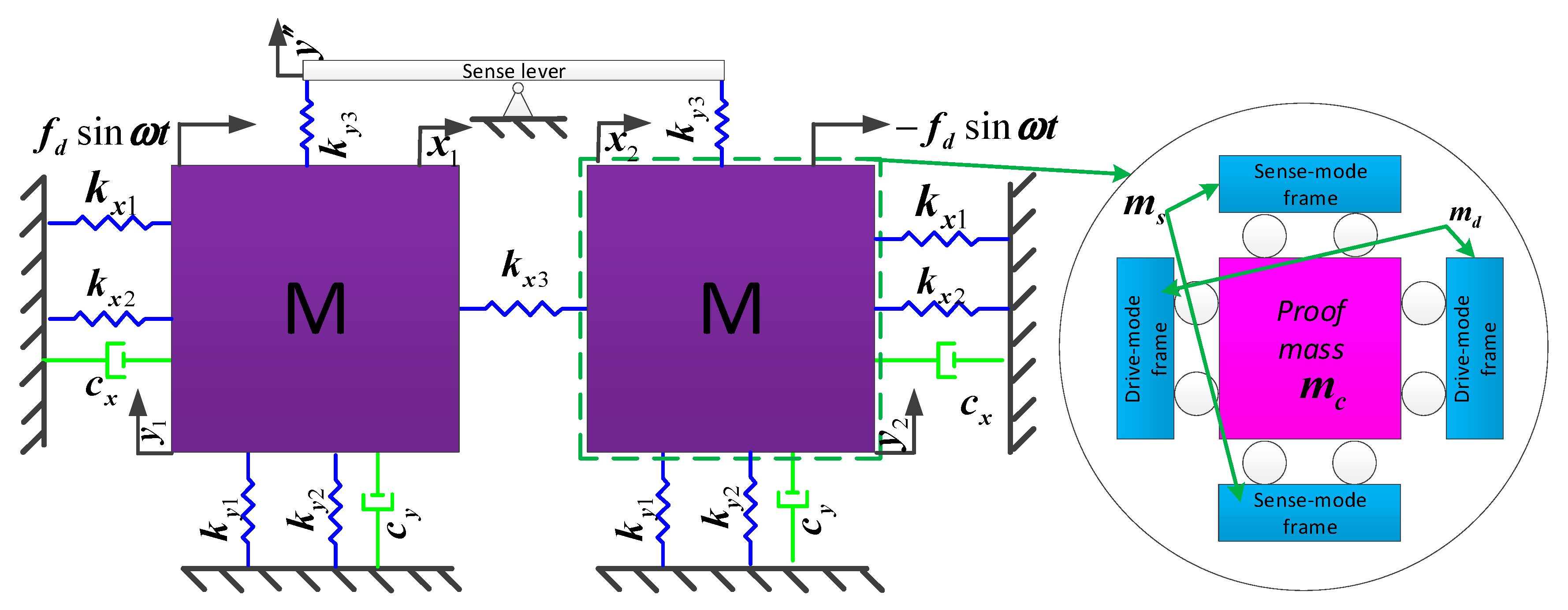
3. Theoretical Analysis
3.1. Kinematic Analysis of Type A and B
3.2. Optimization Analysis of LR
3.3. Analysis of IRMS
4. FEM Simulation and Analysis
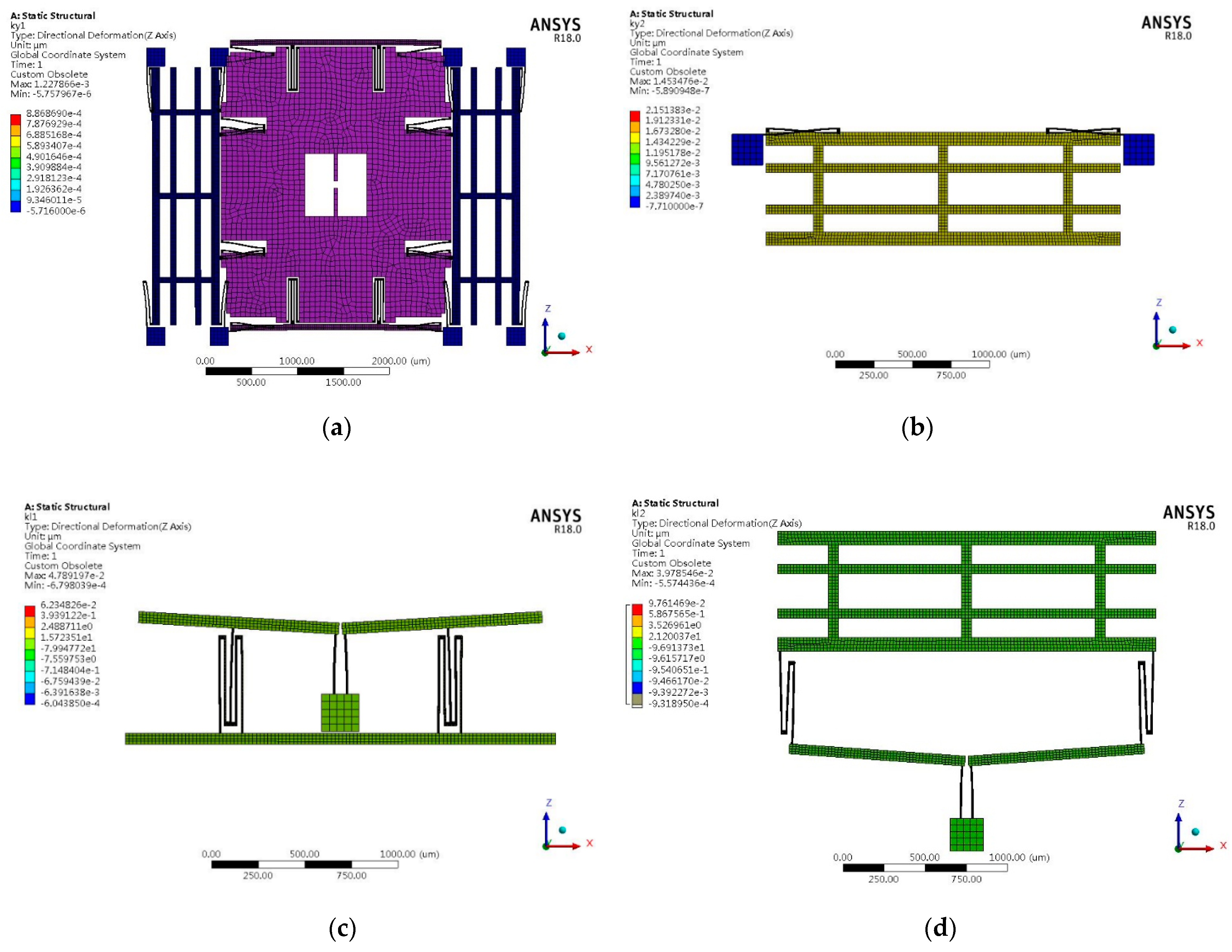
4.1. Analysis of LR and IRMS
4.2. FEM Analysis of Mechanism Sensitivity
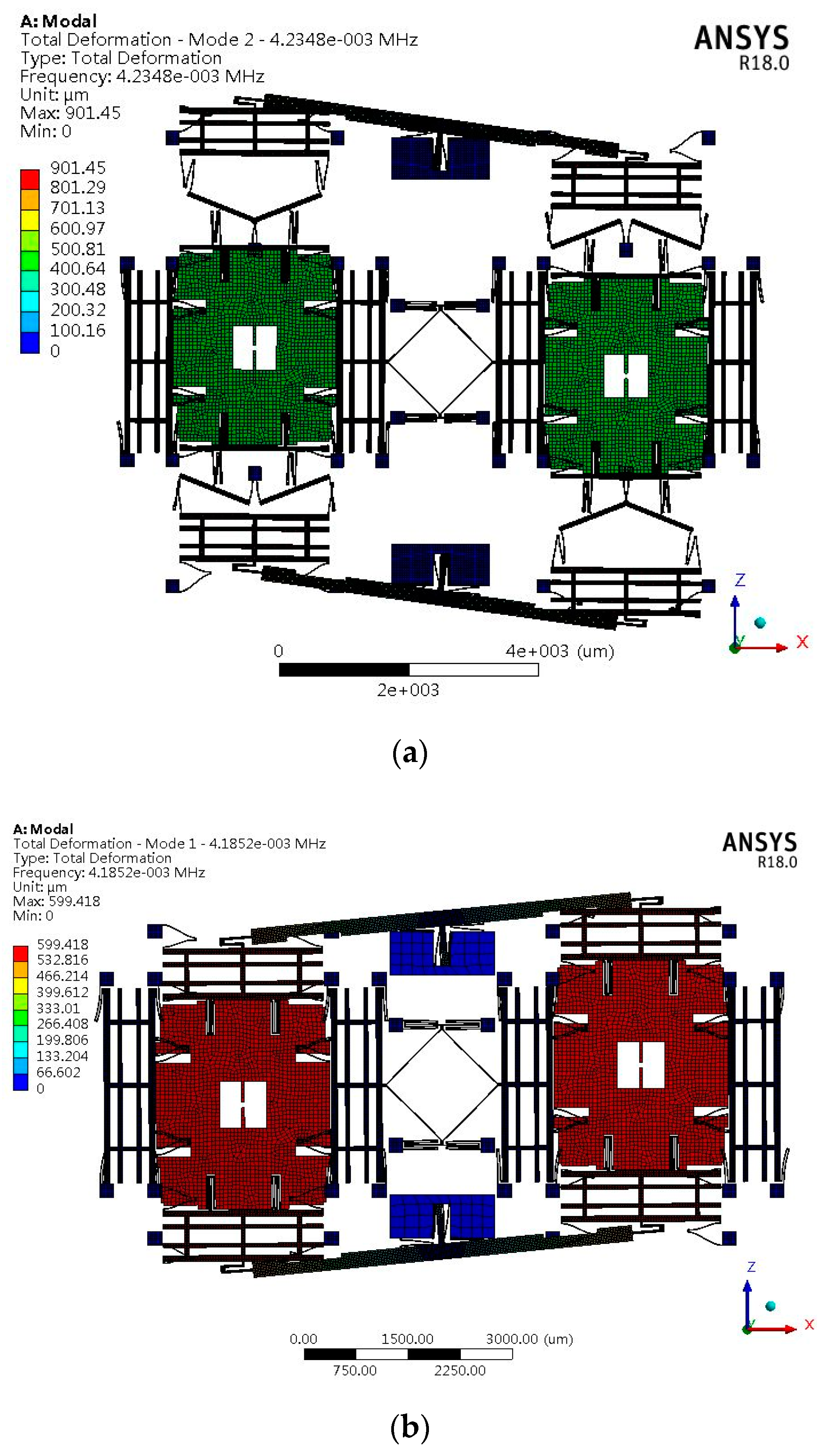
4.2.1. Modal Analysis
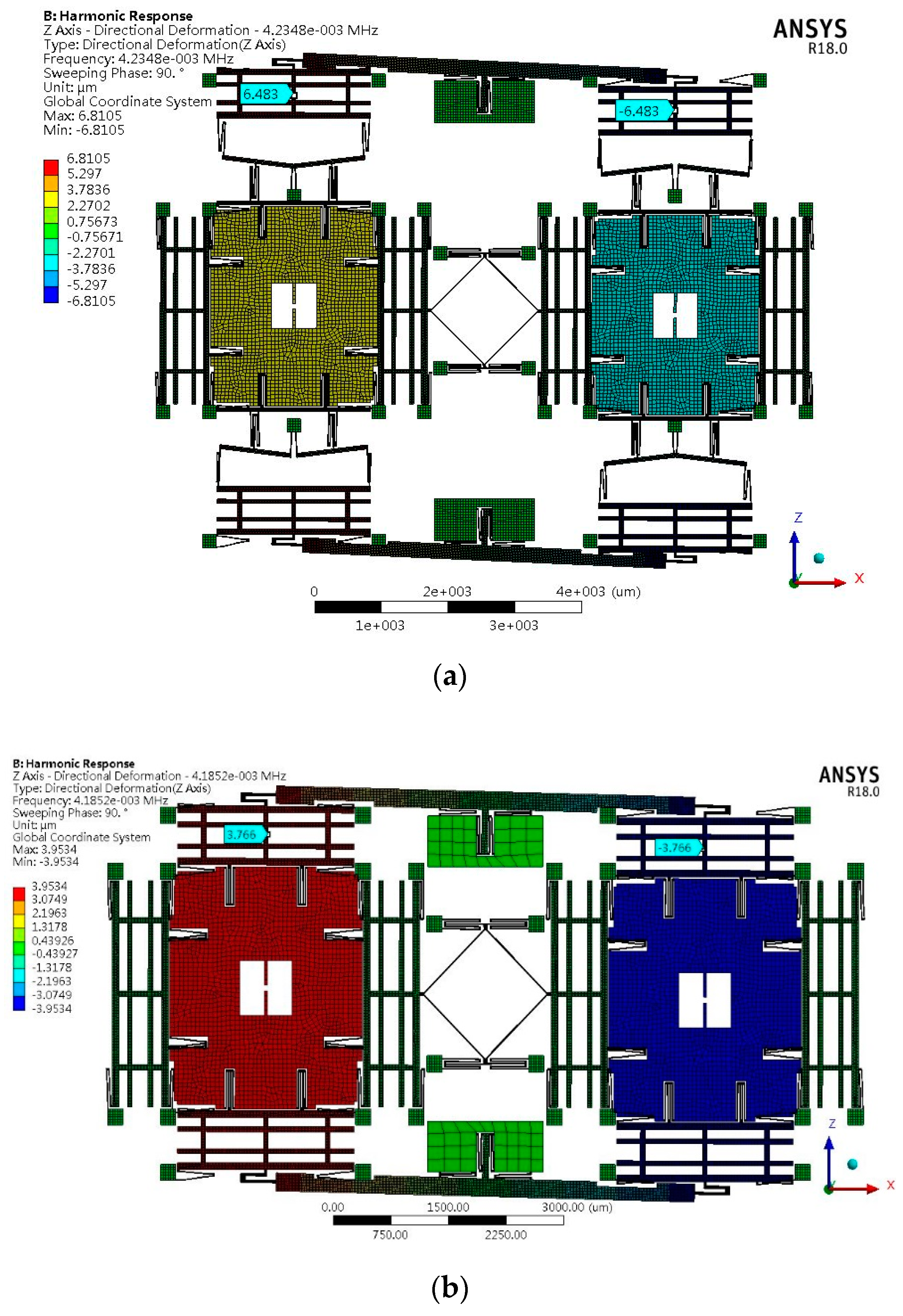
4.2.2. Sensitivity Analysis
4.3. Numerical and Theoretical Comparisons
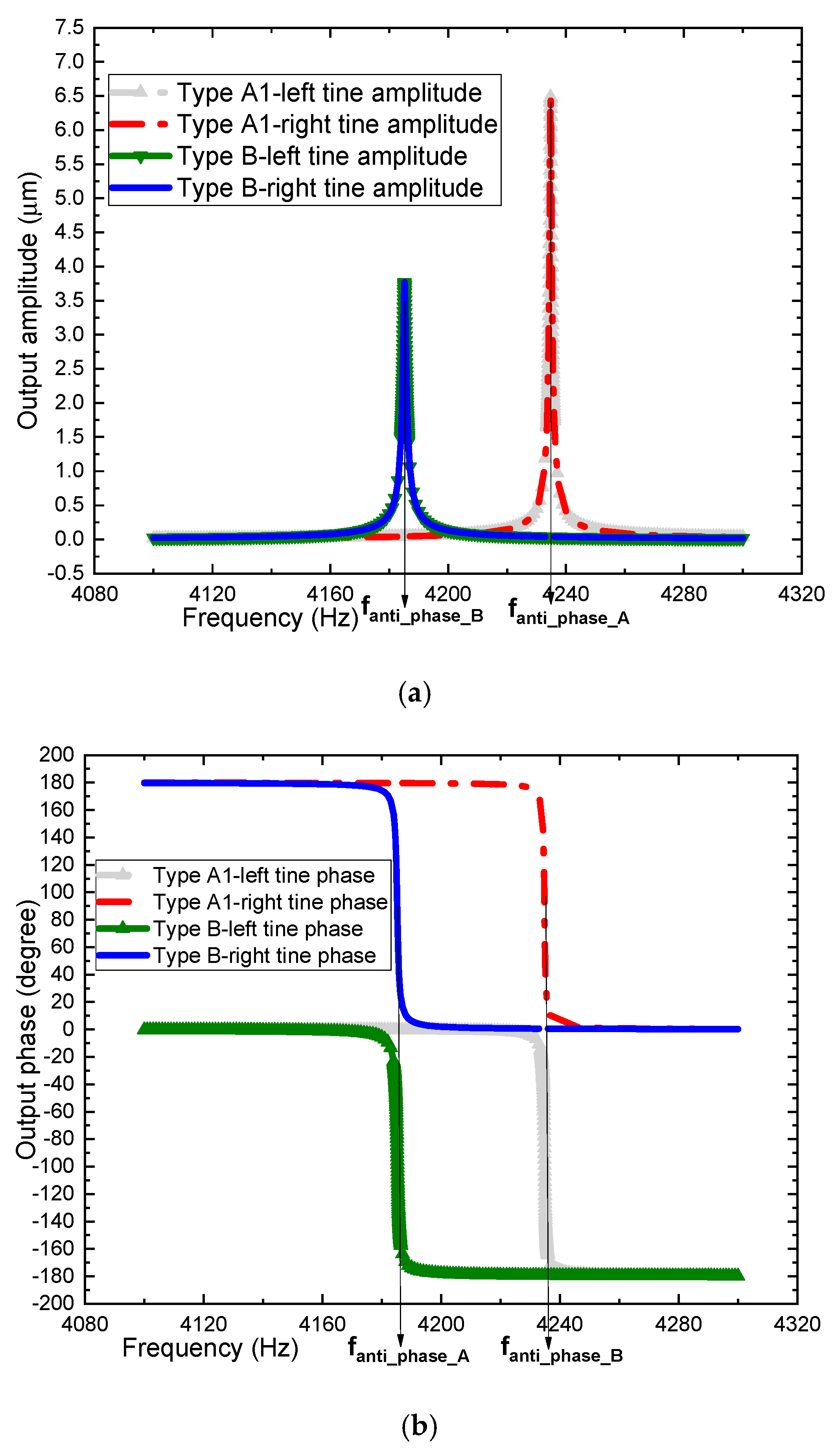
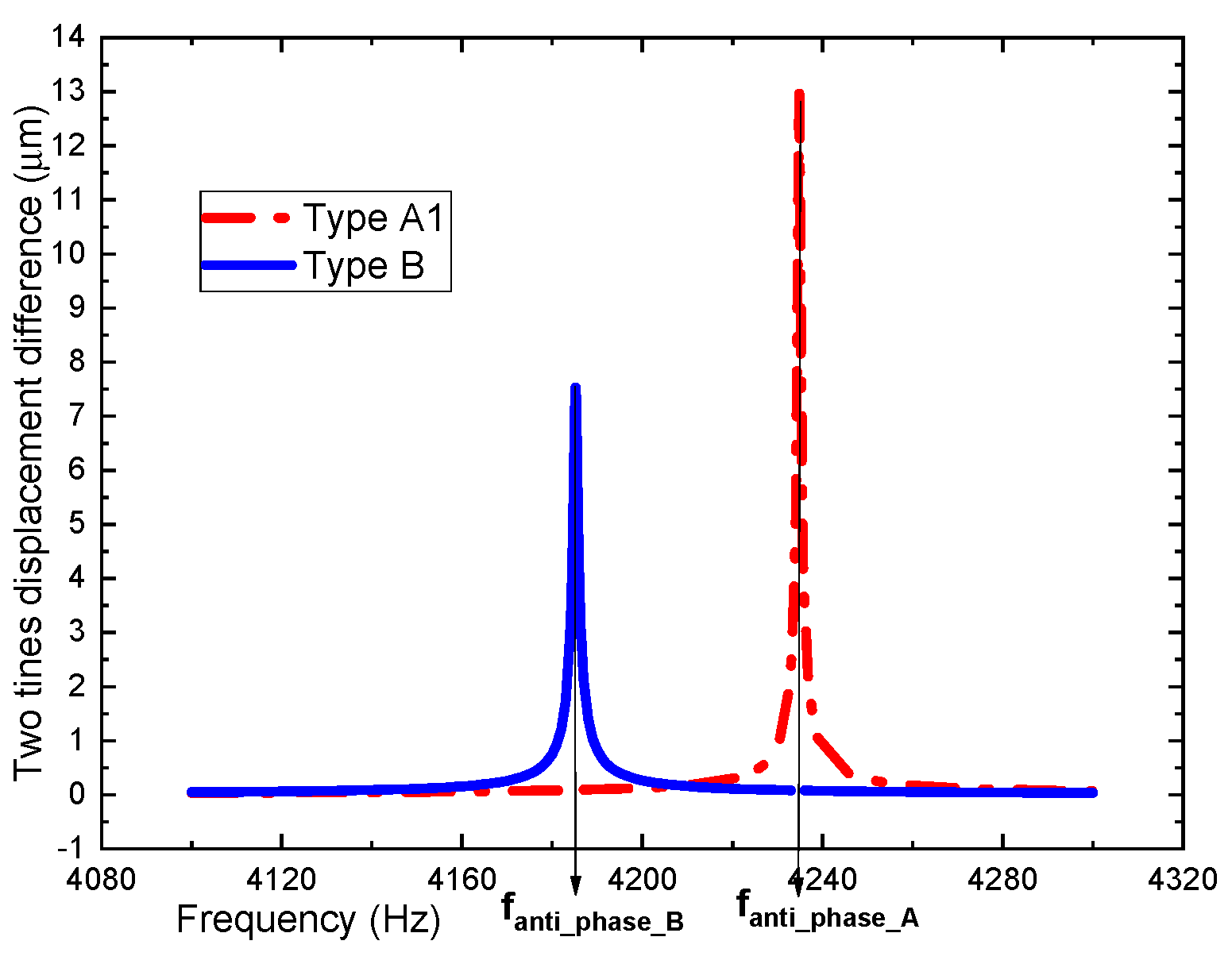
4.4. Nonlinear Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shkel, A.M. Type I and type II micromachined vibratory gyroscopes. In Proceedings of the IEEE/ION Position, Location, and Navigation Symposium, Coronado, CA, USA, 24–27 April 2006; ION: Coronado, CA, USA, 2006; pp. 586–593. [Google Scholar]
- Xia, D.; Yu, C.; Kong, L. The development of micromachined gyroscope structure and circuitry technology. Sensors 2014, 14, 1394–1473. [Google Scholar] [CrossRef] [PubMed]
- Perlmutter, M.; Robin, L. High-performance, low cost inertial MEMS: A market in motion! In Proceedings of the IEEE/ION Position Location and Navigation Symposium (PLANS), Myrtle Beach, SC, USA, 23–26 April 2012; pp. 225–229. [Google Scholar]
- Trusov, A.A. Overview of MEMS Gyroscopes: History, Principles of Operations, Types of Measurements; University of California: Irvine, CA, USA, 2011. [Google Scholar]
- Guan, Y.; Gao, S.; Jin, L.; Cao, L. Design and vibration sensitivity of a MEMS tuning fork gyroscope with anchored coupling mechanism. Microsyst. Technol. 2015, 22, 247–254. [Google Scholar] [CrossRef]
- Guan, Y.; Gao, S.; Liu, H.; Jin, L.; Niu, S. Design and vibration sensitivity analysis of a MEMS tuning fork gyroscope with an anchored diamond coupling mechanism. Sensors 2016, 16, 468. [Google Scholar] [CrossRef] [PubMed]
- Azgin, K.; Temiz, Y.; Akin, T. An SOI-MEMS tuning fork gyroscope with linearly coupled drive mechanism. In Proceedings of the 20th IEEE International Conference on Micro Electro Mechanical Systems (MEMS 2007), Kobe, Japan, 21–25 January 2007; pp. 482–485. [Google Scholar]
- Gomez, U.M.K.; Kuhlmann, B.; Classen, J.; Bauer, W.; Lang, C.; Veith, M.; Frey, J.; Grabmaier, F.; Offterdinger, K.; Raab, T.; et al. New surface micromachined angular rate sensor for vehicle stabilizing systems in automotive applications. In Proceedings of the 13th International Conference on Solid-State Sensors, Actuators and Microsystems, Seoul, Korea, 5–9 June 2005; Volume 1. [Google Scholar]
- Weinberg, M.S.; Kourepenis, A. Error sources in in-plane silicon tuning-fork MEMS gyroscopes. J. Microelectromech. Syst. 2006, 15, 479–491. [Google Scholar] [CrossRef]
- Sahin, K.; Sahin, E.; Alper, S.E.; Akin, T. A wide-bandwidth and high-sensitivity robust microgyroscope. J. Micromech. Microeng. 2009, 19, 074004. [Google Scholar] [CrossRef]
- Gando, R.K.; Kubo, H.; Masunishi, K.; Tomizawa, Y.; Ogawa, E.; Maeda, S.; Hatakeyama, Y.; Itakura, T.; Ikehashi, T. A catch-and-release drive MEMS gyroscope with enhanced sensitivity by mode-matching. In Proceedings of the 4th IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Kauai, HI, USA, 27–30 March 2017; pp. 50–53. [Google Scholar]
- Xia, D.; Kong, L.; Gao, H. A mode matched triaxial vibratory wheel gyroscope with fully decoupled structure. Sensors 2015, 15, 28979–29002. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Li, H.; Ni, Y.; Liu, J.; Huang, L. Frequency tuning of work modes in z-axis dual-mass silicon microgyroscope. J. Sens. 2014, 2014, 891735. [Google Scholar] [CrossRef]
- Bu, F.; Xu, D.; Zhao, H.; Fan, B.; Cheng, M. MEMS gyroscope automatic real-time mode-matching method based on phase-shifted 45 degrees additional force demodulation. Sensors 2018, 18, 3001. [Google Scholar] [CrossRef]
- He, C.; Zhao, Q.; Huang, Q.; Liu, D.; Yang, Z.; Zhang, D.; Yan, G. A MEMS vibratory gyroscope with real-time mode-matching and robust control for the sense-mode. IEEE Sens. J. 2015, 15, 2069–2077. [Google Scholar] [CrossRef]
- Zaman, M.F.; Sharma, A.; Hao, Z.; Ayazi, F. A mode-matched silicon-yaw tuning-fork gyroscope with subdegree-per-hour allan deviation bias instability. J. Microelectromech. Syst. 2008, 17, 1526–1536. [Google Scholar] [CrossRef]
- Sharma, A.; Zaman, M.F.; Ayazi, F. A sub-0.2°/hr bias drift micromechanical silicon gyroscope with automatic CMOS mode-matching. IEEE J. Solid-State Circuits 2009, 44, 1593–1608. [Google Scholar] [CrossRef]
- Xu, L.; Li, H.; Yang, C.; Huang, L. Comparison of three automatic mode-matching methods for silicon micro-gyroscopes based on phase characteristic. IEEE Sens. J. 2016, 16, 610–619. [Google Scholar] [CrossRef]
- Trusov, A.A.; Schofield, A.R.; Shkel, A.M. Micromachined rate gyroscope architecture with ultra-high quality factor and improved mode ordering. Sens. Actuators A Phys. 2011, 165, 26–34. [Google Scholar] [CrossRef]
- Schofield, A.R.; Trusov, A.A.; Shkel, A.M. Versatile vacuum packaging for experimental study of resonant MEMS. In Proceedings of the 23rd IEEE International Conference on Micro Electro Mechanical Systems (MEMS 2010), Hong Kong, China, 24–28 January 2010; pp. 516–519. [Google Scholar]
- Trusov, A.A.; Schofield, A.R.; Shkel, A.M. A substrate energy dissipation mechanism in in-phase and anti-phase micromachined z-axis vibratory gyroscopes. J. Micromech. Microeng. 2008, 18, 095016. [Google Scholar] [CrossRef]
- Zotov, S.A.; Simon, B.R.; Prikhodko, I.P.; Trusov, A.A.; Shkel, A.M. Quality factor maximization through dynamic balancing of tuning fork resonator. Sens. J. IEEE 2014, 14, 2706–2714. [Google Scholar] [CrossRef]
- Larkin, K.; Ghommem, M.; Abdelkefi, A. Significance of size dependent and material structure coupling on the characteristics and performance of nanocrystalline micro/nano gyroscopes. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 99, 169–181. [Google Scholar] [CrossRef]
- Zhang, Q.; Feng, L.; Cui, J.; Tang, Y.; Yao, Y. Design of A New Structure Quartz MEMS Gyroscope with High Sensitivity. IOP Conf. Ser. Mater. Sci. Eng. 2018, 382, 042036. [Google Scholar] [CrossRef]
- Jouaneh, M.; Yang, R. Modeling of flexure-hinge type lever mechanisms. Precis. Eng. 2003, 27, 407–418. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y. Analytical modeling, optimization and testing of a compound bridge-type compliant displacement amplifier. Mech. Mach. Theory 2011, 46, 183–200. [Google Scholar] [CrossRef]
- Iqbal, S.; Malik, A.A.; Shakoor, R.I. Design and analysis of novel micro displacement amplification mechanism actuated by chevron shaped thermal actuators. Microsyst. Technol. 2018, 25, 861–875. [Google Scholar] [CrossRef]
- Iqbal, S.; Shakoor, R.I.; Gilani, H.N.; Abbas, H.; Malik, A.M. Performance Analysis of Microelectromechanical System Based Displacement Amplification Mechanism. Iran. J. Sci. Technol. Trans. Mech. Eng. 2018. [Google Scholar] [CrossRef]
- Iqbal, S.; Malik, A.; Shakoor, R.I. Kinematic sensitivity analysis of a novel micro-mechanism for displacement amplification. Trans. Can. Soc. Mech. Eng. 2018, 42, 436–443. [Google Scholar] [CrossRef]
- Iqbal, S.; Shakoor, R.I.; Lai, Y.; Malik, A.M.; Bazaz, S.A. Experimental evaluation of force and amplification factor of three different variants of flexure based micro displacement amplification mechanism. Microsyst. Technol. 2019, 25, 2889–2906. [Google Scholar] [CrossRef]
- Zhang, J.; Su, Y.; Shi, Q.; Qiu, A.P. Microelectromechanical resonant accelerometer designed with a high sensitivity. Sensors 2015, 15, 30293–30310. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Ding, X.; Huang, L.; Li, H. Design and analysis of a novel dual-mass MEMS resonant output gyroscope. AIP Adv. 2018, 8, 025017. [Google Scholar] [CrossRef]
- Gao, Y.; Huang, L.; Ding, X.; Li, H. Design and implementation of a dual-mass MEMS gyroscope with high shock resistance. Sensors 2018, 18, 1037. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Li, H. Investigation of a vacuum packaged MEMS gyroscope architecture’s temperature robustness. Int. J. Appl. Electromagn. Mech. 2013, 41, 495–506. [Google Scholar] [CrossRef]
- Cao, H.; Li, H.; Kou, Z.; Shi, Y.; Tang, J.; Ma, Z.; Shen, C.; Liu, J. Optimization and Experimentation of Dual-Mass MEMS Gyroscope Quadrature Error Correction Methods. Sensors 2016, 16, 71. [Google Scholar] [CrossRef]
- Yoon, S.W.; Lee, S.; Najafi, K. Vibration-induced errors in MEMS tuning fork gyroscopes. Sens. Actuators A Phys. 2012, 180, 32–44. [Google Scholar] [CrossRef]
- Tang, Q.; Wang, X.; Yang, Q. Scale factor model analysis of MEMS gyroscopes. Microsyst. Technol. 2016, 23, 1215–1219. [Google Scholar] [CrossRef]
- Rezaei Kivi, A.; Azizi, S.; Khalkhali, A. Sensitivity enhancement of a MEMS sensor in nonlinear regime. Int. J. Mech. Mater. Des. 2015, 12, 337–351. [Google Scholar] [CrossRef]
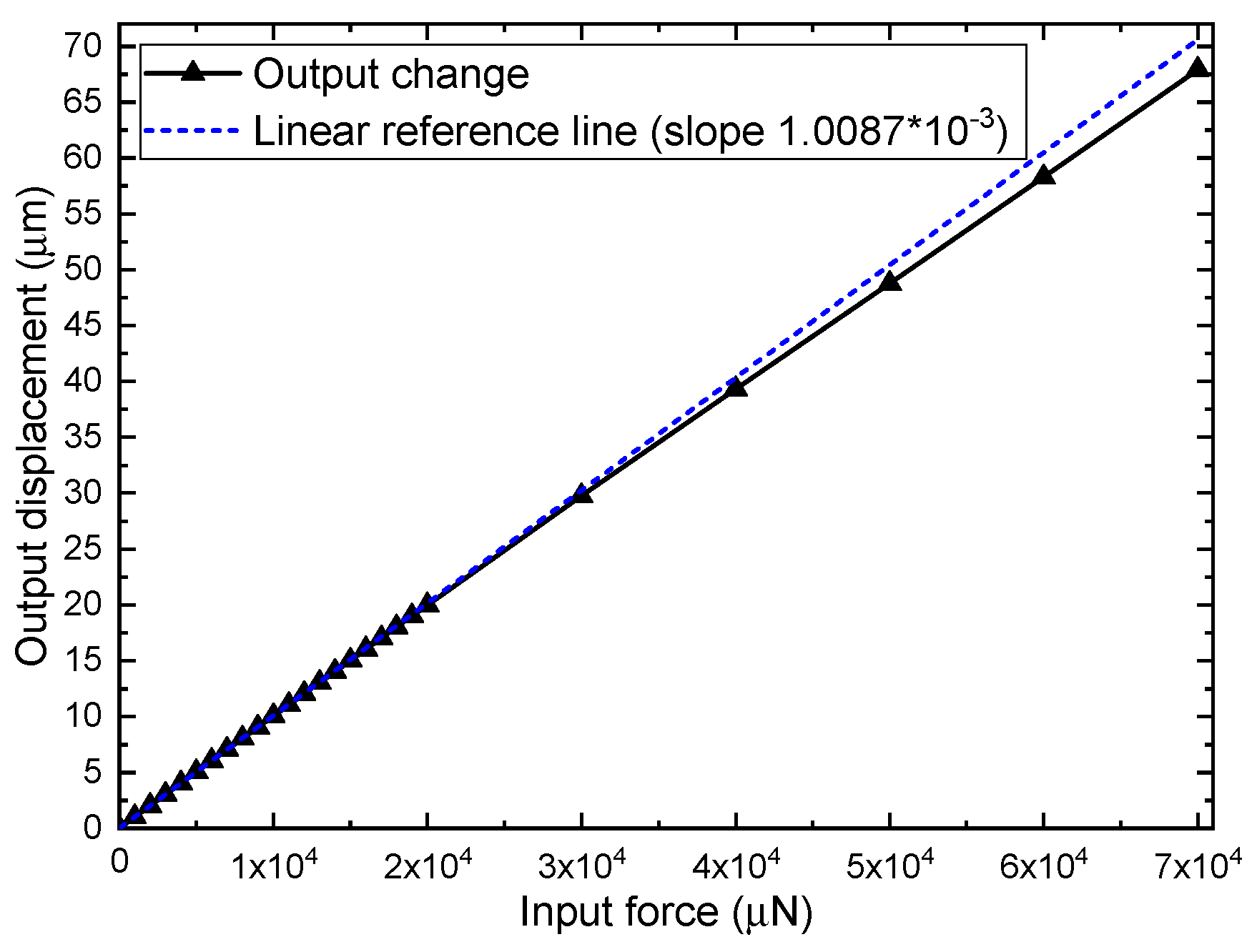
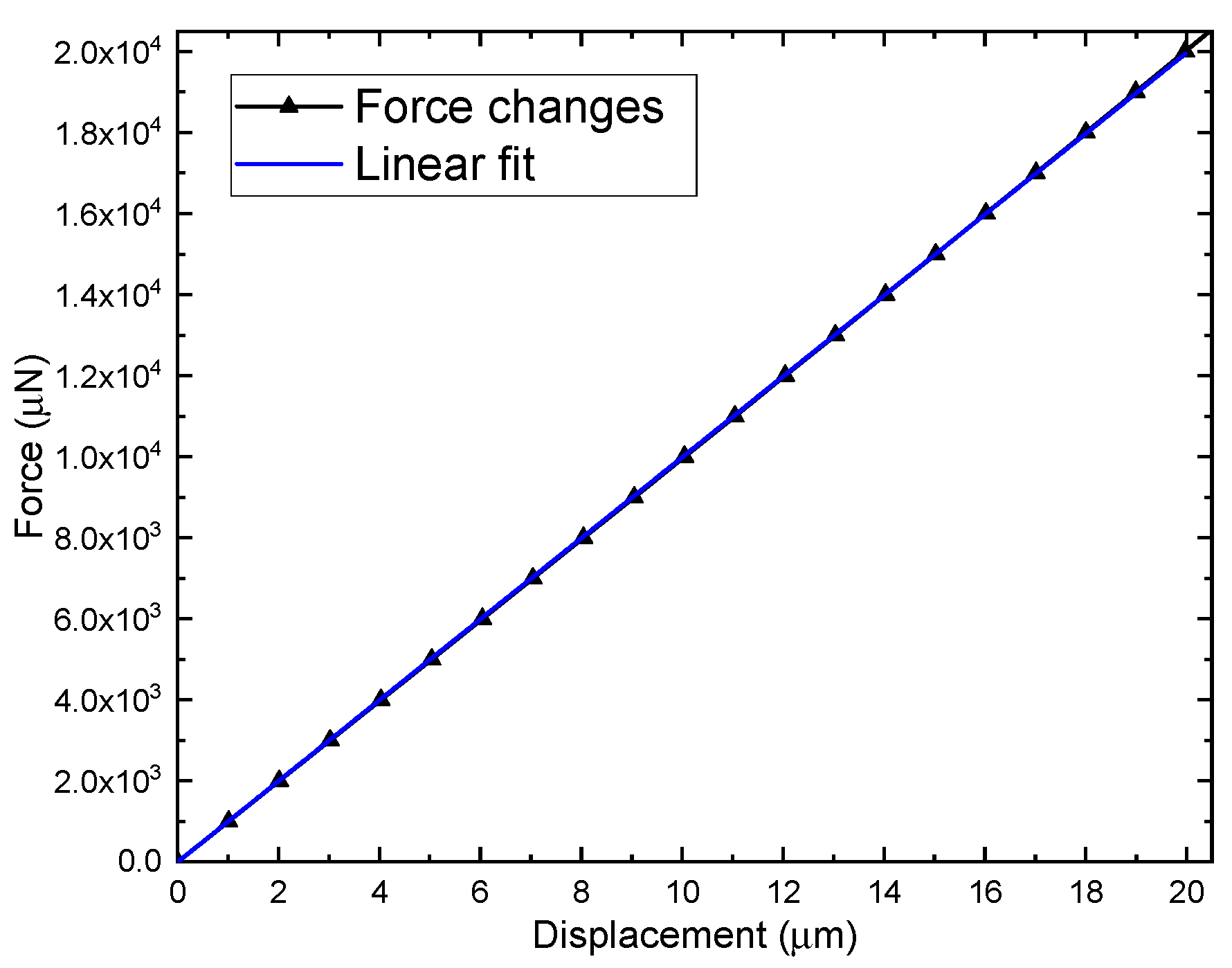
| Parameter | Value |
|---|---|
| Proof mass () | |
| Length of drive spring () | 440 |
| Width of drive spring () | 10 |
| Length of sense spring () | 440 |
| Width of sense spring () | 10 |
| Length of drive coupling leverage () | 1131 |
| Width of drive coupling leverage () | 15 |
| Length of sense coupling leverage () | 5450 |
| Width of sense coupling leverage () | 220 |
| Length of leverage () | 1050 |
| Width of leverage () | 60 |
| Lever arm length ratio | 1.93 |
| Equivalent mass of type A1 () | |
| Equivalent mass of type A2 () | |
| Equivalent mass of type A3 () | |
| Equivalent mass of type B () |
| Parameters | Young’s Modulus (Pa) | Poisson’s Ratio | |
|---|---|---|---|
| Values | 0.28 | 2330 |
| Order | 1 | 2 | 3 | |
|---|---|---|---|---|
| Type | ||||
| Type A1 | Frequency (Hz) | 4227.3 | 4234.8 | 7914.9 |
| Mode of vibration | Anti-phase of drive | Anti-phase of sense | In-phase of sense | |
| Type A2 | Frequency (Hz) | 4227.4 | 4288.9 | 8068.6 |
| Mode of vibration | Anti-phase of drive | Anti-phase of sense | In-phase of sense | |
| Type A3 | Frequency (Hz) | 4227.3 | 4319.2 | 7938.4 |
| Mode of vibration | Anti-phase of drive | Anti-phase of sense | In-phase of sense | |
| Type B | Frequency (Hz) | 4185.2 | 4248 | 6478.9 |
| Mode of vibration | Anti-phase of sense | Anti-phase of drive | In-phase of sense |
| Type | Type A1 | Type B | |||||
|---|---|---|---|---|---|---|---|
| Displacement | Theoretical Value | Simulation Value | Error Rate | Theoretical Value | Simulation Value | Error Rate | |
| Two tines’ displacement difference () | 13.418 | 12.966 | 3.49% | 7.804 | 7.532 | 3.62% | |
| Type | Theoretical Value | Simulation Value | Error Rate |
|---|---|---|---|
| Type A1 | 13.418 | 12.966 | 3.49% |
| Type A2 | 13.585 | 13.098 | 3.72% |
| Type A3 | 12.596 | 12.141 | 3.75% |
| Type | Theoretical Value | Simulation Value |
|---|---|---|
| Type A1 | 79.10% | 72.15% |
| Type A2 | 81.33% | 73.90% |
| Type A3 | 68.06% | 61.19% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Gao, S.; Jin, L.; Liu, H.; Guan, Y.; Peng, S. Design and Mechanical Sensitivity Analysis of a MEMS Tuning Fork Gyroscope with an Anchored Leverage Mechanism. Sensors 2019, 19, 3455. https://doi.org/10.3390/s19163455
Li Z, Gao S, Jin L, Liu H, Guan Y, Peng S. Design and Mechanical Sensitivity Analysis of a MEMS Tuning Fork Gyroscope with an Anchored Leverage Mechanism. Sensors. 2019; 19(16):3455. https://doi.org/10.3390/s19163455
Chicago/Turabian StyleLi, Zezhang, Shiqiao Gao, Lei Jin, Haipeng Liu, Yanwei Guan, and Shigang Peng. 2019. "Design and Mechanical Sensitivity Analysis of a MEMS Tuning Fork Gyroscope with an Anchored Leverage Mechanism" Sensors 19, no. 16: 3455. https://doi.org/10.3390/s19163455
APA StyleLi, Z., Gao, S., Jin, L., Liu, H., Guan, Y., & Peng, S. (2019). Design and Mechanical Sensitivity Analysis of a MEMS Tuning Fork Gyroscope with an Anchored Leverage Mechanism. Sensors, 19(16), 3455. https://doi.org/10.3390/s19163455






