1. Introduction
Nowadays, the Internet of Things (IoT) has received increasing attention from both industry and academia. It is considered an important mean for wireless connections in the fourth industrial revolution. IoT is also being used in the fourth generation (4G) mobile communications and will be applied to the fifth generation (5G). In order to support a large multiuser system such as IoT, the non-orthogonal multiple access (NOMA) is a very potential technique due to its high bandwidth efficiency [
1,
2]. Moreover, compared with conventional orthogonal multiple access (OMA) systems, such as time division multiple access (TDMA), code division multiple access (CDMA), orthogonal frequency division multiple access (OFDMA), the NOMA systems offer better fairness among users, even for users with weak channel conditions such as the cell-edge users. The fundamentals of the NOMA system can be found in Reference [
3] while a study of NOMA system in cellular communication with machine-to-machine in IoT is given in Reference [
4].
Recently, the power supply for terminal devices in wireless networks has become an important matter and has attracted much interest from researchers. Besides using the optimal power allocation for the fifth generation (5G) and sixth generation (6G) networks (6G network will start to enter the market by 2026 [
5]) to reduce the power consumption [
6], another promising method to improve the lifetime of communication devices is to generate electric power from some external energy sources such as solar, wind, and radio frequency (RF) signal to charge the batteries. Unfortunately, natural energy sources are not suitable for small-size mobile devices and in some cases they cannot be used in the healthcare monitoring networks and the sensor networks with real-time requirements. In contrast, the RF energy is often available due to its increased power density and availability, and is independent on environmental conditions, including weather, climate, and temperature. As the result, the RF energy harvesting (EH), also called simultaneous wireless information and power transfer (SWIPT), has been widely used compared with other kinds of energy harvesting techniques [
7,
8,
9]. SWIPT has been applied not only in the point-to-point systems but also in relaying systems because deploying relays can improve the amount of harvested energy and the coverage area of wireless networks. The authors of References [
10,
11] investigated information and energy receiver architecture for SWIPT networks. Reference [
11] especially considered a non-linear energy harvesting model which described the practical system well.
To prolong network lifetime and improve the spectral utilizing efficiency, NOMA is combined with SWIPT [
12]. In Reference [
13], the authors investigated the tradeoff among the energy efficiency, fairness, harvested energy, and system sum rate of NOMA systems in power domain. Investigation of an integrated wireless communication system including NOMA, full-duplex relaying, and energy harvesting techniques was conducted in Reference [
14]. The authors of References [
15,
16] studied the system performance of cooperative NOMA systems and derived the expressions of outage probability in the conditions of perfect successive interference cancellation (SIC) and perfect channel state information (CSI). In Reference [
17], the near users which are close to the base station will harvest the RF energy and forward signals to far users. The analysis results showed that if the time switching ratio in NOMA system with SWIPT is appropriately chosen, the diversity gain will not be impaired. The authors of Reference [
18] proposed a NOMA system where source node communicates with two users via the assistance of the best relay with the RF energy harvesting capability. The exact expressions of the outage probability and throughput were used as the criteria to evaluate the system performance. The effects of power allocation and time switching ratio on the performance of multi-user NOMA system were investigated in Reference [
19]. Specifically, the authors derived the outage probability expression and determined the optimal power allocation coefficient for two NOMA power allocation policies, namely NOMA with fixed power allocation (F-NOMA) and cognitive radio inspired NOMA (CR-NOMA). It was shown that when a reasonable power allocation coefficient is selected, higher system performance can be achieved in comparison with the conventional multi-user system.
We observe that all previous works only mentioned the case of perfect CSI and used only one relay to forward signals to multiple users. Moreover, although the partial relay selection has been widely studied in conventional wireless systems, it has not been analyzed in NOMA systems. Another observation is that the NOMA systems perform superimposing signals in power domain, thus they always require CSI to allocate power for all users. However, due to variation in the communication quality of wireless environment, the imperfect CSI may happen [
20,
21]. Perfect CSI exists if and only if the amount of feedback CSI from users to the base station is large and the length of the pilot sequences which are used to estimate channel is very long. Unfortunately, these conditions rarely happen in practice. Therefore, investigation of the impact of imperfect CSI on the relay selection and power allocation is vitally important to the design of practical NOMA systems.
Motivated by the above issues, in this paper we propose a downlink NOMA relaying system with partial relaying selection. In this system, source node transmits superposition modulated signals to multiple users via the assistance of the best relay. The best relay is chosen from a set of relays which are capable of harvesting RF energy and grouped by their locations. Based on the feedback CSI from all users, the source node performs power allocation and chooses the best communication link. The main contributions of this paper can be summarized as follows:
We overcome the limitation of current multiple access techniques and the energy demand of wireless networks by proposing the downlink NOMA relaying system where the best relay is selected from a set of multiple RF energy harvesting relays.
We study the system performance in terms of the outage probability and the ergodic capacity of each user and the whole system in the condition of imperfect CSI and Rayleigh fading. The imperfection of the CSI is modeled by the correlation coefficient and its impact on the system performance is investigated by using both analysis and simulation approaches. We also compare the outage performance and the ergodic capacity of the proposed NOMA relaying system with those of OMA relaying system.
We determine the optimal time switching ratio to balance between the energy harvesting and the signal processing so that the outage probability can be minimized. All analysis results are validated by simulation results.
The rest of this paper is organized as follows.
Section 2 describes the proposed downlink NOMA relaying system with partial relaying selection and time switching (TS) protocol. The analysis of the outage probability and ergodic capacity of the proposed system are presented in
Section 3 and
Section 4, respectively.
Section 5 shows numerical results to evaluate the system performance. Finally, the conclusions are given in
Section 6.
For the sake of clarity, the frequently used mathematical notations together with their descriptions are summarized in
Table 1.
2. System Model
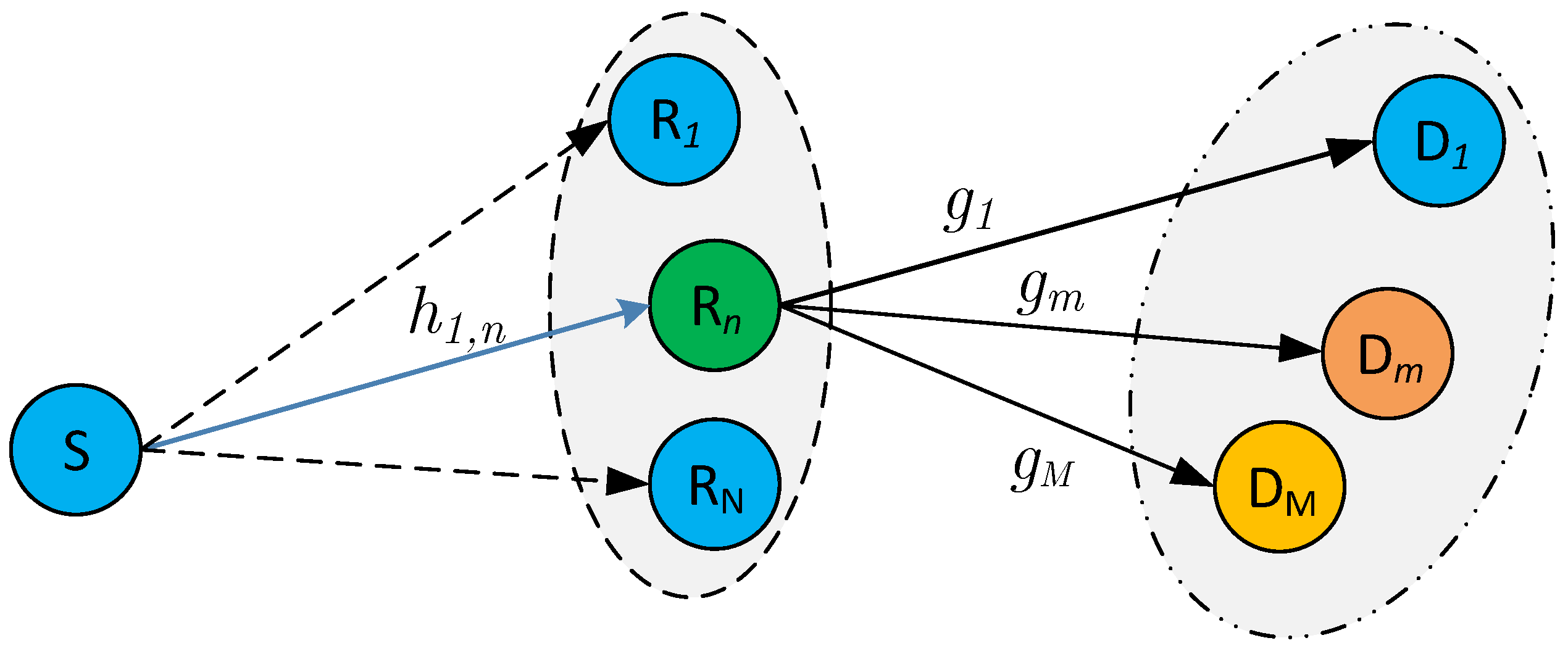
Figure 1 illustrates the proposed downlink NOMA relaying system. In this system, source node
transmits the signals which are coded and superposed in power domain to multiple users
,
, via the assistance of the best relay which is selected from a set of relays
,
. The direct link
-
is assumed not available because the distance between
and
is larger than the coverage area of
or due to deep shadow fading.
We consider that all nodes are equipped with single antenna and operate in half-duplex mode. All channels between
and
and between
and
are influenced by block fading, that is, the symbol rate is larger than channel varying rate so that it can be considered as constant over each symbol duration. The communication links from
to
and from
to
are respectively modeled as complex Gaussian distributions with zero mean and variances
and
, that is,
and
. The Additive White Gaussian Noise (AWGN) at the relays and users are
and
, respectively. Because of the time varying characteristic of wireless channel, its coherent time may be altered when the feedback delay is larger than the transmission block period of a symbol. Thus, the received CSI is always outdated at the transmitter, which often happens in practice [
23,
24].
We denote
,
,
, as the correlation coefficients between the past channel
and the current channel
, similarly for
and
. These coefficients can be considered as the measurements of the fluctuation rate of wireless channels and are related solely to the time delay. Based on the Markov chain, the relationship between
and
and between
and
can be presented as [
25]
where
and
are the circular symmetric complex Gaussian random variables which can be modeled as
and
, respectively.
In this paper, a partial relay selection (PRS) scheme [
26] is used to select the best relay from a set of relays. According to the PRS scheme,
continuously monitors the gain of
–
channels by using the feedback signal and selects the communication link that gives the largest instantaneous channel gain, that is,
where
is the instantaneous SINR of
-
link.
The advantage of using PRS scheme is that the system configuration is simpler and easier than using the full relay selection (FRS) scheme [
27]. In addition, the results in Reference [
28] show that both PRS and FRS schemes have the same average channel capacity in a high SNR regime and the outage probability of PRS is higher than that of FRS when the number of relays is more than 2. On the other hand, FRS scheme may not applicable for multiple-user systems because the distances from the best relay to users are different, thus the calculation complexity of FRS scheme is significantly increased with the number of users.
After a link from the source node to the best relay is established, the transmission period
T for communication process is spitted into two parts (in this system, we use the time-division multiple access (TDMA) scheme). According to the time switching (TS) protocol [
29], a time duration
is used for EH. The remaining time duration
is divided into two equal time sub-slots, which are used for the information transmission. The first half
is used for the information transmission from source node to the relay and the remaining half
is used for the information transmission from the relay to the user. It should be noted that the case
is not considered in this paper because when the energy harvesting time duration takes the whole transmission period
T, i.e., the relay does not process any signals, the basic role in signal forwarding of the relay is eliminated [
30]. Hence, we only consider the time switching ratio
in the range
. Then, the harvested energy of the selected relay in time duration
is expressed as [
29]
where
is the energy conversion efficiency coefficient which varies from 0 to 1 and closely depends on the quality of energy harvesting electric circuitry,
is the transmission power of
.
In our proposed relaying system, since the harvest-use (HU) architecture is used, the relay does not need an energy buffer to store the harvested energy. Since all amounts of harvested energy during EH phase is consumed by
for signal transmission from
to
, from (
4), the transmission power of the best relay is given by
According to the NOMA technique in power domain, during the first time sub-slot
, source node transmits the superimposed signal
, where
and
are the signal and power allocation coefficient of
mth user, respectively. At the end of this time sub-slot, the received signal at
is
where
.
In the remaining second time slot
, the relay employs the AF protocol to broadcast
to all users after multiplying it with an amplifying factor
G. To keep the output power constraint at relay, it is required that
, where
is given in (
5), thus the amplifying factor
G is given by
Therefore, the received signal at
in the case of perfect SIC is expressed as
where
denotes the channel coefficient between
and
.
The received signals at the best relay and each user is comprised of the desired signal and the signals of other users, which are treated as the interferences. Hence, to mitigate the negative effect of the inter-user interference, successive interference cancellation (SIC) method is applied.
For the downlink communication considered in this paper, the optimal SIC algorithm performs decoding signals in an order of increasing channel gain [
31] (
). To ensure the fairness among all users, the power allocation coefficients are assumed to be
, with
. Hence, at the
, the signal of
,
, will be detected and then be removed from the received signal by SIC method. Specifically,
first decodes symbol
while treating
as noise.
Then, the SINR of symbol
at
is given by
where
and
.
At
, SIC will be performed until all signals of
are decoded successfully. Thus, the required SINR at
to successfully decode the signal by itself is given by
We should note that the last user
needs to decode all signals of other users before decoding its signals. Consequently, the SINR for
to decode its own signals can be expressed as
3. Outage Probability Analysis
In this section, we derive the exact closed-form expression of the outage probability, taking into consideration the imperfect CSI and partial relay selection. It is well-known that the event that
can decode the signals of
successfully is
where
is the predefined outage threshold. This threshold is served as the protected value of the SINR to ensure the quality of service of the system and satisfy the target data rate
r of
.
Let us denote
and
. Without loss of generality, we assume that the temperature noise
. Thus from (
12), we can rewrite
as
From (
13) and after some manipulations, we can rewrite (
13) as
where
, step
holds when the condition
is satisfied. It should be noticed that
is a constant and depends on the power allocation coefficient and the target data rate of
.
The outage event occurs at
when it fails to decode its own signal or unsuccessfully performs SIC for the signals of
[
32], i.e.,
. Outage probability of the system occurs when the maximum SNRs at
falls below the threshold to decode signal. Thus, we have
where
is the complementary in the set of
.
The condition in (
14) always occurs, i.e., the outage probability is equal to one, if
. Hence, we need to allocate more power for
to satisfy the following condition
Let us denote
[
33], then the outage probability
of
can be reformulated as
Using the conditional probability property [
34] with respect to
X, and applying the law of joint CDF, we have
To calculate the expression of the outage probability in (
19), we first derive the CDF of
Z and the PDF of
X as follows.
When the
nth relay is selected as the best relay, the PDF of order statistic with respect to
in a set of
N relays is obtained by using the binomial Newton expansion [
35], that is,
where
,
N and
n are non-negative integers,
and
are respectively the CDF and PDF of
, which is the channel gain of each link from source node to relay. According to the probability theory, the PDFs of
and
which are respectively denoted by
and
can be calculated by using the joint PDF, i.e.,
. Another way to calculate the joint PDF of
is based on the properties of conditional probability, that is,
where
Using the joint PDF which is given in ([
36], Equation (9.389)), we can rewrite the numerator of (
22) as
where
is the modified zero order Bessel function of the first kind [
22].
Without loss of generality, all correlation coefficients are assumed to have the same values, that is,
. Substituting (
20), (
22), and (
23) into (
21), after using the equation
which is given in ([
22], Equation (6.614.3)), and then perform some manipulations, we have the PDF of
X in the case of imperfect CSI as
where
.
From (
24), the CDF of
is given by
Based on the result of order statistics which is provided in ([
34], Equation (7.14), p. 246), and after some similar calculations as above, the PDF of the ordered variable
Z is expressed as
where
.
From (
26), we can derive the CDF of
as
Plugging (
27) and (
24) into (
19), and after some manipulations, we obtain the expression of the outage probability as
Let
, (
28) becomes
Using ([
22], Equation (3.324)), we can rewrite the exact closed-form expression of the outage probability as in (
30), where
denotes the modified first order Bessel function of the second kind.
From the expression of the outage probability which is given in (
30), we can see that when the outdated CSI happens, the outage performance is a function of
.
4. Ergodic Capacity Analysis
In this section, we analyze the ergodic capacity of the proposed NOMA relaying system in comparison with that of the OMA relaying system. Due to the fact that the hardware complexity and performance degradation of the NOMA system is directly proportional to the number of users, we also set the number of users be equal to three for both NOMA and OMA systems as used in [
37]. For the OMA system, we consider orthogonal frequency division multiple access (OFDMA). According to the Shannon theory, the instantaneous rate of
is given by
From (
10), when the transmission power is high, we can approximate the required SINR at
as
Substituting (
32) into (
31), we have
where
.
Based on the properties of the logarithmic function, we can rewrite (
33) as
then solve its components by using the partial integration, i.e.,
where
is the CDF of random variable
with
,
, and
.
Using the condition probability, we have CDF of
as
From (
24) and (
27) we can calculate
as
Similarly, for
, we have
where
.
Replacing (
38) into (
35), we obtain
as
where
.
Based on ([
22], Equation (9.343)), we can rewrite (
39) as
Then, using ([
22], Equation (7.811.5)) and after some manipulations, we have
where
is the Meijer’s G-Function ([
22], Equation (9.3)).
Plugging (
38) into (
35), and doing similar manipulations which were used to derive
, we obtain
To compare the ergodic capacities of the NOMA and OMA systems, we let
be the bandwidth which is assigned for
and
be the remaining bandwidth which is assigned for
and
, where
and the whole bandwidth is 1Hz. From ([
38], Equation (7.4)), we can extend the achievable end-to-end ergodic capacity of the OFDMA system with three users as
where
denotes the instantaneous SINR of each user, which is computed as
where
is the equal power allocated for the signal transmission from
to each user
([
38], p. 146). The factor
appears in (
31) and (
43) because source node transmits its signals to all users in two time slots of the transmission period
T.
5. Numerical Results
In this section, we provide the numerical results to evaluate the system performance in terms of the outage probability (OP) and ergodic capacity of the proposed EH-NOMA relaying system with three users. We also determine the optimal time switching ratio to minimize the OP and compare the ergodic capacities of the proposed EH-NOMA relaying system with EH-OMA relaying system. Regarding to the evaluating method, we use the common approach in this field, that is, to drive a closed-form mathematical expression to model the system performance and then compare the analysis results with Monte-Carlo simulation results to validate the derived mathematical expressions. Unlike previous works, which only considered EH-NOMA systems with two users and under perfect CSI, our paper focuses on the theoretical analysis of an EH-NOMA system with more than two users, taking into account the effects of AF relaying protocol and the feedback delay of wireless channels on the system performance. Since, there are not many similar parameters, it may be an unfair comparison between our proposed EH-NOMA relaying system with previous NOMA relaying systems. Therefore, we use the same system model of the proposed EH-NOMA relaying sytem but replace the NOMA with OMA to demonstrate the benefits of utilizing the NOMA technique in the proposed EH relaying system. Unless otherwise stated, the parameter settings of EH-NOMA and EH-OMA relaying systems are summarized in
Table 2. It is noticed that the average
is defined as the ratio of the transmission power of source S to the variance of AWGN, that is,
, ranging from 0 dB to 40 dB.
Figure 2 shows the outage probability of each user versus the average SINR in dB. The outage probability of the EH-NOMA relaying system is also compared with that of EH-OMA relaying system. Firstly, we can see that the OP of
is lowest among all users while the OP of
is highest. The reason is that the channel gain from R to
is highest (the decay of the magnitude power signal is proportional to the squared distance in multipath fading) because
is the closest user to R while
is the farthest one. Another important observation is that the OPs of
and
in the EH-NOMA relaying system are better than those of
and
in the EH-OMA relaying system, while the OP of
in the EH-OMA relaying system is better than in the NOMA relaying system. However, the gap is insignificant because the number of time slots for the transmission in the EH-OMA relaying system is higher than in the EH-NOMA relaying system, thus the probability that outage evens happen in the EH-OMA relaying system is also higher than in the EH-NOMA relaying system. On the other hand, the outage threshold of the OMA user is
, where
. In contrast, the outage threshold of the NOMA user is
. Then, obviously the outage threshold of the OMA user is obviously higher than that of the NOMA user. However, the OP not only depends on the outage threshold but also on the received SINR at user. In addition, we also see that in the low SINR regime (less than 15 dB), the OPs of all OMA users always outperform those of NOMA users. However, in the high SINR regime (larger 15 dB) only the OP of
in the EH-OMA relaying system is better than that in the EH-NOMA relaying system. We can also see in
Figure 2 that the diversity gain of all users is equal to one.
Figure 3 plots the OP of
in the EH-NOMA relaying system versus the average SINR in dB for different channel correlation coefficients
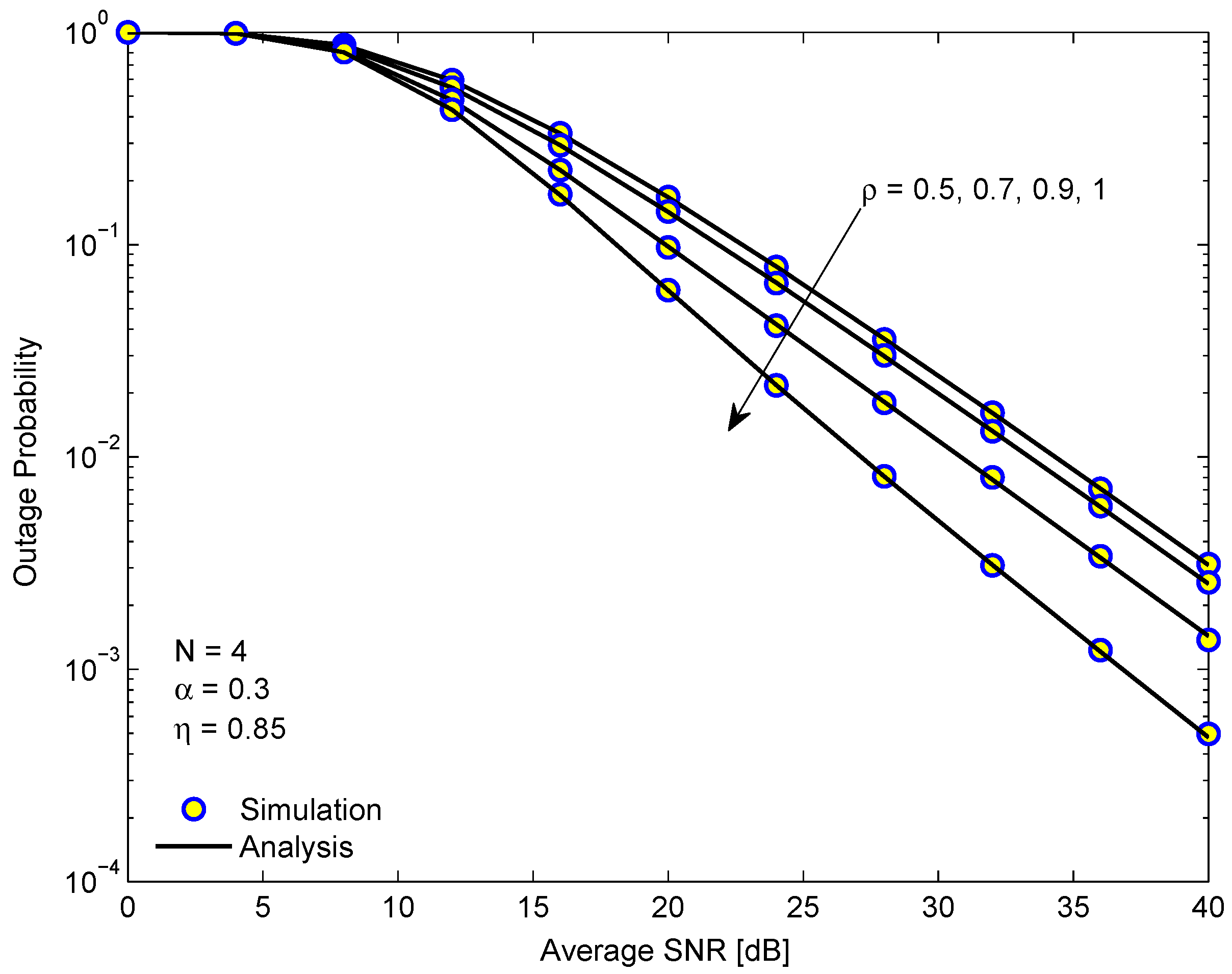
. Firstly, we see that higher
reduces the OP, but the reduction is not remarkable for small
. The improvement in OP is only significant when
is near to 1. We should remind that
indicates the correlation degree between the transmission channel and the feedback channel in time coherent at the transmitter. The analysis results are in excellent agreement with the simulation ones, confirming the correctness of our mathematical analysis.
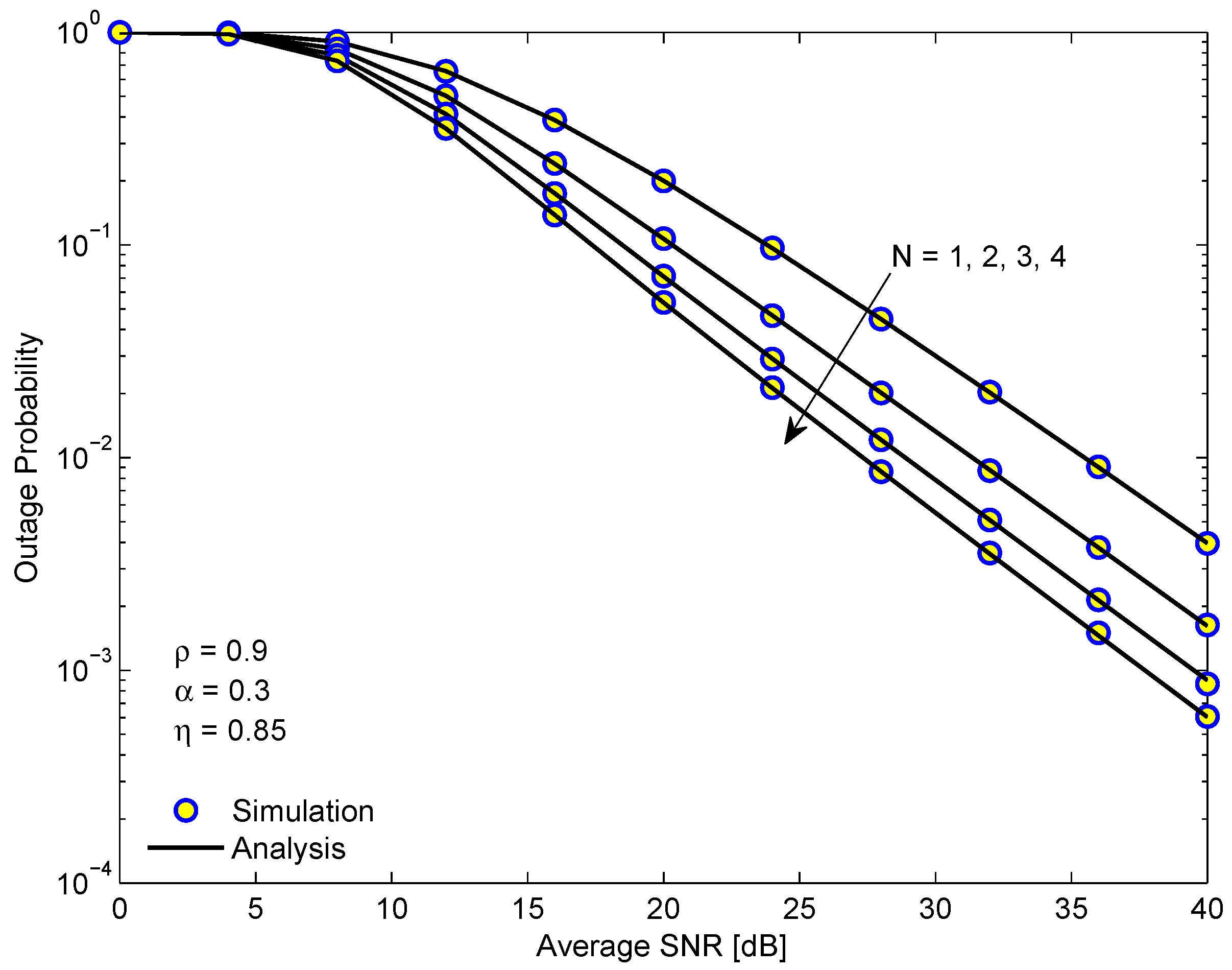
Figure 4 illustrates the OP of
in the NOMA system versus the average SINR in dB for different numbers of relays
N. From
Figure 4, we see that when the number of relays increases, the outage performance of the system is improved. It is because increasing the number of relays will provide more opportunity for selecting the connection links from source node to relay, which not only makes the achievable decoding performance better but also increases the amount of harvested energy. In addition, the diversity gains is not significantly improved with
N because the diversity order of PRS scheme is always equal to one.
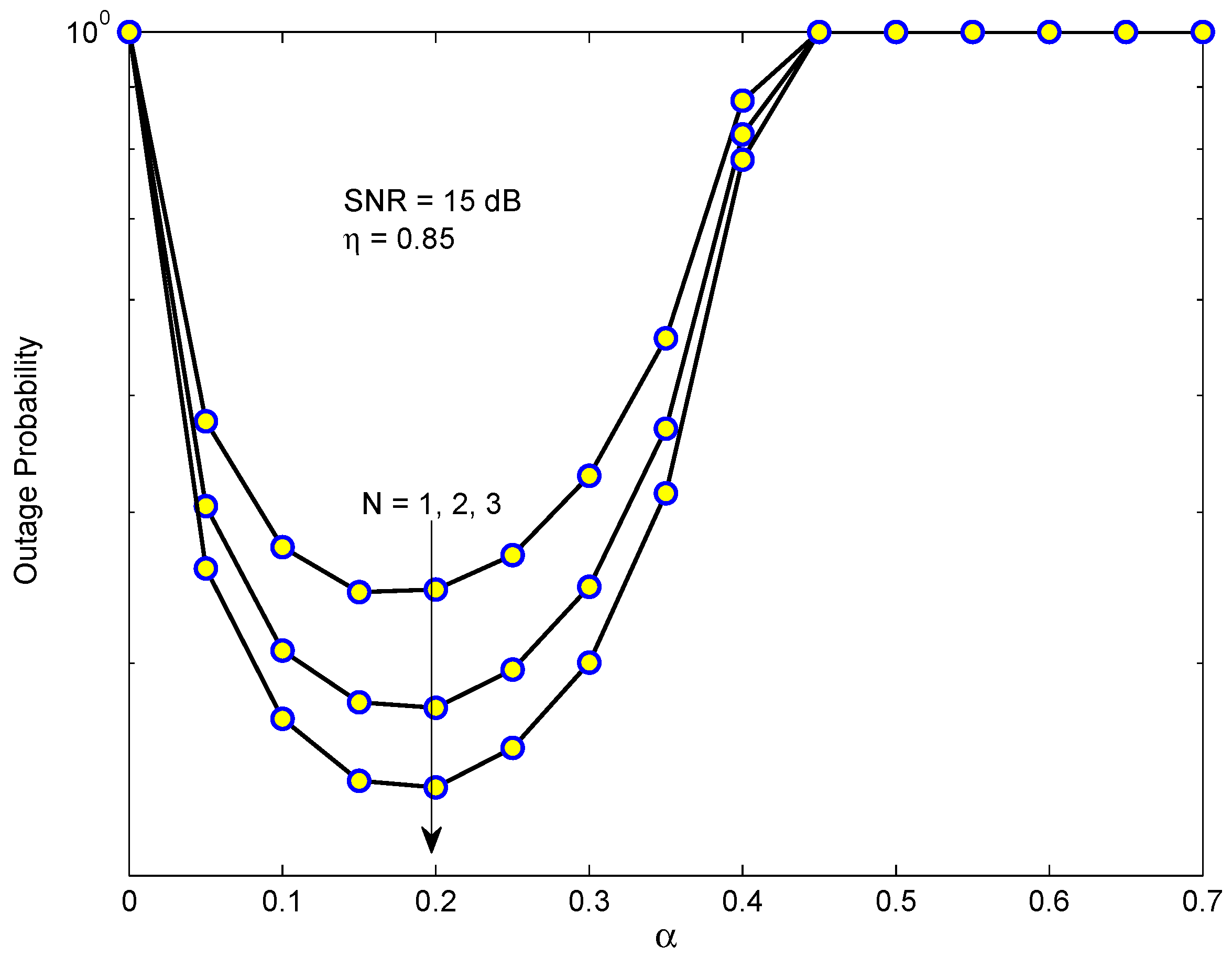
Figure 5 presents the OP of
in the EH-NOMA relaying system versus time switching ratio
for different numbers of relays. The values of
range from 0 to 0.7 while SINR remains at 15 dB. Firstly, we see that there exists an optimal value of
which minimizes the OP. Moreover, the minimum value of OP depends on the number of relays
N, i.e., as
N is higher the minimal OP becomes smaller. The reason is that when
N increases, the SINR of the first hop will be better because the PRS method is used. Another important observation is that the optimal value of
which minimizes the OP is approximately 0.2 regardless of the number of relays.
Figure 6 demonstrates the OP of
in the EH-NOMA relaying system versus the correlation coefficient
for different average SINR. We can see that the OP reduces as
increases. In the worst case
, the instantaneous CSI at the transmission time does not correlate with the instantaneous CSI at the relay-selection time or at the power-allocation time. In contrast, in the best case
, the instantaneous CSI at the transmission time closely correlates with the instantaneous CSI at the relay-selection time or at the power-allocation time. The improvement in the CSI leads to better power allocation and signal processing of the system.
Figure 6 also shows that when
, the enhancement of OP is not significant and the system performance is only improved when the correlation coefficient
is close to 1.
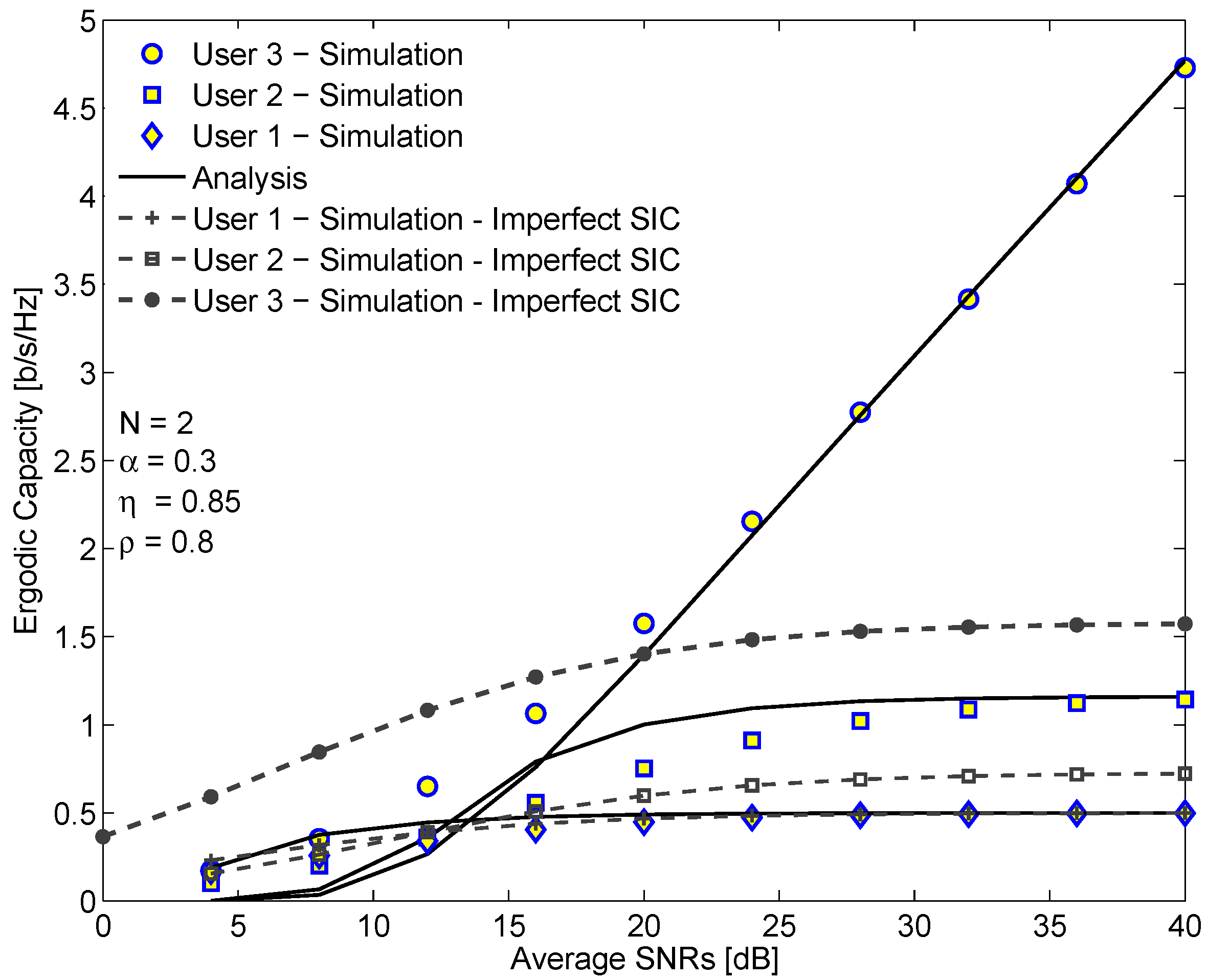
Figure 7 depicts the ergodic capacity of each user in EH-NOMA relaying system versus the average SINR in dB. As observed from
Figure 7, the ergodic capacity of
outperforms the ergodic capacities of
and
. Moreover, the ergodic capacities of
and
increase slightly in the low SINR region and is saturated in the high SINR region. In contrast, the ergodic capacity of
increases exponentially with respect to the SINR. This reason is that
does not use SIC but only detects the signal of itself. Meanwhile,
must use the first-order SIC first and then
uses the second-order SIC. Thus, the impact of interference on
is higher than
and
. However, there exists the trade-off between the complexity and the achievable ergodic capacity of the system. We also see a good match between the analysis results and the simulation results, especially in the high SINR regime. On the other hand, the ergodic capacity in the case of perfect SIC is compared with that in the case of imperfect SIC. We can see that the ergodic capacity in case imperfect SIC is lower. Moreover, the gap between them increases with the SINR. It is because when SINR increases, the interference caused by imperfect SIC also increases. Therefore, the SINR as well as the ergodic capacity become slowly higher. Another feature is that the ergodic capacity of
remains the same in both cases because
does not use SIC when decoding the signals.
Figure 8 provides the simulation results of the ergodic rate of NOMA and OMA systems versus the average SINR in dB. From
Figure 8, we see that the ergodic rate of NONA system is always higher than the OMA system as the number of relays increases. It is because the NOMA system uses the whole bandwidth for each user while the OMA system uses individual bandwidth for each user, resulting in higher spectrum usage efficiency. Another important observation is that when
N gets higher, the difference gap of the ergodic capacities of these two systems does not increase linearly. Thus, we do not need to use a large number of relays for partial relay selection scheme because it may increase the complexity of the system but not significantly enhance its performance.