1. Introduction
Internet of Things (IoT) is becoming rapidly ubiquitous with Bluetooth Low Energy (BLE) as its core wireless network technology [
1]. BLE also called BLE smart offers very interesting features such as low power consumption and cost, long-range and battery life, small size and portability and secure and simple efficient communication protocols [
2,
3]. Such features have allowed BLE to be widely embedded in common consumer electronic devices and to be an integral part of smart gadgets (such as smartphones, smartwatches and, laptops, etc.). These BLE based wireless devices intercommunicate with one another and form an IoT network that provides different services and applications to people in outdoor as well as indoor environments [
4]. As people spend a substantial proportion of their time in indoor environments, the interaction of smart devices and gadgets interaction provide the basis for many novel IoT applications, such as indoor positioning, object tracking and indoor navigation, home automation, health monitoring, proximity-based advertisement and retail marketing [
5,
6,
7]. The extensive use of BLE devices in IoT applications has laid the foundation of a virtual BLE infrastructure in different kinds of indoor environments such as buildings, offices, homes and shops [
8]. For example in
Figure 1, BLE based IoT network deployed in a home can be used to locate people, valuables or objects of interest [
9]. A pre-deployed BLE based IoT network in an office building can help the company to maintain the time records of its employees [
10]. Whereas, a BLE based IoT network installed in a retail shop can be used to provide information on the time spent by different customers in front of different items of their interest [
11]. Similarly, a BLE based IoT network deployed in hospitals can be used to provide critical information about the daily routines of patients and can help to develop performance indicators to maintain a healthy environment [
12]. In all of these applications, the location of the target (human, object or robot) is of prime importance and to estimate the coordinates is a challenging task. In this context, the pre-deployed BLE IoT network can be exploited to form Wireless Indoor Localization System (WILS) that can provide strategic information of the targets, thus augmenting the use of existing applications [
13].
In light of the motivation presented above, BLE based WILS can be formed by smart use of the existing BLE based IoT network infrastructure in different indoor environments. Such a BLE based WILS would be a low-cost system, as it will only consist of the pre-deployed BLE devices. At the same time, the system is simple in use because the Received Signal Strength (RSS) of the BLE devices is used to derive the location(s) of the different target(s) with the use of suitable signal based localization algorithms. Wireless signal based localization algorithms derive absolute or relative coordinates of the target through the RSS of the devices in an indoor environment such as proximity [
8], fingerprinting [
14] and trilateration [
15,
16]. Proximity algorithm only indicates an approximate presence of the target(s) (also referred to as a tag(s)) in reference to a known location of a BLE transmitting device(s) (also referred to as an anchor(s)) [
17]. Whereas wireless fingerprinting requires the matching of pre-recorded RSS or fingerprints of the BLE anchors with the RSS recorded by the target for localization within the indoor environment that introduces unnecessary off-line workload before matching of the online fingerprints to locate the target [
18]. Unlike proximity and fingerprinting, the trilateration algorithm estimates the absolute or relative location of the target with reference to the locations of (at least 3) BLE devices [
19]. It uses a path loss model to derive the distance from the corresponding RSS samples. Trilateration algorithm is widely used for its simplicity and ability to calculate the target location(s) from the RSS of the pre-deployed BLE devices.
The efficacy of the WILS depends on the localization accuracy and location precision. The localization accuracy of the WILS defines the measure of correctness of the estimated location of the target [
20,
21,
22]. Whereas, the location precision of the WILS defines the percentage of the estimated location of the target of a certain localization accuracy sustained for the defined interval of time [
20]. To design a low-cost BLE based WILS with a high localization accuracy and high precision is a key requirement in enabling IoT applications but it is equally challenging and difficult. Since RSS is used to locate the target, the localization accuracy and precision depends on the stability of the BLE RSS, which in fact, depends on the transmission power used by the BLE devices. As the BLE wireless standard allows BLE devices to operate at multiple transmission power levels, it is intuitive that at a high transmission power level, BLE RSS is more stable compared to BLE RSS at a low transmission power level [
23,
24]. This issue is not often discussed as most works on localization algorithms use the highest power levels but it has important practical implications for energy efficiency, e.g., if a designer would like to trade-off localization performance and anchor’s battery lifetime. Furthermore, BLE RSS is susceptible to fast fading noise [
14] and multi-path effects [
25] caused by clutter present in the indoor environment, regardless of the transmission power level used by the wireless devices [
26]. There are other factors such as the effects of the non-linear amplifiers of the BLE devices, the antenna gain variation of the signal transmitters and different kinds of antennae used by various vendors [
27]. But their effect is of constant proportion in comparison to the effects of fast fading noise [
28], the change in transmission power levels [
29] and interference level of multi-paths [
23,
24]. Regardless of the gain, antennae and device heterogeneity, the random variation persists in every BLE signal mainly due to its low energy characteristic. A significant BLE RSS variation occurs when devices operate from high to low transmission power levels. As such, we investigate the extent of localization degradation when we use lower transmission power levels.
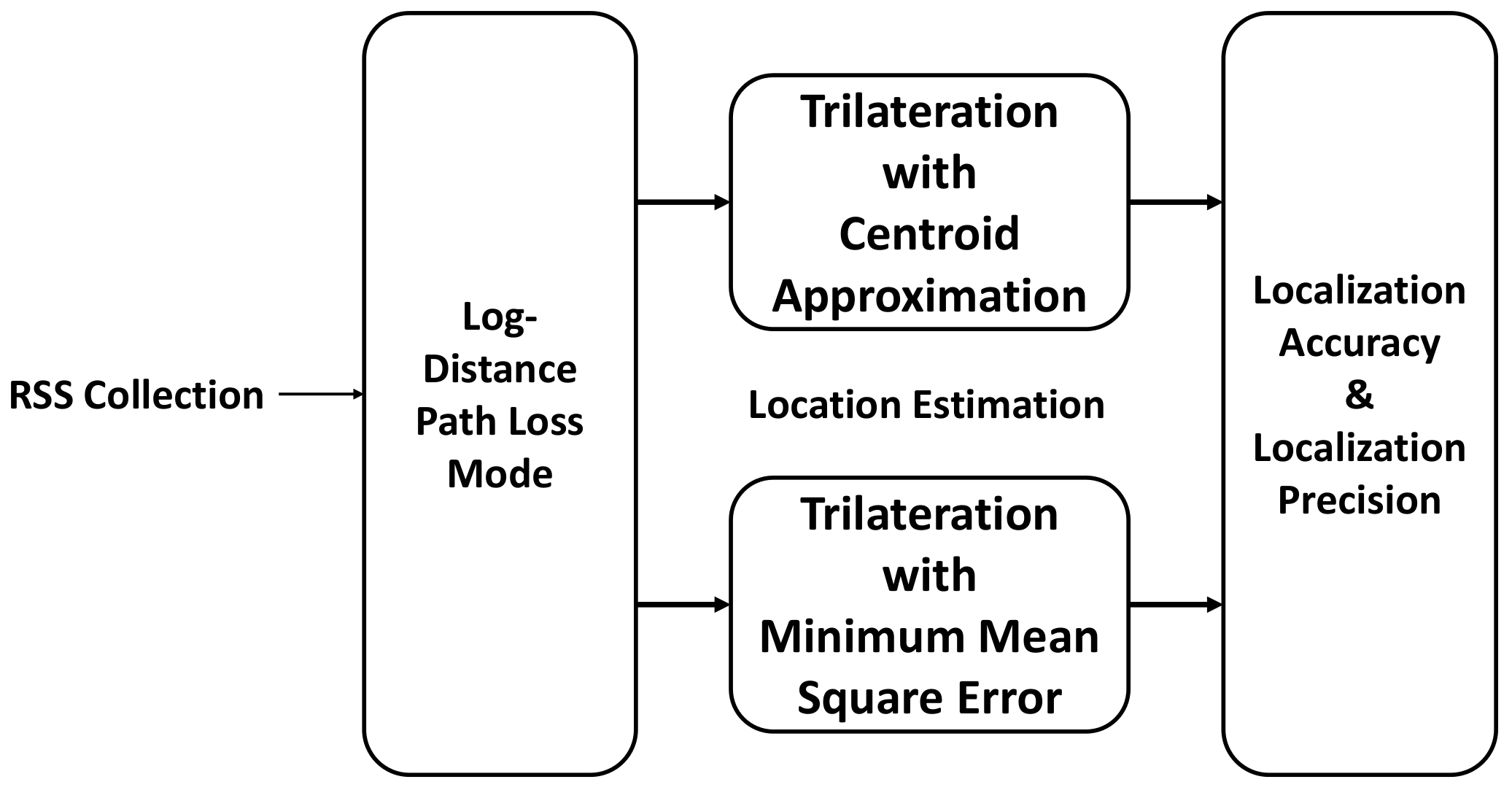
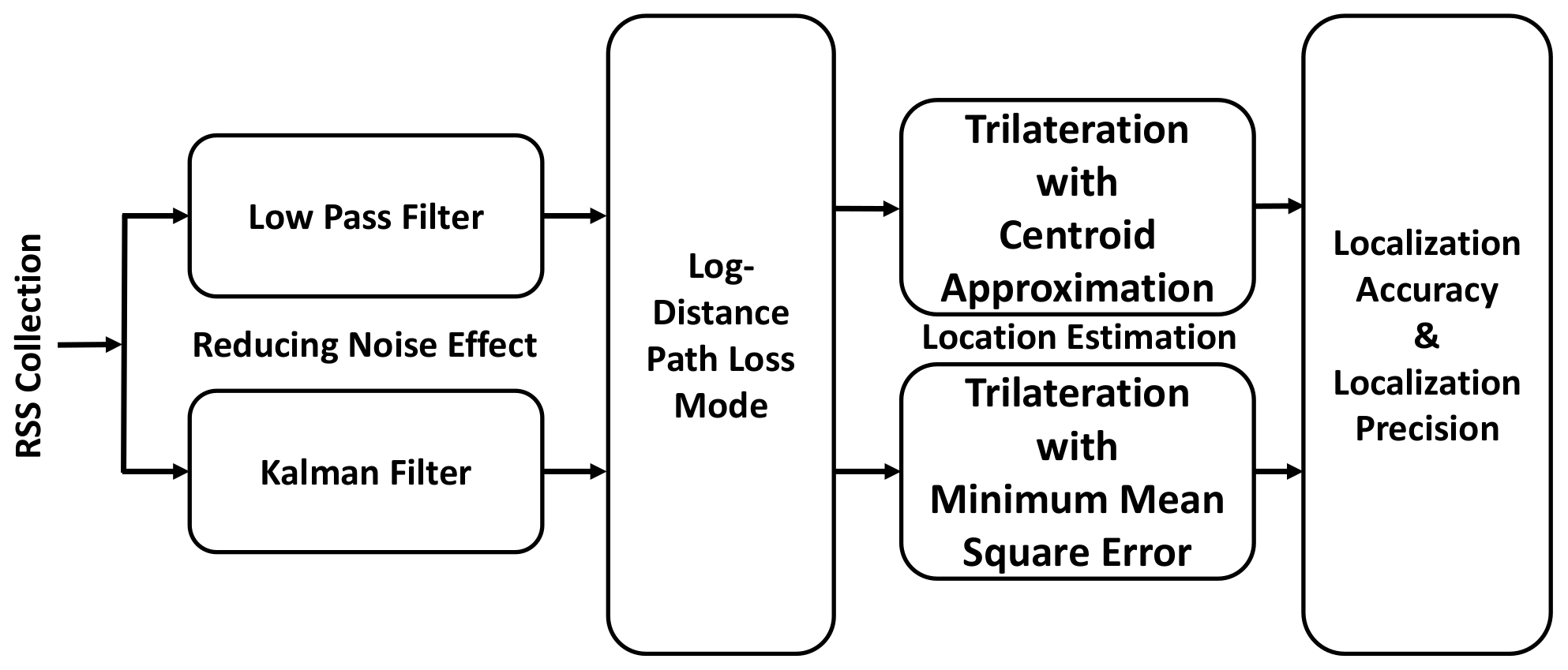
Therefore, the focus of this paper is to investigate the implications of BLE signal variation due to the use of multiple transmission power levels on WILS. To do so, we use the well-known and established trilateration based localization with Centroid Approximation (CA) method and Minimum Mean Square Error (MMSE) method. The trilateration based localization model is used to analyze the BLE RSS variations. The RSS variation causes the WILS to deviate, that results in low localization accuracy and low localization precision. To address this problem, we further investigate two different filters i.e., a Low Pass Filter (LPF) and Kalman Filter (KF) with trilateration based localization model and analyze their performance in eliminating the random variations from BLE RSS at multiple transmission power levels. Furthermore, we compare the performance of the two filters in terms of localization accuracy and localization precision with BLE based WILS operating at multiple transmission power levels. Thus, the contributions of this paper are as follows:
We investigate the problem of BLE RSS variation caused by the multiple transmission power levels in a BLE based WILS.
We evaluate the effects of BLE RSS variation on localization accuracy and localization precision of the WILS.
We further investigate and compare the performance of LPF and KF to improve localization accuracy and localization precision.
Lastly, we evaluate the implications of lower power levels on WILS which is practically useful for realizing the trade-off between accuracy along with precision and the device lifetime when deploying energy efficient WILS where lower power transmission levels are used.
The rest of the paper is organized as follows.
Section 2 reviews the relevant work present in the literature and discuss how is our work different from others. In
Section 3, we present the concept of BLE based WILS along with the set of assumptions considered to investigate the problem of BLE RSS variation with multiple transmission power levels. In
Section 4, we briefly explain the trilateration based localization model and discuss the limitations of the BLE based WILS. In
Section 5, we explain in detail the extended localization model in which two filters i.e., LPF and KF, are introduced in a simple trilateration based model.
Section 6 presents the details on the set of experiments and discusses the results. Finally,
Section 7 concludes the paper and presents future work.
2. Related Work
BLE is widely adopted as the de facto wireless standard for IoT applications as it continues to progress to meet their requirements [
30]. The evolution from the classical Bluetooth wireless technology to the BLE has been extensively discussed in [
31], along with the discussion on its features, specification, use in existing IoT applications [
8] and its viability in future IoT applications in light of the different commercial and noncommercial BLE systems present in the market [
11]. BLE features [
2] such as low power consumption and cost, long-range and battery life, secure and fast efficient communication and small size and portability, allows BLE to be tagged to any entity (stationary or moving) in comparison to other wireless standards (such as WiFi [
32], RFID [
33], UWB [
34], Infrared [
35] and Ultrasound [
36]) that rely more on a static network [
37]. The existing IoT applications have already laid the foundation of a BLE based IoT network infrastructure that can be used for applications such as micro-positioning and indoor localization, to make the existing applications smarter [
38]. The foresight that the pre-deployed BLE based IoT network infrastructure for sensing, monitoring and control IoT applications in different indoor environments can be used for additional applications, such as BLE based WILS.
In the context of WILS, BLE has been extensively studied and evaluated for target localization in indoor environments [
27,
39,
40,
41]. These studies mainly focus on analyzing the impact of the different parameters such as scanning window, transmission interval, number of frequency channels, the orientation of the devices, different indoor structures, device density and presence of line of sight (LOS) [
42] and Non-Line of Sight (NLOS) with different objects [
41] over BLE RSS in an indoor environment. For target localization, BLE is used with different approaches to estimate the location, such as wireless signal based localization algorithms, e.g., proximity [
15], fingerprinting [
14] and trilateration techniques [
43]. Some researchers have proposed alternative approaches such as geometric methods [
17], machine learning algorithms e.g supervised learning [
44,
45] and unsupervised learning [
46] and crowdsourcing approaches [
47]. In reference to the preferable range of localization accuracy for different targets in an indoor environment, Dahlgren et al. [
48] evaluated BLE RSS for indoor localization to achieve localization accuracy within the range of 2 m to 5 m (i.e., <2 m, <3 m, <4 m, <5 m and >5 m) with different commercial BLE commercial systems and in different indoor environments such as offices, corridors and rooms, etc. The authors conclude that the BLE RSS variations caused by the noise effects that are induced by the clutter present in the indoor environment to be the prime reason that effects the localization accuracy and reported maximum localization accuracy achieved was approximately 3 m.
To deal with the BLE RSS variation, a filter based approach is the most common method to address the randomness in wireless signals. Researchers have proposed different filters, such as moving average filter [
49], median filter [
14], LPF [
49], KF [
50], extended-KF [
51] and particle filter [
52], along with trilateration algorithms. In [
53] the authors used filter based approach for localization and reported a localization accuracy less than 1 m by using a KF with trilateration. In [
54] the authors used the channel diversity of the BLE signals for indoor localization. The authors used KF to remove the fluctuations from the RSS of the BLE devices and reported a localization accuracy of less than 1 m with trilateration technique however all experiments conducted were on default transmission power setting.
In comparison to filter based approach, a number of researchers have proposed non-filter based approach in which the multiple transmission power level feature of BLE is analyzed in context of reducing the noise effects that causes the fluctuations in RSS. A detailed study is presented in [
24] in which the authors have analyzed the effects of multiple transmission power levels on BLE RSS. The authors show the presence of multi-path fading effects at different transmission power levels and propose machine learning algorithms such as Support Vector Machines and K-Nearest Neighbour algorithms along with wireless fingerprinting technique with BLE based WILS for indoor localization. In [
23], the authors also proposed a multiple transmission power level feature to address multi-path effects in BLE RSS. From their experiments the authors show that at low transmission power level, the effects of the multi-paths is low. The reason being that at low transmission power level, the majority of the multi-paths fades away while propagating towards the destination node. In the experiments, the authors attached the BLE devices to a ceiling that operates with two transmission power levels, i.e.,
dBm and
dBm, which is in LOS with a laptop at a distance of approximately 2 m, showing that the RSS is more stable and the estimated localization error is 1 m. The experimental setup of the work in [
23], is highly impractical in a real-world scenario and the RSS of BLE at such low transmission power levels can hardly be recorded beyond a 1 m distance.
Recently, multiple transmission power level is used with filter-based approach. The authors in [
28] explored different transmission power levels (i.e., 4 dBm, 0 dBm,
dBm and −8 dBm) and studied their effect on RSS with distance. The authors used a K-Nearest Neighbour (KNN) based fingerprinting technique and four different filters to smooth the RSS. The authors reported the result with a maximum localization accuracy of 2.9 m when all devices operate at the highest transmission power level i.e., 4 dBm. Golestanian et al. in [
55] exploited and proposed multiple transmission power level feature of BLE based WILS to deal with unreliability of the RSS. The authors analyzed the variation of BLE RSS at −4 dBm,
dBm,
dBm and
dBm and used moving average filter to remove the variation in the RSS which ultimately reduces the error in distance estimation.
The works presented in [
24,
28] motivated us to conduct a comprehensive evaluation of a BLE based WILS by exploring the multiple power transmission feature for target localization in an indoor environment. In [
56], we analyzed a BLE based WILS with multiple transmission power levels and used a trilateration algorithm for target localization. We conducted a set of experiments in a classroom environment and estimated the location of the 3 targets in the presence of LOS and NLOS. Out of 5 transmission power levels, the maximum localization accuracy achieved was 2.2 m when all BLE devices operated at 10 dBm, which is the highest transmission power level, and localization accuracy of 5 m with −8 dBm, which is the lowest transmission power level. The reason is that BLE devices operate at low transmission power levels, hence the RSS gets weak and attenuated due to multi-path effects and clutter present within the environment. The reported results were achieved by using the average of the collected raw RSS samples. The studies [
49,
54] provided the result that as high as a 1 m localization accuracy can be achieved with the use of the filters with BLE by using a trilateration algorithm. To the best of our knowledge, the majority of the researchers have addressed the problem of RSS variation at default transmission power level or at higher transmission power levels with filters to achieve high localization accuracy. The problem of RSS variation caused by the change in transmission power levels in BLE based WILS localization accuracy and precision has not been highlighted and addressed.
Localization accuracy and localization precision are two important parameters in WILS. It is important that the system should be able to sustain the high localization accuracy with high location precision. Most of the researchers calculate the mean localization error derived from the average of the RSS sample collected. However, for real-time localization, the use of instantaneous samples is also preferred. But, instantaneous RSS samples are erroneous, such data is usually averaged to derive an approximate value. By the use of a filter, the erroneous samples can be removed to result in a smooth RSS. To the best of our knowledge, the majority of the researchers have addressed the problem of RSS variation at the default transmission power level. In this paper, we comprehensively highlight the problem of RSS variation with change in multiple transmission power levels and propose a simple solution to address the highlighted problem.
3. Bluetooth Low Energy (BLE) Based Wireless Indoor Localization System (WILS)
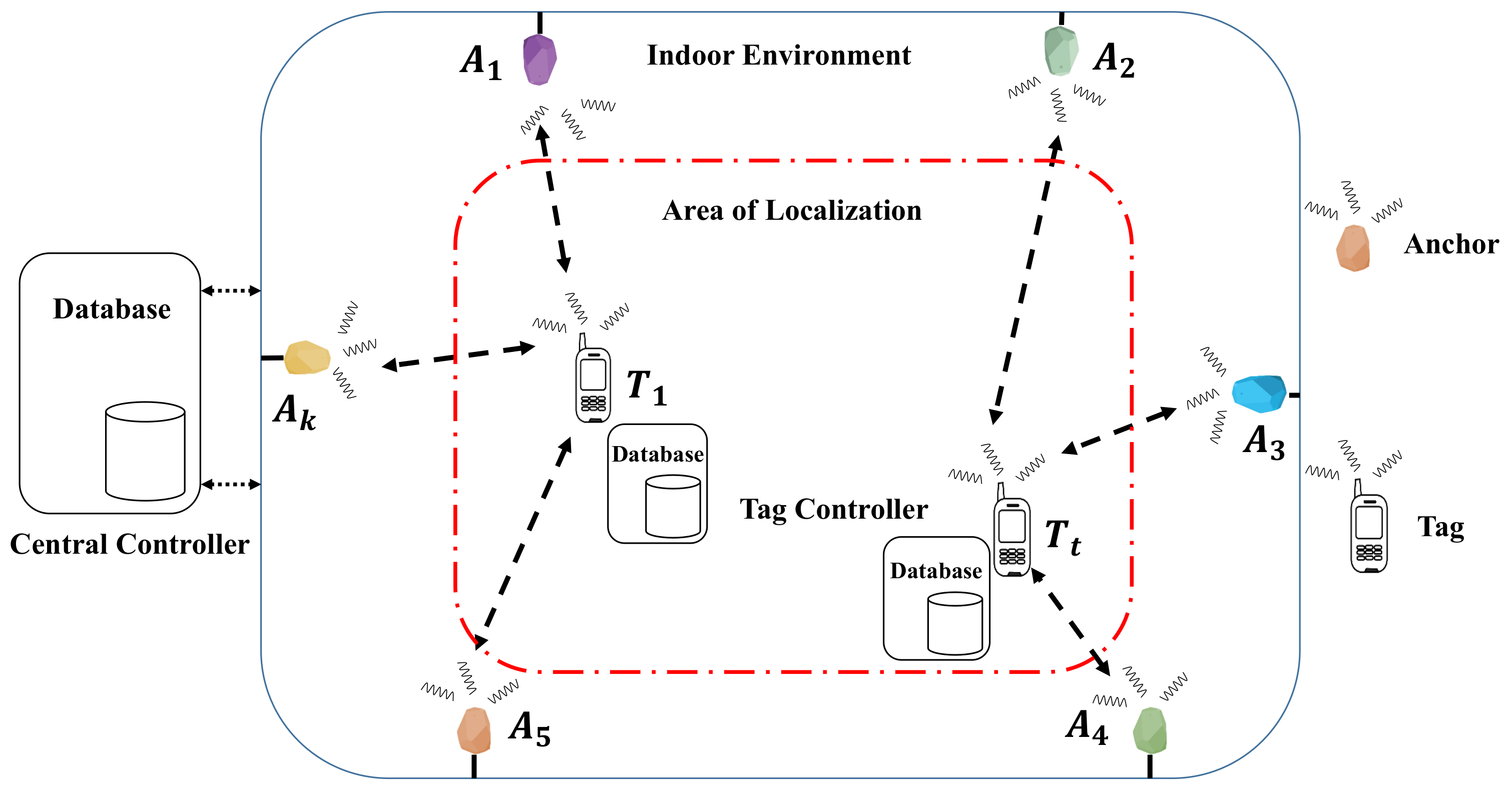
In this section, we shall explain the generic model of BLE based WILS. Generally, a WILS consists of a set of pre-deployed access points or anchors, denoted by
, where
k represents the
kth anchor and a set of targets or tags, denoted by
, where
t represents the
tth tag in an indoor environment as shown in
Figure 2. The location of the anchors, denoted by (
) is fixed and known. Whereas, the tag location, denoted by (
), needs to be estimated in an area referred to as Area of Localization (AoL). In a typical BLE based WILS both the anchors and tags are wireless devices, embedded with BLE wireless transceivers that allow them to operate in the 2.4 GHz license-free band. In a BLE based system, 2.4 GHz ISM band is divided into 40 BLE channels, each 2 MHz [
14]. Out of the 40 BLE channels, 3 channels (i.e., 37, 38 and 39 of the BLE 2.4 GHz ISM band) are designated as advertising channels, while the remaining 37 are communication channels [
14]. The BLE wireless standard allows each BLE device (i.e., anchor and tag) to be identified by a Universal Unique Identifier (UUID) [
57]. The UUID is advertised in small data packets called beacons, by hopping pseudo-randomly between 3 advertising BLE channels. The rate at which the beacons are advertised is defined by an advertising interval, denoted by
, that ranges approximately from 2000 ms to 100 ms [
57]. A large advertising interval corresponds to low beaconing whereas a small advertising interval corresponds to high beaconing. Each anchor has the capability to transmit the beacons at multiple transmission power levels [
25]. These transmission power levels are listed in [
56] and shown in
Table 1. The transmission power level is denoted by
, where
l is the index of the power level as listed in
Table 1. The transmission power level defines the transmission range of the device. High transmission power corresponds to a large transmission range and vice versa. We assume at a time instance
all anchors of the anchor set
A operate at similar transmission power levels
. With that what we mean is, at a time instance
, all anchors will operate at a single transmission power level, i.e.,
. Any BLE device that resides within the range of an anchor can scan for their beacons if they are advertised. The rate of scanning beacons is defined by the scanning interval [
57], denoted by
. A large scanning interval allows many beacons to be collected, whereas a small scanning interval allows less beacons to be collected. Generally,
1 s, is the default scanning interval which is adopted universally and a
250 ms is the most optimal setting considering scanning interval
1 s. It is assumed that the tag is in Line of Sight (LOS) and resides within the transmission range of at least 3 anchors at all times.
In a typical BLE based WILS, all these anchors are further wired with a central controller, that hosts a central database, where the data reported by each anchor is stored and processed to estimate the location of the tag. Similarly, a tag also hosts a tag controller and associated with the tag controller is its database in which the tag controller stores and process the data that it receives from the anchors. The data here is basically the raw RSS of the BLE devices, e.g., if the anchors are residing within the transmission range of the tag, the anchors report to the central controller with the RSS of the tag and the controller updates the data stored in its database. Similarly, the tag reports to its controller with the RSS of the anchors and the tag controller updates the data stored in its database. Whenever a target arrives in the range of 3 or more anchors, the central controller or the tag controller, or both, can initiate the process of localization and estimate the location of the tag. The entire system is shown in the
Figure 2 and the symbol along with their definitions used in the model are listed in
Table 2.
The initiation of the localization process can be triggered by the anchor or by the tag or both. If a tag is a lost valuable, the localization process is initiated by anchors and the central controller, whereas if the person wants to know its location inside a building the person triggers the localization process through his/her cell phone that acts as a tag. BLE devices are resource constrained i.e., they have limited computational power, memory and limited battery life.
The multiple transmission power level features of BLE devices allow them to operate from higher to lower transmission power. The main advantage of operating at a high transmission power level is that the BLE signal is less susceptible to noise effects at a significantly larger distance. At high transmission power levels, two BLE devices (central-peripheral roles) are able to pair in a very short time interval (in order of 1–2 ms) because of low Bit Error Rate (BER) and low latency in the link between the two devices. As a disadvantage, the continuous transmission at high transmission power levels drains the battery of the BLE devices that ultimately leads to the short lifespan of the device. The advantage of operating at low transmission power increases the overall lifespan of the BLE devices but the ability of BLE devices to transmit at large distances is restricted. At low transmission power levels, the BLE signal is prone to noise effects that result in high BER and link latency which increases the overall connection interval and pairing time between the two BLE devices [
26]. In the context of wireless localization, transmission power plays an important role in localization specifically in indoor environments. The high transmission power leverages the coverage area of an individual device therefore, fewer devices can be used to locate a large number of targets in an AoL with a reasonable localization accuracy and precision at the cost of battery lifetime. Whereas, operating at low transmission power levels increases the battery lifetime but restricts the coverage area that demands a significant number of devices to be deployed to cover an AoL and locate the targets with a reasonable localization accuracy and precision. In this regard, the researchers have devised transmission power management schemes to optimize the energy efficiency and overall battery lifetime of the BLE devices [
58,
59,
60]. Regardless of the transmission power management schemes, the change in the transmission power affects the BLE RSS. This change in the RSS will affect the overall localization accuracy and localization precision of the WILS. Because at low transmission power levels, RSS is highly unstable due to multi-path effects and clutters present in the indoor environment. In the next section, we present the set of techniques to estimate the localization system and investigate the effect caused by the change in multiple transmission power levels over localization accuracy and localization precision.
6. Experiments and Results
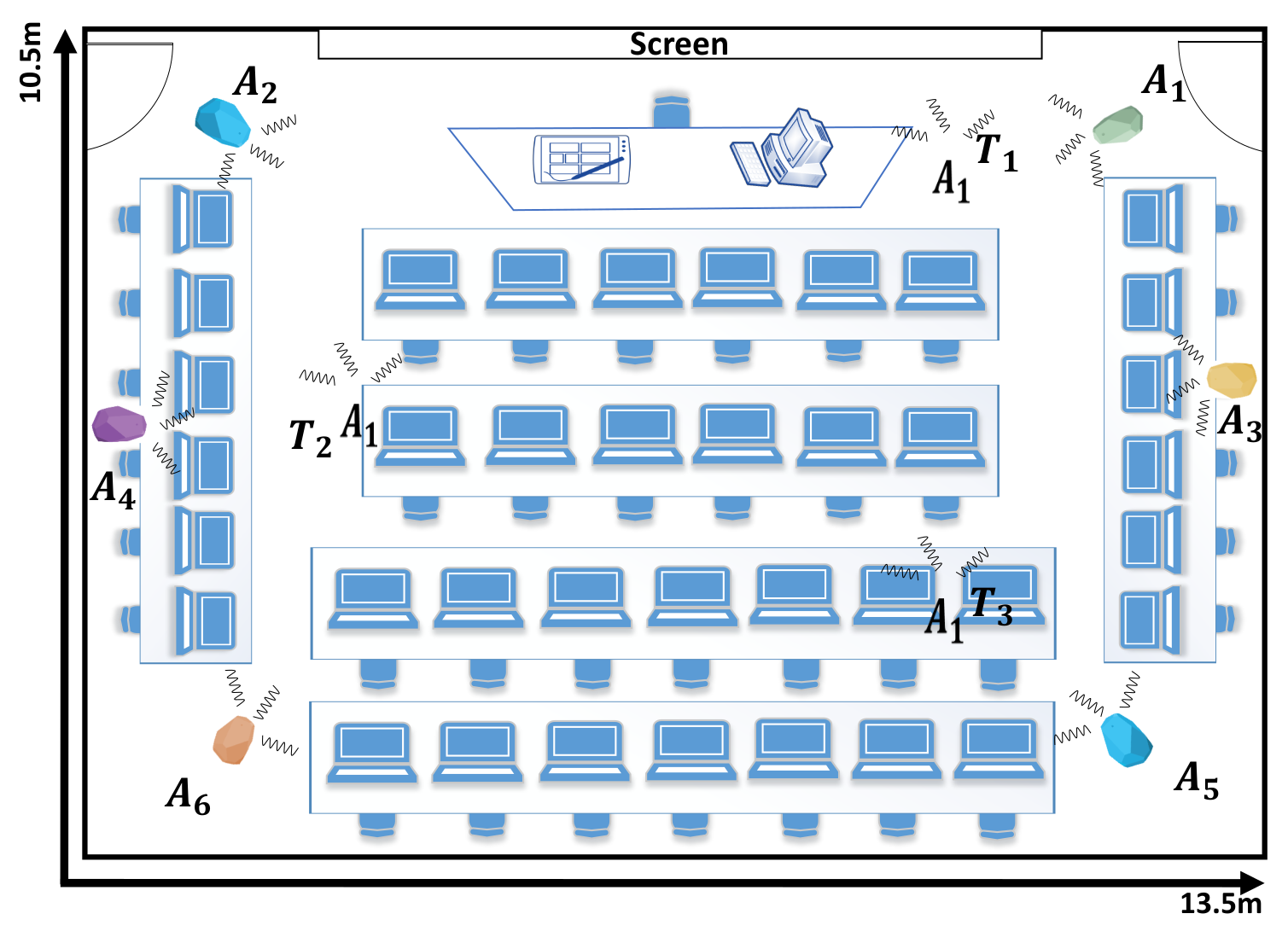
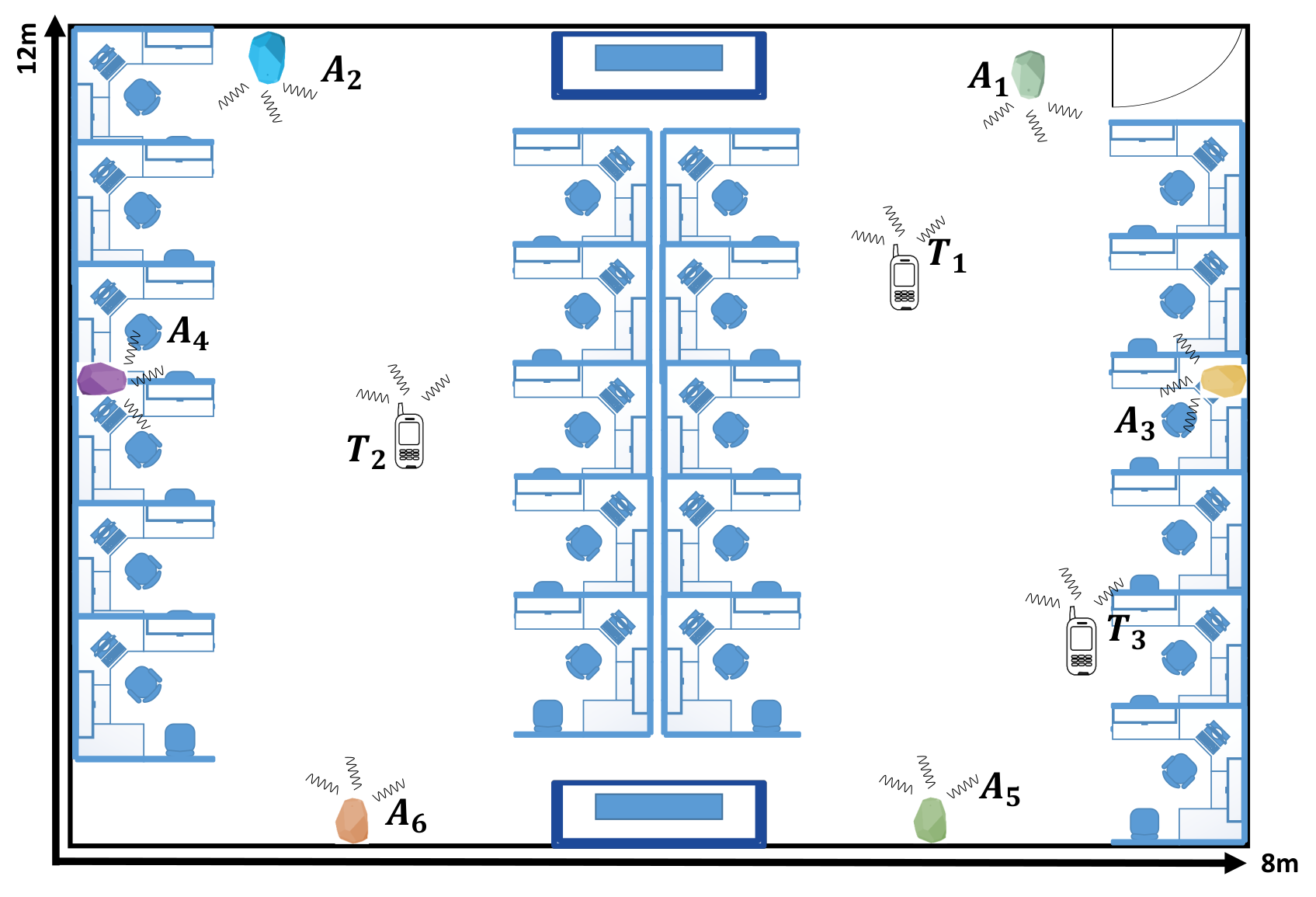
In this section, we present the set of experiments that we conducted to assess the BLE based WILS and compare the results based on the different techniques that were discussed in the above sections. We conducted experiments in the two indoor environments shown in
Figure 4 and
Figure 5 and compare our results based on the experimental settings deployed in the two indoor environments. In the both indoor environments, a total of 6 BLE anchors were chosen to locate a tag at three different locations. In this experiment, we have used Estimote BLE beacons [
69] with ibeacon configurations as anchors and a Samsung Galaxy Note 3 as a tag to record the BLE beacons. The locations of the anchors and tag, in 2-dimensional coordinates, are provided in
Table 3. All anchors operate with same transmission power level. However, we configure the transmission power level sequentially from 10 dBm to
dBm. For each configuration (let say when all anchors operate at 10 dBm) we conduct an experiment and collect 200 samples of RSS data of all anchors at all 3 target locations in two different environments as shown in
Figure 4 and
Figure 5. In a similar manner, we will conduct experiments for the remaining 4 configurations, repeat the experiments and compare the results. Initially, we will assess the effect of LPF and KF techniques over RSS at multiple transmission power levels. Then we will estimate the location of tag by using filter-based trilateration with CA & MMSE methods and present comparative analysis based on the estimated localization accuracy and localization precision respectively.
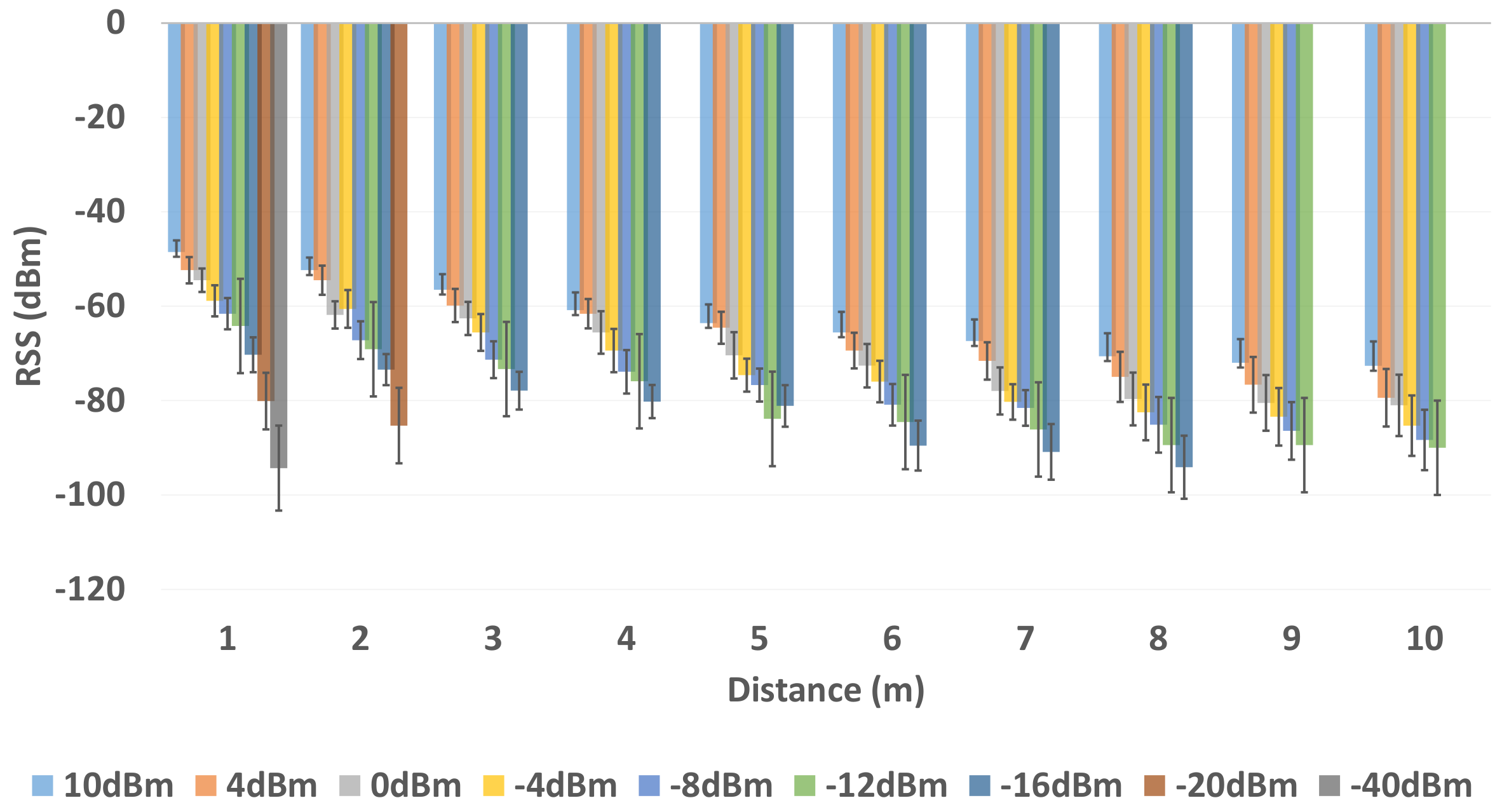
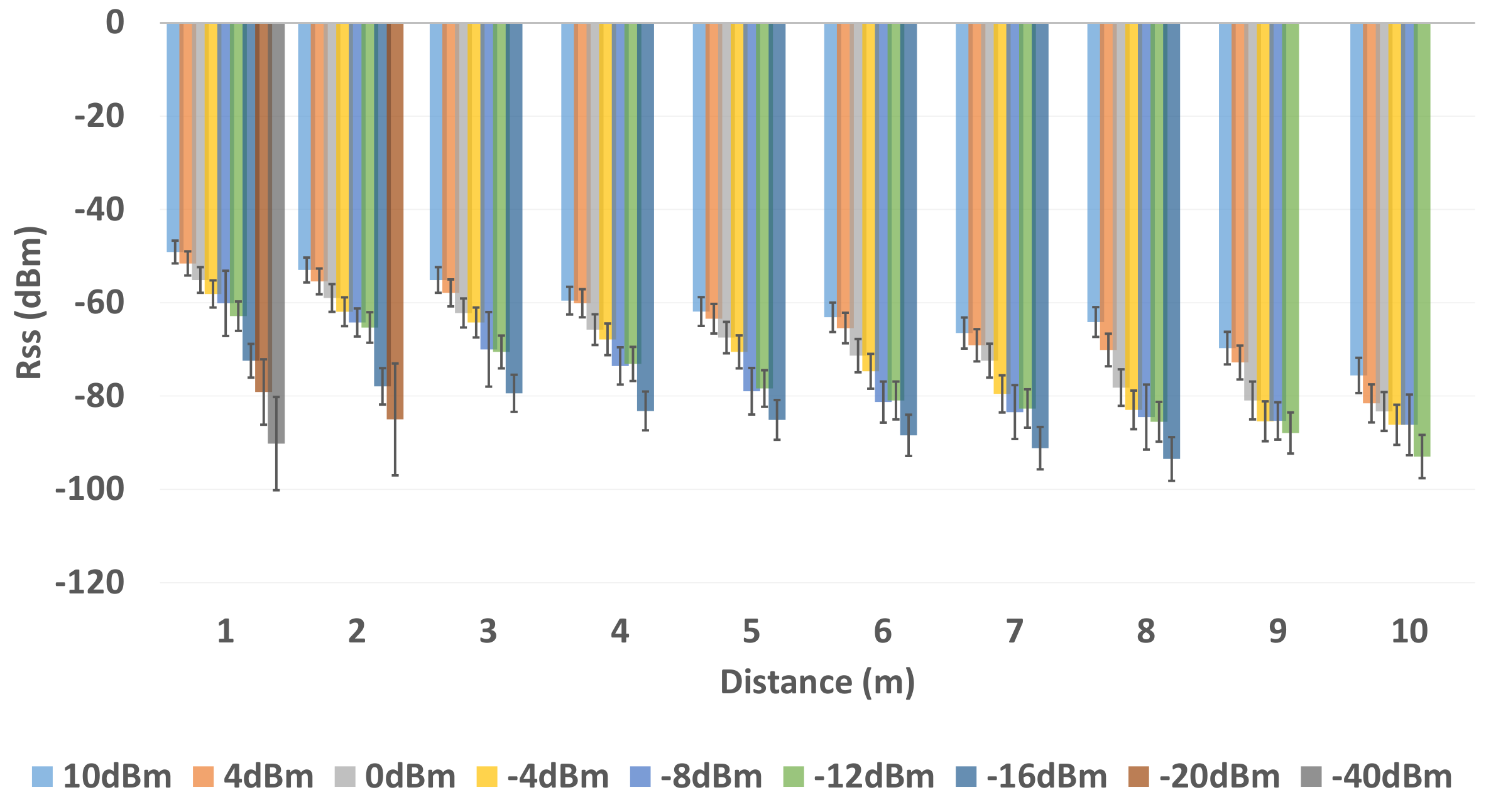
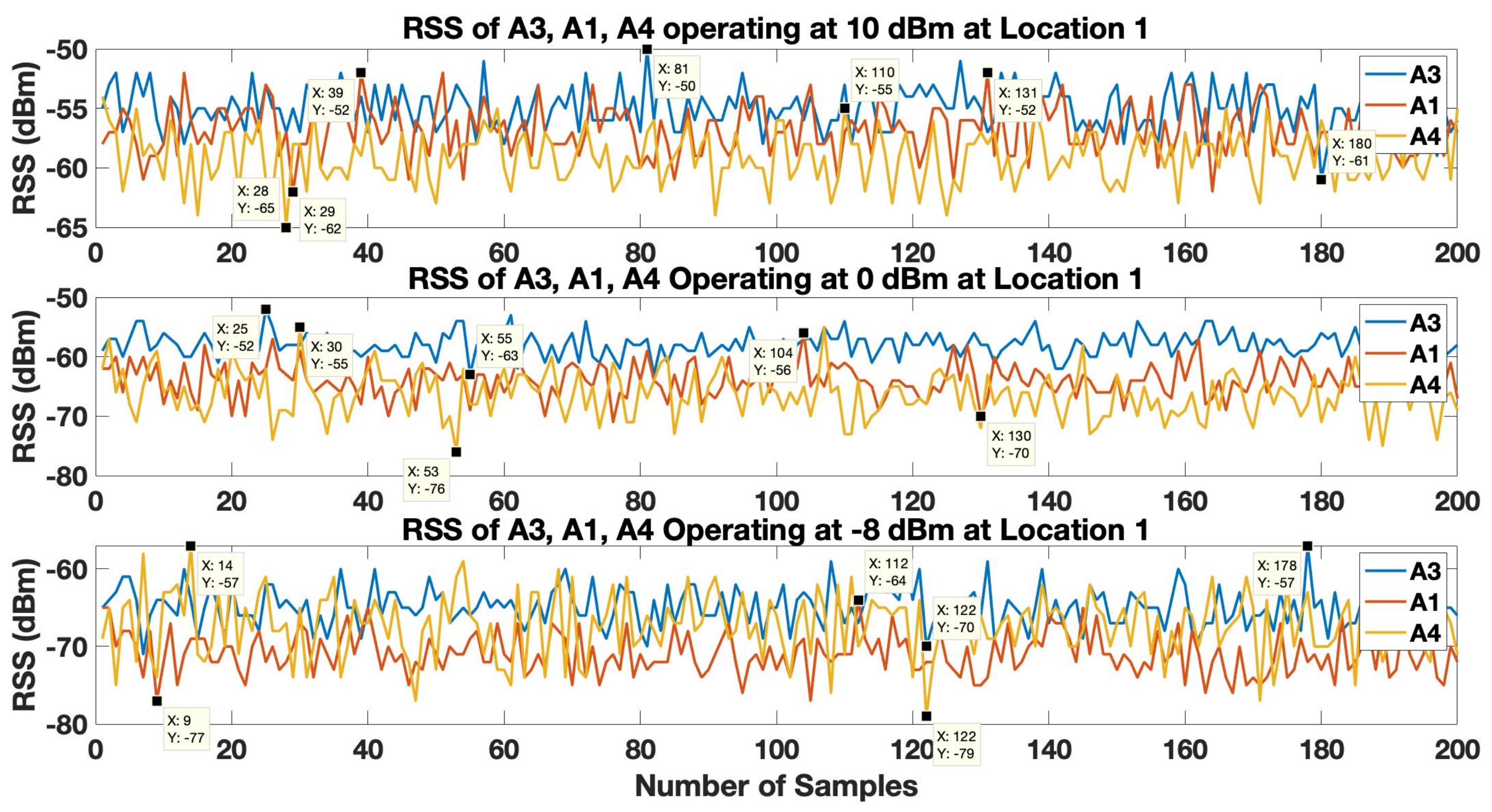
6.1. Effects on RSS
Initially, at each tag location 200 samples (approximately 1 min of datum) were recorded by the tag of all the anchors operating at multiple transmission power levels. LPF and KF were applied to the RSS datum.
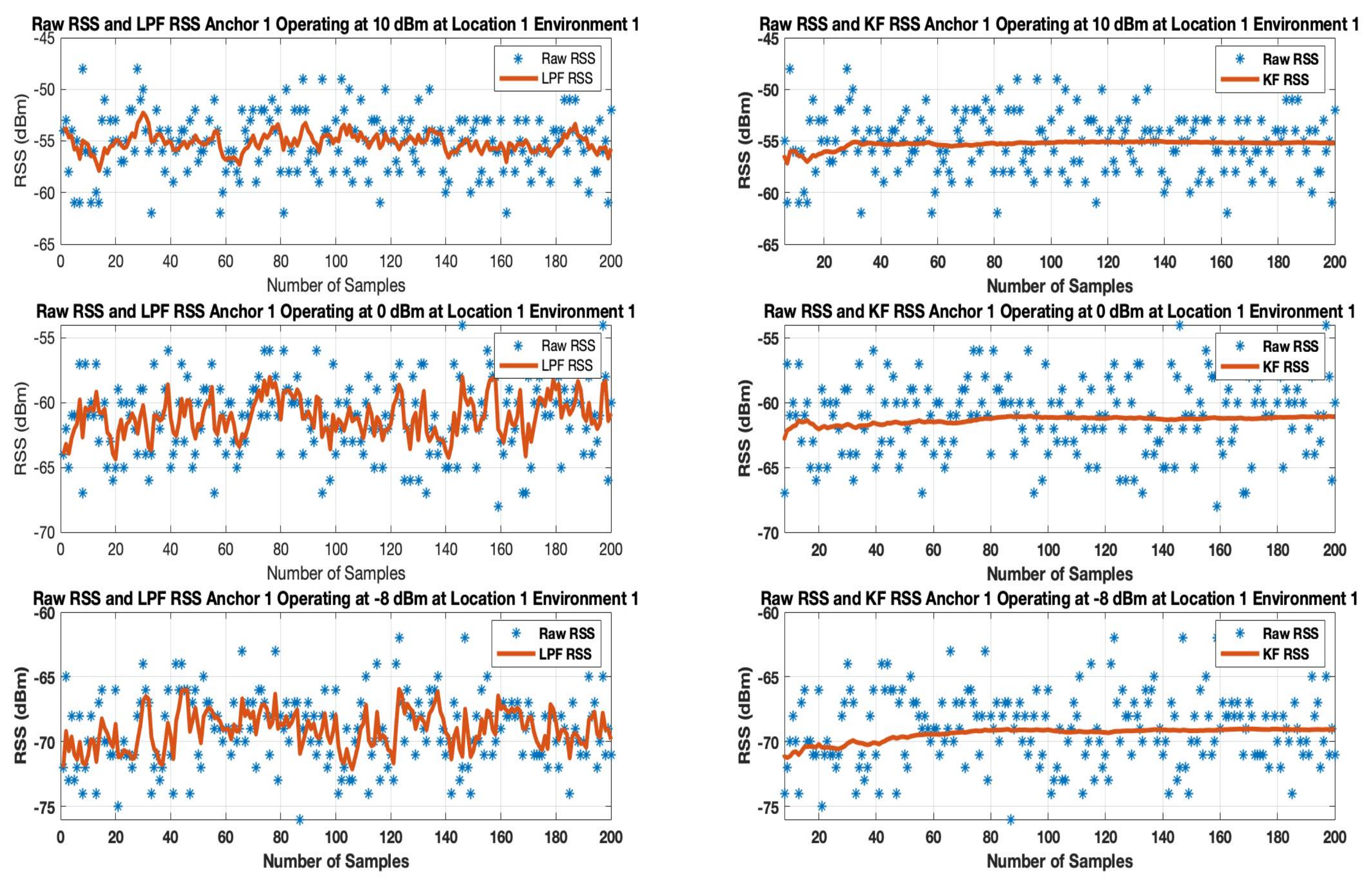
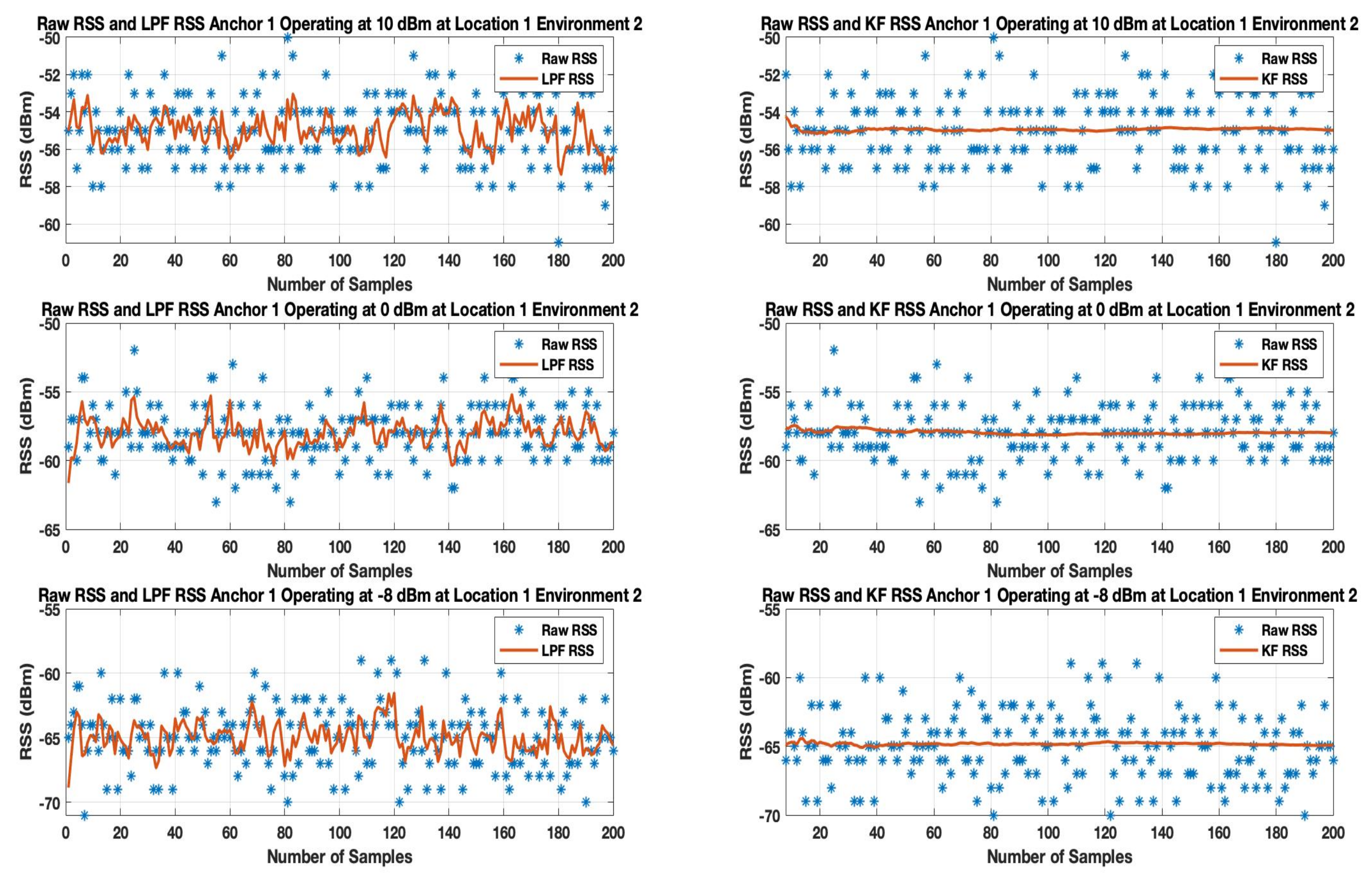
Figure 11 and
Figure 12 show the results when LPF and KF are applied on anchor 1 operating on the highest (10 dBm), default (0 dBm) and the lowest (
dBm) transmission power level in environment 1 and environment 2.
The results show the random variation of the unfiltered BLE RSS of anchor
increases as the BLE device operates from 10 dBm to -8 dBm for both indoor environments. When an LPF is applied to a BLE operating at 10 dBm as shown in
Figure 11 and
Figure 12, the result shows a reasonable smooth RSS. However, LPF struggles to maintain the smooth RSS, as a BLE operates from a high to low transmission power level. This is because LPF fails to map the deviated samples of RSS to their actual value of the RSS samples. A similar trend is observed in an environment as shown in
Figure 12 in which LPF fails to be absolute resilient against a much deviated RSS, especially when a BLE based WILS operates at low transmission power levels. In comparison to LPF, the performance of KF in removing the effect of deviated RSS samples and smoothing the RSS sample vector outperforms the LPF as shown in
Figure 11 and
Figure 12. Whereas, based on the initial setting, KF converges quickly (in 1 s to 2 s). This results in extremely smooth RSS in both environments for devices operating at multiple transmission power levels.
In conclusion, both filters are able to remove the random variations from the RSS. However, KF is proved to be more effective in comparison to LPF. Thus, in terms of smoothing, KF appears to be smoother than LPF. For localization, filtered RSS streams are most likely to result in much stable localization accuracy and precision. Therefore, both filters, i.e., LPF and KF, are applied to the 3 anchors with the strongest RSS.
6.2. Estimating the Localization Accuracy and Localization Precision with Filter Based Approach
The filtered stream of RSS samples can now be used to estimate the location of the tag. The filters allow the RSS to be smooth by removing the random fluctuations as much as possible. This stream of filtered RSS is used to estimate the location of the tag with a filter based trilateration localization algorithm with CA and MMSE methods. The methodology used to achieve the results is defined in
Section 4.4.2 in which the unfiltered RSS sample vector (i.e., 200 RSS samples corresponding to 1 min of data) is first filtered through LPF filter and KF filter. This filtered stream of RSS sample vector is used to achieve localization accuracy and localization precision. The experiments are repeated 5 times with 5 different transmission power settings at all tag locations in the two environments. The best results with filter-based approach are reported in
Table 7 and
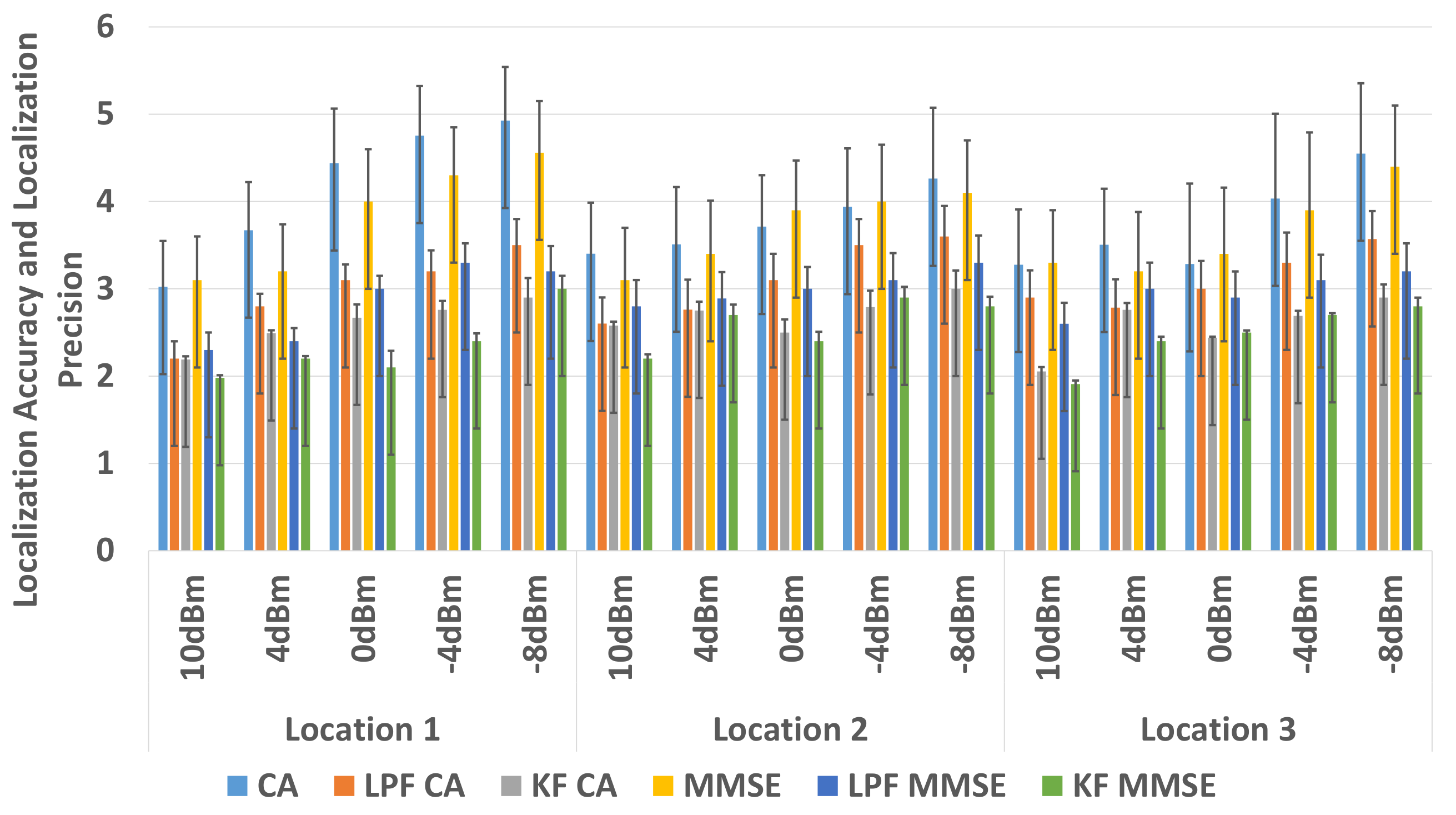
Table 8. The localization accuracy and localization precision achieved for each transmission power level are shown in their respective columns.
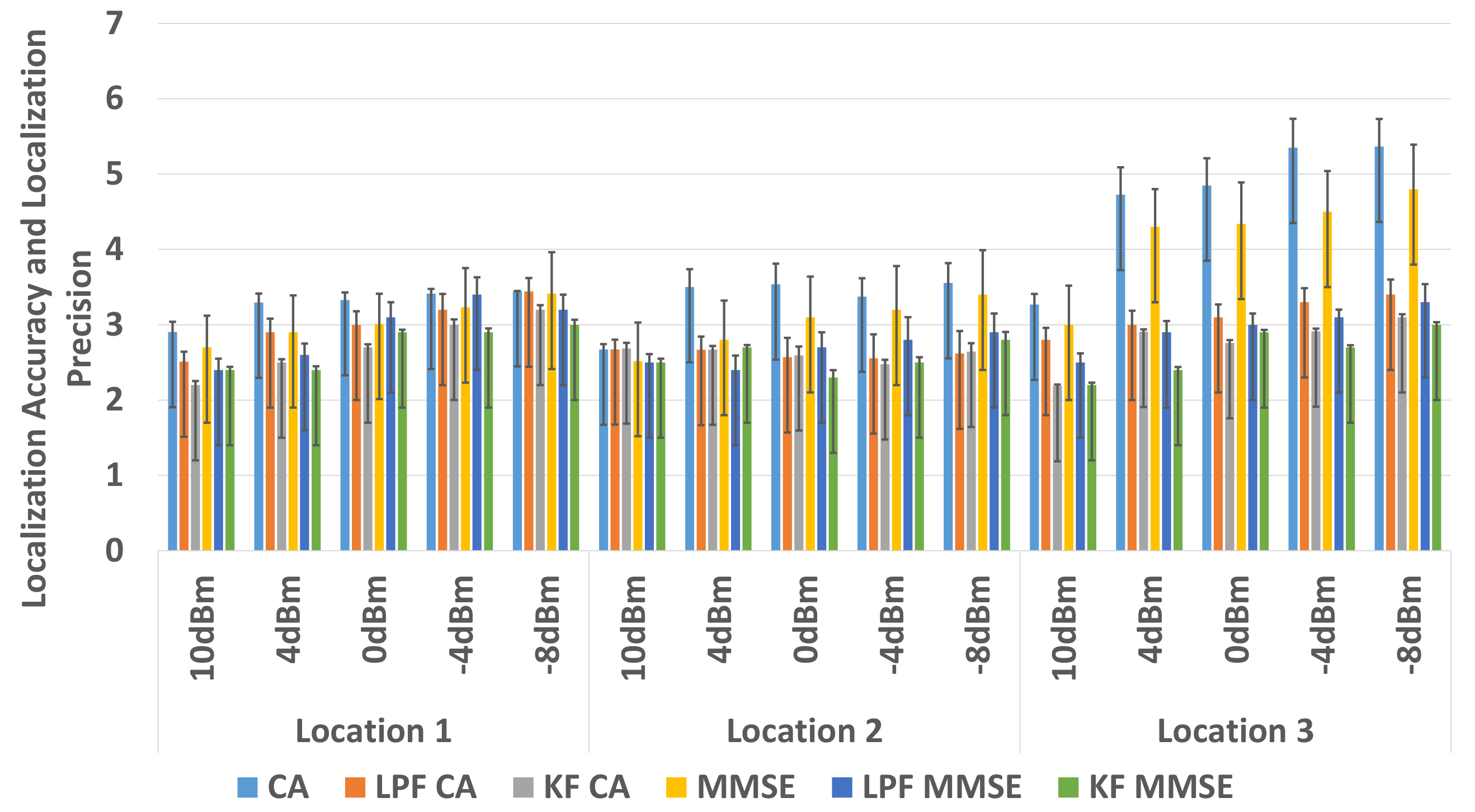
The results show an improvement in the overall localization accuracy and localization precision at all transmission power levels with filter-based approach. A significant improvement can be observed in the localization accuracy and localization precision for the anchors that operate at low transmission power levels, i.e., dBm and dBm at all 3 tag locations. At a low transmission power level, the RSS tends to vary more compared to RSS at high transmission power levels. This change in the RSS sample stream causes large deviations that result in large errors.
In comparison to the non-filter based approach, an average of 0.8 m of improvement is observed in localization accuracy and an approximately 36% improvement in localization precision of the WILS is observed when LPF using CA method for BLE based WILS in environment 1. An average of 1.2 m of improvement is observed in localization accuracy and an approximately 38% improvement in localization precision by the using CA method in environment 2. An average of 1.3 m improvement in localization accuracy and approximately 50% improvement in localization precision is observed with KF using CA method in environment 1. And an average of 1.4 m improvement in localization accuracy and approximately 56% improvement in localization precision is observed with KF with CA method in environment 2. With the MMSE method, an average of 0.3 m of improvement is observed in localization accuracy and an approximately 33% improvement in localization precision of the WILS is observed by using LPF in BLE based WILS in environment 1. An average of 1.4 m of improvement is observed in localization accuracy and an approximately 33.5% improvement in localization precision of the WILS is observed by using LPF in BLE based WILS for environment 2. Similarly, An average of 1 m improvement in localization accuracy and approximately 46% improvement in localization precision is observed with KF using MMSE method in BLE based WILS for environment 1. And an average of 1.4 m improvement in localization accuracy and approximately 54% improvement in localization precision is observed by using KF with MMSE method in BLE based WILS for environment 2. From the comparative analysis as shown in
Figure 13 and
Figure 14, it is concluded KF based MMSE method, outperforms all other methods with different transmission power levels, at all 3 locations in the two indoor environments.
Therefore, in comparison to LPF based trilateration localization with CA, the performance of a KF based trilateration localization with MMSE is far better. An average of 0.5 m improvement in localization accuracy and 10% improvement in localization precision is observed with a KF based trilateration localization with MMSE in both environments with BLE based WILS operating at multiple transmission power levels.
6.3. Comparison with the State-of-the-Art
In this section, we shall compare our results with results of the two relevant works i.e., [
24,
28], present in the literature. The best result reported in [
24] is a localization accuracy of 2 m with matching precision (localization precision) of approximately 86.74% by using 5 BLE anchors with Mode-KNN based signal pattern matching method. Whereas, the best results reported in [
28] is a localization accuracy of 2.8 m only, achieved by using 3 BLE anchors with minimum signal replacement based signal patter matching method.
In comparison to the results reported above, we have been able to achieve localization accuracy is approximately 2.2 m meters with a localization precision 95% by using 3 BLE anchors with KF based trilateration method.
7. Conclusions and Future Work
BLE based WILS with high accuracy and high precision is extremely important to improve the location-based BLE IoT applications. In this paper, we investigated the problem of RSS variation incurred by the use of multiple transmission power feature in BLE based WILS. To highlight this problem, we deployed BLE based WILS in two different kinds of indoor environments as shown in
Figure 4 and
Figure 5 that consisted of 6 anchors to estimate at tag coordinates at 3 different tag locations with a trilateration based localization model. It was observed that the RSS, localization accuracy and localization precision tends to decrease as the anchors operate from high to low transmission power levels. We initially used a non-filter based approach in which we compared the results of two commonly used trilateration methods i.e., CA method and MMSE method. Furthermore, we analyzed the results and concluded that the trilateration based localization model with MMSE outperformed the CA method in terms of localization accuracy and localization precision in both indoor environments.
To improve the overall localization accuracy and localization precision of BLE based WILS, we further investigated the effects of the use of two filters i.e., LPF and KF in trilateration based localization model with CA and MMSE methods. In comparison to the non-filter based approach, we observed a great improvement in localization accuracy and localization precision with filter-based approach in the two indoor environments. We compared the results of LPF and KF as shown
Figure 13 and
Figure 14. We observed the results obtained with the use of KF in trilateration based localization with MMSE were far better than the results obtained with LPF in the trilateration based localization model with CA and MMSE methods. In conclusion, the use of KF in trilateration based localization model with MMSE method proved more effective in eradicating random variations in RSS with the change in multiple transmission power levels, thus resulting in a BLE based WILS with high accuracy and high precision.
In future, we are focusing to address the KF error drift issue. In our case, whenever KF is invoked, it starts from the initial values (reset each time to 0) which is one method to address this problem. Another approach is that the KF starts with an initial value of the RSS for each anchor to help in quick convergence (less than 1–2 s). However, there are two problems in this approach, (1) the setting initial RSS values for each anchor add extra workload and (2) with each filter error is added with the initial settings (error drift issue) which can drift the KF result overtime. Also, the problem of BLE RSS signal variation caused by the change in transmission power levels needs to be investigated with semi-dynamic and dynamic targets in an indoor environment. In this regard, it would be interesting to see the impact of the Extended Kalman Filter (EKF) and Particle Filter (PF). Furthermore, these filters can also be used in conjunction with fingerprinting-based localization algorithms. We could also consider security of ranging as this has become an interesting requirement in some applications [
70]. Thus, we plan to extend our work in these dimensions as our future work.