A Framework of Human-Motion Based Structural Dynamics Simulation Using Mobile Devices
Abstract
1. Introduction
2. System Development
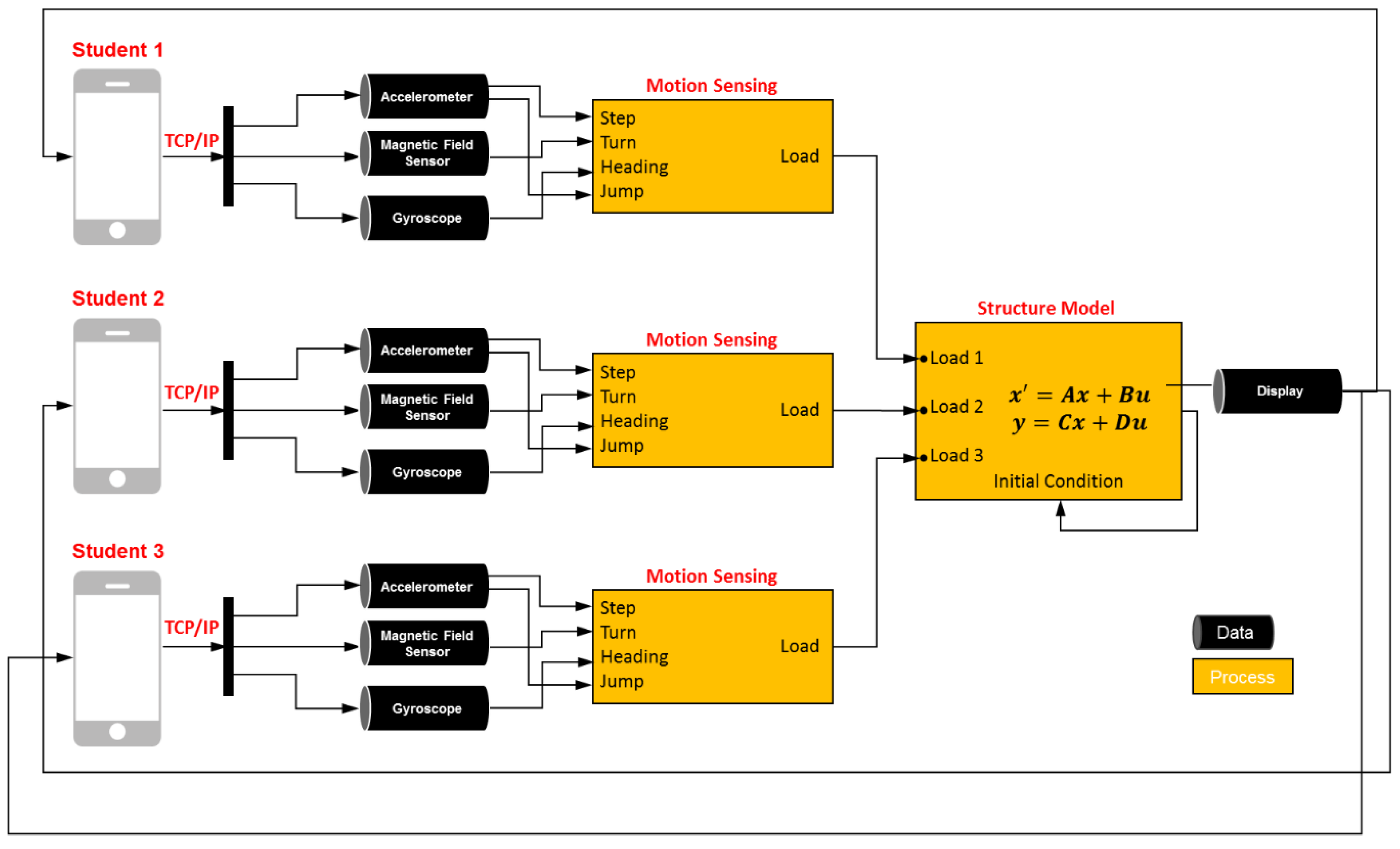
2.1. Overview
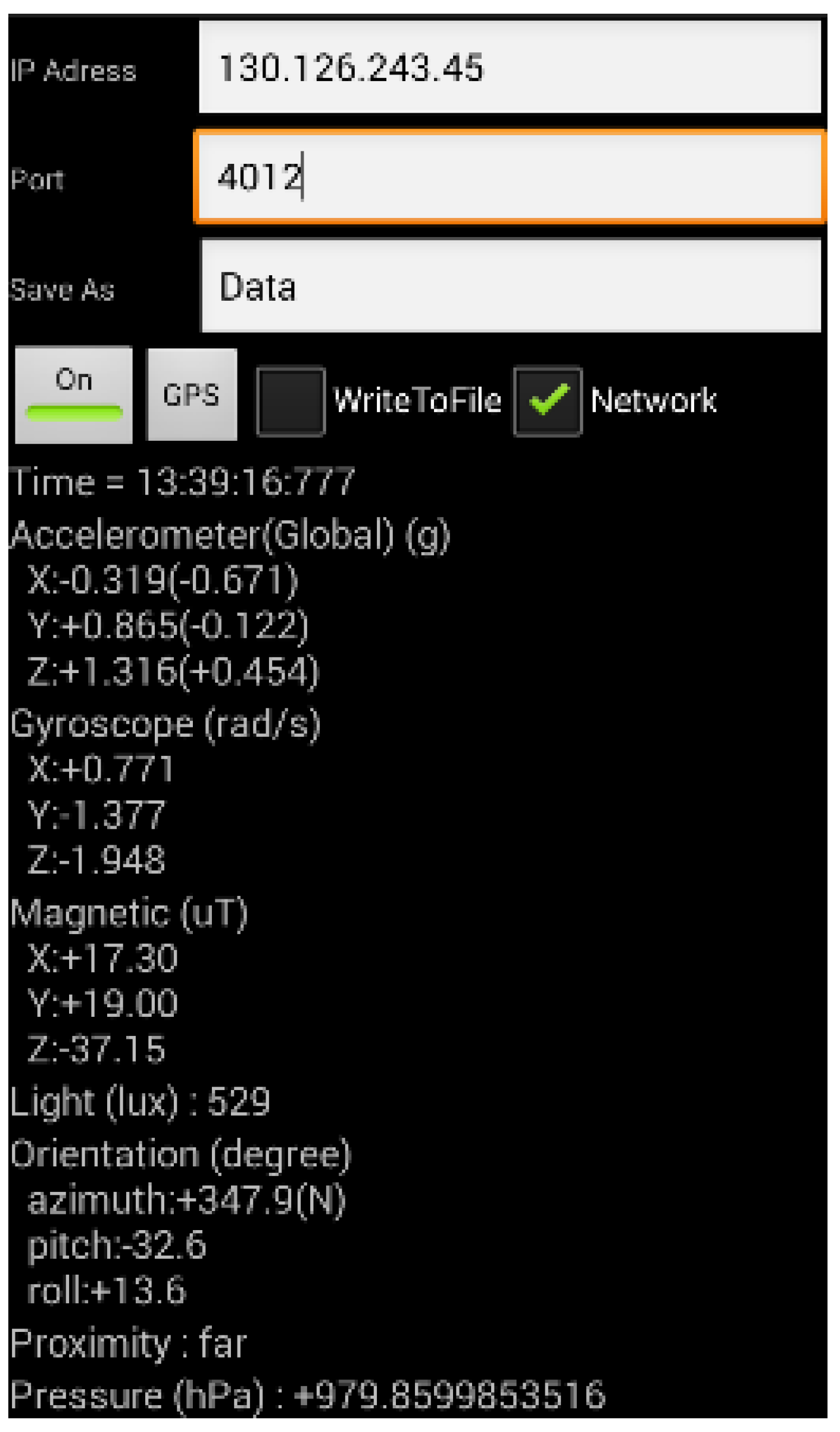
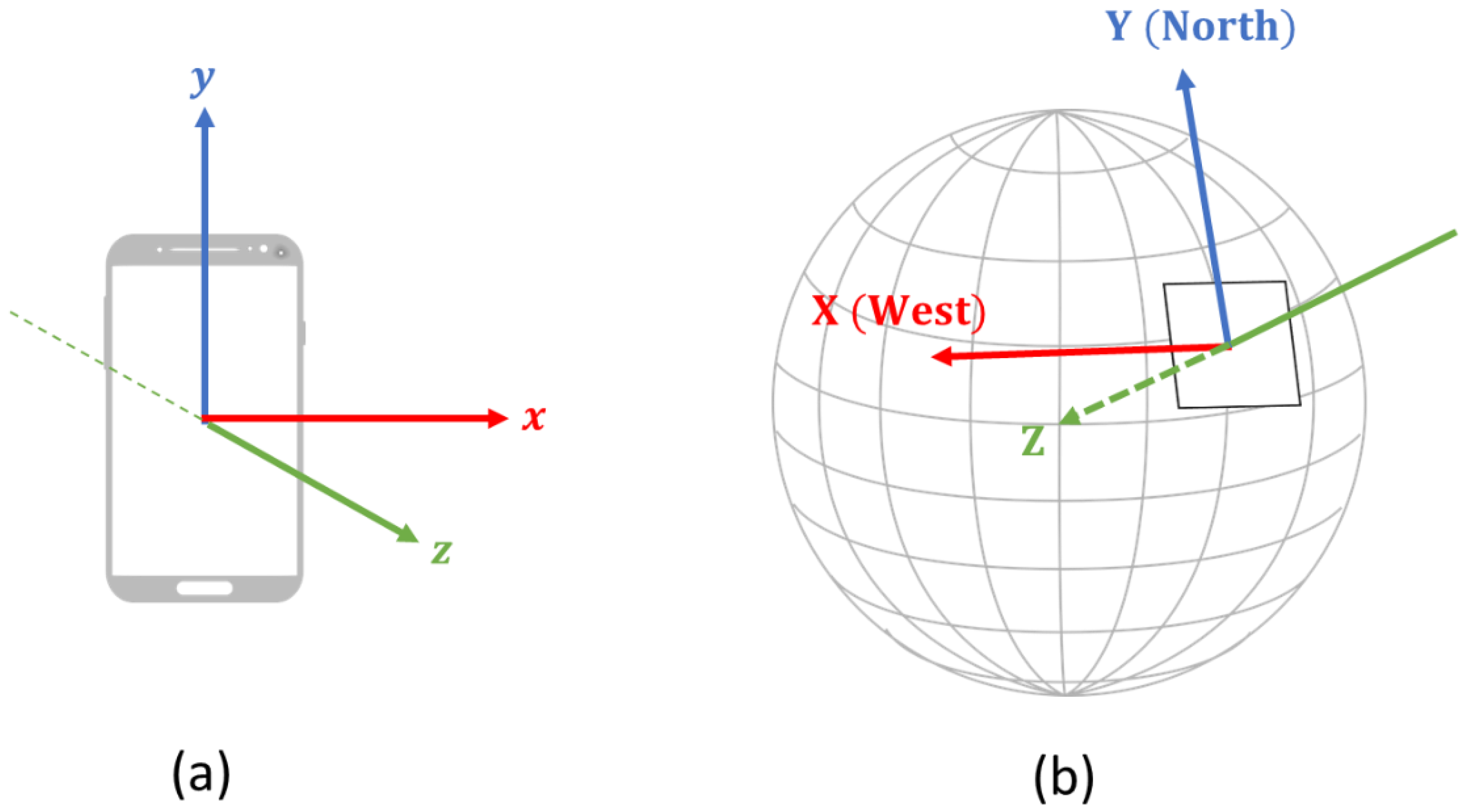
2.2. Data Collection
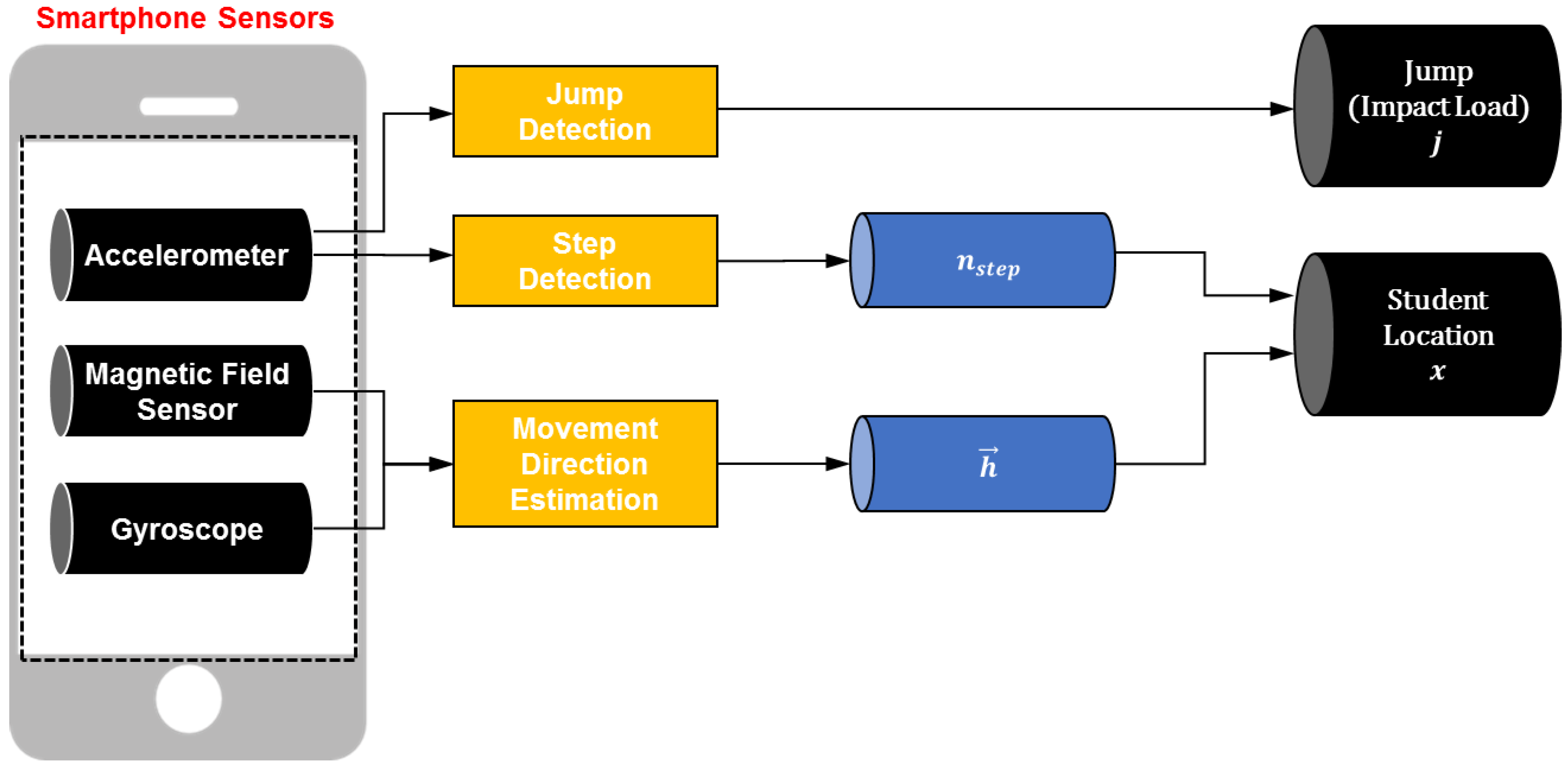
2.3. Motion Sensing
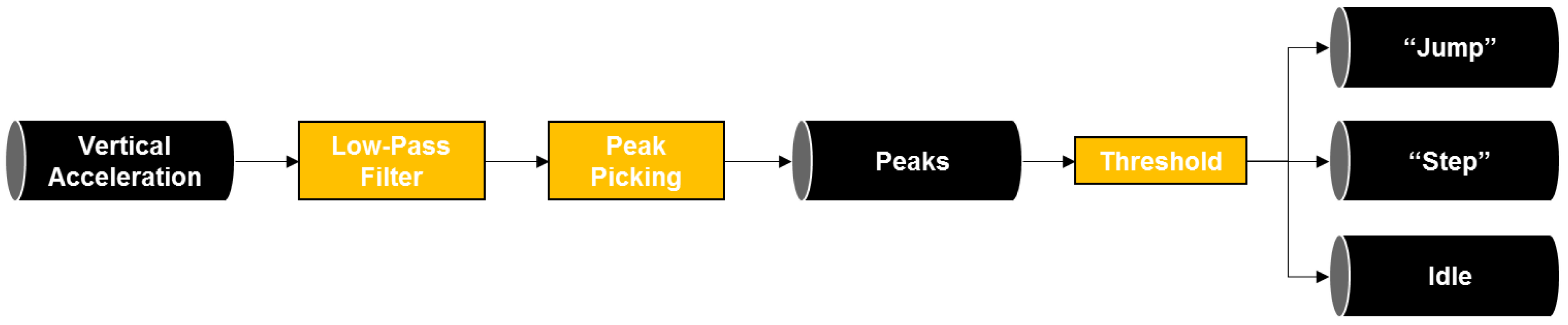
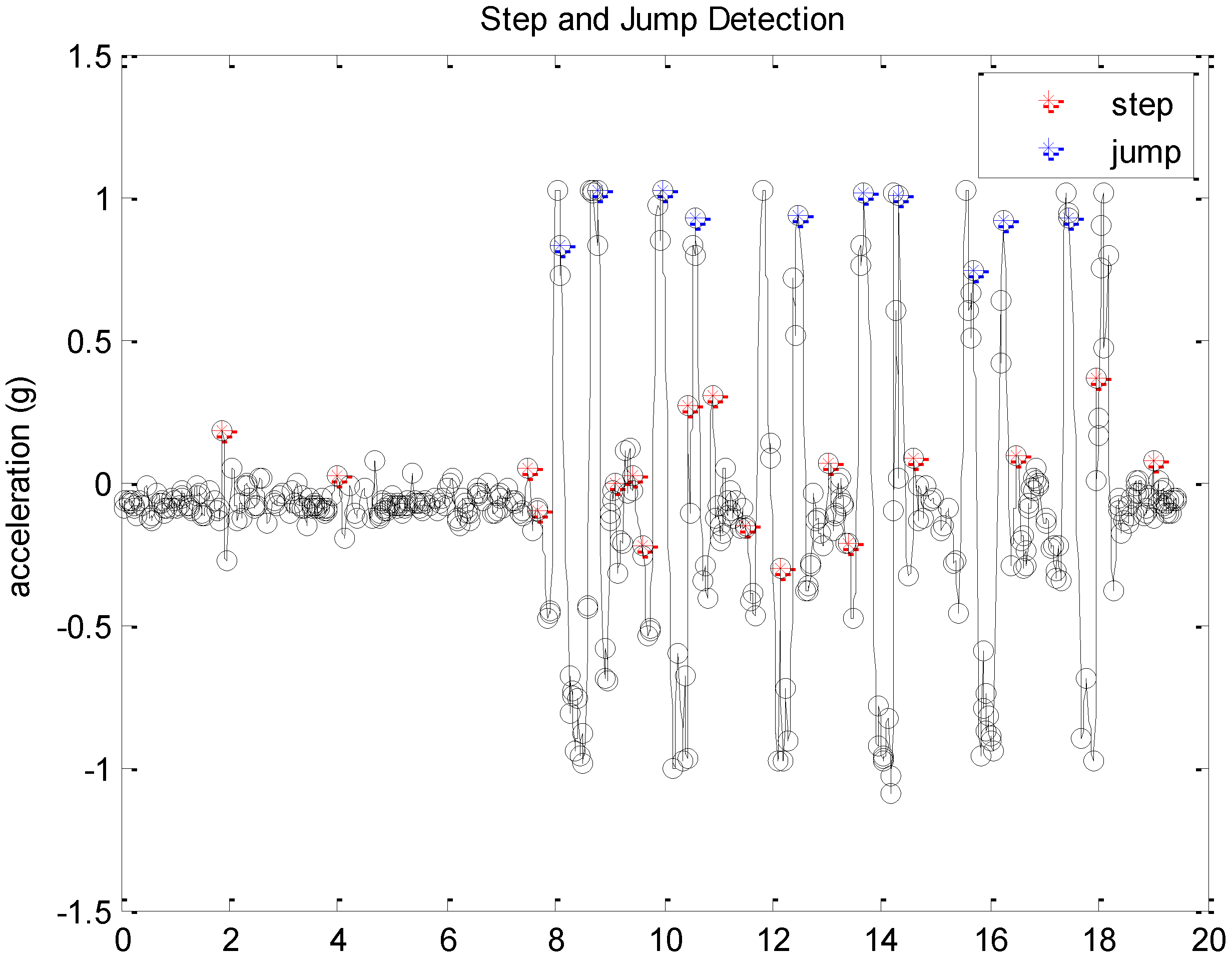
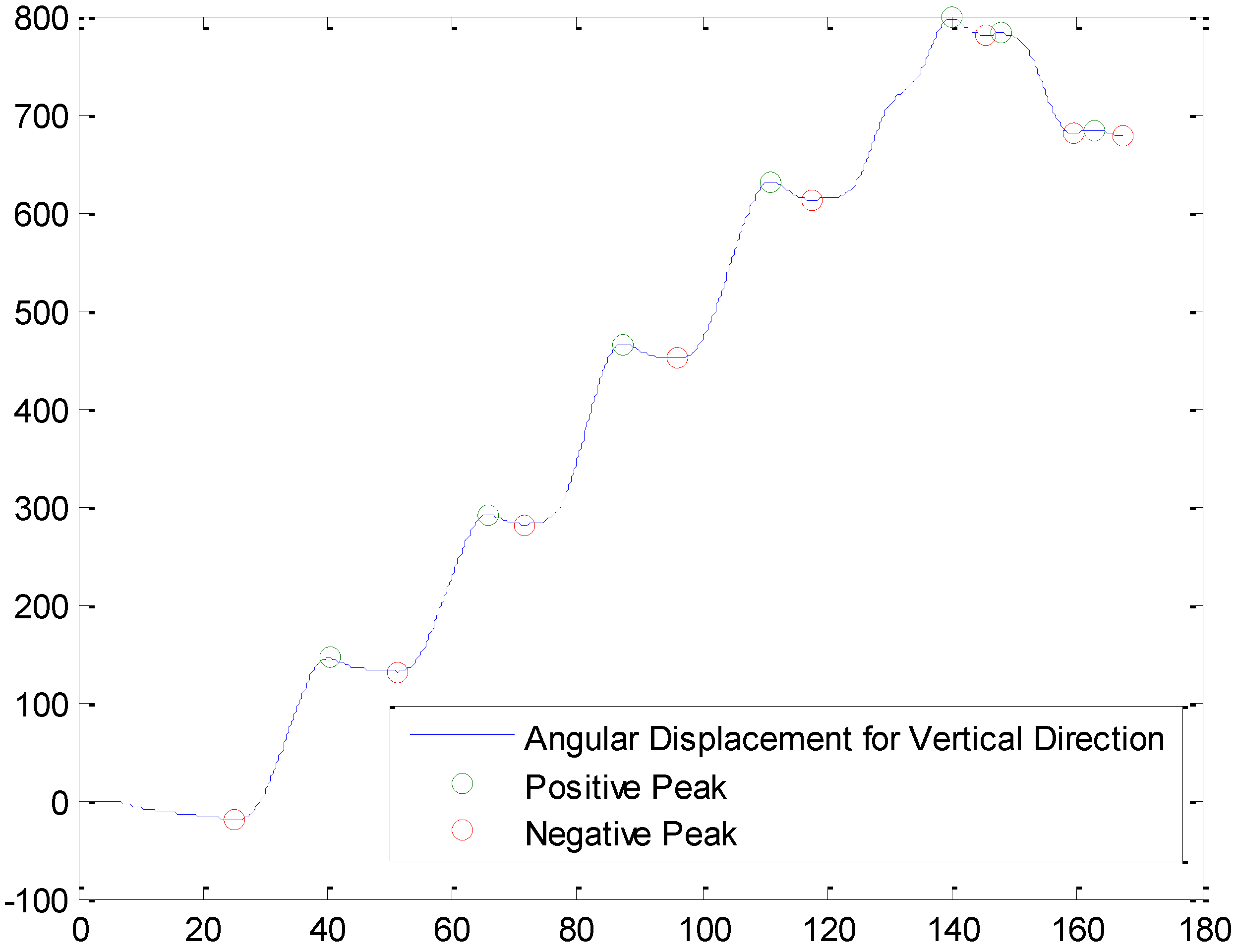
2.3.1. Step & Jump Detection
2.3.2. Movement Direction Estimation
2.4. Structure Dynamics Analysis Based on Motion Sensing
2.4.1. Equation of Motion (EOM)
2.4.2. State Space Representation
2.4.3. Combining with Motion Sensing
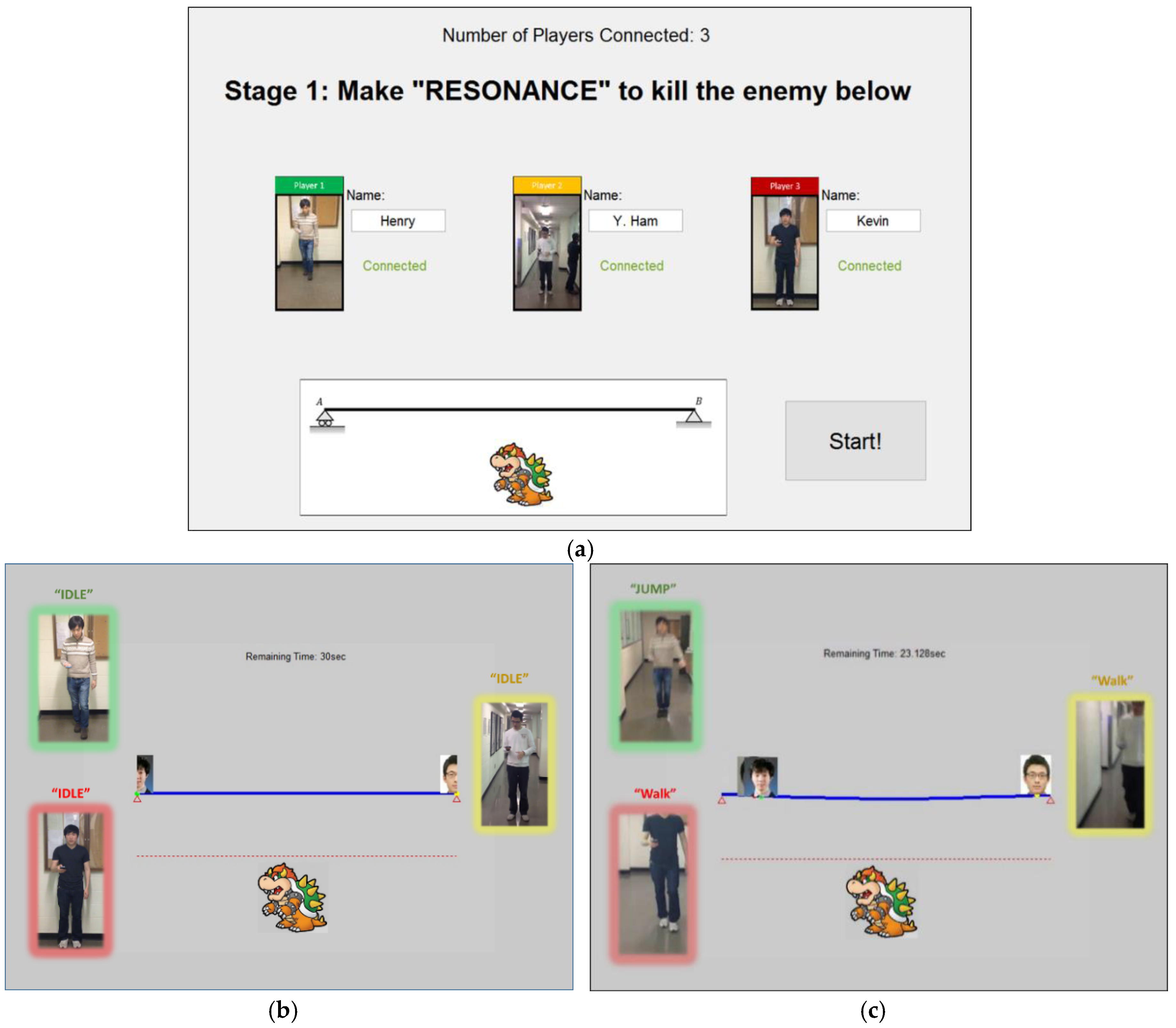
3. Experiments
3.1. Experimental Setup and Results
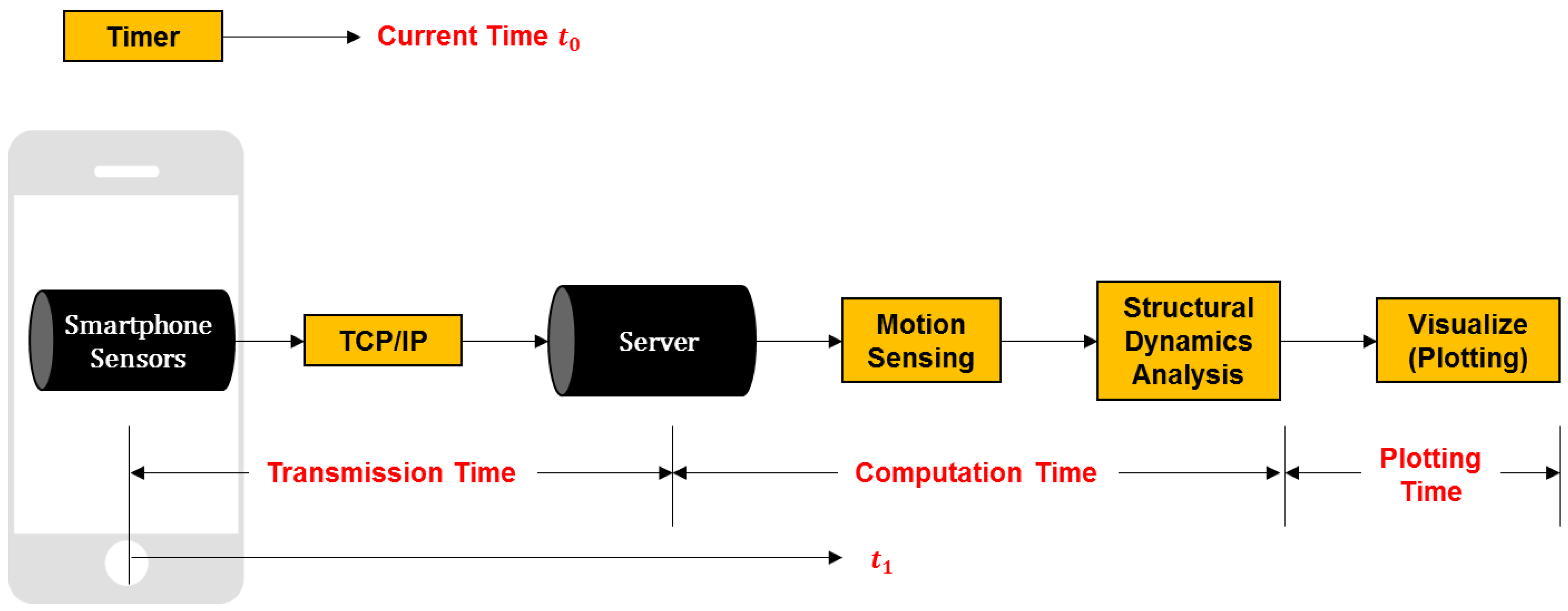
3.2. Time & Data Synchronization
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mann, B.D.; Eidelson, B.M.; Fukuchi, S.G.; Nissman, S.A.; Robertson, S.; Jardines, L. The development of an interactive game-based tool for learning surgical management algorithms via computer. Am. J. Surg. 2002, 183, 305–308. [Google Scholar] [CrossRef]
- Ebner, M.; Walder, U. E-learning in civil engineering-six years of experience at graz university of technology. In Proceedings of the 24th W78 Conference Maribor, Maribor, Slovenia, 26–29 June 2007; pp. 749–754. [Google Scholar]
- Ebner, M.; Holzinger, A. Successful implementation of user-centered game based learning in higher education: An example from civil engineering. Comput. Educ. 2007, 49, 873–890. [Google Scholar] [CrossRef]
- Zechner, J.; Ebner, M. Playing a game in civil engineering—The internal force master for structural analysis. In Proceedings of the 14th International Conference on Interactive Collaborative Learning, Piestany, Slovakia, 21–23 September 2011; pp. 417–422. [Google Scholar]
- Engineering.com. Cargo Bridge. Available online: http://www.engineering.com/GamesPuzzles/CargoBridge.aspx (accessed on 5 May 2017).
- Engineering.com. Bridge Builder. Available online: http://www.engineering.com/GamesPuzzles/BridgeBuilder/tabid/5172/Default.aspx (accessed on 5 May 2017).
- Media, A. Bridge Builder Simulator; Apple App Store: Cupertino, CA, USA, 2017. [Google Scholar]
- Media, A. Bridge Construction Simulator 3D; Apple App Store: Cupertino, CA, USA, 2017. [Google Scholar]
- LLC, J.I. Civil Engineering Calculation; Apple App Store: Cupertino, CA, USA, 2017. [Google Scholar]
- Freeman, S.; Eddy, S.L.; McDonough, M.; Smith, M.K.; Okoroafor, N.; Jordt, H.; Wenderoth, M.P. Active learning increases student performance in science, engineering, and mathematics. Proc. Natl. Acad. Sci. USA 2014, 111, 8410–8415. [Google Scholar] [CrossRef] [PubMed]
- ASCE. The Vision for Civil Engineering in 2025; American Society of Civil Engineers: Leston, VA, USA, 2007. [Google Scholar]
- Bressler, D.; Bodzin, A. A mixed methods assessment of students’flow experiences during a mobile augmented reality science game. J. Comput. Assist. Learn. 2013, 29, 505–517. [Google Scholar] [CrossRef]
- Kamarainen, A.M.; Metcalf, S.; Grotzer, T.; Browne, A.; Mazzuca, D.; Tutwiler, M.S.; Dede, C. EcoMOBILE: Integrating augmented reality and probeware with environmental education field trips. Comput. Educ. 2013, 68, 545–556. [Google Scholar] [CrossRef]
- Klopfer, E.; Squire, K. Environmental Detectives—The development of an augmented reality platform for environmental simulations. Educ. Technol. Res. Dev. 2008, 56, 203–228. [Google Scholar] [CrossRef]
- Vassigh, S.; Newman, W.; Mostafavi, A.; Behzadan, A. Hybrid Technologies for Interdisciplinary Education. J. Civil Environ. Eng. 2015, 5, 201. [Google Scholar] [CrossRef]
- Holzinger, A.; Ebner, M. Interaction and Usability of Simulations and Animations: A Case Study of the Flash Technology. In Proceedings of the Interact, Zurich, Switzerland, 1–5 September 2003; pp. 777–780. [Google Scholar]
- Kettanurak, V.N.; Ramamurthy, K.; Haseman, W.D. User attitude as a mediator of learning performance improvement in an interactive multimedia environment: An empirical investigation of the degree of interactivity and learning styles. Int. J. Hum. Comput. Stud. 2001, 54, 541–583. [Google Scholar] [CrossRef]
- De Jong, T.; Linn, M.C.; Zacharia, Z.C. Physical and virtual laboratories in science and engineering education. Science 2013, 340(6130), 305–308. [Google Scholar] [CrossRef] [PubMed]
- Kontra, C.; Lyons, D.J.; Fischer, S.M.; Beilock, S.L. Physical experience enhances science learning. Psychol. Sci. 2015, 26(6), 737–749. [Google Scholar] [CrossRef] [PubMed]
- Yoon, H.; Ham, Y.; Golparvar-Fard, M.; Spencer, B.F. Forward-Backward Approach for 3D Event Localization Using Commodity Smartphones for Ubiquitous Context-Aware Applications in Civil and Infrastructure Engineering. Comput. Aided Civil Infrastruct. Eng. 2016, 31, 245–260. [Google Scholar] [CrossRef]
- Yoon, H.; Shiftehfar, R.; Cho, S.; Spencer, B.F., Jr.; Nelson, M.E.; Agha, G. Victim localization and assessment system for emergency responders. J. Comput. Civil Eng. 2015, 30, 04015011. [Google Scholar] [CrossRef]

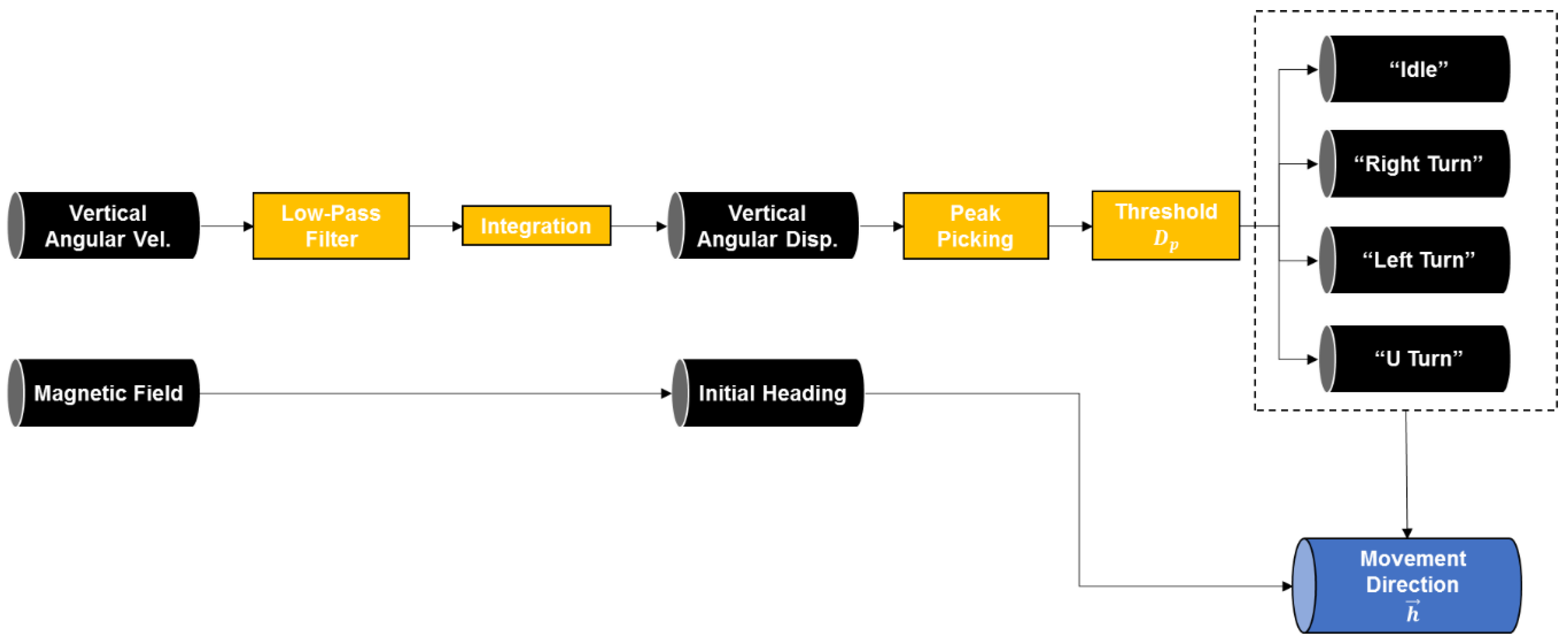



| Range of Dp | |
|---|---|
| −135 < Dp < −45 | Right Turn |
| −45 < Dp < 45 | Idle |
| 45 < Dp < 135 | Left Turn |
| 135 < Dp or −135 > Dp | U Turn |
| Case | Transmission Time (ms) | Computation Time (ms) | Plotting Time (ms) | Overall (ms) |
|---|---|---|---|---|
| 1 | 9 | 122 | 269 | 400 |
| 2 | 10 | 109 | 147 | 266 |
| 3 | 20 | 121 | 151 | 292 |
| 4 | 13 | 120 | 155 | 288 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, H.; Han, K.; Ham, Y. A Framework of Human-Motion Based Structural Dynamics Simulation Using Mobile Devices. Sensors 2019, 19, 3258. https://doi.org/10.3390/s19153258
Yoon H, Han K, Ham Y. A Framework of Human-Motion Based Structural Dynamics Simulation Using Mobile Devices. Sensors. 2019; 19(15):3258. https://doi.org/10.3390/s19153258
Chicago/Turabian StyleYoon, Hyungchul, Kevin Han, and Youngjib Ham. 2019. "A Framework of Human-Motion Based Structural Dynamics Simulation Using Mobile Devices" Sensors 19, no. 15: 3258. https://doi.org/10.3390/s19153258
APA StyleYoon, H., Han, K., & Ham, Y. (2019). A Framework of Human-Motion Based Structural Dynamics Simulation Using Mobile Devices. Sensors, 19(15), 3258. https://doi.org/10.3390/s19153258







