Orthogonal Demodulation Pound–Drever–Hall Technique for Ultra-Low Detection Limit Pressure Sensing
Abstract
:1. Introduction
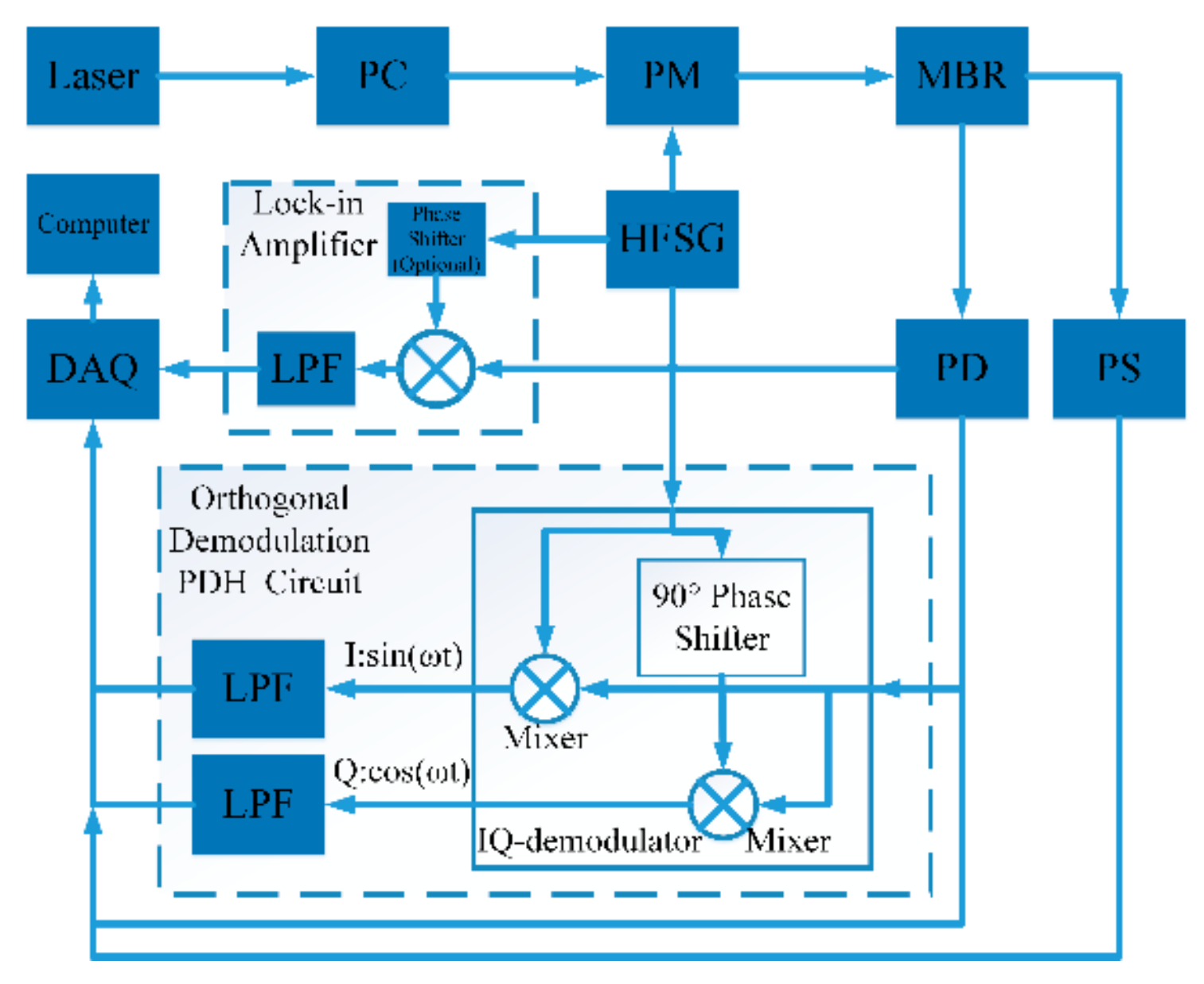
2. Experimental Setup and Principle
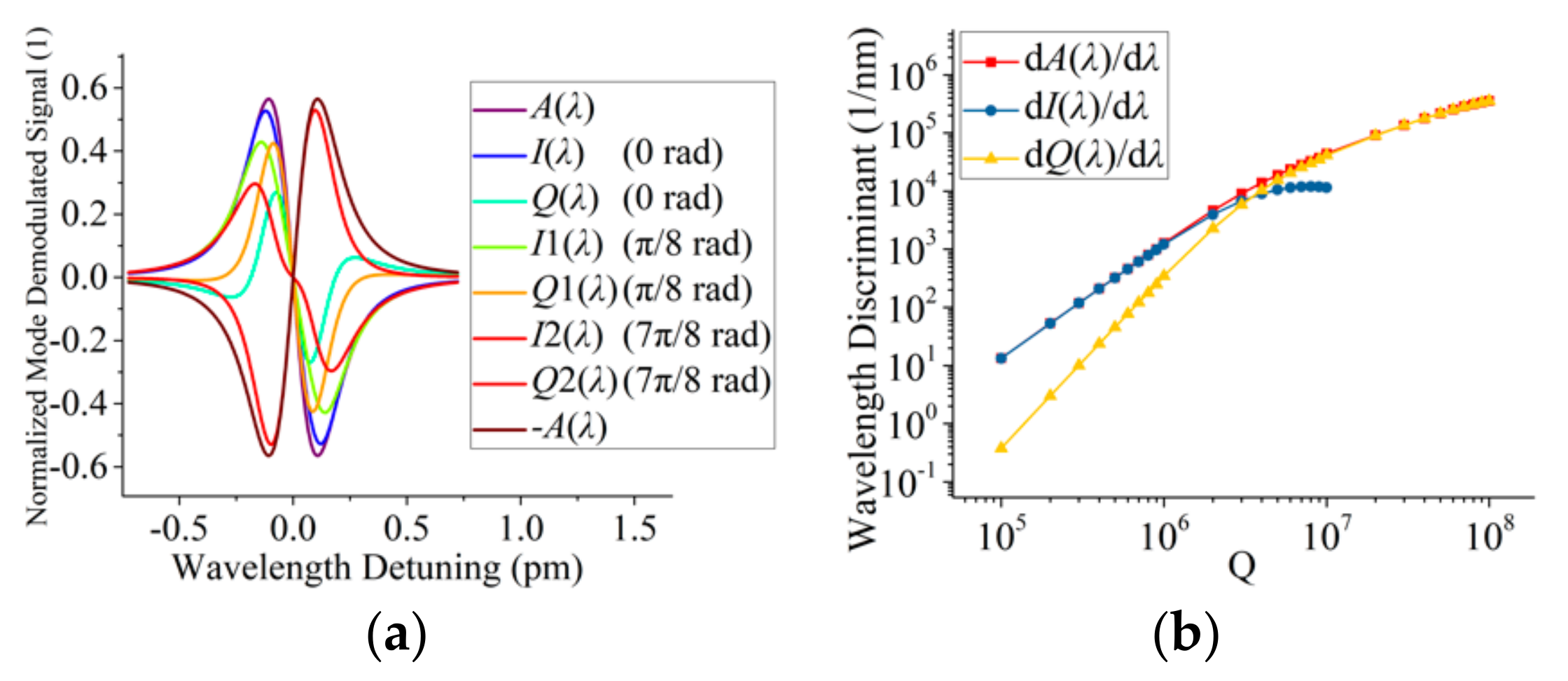
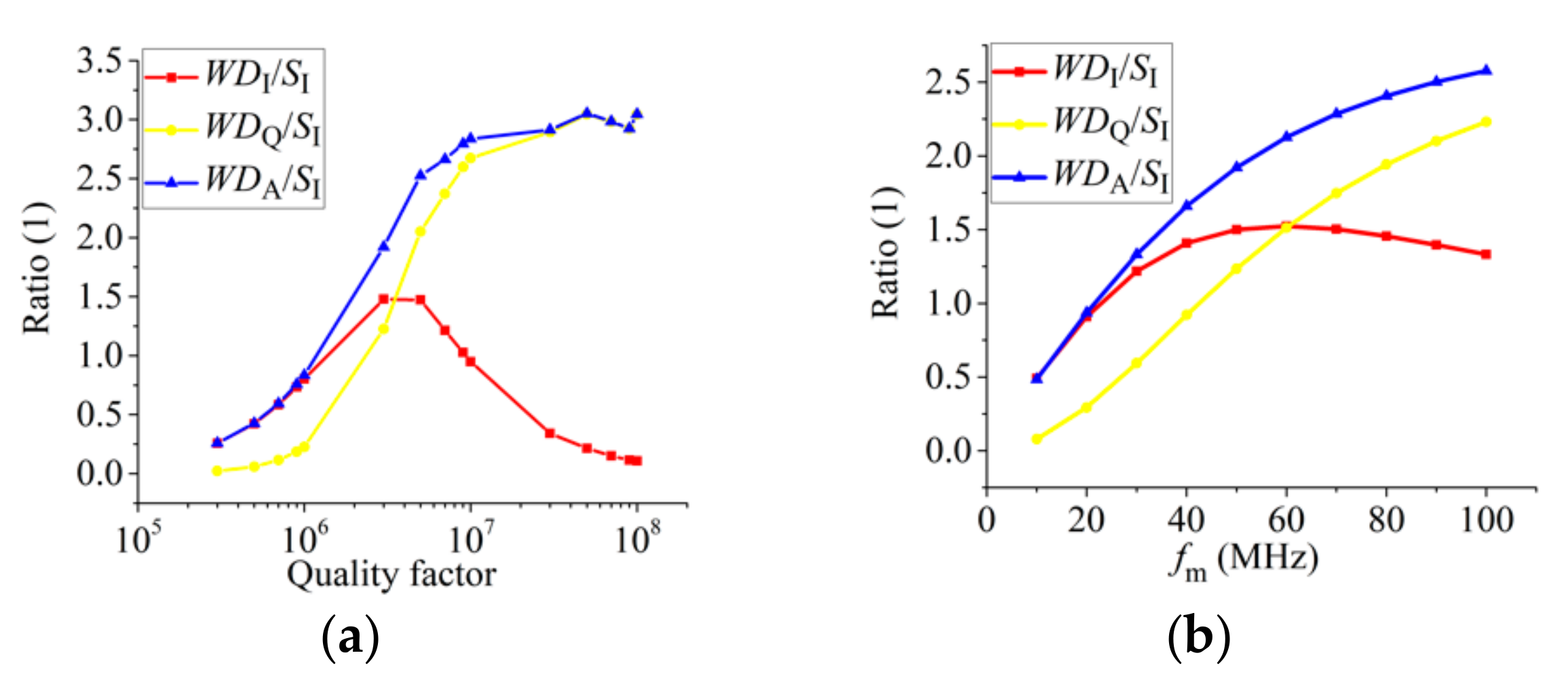
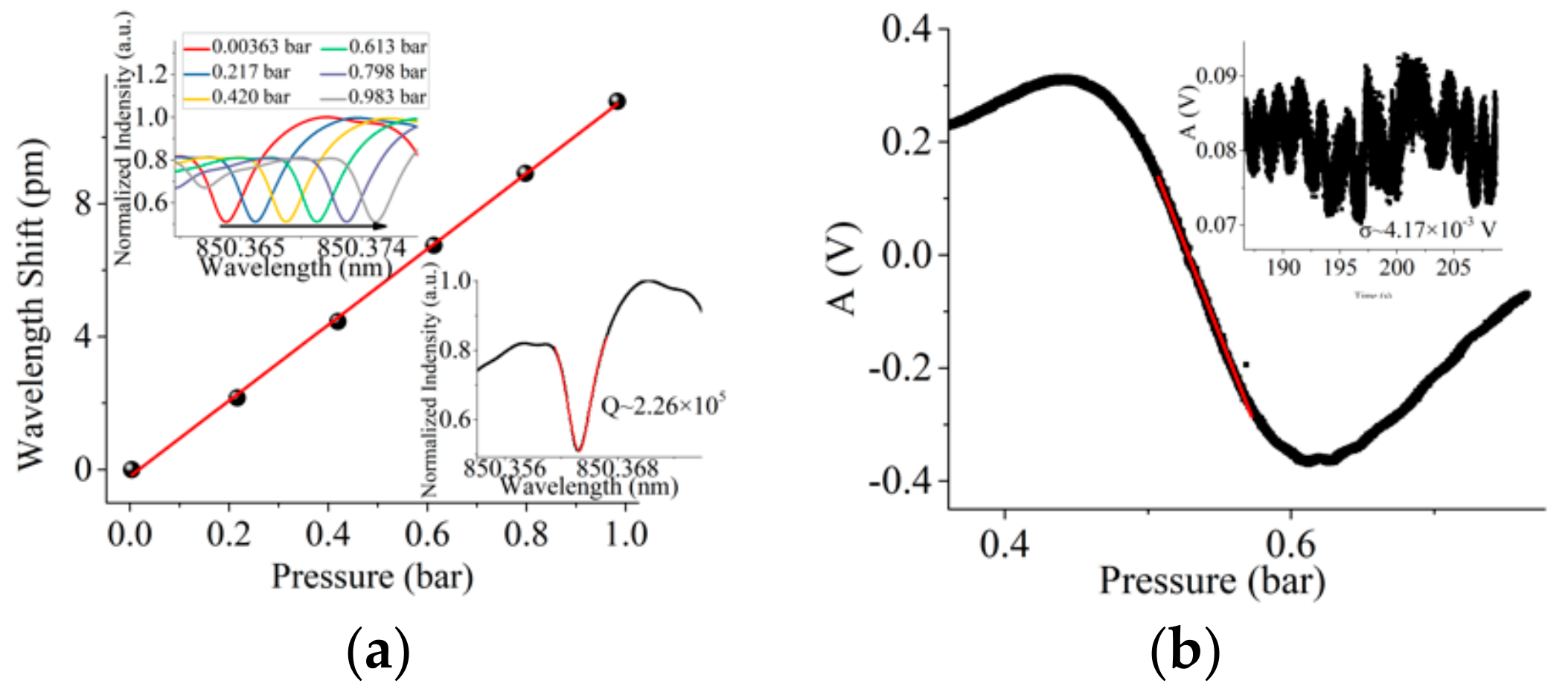
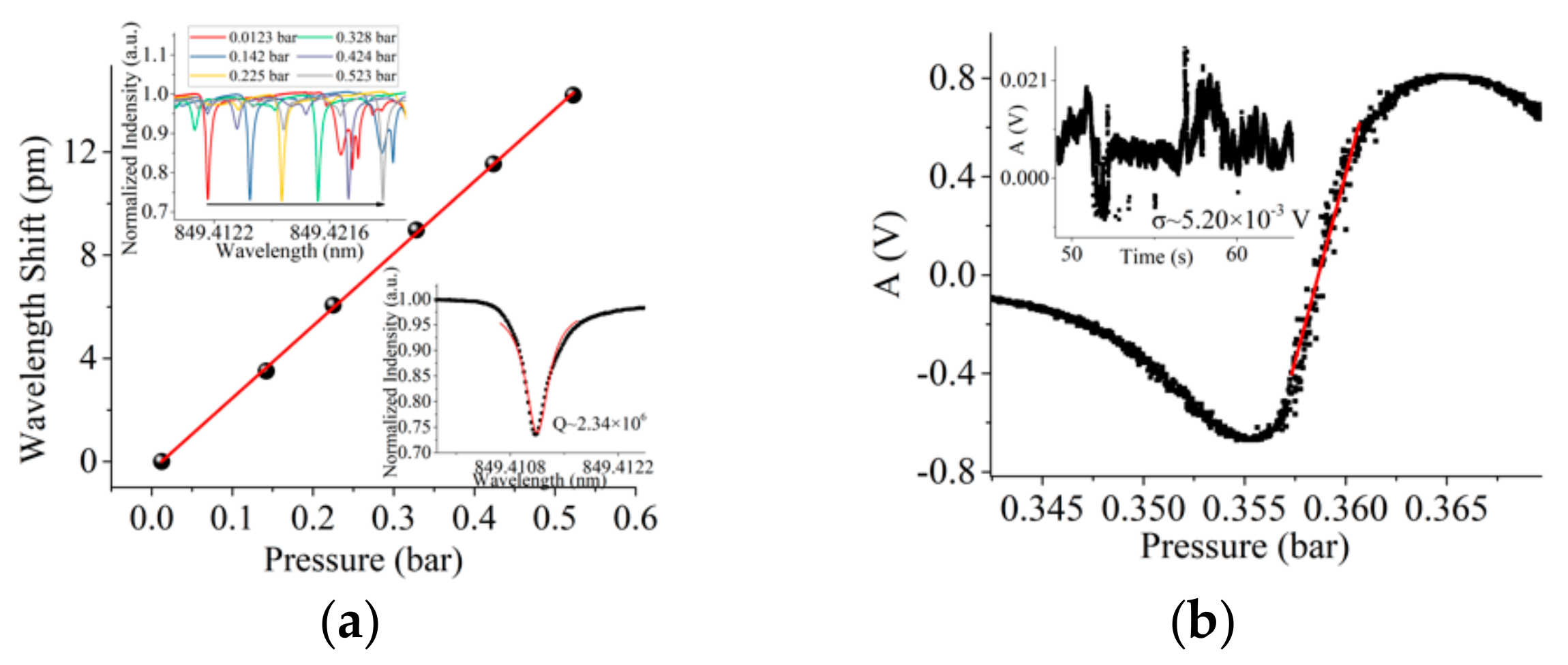
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Drever, R.; Hall, J.L.; Kowalski, F.; Hough, J.; Ford, G.; Munley, A.; Ward, H. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 1983, 31, 97–105. [Google Scholar] [CrossRef]
- Black, E.D. An introduction to Pound-Drever-Hall laser frequency stabilization. Am. J. Phys 2001, 69, 79–87. [Google Scholar] [CrossRef]
- Sanders, G.A.; Prentiss, M.; Ezekiel, S. Passive ring resonator method for sensitive inertial rotation measurements in geophysics and relativity. Opt. Lett. 1981, 6, 569–571. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, J.J.; Ma, H.L.; Jin, Z.H. High-frequency Pound-Drever-Hall sensing of a short and high-finesse fiber ring resonator. In Proceedings of the 15th International Conference on Optical Communications and Networks (ICOCN), Hangzhou, China, 24–27 September 2016. [Google Scholar]
- Barnes, J.; Li, S.J.; Goyal, A.; Abolmaesumi, P.; Mousavi, P.; Loock, H.-P. Broadband Vibration Detection in Tissue Phantoms Using a Fiber Fabry--Perot Cavity. IEEE Trans. Biomed. Eng. 2018, 65, 921–927. [Google Scholar] [CrossRef]
- Huang, W.Z.; Feng, S.W.; Zhang, W.T.; Li, F. DFB fiber laser static strain sensor based on beat frequency interrogation with a reference fiber laser locked to a FBG resonator. Opt. Express 2016, 24, 12321–12329. [Google Scholar] [CrossRef]
- Zhao, S.X.; Liu, Q.W.; Chen, J.G.; He, Z.Y. pε-Resolution Fiber Grating Sensor With Adjustable Measurement Range and Ultralow Probe Power. IEEE Photonics Technol. Lett. 2019, 31, 19–22. [Google Scholar] [CrossRef]
- Gatti, D.; Galzerano, G.; Janner, D.; Longhi, S.; Laporta, P. Fiber strain sensor based on a pi-phase-shifted Bragg grating and the Pound-Drever-Hall technique. Opt. Express 2008, 16, 1945–1950. [Google Scholar] [CrossRef]
- Chow, J.H.; Littler, I.C.; De Vine, G.; McClelland, D.E.; Gray, M.B. Phase-sensitive interrogation of fiber Bragg grating resonators for sensing applications. J. Lightwave Technol. 2005, 23, 1881. [Google Scholar] [CrossRef]
- An, P.L.; Zheng, Y.Q.; Yan, S.B.; Xue, C.Y.; Wang, W.J.; Liu, J. High-Q microsphere resonators for angular velocity sensing in gyroscopes. Appl. Phys. Lett. 2015, 106, 063504. [Google Scholar] [CrossRef]
- Swaim, J.D.; Knittel, J.; Bowen, W.P. Detection of nanoparticles with a frequency locked whispering gallery mode microresonator. Appl. Phys. Lett. 2013, 102, 183106. [Google Scholar] [CrossRef] [Green Version]
- Knittel, J.; Chow, J.H.; Gray, M.B.; Taylor, M.A.; Bowen, W.P. Ultrasensitive real-time measurement of dissipation and dispersion in a whispering-gallery mode microresonator. Opt. Lett. 2013, 38, 1915–1917. [Google Scholar] [CrossRef] [PubMed]
- Madugani, R.; Yang, Y.; Le, V.H.; Ward, J.M.; Chormaic, S.N. Linear laser tuning using a pressure-sensitive microbubble resonator. IEEE Photonics. Technol. Lett. 2016, 28, 1134–1137. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Vollmer, F.; Arnold, S. Whispering-gallery-mode biosensing: label-free detection down to single molecules. Nat. Methods 2008, 5, 591–596. [Google Scholar] [CrossRef] [PubMed]
- Armani, A.M.; Kulkarni, R.P.; Fraser, S.E.; Flagan, R.C.; Vahala, K.J. Label-free, single-molecule detection with optical microcavities. Science 2007, 317, 783–787. [Google Scholar] [CrossRef] [PubMed]
- He, L.N.; Özdemir, Ş.K.; Zhu, J.G.; Kim, W.; Yang, L. Detecting single viruses and nanoparticles using whispering gallery microlasers. Nat. Nanotechnol. 2011, 6, 428–432. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.W.; Liu, L.Y.; Xu, L. Ultralow sensing limit in optofluidic micro-bottle resonator biosensor by self-referenced differential-mode detection scheme. Appl. Phys. Lett. 2014, 104, 033703. [Google Scholar] [CrossRef]
- Li, M.; Wu, X.; Liu, L.Y.; Fan, X.D.; Xu, L. Self-referencing optofluidic ring resonator sensor for highly sensitive biomolecular detection. Anal. Chem. 2013, 85, 9328–9332. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Vahala, K.J. Cavity opto-mechanics. Opt. Express 2007, 15, 17172–17205. [Google Scholar] [CrossRef]
- Li, M.; Wu, X.; Liu, L.Y.; Xu, L. Kerr parametric oscillations and frequency comb generation from dispersion compensated silica micro-bubble resonators. Opt. Express 2013, 21, 16908–16913. [Google Scholar] [CrossRef]
- Lee, W.; Sun, Y.Z.; Li, H.; Reddy, K.; Sumetsky, M.; Fan, X.D. A quasi-droplet optofluidic ring resonator laser using a micro-bubble. Appl. Phys. Lett. 2011, 99, 091102. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.F.; Wang, T.; Qiang, L.; Ye, T.; Zhang, Z.Y.; Qiu, M.; Su, Y.K. Compact optical temporal differentiator based on silicon microring resonator. Opt. Express 2008, 16, 15880–15886. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, W.L.; Li, M.; Guzzon, R.S.; Norberg, E.J.; Parker, J.S.; Lu, M.Z.; Coldren, L.A.; Yao, J.P. A fully reconfigurable photonic integrated signal processor. Nat. Photonics 2016, 10, 190–195. [Google Scholar] [CrossRef]
- Liao, J.; Wu, X.; Liu, L.Y.; Xu, L. Fano resonance and improved sensing performance in a spectral-simplified optofluidic micro-bubble resonator by introducing selective modal losses. Opt. Express 2016, 24, 8574–8580. [Google Scholar] [CrossRef] [PubMed]
- Ioppolo, T.; Ötügen, M.V. Pressure tuning of whispering gallery mode resonators. J. Opt. Soc. Am. B 2007, 24, 2721–2726. [Google Scholar] [CrossRef] [Green Version]
- Martin, L.L.; León-Luis, S.; Pérez-Rodríguez, C.; Martín, I.; Rodríguez-Mendoza, U.; Lavín, V. High pressure tuning of whispering gallery mode resonances in a neodymium-doped glass microsphere. J. Opt. Soc. Am. B 2013, 30, 3254–3259. [Google Scholar] [CrossRef] [Green Version]
- Henze, R.; Seifert, T.; Ward, J.; Benson, O. Tuning whispering gallery modes using internal aerostatic pressure. Opt. Lett. 2011, 36, 4536–4538. [Google Scholar] [CrossRef]
- Yang, Y.; Saurabh, S.; Ward, J.M.; Chormaic, S.N. High-Q, ultrathin-walled microbubble resonator for aerostatic pressure sensing. Opt. Express 2016, 24, 294–299. [Google Scholar] [CrossRef] [Green Version]
- Yang, L. Fabrication and characterization of microlasers by the sol-gel method. PhD Thesis, California Institute of Technology, Pasadena, CA, USA, May 2005. [Google Scholar]
- Yang, Y.; Saurabh, S.; Ward, J.; Chormaic, S.N. Coupled-mode-induced transparency in aerostatically tuned microbubble whispering-gallery resonators. Opt. Lett. 2015, 40, 1834–1837. [Google Scholar] [CrossRef] [Green Version]
- Lu, Q.J.; Liao, J.; Liu, S.; Wu, X.; Liu, L.Y.; Xu, L. Precise measurement of micro bubble resonator thickness by internal aerostatic pressure sensing. Opt. Express 2016, 24, 20855–20861. [Google Scholar] [CrossRef]
- Murugan, G.S.; Petrovich, M.N.; Jung, Y.; Wilkinson, J.S.; Zervas, M.N. Hollow-bottle optical microresonators. Opt. Express 2011, 19, 20773–20784. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Guo, Y.B.; Sun, Y.Z.; Reddy, K.; Fan, X.D. Analysis of single nanoparticle detection by using 3-dimensionally confined optofluidic ring resonators. Opt. Express 2010, 18, 25081–25088. [Google Scholar] [CrossRef] [PubMed]
- Foreman, M.R.; Swaim, J.D.; Vollmer, F. Whispering gallery mode sensors. Adv. Opt. Photonics 2015, 7, 168–240. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Liu, S.; Wu, X.; Liu, L.; Xu, L. Orthogonal Demodulation Pound–Drever–Hall Technique for Ultra-Low Detection Limit Pressure Sensing. Sensors 2019, 19, 3223. https://doi.org/10.3390/s19143223
Hu J, Liu S, Wu X, Liu L, Xu L. Orthogonal Demodulation Pound–Drever–Hall Technique for Ultra-Low Detection Limit Pressure Sensing. Sensors. 2019; 19(14):3223. https://doi.org/10.3390/s19143223
Chicago/Turabian StyleHu, Jinliang, Sheng Liu, Xiang Wu, Liying Liu, and Lei Xu. 2019. "Orthogonal Demodulation Pound–Drever–Hall Technique for Ultra-Low Detection Limit Pressure Sensing" Sensors 19, no. 14: 3223. https://doi.org/10.3390/s19143223
APA StyleHu, J., Liu, S., Wu, X., Liu, L., & Xu, L. (2019). Orthogonal Demodulation Pound–Drever–Hall Technique for Ultra-Low Detection Limit Pressure Sensing. Sensors, 19(14), 3223. https://doi.org/10.3390/s19143223




