Moving Object Detection Based on Optical Flow Estimation and a Gaussian Mixture Model for Advanced Driver Assistance Systems
Abstract
1. Introduction
2. Related Work
2.1. Brox Optical Flow Estimation
2.2. Gaussian Mixture Model
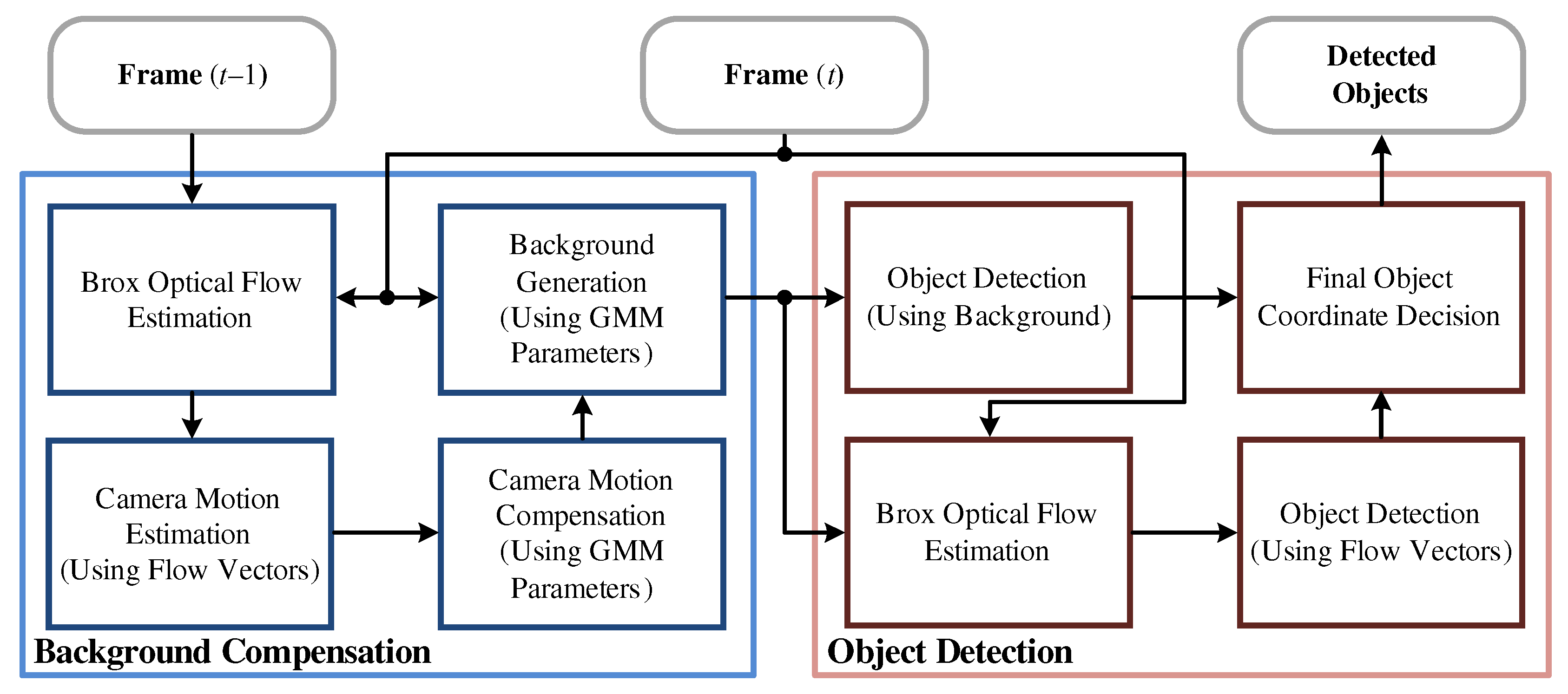
3. Proposed Moving Object Detection Algorithm
3.1. Background Compensation
3.2. Object Detection
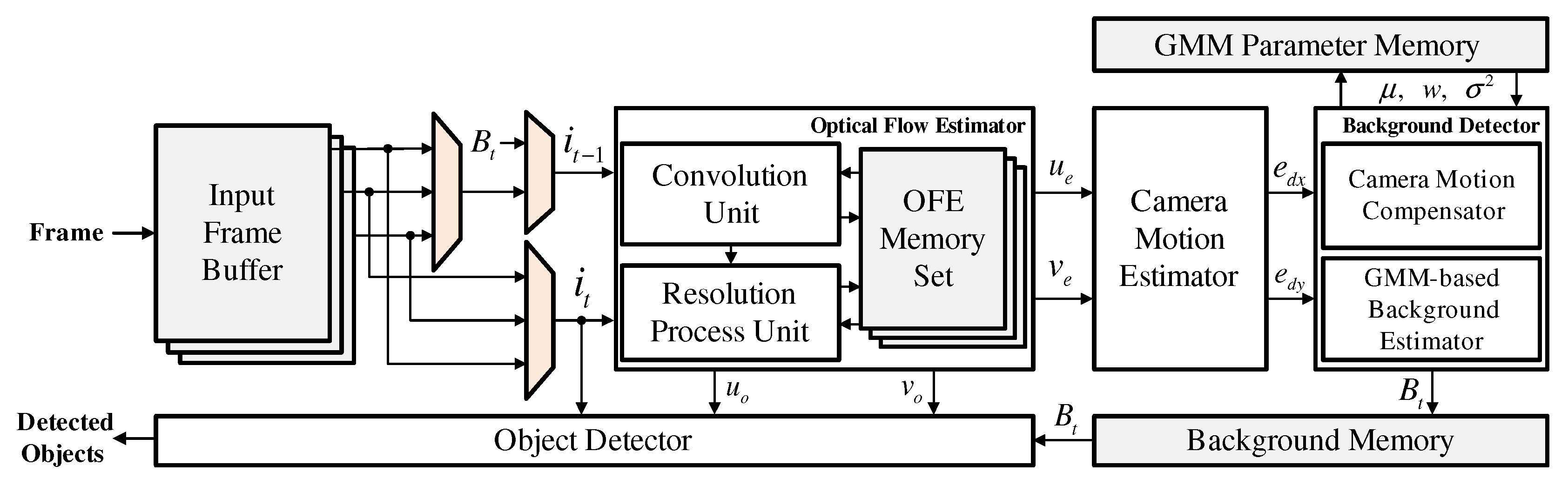
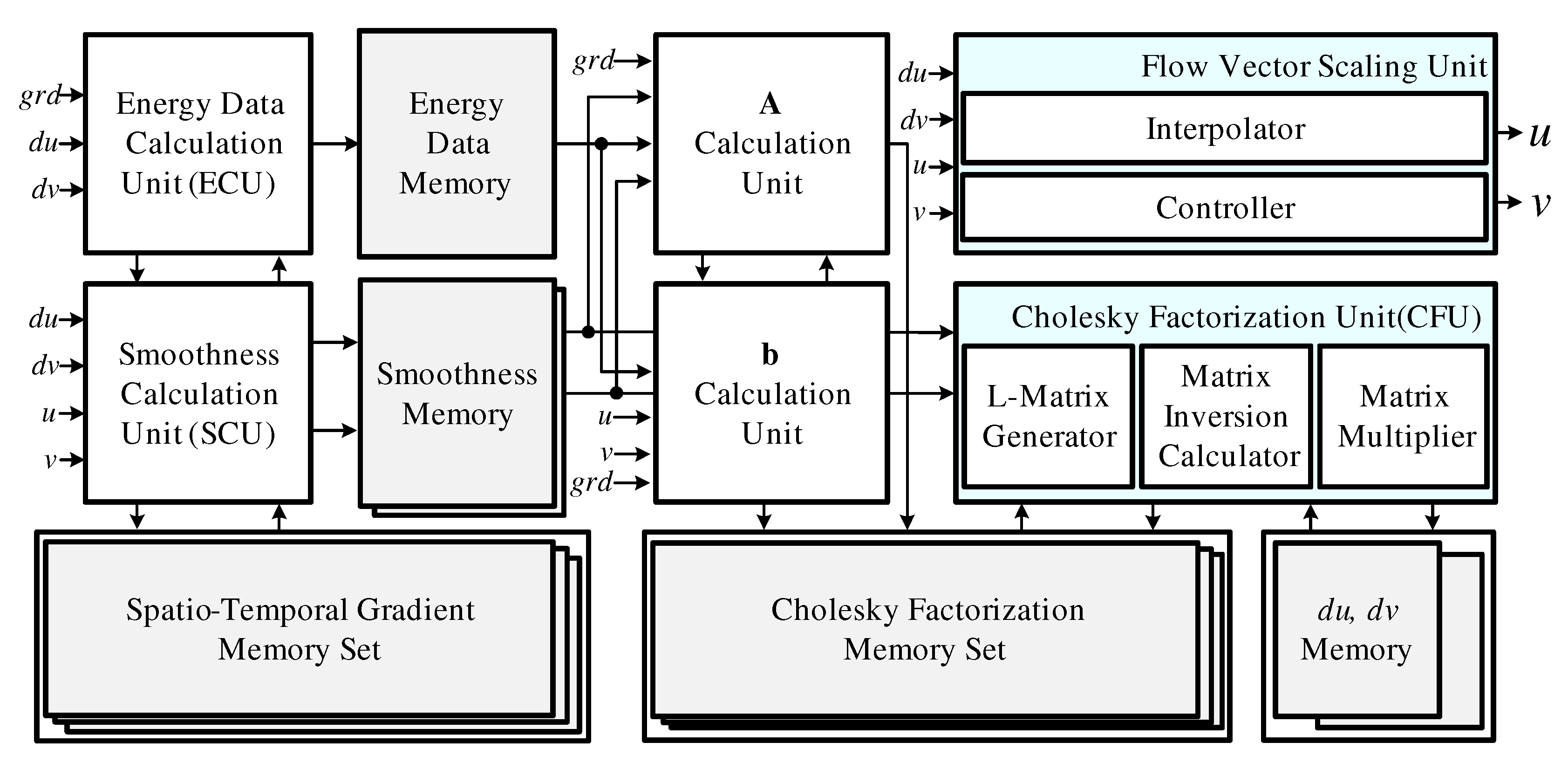
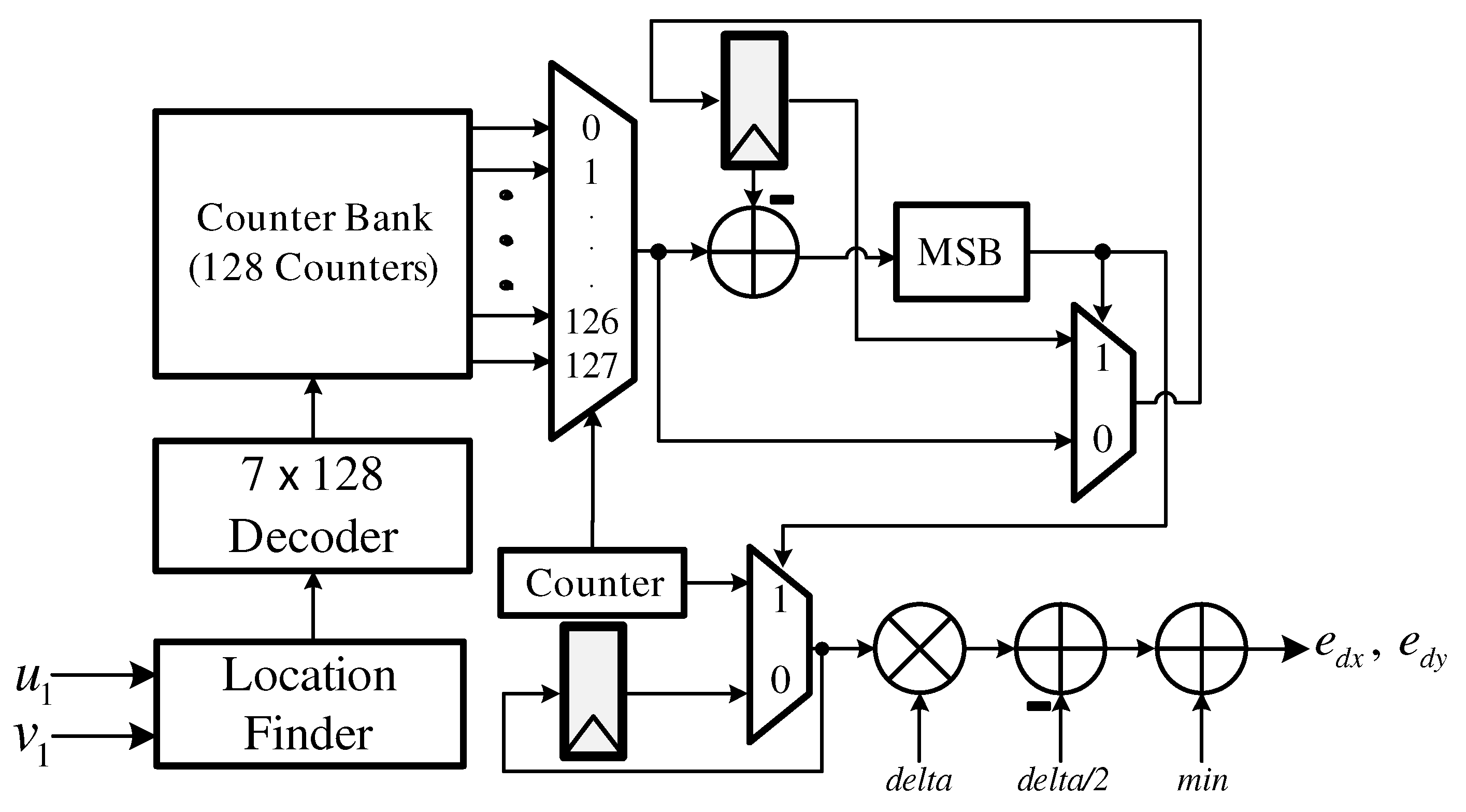
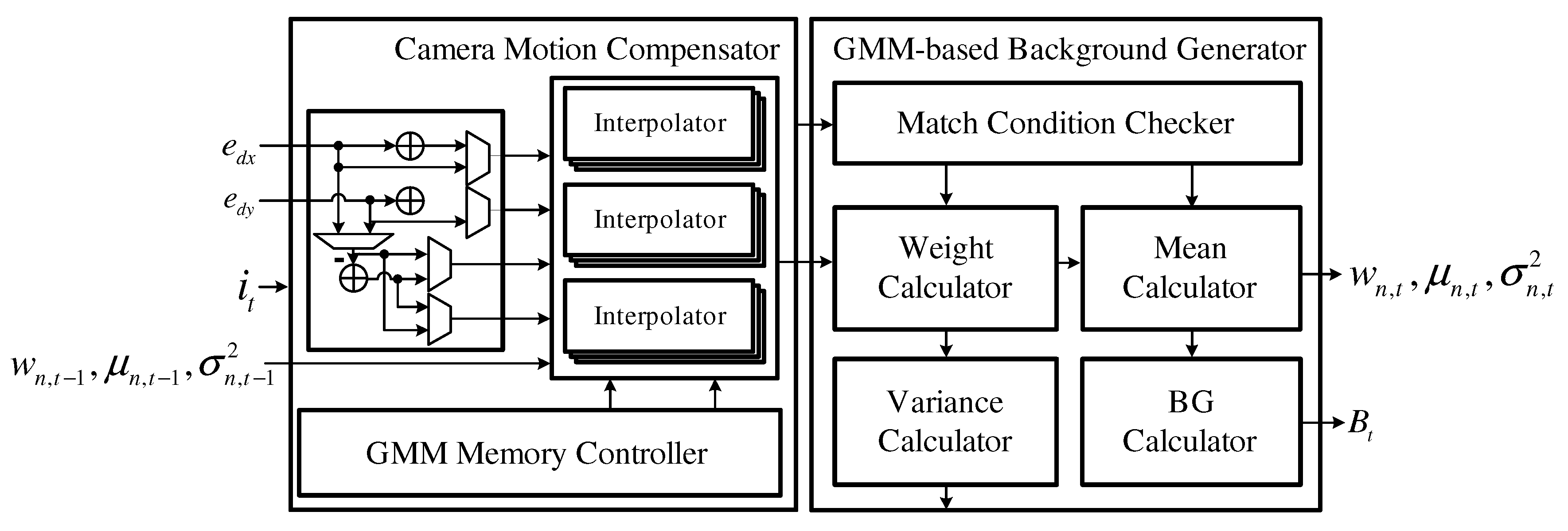
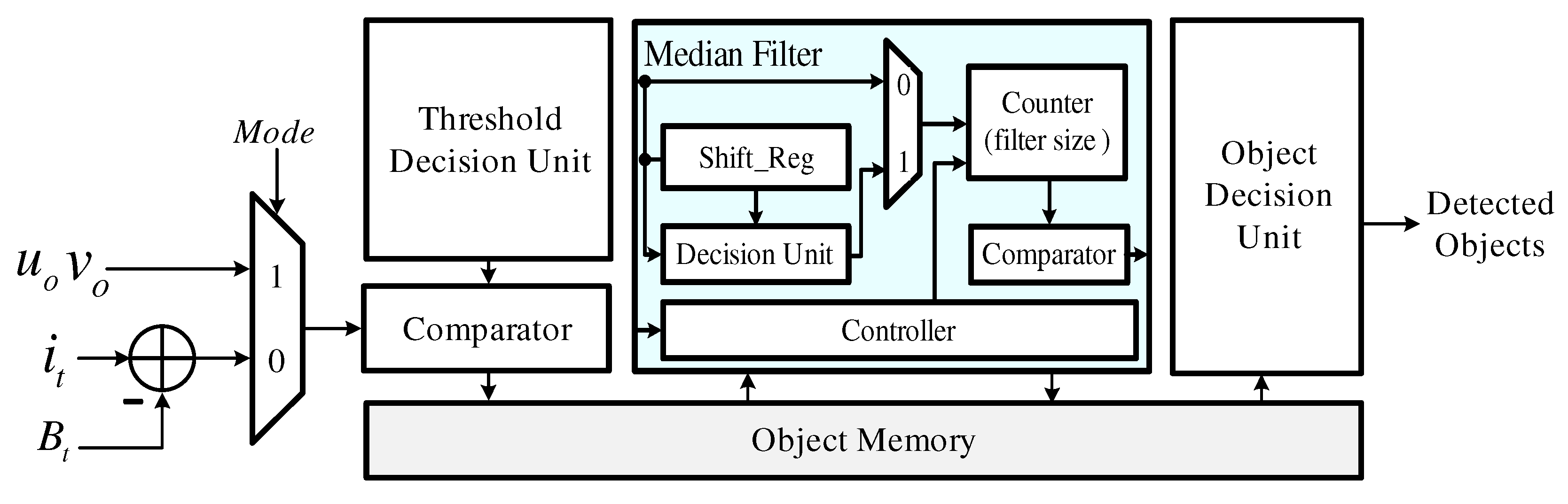
4. Hardware Architecture Design
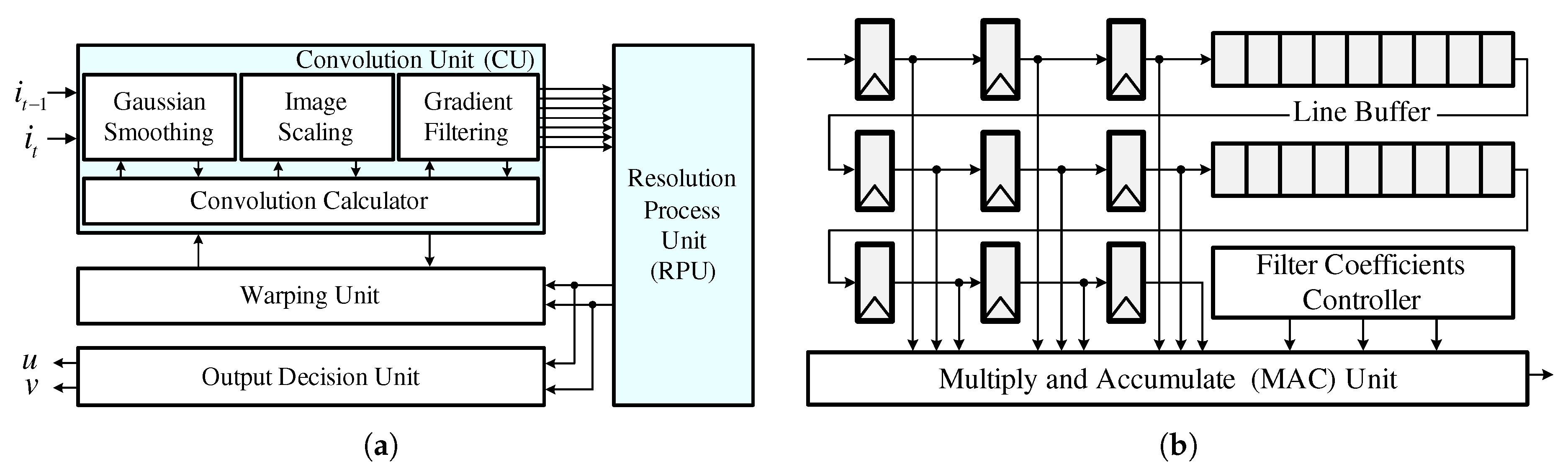
4.1. Optical Flow Estimator
4.2. Camera Motion Estimator
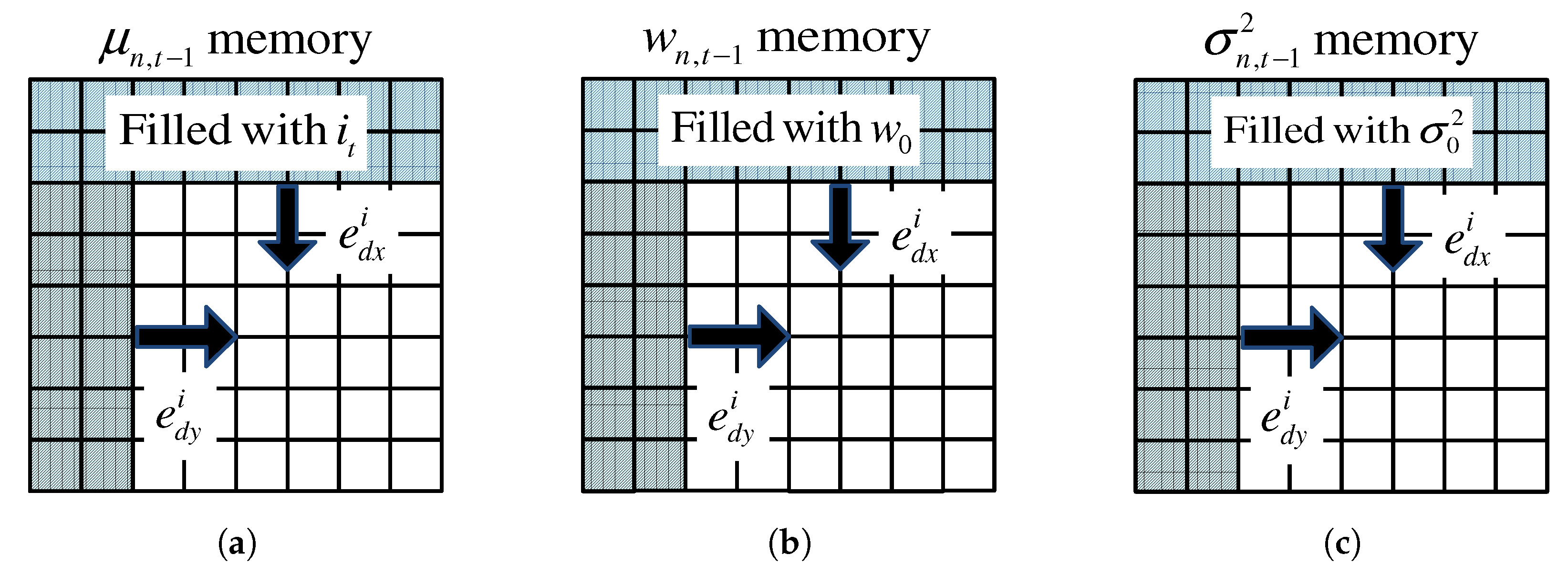
4.3. Background Detector
4.4. Object Detector
5. Experimental Results
5.1. FPGA Implementation
5.2. Performance Evaluation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bengler, K.; Dietmayer, K.; Farber, B.; Maurer, M.; Stiller, C.; Winner, H. Three decades of driver assistance systems: Review and future perspectives. IEEE Intell. Transp. Syst. Mag. 2014, 6, 6–22. [Google Scholar] [CrossRef]
- Khan, M.Q.; Lee, S. A comprehensive survey of driving monitoring and assistance systems. Sensors 2019, 19, 2574. [Google Scholar] [CrossRef]
- Chen, K.P.; Hsiung, P.A. Vehicle collision prediction under reduced visibility conditions. Sensors 2018, 18, 3026. [Google Scholar] [CrossRef]
- Mukhtar, A.; Xia, L.; Tang, T.B. Vehicle detection techniques for collision avoidance systems: A review. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2318–2338. [Google Scholar] [CrossRef]
- Sualeh, M.; Kim, G.W. Dynamic multi-lidar based multiple object detection and tracking. Sensors 2019, 19, 1474. [Google Scholar] [CrossRef]
- Zhao, Y.; Su, Y. Vehicles detection in complex urban scenes using Gaussian mixture model with FMCW radar. IEEE Sens. 2017, 17, 5948–5953. [Google Scholar] [CrossRef]
- Nieto, M.; Otaegui, O.; Velez, G.; Ortega, J.D.; Cortes, A. On creating vision-based advanced driver assistance systems. IET Intell. Transp. Syst. 2015, 9, 59–66. [Google Scholar] [CrossRef]
- Zhan, C.; Duan, X.; Xu, S.; Song, Z.; Luo, M. An improved moving object detection algorithm based on frame difference and edge detection. In Proceedings of the Fourth International Conference on Image and Graphics, Chengdu, China, 22–24 August 2007. [Google Scholar]
- Sharmin, N.; Brad, R. Optimal filter estimation for Lucas-Kanade optical flow. Sensors 2012, 12, 12694–12709. [Google Scholar] [CrossRef]
- Stauffer, C.; Grimson, W.E.L. Adaptive background mixture models for real-time tracking. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Fort Collins, CO, USA, 23–25 June 1999. [Google Scholar]
- Lee, D. Effective Gaussian mixture learning for video background subtraction. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 827–832. [Google Scholar]
- Bouwmans, T.; Baf, F.E.; Vachon, B. Background modeling using mixture of Gaussians for foreground detection: A survey. Recent Pat. Comput. Sci. 2008, 1, 219–237. [Google Scholar] [CrossRef]
- Shah, M.; Deng, J.D.; Woodford, B.J. Video background modeling: Recent approaches, issues and our proposed techniques. Mach. Vis. Appl. 2014, 25, 1105–1119. [Google Scholar] [CrossRef]
- Wang, R.; Bunyak, F.; Seetharaman, G.; Palaniappan, K. Static and moving object detection using flux tensor with split Gaussian models. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshop, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Casares, M.; Velipasalar, S.; Pinto, A. Light-weight salient foreground detection for embedded smart cameras. Comput. Vis. Image Underst. 2010, 114, 1223–1237. [Google Scholar] [CrossRef]
- Cuevas, C.; Garcia, N. Efficient moving object detection for lightweight applications on smart cameras. IEEE Trans. Circuits Syst. Video Technol. 2013, 23, 1–14. [Google Scholar] [CrossRef]
- Azmat, S.; Wills, L.; Wills, S. Spatio-temporal multimodal mean. In Proceedings of the IEEE Southwest Symposium on Image Analysis and Interpretation, San Diego, CA, USA, 6–8 April 2014. [Google Scholar]
- Guo, J.; Hsia, C.; Liu, Y.; Shih, M.; Chang, C.; Wu, J. Fast background subtraction based on a multilayer codebook model for moving object detection. IEEE Trans. Circuts Syst. Video Technol. 2013, 23, 1809–1821. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, C.; Yu, W. Moving object detection by detecting contiguous outliers in the low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 597–610. [Google Scholar] [CrossRef] [PubMed]
- Sheikh, Y.; Javed, O.; Kanade, T. Background subtraction for freely moving cameras. In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009. [Google Scholar]
- Huang, S.C.; Do, B.H. Radial basis function based neural network for motion detection in dynamic scenes. IEEE Trans. Cybern. 2013, 44, 114–125. [Google Scholar] [CrossRef] [PubMed]
- Zamalieva, D.; Yilmaz, A. Background subtraction for the moving camera: A geometric approach. Comput. Vis. Image Underst. 2014, 127, 73–85. [Google Scholar] [CrossRef]
- Jo, K.; Yu, Y.; Kurnianggoro, L. Moving object detection for a moving camera based on global motion compensation and adaptive background model. Int. J. Control Autom. Syst. 2019, 17, 1866–1874. [Google Scholar]
- Bhaskar, H.; Dwivedi, K.; Dogra, D.; Al-Mualla, M.; Mihaylova, L. Autonomous detection and tracking under illumination changes, occlusions and moving camera. Signal Process. 2015, 117, 343–354. [Google Scholar] [CrossRef]
- Yazdi, M.; Bouwmans, T. New trends on moving object detection in video images captured by a moving camera: A survey. Comput. Sci. Rev. 2018, 28, 157–177. [Google Scholar] [CrossRef]
- Heo, B.; Yun, K.; Choi, J. Appearance and motion based deep learning architecture for moving object detection in moving camera. In Proceedings of the IEEE International Conference on Image Processing, Beijing, Chaina, 17–20 September 2011. [Google Scholar]
- Dike, H.U.; Wu, Q.; Zhou, Y.; Liang, G. Unmanned aerial vehicle (UAV) based running person detection from a real-time moving camera. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Kuala Lumpur, Malaysia, 12–15 December 2018. [Google Scholar]
- Babaee, M.; Dinh, D.T.; Rigoll, G. A deep convolutional neural network for video sequence background subtraction. Pattern Recognit. 2018, 76, 635–649. [Google Scholar] [CrossRef]
- Kim, D.; Kwon, J. Moving object detection on a vehicle mounted back-up camera. Sensors 2016, 16, 23. [Google Scholar] [CrossRef] [PubMed]
- Horn, B.K.P.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef]
- Brox, T.; Bruhn, A.; Papenberg, N.; Weickert, J. High accuracy optical flow estimation based on a theory for warping. In Proceedings of the European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004. [Google Scholar]
- Zach, C.; Pock, T.; Bischof, H. A Duality based approach for realtime TV-L1 optical flow. In Proceedings of the Joint Pattern Recognition Symposium, Heidelberg, Germany, 12–14 September 2007. [Google Scholar]
- Lempitsky, V.; Roth, S.; Rother, C. FusionFlow: Discrete-continuous optimization for optical flow estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- OpenCV Library. Source Forge. Available online: https://sourceforge.net/projects/opencvlibrary/ (accessed on 15 July 2019).
- Genovese, M.; Napoli, E.; Caro, D.D.; Petra, N.; Strollo, A.G.M. FPGA implementation of Gaussian mixture model algorithm for 47fps segmentation of 1080p video. J. Electr. Comput. Eng. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Genovese, M.; Napoli, E. ASIC and FPGA implementation of the Gaussian mixture model algorithm for real-time segmentation of high definition video. IEEE Trans. VLSI Syst. 2014, 22, 537–547. [Google Scholar] [CrossRef]
- Arivazhagan, S.; Kiruthika, K. FPGA implementation of GMM algorithm for background subtractions in video sequences. In Proceedings of the International Conference on Computer Vision and Image Processing, Roorkee, India, 26–28 February 2016. [Google Scholar]
- Krishnamoorthy, A.; Menon, D. Matrix inversion using Cholesky decomposition. In Proceedings of the IEEE Conference on Signal Processing: Algorithms, Architectures, Arrangements, and Applications, Poznan, Poland, 26–28 September 2013. [Google Scholar]
- Sand, P.; Teller, S. Particle video: Long-range motion estimation using point trajectories. Int. J. Comput. Vis. 2008, 80, 72–91. [Google Scholar] [CrossRef]


| Block | FPGA Logic Slices (/51840) | DSP48s (/192) | Block RAM (/972) |
|---|---|---|---|
| Optical flow estimator | 12,312 | 96 | 108 |
| Camera motion estimator | 326 | 1 | 0 |
| Background detector | 443 | 5 | 50 |
| Object detector | 164 | 2 | 5 |
| Total | 13,245 (25.55%) | 104 (54.16%) | 163 (16.77%) |
| Target FPGA | Circuit | LUT | Slice | DSP48s |
|---|---|---|---|---|
| Virtex5 | Proposed | 729 | 325 | 3 |
| [35] | 1066 | 346 | 10 | |
| [36] | 724 | 323 | 3 | |
| Virtex6 | Proposed | 794 | 352 | 3 |
| [36] | 788 | 349 | 3 |
| Image Size | Processing Speed (fps) | |
|---|---|---|
| Fast MOD [23] | Proposed | |
| 480 × 704 | 14.8 | 27.2 |
| 368 × 580 | 22.7 | 43.1 |
| 340 × 570 | 24.6 | 47.5 |
| 240 × 320 | 51.2 | 119.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, J.; Jung, Y.; Kim, D.-S.; Lee, S.; Jung, Y. Moving Object Detection Based on Optical Flow Estimation and a Gaussian Mixture Model for Advanced Driver Assistance Systems. Sensors 2019, 19, 3217. https://doi.org/10.3390/s19143217
Cho J, Jung Y, Kim D-S, Lee S, Jung Y. Moving Object Detection Based on Optical Flow Estimation and a Gaussian Mixture Model for Advanced Driver Assistance Systems. Sensors. 2019; 19(14):3217. https://doi.org/10.3390/s19143217
Chicago/Turabian StyleCho, Jaechan, Yongchul Jung, Dong-Sun Kim, Seongjoo Lee, and Yunho Jung. 2019. "Moving Object Detection Based on Optical Flow Estimation and a Gaussian Mixture Model for Advanced Driver Assistance Systems" Sensors 19, no. 14: 3217. https://doi.org/10.3390/s19143217
APA StyleCho, J., Jung, Y., Kim, D.-S., Lee, S., & Jung, Y. (2019). Moving Object Detection Based on Optical Flow Estimation and a Gaussian Mixture Model for Advanced Driver Assistance Systems. Sensors, 19(14), 3217. https://doi.org/10.3390/s19143217







