DEM Generation from Fixed-Wing UAV Imaging and LiDAR-Derived Ground Control Points for Flood Estimations
Abstract
:1. Introduction
2. Equipment and Methods
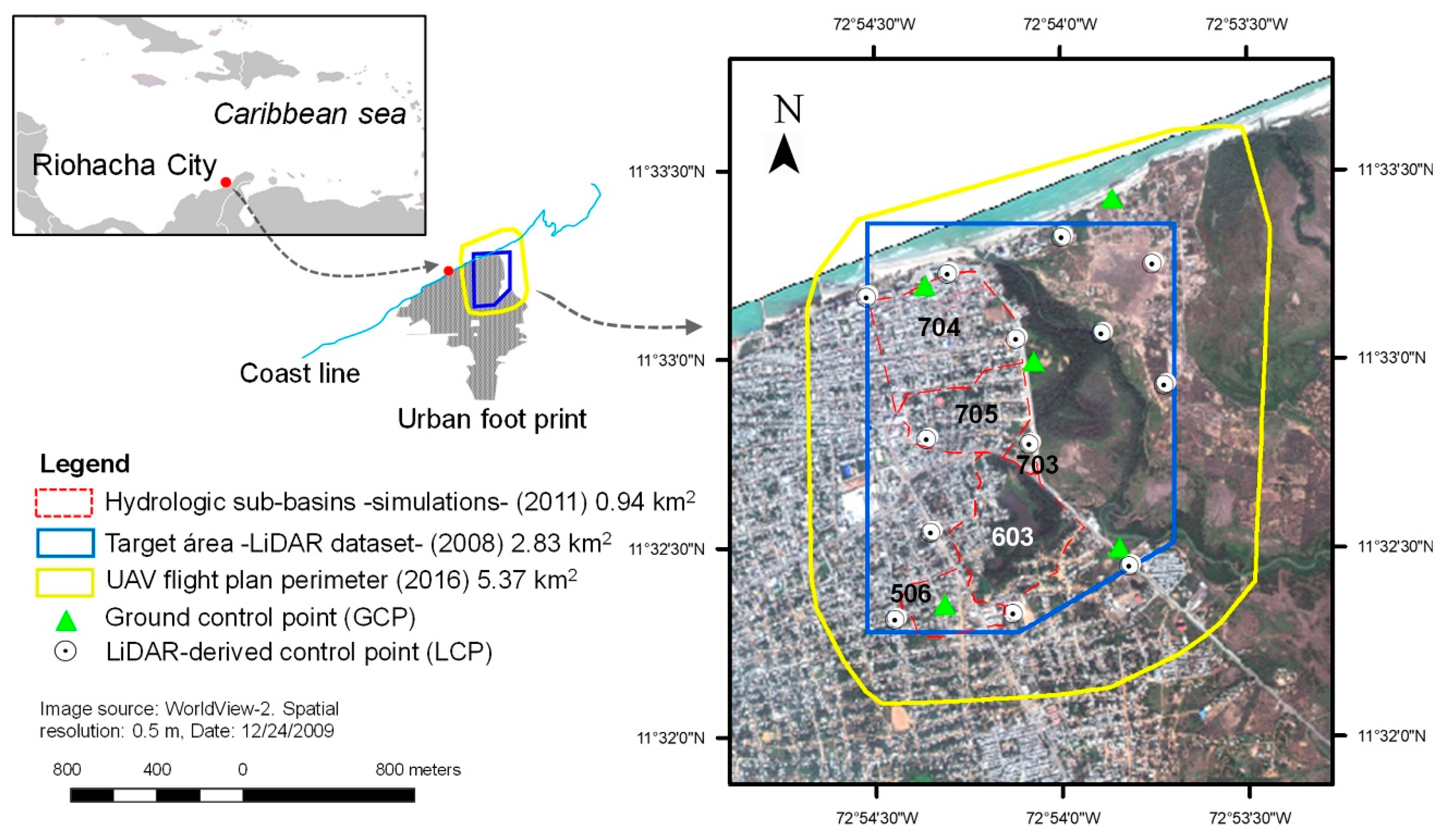
2.1. Case Study Description
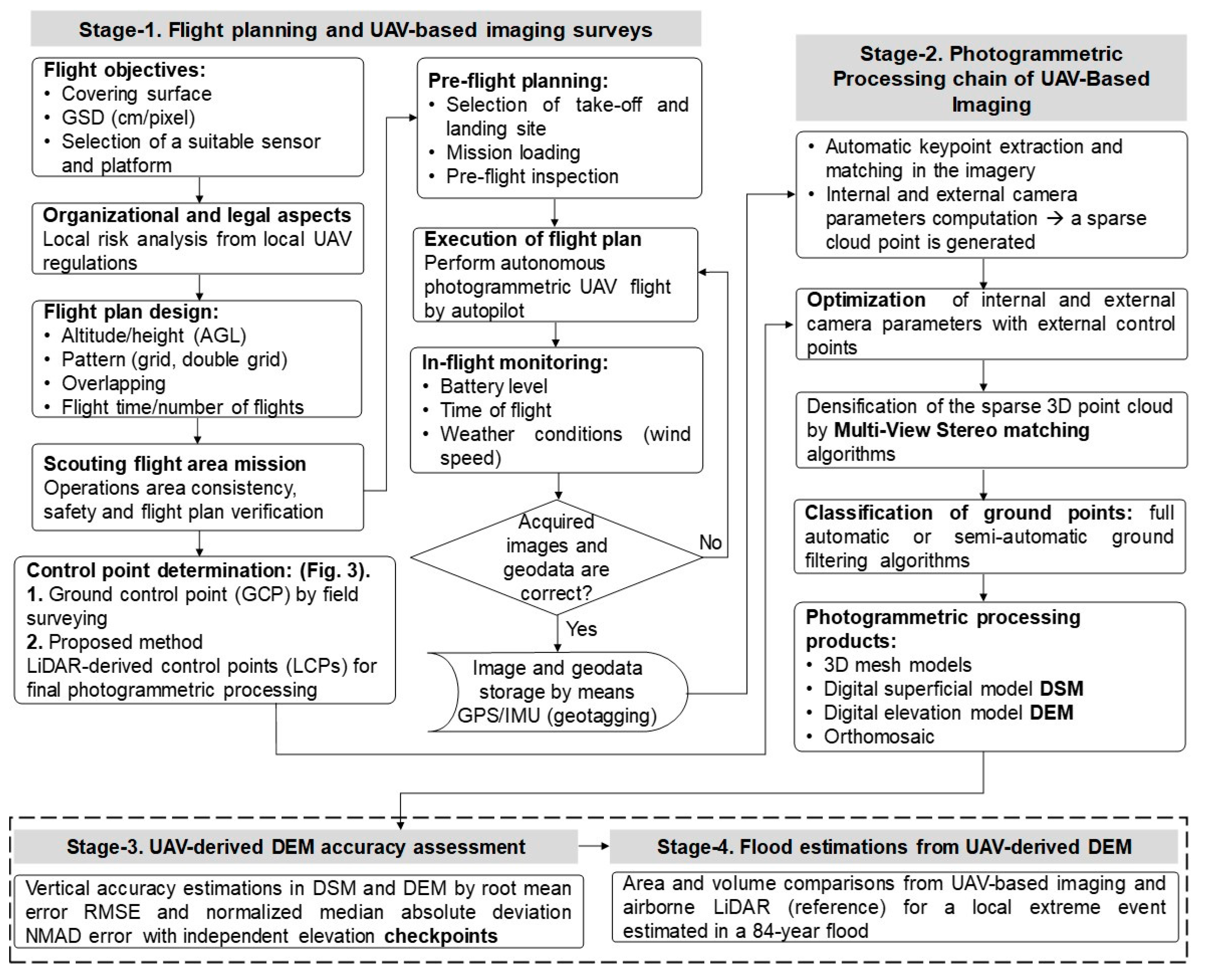
2.2. Methodology
2.2.1. Stage 1. Flight Planning, UAV-Based Surveys and LCPs (Proposed Method)
2.2.2. Stage 2. Photogrammetric Processing of UAV-Based Imaging for DEM Generation
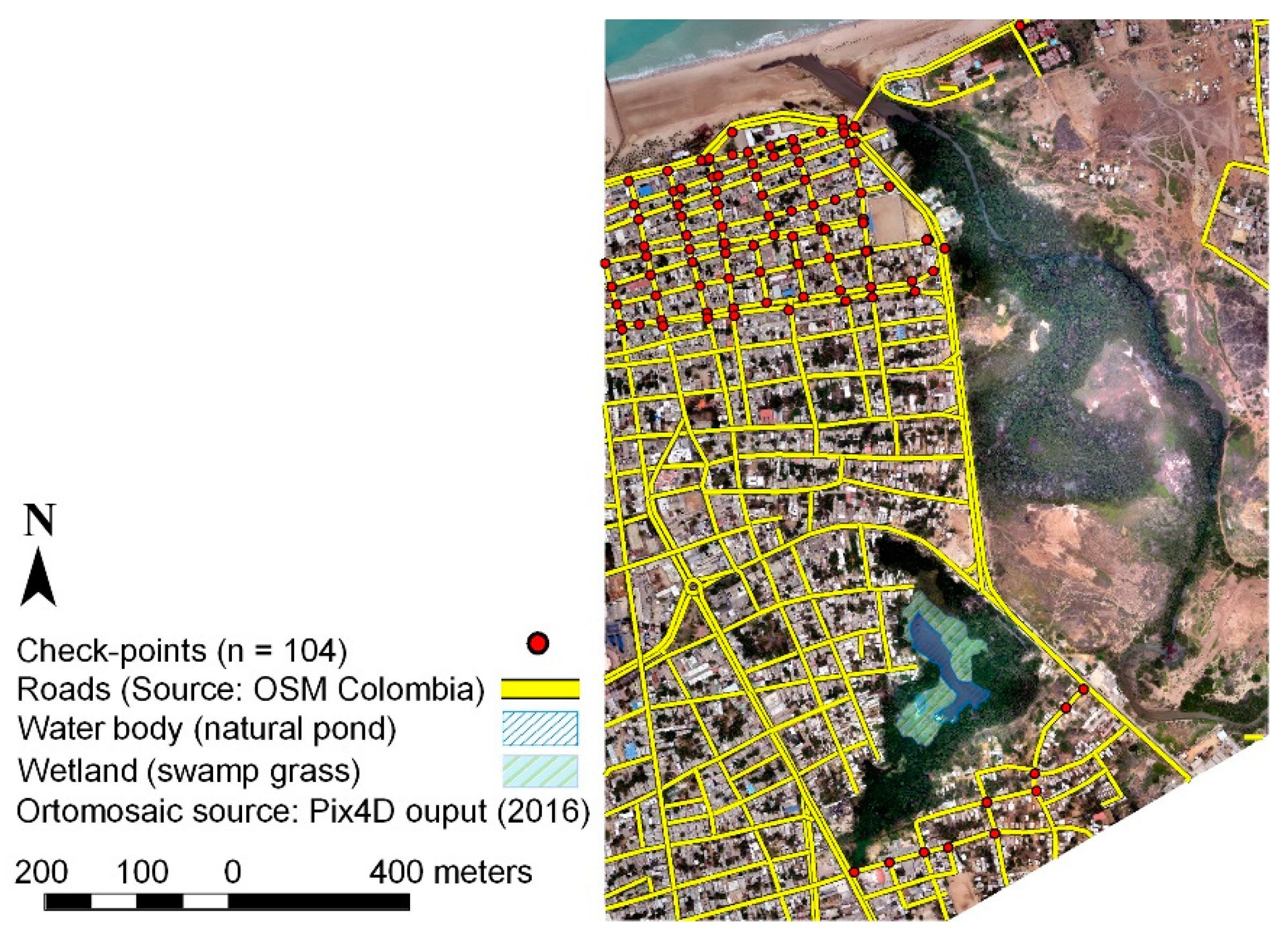
2.2.3. Stage 3. UAV-Derived DEM Accuracy Assessment
2.2.4. Stage 4. Flood Estimations from UAV-Derived DEMs
3. Results
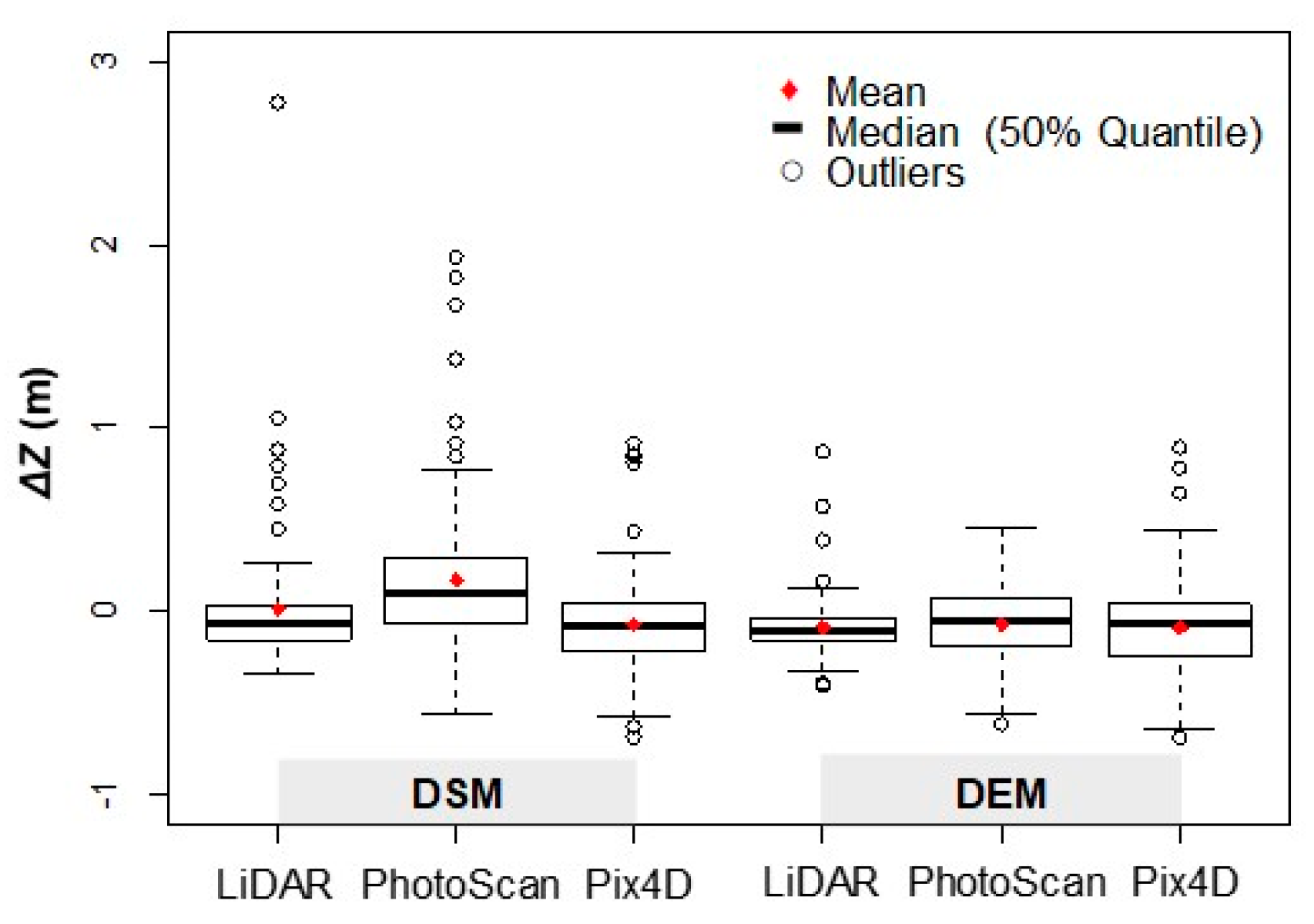
3.1. UAV-Derived DEM Accuracy Assessment
3.2. Flood Estimations from UAV-Derived DEMs
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Aircraft | Specs |
|---|---|
| Model/ wingspan | “eBee ™ SenseFly drone mapping”/ 0.96 m (delta type) |
| Weight (include battery + sensor) | approx. 0.7 kg (micro-UAV weight criteria found in Hassanalian et al., [12]) |
| Cruise speed/ Wind resistance | 40-90 km/h/ Up to 45 km/h |
| Maximum flight time/Radio Link | up to 50 min (depending on climate factors, as wind velocity)/ up to 3 km |
| Camera RGB | |
| Model | Canon IXUS 127 with CMOS imaging sensor technology |
| Sensor resolution/ Shutter speed | ~16 million pixels (4608 × 3456)/ 1/2000 seg |
| Focal length/ sensor size | 4.3 mm (35 mm film equivalent: 24 mm)/6.16 × 4.62 mm |
| Processing Hardware (CPU/GPU) | Intel® Core™ i7-6700 HQ CPU @2.60GHz RAM: 32GB /Intel® HD Graphics 530 |
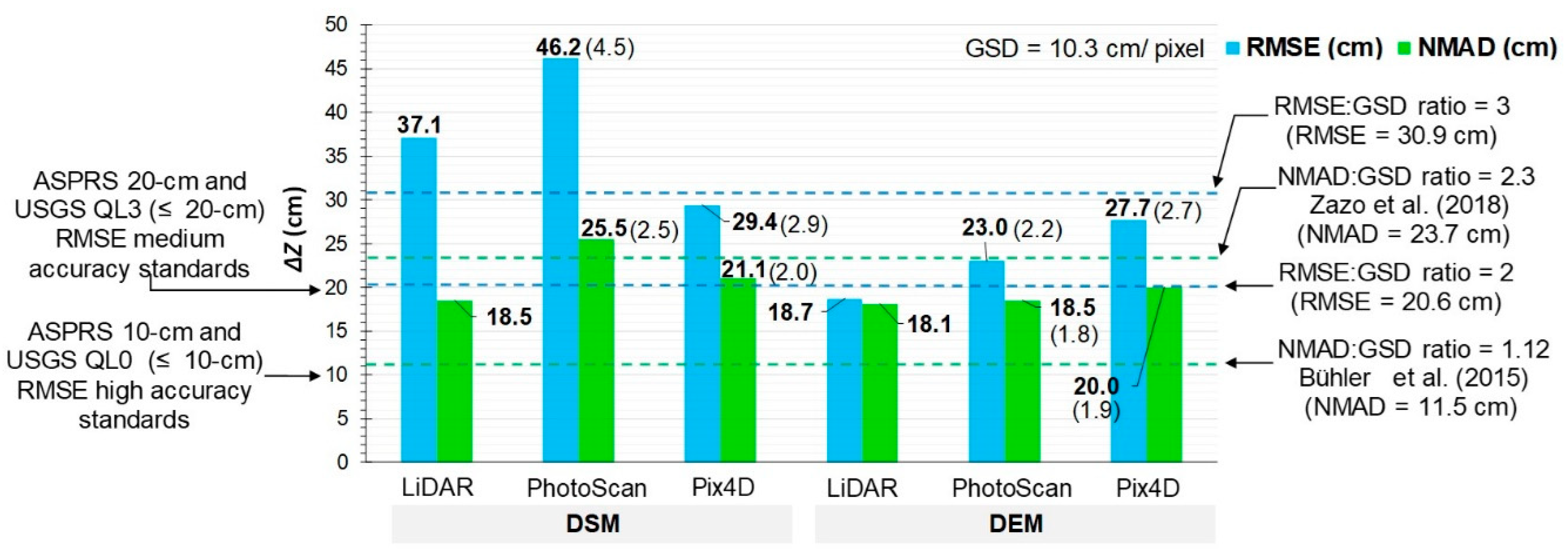
| Autor | Platform | GSD (cm/pix) | Area (km2) | NMAD (cm) | NMAD:GSD Ratio |
|---|---|---|---|---|---|
| Present study | eBee™ | 10.3 | 5.37 | 18.5–25.5 | 1.8–2.5 (2.15)1 |
| Zazo et al., 2018 [67] | manned ultra-light motor | 2.6 | 0.78 | 6 | 2.3 |
| Brunier et al., 2016 [84] | Manned Savannah ICP | 3.35 | No data | 6.96 | 2.1 |
| Bühler et al., 2015 [29] | utility aircraft | 25 | 145 | 28 | 1.1 |
| RMSE (cm) | RMSE:GSD ratio | ||||
| Present study | eBee™ | 10.3 | 5.37 | 23.0–46.2 | 2.2–4.5 (3.4) |
| Hugenholtz et al., 2013 [85] | RQ-84Z AreoHawk | 10 | 1.95 | 29 | 2.9 |
| Hugenholtz et al., 2016 [31] | eBee™ RTK | 5.2 | 0.48 | 5.7–7.2 | 1.1–1.4 (1.2) |
| Roze et al., 2014 [48] | eBee™ RTK | 2.5–5.0 | 0.2 | 3.1–7.0 | 1.2–1.4 (1.3) |
| Benassi et al., 2017 [86] | eBee™ RTK | ~2.0 | 0.25 | 2.0–10.0 | 1.0–5.0 (3.0) |
| Leitão et al., 2016 [20] | eBee™ | 2.5–10.0 | 0.039 | No data | No data |
| Gindraux et al., 2017 [87] | eBee™ | 6 | 1.4–6.9 | 10–25 | 1.7–4.2 (2.9) |
| Immerzeel et al., 2014 [88] | Swinglet CAM™ | 3–5 | 3.75 | No data | No data |
| Yilmaz et al., 2018 [89] | Gatewing™ X100 | 5.0–6.0 3 | 2.0 | 5.0 – 33.0 | 1.0–5.5 (3.3) |
| Coveney et al., 2017 [16] | Swinglet CAM™ | 3.5 | 0.29 | 9 | 2.6 |
| Langhammer et al., 2017 [19] | Mikrokopter® Hexa 2 | 1.5 | ~0.14 3 | 2.5 | 1.7 |
| Gbenga et al., 2017 [90] | DJI™ Phantom 2 2 | 10.91 | 0.81 | 46.87 | 4.3 |
References
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood risk and climate change: Global and regional perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- United Nations Sustainable Development Goals. Available online: https://www.un.org/sustainabledevelopment/cities/ (accessed on 29 May 2019).
- Hafezi, M.; Sahin, O.; Stewart, R.A.; Mackey, B. Creating a novel multi-layered integrative climate change adaptation planning approach using a systematic literature review. Sustainability 2018, 10, 4100. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, A.S.; Fu, G.; Djordjević, S.; Zhang, C.; Savić, D.A. An integrated framework for high-resolution urban flood modelling considering multiple information sources and urban features. Environ. Model. Softw. 2018, 107, 85–95. [Google Scholar] [CrossRef]
- Polat, N.; Uysal, M. An experimental analysis of digital elevation models generated with Lidar Data and UAV photogrammetry. J. Indian Soc. Remote Sens. 2018, 46, 1135–1142. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, B.; Devereux, B. State-of-the-Art: DTM generation using airborne LIDAR Data. Sensors 2017, 17, 150. [Google Scholar] [CrossRef] [PubMed]
- Liu, X. Airborne LiDAR for DEM generation: Some critical issues. Prog. Phys. Geogr. 2008, 32, 31–49. [Google Scholar]
- Wedajo, G.K. LiDAR DEM Data for flood mapping and assessment; opportunities and challenges: A Review. J. Remote Sens. GIS 2017, 6, 2015–2018. [Google Scholar] [CrossRef]
- Arrighi, C.; Campo, L. Effects of digital terrain model uncertainties on high-resolution urban flood damage assessment. J. Flood Risk Manag. 2019, e12530. [Google Scholar] [CrossRef]
- Bermúdez, M.; Zischg, A.P. Sensitivity of flood loss estimates to building representation and flow depth attribution methods in micro-scale flood modelling. Nat. Hazards 2018, 92, 1633–1648. [Google Scholar] [CrossRef] [Green Version]
- Laks, I.; Sojka, M.; Walczak, Z.; Wróżyński, R. Possibilities of using low quality digital elevation models of floodplains in Hydraulic numerical models. Water 2017, 9, 283. [Google Scholar] [CrossRef]
- Hassanalian, M.; Abdelkefi, A. Classifications, applications, and design challenges of drones: A review. Prog. Aerosp. Sci. 2017, 91, 99–131. [Google Scholar] [CrossRef]
- Fonstad, M.A.; Dietrich, J.T.; Courville, B.C.; Jensen, J.L.; Carbonneau, P.E. Topographic structure from motion: A new development in photogrammetric measurement. Earth Surf. Process. Landforms 2013, 38, 421–430. [Google Scholar] [CrossRef]
- Singh, K.K.; Frazier, A.E. A meta-analysis and review of unmanned aircraft system (UAS) imagery for terrestrial applications. Int. J. Remote Sens. 2018, 39, 5078–5098. [Google Scholar] [CrossRef]
- Remondino, F.; Nocerino, E.; Toschi, I.; Menna, F. A critical review of automated photogrammetric processing of large datasets. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2017, 42, 591–599. [Google Scholar] [CrossRef]
- Coveney, S.; Roberts, K. Lightweight UAV digital elevation models and orthoimagery for environmental applications: Data accuracy evaluation and potential for river flood risk modelling. Int. J. Remote Sens. 2017, 38, 3159–3180. [Google Scholar] [CrossRef]
- Schumann, G.J.P.; Muhlhausen, J.; Andreadis, K.M.; Schumann, G.J.P.; Muhlhausen, J.; Andreadis, K.M. Rapid mapping of small-scale river-floodplain environments using UAV SfM supports classical theory. Remote Sens. 2019, 11, 982. [Google Scholar] [CrossRef]
- Izumida, A.; Uchiyama, S.; Sugai, T. Application of UAV-SfM photogrammetry and aerial LiDAR to a disastrous flood: Multitemporal topographic measurement of a newly formed crevasse splay of the Kinu River, central Japan. Nat. Hazards Earth Syst. Sci. Discuss. 2017, 17, 1505. [Google Scholar] [CrossRef]
- Langhammer, J.; Bernsteinová, J.; Mirijovský, J. Building a high-precision 2D hydrodynamic flood model using UAV Photogrammetry and Sensor Network Monitoring. Water 2017, 9, 861. [Google Scholar] [CrossRef]
- Leitão, J.P.; Moy de Vitry, M.; Scheidegger, A.; Rieckermann, J. Assessing the quality of digital elevation models obtained from mini unmanned aerial vehicles for overland flow modelling in urban areas. Hydrol. Earth Syst. Sci. 2016, 20, 1637–1653. [Google Scholar] [CrossRef] [Green Version]
- Yalcin, E. Two-dimensional hydrodynamic modelling for urban flood risk assessment using unmanned aerial vehicle imagery: A case study of Kirsehir, Turkey. J. Flood Risk Manag. 2018, e12499. [Google Scholar] [CrossRef]
- Rinaldi, P.; Larrabide, I.; D’Amato, J.P. Drone based DSM reconstruction for flood simulations in small areas: A pilot study. In World Conference on Information Systems and Technologies; Springer: Cham, Switzerland, 2019; pp. 758–764. [Google Scholar]
- Hashemi-Beni, L.; Jones, J.; Thompson, G.; Johnson, C.; Gebrehiwot, A. Challenges and opportunities for UAV-based digital elevation model generation for flood-risk management: A case of princeville, north carolina. Sensors 2018, 18, 3843. [Google Scholar] [CrossRef] [PubMed]
- Boccardo, P.; Chiabrando, F.; Dutto, F.; Tonolo, F.G.; Lingua, A. UAV deployment exercise for mapping purposes: Evaluation of emergency response applications. Sensors 2015, 15, 15717–15737. [Google Scholar] [CrossRef] [PubMed]
- Şerban, G.; Rus, I.; Vele, D.; Breţcan, P.; Alexe, M.; Petrea, D. Flood-prone area delimitation using UAV technology, in the areas hard-to-reach for classic aircrafts: Case study in the north-east of Apuseni Mountains, Transylvania. Nat. Hazards 2016, 82, 1817–1832. [Google Scholar] [CrossRef]
- Manfreda, S.; Herban, S.; Arranz Justel, J.; Perks, M.; Mullerova, J.; Dvorak, P.; Vuono, P. Assessing the Accuracy of Digital Surface Models Derived from Optical Imagery Acquired with Unmanned Aerial Systems. Drones 2019, 3, 15. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Draeyer, B.; Strecha, C. Pix4D White Paper-How Accurate Are UAV Surveying Methods; Pix4D White Paper: Lausanne, Switzerland, 2014. [Google Scholar]
- Bühler, Y.; Marty, M.; Egli, L.; Veitinger, J.; Jonas, T.; Thee, P.; Ginzler, C. Snow depth mapping in high-alpine catchments using digital photogrammetry. Cryosphere 2015, 9, 229–243. [Google Scholar] [CrossRef] [Green Version]
- Carbonneau, P.E.; Dietrich, J.T. Cost-effective non-metric photogrammetry from consumer-grade sUAS: Implications for direct georeferencing of structure from motion photogrammetry. Earth Surf. Process. Landforms 2017, 42, 473–486. [Google Scholar] [CrossRef]
- Hugenholtz, C.; Brown, O.; Walker, J.; Barchyn, T.; Nesbit, P.; Kucharczyk, M.; Myshak, S. Spatial accuracy of UAV-derived orthoimagery and topography: Comparing photogrammetric models processed with direct geo-referencing and ground control points. Geomatica 2016, 70, 21–30. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; D’Oleire-Oltmanns, S.; Niethammer, U. Optimising UAV topographic surveys processed with structure-from-motion: Ground control quality, quantity and bundle adjustment. Geomorphology 2017, 280, 51–66. [Google Scholar] [CrossRef] [Green Version]
- James, M.R.; Robson, S.; Smith, M.W. 3-D uncertainty-based topographic change detection with structure-from-motion photogrammetry: Precision maps for ground control and directly georeferenced surveys. Earth Surf. Process. Landforms 2017, 42, 1769–1788. [Google Scholar] [CrossRef]
- Tonkin, T.N.; Midgley, N.G. Ground-control networks for image based surface reconstruction: An investigation of optimum survey designs using UAV derived imagery and structure-from-motion photogrammetry. Remote Sens. 2016, 8, 786. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.; Peterson, J.; Chandra, S. LiDAR-derived high quality ground control information and DEM for image orthorectification. Geoinformatica 2007, 11, 37–53. [Google Scholar] [CrossRef]
- Mitishita, E.; Habib, A.; Centeno, J.; Machado, A.; Lay, J.; Wong, C. Photogrammetric and Lidar Data Integration Using the Centroid of Rectangular Roof as a Control Point. Photogramm. Rec. 2008, 23, 19–35. [Google Scholar] [CrossRef]
- James, T.D.; Murray, T.; Barrand, N.E.; Barr, S.L. Extracting photogrammetric ground control from LiDAR DEMs for change detection. Photogramm. Rec. 2006, 21, 312–328. [Google Scholar] [CrossRef]
- Gneeniss, A.S.; Mills, J.P.; Miller, P.E. Reference Lidar Surfaces for Enhanced Aerial Triangulation and Camera Calibration. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 1, 111–116. [Google Scholar] [CrossRef]
- Gruen, A.; Huang, X.; Qin, R.; Du, T.; Fang, W.; Boavida, J.; Oliveira, A. Joint Processing of UAV Imagery and Terrestrial Mobile Mapping System Data for Very High Resolution City Modeling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-1/W2, 4–6. [Google Scholar] [CrossRef]
- Persad, R.A.; Armenakis, C. Alignment of Point Cloud DMSs from TLS and UAV Platforms. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 369–373. [Google Scholar] [CrossRef]
- Persad, R.A.; Armenakis, C.; Hopkinson, C.; Brisco, B. Automatic registration of 3-D point clouds from UAS and airborne LiDAR platforms. J. Unmanned Veh. Syst. 2017, 5, 159–177. [Google Scholar]
- Abdullah, Q.; Maune, D.; Smith, D.; Heidemann, H.K. New Standard for New Era: Overview of the 2015 ASPRS Positional Accuracy Standards for Digital Geospatial Data. Photogramm. Eng. Remote Sens. 2015, 81, 173–176. [Google Scholar]
- Höhle, J.; Höhle, M. Accuracy assessment of digital elevation models by means of robust statistical methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef] [Green Version]
- Nardini, A.; Miguez, M.G. An integrated plan to sustainably enable the City of Riohacha (Colombia) to cope with increasing urban flooding, while improving its environmental setting. Sustainability 2016, 8, 198. [Google Scholar] [CrossRef]
- Nardini, A.; Cardenas Mercado, L.; Perez Montiel, J. MODCEL vs. IBER: A comparison of flooding models in Riohacha, a coastal town of La Guajira, Colombia. Contemp. Eng. Sci. 2018, 11, 3253–3266. [Google Scholar] [CrossRef]
- OpenStreetMap Colombia, Mapatón Por La Guajira—OpenStreetMap Colombia. Available online: https://openstreetmapcolombia.github.io/2016/03/23/reporte/ (accessed on 5 February 2019).
- Stöcker, C.; Bennett, R.; Nex, F.; Gerke, M.; Zevenbergen, J. Review of the current state of UAV regulations. Remote Sens. 2017, 9, 459. [Google Scholar] [CrossRef]
- Roze, A.; Zufferey, J.C.; Beyeler, A.; Mcclellan, A. eBee RTK Accuracy Assessment; White Paper: Lausanne, Switzerland, 2014. [Google Scholar]
- Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. Assessment of photogrammetric mapping accuracy based on variation ground control points number using unmanned aerial vehicle. Meas. J. Int. Meas. Confed. 2017, 98, 221–227. [Google Scholar] [CrossRef]
- Corbley, K. Merrick Extends Life of LiDAR Sensor by Modifying Flight Operations. Leica ALS40 Contributes to Colombian Market and History. LiDAR Mag. 2014, 4, 6. [Google Scholar]
- Afanador Franco, F.; Orozco Quintero, F.J.; Gómez Mojica, J.C.; Carvajal Díaz, A.F. Digital orthophotography and LIDAR data to control and management of Tierra Bomba island littoral, Colombian Caribbean. Boletín Científico CIOH 2008, 26, 86–103. [Google Scholar] [CrossRef]
- Heidemann, H.K. Lidar base specification (ver. 1.3, February 2018). In U.S. Geological Survey Techniques and Methods; Geological Survey: Reston, Virginia, 2018; Chapter B4. [Google Scholar]
- Zhang, K.; Gann, D.; Ross, M.; Biswas, H.; Li, Y.; Rhome, J. Comparison of TanDEM-X DEM with LiDAR Data for Accuracy Assessment in a Coastal Urban Area. Remote Sens. 2019, 11, 876. [Google Scholar] [CrossRef]
- Escobar-Villanueva, J.; Nardini, A.; Iglesias-Martínez, L. Assessment of LiDAR topography in modeling urban flooding with MODCEL©. Applied to the coastal city of Riohacha, La Guajira (Colombian Caribbean). In Proceedings of the XVI Congreso de la Asociación Española de Teledetección, Sevilla, Spain, 21–23 October 2015; pp. 368–383. [Google Scholar]
- Granshaw, S.I. Photogrammetric Terminology: Third Edition. Photogramm. Rec. 2016, 31, 210–252. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Watson, C. An Automated Technique for Generating Georectified Mosaics. Remote Sens. 2012, 4, 1392–1410. [Google Scholar] [CrossRef]
- Agisoft LLC. Agisoft PhotoScan User Manual—Professional Edition; Agisoft LLC: St. Petersburg, Russia, 2016; Version 1.2. [Google Scholar]
- Pix4D SA Pix4Dmapper 4.1 USER MANUAL; Pix4D SA: Lausanne, Switzerland, 2017.
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle Adjustment—A Modern Synthesis. In Vision Algorithms: Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2000; pp. 298–372. [Google Scholar]
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F. State of the art in high density image matching. Photogramm. Rec. 2014, 29, 144–166. [Google Scholar] [CrossRef] [Green Version]
- Agisoft LLC. Agisoft LLC Orthophoto and DEM Generation with Agisoft PhotoScan Pro 1.0.0; Agisoft LLC: St. Petersburg, Russia, 2013. [Google Scholar]
- Axelsson, P. DEM Generation from Laser Scanner Data Using adaptive TIN Models. Int. Arch. Photogramm. Remote Sens. 2000, 23, 110–117. [Google Scholar]
- Becker, C.; Häni, N.; Rosinskaya, E.; D’Angelo, E.; Strecha, C. Classification of Aerial Photogrammetric 3D Point Clouds. Photogramm. Eng. Remote Sens. 2018, 84, 287–295. [Google Scholar] [CrossRef]
- Planning Department—Municipality of Riohacha (Colombia). Rehabilitation of Sewerage Pipe Networks for the “Barrio Arriba” of the Municipality of Riohacha; Planning Department—Municipality of Riohacha (Colombia): Riohacha, Colombia, 2018. [Google Scholar]
- Alidoost, F.; Samadzadegan, F. Statistical Evaluation of Fitting Accuracy of Global and Local Digital Elevation Models in Iran. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-1/W3, 19–24. [Google Scholar] [CrossRef]
- Zazo, S.; Rodríguez-Gonzálvez, P.; Molina, J.L.; González-Aguilera, D.; Agudelo-Ruiz, C.A.; Hernández-López, D. Flood hazard assessment supported by reduced cost aerial precision photogrammetry. Remote Sens. 2018, 10, 1566. [Google Scholar] [CrossRef]
- Ruzgiene, B.; Berteška, T.; Gečyte, S.; Jakubauskiene, E.; Aksamitauskas, V.Č. The surface modelling based on UAV Photogrammetry and qualitative estimation. Meas. J. Int. Meas. Confed. 2015, 73, 619–627. [Google Scholar] [CrossRef]
- Teknomo, K. Similarity Measurement. Available online: http://people.revoledu.com/kardi/tutorial/Similarity/BrayCurtisDistance.html (accessed on 24 June 2018).
- Nartiss, M. r.Lake.xy Module. Available online: https://grass.osgeo.org/grass74/manuals/r.lake.html (accessed on 9 July 2018).
- Miguez, M.G.; Battemarco, B.P.; De Sousa, M.M.; Rezende, O.M.; Veról, A.P.; Gusmaroli, G. Urban flood simulation using MODCEL-an alternative quasi-2D conceptual model. Water 2017, 9, 445. [Google Scholar] [CrossRef]
- Hodgson, M.; Bresnahan, P. Accuracy of Airborne LIDAR Derived Elevation: Empirical Assessment and Error Budget. Photogramm. Eng. Remote Sens. 2004, 70, 331. [Google Scholar] [CrossRef]
- Huang, R.; Zheng, S.; Hu, K.; Huang, R.; Zheng, S.; Hu, K. Registration of Aerial Optical Images with LiDAR Data Using the Closest Point Principle and Collinearity Equations. Sensors 2018, 18, 1770. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, X. Advances in fusion of optical imagery and LiDAR point cloud applied to photogrammetry and remote sensing. Int. J. Image Data Fusion 2017, 8, 1–31. [Google Scholar] [CrossRef]
- Giordan, D.; Hayakawa, Y.; Nex, F.; Remondino, F.; Tarolli, P. Review article: The use of remotely piloted aircraft systems (RPASs) for natural hazards monitoring and management. Nat. Hazards Earth Syst. Sci. 2018, 4, 1079–1096. [Google Scholar] [CrossRef]
- Yurtseven, H. Comparison of GNSS-, TLS- and Different Altitude UAV-Generated Datasets on The Basis of Spatial Differences. ISPRS Int. J. Geo-Inf. 2019, 8, 175. [Google Scholar] [CrossRef]
- Park, J.; Kim, P.; Cho, Y.K.; Kang, J. Framework for automated registration of UAV and UGV point clouds using local features in images. Autom. Constr. 2019, 98, 175–182. [Google Scholar] [CrossRef]
- Shaad, K.; Ninsalam, Y.; Padawangi, R.; Burlando, P. Towards high resolution and cost-effective terrain mapping for urban hydrodynamic modelling in densely settled river-corridors. Sustain. Cities Soc. 2016, 20, 168–179. [Google Scholar] [CrossRef]
- Šiljeg, A.; Barada, M.; Marić, I.; Roland, V. The effect of user-defined parameters on DTM accuracy—development of a hybrid model. Appl. Geomat. 2019, 11, 81–96. [Google Scholar] [CrossRef]
- Jeunnette, M.N.; Hart, D.P. Remote sensing for developing world agriculture: Opportunities and areas for technical development. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XVIII, Edinburgh, UK, 26–29 September 2016; Volume 9998, pp. 26–29. [Google Scholar]
- SESAR Providing Operations of Drones with Initial Unmanned Aircraft System Traffic Management (PODIUM). Available online: https://vimeo.com/259880175 (accessed on 31 May 2019).
- Wild, G.; Murray, J.; Baxter, G.; Wild, G.; Murray, J.; Baxter, G. Exploring Civil Drone Accidents and Incidents to Help Prevent Potential Air Disasters. Aerospace 2016, 3, 22. [Google Scholar] [CrossRef]
- Altawy, R.; Youssef, A.M. Security, Privacy, and Safety Aspects of Civilian Drones. ACM Trans. Cyber-Phys. Syst. 2016, 1, 1–25. [Google Scholar] [CrossRef]
- Brunier, G.; Fleury, J.; Anthony, E.J.; Gardel, A.; Dussouillez, P. Close-range airborne Structure-from-Motion Photogrammetry for high-resolution beach morphometric surveys: Examples from an embayed rotating beach. Geomorphology 2016, 261, 76–88. [Google Scholar] [CrossRef]
- Hugenholtz, C.H.; Whitehead, K.; Brown, O.W.; Barchyn, T.E.; Moorman, B.J.; LeClair, A.; Riddell, K.; Hamilton, T. Geomorphological mapping with a small unmanned aircraft system (sUAS): Feature detection and accuracy assessment of a photogrammetrically-derived digital terrain model. Geomorphology 2013, 194, 16–24. [Google Scholar] [CrossRef] [Green Version]
- Benassi, F.; Dall’Asta, E.; Diotri, F.; Forlani, G.; Morra di Cella, U.; Roncella, R.; Santise, M. Testing accuracy and repeatability of UAV blocks oriented with GNSS-supported aerial triangulation. Remote Sens. 2017, 9, 172. [Google Scholar] [CrossRef]
- Gindraux, S.; Boesch, R.; Farinotti, D. Accuracy assessment of digital surface models from Unmanned Aerial Vehicles’ imagery on glaciers. Remote Sens. 2017, 9, 186. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Kraaijenbrink, P.D.A.; Shea, J.M.; Shrestha, A.B.; Pellicciotti, F.; Bierkens, M.F.P.; De Jong, S.M. High-resolution monitoring of Himalayan glacier dynamics using unmanned aerial vehicles. Remote Sens. Environ. 2014, 150, 93–103. [Google Scholar] [CrossRef]
- Yilmaz, V.; Konakoglu, B.; Serifoglu, C.; Gungor, O.; Gökalp, E. Image classification-based ground filtering of point clouds extracted from UAV-based aerial photos. Geocarto Int. 2018, 33, 310–320. [Google Scholar] [CrossRef]
- Gbenga Ajayi, O.; Palmer, M.; Salubi, A.A. Modelling farmland topography for suitable site selection of dam construction using unmanned aerial vehicle (UAV) photogrammetry. Remote Sens. Appl. Soc. Environ. 2018, 11, 220–230. [Google Scholar]

| Parameter | Result |
|---|---|
| Imagery acquisition date: | 17/02/2016 (6 to 10 am); cloudy day and low wind velocity [46]. |
| Flight plan area | 5.37 km2 (537 ha). Flight 1: 0.9 km2; flight 2: 2.2 km2 and flight 3: 2.2 km2 (see Figure 1): |
| Ground sample distance, GSD | ~ 10.3 cm/ pixel (single image footprint on the ground ~473 m × 355 m) |
| Flight height: | ~ 325 m AGL (height above ground level). Reported by on-board GPS flight log |
| Overlap/ grid pattern/ strips | 80% (longitudinal)/ simple grid [24]/ 19 overlapping strips captured at nadir angle |
| Number of flights/images: | 3 flights, one of 8 min and two of 20 min each, approximately 467 images acquired |
| PhotoScan (semi-automatic) | Pix4Dmapper (automatic) | ||
|---|---|---|---|
| Parameter | Selected/ Value 1,2,3 | Parameter | Selected/ Value 1,2,3 |
| Align photos | Initial processing | ||
| Accuracy | “High” | Keypoint image scale | “Full” |
| Pair selection | “Reference” | Matching image pairs | “Aerial Grid or Corridor” |
| Reprojection error (pix) 1 | 1.97 | Reprojection error (pix) 1 | 0.19 |
| Control point accuracy (pix) 2 | 0.16 | Control point accuracy (pix) 2 | 0.65 |
| Camera optimization (%) 3 | 1.90 | Camera optimization (%) 3 | 0.21 |
| Sparse cloud (point/m2) | 0.04 | Sparse cloud (point/m2) | 0.12 |
| Build dense Cloud | Point cloud densification | ||
| Quality | “Medium” | Point density | “Optimal” |
| Deep filtering | “Mild” | Min. number of matched | “3” |
| Dense cloud (point/m2) | 6.4 | Dense cloud (point/m2) | 6.6 |
| Classifying dense cloud points | “Ground points” | Point cloud classification | “Classify Point Cloud” |
| Cell size (m) | “40” | - | - |
| Max distance (m) | “0.3” | - | - |
| Max angle (deg) | “5” | - | - |
| Ground cloud (points/m2) | 2.09 | Ground cloud (points/m2) | 3.51 |
| Build mesh | - | - | |
| Source type | “Height field (2.5D)” | - | - |
| Point classes | - | - | |
| [Surface mesh] | “Created (Never classified)” | - | - |
| [Terrain mesh] | “Ground” | - | - |
| Build DEM ← [from surface mesh] | Raster DSM | ||
| Source data | “mesh” | Method | “Inv. Dist. Weighting” |
| Interpolation | “Enable (default)” | DSM filters | [all checked] |
| Resolution | [default value] | Resolution | “Automatic” [1 × GSD] |
| 40.84 × 40.84 cm | 10.35 × 10.35 cm | ||
| Build DEM ← [from terrain mesh] | Additional outputs | ||
| Source data | “mesh” | Raster DTM 4 | [checked] |
| Interpolation | “Enable (default)” | ||
| Resolution | [default value] | Resolution | “Automatic” [5 × GSD] |
| 40.83 × 40.83 cm | 51.73 × 51.73 cm | ||
| Sub-Basin | Comment 1 | LiDAR H | PhotoScan H | Pix4D H |
|---|---|---|---|---|
| 704 | Constituted entirely by urban cover (0.32 km2); h = 1.22 | 1.48 | 1.35 | 1.80 |
| 705 | Also constituted by urban cover (0.19 km2); h = 0.29 | 1.32 | 0.79 | 1.28 |
| 703 | Adjoining outlet of Sub-basin 603 (0.02 km2); h = 1.78 | 1.87 | 1.74 | 2.02 |
| 603 | Pond, wetland and urban cover (0.29 km2); h = 1.63 | 1.85 | 2.01 | 1.63 |
| 506 | Adjoining inlet of Sub-basin 603 (0.1 km2); h = 1.12 | 3.15 | 3.10 | 3.78 |
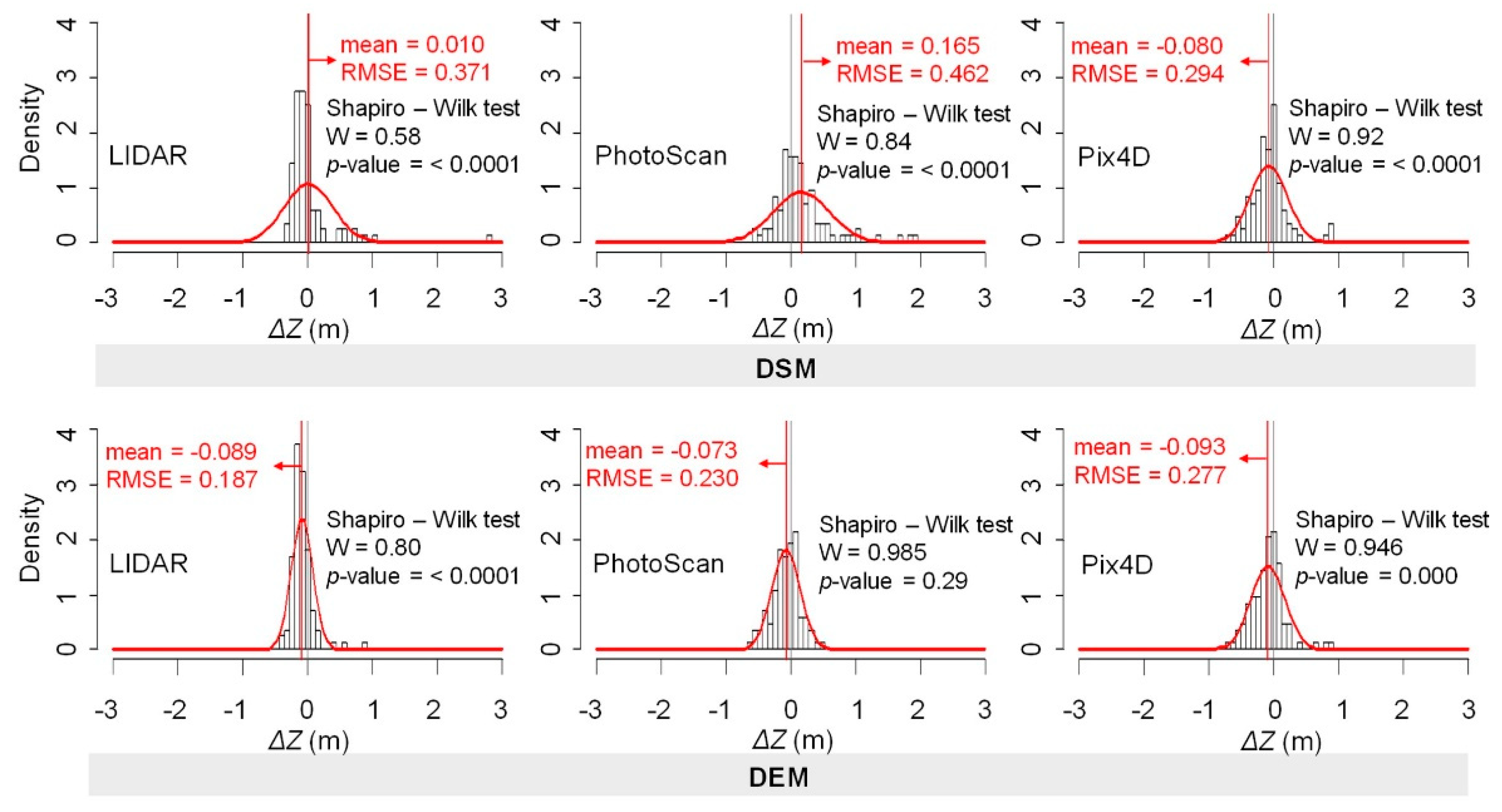
| Accuracy Estimators by Assumption of the ΔZ Distribution: | DSM | DEM | ||||
|---|---|---|---|---|---|---|
| LiDAR | PhotoScan | Pix4D | LiDAR | PhotoScan | Pix4D | |
| Normal | ||||||
| Mean (m) | 0.010 | 0.165 | −0.080 | −0.089 | −0.073 | −0.093 |
| Standard deviation, SD (m) | 0.373 | 0.433 | 0.284 | 0.166 | 0.219 | 0.262 |
| RMSE 1 (m) | 0.371 | 0.462 | 0.294 | 0.187 | 0.230 | 0.277 |
| RMSE:GSD 2 ratio | - | 4.5 | 2.9 | - | 2.2 | 2.7 |
| Non-normal (robust method) | ||||||
| Median (m) | 0.125 | 0.172 | 0.142 | 0.123 | 0.131 | 0.135 |
| NMAD 3 (m) | 0.185 | 0.255 | 0.211 | 0.181 | 0.185 | 0.200 |
| NMAD:GSD 2 ratio | - | 2.5 | 2.0 | - | 1.8 | 1.9 |
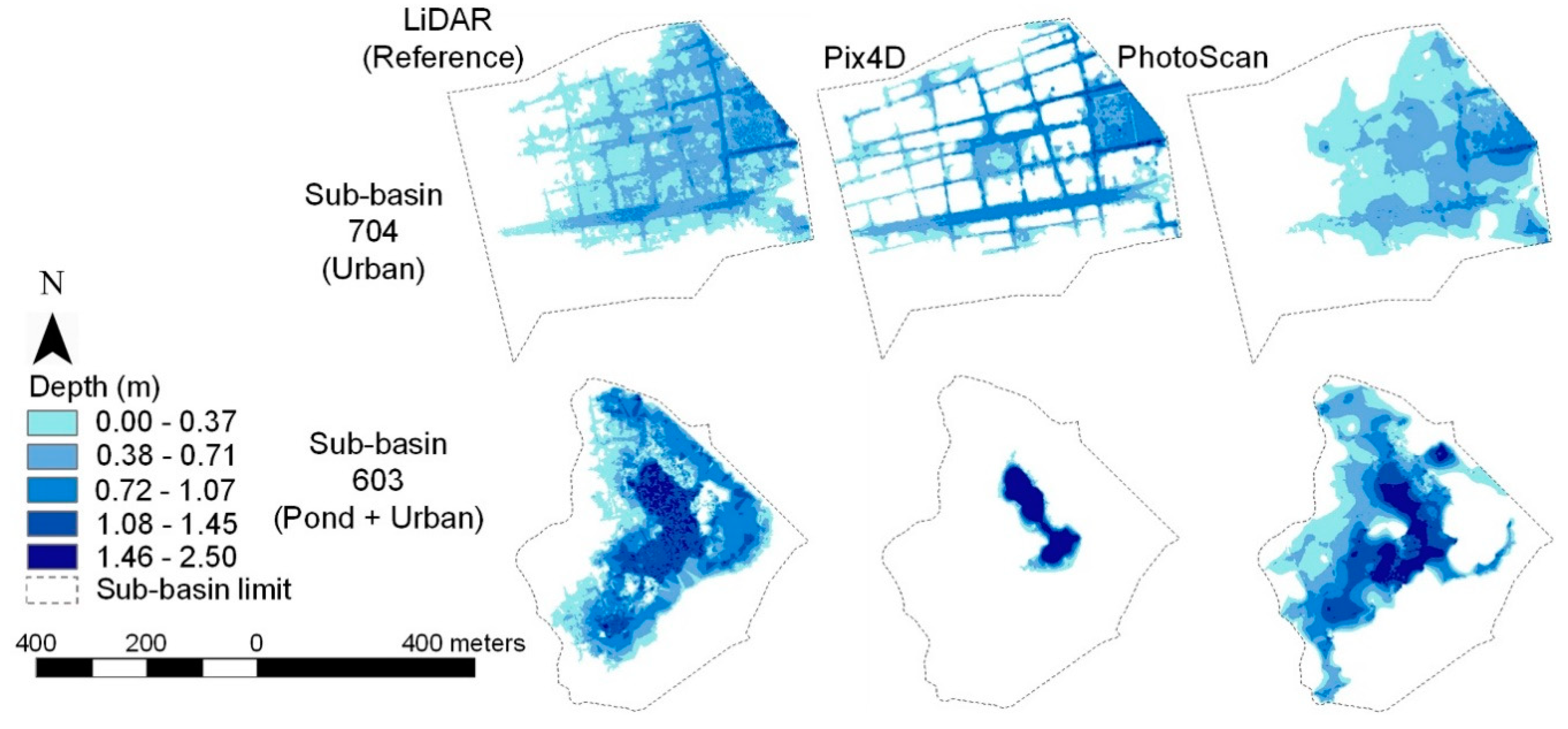
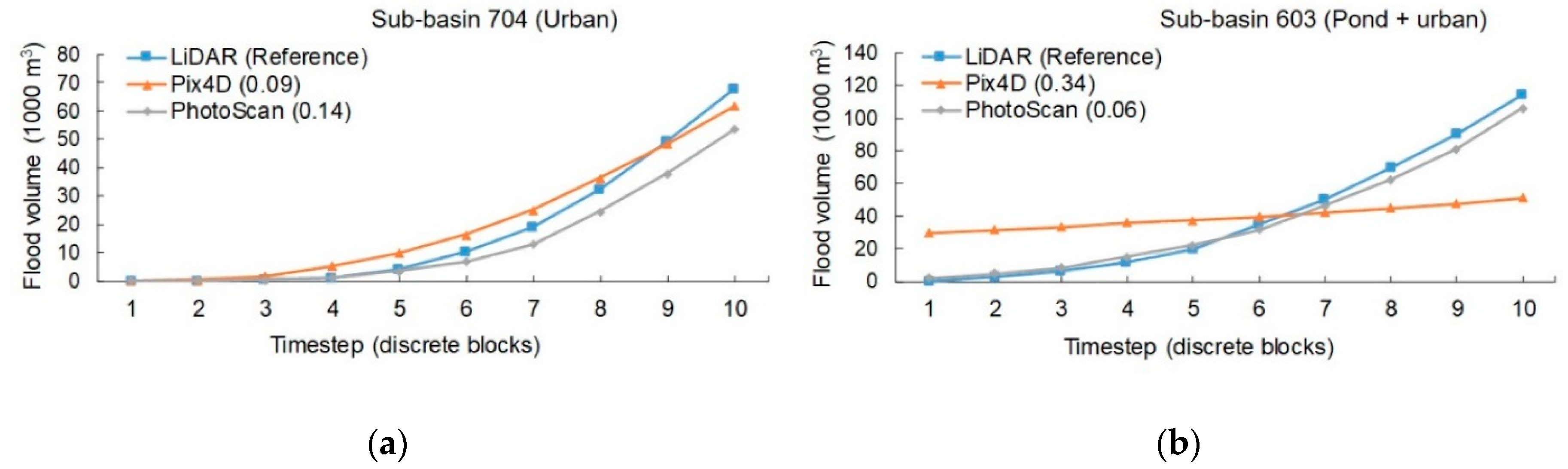
| Sub-Basin | Volume, Area V (m3), A (m2) | LiDAR | Pix4D | PhotoScan | Pix4D | PhotoScan |
|---|---|---|---|---|---|---|
| Difference (%) 2 | ||||||
| 704 (Urban) | V | 68,072 | 61,728 | 53,699 | 9.3 | 21.1 |
| A | 166,385 | 114,940 | 141,985 | 30.9 | 14.7 | |
| 705 (Urban) | V | 4,065 | 185 | 126 | 95.4 | 96.9 |
| A | 16,682 | 941 | 758 | 94.4 | 95.5 | |
| 703 (Outlet of 603) | V | 13,986 | 4,294 | 7,638 | 69.3 | 45.4 |
| A | 15,646 | 5,756 | 11,793 | 63.2 | 24.6 | |
| 603 (Pond + urban) | V | 114,311 | 51,103 | 106,135 | 55.3 | 7.2 |
| A | 155,245 | 21,015 | 146,596 | 86.5 | 5.6 | |
| 506 (Inlet of 603) | V | 2,589 | 5,690 | 7,180 | 119.8 | 177.3 |
| A | 7,878 | 11,206 | 14,514 | 42.2 | 84.2 | |
| Difference (absolute) | ||||||
| Total (Σ) 1 | V | 203,023 | 123,000 | 174,778 | 80,023 | 28,245 |
| A | 361,836 | 153,858 | 315,646 | 207,978 | 46,190 | |
| Overall difference (%) 2 | V | 42.5 | 18.4 | |||
| A | 59.3 | 16.4 | ||||
| Sub-Basin | Pix4D | PhotoScan | Pix4D | PhotoScan |
|---|---|---|---|---|
| Volume 1 | Area 1 | |||
| 704 (urban) | 0.09 | 0.14 | 0.16 | 0.12 |
| 705 (urban) | 0.85 | 0.91 | 0.79 | 0.85 |
| 703 (outlet of 603) | 0.47 | 0.27 | 0.51 | 0.19 |
| 603 (pond + urban) | 0.34 | 0.06 | 0.69 | 0.07 |
| 506 (inlet of 603) | 0.46 | 0.54 | 0.33 | 0.44 |
| Overall average score | 0.44 | 0.38 | 0.50 | 0.33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escobar Villanueva, J.R.; Iglesias Martínez, L.; Pérez Montiel, J.I. DEM Generation from Fixed-Wing UAV Imaging and LiDAR-Derived Ground Control Points for Flood Estimations. Sensors 2019, 19, 3205. https://doi.org/10.3390/s19143205
Escobar Villanueva JR, Iglesias Martínez L, Pérez Montiel JI. DEM Generation from Fixed-Wing UAV Imaging and LiDAR-Derived Ground Control Points for Flood Estimations. Sensors. 2019; 19(14):3205. https://doi.org/10.3390/s19143205
Chicago/Turabian StyleEscobar Villanueva, Jairo R., Luis Iglesias Martínez, and Jhonny I. Pérez Montiel. 2019. "DEM Generation from Fixed-Wing UAV Imaging and LiDAR-Derived Ground Control Points for Flood Estimations" Sensors 19, no. 14: 3205. https://doi.org/10.3390/s19143205
APA StyleEscobar Villanueva, J. R., Iglesias Martínez, L., & Pérez Montiel, J. I. (2019). DEM Generation from Fixed-Wing UAV Imaging and LiDAR-Derived Ground Control Points for Flood Estimations. Sensors, 19(14), 3205. https://doi.org/10.3390/s19143205






