A Robust Vision-Based Method for Displacement Measurement under Adverse Environmental Factors Using Spatio-Temporal Context Learning and Taylor Approximation
Abstract
1. Introduction
1.1. Background
1.2. Motivations and Objectives
2. Methodology
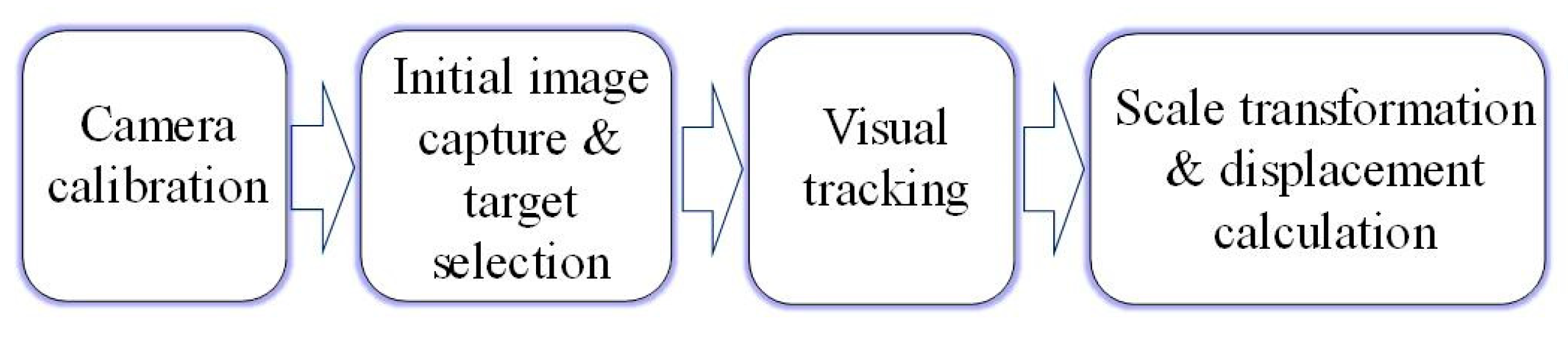
2.1. General Procedure of the Vision-Based Displacement Measurement Methods
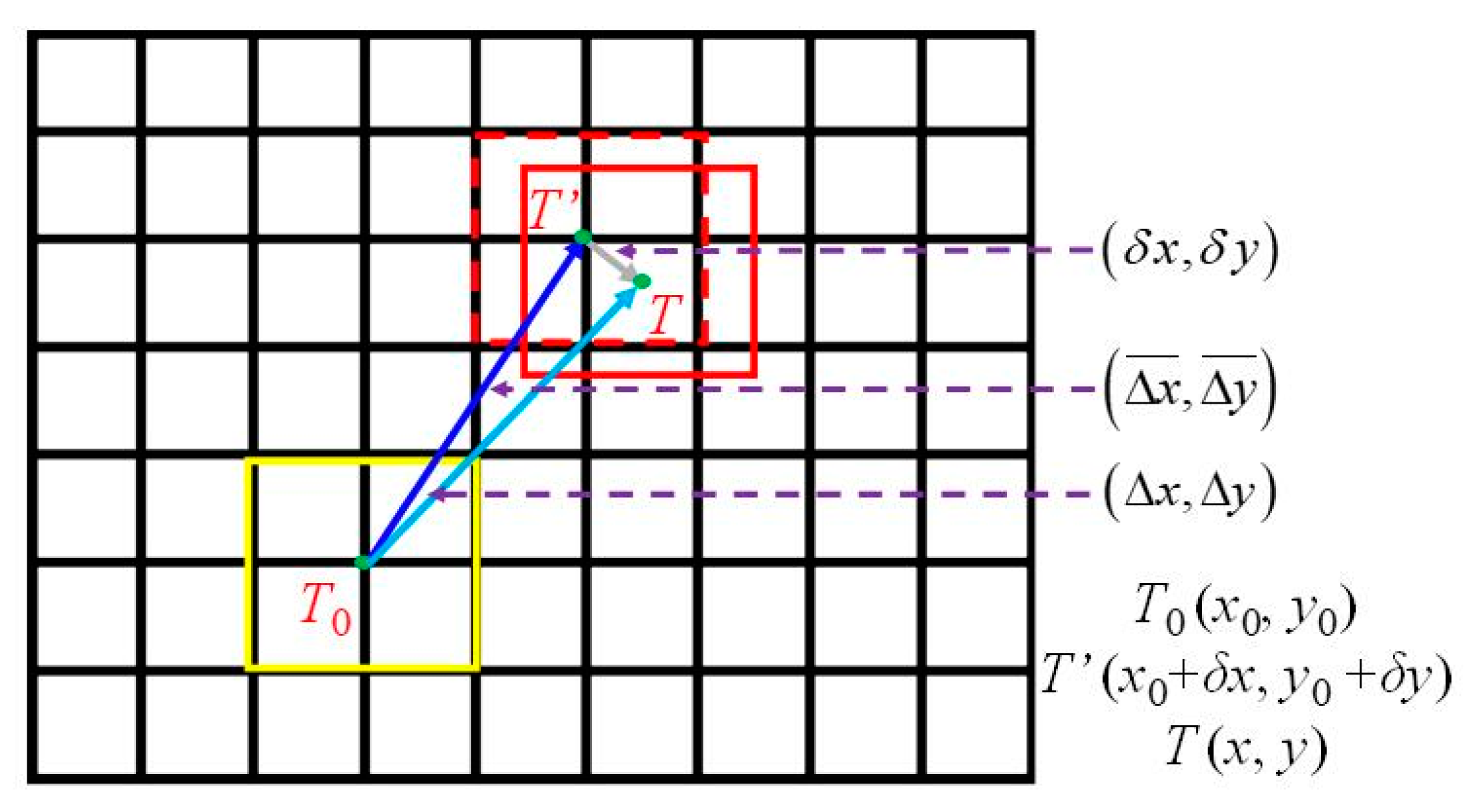
2.2. Visual Tracking Using Spatio-Temporal Context (STC) Learning
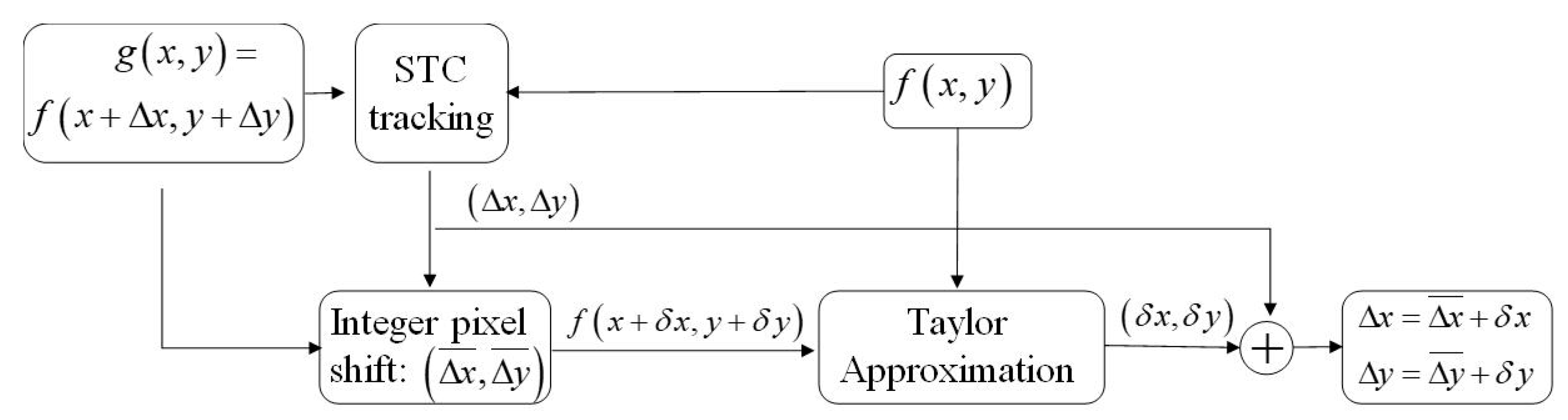
2.3. Subpixel Level Estimation Using Taylor Approximation
3. Laboratory Verification
3.1. Experimental Setup
- Case 1:
- The truck moves on the bridge in ideal conditions and no adverse factors are imposed in the measuring environment. A light meter (Dr. Meter LX1010B Digital Illuminance, London, England) is used to measure the illumination change. The illumination is 34 lux and the relative humidity is 49% at the displacement measurement location under the ideal conditions;
- Case 2:
- The truck moves on the bridge while the illumination of the laboratory is changed several times by switching a manual controller. Normally, 9 light panels in the lab are on and the illumination at the measurement location is 34 lux. By turning off the 3 light panels, which are close to the measurement target, the illumination drops to 18 lux. As shown in Figure 6, the left image is lighter, which was taken when the illumination was 34 lux, while the right image is darker which was taken when the illumination was 18 lux;
- Case 3:
- A humidifier (Honeywell HUL520B Mistmate Cool Mist Humidifier, Seattle, WA, USA) is placed between the camera and measuring targets (Figure 7). The humidifier produces a mist at the maximum status to simulate natural fog which decreases the visibility in the camera’s field of view. Normally, the temperature is 24 °C and the relative humidity is 49%. While in the center of the mist, the temperature is 20.3 °C and the relative humidity is 95%.
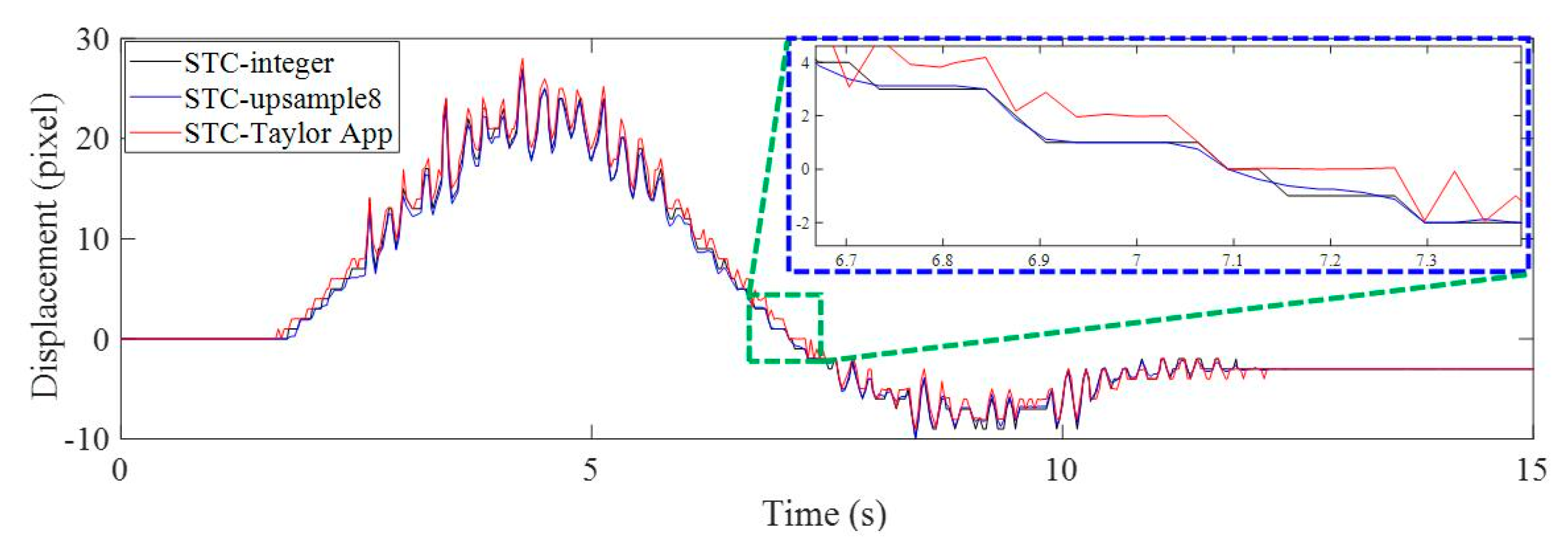
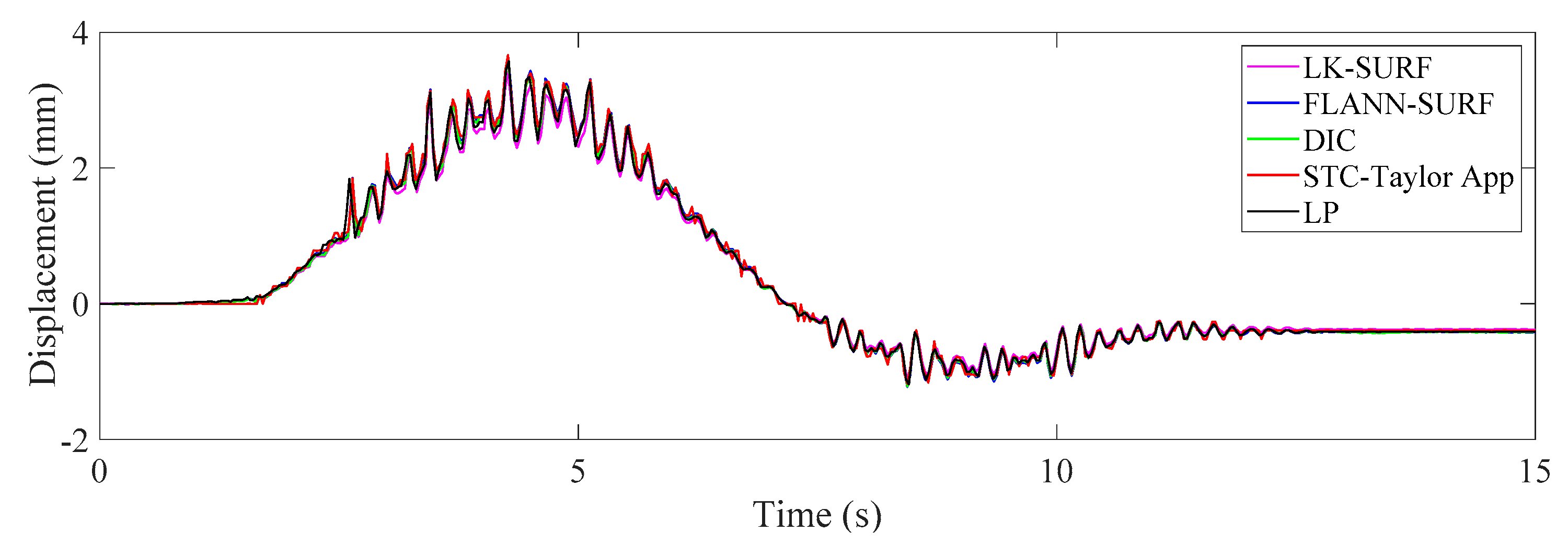
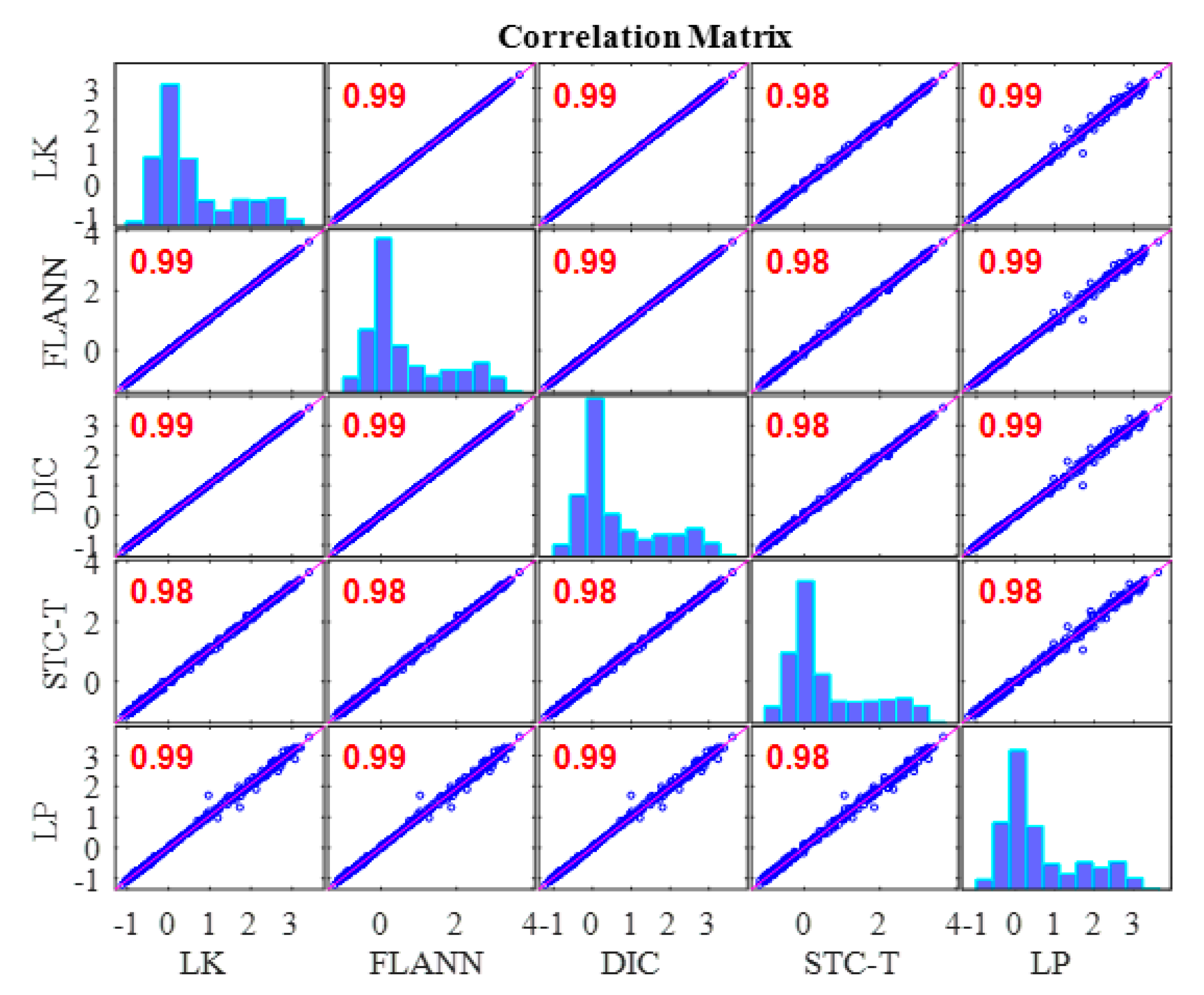
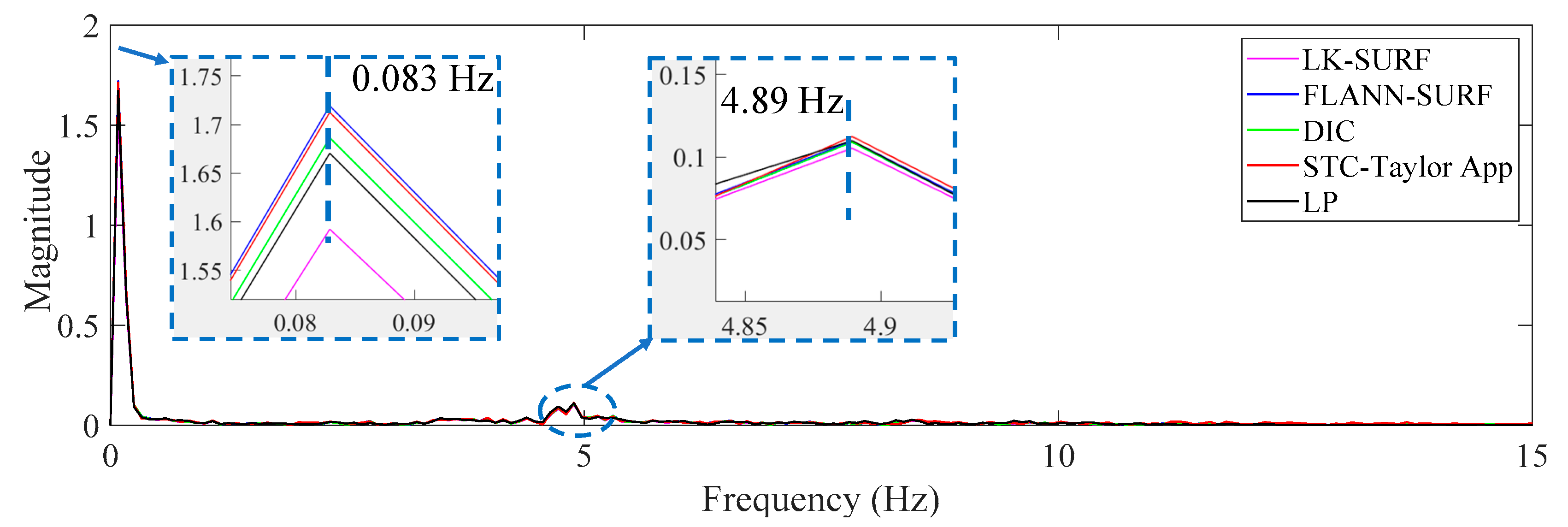
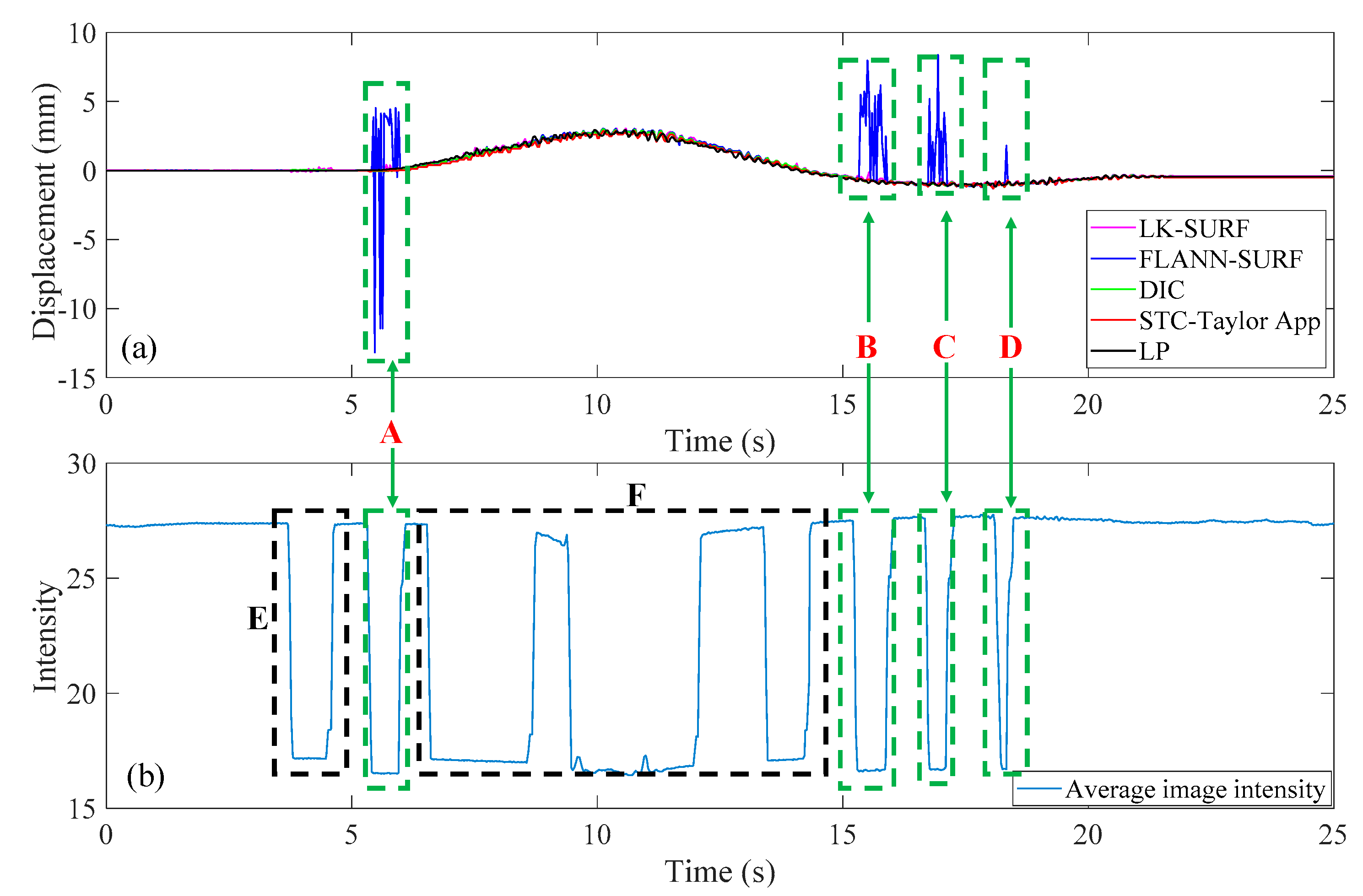
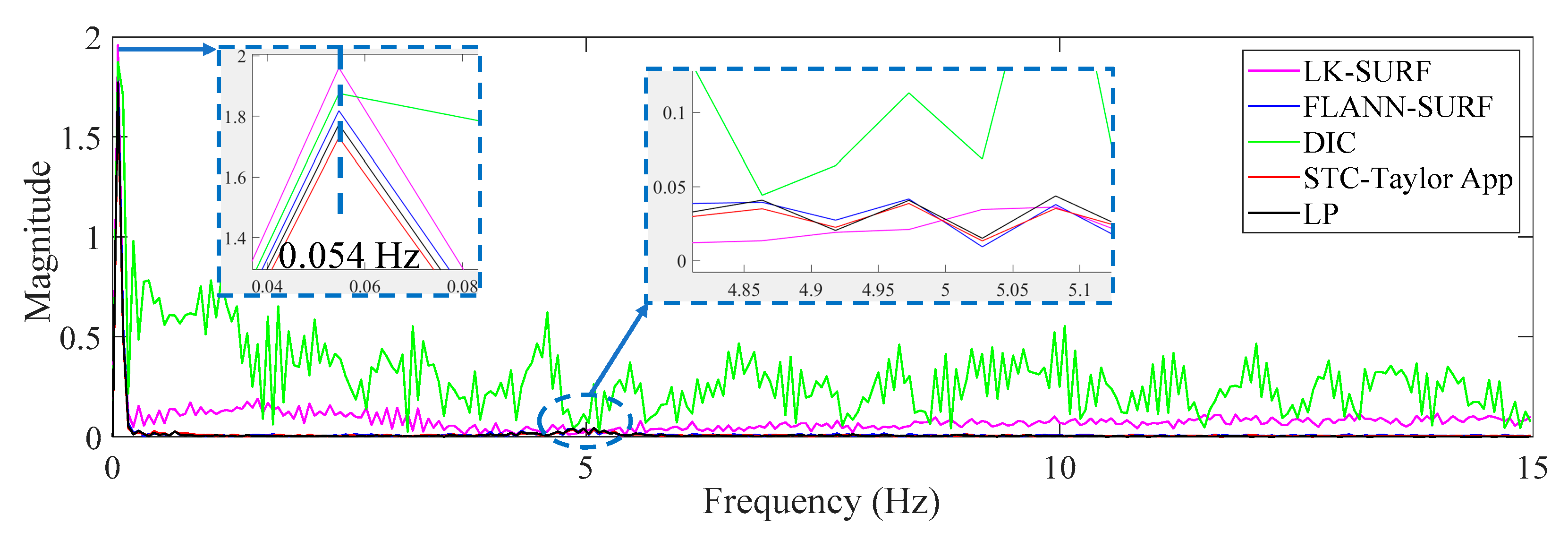
3.2. Results Analysis and Comparative Study of Case 1 (Ideal Case)
3.3. Results Analysis and Comparative Study of Case 2 (Illumination Change)
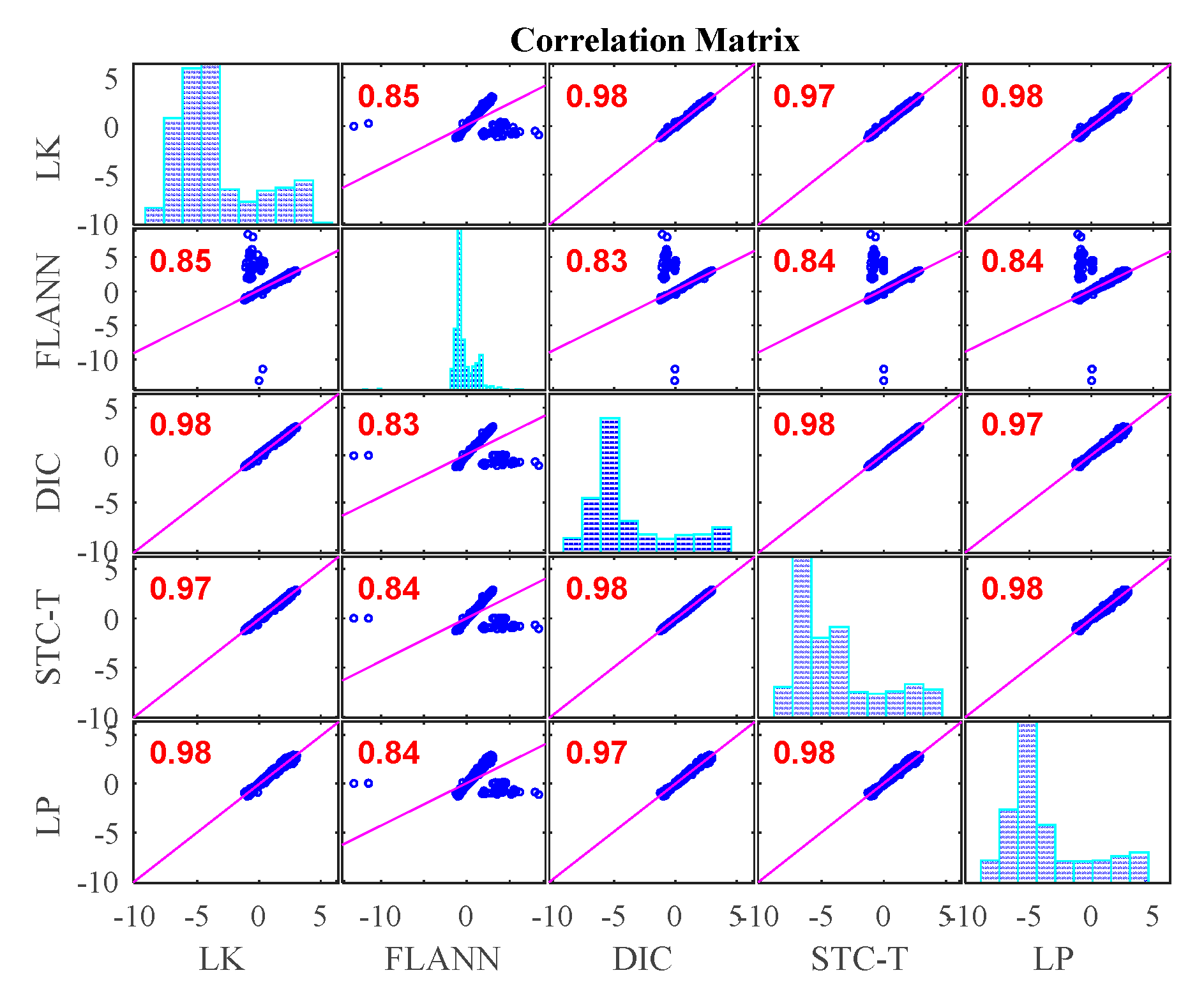
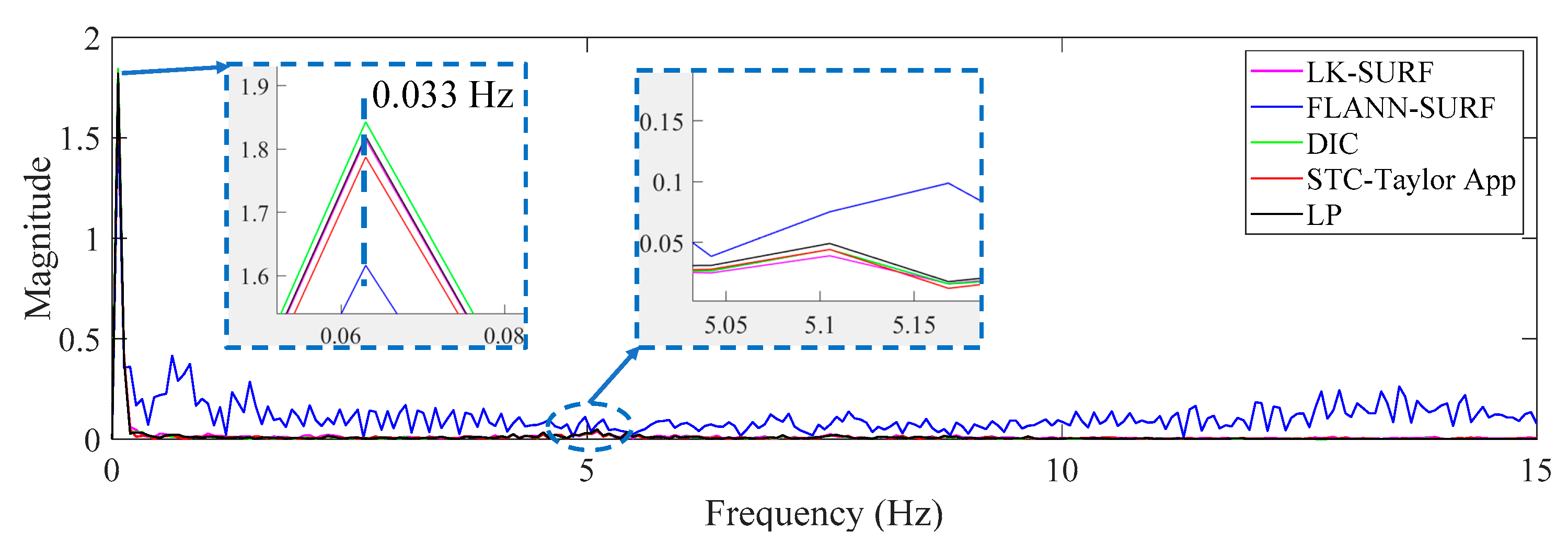
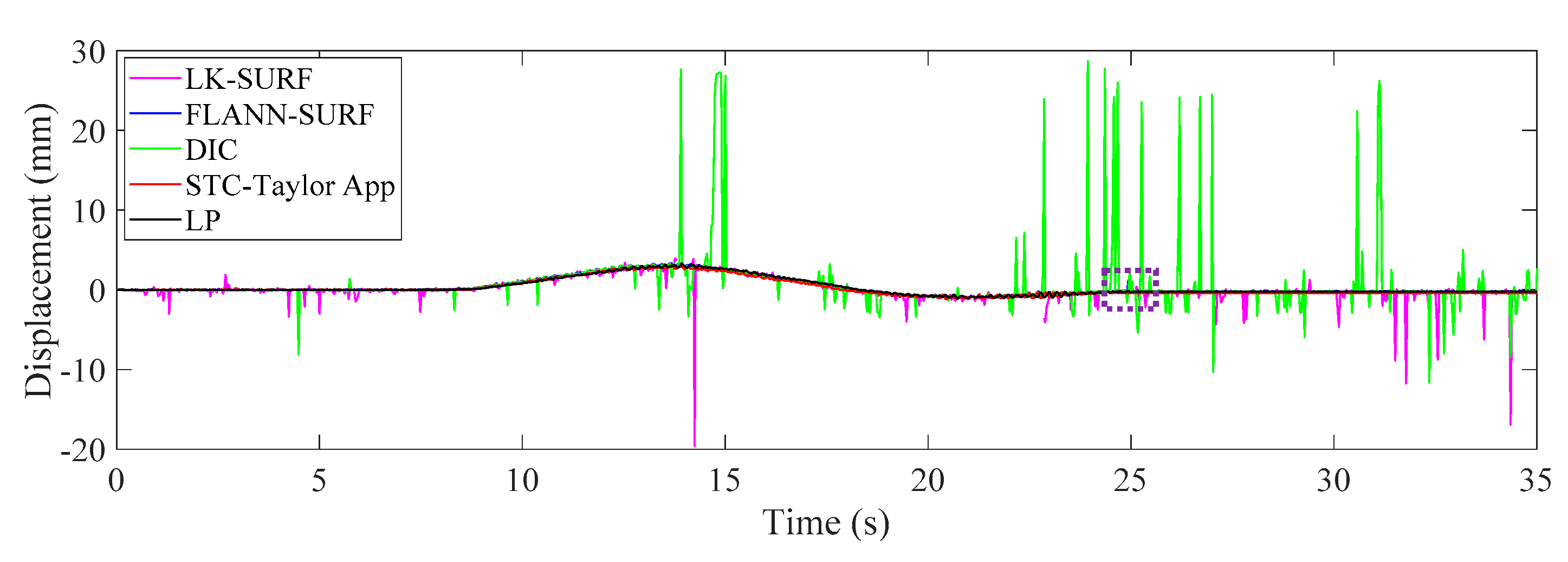
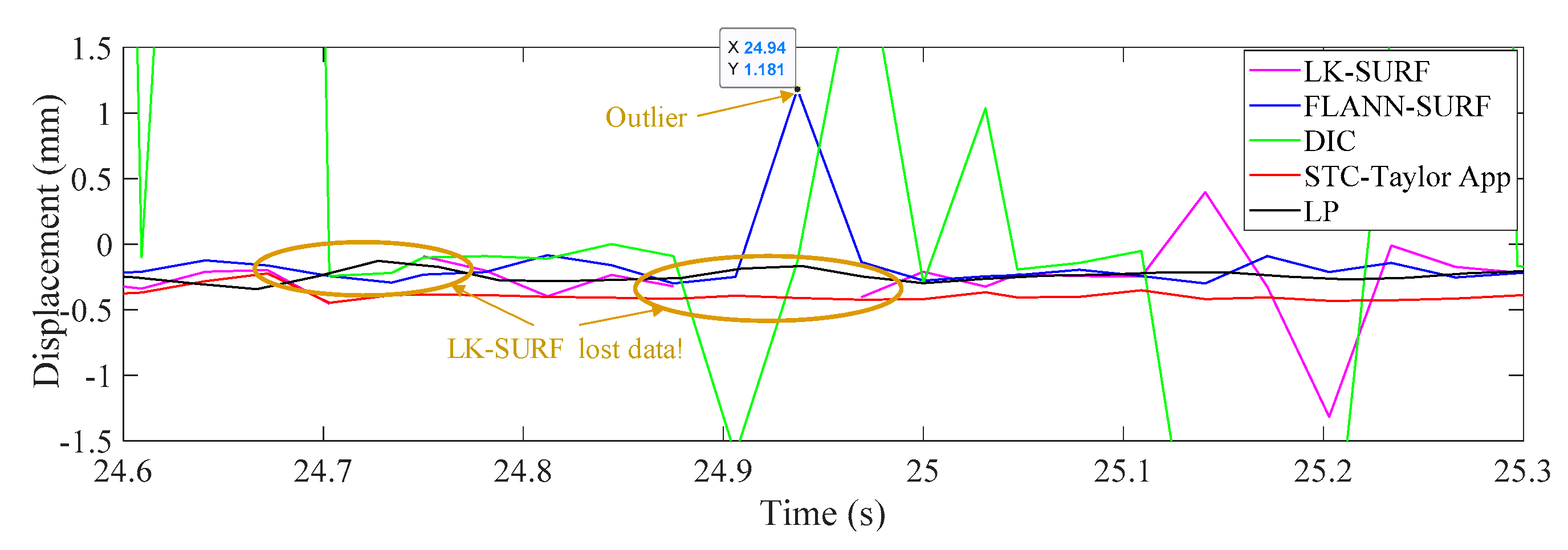
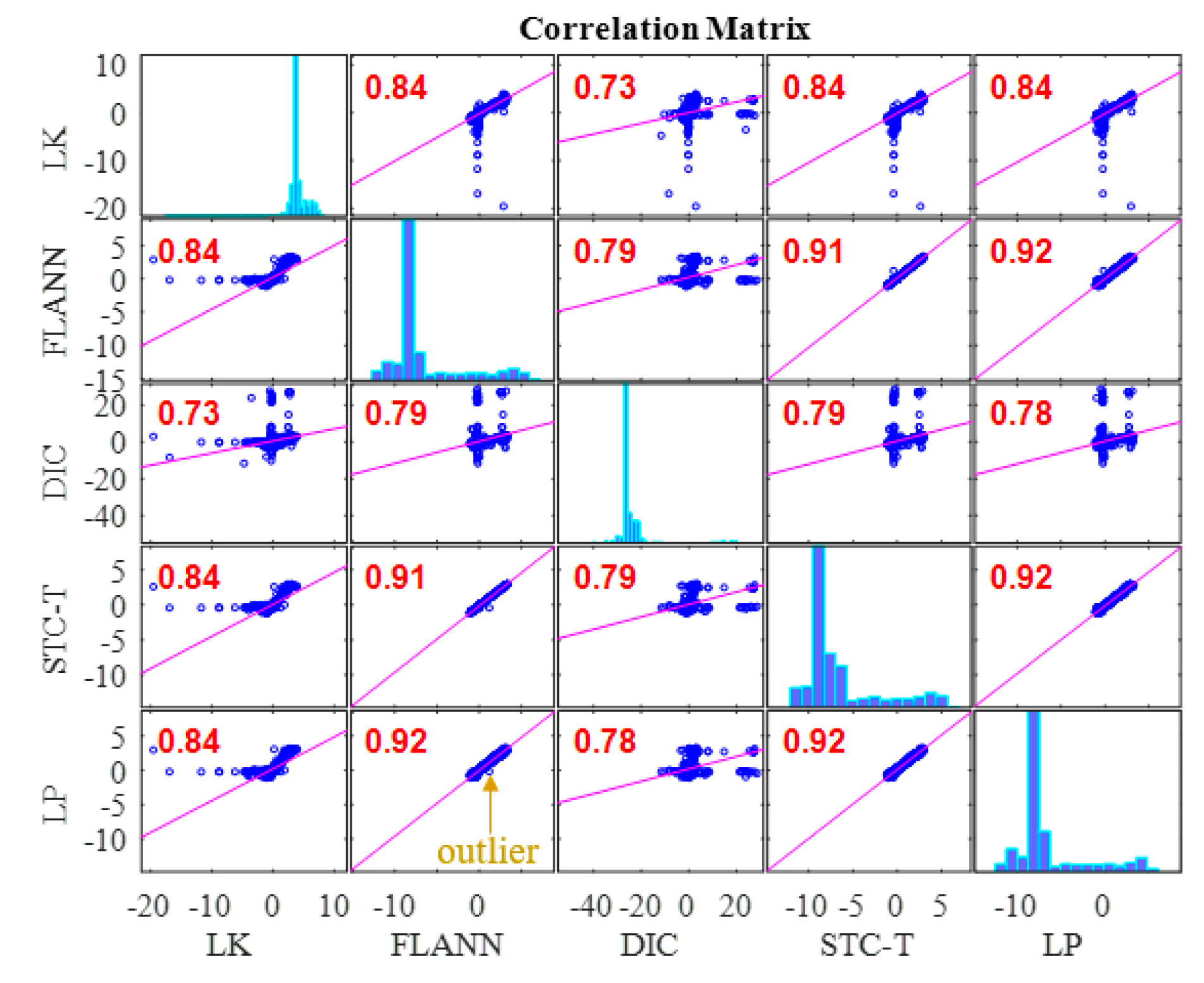
3.4. Results Analysis and Comparative Study of Case 3 (Fog Interference)
4. Conclusions
- In Case 1, there were no adverse environmental factors and the measurement condition was desirable for vision-based systems. The correlation coefficients of the LK-SURF, FLANN-SURF, and DIC with the ground truth, i.e., LP, were all 0.99, while the correlation coefficient between the proposed method, STC-Taylor App, and LP was 0.98, which was also quite good. It indicated that that at least in a desirable measurement environment, the proposed method is a strong competitor of the current methods.
- In Case 2, with the illumination change, the correlation coefficient of the time histories between that obtained from FLANN-SURF and the ground truth, LP, dropped to 0.84, while LK-SURF’s and DIC’s only dropped from 0.99 to 0.98 and from 0.99 to 0.97, respectively, compared with the correlation matrix obtained from Case 1. However, the correlation coefficient of the time histories between that obtained from the proposed method, STC-Taylor App, and the ground truth, LP, was still 0.98 comparing to that of Case 1.
- In Case 3, with the fog interference, the correlation coefficient between LK-SURF and LP dropped from 0.99 to 0.84, while DIC’s drops from 0.99 to 0.78, which was the worst performance. The FLANN-SURF’s dropped from 0.99 to 0.92 and the proposed method, STC-Taylor App, dropped from 0.98 to 0.92.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schumacher, T.; Shariati, A. Monitoring of structures and mechanical systems using virtual visual sensors for video analysis: Fundamental concept and proof of feasibility. Sensors 2013, 13, 16551–16564. [Google Scholar] [CrossRef]
- Dong, C.Z.; Celik, O.; Catbas, F.N. Marker free monitoring of the grandstand structures and modal identification using computer vision methods. Struct. Heal. Monit. 2018. [Google Scholar] [CrossRef]
- Khuc, T.; Catbas, F.N. Completely contactless structural health monitoring of real-life structures using cameras and computer vision. Struct. Control Heal. Monit. 2017, 24, e1852. [Google Scholar] [CrossRef]
- Xu, Y.; Brownjohn, J.M.W. Review of machine-vision based methodologies for displacement measurement in civil structures. J. Civ. Struct. Heal. Monit. 2018, 8, 91–110. [Google Scholar] [CrossRef]
- Brownjohn, J.M.W.; Xu, Y.; Hester, D. Vision-based bridge deformation monitoring. Front. Built Environ. 2017, 3, 1–16. [Google Scholar] [CrossRef]
- Yoon, H.; Elanwar, H.; Choi, H.; Golparvar-Fard, M.; Spencer, B.F. Target-free approach for vision-based structural system identification using consumer-grade cameras. Struct. Control Heal. Monit. 2016, 23, 1405–1416. [Google Scholar] [CrossRef]
- Celik, O.; Dong, C.Z.; Catbas, F.N. A computer vision approach for the load time history estimation of lively individuals and crowds. Comput. Struct. 2018, 200, 32–52. [Google Scholar] [CrossRef]
- Lydon, D.; Taylor, S.; Martinez del Rincon, J.; Hester, D.; Lydon, M.; Robinson, D. Field investigation of contactless displacement measurement using computer vision systems for civil engineering applications. In Proceedings of the Irish Machine Vision and Image Processing Conference-NUIG, Galway, UK, 25–26 August 2016. [Google Scholar]
- Chen, Y.; Joffre, D.; Avitabile, P. Underwater dynamic response at limited points expanded to full-field strain response. J. Vib. Acoust. 2018, 140, 051016. [Google Scholar] [CrossRef]
- Feng, M.Q.; Fukuda, Y.; Feng, D.; Mizuta, M. Nontarget vision sensor for remote measurement of bridge dynamic response. J. Bridg. Eng. 2015, 20, 4015023. [Google Scholar] [CrossRef]
- Fukuda, Y.; Feng, M.Q.; Shinozuka, M. Cost-effective vision-based system for monitoring dynamic response of civil engineering structures. Struct. Control Heal. Monit. 2010, 17, 918–936. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Vision-based multipoint displacement measurement for structural health monitoring. Struct. Control Heal. Monit. 2016, 23, 876–890. [Google Scholar] [CrossRef]
- Fukuda, Y.; Feng, M.Q.; Narita, Y.; Tanaka, T. Vision-based displacement sensor for monitoring dynamic response using robust object search algorithm. IEEE Sens. J. 2013, 13, 4725–4732. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q.; Ozer, E.; Fukuda, Y. A vision-based sensor for noncontact structural displacement measurement. Sensors 2015, 15, 16557–16575. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Experimental validation of cost-effective vision-based structural health monitoring. Mech. Syst. Signal Process. 2017, 88, 199–211. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Computer vision for SHM of civil infrastructure: From dynamic response measurement to damage detection-A review. Eng. Struct. 2018, 156, 105–117. [Google Scholar] [CrossRef]
- Khuc, T.; Catbas, F.N. Computer vision-based displacement and vibration monitoring without using physical target on structures. Struct. Infrastruct. Eng. 2016, 13, 1–12. [Google Scholar]
- Dong, C.Z.; Celik, O.; Catbas, N.F.; OBrien, E.J.; Taylor, S.E. Structural displacement monitoring using deep learning-based full field optical flow methods. Struct. Infrastruct. Eng. 2019. accepted. [Google Scholar]
- Dong, C.Z.; Catbas, F.N. A non-target structural displacement measurement method using advanced feature matching strategy. Adv. Struct. Eng. 2019. [Google Scholar] [CrossRef]
- Ye, X.W.; Yi, T.-H.; Dong, C.Z.; Liu, T.; Bai, H. Multi-point displacement monitoring of bridges using a vision-based approach. Wind Struct. Int. J. 2015, 20, 315–326. [Google Scholar] [CrossRef]
- Chen, J.G.; Wadhwa, N.; Cha, Y.J.; Durand, F.; Freeman, W.T.; Buyukozturk, O. Modal identification of simple structures with high-speed video using motion magnification. J. Sound Vib. 2015, 345, 58–71. [Google Scholar] [CrossRef]
- Chen, Y.; Logan, P.; Avitabile, P.; Dodson, J. Non-model based expansion from limited points to an augmented set of points using chebyshev polynomials. Exp. Tech. 2019, 1–23. [Google Scholar] [CrossRef]
- Lee, J.J.; Cho, S.; Shinozuka, M. Evaluation of bridge load carrying capacity based on dynamic displacement measurement using real-time image processing techniques. Steel Struct. 2006, 6, 377–385. [Google Scholar]
- Ojio, T.; Carey, C.H.; OBrien, E.J.; Doherty, C.; Taylor, S.E. Contactless Bridge weigh-in-motion. J. Bridg. Eng. 2016, 21, 04016032. [Google Scholar] [CrossRef]
- Dong, C.Z.; Bas, S.; Catbas, F.N. A completely non-contact recognition system for bridge unit influence line using portable cameras and computer vision. Smart Struct. Syst. 2019. accepted. [Google Scholar]
- Khuc, T.; Catbas, F.N. Structural identification using computer vision–based bridge health monitoring. J. Struct. Eng. 2018, 144. [Google Scholar] [CrossRef]
- Catbas, F.N.; Dong, C.Z.; Celik, O.; Khuc, T. A vision for vision-based technologies for bridge health monitoring. In Proceedings of the Ninth International Conference on Bridge Maintenance, Safety and Management (IABMAS 2018), Melbourne, Australia, 9–13 July 2018; p. 54. [Google Scholar]
- Ji, Y.F.; Chang, C.C. Nontarget image-based technique for small cable vibration measurement. J. Bridg. Eng. 2008, 13, 34–42. [Google Scholar] [CrossRef]
- Ji, Y.F.; Chang, C.C. Nontarget stereo vision technique for spatiotemporal response measurement of line-like structures. J. Eng. Mech. 2008, 134, 466–474. [Google Scholar] [CrossRef]
- Chen, C.C.; Wu, W.H.; Tseng, H.Z.; Chen, C.H.; Lai, G. Application of digital photogrammetry techniques in identifying the mode shape ratios of stay cables with multiple camcorders. Meas. J. Int. Meas. Confed. 2015, 75, 134–146. [Google Scholar] [CrossRef]
- Poozesh, P.; Baqersad, J.; Niezrecki, C.; Avitabile, P.; Harvey, E.; Yarala, R. Large-area photogrammetry based testing of wind turbine blades. Mech. Syst. Signal Process. 2017, 86, 98–115. [Google Scholar] [CrossRef]
- Dong, C.Z.; Ye, X.W.; Jin, T. Identification of structural dynamic characteristics based on machine vision technology. Meas. J. Int. Meas. Confed. 2018, 126, 405–416. [Google Scholar] [CrossRef]
- Fioriti, V.; Roselli, I.; Tatì, A.; Romano, R.; De Canio, G. Motion Magnification Analysis for structural monitoring of ancient constructions. Meas. J. Int. Meas. Confed. 2018, 129, 375–380. [Google Scholar] [CrossRef]
- Yang, Y.; Dorn, C.; Mancini, T.; Talken, Z.; Theiler, J.; Kenyon, G.; Farrar, C.; Mascareñas, D. Reference-free detection of minute, non-visible, damage using full-field, high-resolution mode shapes output-only identified from digital videos of structures. Struct. Heal. Monit. 2018, 17, 514–531. [Google Scholar] [CrossRef]
- Yang, Y.; Dorn, C.; Mancini, T.; Talken, Z.; Nagarajaiah, S.; Kenyon, G.; Farrar, C.; Mascarenas, D. Blind identification of full-field vibration modes of output-only structures from uniformly-sampled, possibly temporally-aliased (sub-Nyquist), video measurements. J. Sound Vib. 2017, 390, 232–256. [Google Scholar] [CrossRef]
- Yang, Y.; Dorn, C.; Mancini, T.; Talken, Z.; Kenyon, G.; Farrar, C.; Mascarenas, D. Blind identification of full-field vibration modes from video measurements with phase-based video motion magnification. Mech. Syst. Signal Process. 2017, 85, 567–590. [Google Scholar] [CrossRef]
- Cha, Y.J.; Chen, J.G.; Büyüköztürk, O. Output-only computer vision based damage detection using phase-based optical flow and unscented Kalman filters. Eng. Struct. 2017, 132, 300–313. [Google Scholar] [CrossRef]
- Yang, Y.; Nagarajaiah, S. Dynamic Imaging: Real-time detection of local structural damage with blind separation of low-rank background and sparse innovation. J. Struct. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Model updating of railway bridge using in situ dynamic displacement measurement under trainloads. J. Bridg. Eng. 2015, 20, 1–12. [Google Scholar] [CrossRef]
- Ye, X.W.; Dong, C.Z.; Liu, T. Force monitoring of steel cables using vision-based sensing technology: Methodology and experimental verification. Smart Struct. Syst. 2016, 18, 585–599. [Google Scholar] [CrossRef]
- Feng, D.; Scarangello, T.; Feng, M.Q.; Ye, Q. Cable tension force estimate using novel noncontact vision-based sensor. Meas. J. Int. Meas. Confed. 2017, 99, 44–52. [Google Scholar] [CrossRef]
- Ye, X.W.; Dong, C.Z.; Liu, T. A review of machine vision-based structural health monitoring: Methodologies and applications. J. Sensors 2016, 2016, 7103039. [Google Scholar] [CrossRef]
- Ma, S.; Pang, J.; Ma, Q. The systematic error in digital image correlation induced by self-heating of a digital camera. Meas. Sci. Technol. 2012, 23, 025403. [Google Scholar] [CrossRef]
- Ye, X.W.; Yi, T.H.; Dong, C.Z.; Liu, T. Vision-based structural displacement measurement: System performance evaluation and influence factor analysis. Meas. J. Int. Meas. Confed. 2016, 88, 372–384. [Google Scholar] [CrossRef]
- Dong, C.Z.; Ye, X.W.; Liu, T. Non-contact structural vibration monitoring under varying environmental conditions. Vibroeng. Procedia 2015, 5, 217–222. [Google Scholar]
- Ye, X.W.; Dong, C.Z.; Liu, T. Environmental effect on vision-based structural dynamic displacement monitoring. In Proceedings of the Second International Conference on Performance–based and Life-cycle Structural Engineering (PLSE 2015), Brisbane, Australia, 9–15 December 2015; Dilum, F., Teng, J.-G., Torero, J.L., Eds.; University of Queensland: Brisbane, Australia, 2015; pp. 261–265. [Google Scholar]
- Zhang, K.; Zhang, L.; Yang, M.H.; Zhang, D. Fast tracking via spatio-temporal context learning. arXiv 2013, arXiv:1311.1939, 1–16. [Google Scholar]
- Chan, S.H.; Vo, D.T.; Nguyen, T.Q. Subpixel motion estimation without interpolation. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, La Jolla, CA, USA, 14–19 March 2010; pp. 722–725. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration (technical report). IEEE Trans. Pattern Anal. Mach. Intell. 2002, 22, 1330–1334. [Google Scholar] [CrossRef]
- Ye, X.W.; Dong, C.Z.; Liu, T. Image-based structural dynamic displacement measurement using different multi-object tracking algorithms. Smart Struct. Syst. 2016, 17, 935–956. [Google Scholar] [CrossRef]
- Ye, X.W.; Dong, C.Z. Fatigue cracking identification of reinforced concrete bridges using vision-based sensing technology. In Proceedings of the 24th Australasian Conference on the Mechanics of Structures and Materials, Perth, Australia, 6 June 2017; pp. 1141–1146. [Google Scholar]
- Oppenheim, A.V.; Willsky, A.S.; Nawab, S.H. Signals and Systems, 2nd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1996; ISBN 0-13-814757-4. [Google Scholar]
- BEI 9600 Series Sensors. Available online: https://www.mouser.com/datasheet/2/657/linear-position-sensor_9600-1062977.pdf (accessed on 18 July 2019).




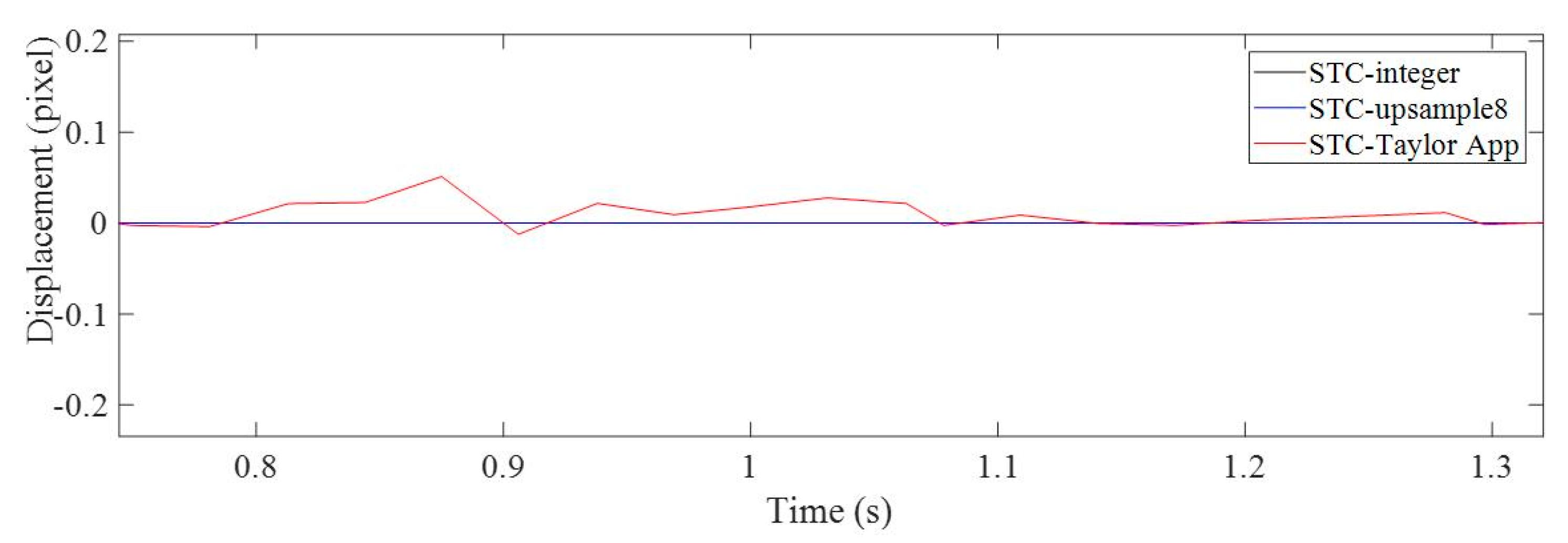
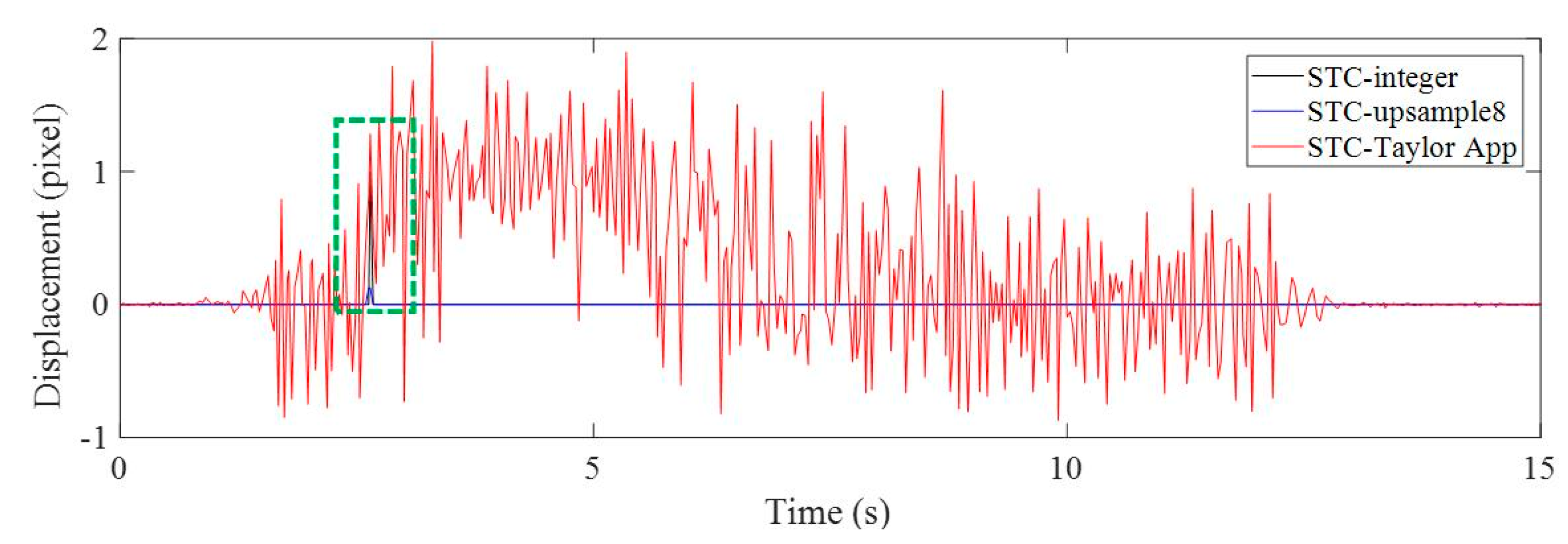
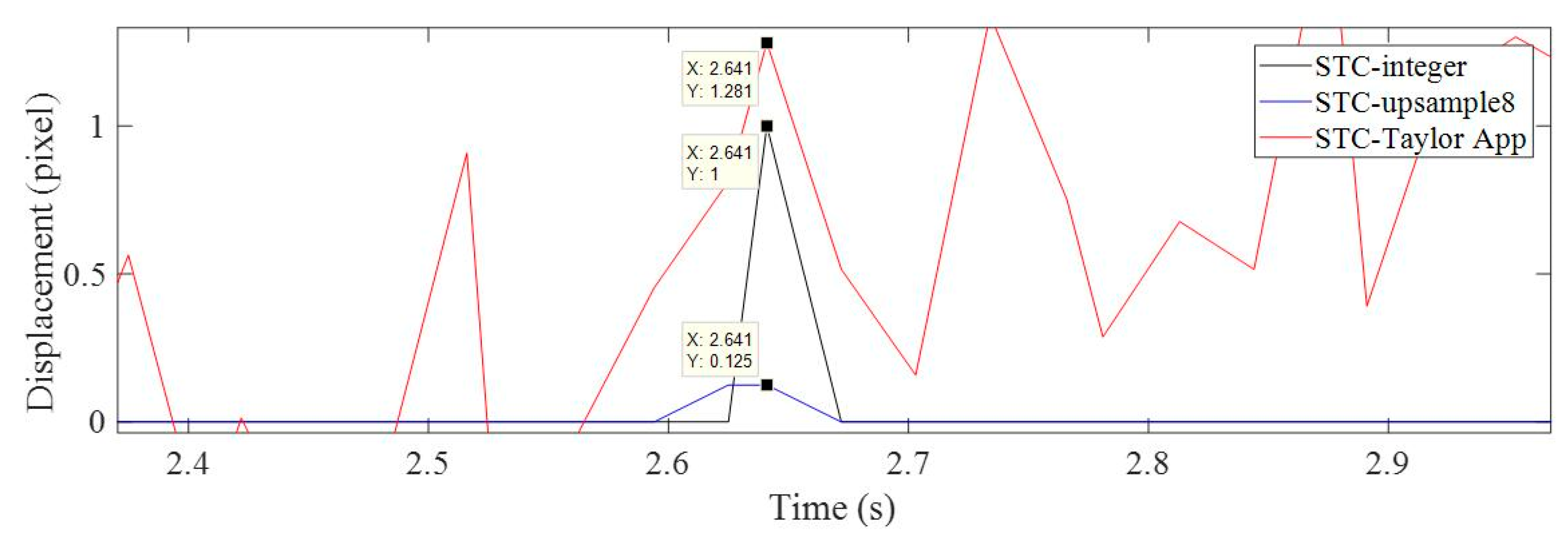

| Methods | STC-Integer | STC-Upsample8 | STC-Taylor App |
|---|---|---|---|
| Time(s) | 0.0481 | 2.4895 | 0.0495 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, C.-Z.; Celik, O.; Catbas, F.N.; OBrien, E.; Taylor, S. A Robust Vision-Based Method for Displacement Measurement under Adverse Environmental Factors Using Spatio-Temporal Context Learning and Taylor Approximation. Sensors 2019, 19, 3197. https://doi.org/10.3390/s19143197
Dong C-Z, Celik O, Catbas FN, OBrien E, Taylor S. A Robust Vision-Based Method for Displacement Measurement under Adverse Environmental Factors Using Spatio-Temporal Context Learning and Taylor Approximation. Sensors. 2019; 19(14):3197. https://doi.org/10.3390/s19143197
Chicago/Turabian StyleDong, Chuan-Zhi, Ozan Celik, F. Necati Catbas, Eugene OBrien, and Su Taylor. 2019. "A Robust Vision-Based Method for Displacement Measurement under Adverse Environmental Factors Using Spatio-Temporal Context Learning and Taylor Approximation" Sensors 19, no. 14: 3197. https://doi.org/10.3390/s19143197
APA StyleDong, C.-Z., Celik, O., Catbas, F. N., OBrien, E., & Taylor, S. (2019). A Robust Vision-Based Method for Displacement Measurement under Adverse Environmental Factors Using Spatio-Temporal Context Learning and Taylor Approximation. Sensors, 19(14), 3197. https://doi.org/10.3390/s19143197






