1. Introduction
With the development of mobile networks and smart terminals, mobile crowdsourcing [
1,
2] has gradually evolved into a novel distributed problem-solving paradigm, which uses popular mobile users to collect and process data beyond the past possible range and has become an important research hotspot. The proliferation of smartphones makes mobile crowdsensing applications possible. Newzoo’s “2018 Global Mobile Markets Report” [
3] shows that the number of global smartphone users has exceeded 3.3 billion so far. As mobile data and hardware become cheaper in the next few years, the number of smartphone users is expected to reach 3.8 billion by 2021, which means there are a large number of potential users in mobile crowdsourcing applications. Furthermore, smartphones are equipped with a variety of powerful built-in sensors, such as GPS, camera, accelerometer, microphone, etc., which enable crowdsourcing users to easily collect basic data of various applications and send sensing data to crowdsourcing platforms.
Inspired by the current popular smart city testbeds [
4,
5], a typical mobile crowdsourcing platform was proposed. As shown in
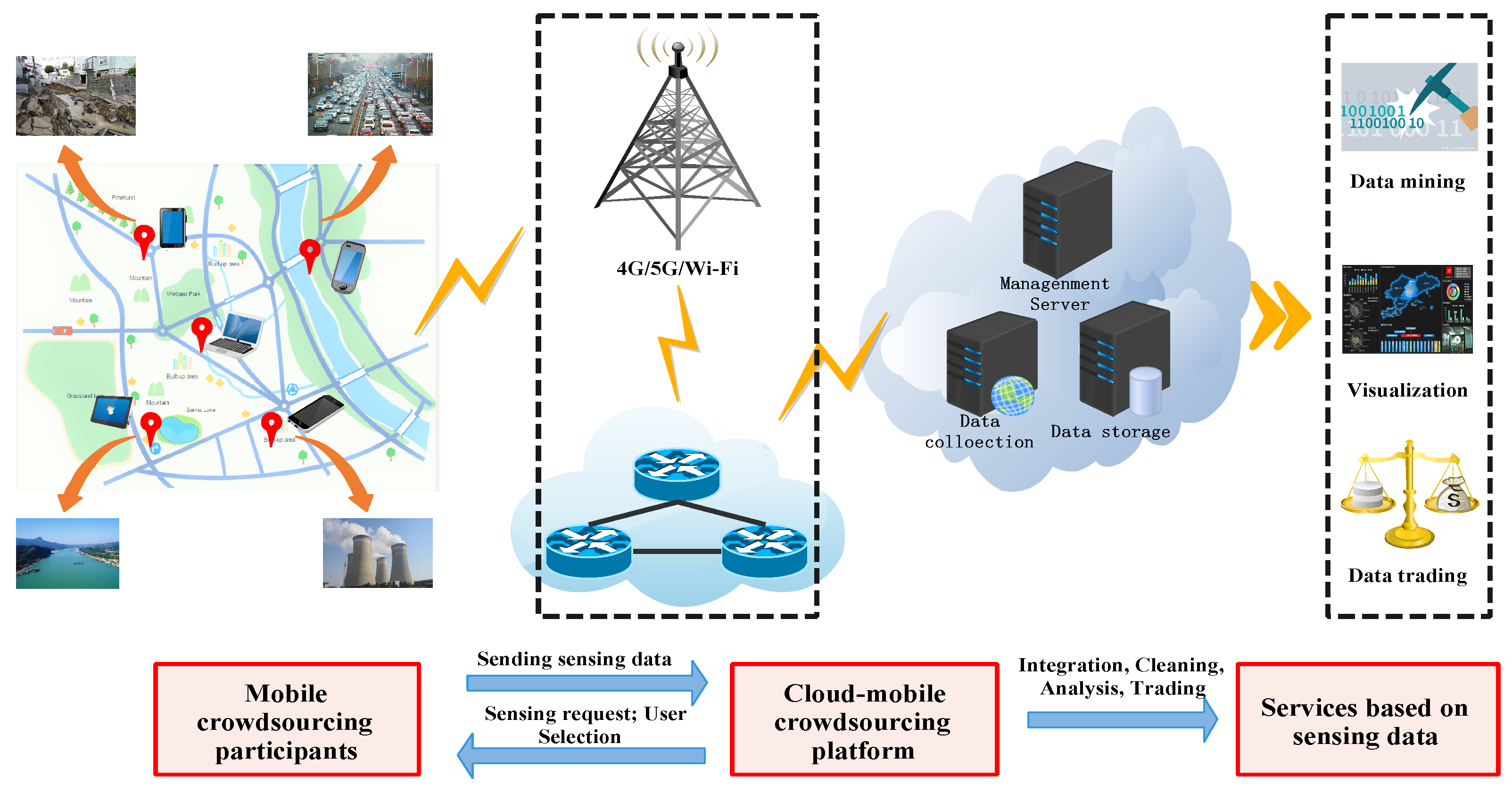
Figure 1, the mobile crowdsourcing system consists of a large group of crowdsourcing participants distributed in a specific area and a crowdsourcing platform in the cloud, which is connected by mobile network or WiFi. Crowdsourcing participants(a.k.a, Users) use smart devices for road condition monitoring [
6], pollution monitoring [
7], location services [
8], natural disaster assessment [
9], etc., and send sensing data to crowdsourcing platforms. However, users consume their resources in performing tasks, such as batteries and computing power. Due to the diversity of individuals and smart devices, the cost of performing tasks is not the same. So they need to get different rewards from crowdsourcing platforms to continue their cooperation. Crowdsourcing platform provides a centralized management platform for sensing data receipt, integration, cleaning, analysis, and further building applications of interest, such as data mining, visualization and data trading, etc. In addition, the crowdsourcing platform has the right to publish tasks and select users.
To maximize crowdsourcing quality, the crowdsourcing platform needs to select the best subset of users available by matching the task requirements to the user’s profile, which is not easy. Crowdsourcing quality is affected by many factors. In addition to spatial location, existing research [
10,
11] has shown that user reputation, credibility, and time required to complete a perceived task have a significant impact on the quality of crowdsourcing. However, meeting the multi-objective constraints of mobile crowdsourcing remains a challenge. We need to consider not only the distance between the user and the task, but also the completion time of the task, the reputation and credibility of the users. In addition, under the above constraints, how to further select suitable users for the existing mobile crowdsourcing tasks to maximize the quality of crowdsourcing and minimize the incentive budget (i.e., minimum the total incentive cost of the selected users) is a major challenge for the crowdsourcing platform, which is called the mobile crowdsourcing user selection (MCUS) problem.
In truth, these two objectives are contradictory. If we improve one objective, the other will be reduced accordingly. As shown in literature [
12], there is no optimal solution that can improve multi-objectives at the same time, but a set of pareto optimal solutions. To solve the problem, there are two standard approaches to formalize the problem: one is to find a subset of users that maximizes the crowdsourcing quality under a given budget; the other is to find a subset of users that minimizes the budget while meeting the minimum crowdsourcing quality requirements.
However, neither of the above methods is ideal in our context, because they all have an artificial predefined condition. Until the available users are selected, the mobile crowdsourcing platform often does not know how well the published tasks match the users. Therefore, it is unrealistic to require the crowdsourcing platform to predetermine a reasonable boundary to achieve a satisfactory compromise between multi-objective. The following two examples illustrate the limitations of both approaches.
Example 1. For simplicity, two potential users are shown in Table 1a, where Quality is the quality of service for users and Cost is the compensation for users. Assume that the upper limit of the budget cost of the crowdsourcing platform is pre-specified at $10. Not surprisingly, User X will be selected and not further inspect User Y. In fact, we can increase the cost slightly to get a more substantial profit. In other words, we increase the cost by $1, but we can get 80% of the service quality (improved by 30%). Arguably, it is worth spending some extra resources. Example 2. Similarly, two other users are shown in Table 1b. Assuming that the lower bound of the crowdsourcing quality is predetermined to be 80%, then User A will be selected and User B will not be further examined. In fact, achieving a cost reduction of $6 by slightly relaxing the requirements for crowdsourcing quality (i.e., 2%) is significantly cost effective. In practice, both of these scenarios are inevitable because we do not know the distribution of the different solutions and may miss a more desirable solution. Therefore, we need to find all the marginal points before we stop investigation. In other words, we will provide all the pareto-optimal solutions for the crowdsourcing platform to make a reasonable decision.
As mentioned earlier, we can’t use the previous methods to solve the user selection problem in mobile crowdsourcing, which is provably a NP-hard problem. To address this challenge, we have made the following significant contributions.
We propose a scheme inspired by the principle of marginalism in microeconomics, and the problem of user selection in mobile crowdsourcing is formally defined in
Section 3. Assuming that the same unit can be used to measure gain and cost in a crowdsourcing platform, we wish to stop selecting new users when the marginal gain is lower than the marginal cost. The marginal gain here refers to the difference between the benefit after and before the selection of users.
In
Section 4, we propose various gain-cost models driven by the Quality of Service (QoS), which provides a basis for evaluating the value of users’ contribution.
We prove that user selection problem is NP-hard in
Section 4.1. Then we propose a greedy random adaptive procedure with annealing randomness (GRASP-AR) to solve the user selection problem in
Section 4.2.
We conduct extensive experiments using real-world and synthetic data sets to evaluate our proposed algorithms on large-scale environment. The results show the effectiveness and efficiency of our proposed approaches in
Section 5.
In addtion, we review the previous work on mobile crowdsourcing in
Section 2.
Section 6 concludes the paper and lay out a research agenda.
4. Optimization Algorithm
In this section, we first analyze the complexity of solving MCUS Marginalism problem, and we rigorously prove that MCUS Marginalism problem is a NP-hard problem. Then we propose a greedy random adaptive procedure with annealing randomness(GRASP-AR), which attempt to overcome the limitations of deterministic algorithms (based on adding what is apparently the best element to the partial solution), that is, our algorithms strive to ensure that the solution is globally optimal because they explore the search space in a comprehensive way.
4.1. Complexity Analysis of MCUS Marginalism Problem
It is very important to solve the MCUS Marginalism problem with an efficient algorithm. Unfortunately, as we will prove next, MCUS Marginalism problem is a NP-hard.
Theorem 1. MCUS Marginalism problem defined in Defintion 7 is a NP-hard Problem.
Proof. The Marginalism problem can be proved by reducing problem. Further, we can prove that the decision version of is NP-complete. Next, we should find a known NPC problem and then try to reduce it.
We use the knapsack problem as a known NP complete problem. The knapsack problem is defined as follows. For an instance A of knapsack problem and a set of object with value and weight, where is represented by and respectively. The question is whether exists a set that maximizes the value of members from (i.e., ), and further , where is upper bound of the capability.
Next, we change instance A to an instance of . We construct a user instance B with cost upper bound , and represent it as . For each , its gain and cost are and , respectively. The problem is to find a set to maximize the gain from the members of (i.e., ), and further . We assume that can be used as a solution for instance A. By trying to select users in the set U, the formed can be used as a solution for .
With the construction approach of the solution, and a maximal imply and a maximal , respectively.
Then, we can simply see that the reduction from A to B ends in polynomial time, since the knapsack problem is a NP-hard problem, so the is NP-hard. While Marginalism problem can be reduced to , so Marginalism problem is also a NP-hard problem. □
4.2. GRASP with Annealing Randomness (GRASP-AR)
In the previous section, we have shown that MCUS marginalism problem is a NP-hard problem. As the scale of users continues to expand, solving MCUS Marginalism problem is limited by both memory and time. In practice, the number of decision variables increases exponentially as the scale of users increases. Even if computing resources can increase indefinitely, the exact solution may not be found in a reasonable amount of time. To address the problem, we proposed a greedy randomized adaptive search procedure with annealing randomness as a trade-off between computation time and quality of found solutions.
GRASP [
39,
40] is a multi-start meta-heuristic algorithm, which consists of two phases: construction phase and local search phase. In the construction phase, the iterative constructs a feasible solution, one element at a time. The greedy randomized algorithm is first used to select the top-
k candidates from the generated profits, and the best solution is selected from multiple iterations. The algorithm is adaptive and provides a good initial solution while maintaining a certain degree of diversification to avoid convergence toward local optima. In the local search phase, we introduce a simulated annealing (SA) [
41] meta-heuristic, whose effectiveness depends on the fact that it accepts a non-improved solution within a certain probability. In other words, it can accept a solution that is worse than the best solution found at the time. The probability of this solution depends on the degree to which the new solution differs from the optimal solution and a further parameter, the synthesis temperature excited by the metallurgical annealing process. As the value of the parameter decreases gradually, the randomness of the method also gradually decreases (the lower the value, the lower the randomness). Because SA can search for feasible solutions in a larger range, making it possible for the algorithm to jump out of the local optimal solution and find a global optimal solution.
| Algorithm 1: GRASP-AR. |
![Sensors 19 03158 i001 Sensors 19 03158 i001]() |
Algorithm 1 introduces the main processing phases of GRASP-AR. The algorithm ensures that a subset of users with the largest marginal gain is found. The algorithm performs iterations. In each iteration, the construction phase constructs an initial solution , then the local search phase uses a simulated annealing strategy to further find a viable solution in the neighborhood. Finally, it returns the best solution from all iterations.
The construction process of greedy randomized is given in Algorithm 2. First, a given set of candidate users is initialized and a group of users is added iteratively in a greedy randomized. In each iteration (Step. 2–14), we select the user with the maximum incremental gain from the remaining user set U∖ (Step. 5). In other words, we check one by one whether the maximum gain achieved by the remaining users can exceed the current best solution, and skips the user if not. Next, Step. 6 evaluates the difference between the marginal gain and marginal cost of the selected users. The top-k user sets are selected in this way (Step. 7–10). Finally, Step. 12–15 choose subset of users with the highest gain.
| Algorithm 2: Procedure BuildSolution(). |
![Sensors 19 03158 i002 Sensors 19 03158 i002]() |
| Algorithm 3: Procedure LocalSearch(U, , G, C, k). |
![Sensors 19 03158 i003 Sensors 19 03158 i003]() |
The local search phase takes the initial solution as input and iteratively explores its neighborhood for a better solution. In this work, we introduce SA meta heuristic method. SA is a general probability algorithm. Its starting point is based on the annealing process of solid materials in metallurgical processes. It is initialized with a parameter called temperature, denoted T, which accepts a non-improved solution within a certain probability. According to the cooling rate factor , the temperature slowly drops during execution. The lower the temperature, the lower the probability of choosing a worse solution in the next iteration.
The proposed SA is given in Algorithm 3. First, it takes the construction phase of the solution as input, which is the best solution found so far. Next, in each iteration, it compares the current solution with (1) the solution of removing u (2) the candidate solution with the remaining user subset replacement u, and represents the difference between them as . If the candidate solution is better, consider it as the current solution and update the best solution found. If the candidate solution is worse, it is accepted as the new current solution with the probability . Finally, the temperature decreases with the cooling factor until the preset minimum temperature stops.