Compressed Sensing Radar Imaging: Fundamentals, Challenges, and Advances
Abstract
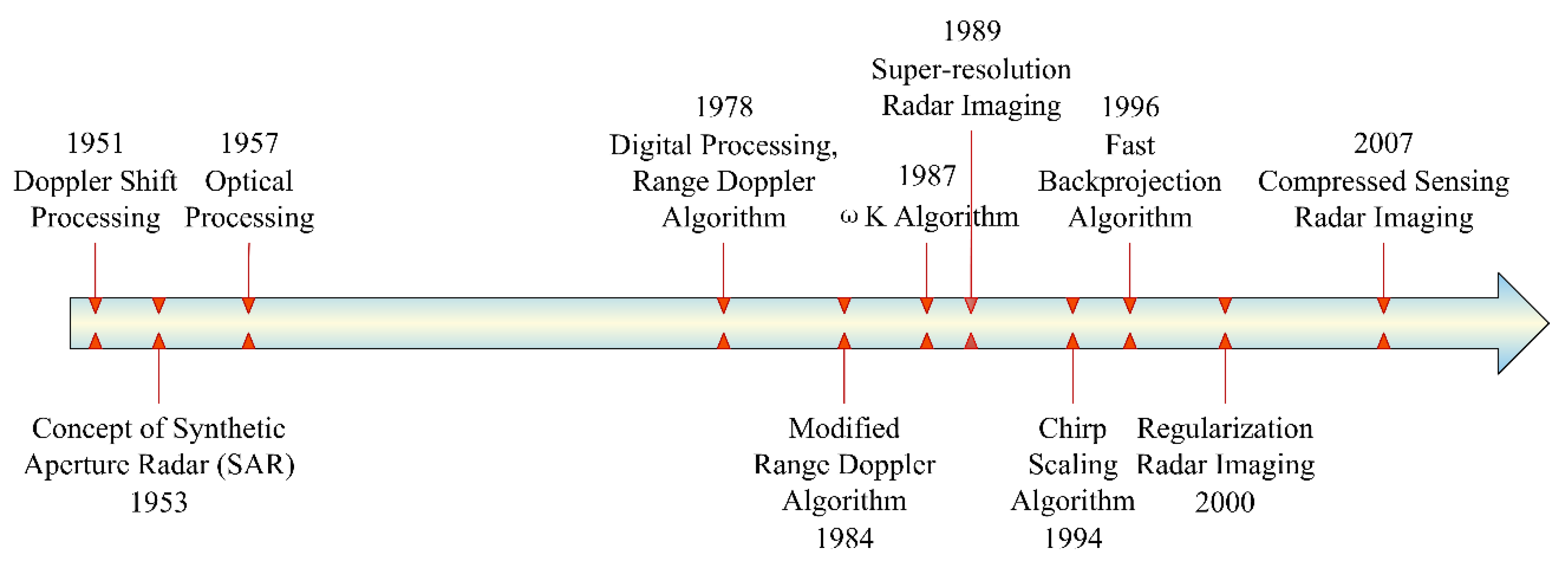
1. Introduction
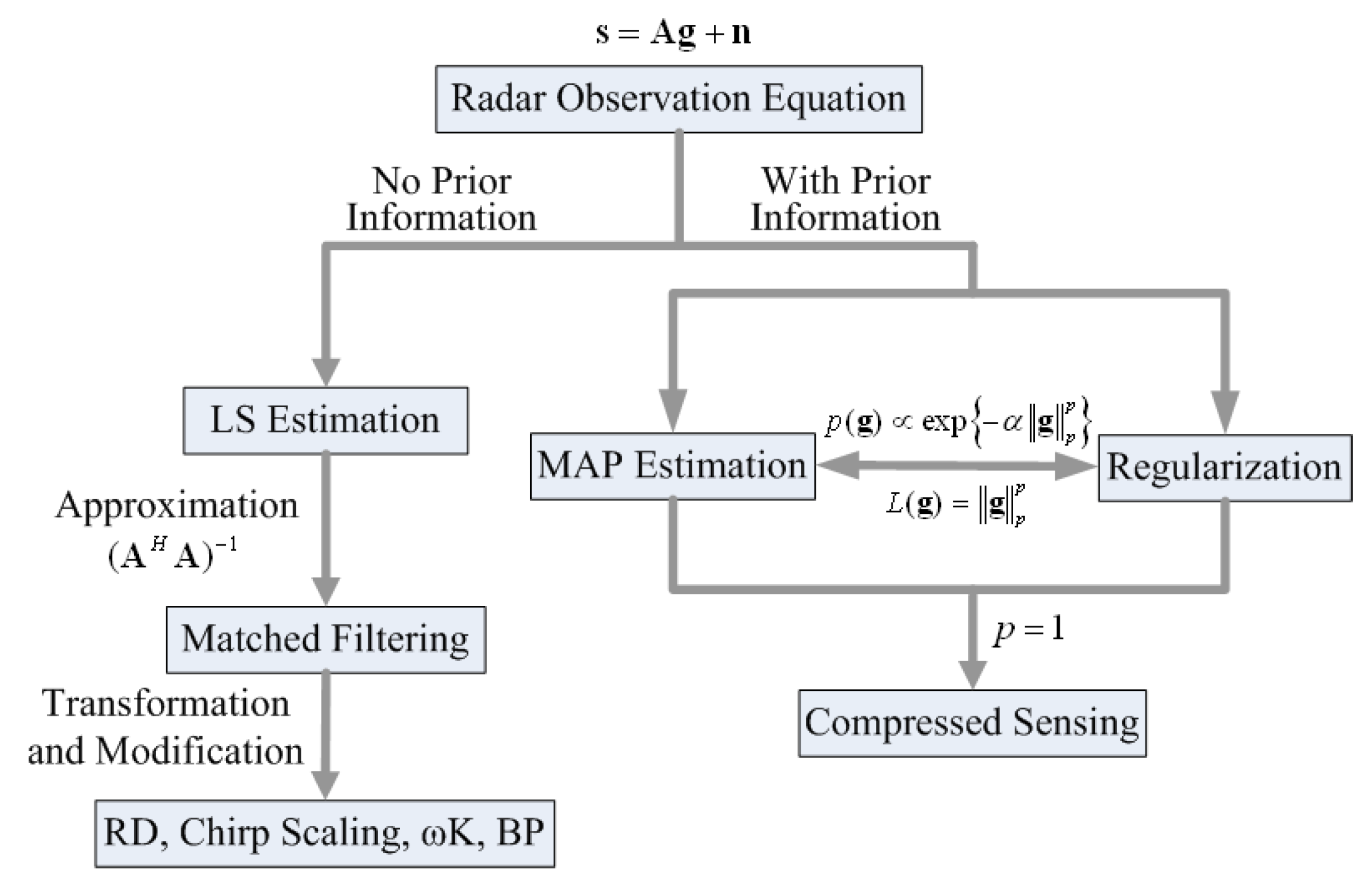
2. Mathematical Fundamentals of Radar Imaging
2.1. Radar Observation Model
2.2. Best Linear Unbiased Estimate and Least Squares Estimate of the Scene
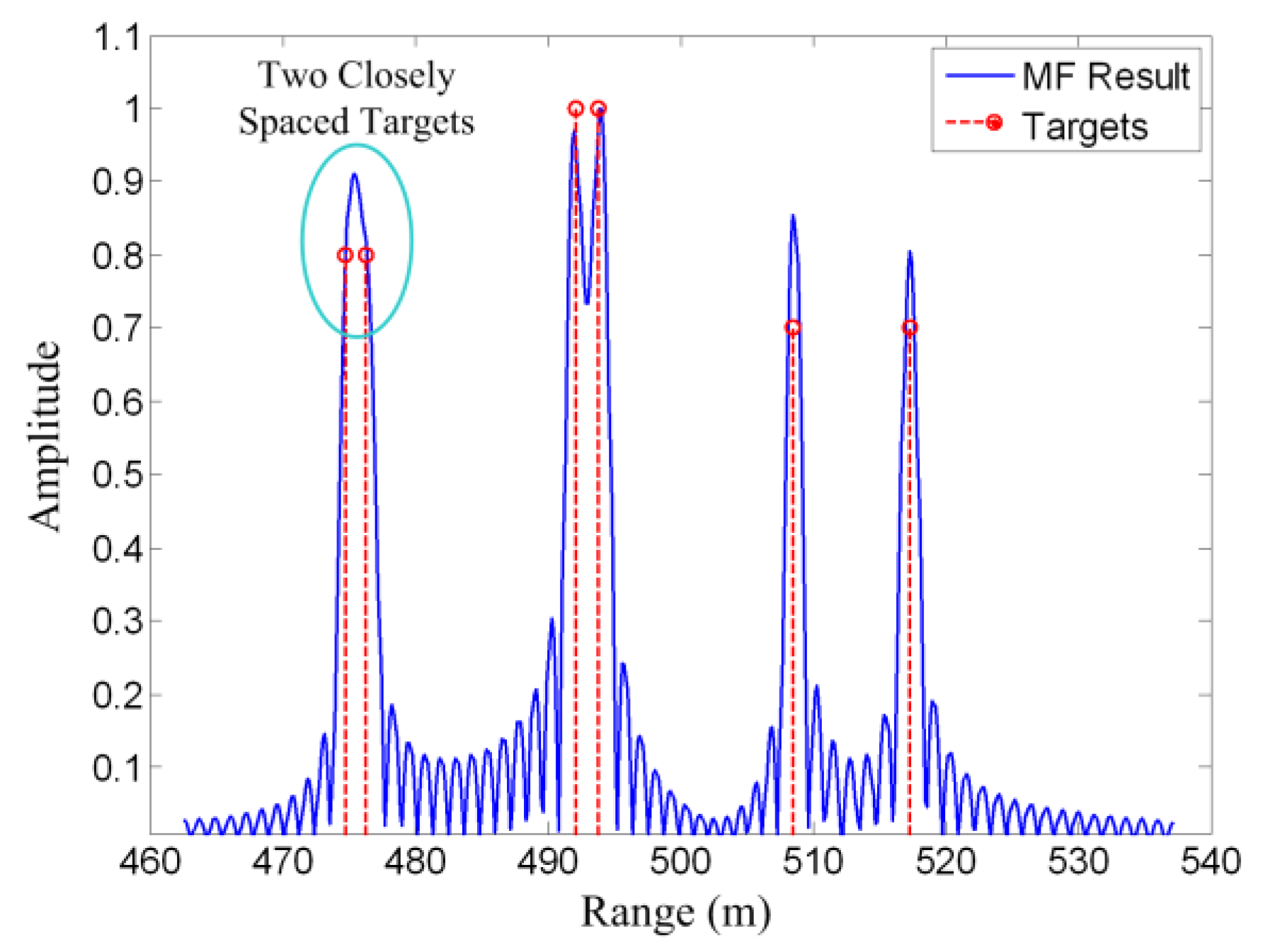
2.3. Matched Filtering Method
2.4. Regularization Method
2.5. Bayesian Maximum a Posteriori Estimation
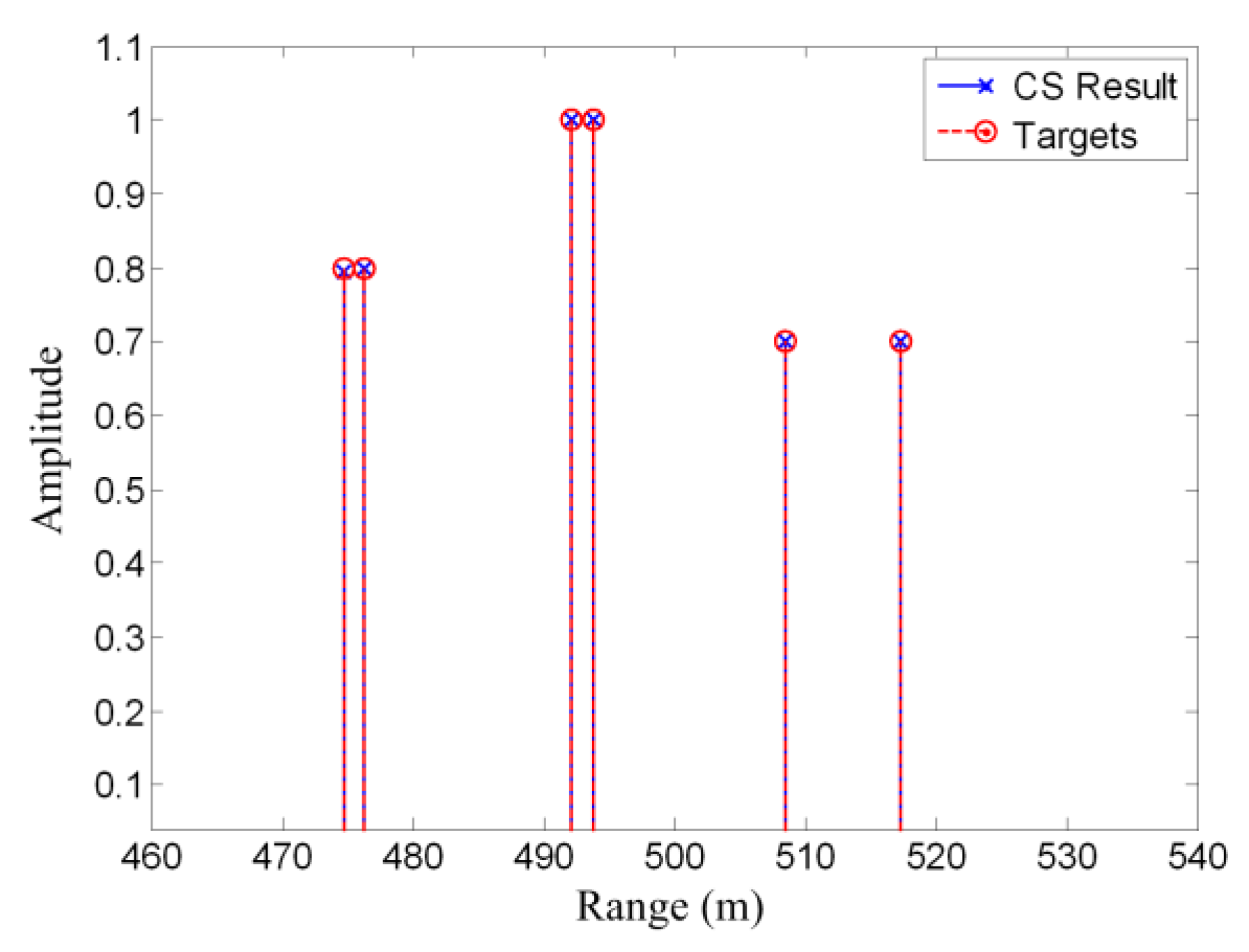
2.6. Compressed Sensing Method
2.7. Summary of Radar Imaging Methods
3. Challenges and Advances in Compressed Sensing-Based Radar Imaging
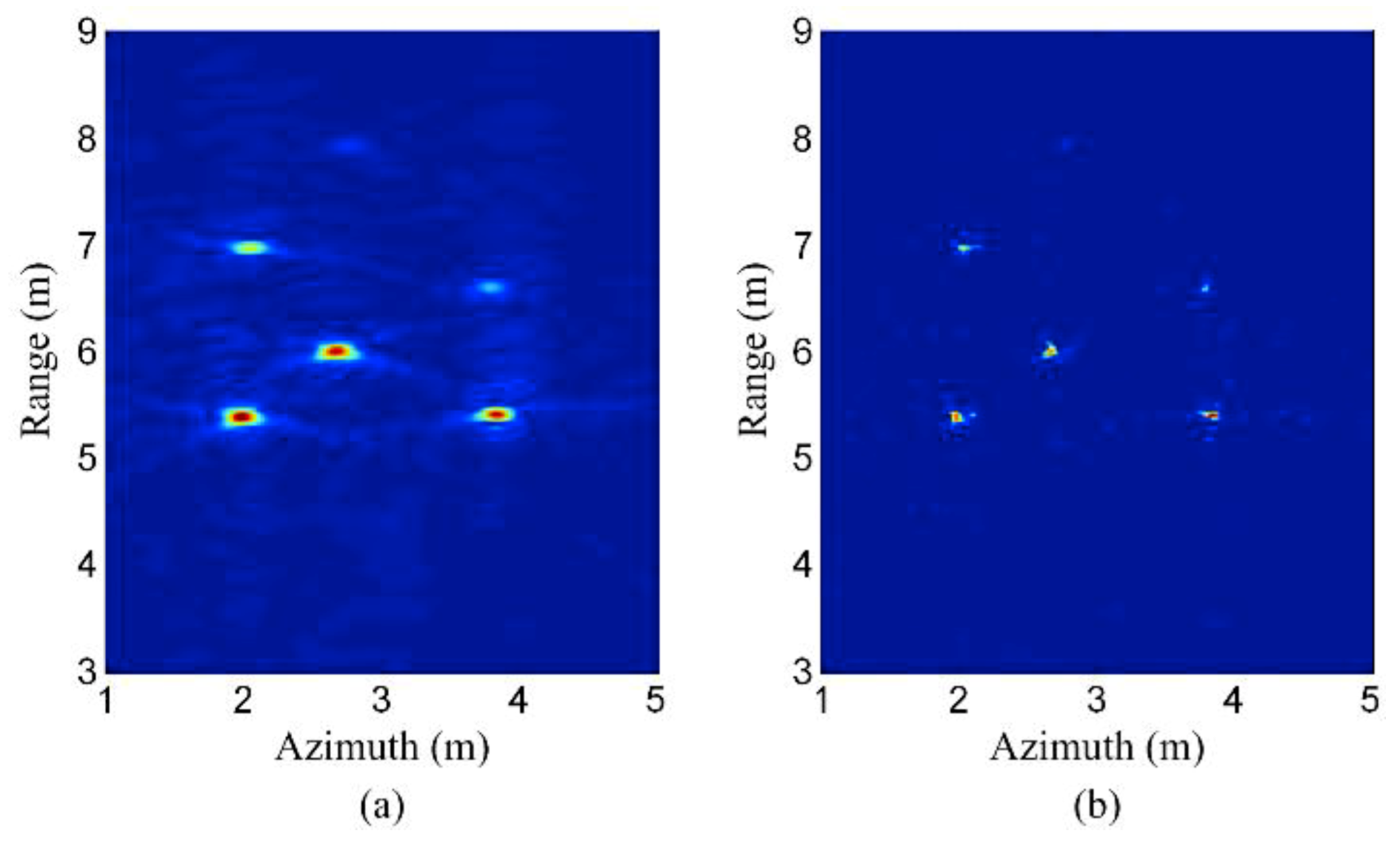
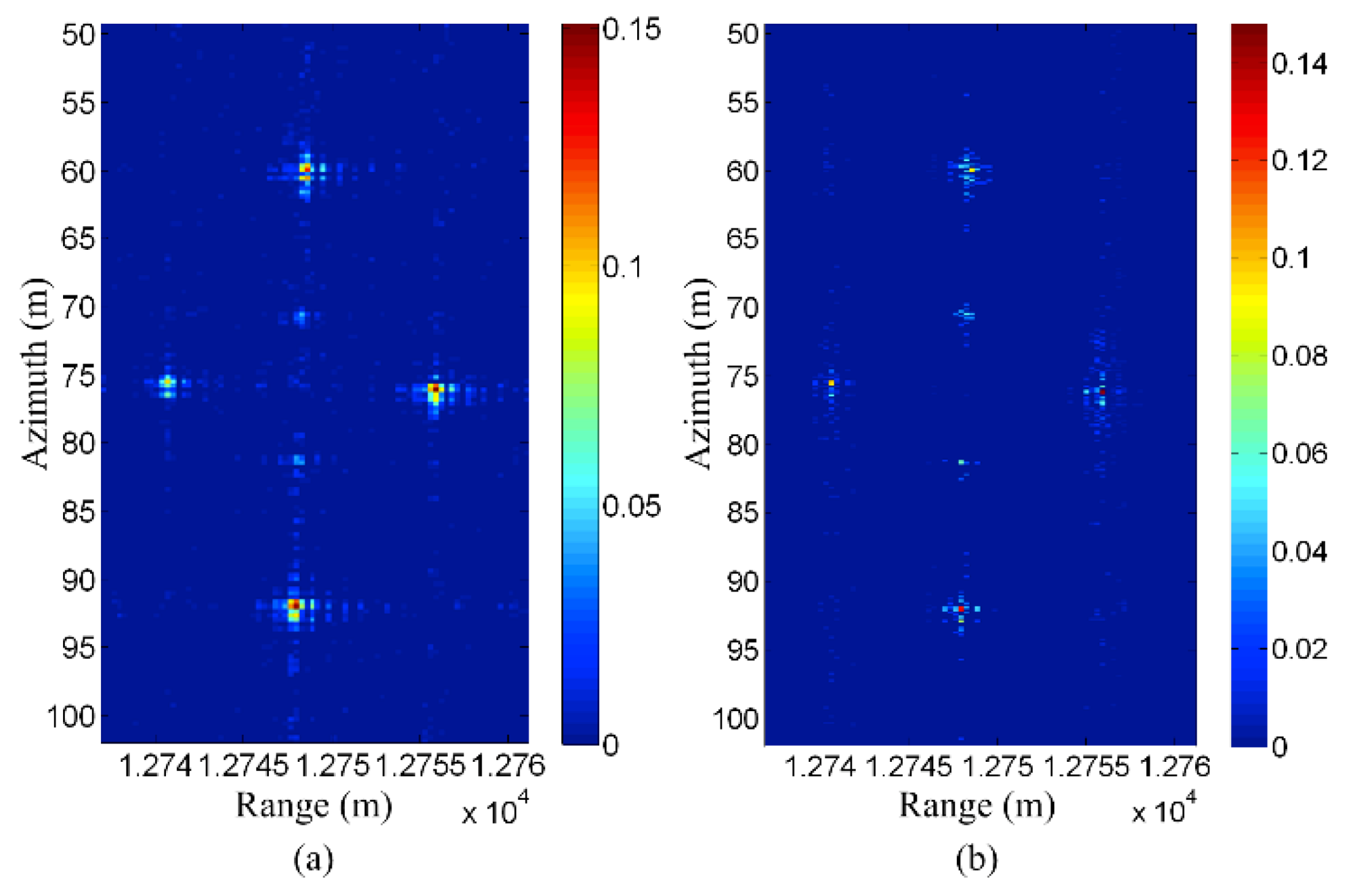
3.1. Sampling Scheme
3.2. Computational Complexity
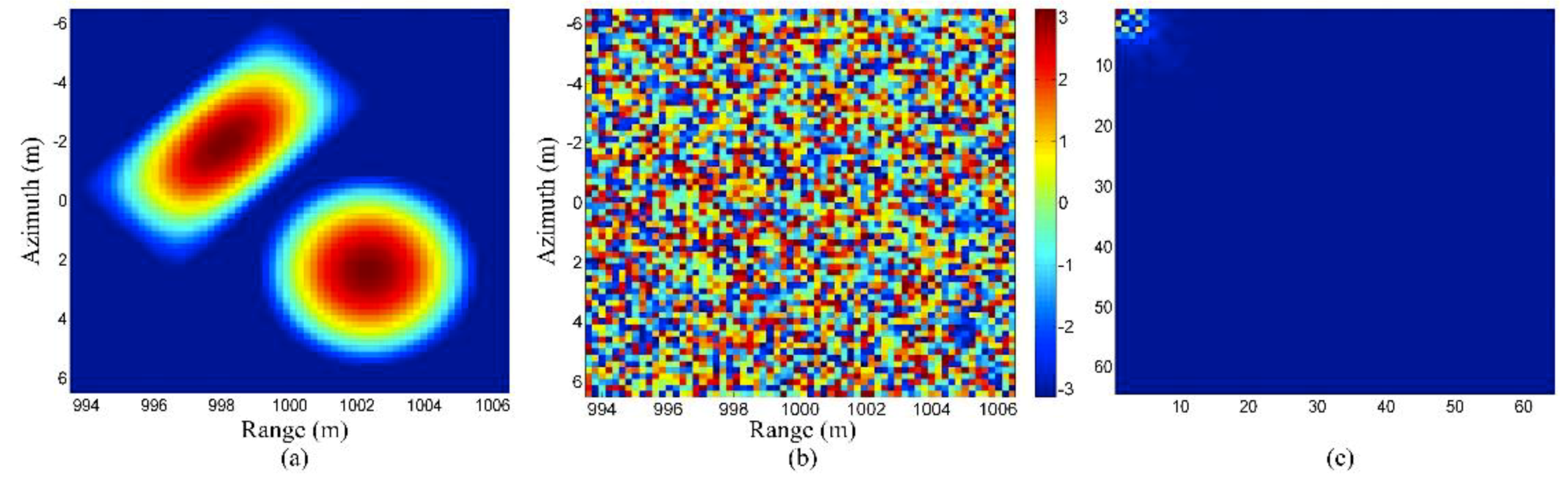
3.3. Sparsity and Sparse Representation
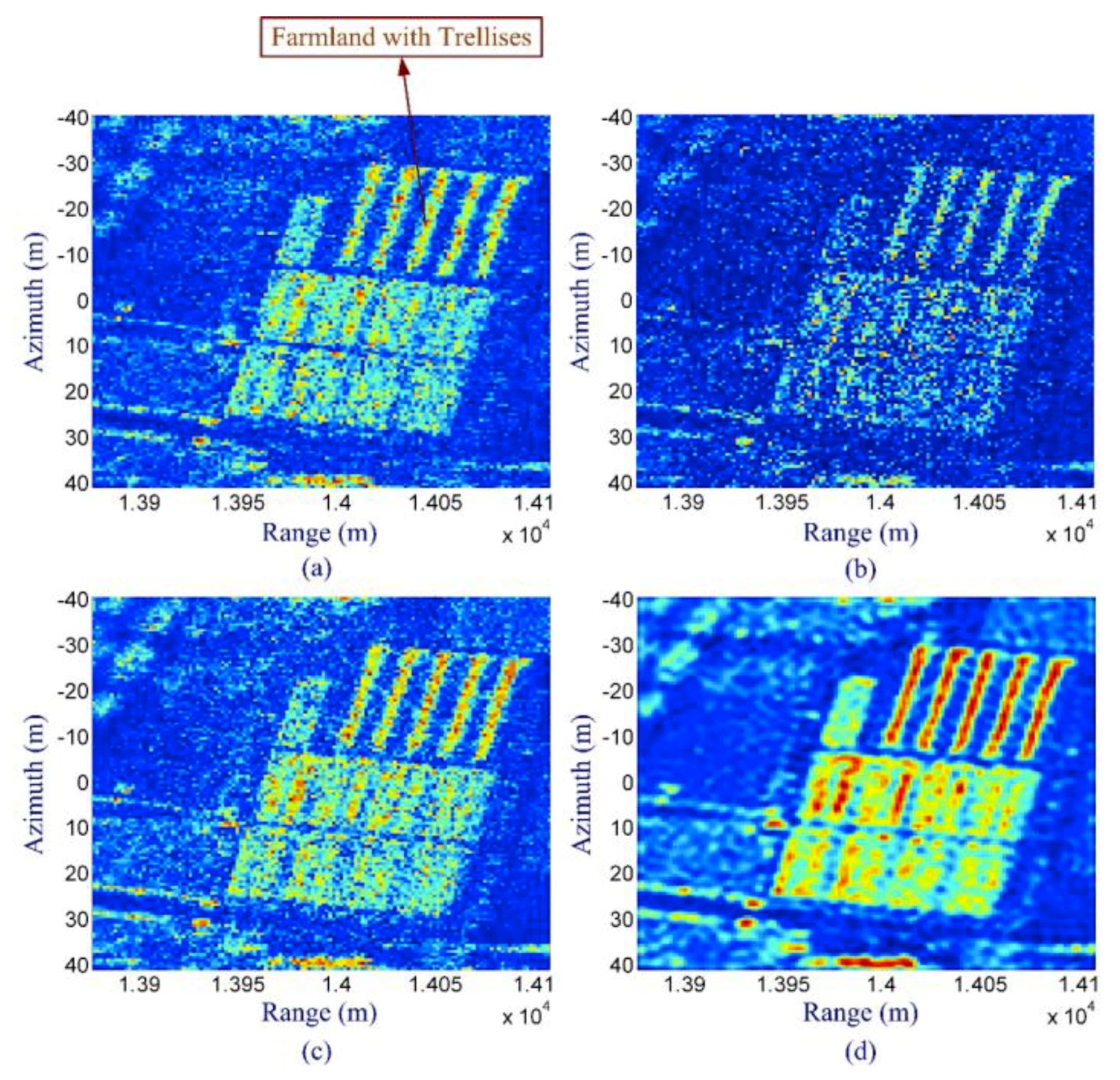
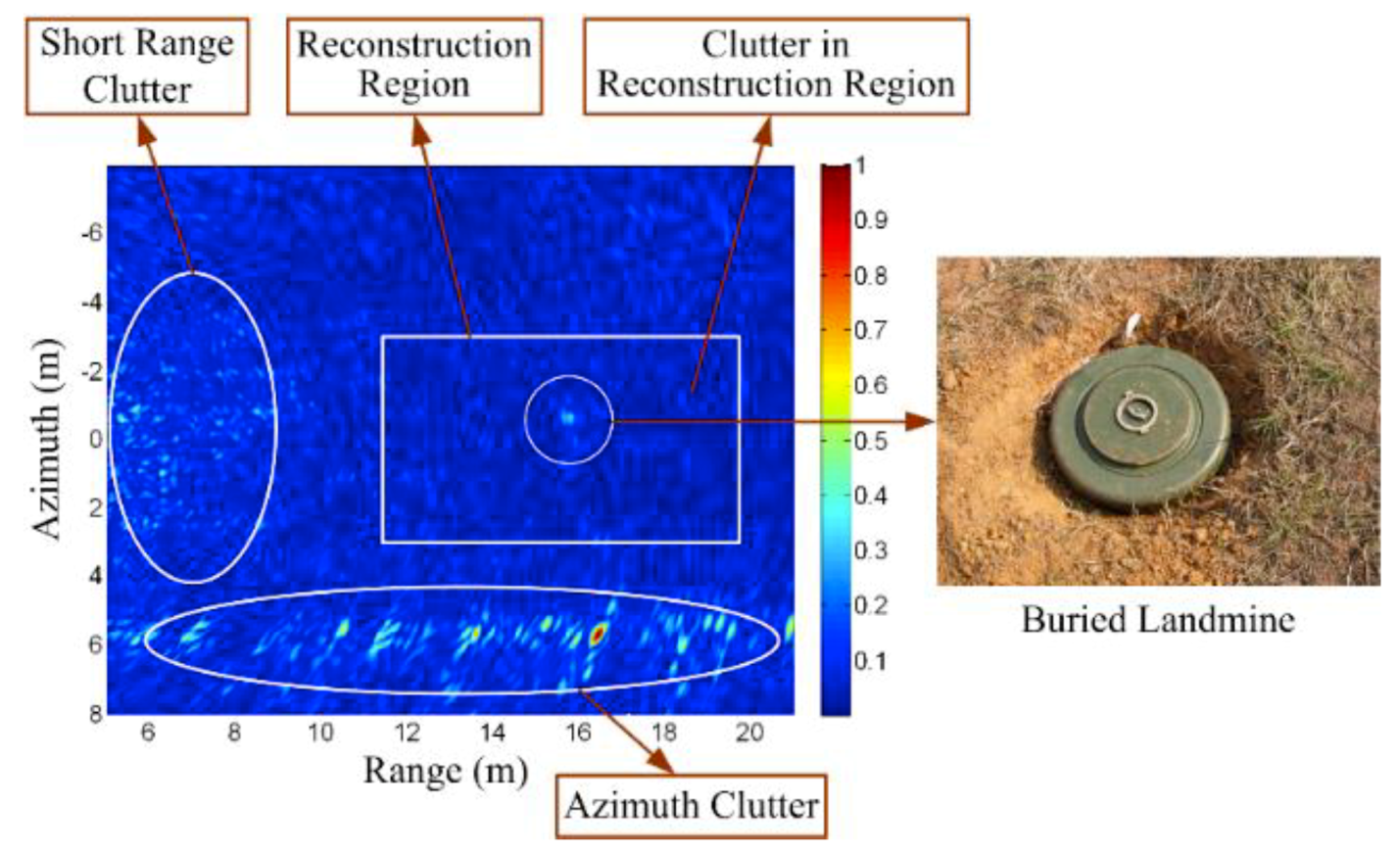
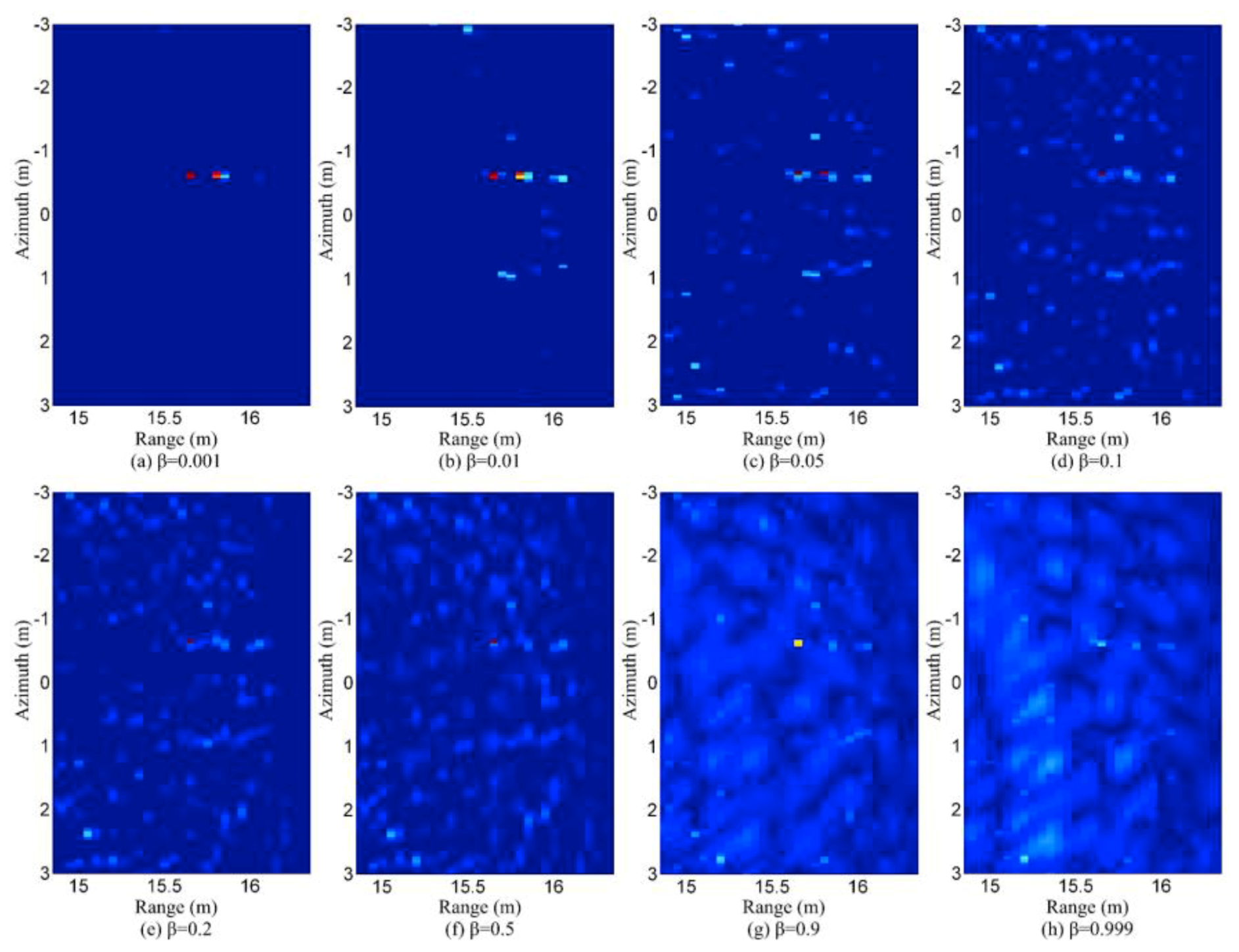
3.4. Influence of Clutter
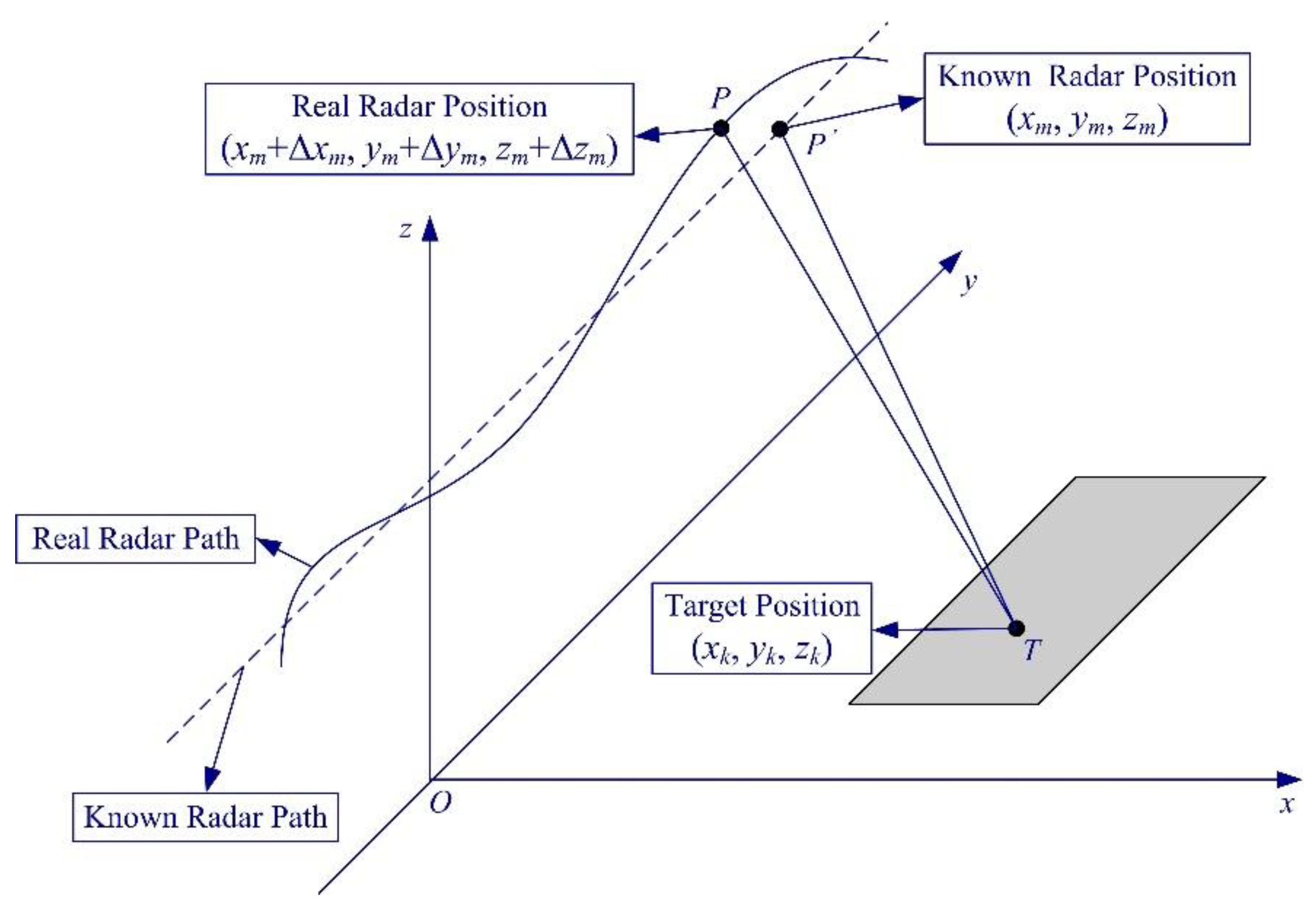
3.5. Model Error Compensation
4. Conclusions
Funding
Conflicts of Interest
References
- Cumming, I.; Wong, F. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Boston, MA, USA, 2005. [Google Scholar]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Mensa, D.L. High Resolution Radar Imaging; Artech House: Norwood, MA, USA, 1981. [Google Scholar]
- Potter, L.C.; Ertin, E.; Parker, J.T.; Çetin, M. Sparsity and compressed sensing in radar imaging. Proc. IEEE 2010, 98, 1006–1020. [Google Scholar] [CrossRef]
- Mohammad-Djafari, A. Inverse Problems in Vision and 3D Tomography; ISTE: London, UK; John Wiley and Sons: New York, NY, USA, 2010. [Google Scholar]
- Mohammad-Djafari, A. Bayesian approach with prior models which enforce sparsity in signal and image processing. EURASIP J. Adv. Signal Process. 2012, 2012, 52. [Google Scholar] [CrossRef]
- Mohammad-Djafari, A.; Daout, F.; Fargette, P. Fusion and inversion of SAR data to obtain a superresolution image. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Cario, Egypt, 7–10 November 2009; pp. 569–572. [Google Scholar]
- Groetsch, C.W. The Theory of Tikhonov Regularization for Fredholm Equations of the First Kind; Pitman Publishing Limited: London, UK, 1984. [Google Scholar]
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of Ill-Posed Problems; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Miller, K. Least squares methods for ill-posed problems with a prescribed bound. SIAM J. Math. Anal. 1970, 1, 52–57. [Google Scholar] [CrossRef]
- Blacknell, D.; Quegan, S. SAR super-resolution with a stochastic point spread function. In Proceedings of the IEE Colloquium on Synthetic Aperture Radar, London, UK, 29 November 1989. [Google Scholar]
- Pryde, G.C.; Delves, L.M.; Luttrell, S.P. Transputer based super resolution of SAR images: Two approaches to a parallel solution. In Proceedings of the IEE Colloquium on Transputers for Image Processing Applications, London, UK, 13 February 1989. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Bouman, C.; Sauer, K. A generalized Gaussian image model for edge-preserving MAP estimation. IEEE Trans. Image Process. 1993, 2, 296–310. [Google Scholar] [CrossRef] [PubMed]
- Chang, L.T.; Gupta, I.J.; Burnside, W.D.; Chang, C.T. A data compression technique for scattered fields from complex targets. IEEE Trans. Antennas Propag. 1997, 45, 1245–1251. [Google Scholar] [CrossRef]
- Candès, E.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive sensing. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Jafarpour, S.; Weiyu, X.; Hassibi, B.; Calderbank, R. Efficient and robust compressed sensing using optimized expander graphs. IEEE Trans. Inf. Theory 2009, 55, 4299–4308. [Google Scholar] [CrossRef]
- Yuejie, C.; Scharf, L.L.; Pezeshki, A.; Calderbank, R. Sensitivity to basis mismatch in compressed sensing. IEEE Trans. Signal Process. 2011, 59, 2182–2195. [Google Scholar]
- Raginsky, M.; Jafarpour, S.; Harmany, Z.T.; Marcia, R.F.; Willett, R.M.; Calderbank, R. Performance bounds for expander-based compressed sensing in Poisson noise. IEEE Trans. Signal Process. 2011, 59, 4139–4153. [Google Scholar] [CrossRef]
- Logan, C.L. An Estimation-Theoretic Technique for Motion Compensated Synthetic-Aperture Array Imaging. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2000. [Google Scholar]
- Browne, K.E.; Burkholder, R.J.; Volakis, J.L. Fast optimization of through-wall radar images via the method of Lagrange multipliers. IEEE Trans. Antennas Propag. 2013, 61, 320–328. [Google Scholar] [CrossRef]
- Romberg, J. Imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 14–20. [Google Scholar] [CrossRef]
- Çetin, M.; Karl, W.C. Feature-enhanced synthetic aperture radar image formation based on nonquadratic regularization. IEEE Trans. Antennas Propag. 2001, 10, 623–631. [Google Scholar]
- Kalogerias, D.; Sun, S.; Petropulu, A.P. Sparse sensing in colocated MIMO radar: A matrix completion approach. In Proceedings of the 2013 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Athens, Greece, 12–15 December 2013; pp. 496–502. [Google Scholar]
- Yao, Y.; Petropulu, A.P.; Poor, H.V. Measurement matrix design for compressive sensing-based MIMO radar. IEEE Trans. Signal Process. 2011, 59, 5338–5352. [Google Scholar]
- Yao, Y.; Petropulu, A.P.; Poor, H.V. MIMO radar using compressive sampling. IEEE J. Sel. Top. Signal Process. 2010, 4, 146–163. [Google Scholar]
- Rossi, M.; Haimovich, A.M.; Eldar, Y.C. Spatial compressive sensing for MIMO radar. IEEE Trans. Signal Process. 2014, 62, 419–430. [Google Scholar] [CrossRef]
- Rossi, M.; Haimovich, A.M.; Eldar, Y.C. Global methods for compressive sensing in MIMO radar with distributed sensors. In Proceedings of the Forty Fifth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, CA, USA, 6–9 November 2011; pp. 1506–1510. [Google Scholar]
- Rossi, M.; Haimovich, A.M.; Eldar, Y.C. Spatial compressive sensing in MIMO radar with random arrays. In Proceedings of the 46th Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 21–23 March 2012. [Google Scholar]
- Herman, M.; Strohmer, T. Compressed sensing radar. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008. [Google Scholar]
- Herman, M.; Strohmer, T. High-resolution radar via compressed sensing. IEEE Trans. Signal Process. 2009, 57, 2275–2284. [Google Scholar] [CrossRef]
- Herman, M.; Strohmer, T. General deviants: An analysis of perturbations in compressed sensing. IEEE J. Sel. Top. Signal Process. 2010, 4, 342–349. [Google Scholar] [CrossRef]
- Baraniuk, R.G.; Steeghs, P. Compressive radar imaging. In Proceedings of the 2007 IEEE Radar Conference, Boston, MA, USA, 17–20 April 2007; pp. 128–133. [Google Scholar]
- Ender, J.H.G. On compressive sensing applied to radar. Signal Process. 2010, 90, 1402–1414. [Google Scholar] [CrossRef]
- Çetin, M.; Stojanovic, I.; Önhon, N.Ö.; Varshney, K.; Samadi, S.; Karl, W.C.; Willsky, A. Sparsity-driven synthetic aperture radar imaging: Reconstruction, autofocusing, moving targets, and compressed sensing. IEEE Signal Process. Mag. 2014, 31, 27–40. [Google Scholar] [CrossRef]
- Zhang, B.; Hong, W.; Wu, Y. Sparse microwave imaging: Principles and applications. Sci. China Inf. Sci. 2012, 55, 1722–1754. [Google Scholar] [CrossRef]
- Bi, H.; Zhang, B.; Zhu, X.; Jiang, C.; Hong, W. Extended chirp scaling-baseband azimuth scaling-based azimuth-range decouple L1 regularization for TOPS SAR imaging via CAMP. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3748–3763. [Google Scholar] [CrossRef]
- Patel, V.M.; Easley, G.R.; Healy, D.M., Jr.; Chellappa, R. Compressed synthetic aperture radar. IEEE J. Sel. Top. Signal Process. 2010, 4, 244–254. [Google Scholar] [CrossRef]
- Alonso, M.T.; López-Dekker, P.; Mallorquí, J.J. A novel strategy for radar imaging based on compressive sensing. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4285–4295. [Google Scholar] [CrossRef]
- Samadi, S.; Çetin, M.; Masnadi-Shirazi, M.A. Sparse representation-based synthetic aperture radar imaging. IET Radar Sonar Navig. 2011, 5, 182–193. [Google Scholar] [CrossRef]
- Yang, L.; Zhou, J.; Hu, L.; Xiao, H. A Perturbation-Based Approach for Compressed Sensing Radar Imaging. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 87–90. [Google Scholar] [CrossRef]
- Zhang, L.; Qiao, Z.; Xing, M.; Li, Y.; Bao, Z. High-Resolution ISAR imaging with sparse stepped-frequency waveforms. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4630–4651. [Google Scholar] [CrossRef]
- Wang, H.; Quan, Y.; Xing, M.; Zhang, S. ISAR Imaging via sparse probing frequencies. IEEE Geosci. Remote Sens. Lett. 2011, 8, 451–455. [Google Scholar] [CrossRef]
- Du, X.; Duan, C.; Hu, W. Sparse representation based autofocusing technique for ISAR images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1826–1835. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. Tomographic SAR inversion by L1-norm regularization-the compressive sensing approach. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3839–3846. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR. IEEE Trans. Geosci. Remote Sens. 2012, 50, 247–258. [Google Scholar] [CrossRef]
- Zhu, X.X.; Ge, N.; Shahzad, M. Joint Sparsity in SAR Tomography for Urban Mapping. IEEE J. Sel. Top. Signal Process. 2015, 9, 1498–1509. [Google Scholar] [CrossRef]
- Budillon, A.; Evangelista, A.; Schirinzi, G. Three-Dimensional SAR Focusing from Multipass Signals Using Compressive Sampling. IEEE Trans. Geosci. Remote Sens. 2011, 49, 488–499. [Google Scholar] [CrossRef]
- Xilong, S.; Anxi, Y.; Zhen, D.; Diannong, L. Three-dimensional SAR focusing via compressive sensing: The case study of angel stadium. IEEE Geosci. Remote Sens. Lett. 2012, 9, 759–763. [Google Scholar] [CrossRef]
- Aguilera, E.; Nannini, M.; Reigber, A. Multisignal compressed sensing for polarimetric SAR tomography. IEEE Geosci. Remote Sens. Lett. 2012, 9, 871–875. [Google Scholar] [CrossRef]
- Kajbaf, H. Compressed Sensing for 3D Microwave Imaging Systems. Ph.D. Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2012. [Google Scholar]
- Zhang, S.; Dong, G.; Kuang, G. Superresolution downward-looking linear array three-dimensional SAR imaging based on two-dimensional compressive sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2184–2196. [Google Scholar] [CrossRef]
- Tian, H.; Li, D. Sparse flight array SAR downward-looking 3-D imaging based on compressed sensing. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1395–1399. [Google Scholar] [CrossRef]
- Lin, Y.G.; Zhang, B.C.; Hong, W.; Wu, Y.R. Along-track interferometric SAR imaging based on distributed compressed sensing. Electron. Lett. 2010, 46, 858–860. [Google Scholar] [CrossRef]
- Prünte, L. Compressed sensing for joint ground imaging and target indication with airborne radar. In Proceedings of the 4th Workshop on Signal Processing with Adaptive Sparse Structured Representations, Edinburgh, UK, 27–30 June 2011. [Google Scholar]
- Wu, Q.; Xing, M.; Qiu, C.; Liu, B.; Bao, Z.; Yeo, T.S. Motion parameter estimation in the SAR system with low PRF sampling. IEEE Geosci. Remote Sens. Lett. 2010, 7, 450–454. [Google Scholar] [CrossRef]
- Stojanovic, I.; Karl, W.C. Imaging of moving targets with multi-static SAR using an overcomplete dictionary. IEEE J. Sel. Top. Signal Process. 2010, 4, 164–176. [Google Scholar] [CrossRef]
- Önhon, N.Ö.; Çetin, M. SAR moving target imaging in a sparsity-driven framework. In Proceedings of the SPIE Optics + Photonics Symposium, Wavelets and Sparsity XIV, San Diego, CA, USA, 21–25 August 2011; Volume 8138, pp. 1–9. [Google Scholar]
- Prünte, L. Detection performance of GMTI from SAR images with CS. In Proceedings of the 2014 European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014. [Google Scholar]
- Prünte, L. Compressed sensing for removing moving target artifacts and reducing noise in SAR images. In Proceedings of the European Conference on Synthetic Aperture Radar, Hamburg, Germany, 6–9 June 2016. [Google Scholar]
- Suksmono, A.B.; Bharata, E.; Lestari, A.A.; Yarovoy, A.G.; Ligthart, L.P. Compressive stepped-frequency continuous-wave ground-penetrating radar. IEEE Geosci. Remote Sens. Lett. 2010, 7, 665–669. [Google Scholar] [CrossRef]
- Gurbuz, A.C.; McClellan, J.H.; Scott, W.R. A compressive sensing data acquisition and imaging method for stepped frequency GPRs. IEEE Trans. Signal Process. 2009, 57, 2640–2650. [Google Scholar] [CrossRef]
- Tuncer, M.A.C.; Gurbuz, A.C. Ground reflection removal in compressive sensing ground penetrating radars. IEEE Geosci. Remote Sens. Lett. 2012, 9, 23–27. [Google Scholar] [CrossRef]
- Lagunas, E.; Amin, M.G.; Ahmad, F.; Nájar, M. Joint wall mitigation and compressive sensing for indoor image reconstruction. IEEE Trans. Geosci. Remote Sens. 2013, 51, 891–906. [Google Scholar] [CrossRef]
- Amin, M.G. Through-the-Wall Radar Imaging; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Ahmad, F.; Amin, M.G. Through-the-wall human motion indication using sparsity-driven change detection. IEEE Trans. Geosci. Remote Sens. 2013, 51, 881–890. [Google Scholar] [CrossRef]
- Strohmer, T. Radar and compressive sensing—A perfect couple? In Proceedings of the Keynote Speak of 1st International Workshop on Compressed Sensing Applied to Radar (CoSeRa 2012), Bonn, Germany, 14–16 May 2012. [Google Scholar]
- Yang, J.; Thompson, J.; Huang, X.; Jin, T.; Zhou, Z. Random-frequency SAR imaging based on compressed sensing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 983–994. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Wu, Q.; Amin, M. Large-scale sparse reconstruction through partitioned compressive sensing. In Proceedings of the International Conference on Digital Signal Processing, Hong Kong, China, 20–23 August 2014; pp. 837–840. [Google Scholar]
- Yang, J.; Thompson, J.; Huang, X.; Jin, T.; Zhou, Z. Segmented reconstruction for compressed sensing SAR imaging. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4214–4225. [Google Scholar] [CrossRef]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Çetin, M.; Karl, W.C.; Willsky, A.S. Feature-preserving regularization method for complex-valued inverse problems with application to coherent imaging. Opt. Eng. 2006, 45, 017003. [Google Scholar]
- Çetin, M.; Önhon, N.Ö.; Samadi, S. Handling phase in sparse reconstruction for SAR: Imaging, autofocusing, and moving targets. In Proceedings of the EUSAR 2012—9th European Conference on Synthetic Aperture Radar, Nuremberg, Germany, 23–26 April 2012. [Google Scholar]
- Varshney, K.R.; Çetin, M.; Fisher, J.W., III; Willsky, A.S. Sparse representation in structured dictionaries with application to synthetic aperture radar. IEEE Trans. Signal Process. 2008, 56, 3548–3560. [Google Scholar] [CrossRef]
- Abolghasemi, V.; Gan, L. Dictionary learning for incomplete SAR data. In Proceedings of the CoSeRa 2012, Bonn, Germany, 14–16 May 2012. [Google Scholar]
- Halman, J.; Burkholder, R.J. Sparse expansions using physical and polynomial basis functions for compressed sensing of frequency domain EM scattering. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1048–1051. [Google Scholar] [CrossRef]
- Van Den Berg, E.; Friedlander, M.P. Probing the Pareto frontier for basis pursuit solutions. SIAM J. Sci. Comput. 2008, 31, 890–912. [Google Scholar] [CrossRef]
- Yang, J.; Jin, T.; Huang, X. Compressed sensing radar imaging with magnitude sparse representation. IEEE Access 2019, 7, 29722–29733. [Google Scholar] [CrossRef]
- Yang, J.; Jin, T.; Huang, X.; Thompson, J.; Zhou, Z. Sparse MIMO array forward-looking GPR imaging based on compressed sensing in clutter environment. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4480–4494. [Google Scholar] [CrossRef]
- Önhon, N.Ö.; Çetin, M. A sparsity-driven approach for joint SAR imaging and phase error correction. IEEE Trans. Antennas Propag. 2012, 21, 2075–2088. [Google Scholar]
- Kelly, S.I.; Yaghoobi, M.; Davies, M.E. Auto-focus for compressively sampled SAR. In Proceedings of the CoSeRa 2012, Bonn, Germany, 14–16 May 2012. [Google Scholar]
- Wei, S.J.; Zhang, X.L.; Shi, J. An autofocus approach for model error correction in compressed sensing SAR imaging. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2012), Munich, Germany, 22–27 July 2012. [Google Scholar]
- Yang, J.; Huang, X.; Thompson, J.; Jin, T.; Zhou, Z. Compressed sensing radar imaging with compensation of observation position error. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4608–4620. [Google Scholar] [CrossRef]





| Imaging Methods | Mathematical Model | Characteristics | Equivalent Geometric Illustration |
| Least Squares (LS) Estimation | , is usually ill-posed or nonexistent, cannot obtain a stable solution [9,13]. |  | |
| Matched Filtering | Avoids the ill-posed term in the LS solution, but the resolution is limited by the system bandwidth, and side-lobes will appear in the final image [4,21]. | 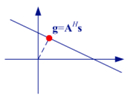 | |
| Range Doppler, Chirp Scaling, ωK, etc. | Approximations and transformations of | Approximations and transformations of the original matched filtering, in order to reduce the computational cost and make it more convenient to implement in practice [1]. | 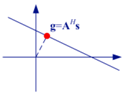 |
| Regularization Method | Add an extra constraint to the LS formula, so that the ill-posed inverse problem becomes well-posed. If the added constraint is chosen appropriately, the result will be better than that for matched filtering [8,9]. | Depends on the expression of . | |
| Sparsity-Driven Regularization | Choose as the -norm (), in order to obtain sparse reconstruction result [6,23]. |  | |
| Bayesian MAP Estimation | For , the MAP estimation will be equivalent to the sparsity-driven regularization method [6,14]. |  | |
| Compressed Sensing (CS) Method | or | For an appropriate choice of , the CS method will be equivalent to the sparsity-driven regularization method [17,23]. | 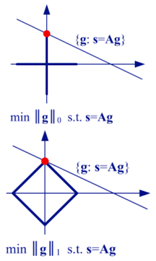 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Jin, T.; Xiao, C.; Huang, X. Compressed Sensing Radar Imaging: Fundamentals, Challenges, and Advances. Sensors 2019, 19, 3100. https://doi.org/10.3390/s19143100
Yang J, Jin T, Xiao C, Huang X. Compressed Sensing Radar Imaging: Fundamentals, Challenges, and Advances. Sensors. 2019; 19(14):3100. https://doi.org/10.3390/s19143100
Chicago/Turabian StyleYang, Jungang, Tian Jin, Chao Xiao, and Xiaotao Huang. 2019. "Compressed Sensing Radar Imaging: Fundamentals, Challenges, and Advances" Sensors 19, no. 14: 3100. https://doi.org/10.3390/s19143100
APA StyleYang, J., Jin, T., Xiao, C., & Huang, X. (2019). Compressed Sensing Radar Imaging: Fundamentals, Challenges, and Advances. Sensors, 19(14), 3100. https://doi.org/10.3390/s19143100





