Comparison of Different Electrocardiography with Vectorcardiography Transformations
Abstract
1. Introduction
2. Methods
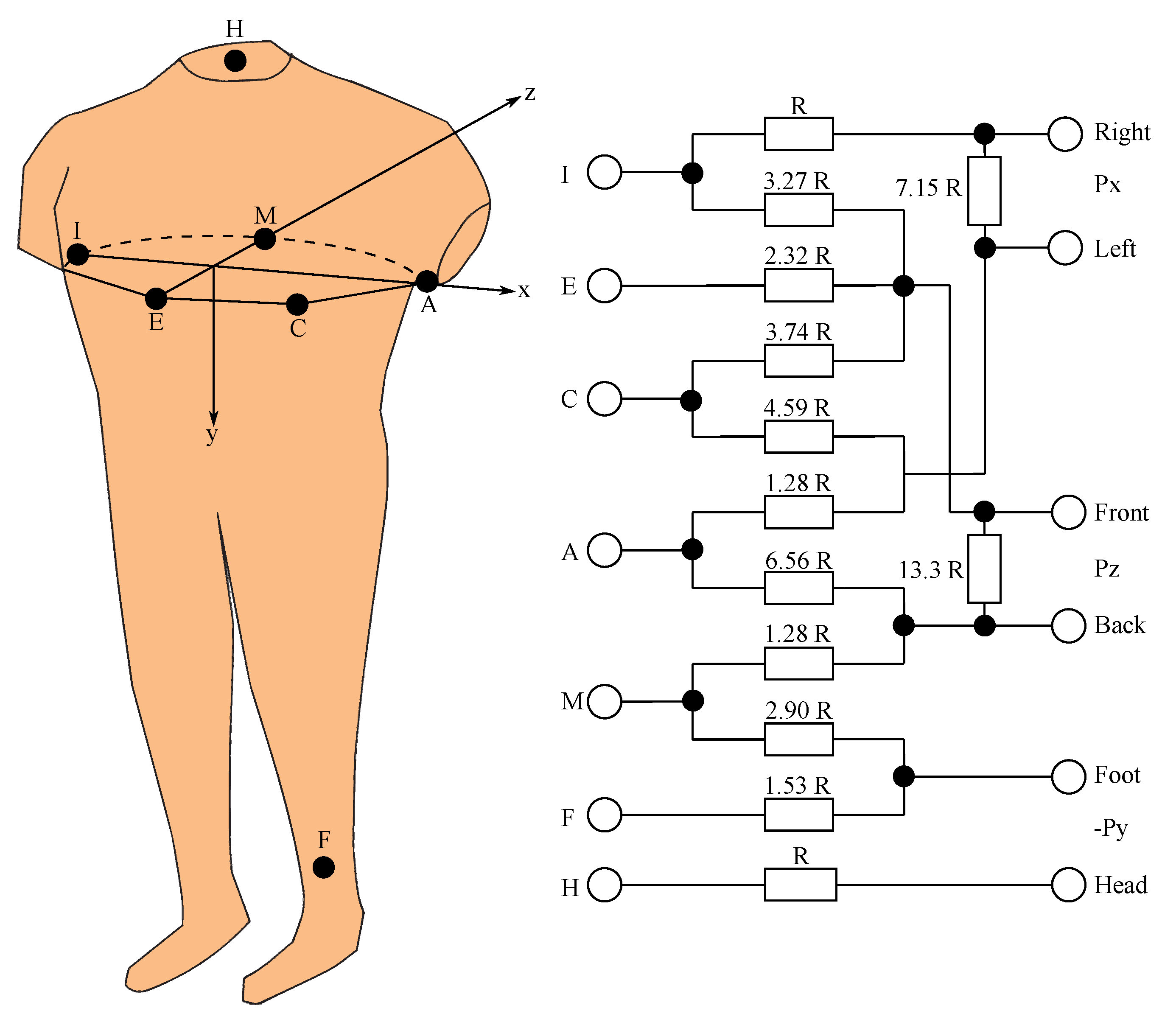
2.1. Kors Quasi-Orthogonal Transformation
2.2. Inverse Dower Transformation
2.3. Kors Regression Transformation
2.4. Linear Regression-Based Transformations
3. Evaluation Parameters
3.1. Correlation Coefficient
3.2. Mean Squared Error
3.3. Statistical Analysis
4. Results
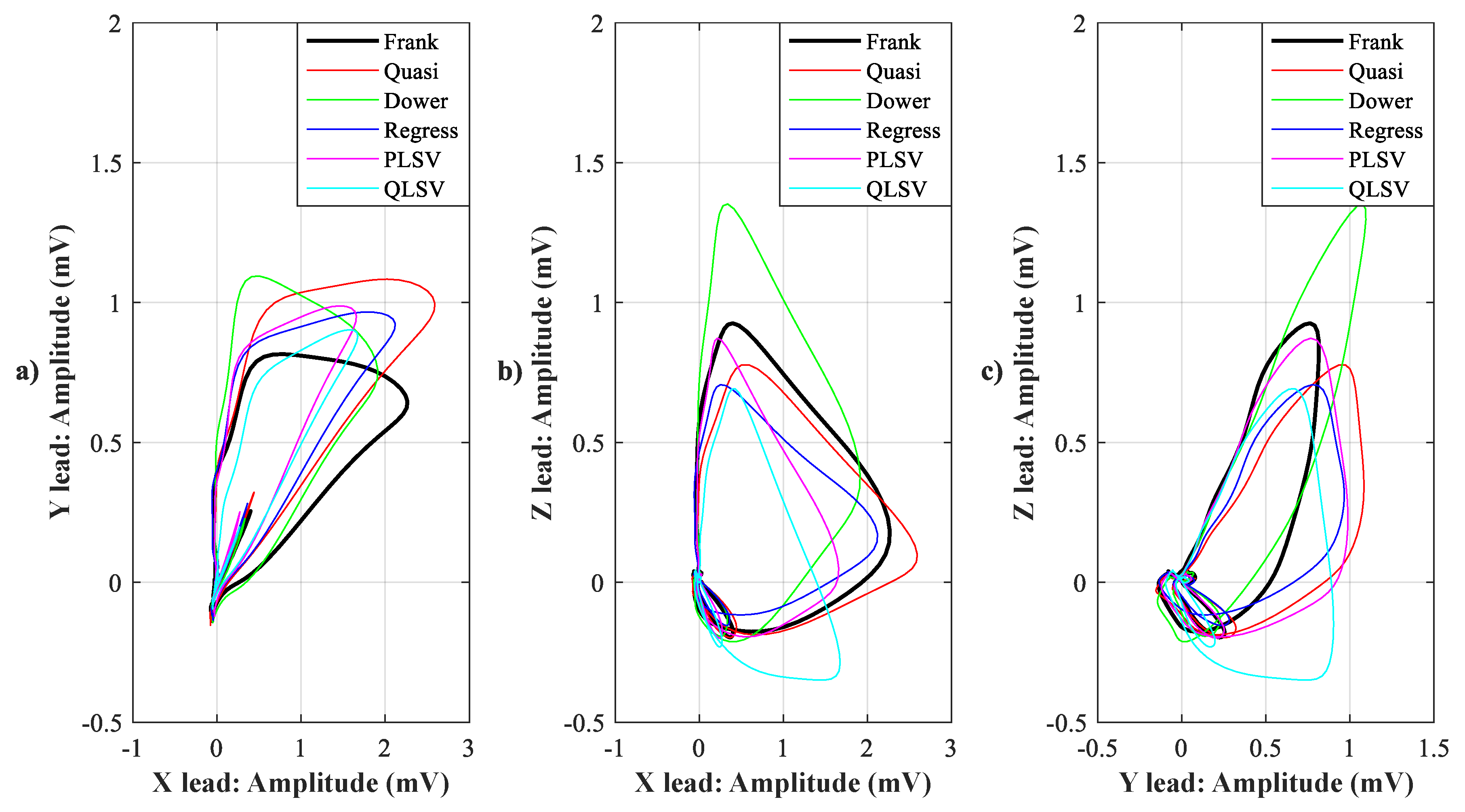
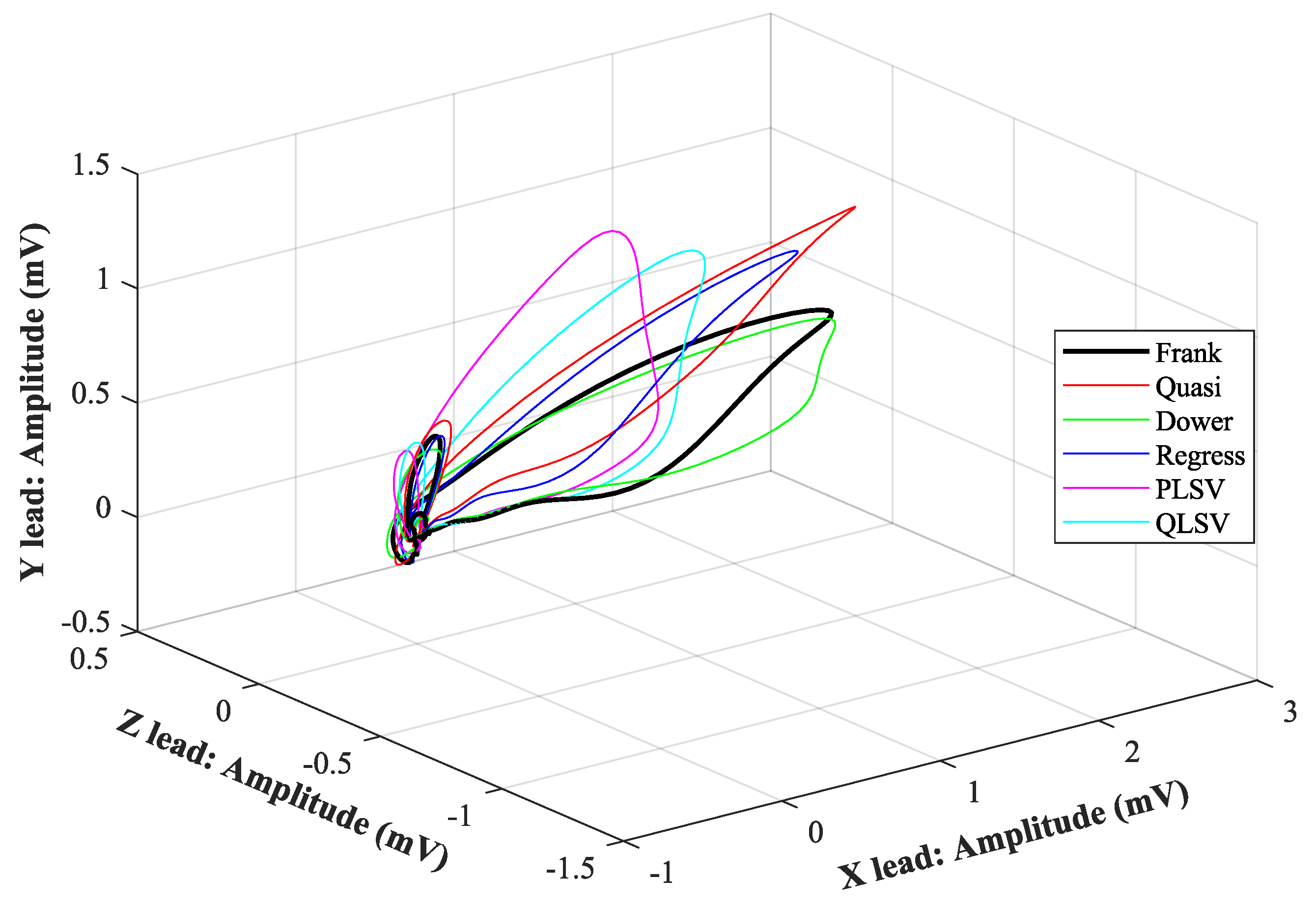
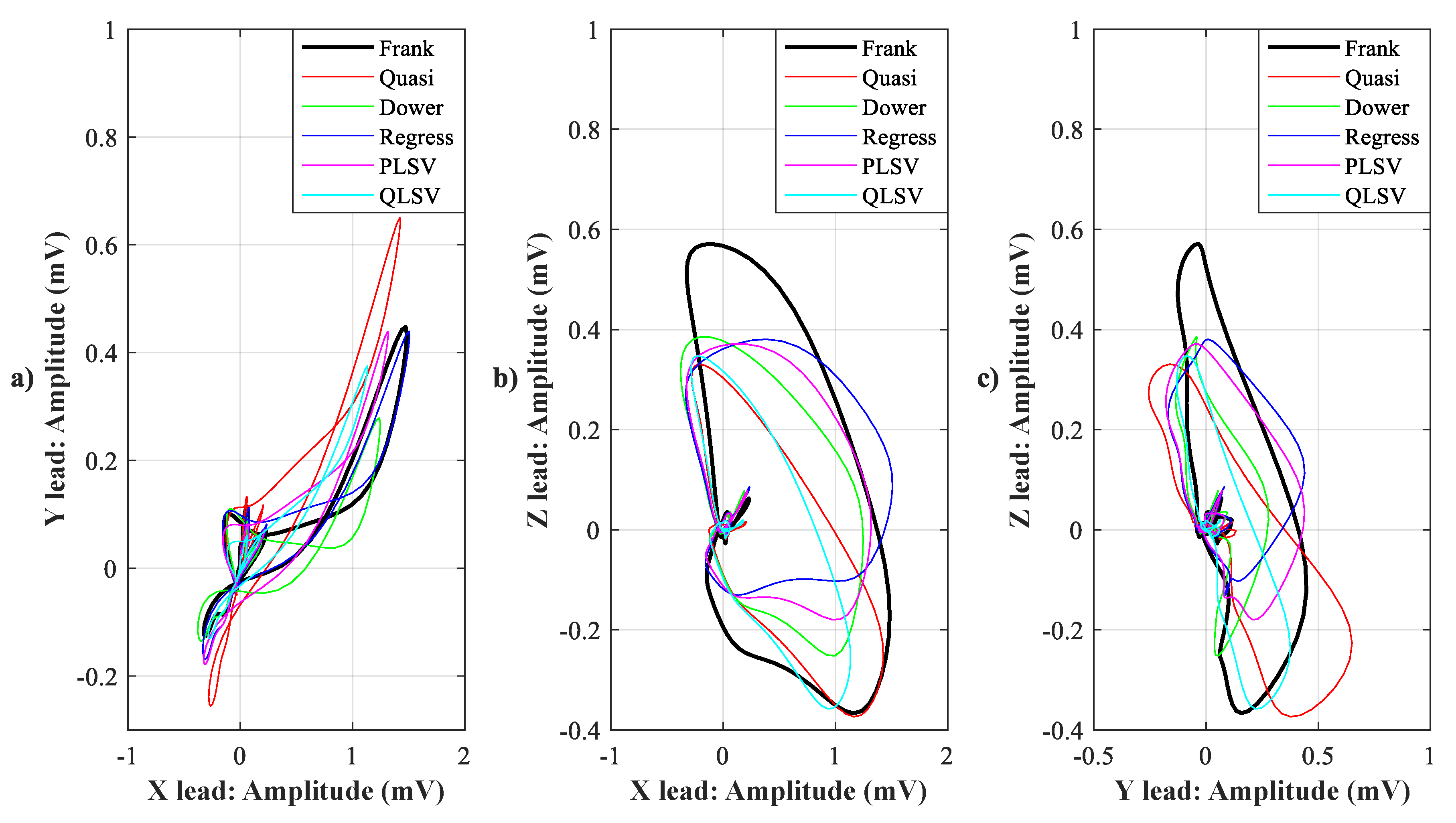
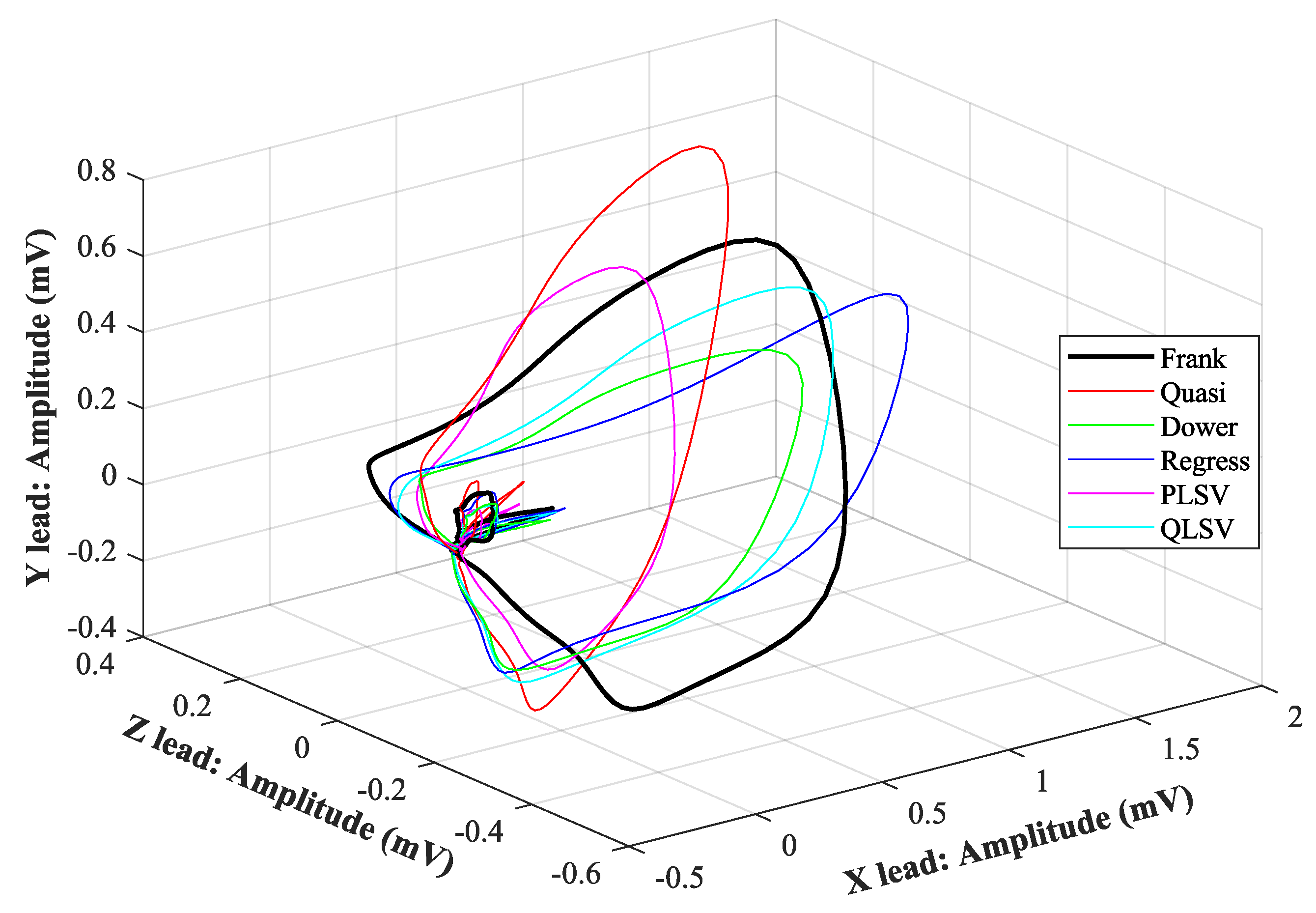
4.1. Visual Evaluation
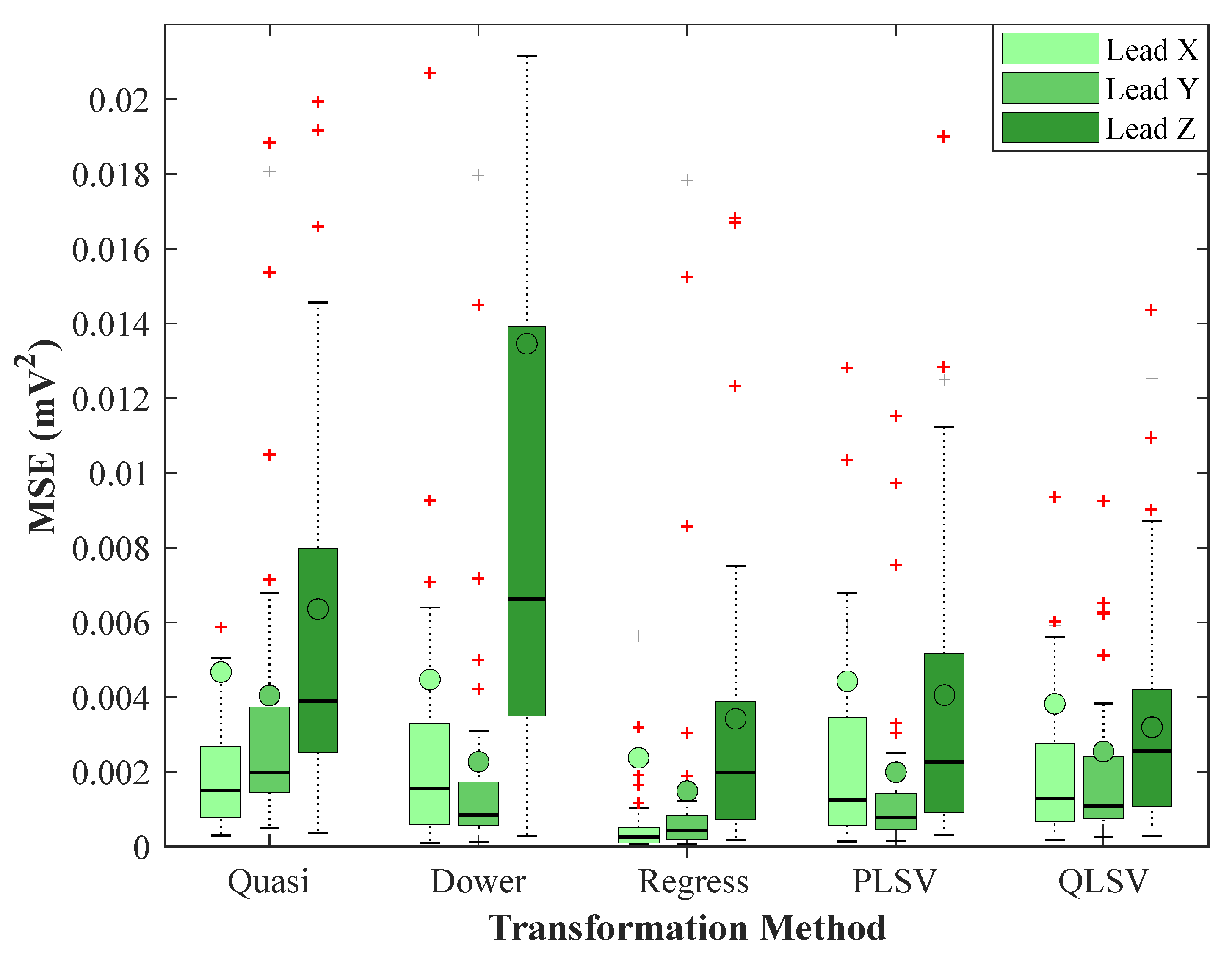
4.2. Statistical Analysis of MSE Results
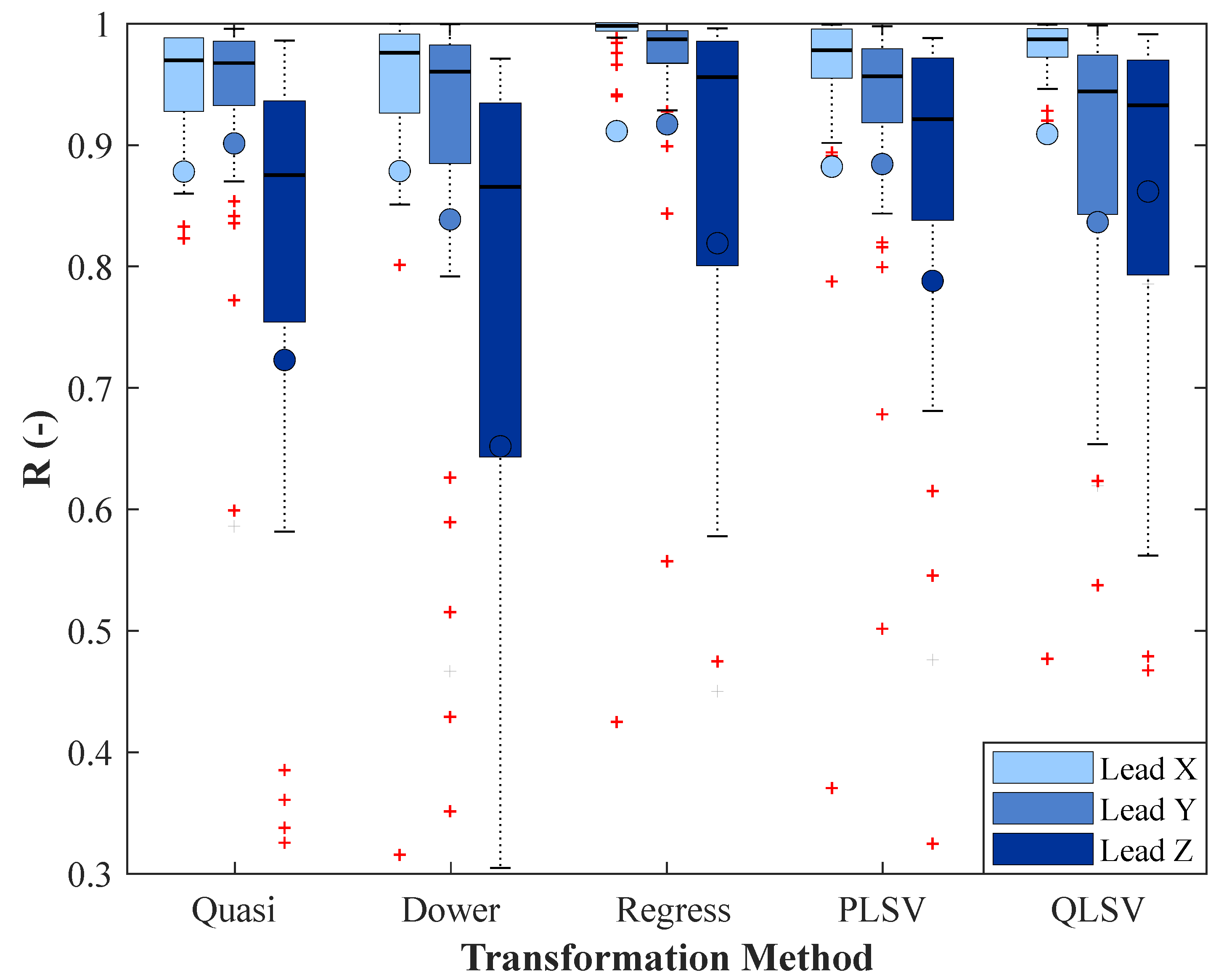
4.3. Statistical Analysis of R Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rubel, P.; Benhadid, I.; Fayn, J. Quantitative assessment of eight different methods for synthesizing Frank VCGs from simultaneously recorded standard ECG leads. J. Electrocardiol. 1991, 24, 197–202. [Google Scholar] [CrossRef]
- Winsor, T. Primer of Vectorcardiography; Lea & Febiger: Philadelphia, PA, USA, 1972. [Google Scholar]
- Levkov, C.L. Orthogonal electrocardiogram derived from the limb and chest electrodes of the conventional 12-lead system. Med. Biol. Eng. Comput. 1987, 25, 155. [Google Scholar] [CrossRef]
- Edenbrandt, L.; Houston, A.; Macfarlane, P.W. Vectorcardiograms synthesized from 12-lead ECGs: A new method applied in 1792 healthy children. Pediatr. Cardiol. 1994, 15, 21–26. [Google Scholar] [CrossRef] [PubMed]
- Lingman, M.; Hartford, M.; Karlsson, T.; Herlitz, J.; Rubulis, A.; Caidahl, K.; Bergfeldt, L. Transient repolarization alterations dominate the initial phase of an acute anterior infarction—A vectorcardiography study. J. Electrocardiol. 2014, 47, 478–485. [Google Scholar] [CrossRef]
- Sederholm, M. The origin of monitoring of acute myocardial infarction with continuous vectorcardiography. J. Electrocardiol. 2014, 47, 418–424. [Google Scholar] [CrossRef]
- Cortez, D.; Bos, J.M.; Ackerman, M.J. Vectorcardiography identifies patients with electrocardiographically concealed long QT syndrome. Heart Rhythm 2017, 14, 894–899. [Google Scholar] [CrossRef] [PubMed]
- Macfarlane, P.W.; Edenbrandt, L.; Pahlm, O. 12-Lead Vectorcardiography; Butterworth-Heinemann: Oxford, UK, 1995. [Google Scholar]
- Guillem, M.S.; Sahakian, A.V.; Swiryn, S. Derivation of orthogonal leads from the 12-lead ECG. Accuracy of a single transform for the derivation of atrial and ventricular waves. In Proceedings of the 2006 Computers in Cardiology, Valencia, Spain, 17–20 September 2006; pp. 249–252, ISBN 978-1-4244-2532-7. [Google Scholar]
- Hyttinen, J.A.; Viik, J.J.; Eskola, H.; Malmivuo, J.A. Optimization and comparison of derived Frank VECG lead systems employing an accurate thorax model. In Proceedings of the Computers in Cardiology 1995, Vienna, Austria, 10–13 September 1995; pp. 385–388. [Google Scholar]
- Malmivuo, P.; Malmivuo, J.A.; Plonsey, R. Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Macfarlane, P.W.; Van Oosterom, A.; Pahlm, O.; Kligfield, P.; Janse, M.; Camm, J. Comprehensive Electrocardiology; Springer Science Business Media: Berlin, Germany, 2010. [Google Scholar]
- McFee, R.; Parungao, A. An orthogonal lead system for clinical electrocardiography. Am. Heart J. 1961, 62, 93–100. [Google Scholar] [CrossRef]
- Simonson, E.; Schmitt, O.H. Present status of vectorcardiography. AMA Arch. Int. Med. 1955, 96, 574–590. [Google Scholar]
- Malmivuo, J.A. The SVEC III vectorcardiographic lead system. IEEE Eng. Med. Biol. Mag. 2004, 23, 47–51. [Google Scholar] [CrossRef] [PubMed]
- Kudaiberdiev, Z. Vectorcardiographic assessment of acute hypoxia effects in pulmonary hypertension due to chronic bronchitis. J. Electrocardiol. 2007, 40, S64. [Google Scholar] [CrossRef]
- Fischmann, E.J.; Elliott, B.J. Experimental comparison of “parallel grid leads” with simple bipolar, and the SVEC-III, Frank, and McFee-Parungao systems. I. Sagittal leads. Am. Heart J. 1964, 67, 792–803. [Google Scholar] [CrossRef]
- Kors, J.A.; Van Herpen, G.; Sittig, A.C.; Van Bemmel, J.H. Reconstruction of the Frank vectorcardiogram from standard electrocardiographic leads: Diagnostic comparison of different methods. Eur. Heart J. 1990, 11, 1083–1092. [Google Scholar] [CrossRef] [PubMed]
- Bjerle, P.; Arvedson, O. Comparison of Frank vectorcardiogram with two different vectorcardiograms derived from conventional ECG-leads. Proc. Eng. Found. 1986, 11, 13–26. [Google Scholar]
- van Bemmel, J.H.; Kors, J.A.; van Herpen, G. Combination of diagnostic classifications from ECG and VCG computer interpretations. J. Electrocardiol. 1992, 25, 126–130. [Google Scholar] [CrossRef]
- Edenbrandt, L.; Pahlm, O. Vectorcardiogram synthesized from a 12-lead ECG: Superiority of the inverse Dower matrix. J. Electrocardiol. 1988, 21, 361–367. [Google Scholar] [CrossRef]
- Schreck, D.M.; Fishberg, R.D. Derivation of the 12-lead electrocardiogram and 3-lead vectorcardiogram. Am. J. Emerg. Med. 2013, 31, 1183–1190. [Google Scholar] [CrossRef]
- Burger, H.C.; Van Milaan, J.B.; Den Boer, W. Comparison of different systems of vectorcardiography. Br. Heart J. 1952, 14, 401. [Google Scholar] [CrossRef]
- Acar, B.; Koymen, H. SVD-based on-line exercise ECG signal orthogonalization. IEEE Trans. Biomed. Eng. 1999, 46, 311–321. [Google Scholar] [CrossRef]
- Dawson, D.; Yang, H.; Malshe, M.; Bukkapatnam, S.T.; Benjamin, B.; Komanduri, R. Linear affine transformations between 3-lead (Frank XYZ leads) vectorcardiogram and 12-lead electrocardiogram signals. J. Electrocardiol. 2009, 42, 622–630. [Google Scholar] [CrossRef]
- Maheshwari, S.; Acharyya, A.; Schiariti, M.; Puddu, P.E. Frank vectorcardiographic system from standard 12 lead ECG: An effort to enhance cardiovascular diagnosis. J. Electrocardiol. 2016, 49, 231–242. [Google Scholar] [CrossRef]
- Vozda, M.; Peterek, T.; Cerny, M. Novel Method for Deriving Vectorcardiographic Leads Based on Artificial Neural Networks. In Proceedings of the 41st International Congress on Electrocardiol, Bratislava, Slovakia, 4–7 June 2014. [Google Scholar]
- Guillem, M.S.; Climent, A.M.; Bollmann, A.; Husser, D.; Millet, J.; Castells, F. Limitations of Dower’s inverse transform for the study of atrial loops during atrial fibrillation. Pacing Clin. Electrophysiol. 2009, 32, 972–980. [Google Scholar] [CrossRef] [PubMed]
- Cortez, D.L.; Schlegel, T.T. When deriving the spatial QRS-T angle from the 12-lead electrocardiogram, which transform is more Frank: Regression or inverse Dower? J. Electrocardiol. 2010, 43, 302–309. [Google Scholar] [CrossRef] [PubMed]
- Cortez, D.; Sharma, N.; Devers, C.; Devers, E.; Schlegel, T.T. Visual transform applications for estimating the spatial QRS–T angle from the conventional 12-lead ECG: Kors is still most Frank. J. Electrocardiol. 2014, 47, 12–19. [Google Scholar] [CrossRef] [PubMed]
- Bousseljot, R.; Kreiseler, D.; Schnabel, A. Nutzung der EKG-Signaldatenbank CARDIODAT der PTB uber das Internet. Biomed. Tech. Biomed. Eng. 1995, 40, 317–318. [Google Scholar] [CrossRef]
- Laguna, P.; Mark, R.G.; Goldberg, A.; Moody, G.B. A database for evaluation of algorithms for measurement of QT and other waveform intervals in the ECG. In Proceedings of the Computers in Cardiology 1997, Lund, Sweden, 7–10 September 1997; pp. 673–676. [Google Scholar]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Ahlgren, P.; Jarneving, B.; Rousseau, R. Requirements for a cocitation similarity measure, with special reference to Pearson’s correlation coefficient. J. Am. Soc. Inf. Sci. Technol. 2003, 54, 550–560. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. Mean squared error: Love it or leave it? A new look at signal fidelity measures. IEEE Signal Process. Mag. 2009, 26, 98–117. [Google Scholar] [CrossRef]
- Andel, J. Fundamentals of Mathematical Statistics; SHTL: Prague, Czech Republic, 1978. [Google Scholar]
- Bris, R.; Litschmannova, M. Statistics I. For Combined and Distance Study; VSB–TU Ostrava: Ostrava, Czech Republic, 2004. [Google Scholar]
- Buendia-Fuentes, F.; Arnau-Vives, M.A.; Arnau-Vives, A.; Jimenez-Jimenez, Y.; Rueda-Soriano, J.; Zorio-Grima, E.; Osa-Sáez, A.; Martínez-Dolz, L.V.; Almenar-Bonet, L.; Palencia-Perez, M.A. High-bandpass filters in electrocardiography: Source of error in the interpretation of the ST segment. ISRN Cardiol. 2012, 2012, 706217. [Google Scholar] [CrossRef]
- Venkatachalam, K.L.; Herbrandson, J.E.; Asirvatham, S.J. Signals and signal processing for the electrophysiologist: Part I: Electrogram acquisition. Circ. Arrhythm. Electrophysiol. 2011, 4, 965–973. [Google Scholar] [CrossRef]
- Venkatachalam, K.L.; Herbrandson, J.E.; Asirvatham, S.J. Signals and signal processing for the electrophysiologist: Part II: Signal processing and artifact. Circ. Arrhythm. Electrophysiol. 2011, 4, 974–981. [Google Scholar] [CrossRef]
- Choudhuri, S.; Ghosal, T.; Goswami, D.P.; Sengupta, A. Planarity of the spatial qrs loop of vectorcardiogram is a crucial diagnostic and prognostic parameter in acute myocardial infarction. Med. Hypotheses 2019, 130, 109251. [Google Scholar] [CrossRef]
- Perez-Riera, A.R.; Barbosa-Barros, R.; Daminello-Raimundo, R.; de Abreu, L.C.; de Almeida, M.C.; Rankinen, J.; Baeub Soler, F.; Nikus, K. Re-evaluating the electro-vectorcardiographic criteria for left bundle branch block. Ann. Noninvasive Electrocardiol. 2019, e12644. [Google Scholar] [CrossRef] [PubMed]
- Prabhakararao, E.; Dandapat, S. A Weighted SVM Based Approach for Automatic Detection of Posterior Myocardial Infarction Using VCG Signals. In Proceedings of the 2019 National Conference on Communications (NCC), Bangalore, India, 20–23 February 2019; pp. 1–6. [Google Scholar]
- Costa, C.M.; Silva, I.S.; de Sousa, R.D.; Hortegal, R.A.; Regis, C.D.M. The association between reconstructed phase space and Artificial Neural Networks for vectorcardiographic recognition of myocardial infarction. J. Electrocardiol. 2018, 51, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Sadhukhan, D.; Datta, J.; Pal, S.; Mitra, M. Automated Identification of Myocardial Infarction Using a Single Vectorcardiographic Feature. In Proceedings of the International Conference on Modelling and Simulation, London, UK, 28–29 September 2017; pp. 641–651. [Google Scholar]
- Tripathy, R.K.; Dandapat, S. Detection of myocardial infarction from vectorcardiogram using relevance vector machine. Signal Image Video Process. 2017, 11, 1139–1146. [Google Scholar] [CrossRef]
- Bonomini, M.P.; Ingallina, F.J.; Barone, V.; Valentinuzzi, M.E.; Arini, P.D. Comparison of electrocardiographic and vectorcardiographic planes on a set of left ventricular hypertrophy patients. In Proceedings of the VI Latin American Congress on Biomedical Engineering CLAIB 2014, Parana, Argentina, 29–31 October 2014; pp. 564–567. [Google Scholar]
- Cortez, D.; Schlegel, T.T.; Ackerman, M.J.; Bos, J.M. ECG-derived spatial QRS-T angle is strongly associated with hypertrophic cardiomyopathy. J. Electrocardiol. 2017, 50, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Nikus, K.; Perez-Riera, A.R.; Konttila, K.; Barbosa-Barros, R. Electrocardiographic recognition of right ventricular hypertrophy. J. Electrocardiol. 2018, 51, 46–49. [Google Scholar] [CrossRef] [PubMed]
- Mather, A.N.; Maredia, N.; Plein, S. Ischemic Heart Disease. In Cardiovascular MR Manual; Springer: Cham, Switzerland, 2015; pp. 371–410. [Google Scholar]
- Cruces, P.D.; Arini, P.D. Quaternion-based study of angular velocity of the cardiac vector during myocardial ischaemia. Int. J. Cardiol. 2017, 248, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Vozda, M.; Cerny, M. Methods for derivation of orthogonal leads from 12-lead electrocardiogram: A review. Biomed. Signal Process. Control 2015, 19, 23–34. [Google Scholar] [CrossRef]
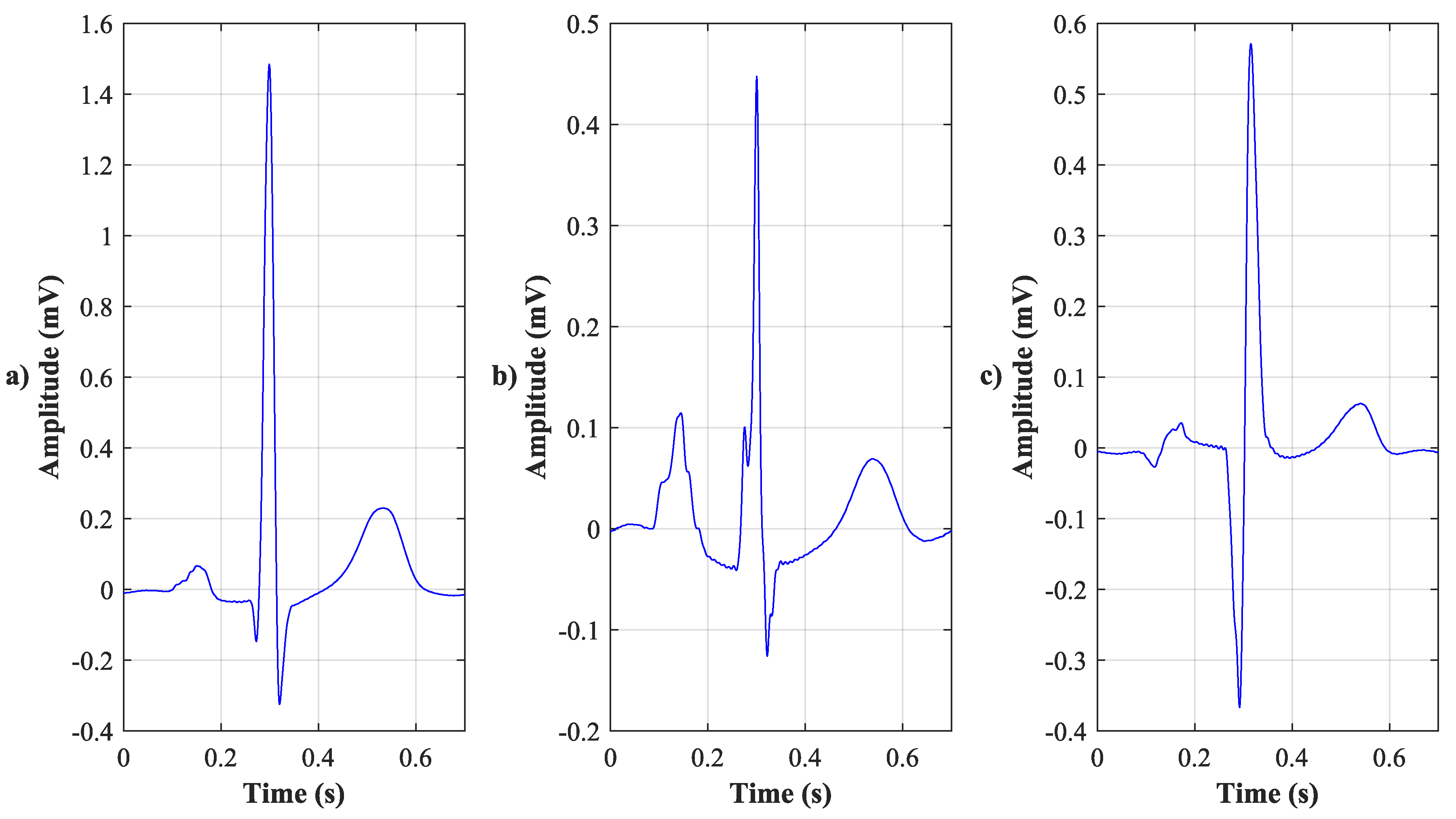
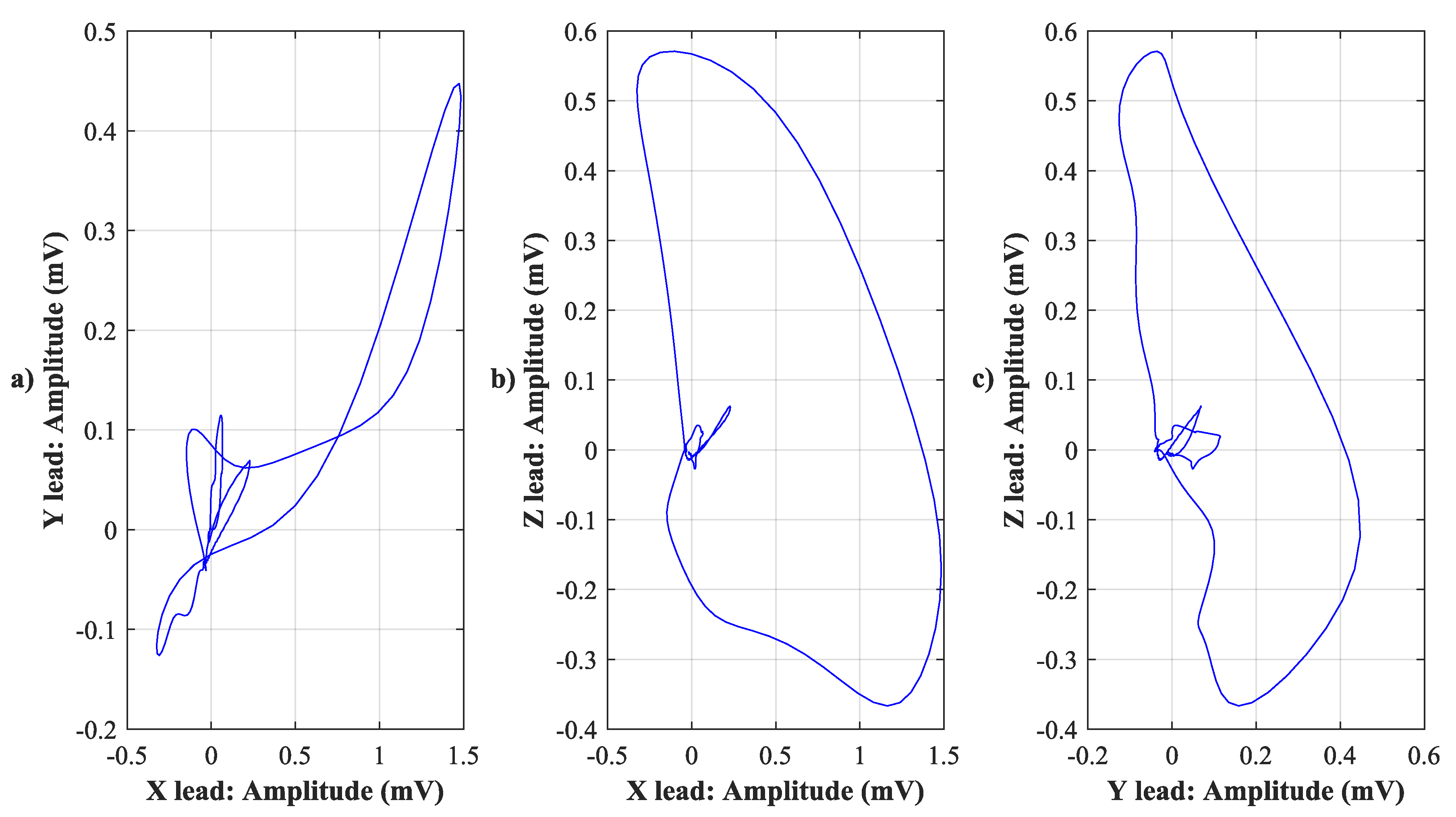
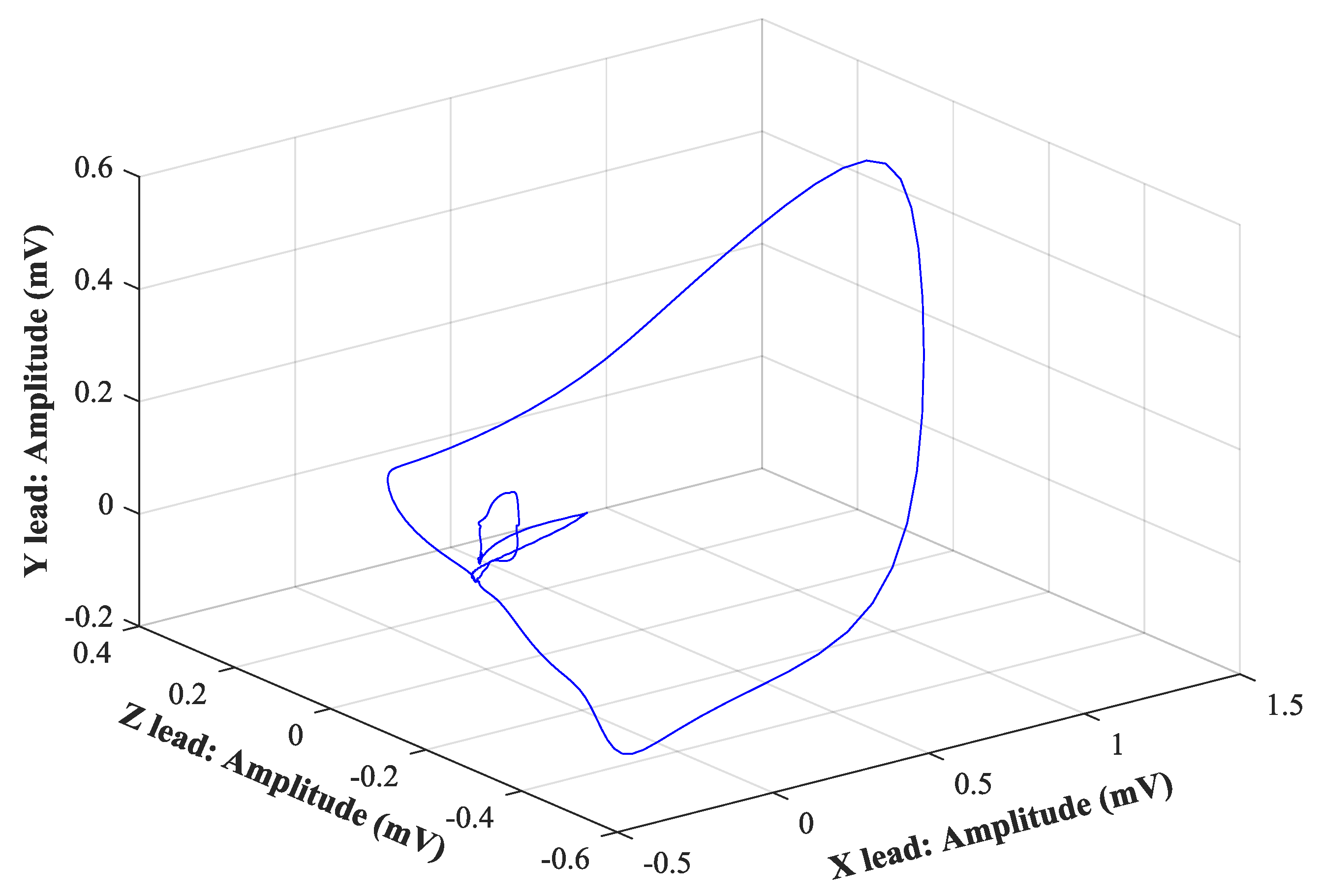
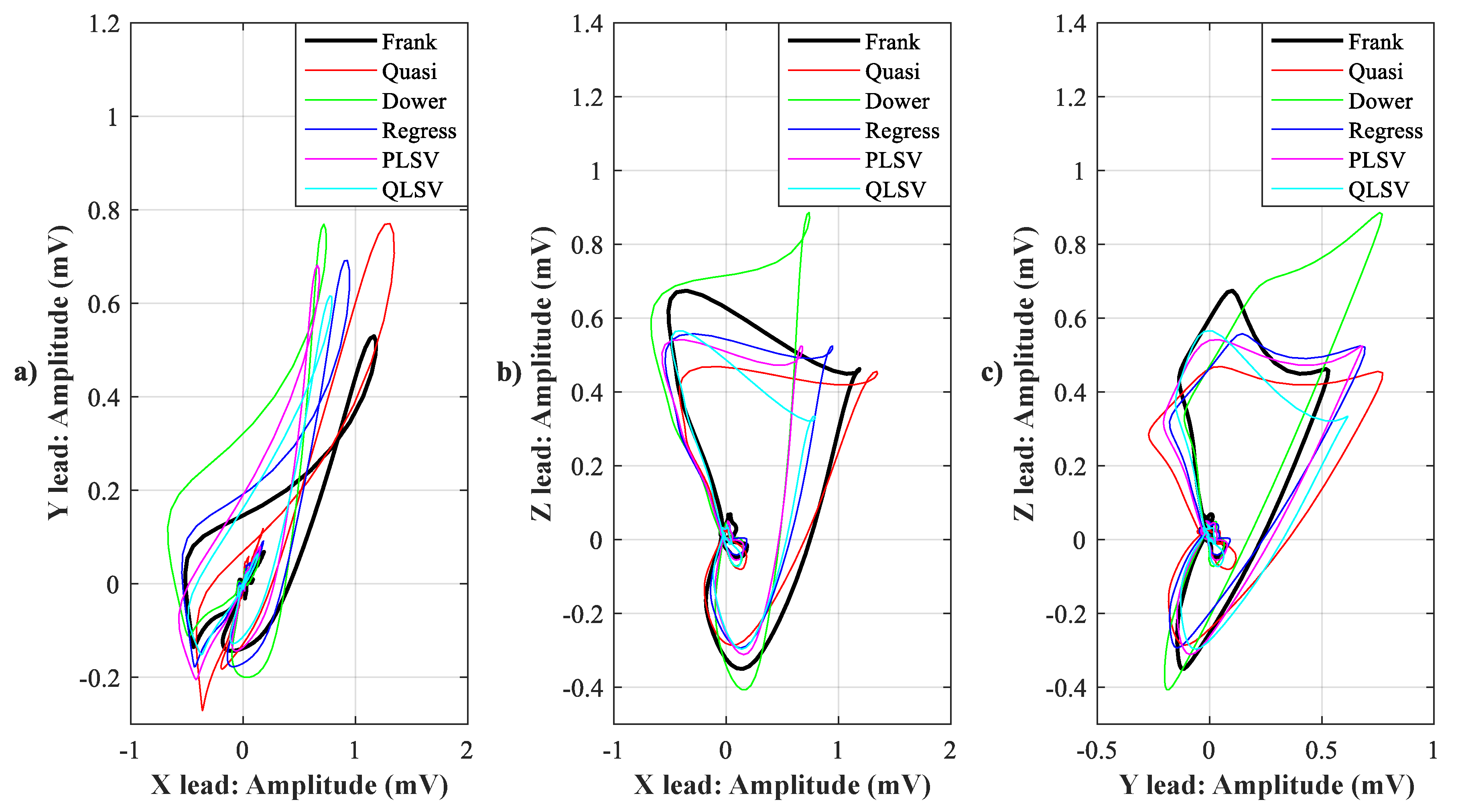
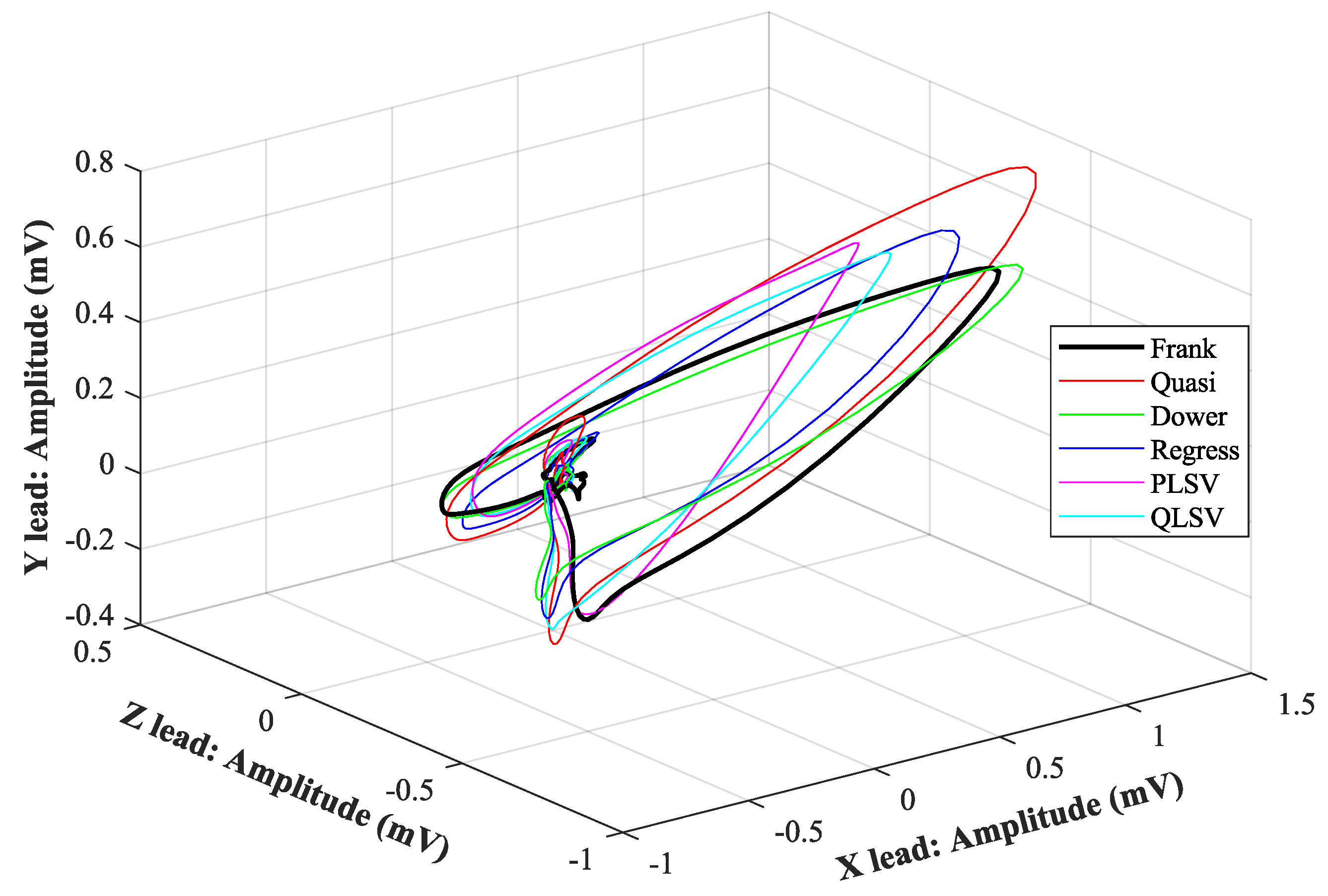
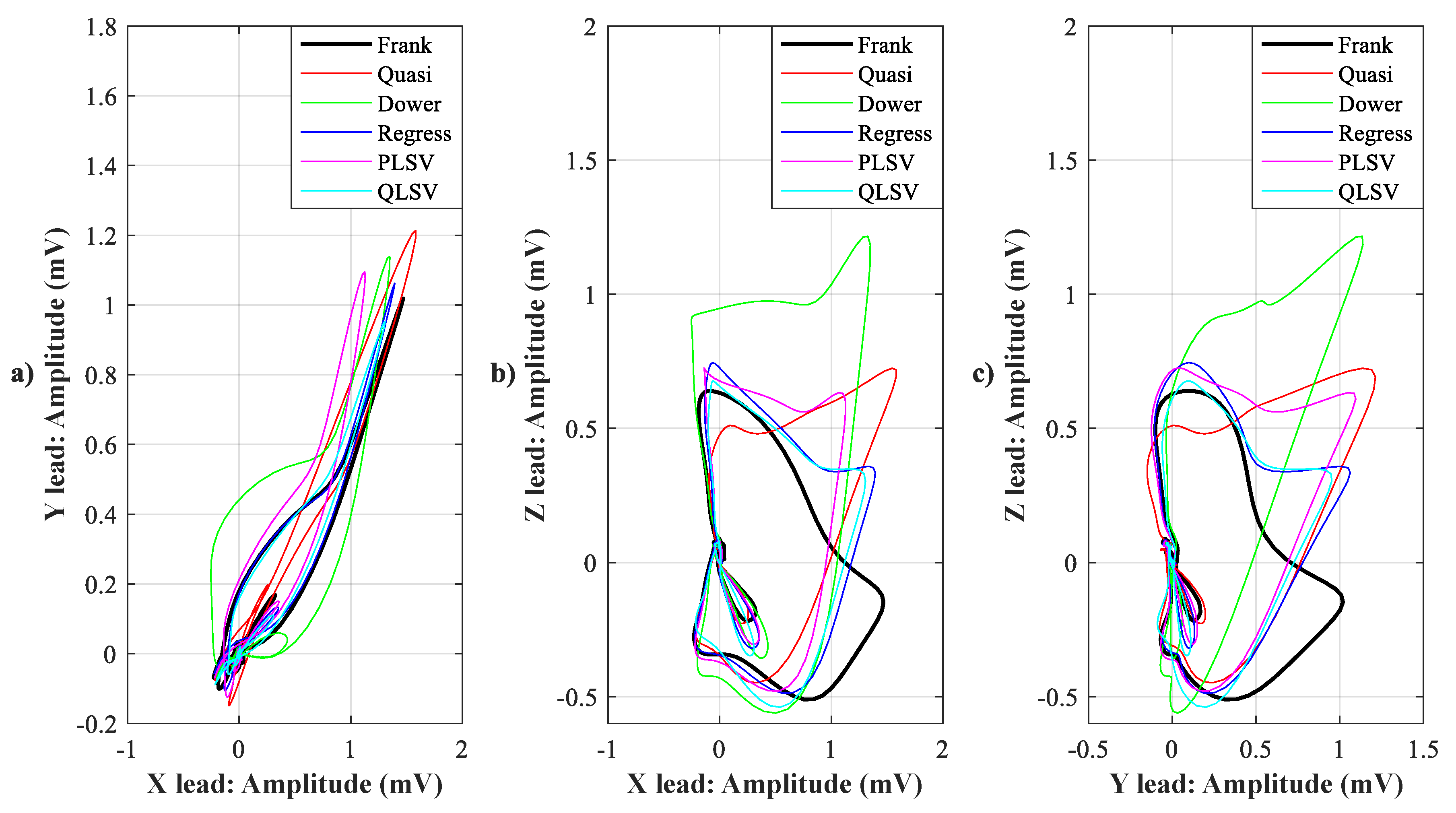
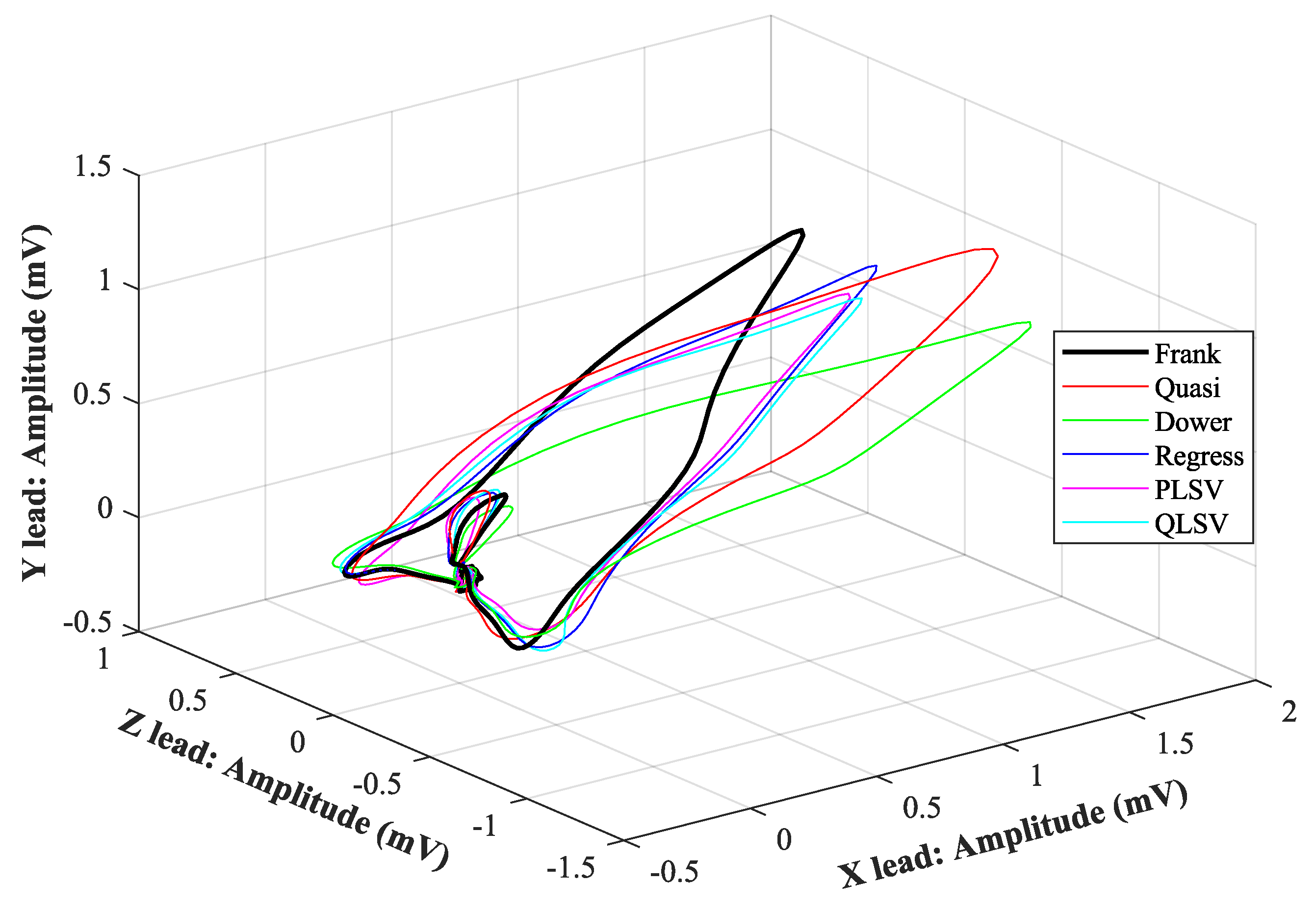
| Lead | X | Y | Z |
|---|---|---|---|
| V1 | −0.172 | 0.057 | −0.229 |
| V2 | −0.074 | −0.019 | −0.310 |
| V3 | 0.122 | −0.106 | −0.246 |
| V4 | 0.231 | −0.022 | −0.063 |
| V5 | 0.239 | 0.041 | 0.055 |
| V6 | 0.194 | 0.048 | 0.108 |
| I | 0.156 | −0.227 | 0.022 |
| II | −0.010 | 0.887 | 0.102 |
| Lead | X | Y | Z |
|---|---|---|---|
| V1 | −0.130 | 0.060 | −0.430 |
| V2 | 0.050 | −0.020 | −0.060 |
| V3 | −0.010 | −0.050 | −0.140 |
| V4 | 0.140 | 0.060 | −0.200 |
| V5 | 0.060 | −0.170 | −0.110 |
| V6 | 0.540 | 0.130 | 0.310 |
| I | 0.380 | −0.070 | 0.110 |
| II | −0.070 | 0.930 | −0.230 |
| Lead | X | Y | Z |
|---|---|---|---|
| V1 | 0.147 | 0.023 | 0.184 |
| V2 | 0.058 | 0.085 | 0.163 |
| V3 | 0.037 | 0.003 | 0.190 |
| V4 | 0.139 | 0.033 | 0.119 |
| V5 | 0.232 | 0.060 | 0.023 |
| V6 | 0.226 | 0.104 | 0.043 |
| I | 0.199 | 0.146 | 0.085 |
| II | 0.018 | 0.503 | 0.130 |
| Lead | X | Y | Z |
|---|---|---|---|
| V1 | −0.266 | 0.088 | −0.319 |
| V2 | 0.027 | −0.088 | −0.198 |
| V3 | 0.065 | 0.003 | −0.167 |
| V4 | 0.131 | 0.042 | −0.099 |
| V5 | 0.203 | 0.047 | −0.009 |
| V6 | 0.22 | 0.067 | 0.06 |
| I | 0.37 | −0.131 | 0.184 |
| II | −0.154 | 0.717 | −0.114 |
| Mean Squared Error | X | Y | Z |
|---|---|---|---|
| Regress Median | 2.2024 · 10 | 3.8445 · 10 | 1.9622 · 10 |
| Quasi Median | 1.5799 · 10 | 1.9417 · 10 | 3.8956 · 10 |
| Dower Median | 1.4880 · 10 | 8.7119 · 10 | 6.5558 · 10 |
| PLSV Median | 1.1881 · 10 | 7.2627 · 10 | 2.3116 · 10 |
| QLSV Median | 1.1887 · 10 | 1.0313 · 10 | 2.5286 · 10 |
| p-value (Regress × Quasi) | 2.4982 · 10 | 3.5755 · 10 | 1.9268 · 10 |
| p-value (Regress × Dower) | 1.2882 · 10 | 5.7956 · 10 | 1.1888 · 10 |
| p-value (Regress × PLSV) | 2.7719 · 10 | 3.6261 · 10 | 0.2878 |
| p-value (Regress × QLSV) | 4.9807 · 10 | 3.2827 · 10 | 0.3576 |
| Correlation Coefficient | X | Y | Z |
|---|---|---|---|
| Regress Median | 0.998397 | 0.994343 | 0.981839 |
| Quasi Median | 0.986784 | 0.986223 | 0.948075 |
| Dower Median | 0.990345 | 0.982841 | 0.944712 |
| PLSV Median | 0.990350 | 0.982036 | 0.966346 |
| QLSV Median | 0.994695 | 0.976752 | 0.971982 |
| p-values (Regress × Quasi) | 2.5482 · 10 | 3.2827 · 10 | 3.0635 · 10 |
| p-values (Regress × Dower) | 6.0021 · 10 | 2.4887 · 10 | 3.6261 · 10 |
| p-values (Regress × PLSV) | 2.1785 · 10 | 9.7206 · 10 | 0.2485 |
| p-values (Regress × QLSV) | 7.1535 · 10 | 1.4784 · 10 | 0.1612 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaros, R.; Martinek, R.; Danys, L. Comparison of Different Electrocardiography with Vectorcardiography Transformations. Sensors 2019, 19, 3072. https://doi.org/10.3390/s19143072
Jaros R, Martinek R, Danys L. Comparison of Different Electrocardiography with Vectorcardiography Transformations. Sensors. 2019; 19(14):3072. https://doi.org/10.3390/s19143072
Chicago/Turabian StyleJaros, Rene, Radek Martinek, and Lukas Danys. 2019. "Comparison of Different Electrocardiography with Vectorcardiography Transformations" Sensors 19, no. 14: 3072. https://doi.org/10.3390/s19143072
APA StyleJaros, R., Martinek, R., & Danys, L. (2019). Comparison of Different Electrocardiography with Vectorcardiography Transformations. Sensors, 19(14), 3072. https://doi.org/10.3390/s19143072






