Sensitivity Enhancement of NMR Spectroscopy Receiving Chain Used in Condensed Matter Physics
Abstract
1. Introduction
2. Noise Figure of NMR System Receiving Chain
2.1. General Approach
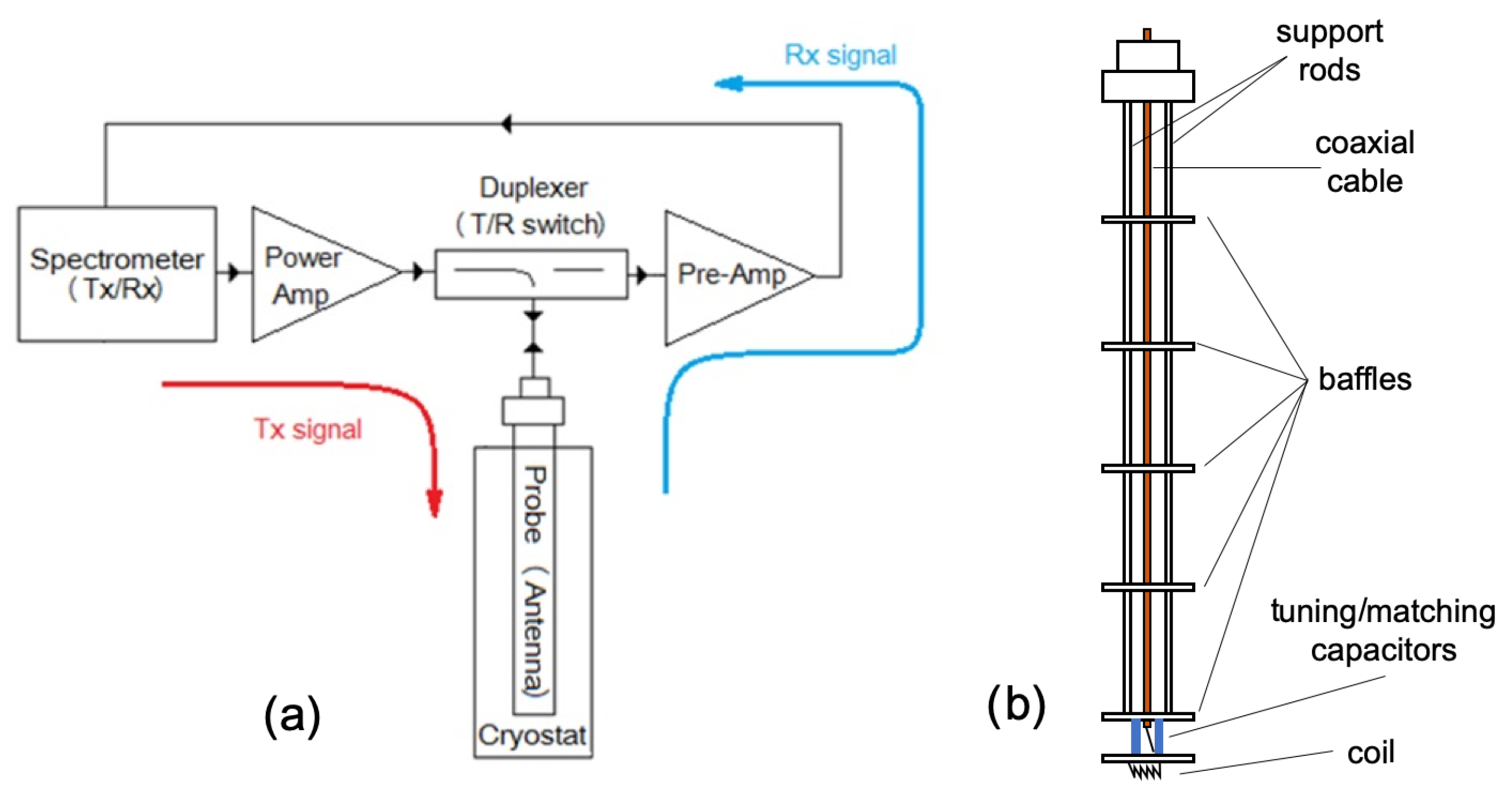
2.2. NMR Spectroscopy System
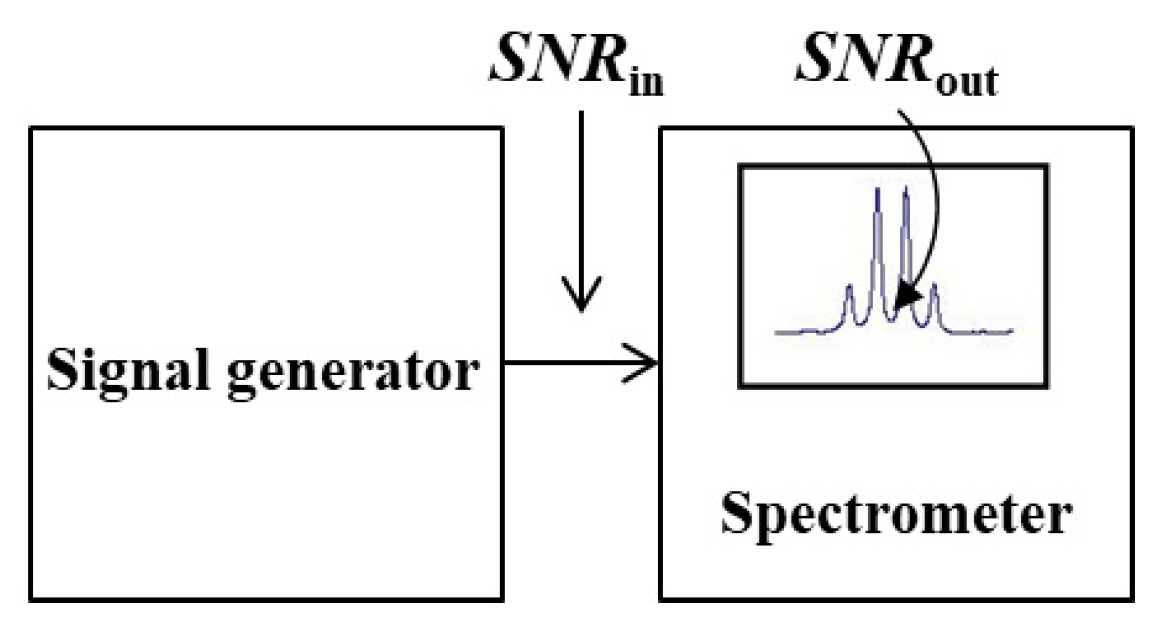
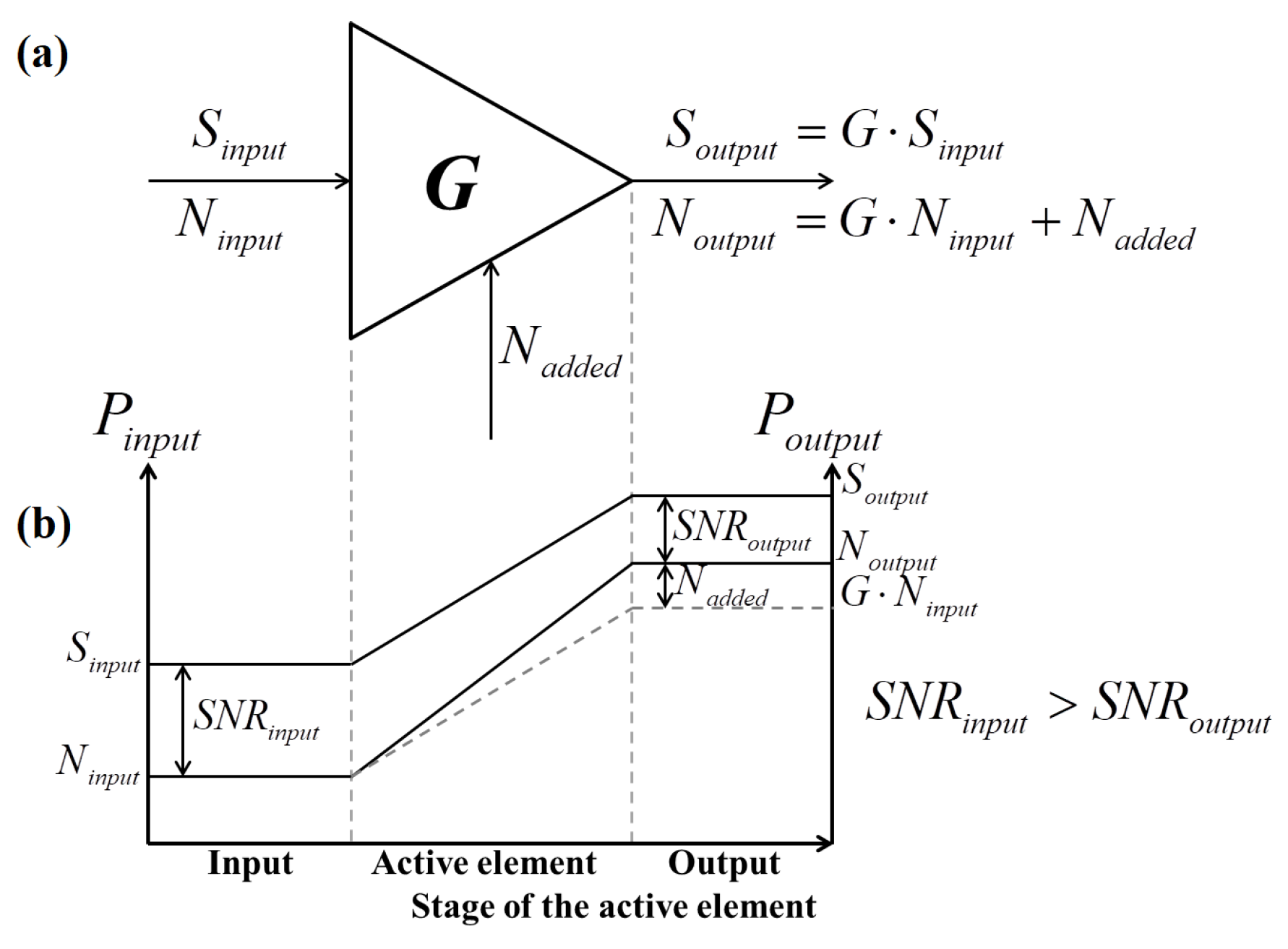
2.3. Concept of Noise Figure
2.4. Noise Model of NMR Receiving Chain
2.5. Preamplifier’s Impedance Mismatch
2.6. Non-Standard Temperature of the Probe
2.7. Signal Averaging
2.8. The Case of a Two-Stage Preamplifier
3. Experimental Verification of Developed Noise Model
3.1. General Approach
3.2. Measurements Description
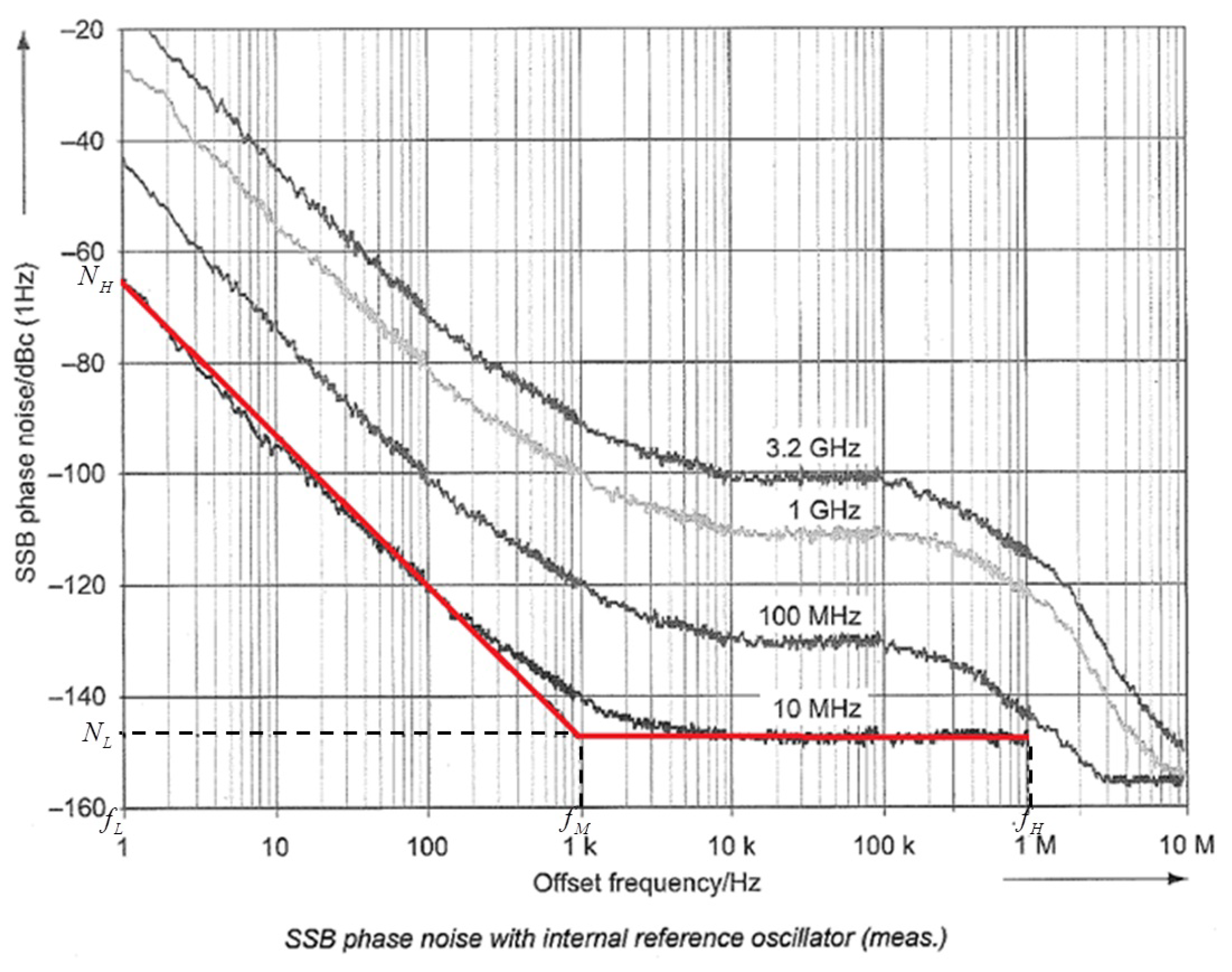
3.3. Results
4. Improvement Suggestions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Spectrometer Noise Figure Determination
References
- Kleckner, I.R.; Foster, M.P. An introduction to NMR-based approaches for measuring protein dynamics. Biochim. Biophys. Acta (BBA) Proteins Proteom. 2011, 1814, 942–968. [Google Scholar] [CrossRef] [PubMed]
- Richards, M.G.; Andrews, A.R.; Lusher, C.P.; Schratter, J. Cryogenic GaAs FET amplifiers and their use in NMR detection. Rev. Sci. Instrum. 1986, 57, 404–409. [Google Scholar] [CrossRef]
- Abragam, A. The Principles of Nuclear Magnetism; Clarendon Press: Oxford, UK, 1989. [Google Scholar]
- Motchenbacher, C.D.; Connelly, J.A. Low-Noise Electronic System Design; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Hoult, D.; Richards, R. The signal-to-noise ratio of the nuclear magnetic resonance experiment. J. Magn. Reson. (1969) 1976, 24, 71–85. [Google Scholar] [CrossRef]
- Fukushima, E.; Roeder, S.B.W. Experimental Pulse NMR: A Nuts and Bolts Approach; Addition-Wesley Publishing Company: Reading, MA, USA, 1981. [Google Scholar]
- Rahman, A.; Choudhary, M.; Wahab, A. Solving Problems with NMR Spectroscopy, 2nd ed.; Elsevier Academic Press: San Diego, CA, USA, 2016. [Google Scholar]
- Pelc, D.; Grafe, H.J.; Gu, G.D.; Požek, M. Cu nuclear magnetic resonance study of charge and spin stripe order in La1.875Ba0.125CuO4. Phys. Rev. B 2017, 95, 054508. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, Z.G.; Huang, Y.C. Implementation of a two-stage digital AGC for spectrum analyzer. In Proceedings of the 2011 International Conference on Applied Superconductivity and Electromagnetic Devices, Sydney, NSW, Australia, 14–16 December 2011; pp. 37–40. [Google Scholar] [CrossRef]
- Levitt, M.H. Spin Dynamics: Basics of Nuclear Magnetic Resonance; John Wiley & Sons, Ltd.: Chichester, UK, 2008. [Google Scholar]
- Hiebel, M. Fundamentals of Vector Network Analysis; Rohde & Schwarz: Munich, Germany, 2014. [Google Scholar]
- Keysight Technologies. Fundamentals of RF and Microwave Noise Figure Measurements. Available online: http://literature.cdn.keysight.com/litweb/pdf/5952-8255E.pdf (accessed on 6 June 2019).
- Davenport, W.B., Jr.; Root, W.L. An Introduction to the Theory of Random Signals and Noise; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1958. [Google Scholar]
- Traficante, D.D. Time averaging. Does the noise really average toward zero? Concepts Magn. Reson. 1991, 3, 83–87. [Google Scholar] [CrossRef]
- Robinson, F.N.H. Noise and Fluctuations in Electronic Devices and Circuits; Clarendon Press: Oxford, UK, 1974. [Google Scholar]
- Cvitanić, T.; Šurija, V.; Prša, K.; Zaharko, O.; Kupčić, I.; Babkevich, P.; Frontzek, M.; Požek, M.; Berger, H.; Magrez, A.; et al. Singlet state formation and its impact on the magnetic structure in the tetramer system SeCuO3. Phys. Rev. B 2018, 98, 054409. [Google Scholar] [CrossRef]
- Cvitanić, T.; Lukas, M.; Grbić, M.S. Two-axis goniometer for single-crystal nuclear magnetic resonance measurements. Rev. Sci. Instrum. 2019, 90, 043903. [Google Scholar] [CrossRef] [PubMed]
- MITEQ AU-1114. Available online: https://nardamiteq.com/docs/1114-1606276-L0910.PDF (accessed on 6 June 2019).
- THAMWAY N141-206AA. Available online: http://www.thamway.co.jp/english/product07-08_e.html (accessed on 6 June 2019).
- Mini-Circuits HELA -10D+. Available online: https://www.minicircuits.com/WebStore/dashboard.html?model=HELA-10%2B (accessed on 6 June 2019).
- Kolar, P.; Hrabar, S.; Grbić, M.S. Towards optimal noise properties of NMR antenna-receiver chain. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 1054–1056. [Google Scholar] [CrossRef]
- Mizuno, T.; Takegoshi, K. Development of a cryogenic duplexer for solid-state nuclear magnetic resonance. Rev. Sci. Instrum. 2009, 80, 124702. [Google Scholar] [CrossRef] [PubMed]
- Bialkowski, M.E.; Ibrahim, S.Z.; Abbosh, A.M. Wideband performance of 3 dB microstrip-slot coupler using different substrates. Microw. Opt. Technol. Lett. 2011, 53, 1618–1624. [Google Scholar] [CrossRef]
- Moskau, D. Application of real time digital filters in NMR spectroscopy. Concepts Magn. Reson. 2002, 15, 164–176. [Google Scholar] [CrossRef]
- Giovannetti, G.; Hartwig, V.; Viti, V.; Gaeta, G.; Francesconi, R.; Landini, L.; Benassi, A. Application of undersampling technique for the design of an NMR signals digital receiver. Concepts Magn. Reson. Part B Magn. Reson. Eng. 2006, 29B, 107–114. [Google Scholar] [CrossRef]
- NMR Spectroscopy Rx Chain Noise Figure Calculator—GitHub. Available online: https://github.com/5ARK/NMR_F_Calc (accessed on 6 June 2019).


| Compound | SeCuO3 | Cs2Cu3SnF12 | |
|---|---|---|---|
| Parameter | Symbol | Values | |
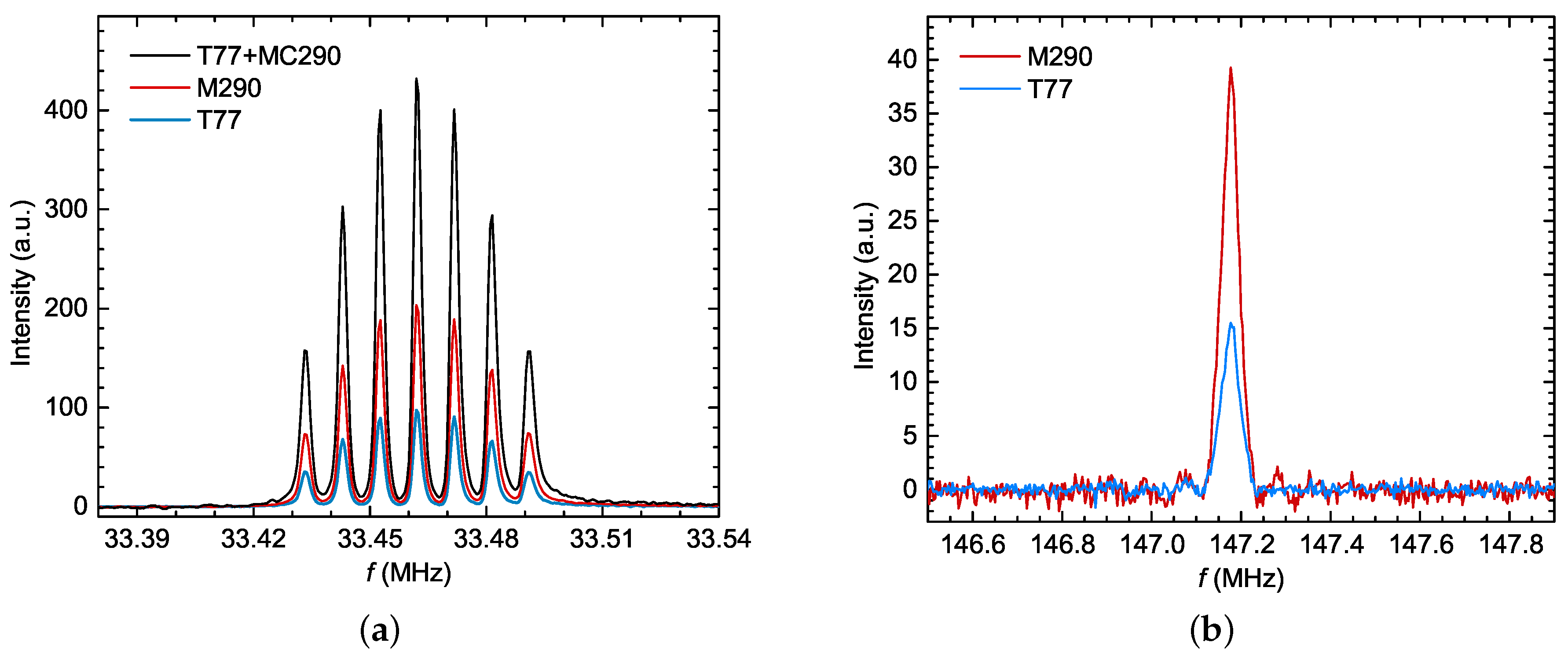
| Measurement frequency (MHz) | - | 147.20 | 33.50 |
| Coil and sample temperature (K) | 20 | 30 | |
| DC magnetic field (T) | 11.90 | 6 | |
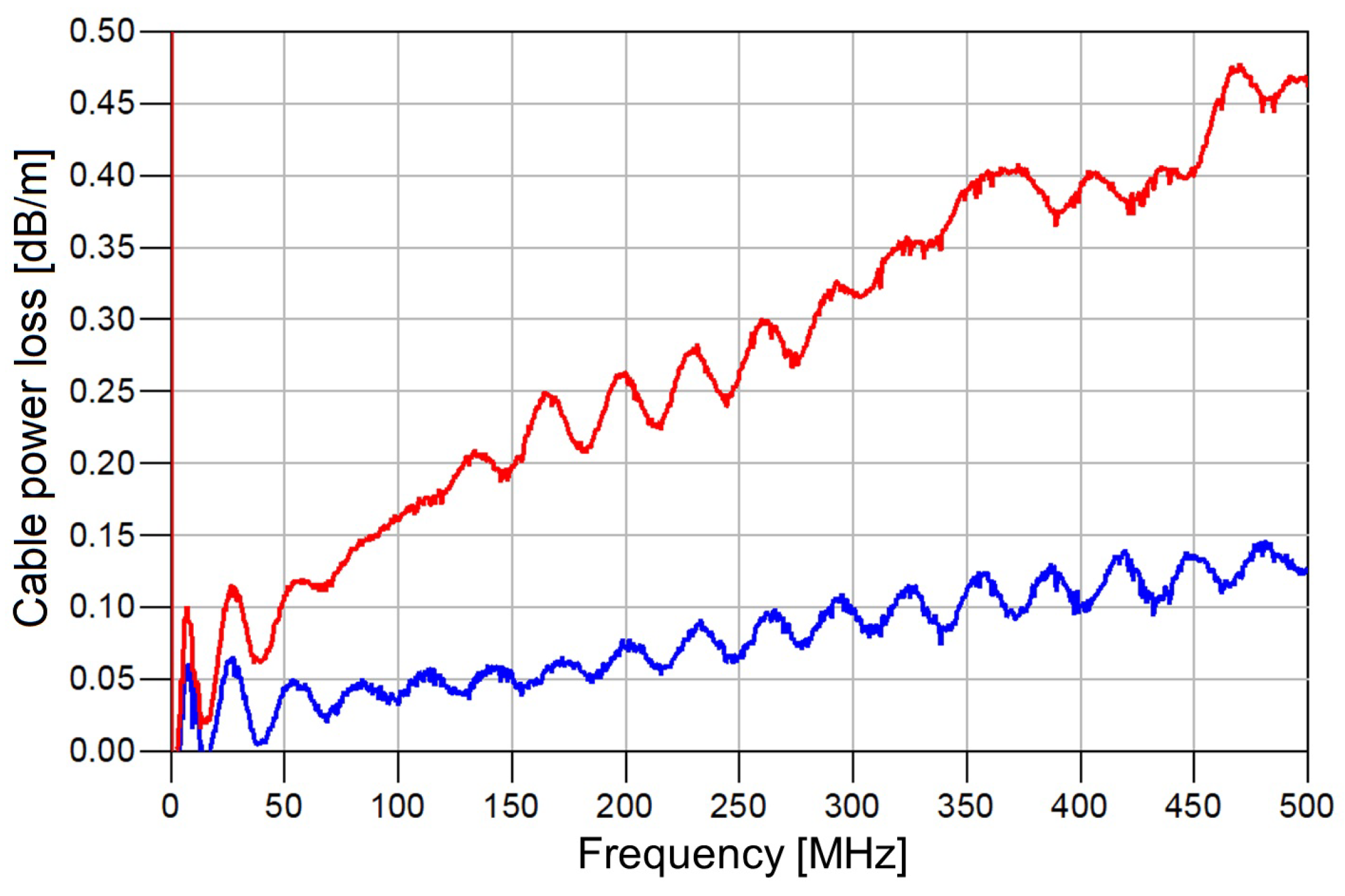
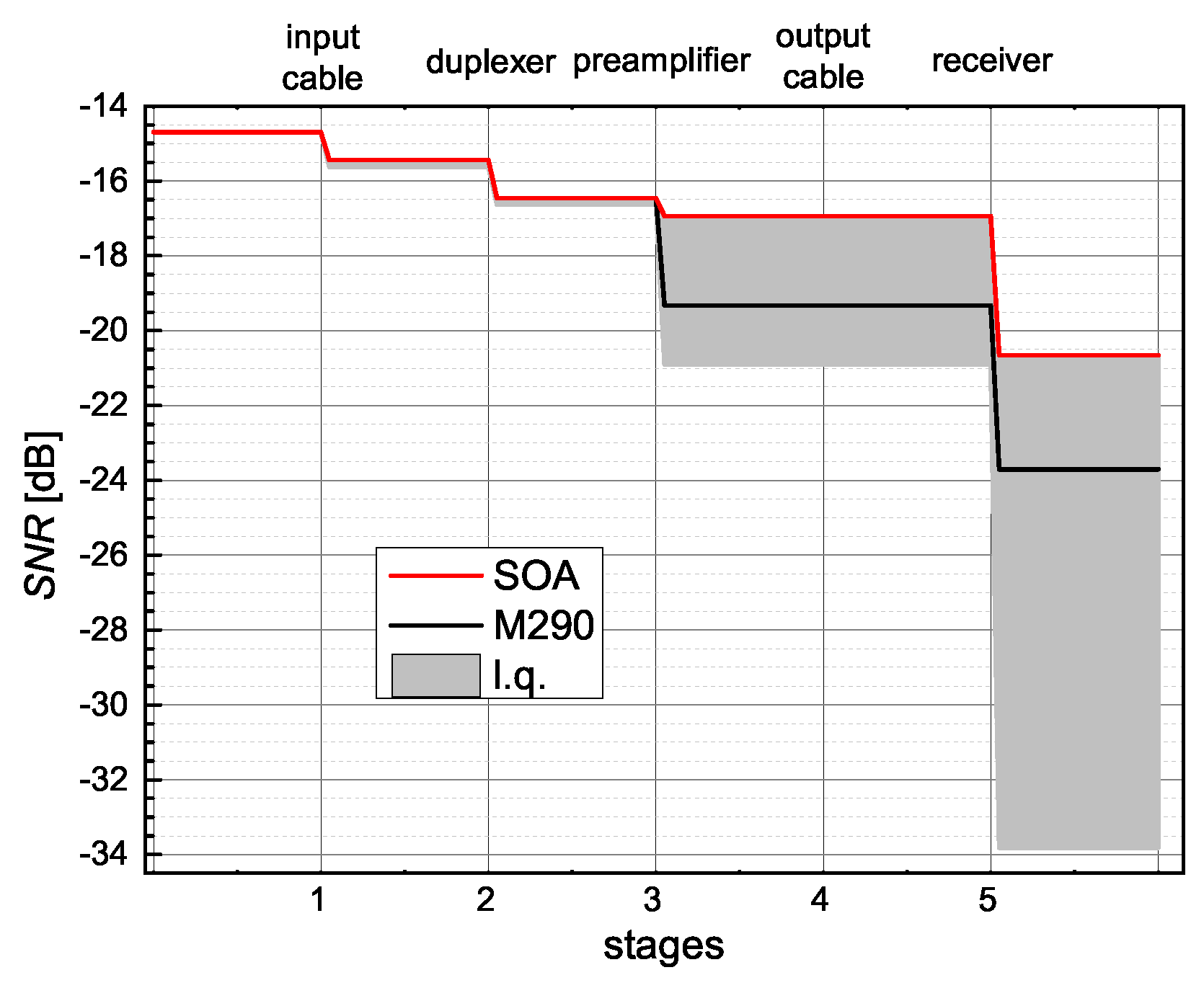
| Input cable loss (dB) | 0.28 | 0.10 | |
| Duplexer loss (dB) | 0.27 | 0.43 | |
| M290 gain (dB) | 36.13 | 36.52 | |
| M290 noise figure (dB) | 1.11 | 1.14 | |
| M290 reflection coefficient (dB) | −16.43 | −13.50 | |
| T77 gain (dB) | , | 28.54 | 27.89 |
| T77 noise figure (dB) | , | 0.32 | 1.07 |
| T77 reflection coefficient (dB) | , | −7.57 | −8.05 |
| MC290 gain (dB) | - | 10.75 | |
| MC290 noise figure (dB) | - | 4.22 | |
| MC290 reflection coefficient (dB) | - | −27.58 | |
| Output cable loss (dB) | 0.46 | 0.62 | |
| Spectrometer noise figure (dB) | 33.50 | 38.40 | |
| Number of measurements | 200 | 400 | |
| Input impedance M290 () | 51.20 | 72.80 | |
| Output impedance M290 () | 54.50 | 45.60 | |
| Input impedance T77 () | 45.77 | 34.70 | |
| Output impedance T77 () | 101.46 | 38.20 | |
| Input impedance MC290 () | 50 | 50 | |
| Output impedance MC290 () | 50 | 50 | |
| Compound | Nucleus | (MHz/T) | Spin | Abundance (%) | Quadrupole Splitting |
|---|---|---|---|---|---|
| SeCuO3 | 63Cu | 11.285 | 3/2 | 69.1 | 48.05 MHz |
| Cs2Cu3SnF12 | 133Cs | 5.5844 | 7/2 | 100 | 9.54 kHz |
| Compound | SeCuO3 | Cs2Cu3SnF12 |
|---|---|---|
| Frequency (MHz) | 147.20 | 33.50 |
| M290 | ||
| Measured (dB) | 30.11 | 56.00 |
| Determined (dB) | −17.95 | −18.46 |
| Calculated via (14) and (3) (dB) | 12.17 | 37.54 |
| T77 | ||
| Measured (dB) | 24.97 | 48.32 |
| Determined (dB) | −12.83 | −10.77 |
| Calculated via (14) and (3) (dB) | 12.14 | 37.55 |
| T77 with MC290 | ||
| Measured | - | 55.65 |
| Determined (dB) | - | −19.41 |
| Calculated via (15) and (3) (dB) | - | 36.24 |
| Calculatedvia (1) (dB) | 15.20 | 35.31 |
| Compound | SeCuO3 | Cs2Cu3SnF12 |
|---|---|---|
| Frequency (MHz) | 147.20 | 33.50 |
| (dB) | 12.17 | 37.54 |
| using M290 (dB) | 30.11 | 56.00 |
| Predicted using SOA (dB) | 32.28 | 58.77 |
| enhancement (dB) | 2.16 | 2.76 |
| enhancement (%) | 65 | 89 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolar, P.; Grbić, M.S.; Hrabar, S. Sensitivity Enhancement of NMR Spectroscopy Receiving Chain Used in Condensed Matter Physics. Sensors 2019, 19, 3064. https://doi.org/10.3390/s19143064
Kolar P, Grbić MS, Hrabar S. Sensitivity Enhancement of NMR Spectroscopy Receiving Chain Used in Condensed Matter Physics. Sensors. 2019; 19(14):3064. https://doi.org/10.3390/s19143064
Chicago/Turabian StyleKolar, Petar, Mihael S. Grbić, and Silvio Hrabar. 2019. "Sensitivity Enhancement of NMR Spectroscopy Receiving Chain Used in Condensed Matter Physics" Sensors 19, no. 14: 3064. https://doi.org/10.3390/s19143064
APA StyleKolar, P., Grbić, M. S., & Hrabar, S. (2019). Sensitivity Enhancement of NMR Spectroscopy Receiving Chain Used in Condensed Matter Physics. Sensors, 19(14), 3064. https://doi.org/10.3390/s19143064





