Self-Adaptive Framework Based on MAPE Loop for Internet of Things †
Abstract
1. Introduction
2. Background and Related Work
2.1. Self-Adaptive Software Framework with Internet of Things
- The monitoring process is responsible for collecting and correlating data from the software and its environment.
- The analyzing (detecting) process is responsible for analyzing the adaptive symptoms by monitoring the data.
- The planning (deciding) process is responsible for determining the required changes and their execution methods (i.e., it is responsible for determining adaptation strategies).
- The executing (acting) process is responsible for applying the adaptation strategy.
2.2. Self-Adaptive Software Modeling by Finite-State Machines
- S is a set of states
- S consists of four subsets: {
- is the transition relationship, and it is classified into two types: and
- is the initial state
- AP is a set of atomic propositions
- L: S is a labeling function ( denotes the power set of AP)
- S is a set of states
- S is classified into three types of subsets, {
- → is the set of transitions, and
- is the transition relationship
- is the initial state
- AP is a set of atomic propositions
- L: S is a labeling function ( denotes the power set of AP)
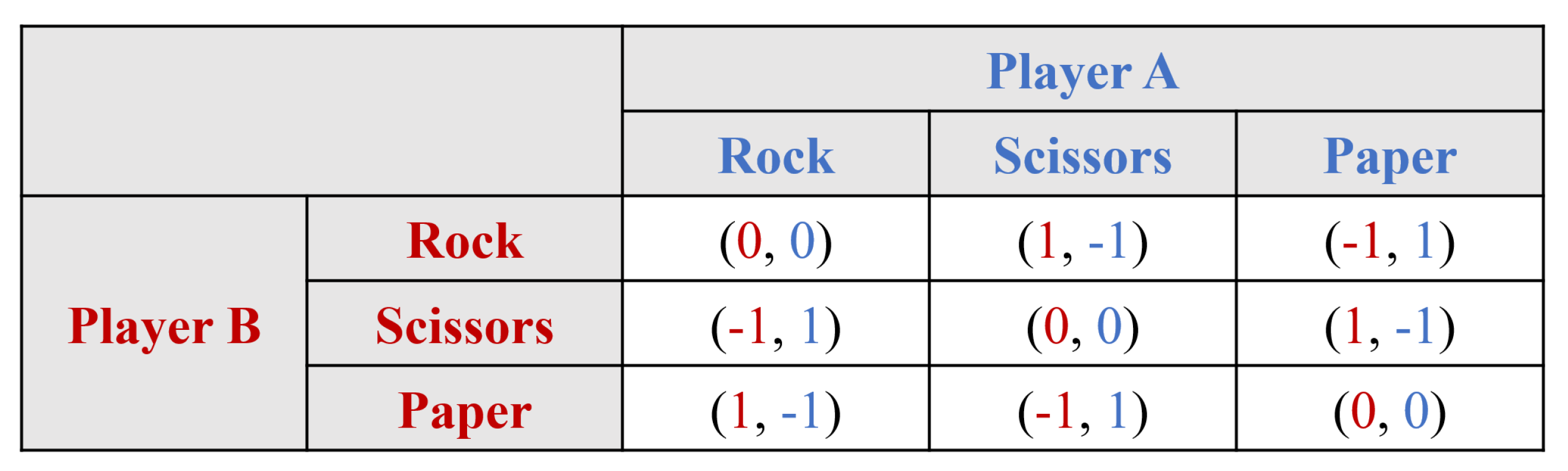
2.3. Nash Equilibrium
- is the strategy set of profile
- Player
- is the payoff function
- A payoff function is evaluated at
- is the strategy profile of player i
- is the strategy profile of players other than i
- Player i selects strategy resulting in strategy profile , and then player i obtains payoff .
- is a Nash equilibrium when .
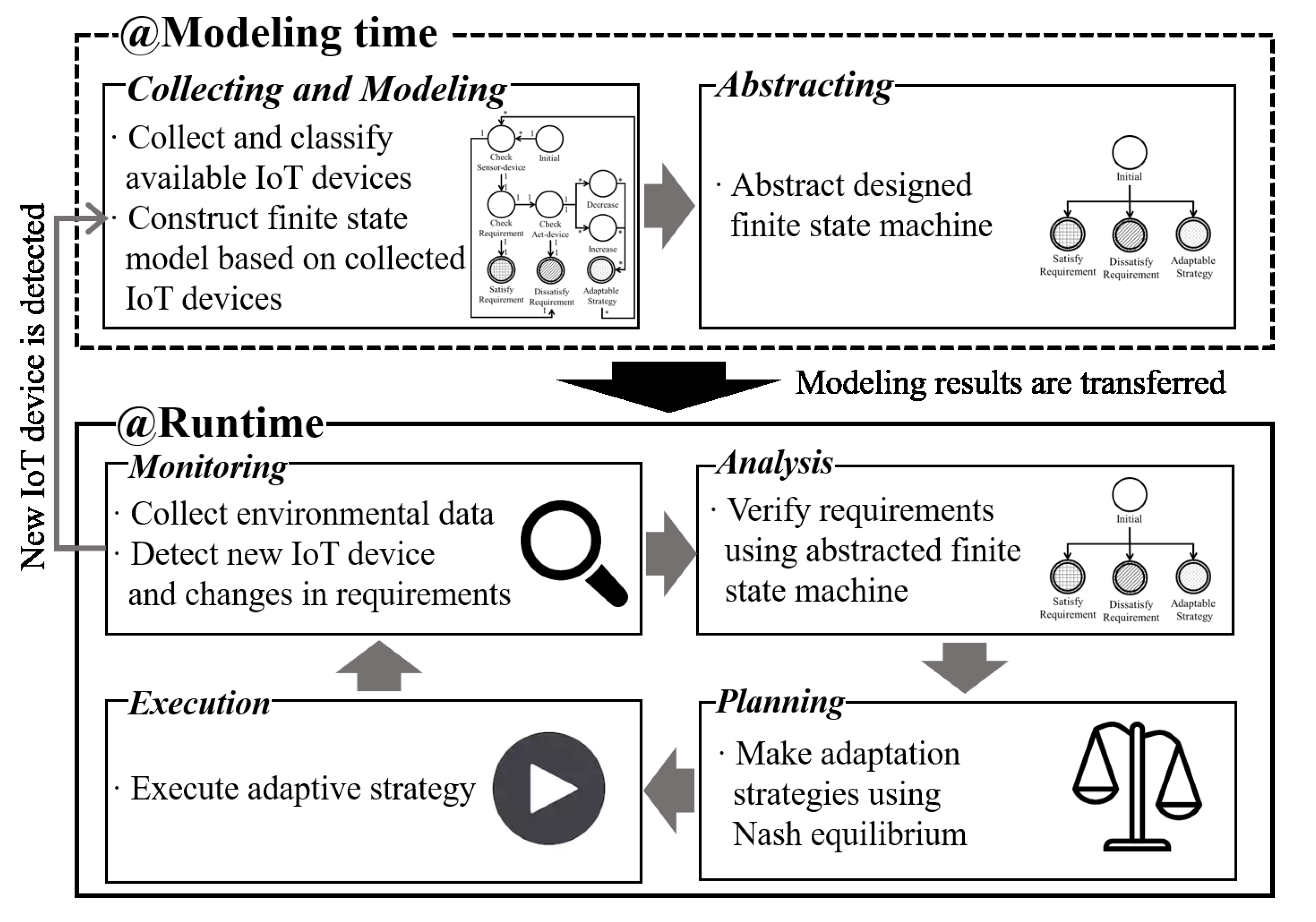
3. Self-Adaptive Framework with Runtime Decision-Making Method
3.1. Overview
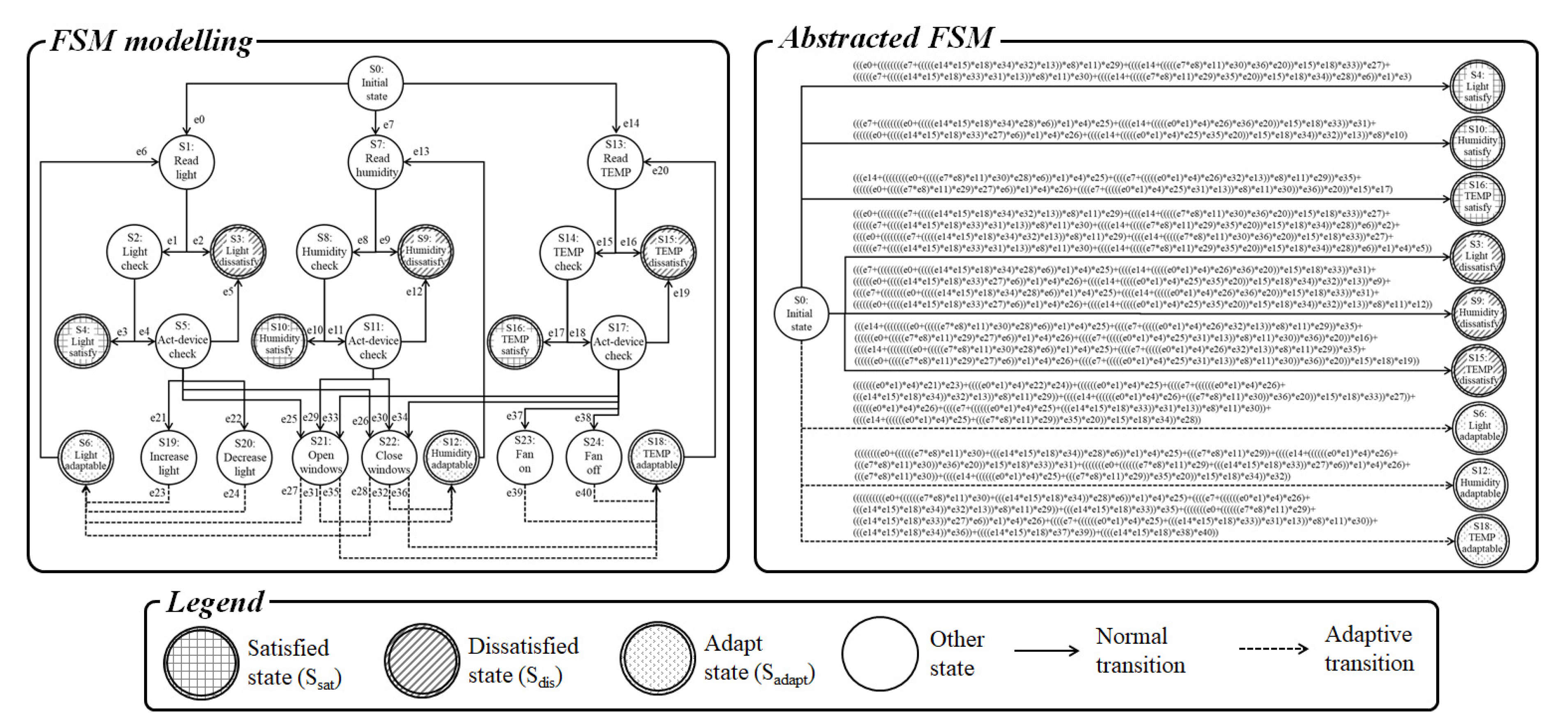
3.2. Finite-State Machine Modeling for IoT Environments
- A sensor-device senses the changes in environment. Therefore, it must have embedded at least one readable sensor-device such as light sensor, humidity sensor, and temperature sensor. In addition, it is assumed that the sensor-device recognizes the requirement that is related to its sensed data.
- An act-device can change the environment. Therefore, it must have embedded at least one physical-device such as an LED, a servomotor, or a fan. In addition, it is assumed that the act-device recognizes the requirements that are associated with its operation.
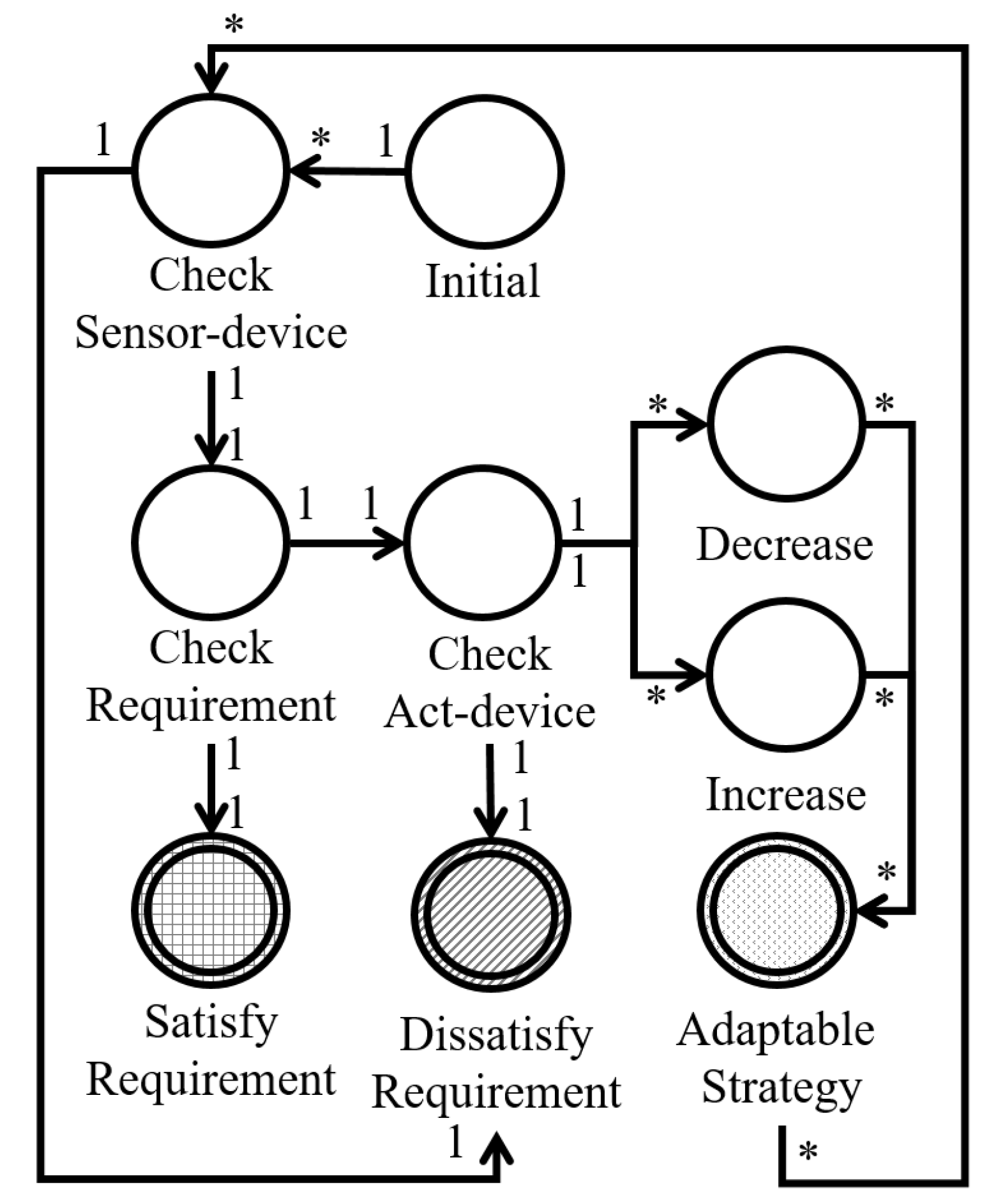
- S is a set of states
- The states are classified into eight types
- are end states
- is the transition relation, and it is classified into eleven types
- is an initial state
- AP is a set of atomic propositions
- L: S is a labeling function ( denotes the power set of AP)
- Initial state () is an initial state.
- Sensor-device state () is a set of sensor-device related states. In this state, the sensor-devices must be related at least once. If a readable sensor-device is available, it reaches a requirement state (i.e., ). However, it is connected to a dissatisfied state (i.e., ) if there is no related sensor-device. Requirement state () is a set of states that verify requirement satisfaction. If the checked requirement is satisfied, the requirement state reaches the satisfied state (i.e., ), else the adaptive state (i.e., ).
- Satisfied state () is a set of end states for which the software requirement is satisfied.
- Dissatisfied state () is a set of end states for which the software requirement is not satisfied. If the finite-state machine has no readable device (i.e., ) or no possible adaptive action (i.e., ), the finite-state machine model reaches this state.
- Act state () is a set of states that check for an actable device. If there are no actable devices, the model reaches the dissatisfied state (i.e., ), else the increase or decrease state (i.e., and , respectively).
- Increase state () and decrease state () are the sets of act-device related states. In these states, at least one actable device is related. If the finite-state machine reaches these states, the related act-device is operated. These states then reach the adaptive state (i.e., and , respectively).
- Adapt state () is one of the end state sets that denotes the possible adaptive activities. Therefore, if the finite-state machine reaches this state, it means that the self-adaptive software must adapt and adaptive strategies do exist. In addition, this state reaches the related requirement sensor-device state to re-verify the requirement satisfaction (i.e., ).
3.3. Game Theoretic Decision-Making and Evaluation
- is the strategy set of profile
- Requirement
- is a payoff function
- A payoff function is evaluated at
- is an act-device profile of requirement i
- is an act-device profile of players other than i
- Requirement i operates act-device resulting in strategy profile and then, requirement i obtains payoff
- is a Nash equilibrium for IoT when
- can be an operation candidate at runtime
- A strategy with the largest number of Nash equilibrium between the requirements is selected and implemented
- The number of satisfied requirements (SR) is the number of requirements that may be satisfied by the execution of a strategy. If an adaptation strategy satisfies multiple requirements, it is more efficient than an adaptive strategy that satisfies lesser requirements.
- The number of related requirements (RR) is the number of requirements that may be affected by the execution of a strategy. For example, if a strategy opens the windows to adjust indoor brightness, it affects humidity, dust density, or temperature. In this case, the requirements of humidity, dust density, and temperature comprise RR. It is more efficient to have fewer RRs.
- The number of act-devices (AD) is the number of act-devices that are executed by the adaptation strategy. It is more efficient to have a smaller value of AD.
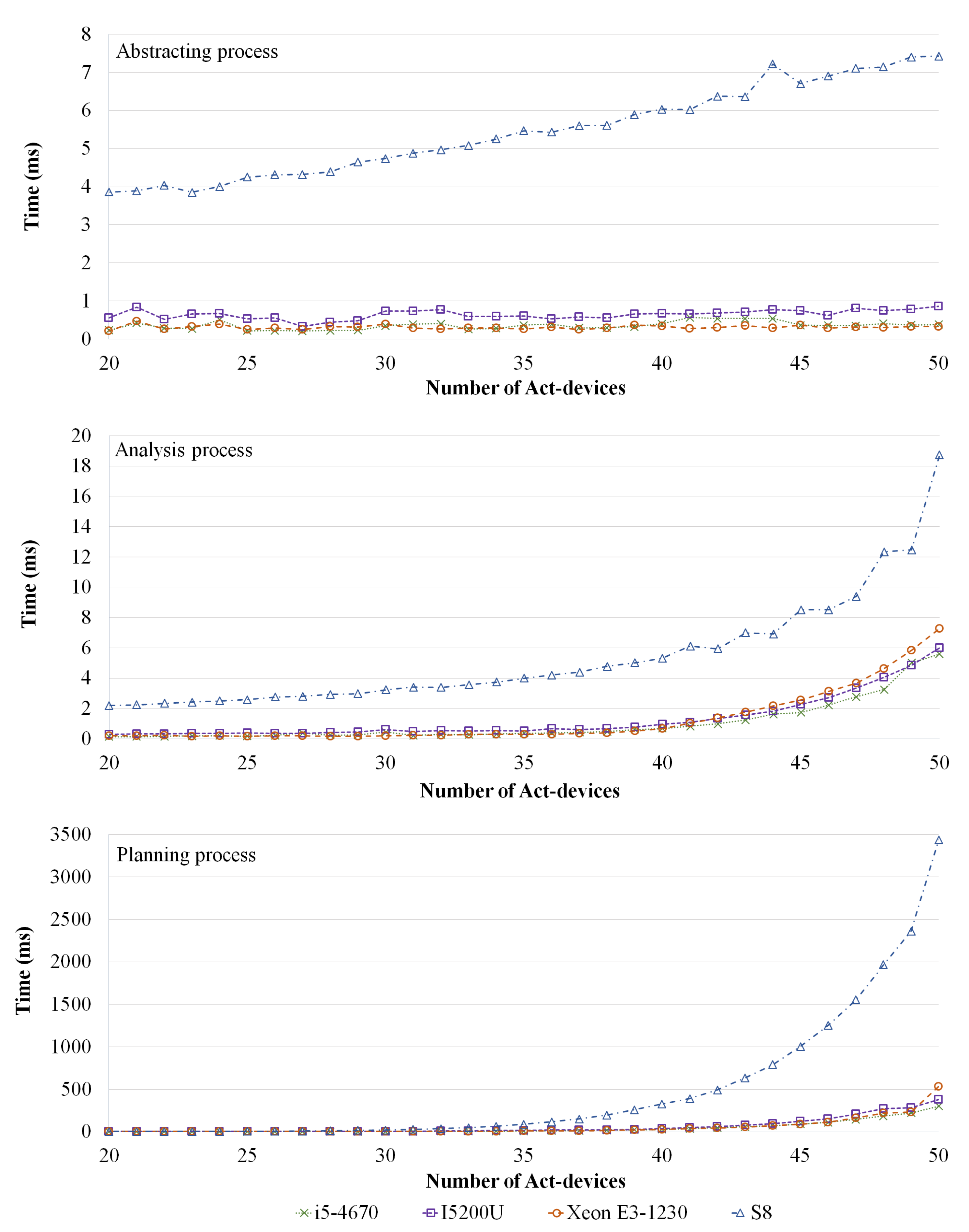
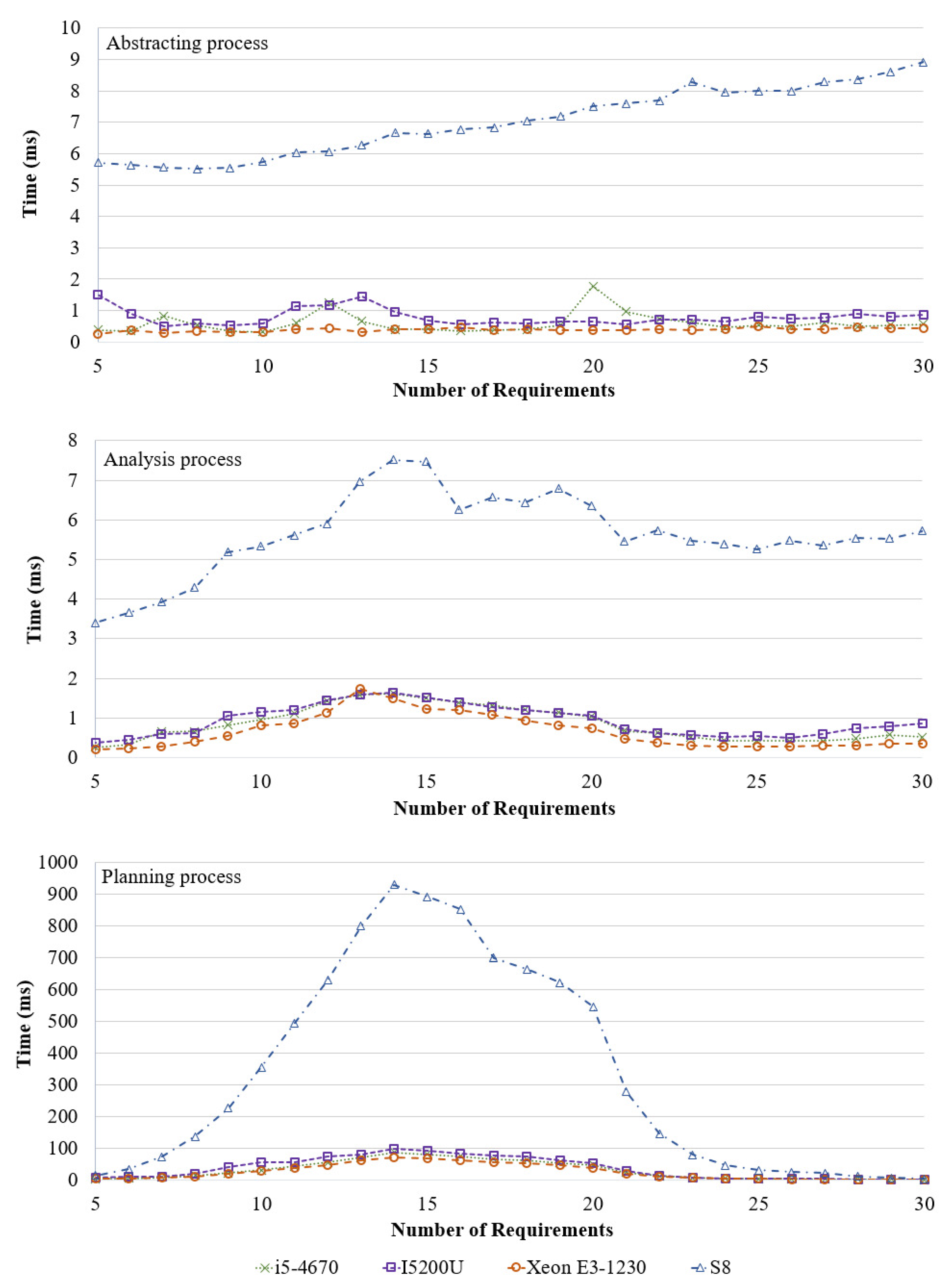
4. Experiment
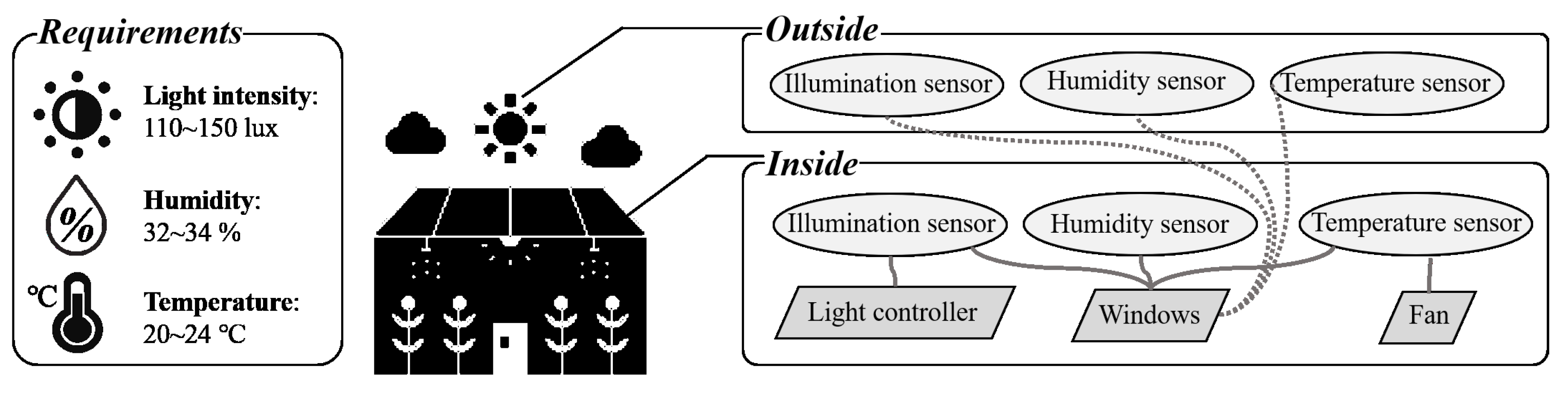
5. Case Study: IoT Based Smart Greenhouse
5.1. Overview of Case Study
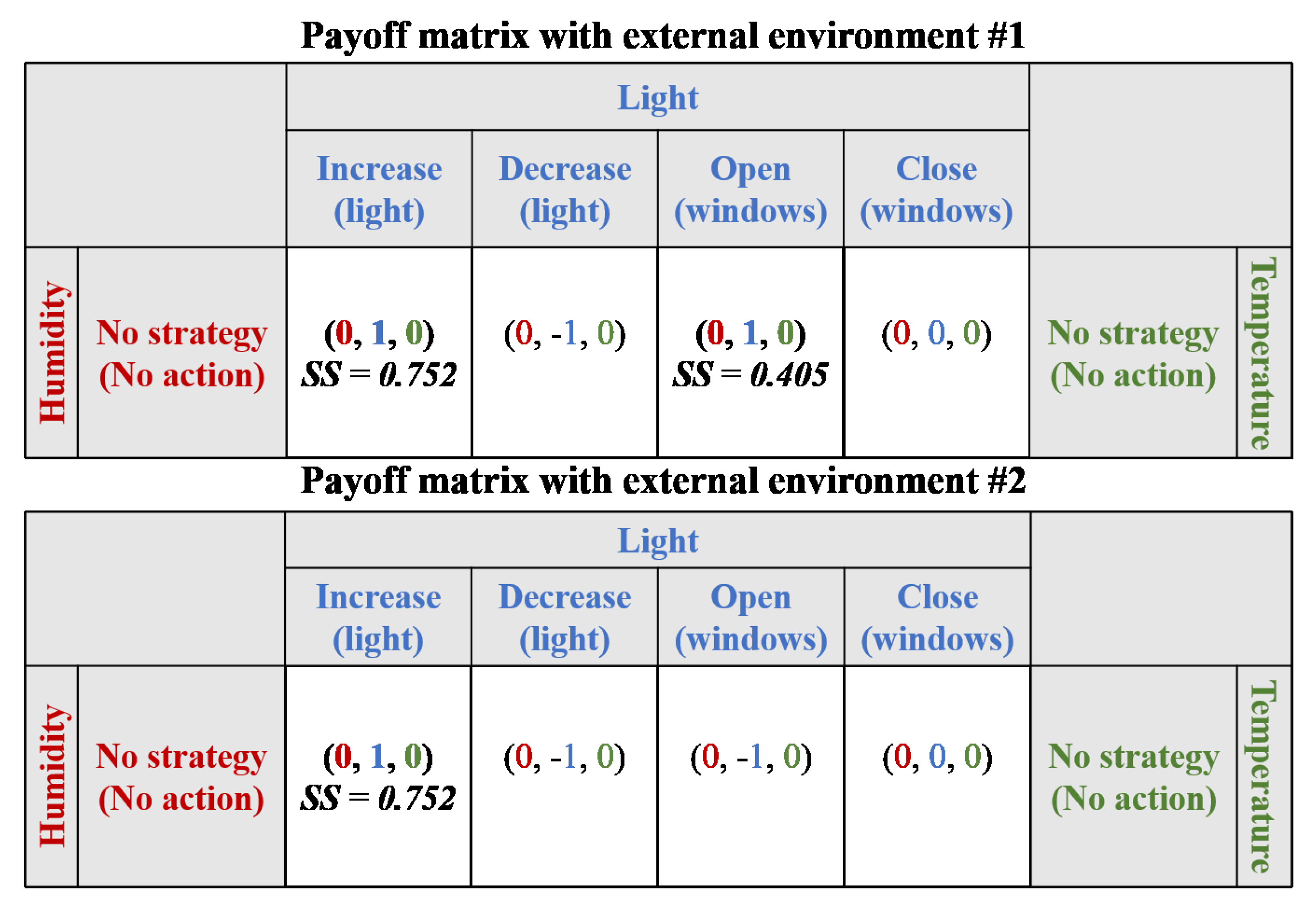
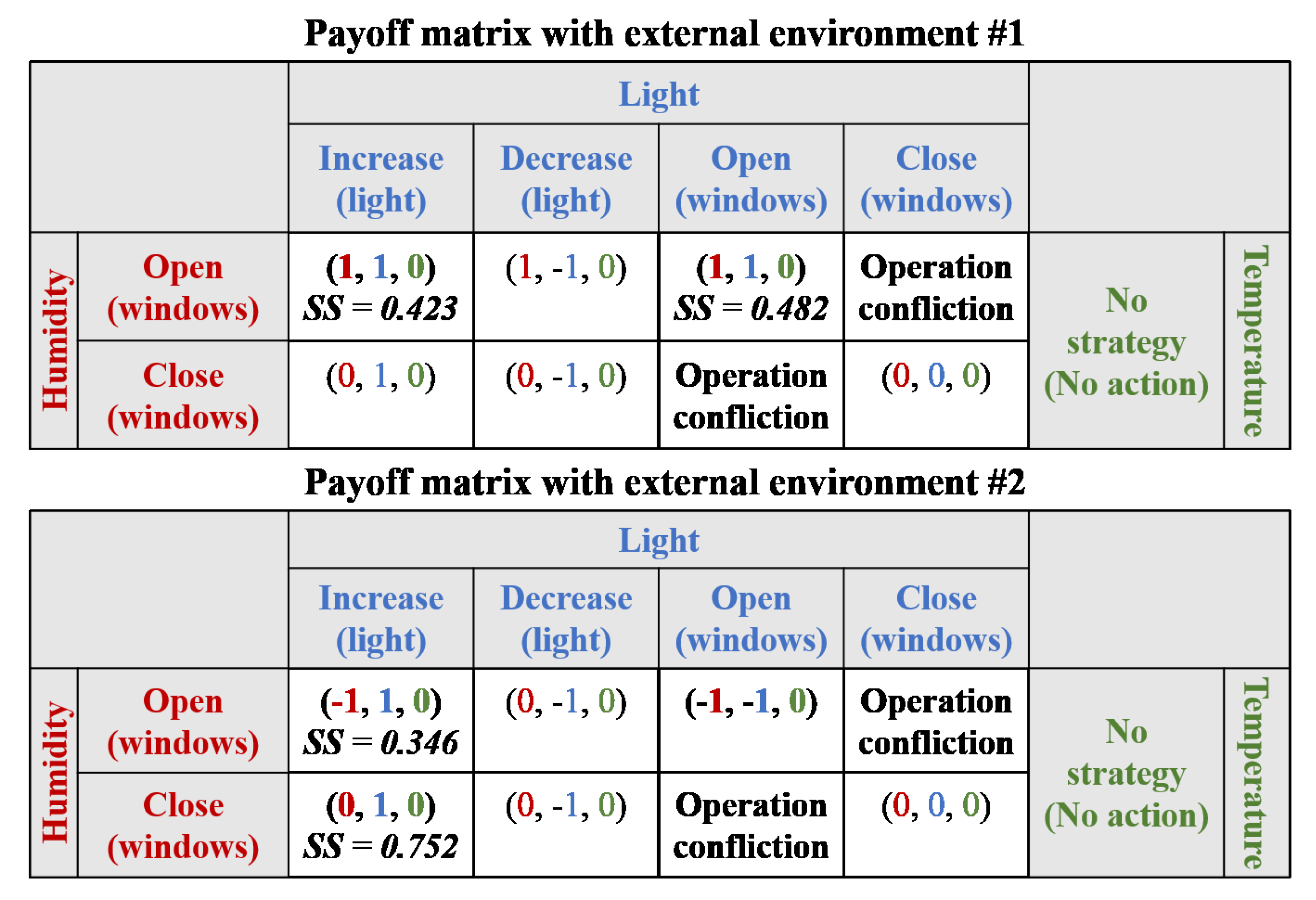
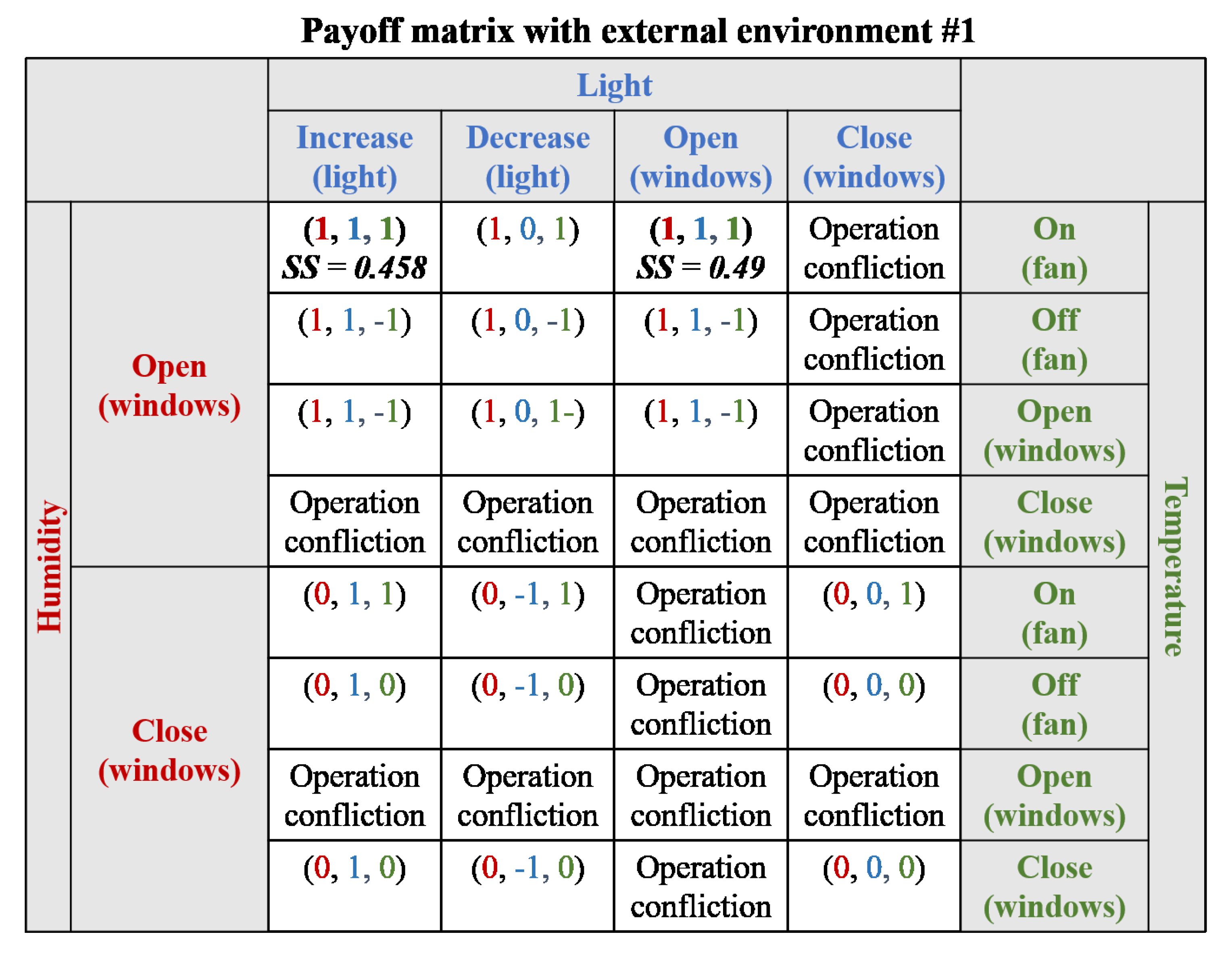
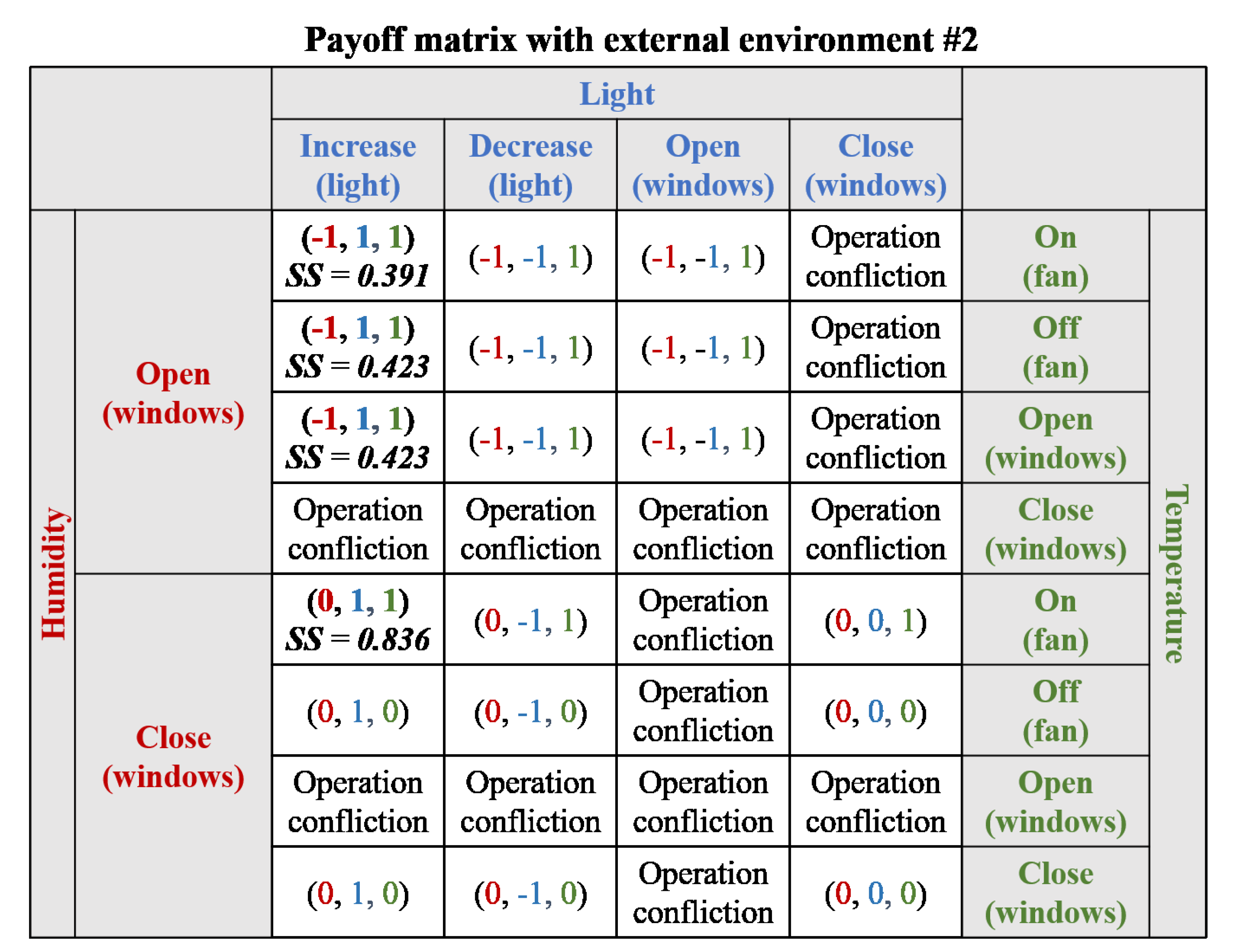
- Scenario #1: The light requirement is not satisfied (80 lux), but the humidity (33%) and temperature (22 °C) requirements are satisfied. The windows are closed, and the level of the light controller is 4 (80 lux). In addition, the fan is turned off.
- Scenario #2: The light (80 lux) and humidity (31%) requirements are not satisfied, but the temperature (22 °C) requirement is satisfied. Both dissatisfied requirements must be increased for adaptation. The windows are closed, and the level of the light controller is 4 (80 lux). In addition, the fan is turned off.
- Scenario #3: All requirements are not satisfied: light (80 lux), humidity (30%), and temperature (26 °C). The light and humidity requirements must be increased for adaptation, but the temperature requirement must be decreased for adaptation. The windows are closed, and the level of the light controller is 4 (80 lux). In addition, the fan is turned off.
- External environment #1: External light is brighter than the light inside (180 lux), and the external humidity and temperature are higher than that of the internal environment (36% and 30 °C).
- External environment #2: External light is darker than the light inside (20 lux) and the external humidity and temperature are lower than that of the internal environment (25% and 15 °C).
5.2. Modeling of Finite-State Machine
5.3. Game Theoretic Decision Making
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, E.; Kim, Y.G.; Seo, Y.D.; Baik, D.K. Self-adaptive framework with game theoretic decision making for Internet of things. In Proceedings of the IEEE TENCON 2018—2018 IEEE Region 10 Conference, Jeju, Korea, 28–31 October 2018; pp. 2092–2097. [Google Scholar]
- Rayes, A.; Samer, S. Internet of things—From hype to reality. In The Road to Digitization; River Publisher Series in Communications; Springer: Basel, Switzerland, 2017; Volume 49. [Google Scholar]
- Balasubramaniam, S.; Jagannath, R. A service oriented iot using cluster controlled decision making. In Proceedings of the 2015 IEEE International Advance Computing Conference (IACC), Banglore, India, 12–13 June 2015; pp. 558–563. [Google Scholar]
- Hughes, D. Self adaptive software systems are essential for the Internet of things. In Proceedings of the 2018 IEEE/ACM 13th International Symposium on Software Engineering for Adaptive and Self-Managing Systems (SEAMS), Gothenburg, Sweden, 27 May–3 June 2018; p. 21. [Google Scholar]
- Salehie, M.; Tahvildari, L. Self-adaptive software: Landscape and research challenges. ACM Trans Auton. Adapt. Syst. (TAAS) 2009, 4, 14. [Google Scholar] [CrossRef]
- Abeywickrama, D.B.; Zambonelli, F. Model checking goal-oriented requirements for self-adaptive systems. In Proceedings of the 2012 IEEE 19th International Conference and Workshops on Engineering of Computer-Based Systems, Novi Sad, Serbia, 11–13 April 2012; pp. 33–42. [Google Scholar]
- Zhang, L.; Alharbe, N.; Atkins, A.S. An IoT application for inventory management with a self-adaptive decision model. In Proceedings of the 2016 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Chengdu, China, 15–18 December 2016; pp. 317–322. [Google Scholar]
- Lunardi, W.T.; Amaral, L.; Marczak, S.; Hessel, F.; Voos, H. Automated decision support iot framework. In Proceedings of the 2016 IEEE 21st International Conference on Emerging Technologies and Factory Automation (ETFA), Berlin, Germany, 6–9 September 2016; pp. 1–8. [Google Scholar]
- Azimi, I.; Anzanpour, A.; Rahmani, A.M.; Pahikkala, T.; Levorato, M.; Liljeberg, P.; Dutt, N. HiCH: Hierarchical fog-assisted computing architecture for healthcare IoT. ACM Trans. Embed. Comput. Syst. (TECS) 2017, 16, 174. [Google Scholar] [CrossRef]
- Mezghani, E.; Exposito, E.; Drira, K. A model-driven methodology for the design of autonomic and cognitive IoT-based systems: Application to healthcare. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 1, 224–234. [Google Scholar] [CrossRef]
- Ouechtati, H.; Azzouna, N.B.; Said, L.B. Towards a self-adaptive access control middleware for the Internet of Things. In Proceedings of the 2018 International Conference on Information Networking (ICOIN), Chiang Mai, Thailand, 10–12 January 2018; pp. 545–550. [Google Scholar]
- Muccini, H.; Spalazzese, R.; Moghaddam, M.T.; Sharaf, M. Self-adaptive IoT architectures: An emergency handling case study. In Proceedings of the ACM 12th European Conference on Software Architecture: Companion Proceedings, Madrid, Spain, 24–28 September 2018; p. 19. [Google Scholar]
- Shekhar, S.; Gokhale, A. Dynamic resource management across cloud-edge resources for performance-sensitive applications. In Proceedings of the 17th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing, Madrid, Spain, 14–17 May 2017; pp. 707–710. [Google Scholar]
- Renart, E.; Balouek-Thomert, D.; Parashar, M. Pulsar: Enabling dynamic data-driven IoT applications. In Proceedings of the 2017 IEEE 2nd International Workshops on Foundations and Applications of Self* Systems (FAS*W), Tucson, AZ, USA, 18–22 Septeber 2017; pp. 357–359. [Google Scholar]
- Liu, C.; Julien, C.; Murphy, A.L. PINCH: Self-organized context neighborhoods for smart environments. In Proceedings of the 2018 IEEE 12th International Conference on Self-Adaptive and Self-Organizing Systems (SASO), Trento, Italy, 3–7 September 2018; pp. 120–129. [Google Scholar]
- Robbe, B.; Danny, W. A QoS-aware adaptive mobility handling approach for LoRa-based IoT systems. In Proceedings of the 2018 IEEE 12th International Conference on Self-Adaptive and Self-Organizing Systems (SASO), Trento, Italy, 3–7 September 2018; pp. 130–139. [Google Scholar]
- Iftikhar, M.U.; Ramachandran, G.S.; Bollansée, P.; Weyns, D.; Hughes, D. DeltaIoT: A self-adaptive Internet of Things exemplar. In Proceedings of the 12th International Symposium on Software Engineering for Adaptive and Self-Managing Systems, Buenos Aires, Argentina, 20–28 May 2017; pp. 76–82. [Google Scholar]
- Nisan, N.; Roughgarden, T.; Tardos, E.; Vazirani, V.V. Algorithmic Game Theory; Cambridge University Press: Cambridge, UK, 2007; Volume 1. [Google Scholar]
- Shoham, Y. Computer science and game theory. Commun. ACM 2008, 51, 74–79. [Google Scholar] [CrossRef]
- Bhatia, M.; Sood, S.K. Game theoretic decision making in IoT-assisted activity monitoring of defence personnel. Multimed. Tools Appl. 2017, 76, 21911–21935. [Google Scholar] [CrossRef]
- Tao, X.; Li, G.; Sun, D.; Cai, H. A game-theoretic model and analysis of data exchange protocols for Internet of Things in clouds. Future Gener. Comput. Syst. 2017, 76, 582–589. [Google Scholar] [CrossRef]
- Semasinghe, P.; Maghsudi, S.; Hossain, E. Game theoretic mechanisms for resource management in massive wireless IoT systems. IEEE Commun. Mag. 2017, 55, 121–127. [Google Scholar] [CrossRef]
- Azzedin, F.; Yahaya, M. Modeling BitTorrent choking algorithm using game theory. Future Gener. Comput. Syst. 2016, 55, 255–265. [Google Scholar] [CrossRef]
- Zheng, J.; Cai, Y.; Chen, X.; Li, R.; Zhang, H. Optimal base station sleeping in green cellular networks: A distributed cooperative framework based on game theory. IEEE Trans. Wirel. Commun. 2015, 14, 4391–4406. [Google Scholar] [CrossRef]
- Kumari, V.; Chakravarthy, S. Cooperative privacy game: A novel strategy for preserving privacy in data publishing. Human-Centic Comput. Inf. Sci. 2016, 6, 12. [Google Scholar] [CrossRef]
- Algur, S.P.; Kumar, N.P. Novel user centric, game theory based bandwidth allocation mechanism in WiMAX. Human-Centic Comput. Inf. Sci. 2013, 3, 20. [Google Scholar] [CrossRef]
- Park, J.K.; Ha, J.; Seo, H.; Kim, J.; Choi, C.W. Stability of game-theoretic energy-aware MAC scheme for wireless sensor networks. In Proceedings of the 2010 IEEE International Conference on Sensor Networks, Ubiquitous, and Trustworthy Computing, Newport Beach, CA, USA, 7–9 June 2010; pp. 384–389. [Google Scholar]
- Muccini, H.; Moghaddam, M.T. Iot architectural styles. In European Conference on Software Architecture; Springer: Berlin, Germany, 2018; pp. 68–85. [Google Scholar]
- Weyns, D.; Schmerl, B.; Grassi, V.; Malek, S.; Mirandola, R.; Prehofer, C.; Wuttke, J.; Andersson, J.; Giese, H.; Göschka, K.M. On patterns for decentralized control in self-adaptive systems. In Software Engineering for Self-Adaptive Systems II; Springer: Berlin, Germany, 2013; pp. 76–107. [Google Scholar]
- Lee, E.; Kim, Y.G.; Seo, Y.D.; Seol, K.; Baik, D.K. Runtime verification method for self-adaptive software using reachability of transition system model. In Proceedings of the ACM Symposium on Applied Computing, Marrakech, Morocco, 3–7 April 2017; pp. 65–68. [Google Scholar]
- Lee, E.; Kim, Y.G.; Seo, Y.D.; Seol, K.; Baik, D. RINGA: Design and verification of finite state machine for self-adaptive software at runtime. Inf. Softw. Technol. 2018, 93, 200–222. [Google Scholar] [CrossRef]
- Garlan, D.; Cheng, S.W.; Huang, A.C.; Schmerl, B.; Steenkiste, P. Rainbow: Architecture-based self-adaptation with reusable infrastructure. Computer 2004, 37, 46–54. [Google Scholar] [CrossRef]
- Knauss, A.; Damian, D.; Franch, X.; Rook, A.; Müller, H.A.; Thomo, A. ACon: A learning-based approach to deal with uncertainty in contextual requirements at runtime. Inf. Softw. Technol. 2016, 70, 85–99. [Google Scholar] [CrossRef]
- Wang, Y.; Mylopoulos, J. Self-repair through reconfiguration: A requirements engineering approach. In Proceedings of the 2009 IEEE/ACM International Conference on Automated Software Engineering, Auckland, New Zealand, 16–20 November 2009; pp. 257–268. [Google Scholar]
- Yang, W.; Xu, C.; Liu, Y.; Cao, C.; Ma, X.; Lu, J. Verifying self-adaptive applications suffering uncertainty. In Proceedings of the 29th ACM/IEEE International Conference on Automated Software Engineering, Vasteras, Sweden, 15–19 September 2014; pp. 199–210. [Google Scholar]
- Tallabaci, G.; Souza, V.E.S. Engineering adaptation with Zanshin: An experience report. In Proceedings of the IEEE 8th International Symposium on Software Engineering for Adaptive and Self-Managing Systems, San Francisco, CA, USA, 20–21 May 2013; pp. 93–102. [Google Scholar]
- Seo, Y.D.; Kim, Y.G.; Lee, E.; Seol, K.S.; Baik, D.K. Design of a smart greenhouse system based on MAPE-K and ISO/IEC-11179. In Proceedings of the 2018 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 12–14 January 2018; pp. 1–2. [Google Scholar]
- Lee, E.; Baik, D.K. A verification technique for self-adaptive software by using model-checking. In Proceedings of the International Conference on Artificial Intelligence (ICAI), The Steering Committee of The World Congress in Computer Science, Computer Engineering and Applied Computing (WorldComp), Las Vegas, NV, USA, 27–30 July 2015; p. 395. [Google Scholar]
- Amaral, L.A.; Tiburski, R.T.; de Matos, E.; Hessel, F. Cooperative middleware platform as a service for Internet of things applications. In Proceedings of the ACM 30th Annual ACM Symposium on Applied Computing, Salamanca, Spain, 13–17 April 2015; pp. 488–493. [Google Scholar]
- Lunardi, W.T.; de Matos, E.; Tiburski, R.; Amaral, L.A.; Marczak, S.; Hessel, F. Context-based search engine for industrial IoT: Discovery, search, selection, and usage of devices. In Proceedings of the 2015 IEEE 20th Conference on Emerging Technologies & Factory Automation (ETFA), Luxembourg, 8–11 September 2015; pp. 1–8. [Google Scholar]
- Ribeiro, A.d.R.L.; de Almeida, F.M.; Moreno, E.D.; Montesco, C.A. A management architectural pattern for adaptation system in Internet of Things. In Proceedings of the IEEE International Wireless Communications and Mobile Computing Conference (IWCMC), Paphos, Cyprus, 5–9 September 2016; pp. 576–581. [Google Scholar]
- De Almeida, F.M.; Ribeiro, A.d.R.L.; Moreno, E.D. An Architecture for self-healing in Internet of Things. In Proceedings of the UBICOMM 2015, Nice, France, 19–24 July 2015; p. 89. [Google Scholar]
- Welsh, K.; Bencomo, N.; Sawyer, P.; Whittle, J. Self-explanation in adaptive systems based on runtime goal-based models. In Transactions on Computational Collective Intelligence XVI; Springer: Berlin, Germany, 2014; pp. 122–145. [Google Scholar]
- Beal, J.; Pianini, D.; Viroli, M. Aggregate programming for the Internet of things. Computer 2015, 48, 22–30. [Google Scholar] [CrossRef]
- Pianini, D.; Montagna, S.; Viroli, M. Chemical-oriented simulation of computational systems with alchemist. J. Simul. 2013, 7, 202–215. [Google Scholar] [CrossRef]
- Bucchiarone, A.; Marconi, A.; Pistore, M.; Raik, H. A context-aware framework for dynamic composition of process fragments in the Internet of services. J. Internet Serv. Appl. 2017, 8, 6. [Google Scholar] [CrossRef]
- Sylla, A.N.; Louvel, M.; Rutten, E.; Delaval, G. Design framework for reliable multiple autonomic loops in smart environments. In Proceedings of the 2017 International Conference on Cloud and Autonomic Computing (ICCAC), Tucson, AZ, USA, 18–22 September; pp. 131–142.
- Renart, E.G.; Diaz-Montes, J.; Parashar, M. Data-driven stream processing at the edge. In Proceedings of the 2017 IEEE 1st International Conference on Fog and Edge Computing (ICFEC), Madrid, Spain, 14–15 May 2017; pp. 31–40. [Google Scholar]
- Jiang, N.; Quiroz, A.; Schmidt, C.; Parashar, M. Meteor: A middleware infrastructure for content-based decoupled interactions in pervasive grid environments. Concur. Comput. Pract. Exp. 2008, 20, 1455–1484. [Google Scholar] [CrossRef]
- Straffin, P.D. Game Theory and Strategy; MAA: Washington, DC, USA, 1993; Volume 36. [Google Scholar]
- Babaioff, M.; Kleinberg, R.; Papadimitriou, C.H. Congestion games with malicious players. Games Econ. Behav. 2009, 67, 22–35. [Google Scholar] [CrossRef]
- Theodorakopoulos, G.; Baras, J.S. Game theoretic modeling of malicious users in collaborative networks. IEEE J. Sel. Areas Commun. 2008, 26, 1317–1327. [Google Scholar] [CrossRef]
- Kim, H.; Lee, E.; Baik, D.k. Self-adaptive software simulation: A lighting control system for multiple devices. In Asian Simulation Conference; Springer: Singapore, 2017; pp. 380–391. [Google Scholar]
- Lee, J.; Lee, E.; Baik, D.K. Simulation and performance evaluation of the self-adaptive light control system. J. Korea Soc. Simul. 2016, 25, 63–74. [Google Scholar] [CrossRef]
| Worked by | Goal | Lifecycle | Approach |
|---|---|---|---|
| Zhang et al. [7] | Inventory management systems with self-adaptive distributed decision support models | Loop with update | - Artificial neural network for recognition of scenarios - Knowledge and rule-based decision-making |
| Lunardi et al. [8] | Automated decision analytics and support for IoT | Loop with update | - Rule-based reasoner |
| Mezghani et al. [10] | Autonomic cognitive design patterns for smart IoT-based systems | Loop with update | - Design patterns for cognitive IoT-based systems - Patterns that provide generic and reusable solutions |
| Ouechtati et al. [11] | A framework for access control in the IoT environment | Dynamic adaptation process (loop) | - Dynamic adaptive process based on risk value, politics, and rule sets |
| Muccini et al. [12] | A framework for IoT modeling | MAPE loop | - Analysis of IoT and self-adaptation control patterns - Bridge and combine the IoT distribution patterns and adaptation logic |
| Shekhar et al. [13] | A framework for adaptive resource management in cyber physical systems and IoT | Feedback loop | - Collect data from cloud and edge resources - Learn and enhance models - Apply enhanced models in a feedback loop |
| Azimi et al. [9] | A hierarchical computing architecture for IoT-based health monitoring system | MAPE-K loop | - A hierarchical computing architecture with cloud and fog enabled IoT - Closed loop for autonomic system - Machine learning data analytics |
| Ribeiro et al. [42] | Management of architectural patterns for self-adaptive system in IoT | MAPE loop | - An architectural pattern for self-adaptive systems with a control loop |
| Welsh et al. [43] | A self-adaptive system with goal-based requirements models to provide self-explanation at runtime | Loop with update | - Goal-based model - Simply structured domain-specific language |
| Beal et al. [44] | Aggregate programming with simplified design, creation, and maintenance for IoT software systems | N/A | - Aggregate programming abstraction layers - Field calculus constructs - Building-block APIs |
| Bucchiarone et al. [46] | A service composition framework with runtime service composition in a dynamic context | Loop with update | - Service model with stateful, non-deterministic, and asynchronous features |
| Renart et al. [14,48] | A data-driven framework to support dynamic data driven IoT applications | N/A | - Associative rendezvous interaction model- Simple rule-based abstraction with two different types of rules |
| Sylla et al. [47] | Self-adaptive framework design with multiple autonomic loops for reliability | MAPE-K | - Multiple autonomic loops |
| Proposed | Self-adaptive framework for IoT | MAPE loop | - Finite-state machine modeling for IoT - Model-checking based runtime verification - Game theory based decision-making method |
| Hardware | CPU Clock (GHz) | Number of CPU Core | Memory (GB) | Operating System |
|---|---|---|---|---|
| Laptop (Intel i5-5200U) | 2.7 | 2 | 8 | Windows 10 |
| Desktop (Intel i5-4670) | 3.4 | 4 | 16 | Windows 10 |
| Server (Intel Xeon E3-1230L v3) | 1.8 | 4 | 4 | Windows 10 |
| Samsung Galaxy S8 | 2.31 | 8 | 4 | Android 8.0.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, E.; Seo, Y.-D.; Kim, Y.-G. Self-Adaptive Framework Based on MAPE Loop for Internet of Things. Sensors 2019, 19, 2996. https://doi.org/10.3390/s19132996
Lee E, Seo Y-D, Kim Y-G. Self-Adaptive Framework Based on MAPE Loop for Internet of Things. Sensors. 2019; 19(13):2996. https://doi.org/10.3390/s19132996
Chicago/Turabian StyleLee, Euijong, Young-Duk Seo, and Young-Gab Kim. 2019. "Self-Adaptive Framework Based on MAPE Loop for Internet of Things" Sensors 19, no. 13: 2996. https://doi.org/10.3390/s19132996
APA StyleLee, E., Seo, Y.-D., & Kim, Y.-G. (2019). Self-Adaptive Framework Based on MAPE Loop for Internet of Things. Sensors, 19(13), 2996. https://doi.org/10.3390/s19132996






