Speckle Noise Filtering in Side-Scan Sonar Images Based on the Tucker Tensor Decomposition
Abstract
1. Introduction
2. Related Works
3. Characteristics of the Speckle Noise and Its Filtering Methods
3.1. Average Filter
3.2. Median Filter
- Take an kernel centered around a pixel .
- Sort the intensity values of the pixels in the kernel into ascending order.
- Select the middle value as the new value for the pixel .
3.3. Frost Filter
3.4. Lee Filter
3.5. Kuan Filter
3.6. Enhanced Lee Filter
4. Tensor-Based Speckle Noise Filtering
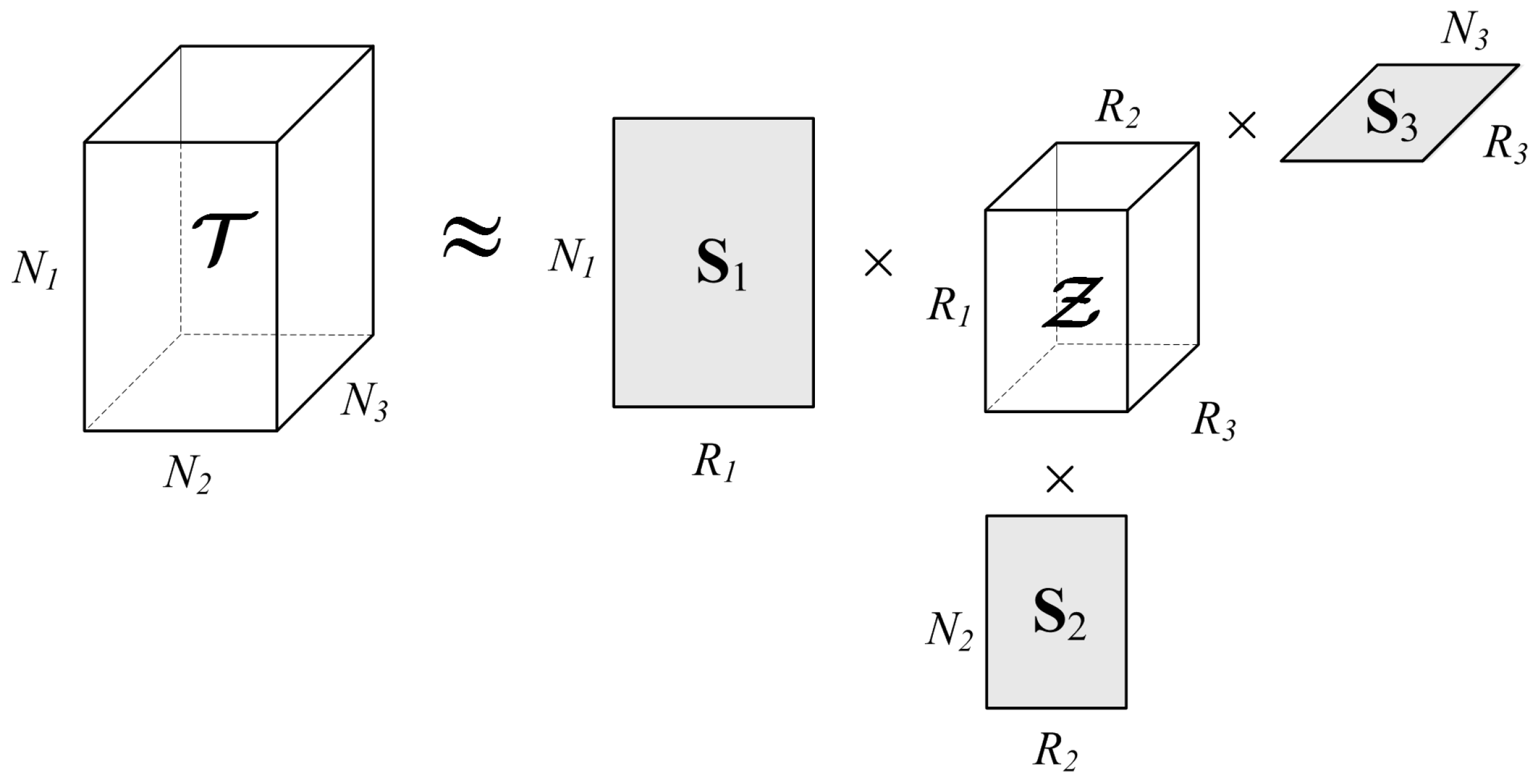
4.1. Multi-Dimensional Signals Filtering in the Tensor Framework
4.2. The Tensor Filtering Algorithm
| Algorithm 1 Tensor assembler. |
|
| Algorithm 2 Filtering algorithm. |
|
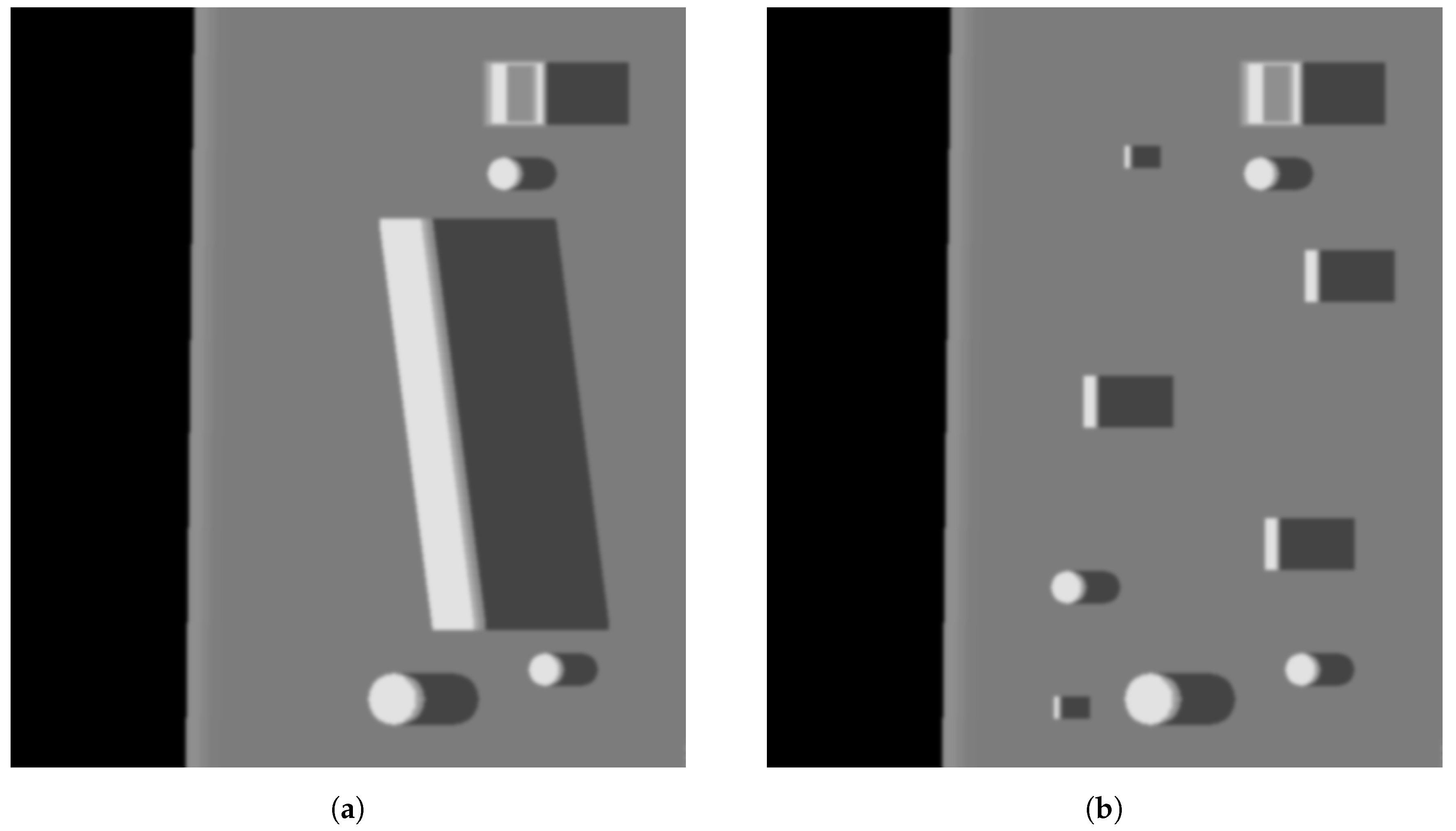
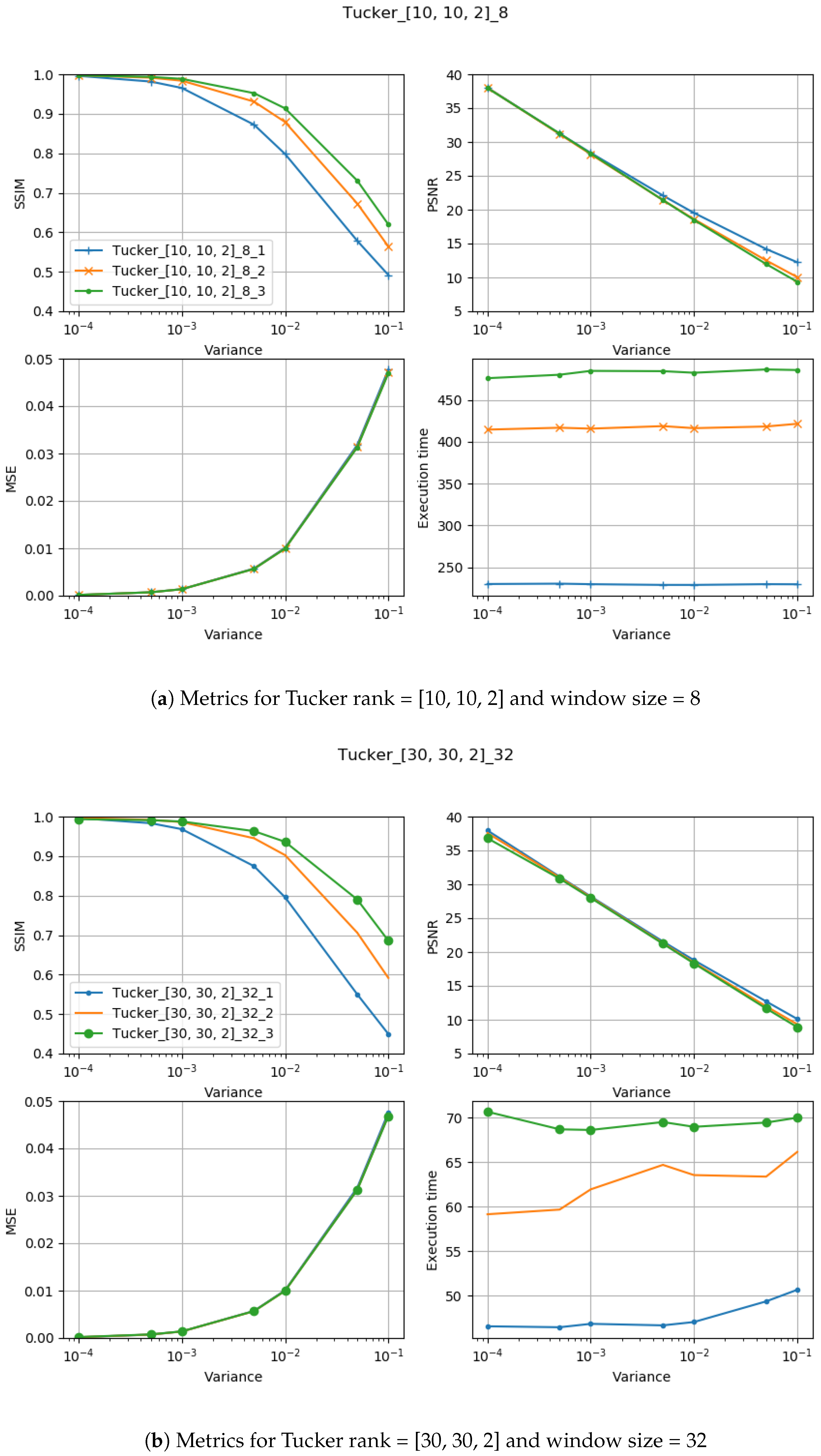
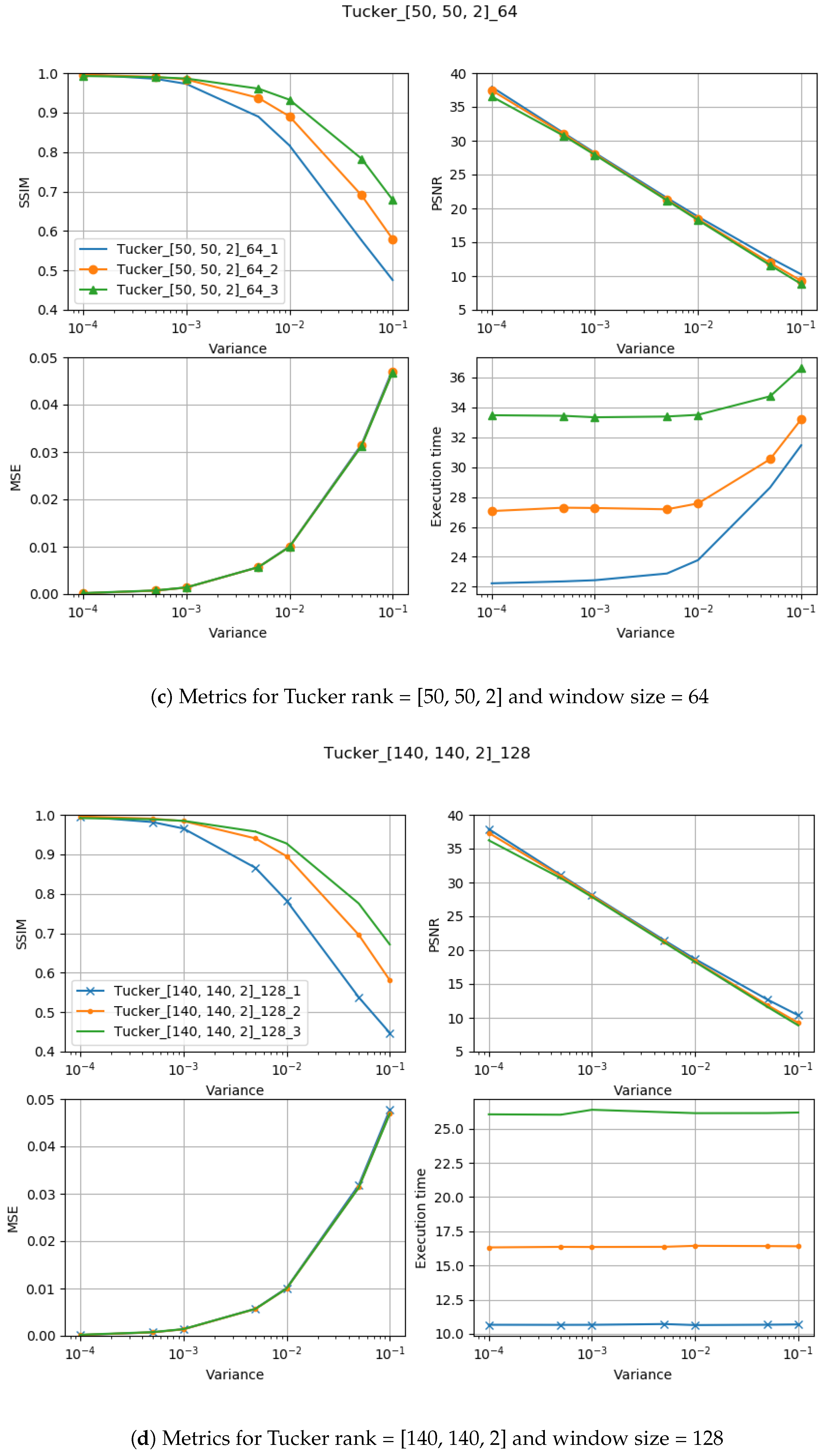
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vanithamani, R.; Umamaheswari, G.; Ezhilarasi, M. Modified hybrid median filter for effective speckle reduction in ultrasound images. In Recent Advances in Networking, Vlsi And Signal Processing; World Scientific and Engineering Academy and Society (WSEAS): Stevens Point, WI, USA, 2010; pp. 166–171. [Google Scholar]
- Adabi, S.; Conforto, S.; Clayton, A.; Podoleanu, A.; Hojjat, A.; Avanaki, M. An intelligent speckle reduction algorithm for optical coherence tomography images. In Proceedings of the 2016 4th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS), Rome, Italy, 27–29 February 2016; pp. 1–6. [Google Scholar]
- Mastriani, M.; Giraldez, A. Enhanced directional smoothing algorithm for edge-preserving smoothing of synthetic-aperture radar images. arXiv 2016, arXiv:1608.01993. [Google Scholar]
- Yu, Y.; Acton, S. Speckle reducing anisotropic diffusion. IEEE Trans. Image Process. 2002, 11, 1260–1270. [Google Scholar]
- Karthikeyan, K.; Rasekar, C. Speckle noise reduction of medical ultrasound images using Bayes shrink wavelet threshold. Int. J. Comput. Appl. 2011, 22, 8–14. [Google Scholar]
- Jaybhay, J.; Shastri, R. A study of speckle noise reduction Filters. Signal Image Process. Int. J. 2015, 6. [Google Scholar] [CrossRef]
- Karabchevsky, S.; Kahana, D.; Ben-harush, O.; Guterman, H. FPGA-based adaptive speckle suppression filter for underwater imaging sonar. IEEE J. Ocean. Eng. 2011, 36, 646–657. [Google Scholar] [CrossRef]
- Maity, A.; Pattanaik, A.; Sagnika, S.; Pani, S. A comparative study on approaches to speckle noise reduction in images. In Proceedings of the 2015 International Conference on Computational Intelligence and Networks, Bhubaneshwar, India, 12–13 January 2015; pp. 148–155. [Google Scholar]
- Cyganek, B. Object Detection and Recognition in Digital Images: Theory and Practice; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Lee, J. Digital image enhancement and noise filtering by use of local statistics. IEEE Trans. Pattern Anal. Mach. Intell. 1980, 2, 165–168. [Google Scholar] [CrossRef] [PubMed]
- Narayanan, S.; Wahidabanu, R. A View on Despeckling in Ultrasound Imaging; Citeseer: University Park, PA, USA, 2009. [Google Scholar]
- Huang, Y.; Vangenderen, J. Evaluation of several speckle filtering techniques for ERS-1&2 imagery. Int. Arch. Photogramm. Remote Sens. 1996, 31, 164–169. [Google Scholar]
- Kolda, T.; Bader, B. Tensor Decompositions and Applications. SIAM Rev. 51.3 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Muti, D.; Bourennane, S. Multidimensional filtering based on a tensor approach. Signal Process. 2005, 85, 2338–2353. [Google Scholar] [CrossRef]
- Cyganek, B.; Smołka, B. Real-time framework for tensor-based image enhancement for object classification. Proc. SPIE 2016, 9897, 98970Q. [Google Scholar]
- De Lathauwer, L.; De Moor, B.; Vandewalle, J. On the best rank-1 and rank-(R1, R2, …, Rn) approximation of higher-order tensors. Siam J. Matrix Anal. Appl. 2000, 21, 1324–1342. [Google Scholar] [CrossRef]
- Cyganek, B.; Krawczyk, B.; Wozniak, M. Multidimensional Data Classification with Chordal Distance Based Kernel and Support Vector Machines. Eng. Appl. Artif. Intell. 2015, 46, 10–22. [Google Scholar] [CrossRef]
- Cyganek, B.; Wozniak, M. Tensor-Based Shot Boundary Detection in Video Streams. New Gener. Comput. 2017, 35, 311–340. [Google Scholar] [CrossRef]
- Marot, J.; Fossati, C.; Bourennane, S. Fast subspace-based tensor data filtering. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 3869–3872. [Google Scholar]
- Kossaifi, J.; Panagakis, Y.; Kumar, A.; Pantic, M. TensorLy: Tensor Learning in Python. arXiv 2018, arXiv:1610.09555. [Google Scholar]
- Grabek, J. Code Repository. Available online: https://github.com/jgrabek/ (accessed on 30 June 2019).
- Gifani, P.; Behnam, H.; Sani, Z. Noise reduction of echo cardiographic images based on temporal information. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2014, 61, 620–630. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]











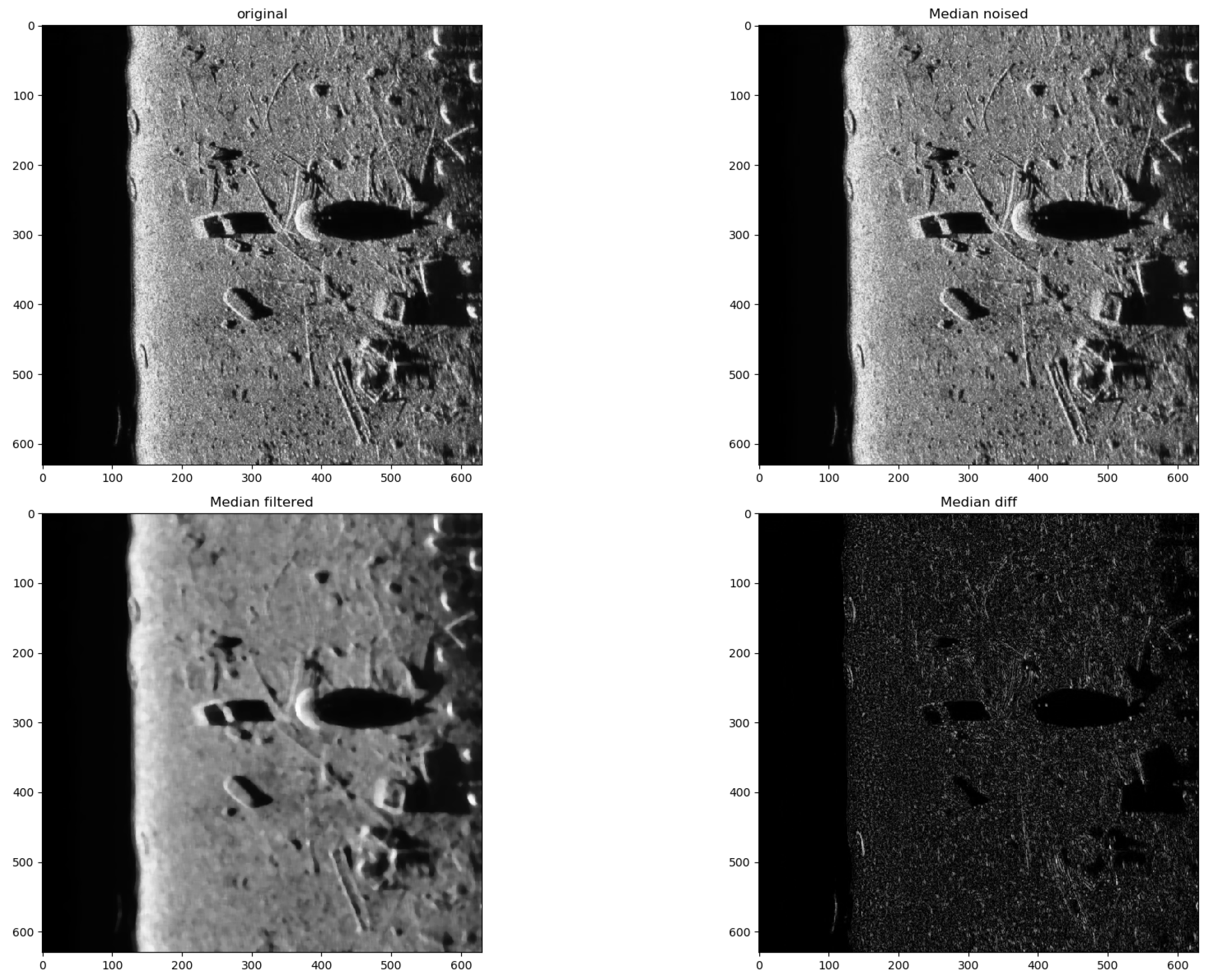
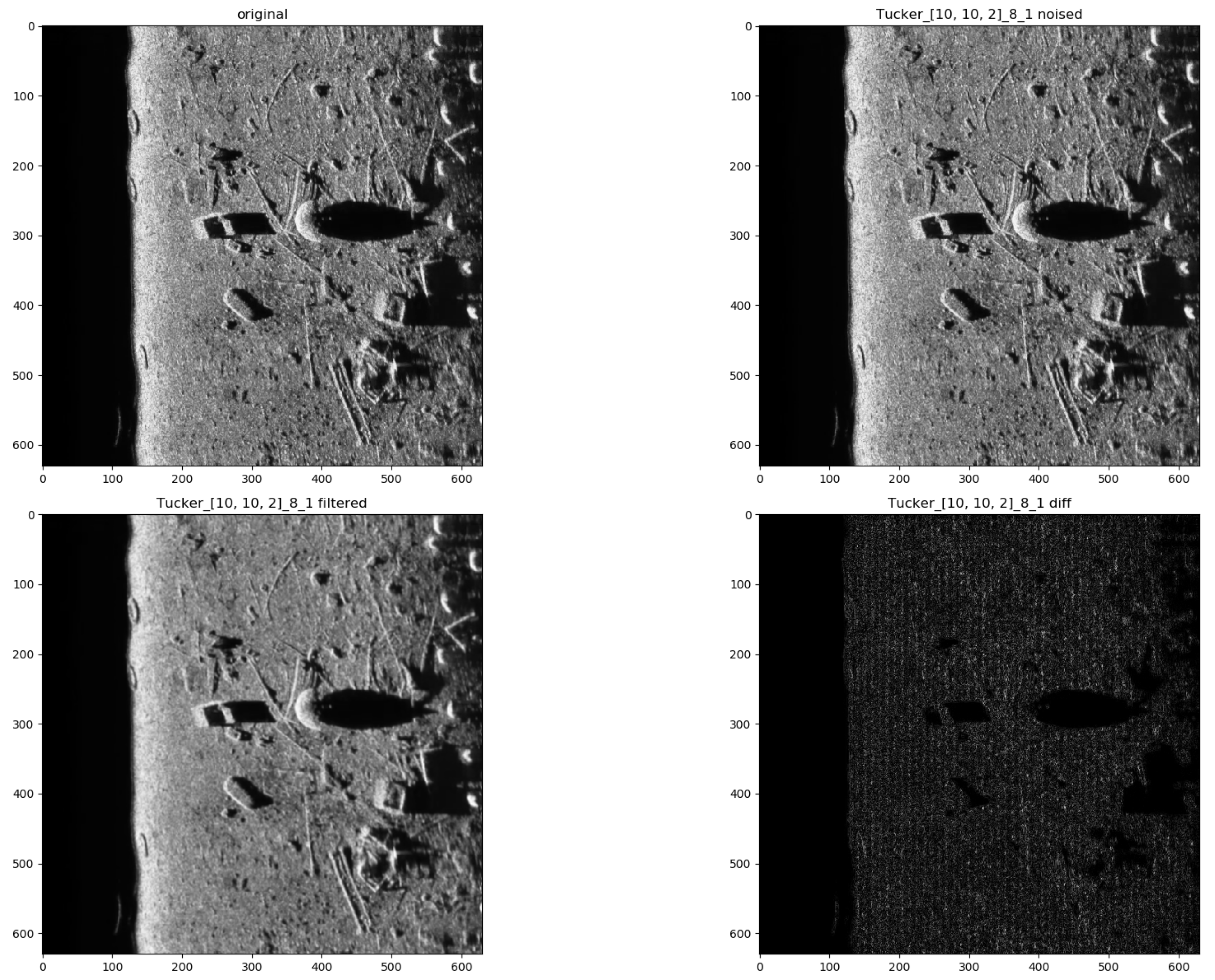

| Index | Methods | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Median | Frost | Lee | Lee Enhanced | Kuan | P1 | P2 | PAuto | ||
| 0.0001 | SSIM | 0.98618 | 0.99462 | 0.99059 | 0.98967 | 0.98871 | 0.98964 | 0.99223 | 0.99595 | 0.9885 |
| PSNR | 33.08012 | 34.28427 | 33.80562 | 33.9245 | 33.23504 | 33.89692 | 34.66237 | 35.536 | 35.59227 | |
| MSE | 4.801 × 10 | 3.701 × 10 | 4.165 × 10 | 4.052 × 10 | 4.655 × 10 | 4.074 × 10 | 3.496 × 10 | 2.932 × 10 | 2.96 × 10 | |
| 0.0005 | SSIM | 0.9832 | 0.99067 | 0.98762 | 0.98663 | 0.98567 | 0.98661 | 0.98882 | 0.98155 | 0.96107 |
| PSNR | 27.7841 | 28.15245 | 28.01909 | 28.06141 | 27.83237 | 28.05204 | 28.42009 | 28.75497 | 28.86646 | |
| MSE | 1.550 × 10 | 1.435 × 10 | 1.478 × 10 | 1.469 × 10 | 1.536 × 10 | 1.472 × 10 | 1.381 × 10 | 1.335 × 10 | 1.348 × 10 | |
| 0.001 | SSIM | 0.97971 | 0.98621 | 0.98424 | 0.98303 | 0.98208 | 0.98303 | 0.9847 | 0.96531 | 0.93043 |
| PSNR | 25.1087 | 25.32174 | 25.24272 | 25.27095 | 25.1348 | 25.26519 | 25.54454 | 25.89716 | 26.05117 | |
| MSE | 2.723 × 10 | 2.613 × 10 | 2.649 × 10 | 2.638 × 10 | 2.710 × 10 | 2.641 × 10 | 2.533 × 10 | 2.499 × 10 | 2.527 × 10 | |
| 0.005 | SSIM | 0.95713 | 0.95753 | 0.9612 | 0.96007 | 0.9592 | 0.96011 | 0.95523 | 0.87239 | 0.83173 |
| PSNR | 18.51647 | 18.58405 | 18.55519 | 18.56429 | 18.52239 | 18.56241 | 18.74906 | 19.55913 | 19.675 | |
| MSE | 9.949 × 10 | 9.900 × 10 | 9.876 × 10 | 9.854 × 10 | 9.938 × 10 | 9.858 × 10 | 9.704 × 10 | 9.746 × 10 | 9.787 × 10 | |
| 0.01 | SSIM | 0.93345 | 0.92814 | 0.93689 | 0.93593 | 0.93518 | 0.93601 | 0.92394 | 0.79781 | 0.74624 |
| PSNR | 15.61236 | 15.65576 | 15.63202 | 15.64155 | 15.61553 | 15.64034 | 15.85178 | 16.95285 | 17.12022 | |
| MSE | 1.670 × 10 | 1.672 × 10 | 1.663 × 10 | 1.660 × 10 | 1.669 × 10 | 1.661 × 10 | 1.644 × 10 | 1.655 × 10 | 1.664 × 10 | |
| 0.05 | SSIM | 0.80955 | 0.78359 | 0.79237 | 0.80542 | 0.81024 | 0.80592 | 0.76942 | 0.57621 | 0.64057 |
| PSNR | 9.02068 | 9.11328 | 9.04919 | 9.16097 | 9.02168 | 9.12861 | 9.43093 | 11.63039 | 11.47503 | |
| MSE | 4.618 × 10 | 4.643 × 10 | 4.616 × 10 | 4.607 × 10 | 4.617 × 10 | 4.608 × 10 | 4.591 × 10 | 4.635 × 10 | 4.605 × 10 | |
| 0.1 | SSIM | 0.71967 | 0.68468 | 0.63478 | 0.48404 | 0.71972 | 0.49222 | 0.66803 | 0.48759 | 0.54534 |
| PSNR | 6.29977 | 6.40971 | 6.45613 | 9.15216 | 6.3006 | 8.96839 | 6.88114 | 9.69316 | 9.4846 | |
| MSE | 6.521 × 10 | 6.557 × 10 | 6.529 × 10 | 6.579 × 10 | 6.520 × 10 | 6.571 × 10 | 6.496 × 10 | 6.561 × 10 | 6.520 × 10 | |
| Parameter | P1 Value | P2 Value |
|---|---|---|
| Tucker rank | 30, 30, 2 | 10, 10, 2 |
| Window size | 32 | 8 |
| Close neighbor distance (CND) | 3 | 1 |
| Method | Mean | Median | Frost | Lee | Lee Enhanced | Kuan | P1 | P2 | PAuto |
|---|---|---|---|---|---|---|---|---|---|
| Average time [s] | 2.86 | 13.83 | 26.06 | 13.42 | 13.29 | 20.12 | 69.44 | 482.34 | 448.52 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grabek, J.; Cyganek, B. Speckle Noise Filtering in Side-Scan Sonar Images Based on the Tucker Tensor Decomposition. Sensors 2019, 19, 2903. https://doi.org/10.3390/s19132903
Grabek J, Cyganek B. Speckle Noise Filtering in Side-Scan Sonar Images Based on the Tucker Tensor Decomposition. Sensors. 2019; 19(13):2903. https://doi.org/10.3390/s19132903
Chicago/Turabian StyleGrabek, Jakub, and Bogusław Cyganek. 2019. "Speckle Noise Filtering in Side-Scan Sonar Images Based on the Tucker Tensor Decomposition" Sensors 19, no. 13: 2903. https://doi.org/10.3390/s19132903
APA StyleGrabek, J., & Cyganek, B. (2019). Speckle Noise Filtering in Side-Scan Sonar Images Based on the Tucker Tensor Decomposition. Sensors, 19(13), 2903. https://doi.org/10.3390/s19132903




