An Adaptive Bluetooth/Wi-Fi Fingerprint Positioning Method based on Gaussian Process Regression and Relative Distance
Abstract
:1. Introduction
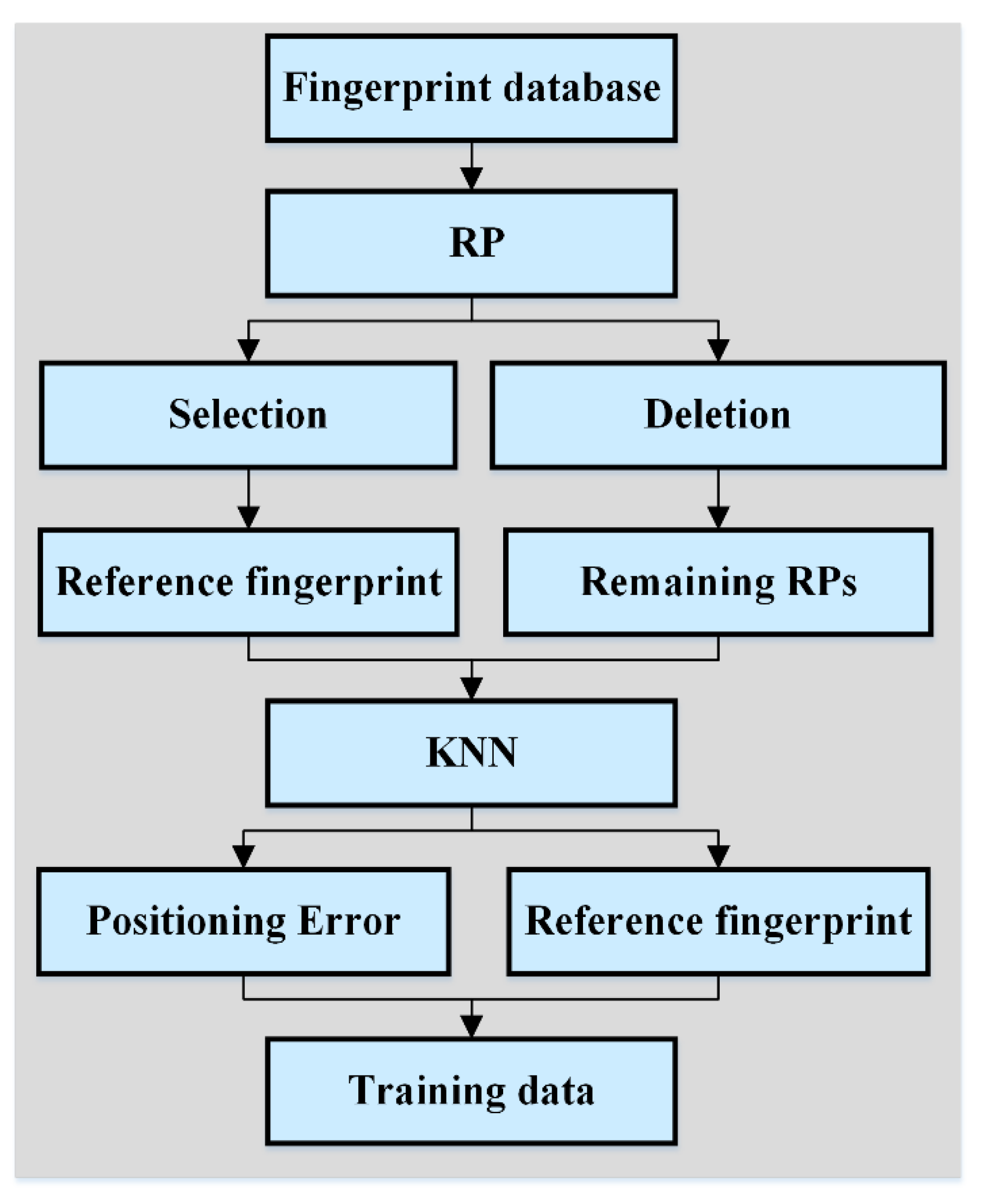
2. Training Data
3. The GPR-Based Fingerprint Positioning Prediction Model
3.1. Gaussian Process Regression
3.2. GPR Hyper-Parameter Estimation
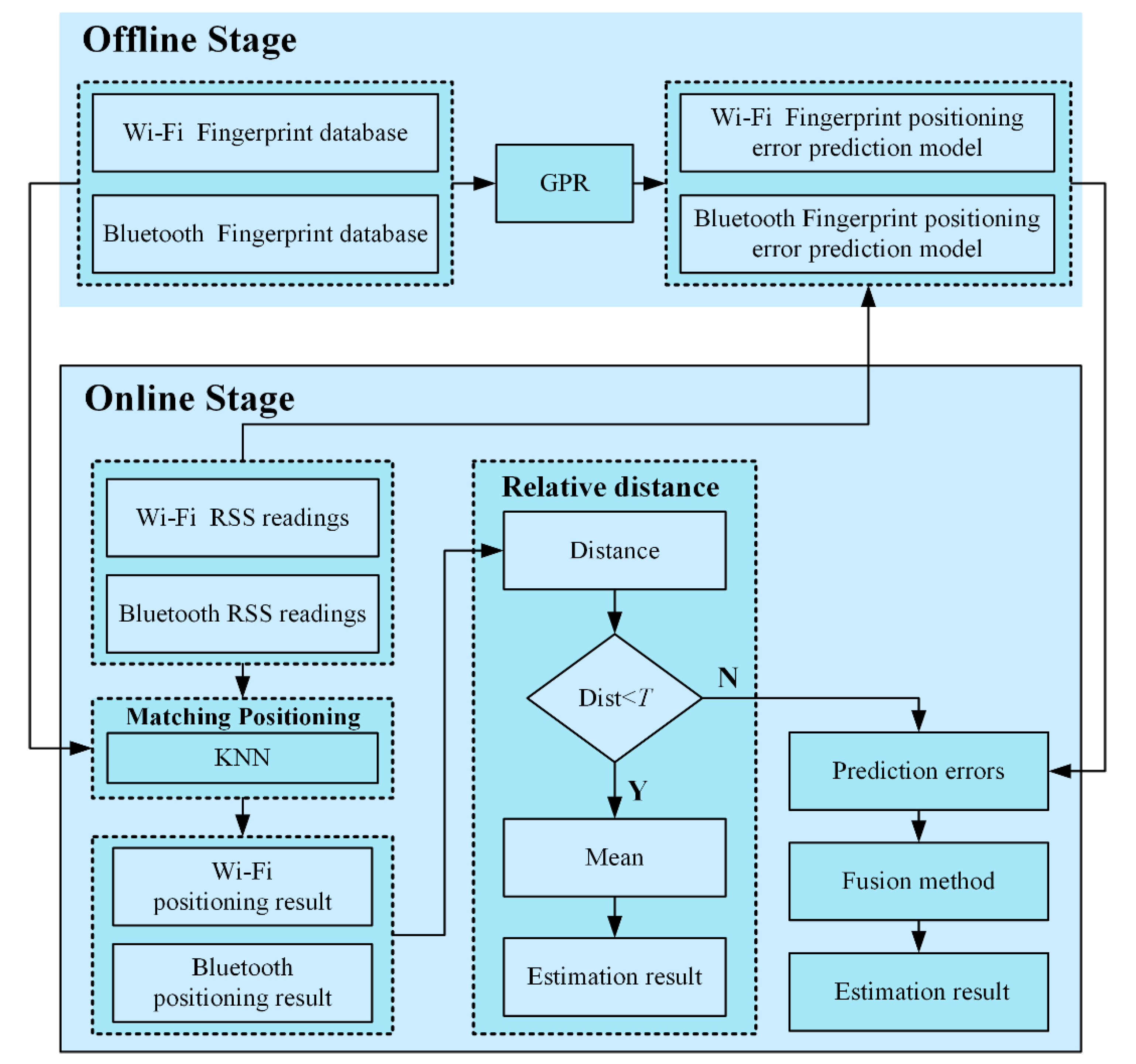
4. Proposed Positioning Method
4.1. Adaptive Fingerprint Positioning Method for Bluetooth and Wi-Fi using GPR and RD
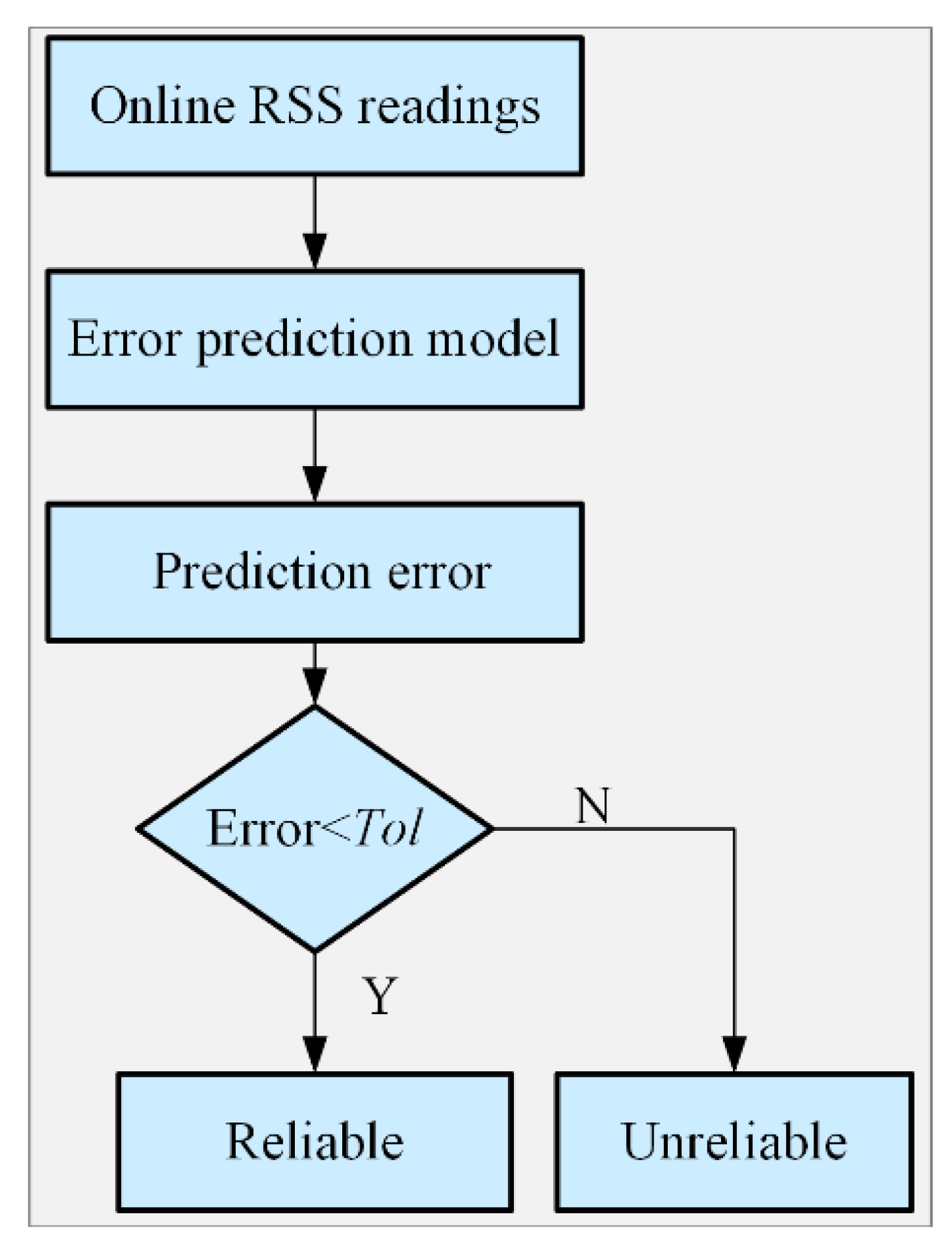
4.2. Threshold Selection
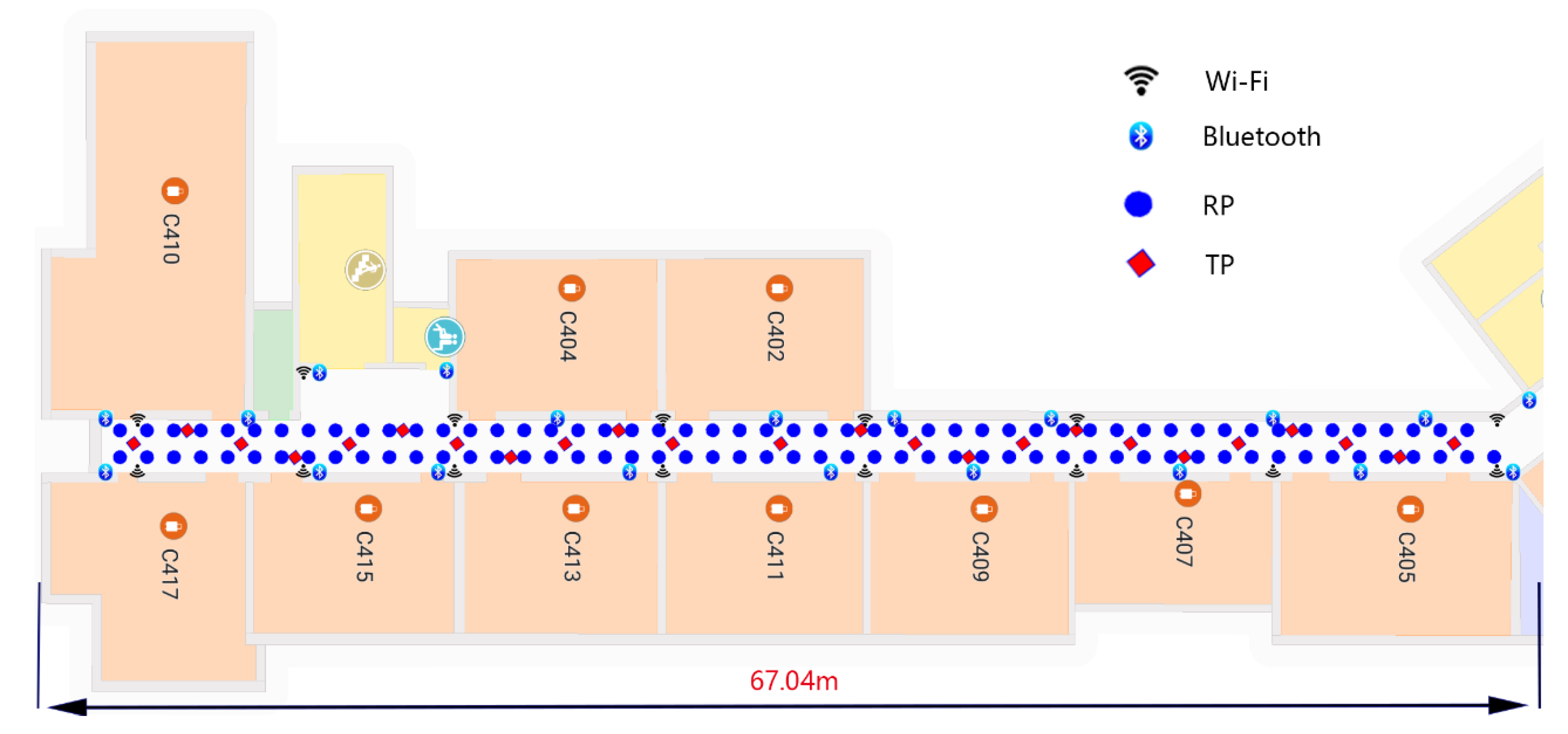
5. Experimental Environment and Analysis
5.1. Experimental Environment
5.2. Effect of Using Relative Distance Alone
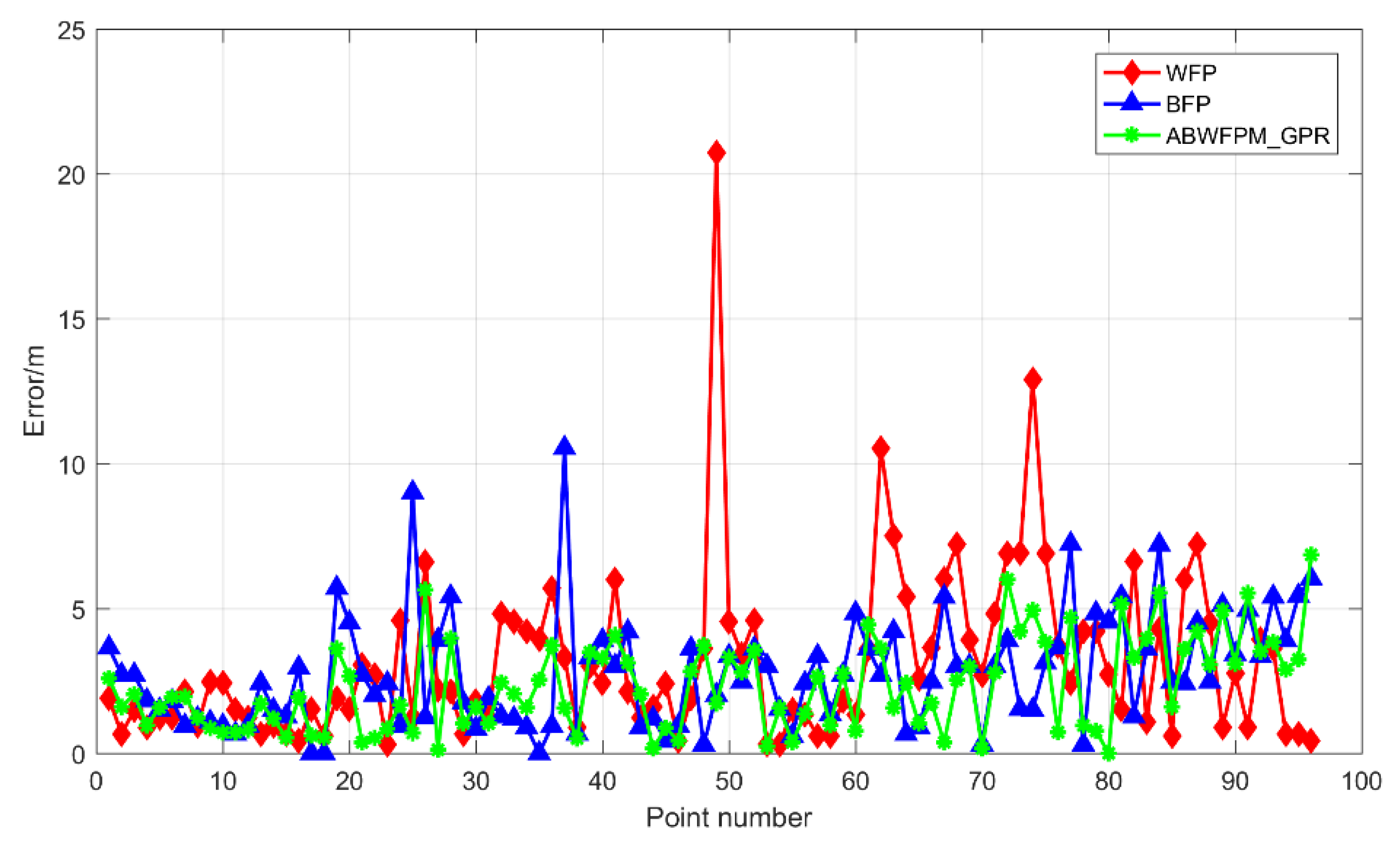
5.3. Effect of Using Gaussian Process Regression Alone
5.4. Adaptive Bluetooth/Wi-Fi Fingerprint Positioning Method Based on GPR and RD
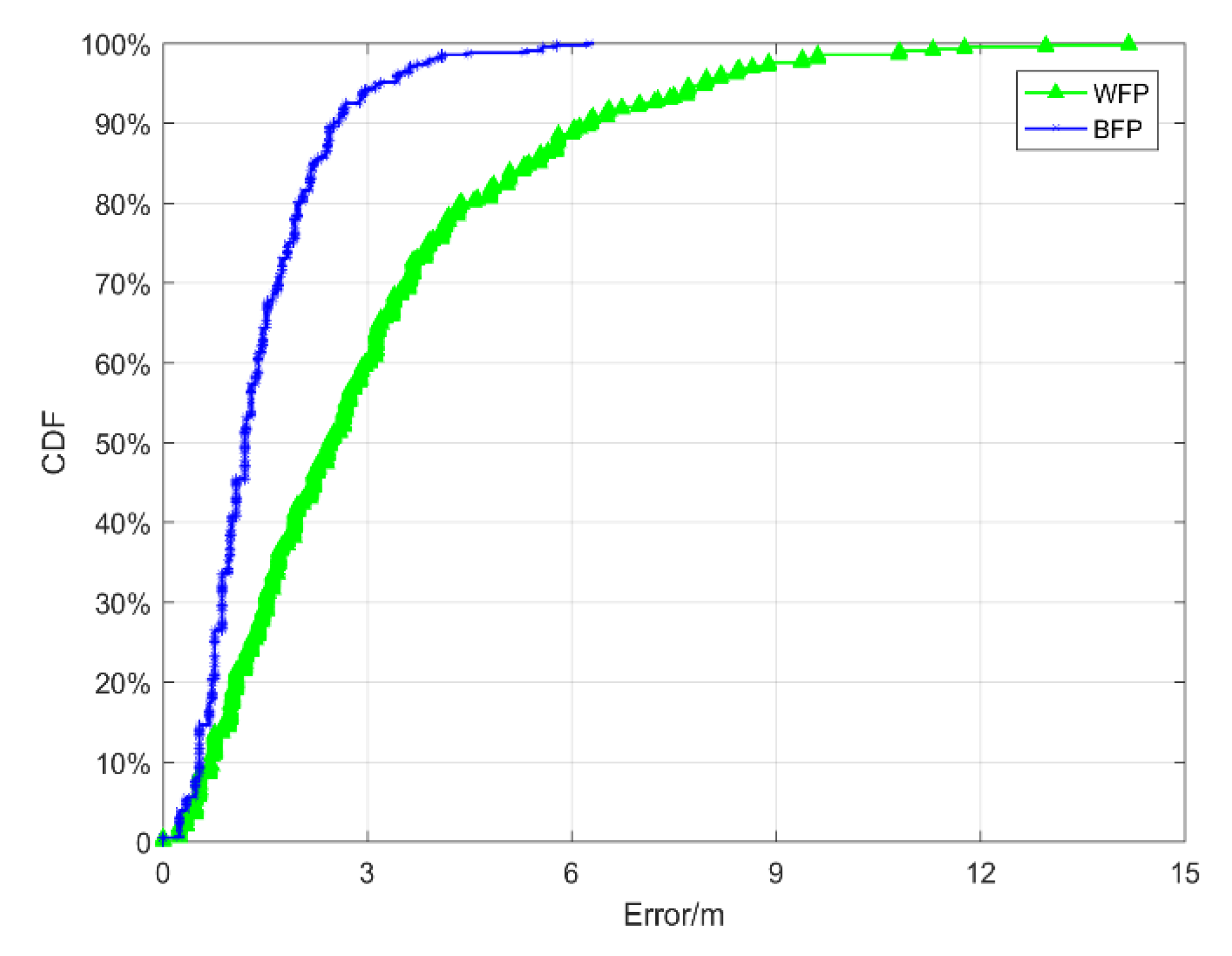
5.4.1. Comparison with BFP and WFP
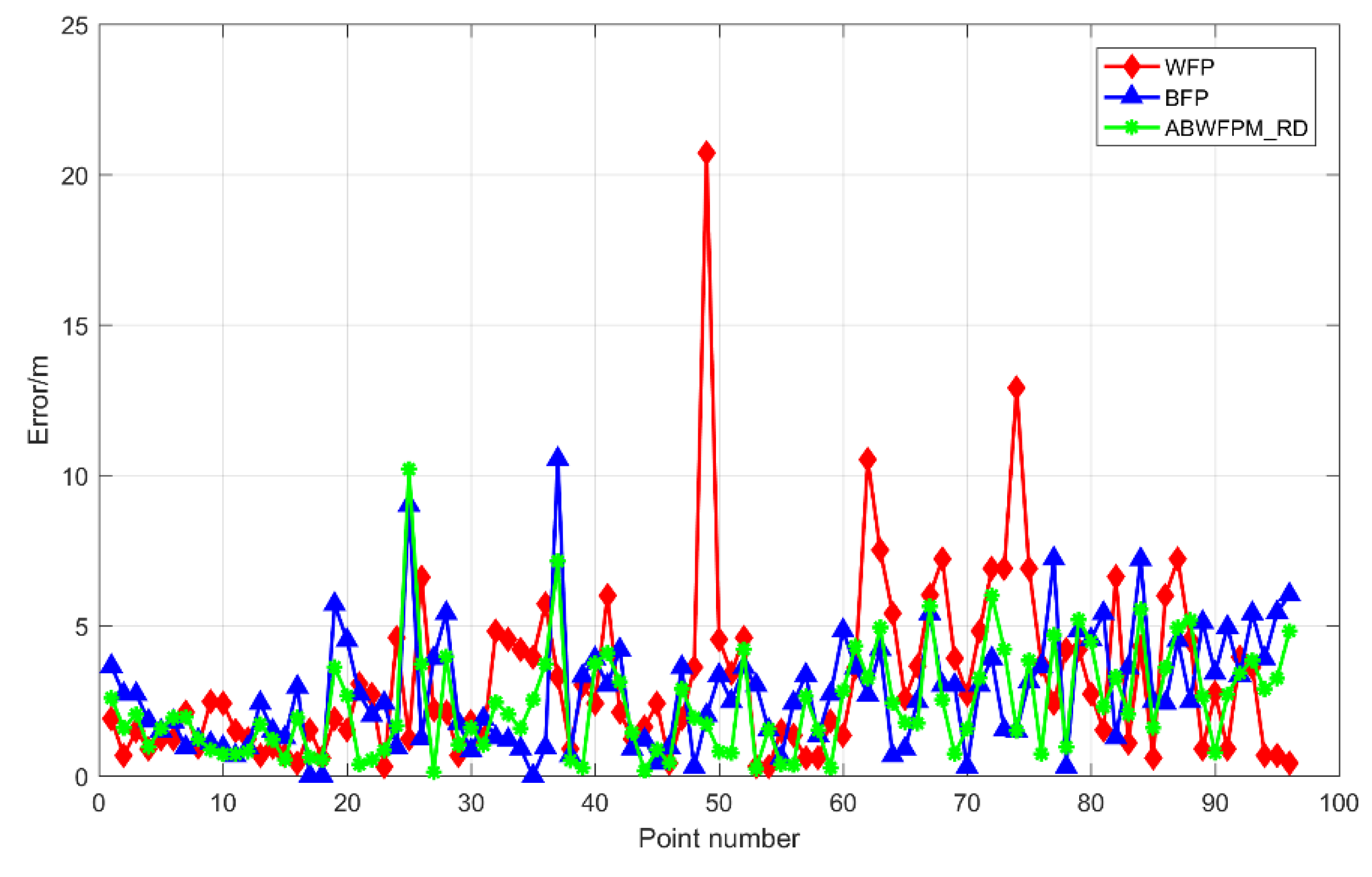
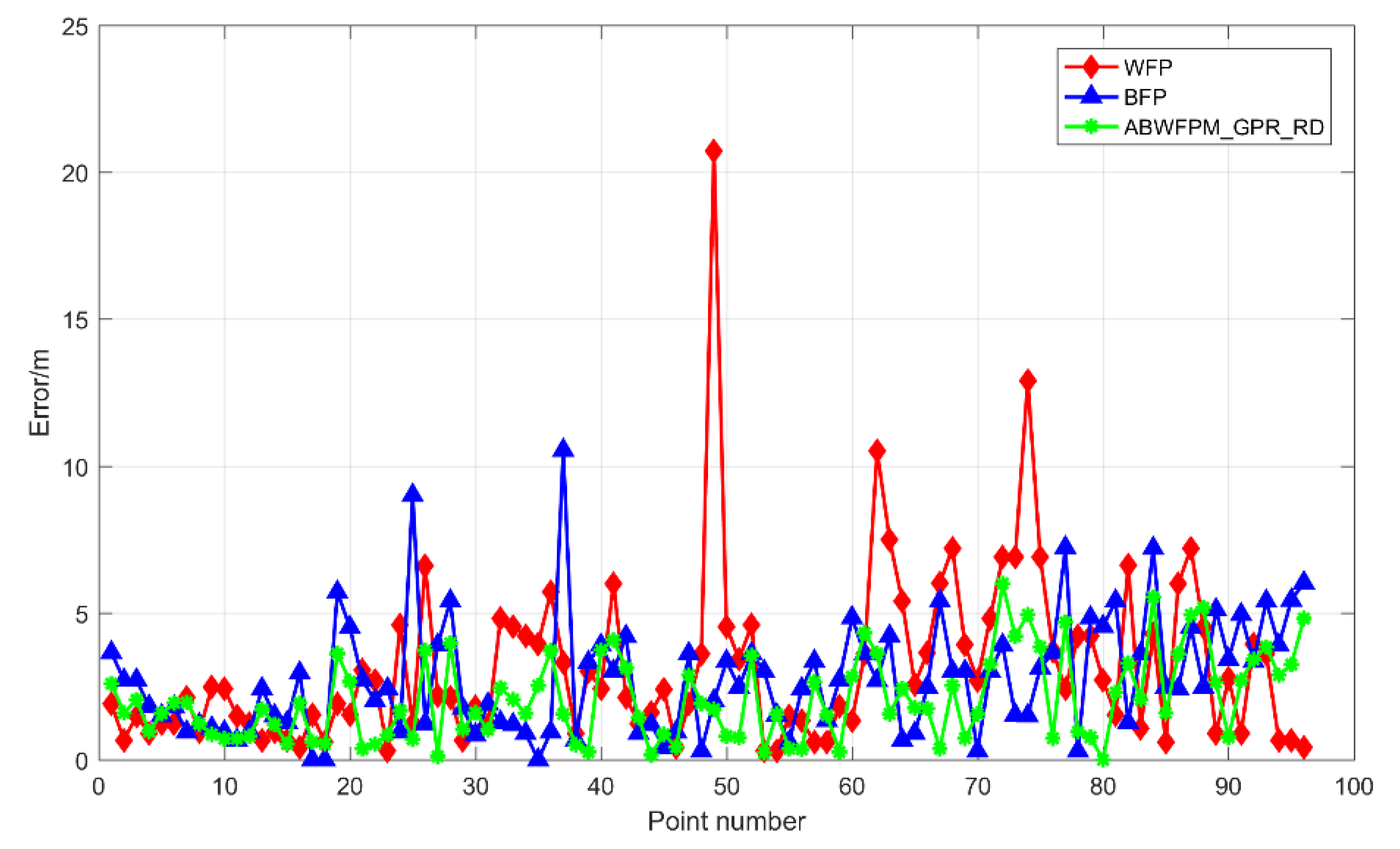
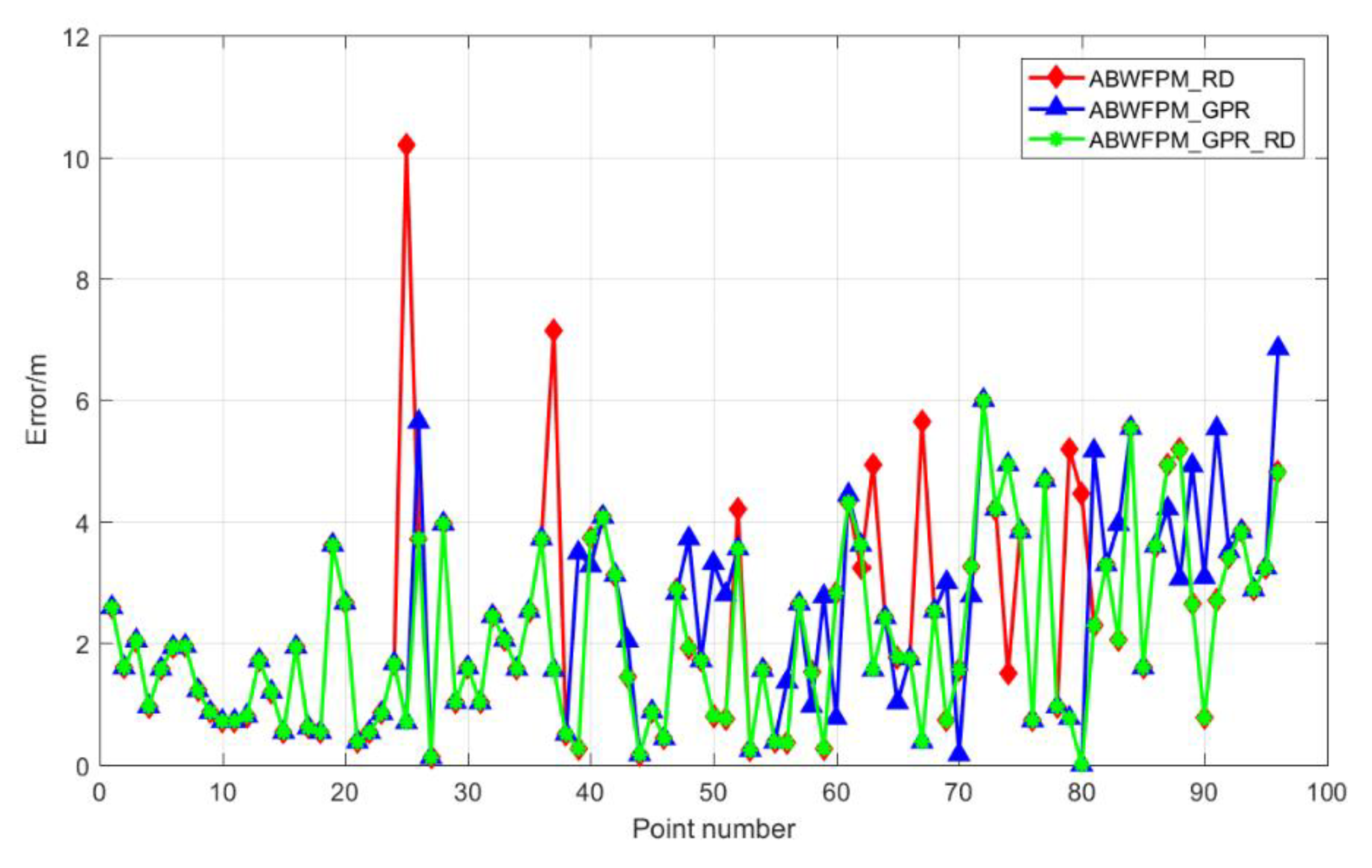
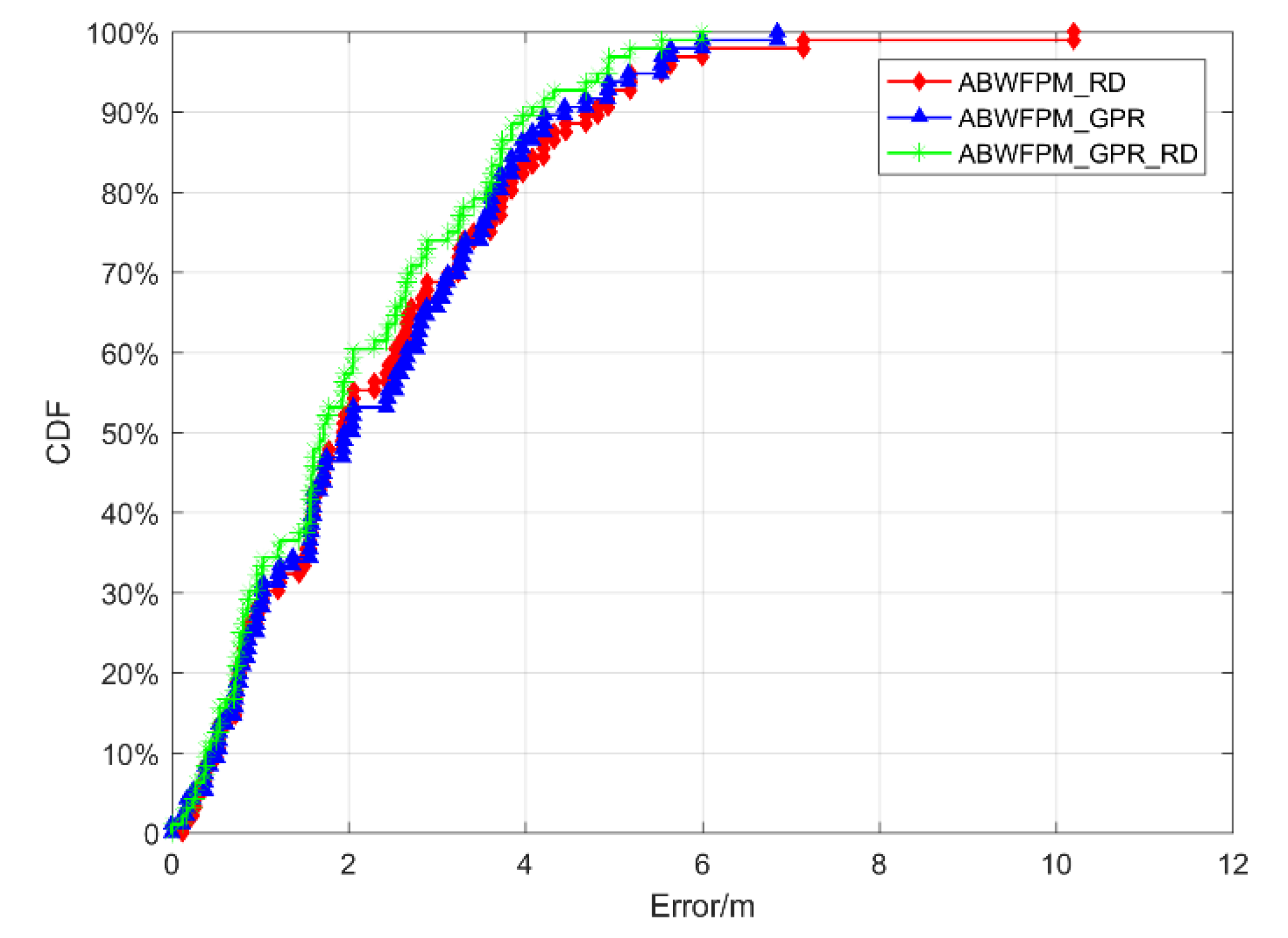
5.4.2. Comparison with ABWFPM_ RD and ABWFPM_GPR
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, S.; Li, G.; Wang, L.; Zhou, Y.; Peng, Y.; Fu, J. A three-dimensional robust ridge estimation positioning method for UWB in a complex environment. Adv. Space Res. 2017, 60, 2763–2775. [Google Scholar] [CrossRef]
- Li, H. Low-Cost 3D bluetooth indoor positioning with least square. Wirel. Pers. Commun. 2014, 78, 1331–1344. [Google Scholar] [CrossRef]
- Rida, M.E.; Liu, F.; Jadi, Y.; Algawhari, A.A.A.; Askourih, A. Indoor location position based on bluetooth signal strength. In Proceedings of the 2nd International Conference on Information Science and Control Engineering, Shanghai, China, 24–26 April 2015; pp. 769–773. [Google Scholar]
- Guo, X.; Li, L.; Ansari, N.; Liao, B. Accurate WiFi localization by fusing a group of fingerprints via a global fusion profile. IEEE Trans. Veh. Technol. 2018, 67, 7314–7325. [Google Scholar] [CrossRef]
- Zhuang, Y.; Syed, Z.; Li, Y.; El-Sheimy, N. Evaluation of two WiFi positioning systems based on autonomous crowdsourcing of handheld devices for indoor navigation. IEEE Trans. Mob. Comput. 2016, 15, 1982–1995. [Google Scholar] [CrossRef]
- Zhang, J.; Lyu, Y.; Patton, J.; Periaswamy, S.C.G.; Roppel, T. BFVP: A probabilistic UHF RFID tag localization algorithm using Bayesian filter and a variable power RFID model. IEEE Trans. Ind. Electron. 2018, 65, 8250–8259. [Google Scholar] [CrossRef]
- Jin, Y.-H.; Ko, K.-W.; Lee, W.-H. An indoor location-based positioning system using stereo vision with the drone camera. Mob. Inf. Syst. 2018, 2018, 13. [Google Scholar] [CrossRef]
- Khyam, M.O.; Noor-A-Rahim, M.; Li, X.; Ritz, C.; Guan, Y.L.; Ge, S.S. Design of chirp waveforms for multiple-access ultrasonic indoor positioning. IEEE Sens. J. 2018, 18, 6375–6390. [Google Scholar] [CrossRef]
- Wang, K.; Nirmalathas, A.; Lim, C.; Alameh, K.; Li, H.; Skafidas, E. Indoor infrared optical wireless localization system with background light power estimation capability. Opt. Express 2017, 25, 22923–22931. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Ou, G.; Peng, A.; Zheng, L.; Shi, J. An INS/WiFi indoor localization system based on the weighted least squares. Sensors 2018, 18, 1458. [Google Scholar] [CrossRef] [PubMed]
- Bahl, P.; Padmanabhan, V.N. RADAR: An in-building RF-based user location and tracking system. In Proceedings of the IEEE Infocom 2000, Nineteenth Joint Conference of the IEEE Computer & Communications Societies, Tel Aviv, Israel, 26–30 March 2000. [Google Scholar]
- Bi, J.; Wang, Y.; Li, X.; Cao, H.; Qi, H.; Wang, Y. A novel method of adaptive weighted K-nearest neighbor fingerprint indoor positioning considering user’s orientation. Int. J. Distrib. Sens. Netw. 2018, 14, 1550147718785885. [Google Scholar] [CrossRef]
- Wu, G.S.; Tseng, P.H. A deep neural network-based indoor positioning method using channel state information. In Proceedings of the International Conference on Computing, Networking and Communications (ICNC), Maui, HI, USA, 5–8 March 2018. [Google Scholar]
- Karegar, P.A. Wireless fingerprinting indoor positioning using affinity propagation clustering methods. Wirel. Netw. 2018, 24, 2825–2833. [Google Scholar] [CrossRef]
- Chen, L.; Pei, L.; Kuusniemi, H.; Chen, Y.; Kröger, T.; Chen, R. Bayesian fusion for indoor positioning using bluetooth fingerprints. Wirel. Pers. Commun. 2013, 70, 1735–1745. [Google Scholar] [CrossRef]
- He, S.; Shin, K.G. Steering crowdsourced signal map construction via Bayesian compressive sensing. In Proceedings of the IEEE INFOCOM 2018-IEEE Conference on Computer Communications, Honolulu, HI, USA, 16–19 April 2018. [Google Scholar]
- Feng, C.; Au, W.S.A.; Valaee, S.; Tan, Z. Received-signal-strength-based indoor positioning using compressive sensing. IEEE Trans. Mob. Comput. 2012, 11, 1983–1993. [Google Scholar] [CrossRef]
- Fang, X.; Nan, L.; Jiang, Z.; Chen, L. Fingerprint localisation algorithm for noisy wireless sensor network based on multi-objective evolutionary model. IET Communications. 2017, 11, 1297–1304. [Google Scholar] [CrossRef]
- Pu, Y.-C.; You, P.-C. Indoor positioning system based on BLE location fingerprinting with classification approach. Appl. Math. Model. 2018, 62, 654–663. [Google Scholar] [CrossRef]
- Seong, J.-H.; Seo, D.-H. Wi-Fi fingerprint using radio map model based on MDLP and euclidean distance based on the Chi squared test. Wirel. Netw. 2018, 25, 3019–3027. [Google Scholar] [CrossRef]
- Galván-Tejada, C.E.; Carrasco-Jiménez, J.C.; Brena, R.F. Bluetooth-WiFi based combined positioning algorithm, implementation and experimental evaluation. Procedia Technol. 2013, 7, 37–45. [Google Scholar] [CrossRef]
- Su, H.; Liao, Z.; Lin, C.; Lin, T. A hybrid indoor-position mechanism based on bluetooth and WiFi communications for smart mobile devices. In Proceedings of the International Symposium on Bioelectronics and Bioinformatics (ISBB), Beijing, China, 14–17 October 2015; pp. 188–191. [Google Scholar]
- De Blasio, G.; Quesada-Arencibia, A.; García, C.R.; Molina-Gil, J.M.; Caballero-Gil, C. Study on an indoor positioning system for harsh environments based on Wi-Fi and bluetooth low energy. Sensors 2017, 17, 1299. [Google Scholar] [CrossRef] [PubMed]
- Ferris, B.; Fox, D.; Lawrence, N.D. WiFi-SLAM using Gaussian process latent variable models. In Proceedings of the International Joint Conference on Artifical Intelligence, Hyderabad, India, 6–12 January 2007. [Google Scholar]
- Yiu, S.; Yang, K. Gaussian process assisted fingerprinting localization. IEEE Internet Things J. 2016, 3, 683–690. [Google Scholar] [CrossRef]
- Kumar, S.; Hegde, R.; Trigoni, N. Gaussian process regression for fingerprinting based localization. Ad Hoc Netw. 2016, 51, 1–10. [Google Scholar] [CrossRef]
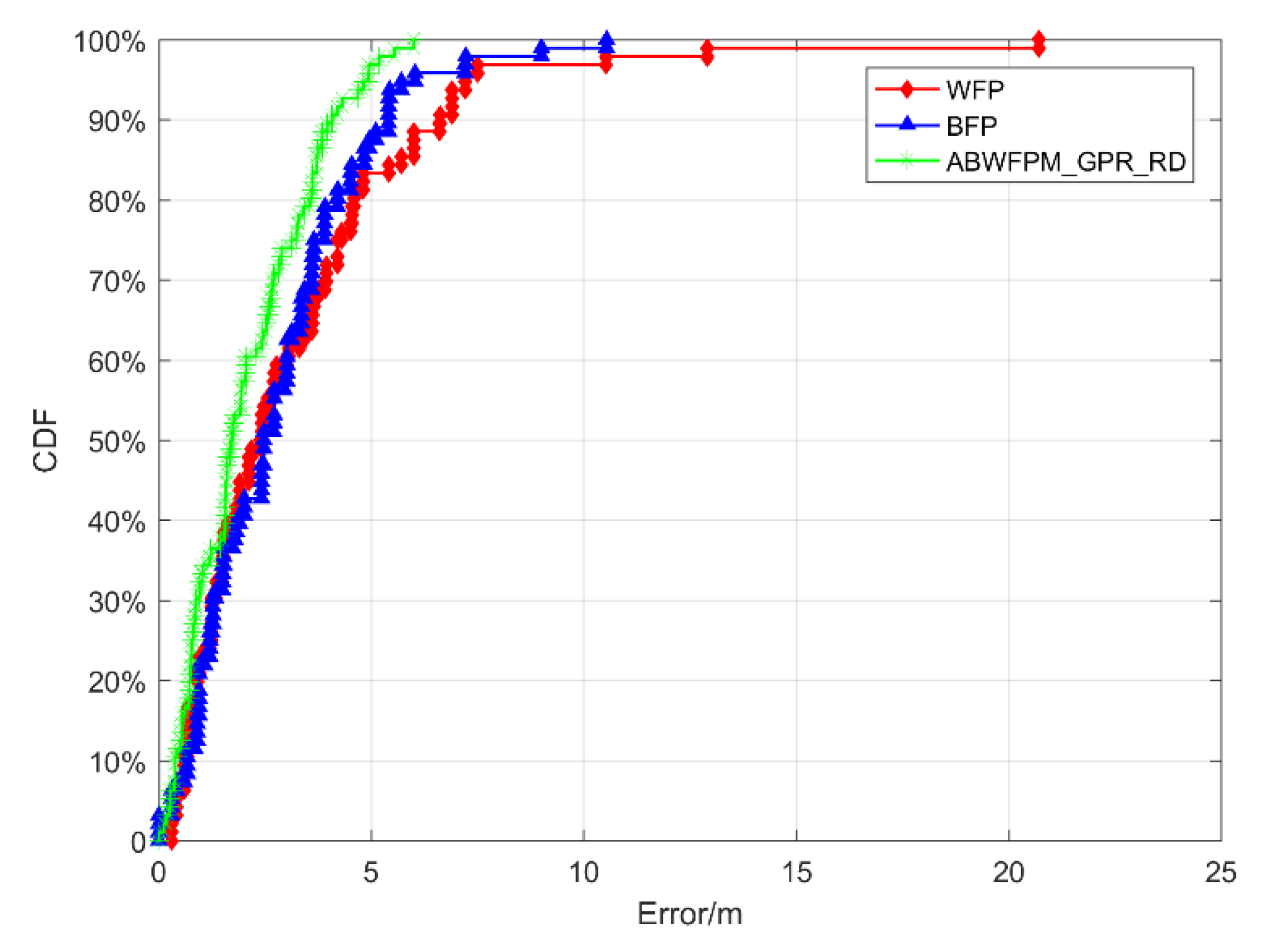
| Method | 50% | 70% | 90% | ME | EM | RMSE |
|---|---|---|---|---|---|---|
| WFP | 2.121 | 3.912 | 6.6 | 20.72 | 3.131 | 2.978 |
| BFP | 2.474 | 3.6 | 5.4 | 10.539 | 2.771 | 1.974 |
| ABWFPM_GPR_RD | 1.601 | 2.664 | 3.967 | 6.001 | 2.06 | 1.449 |
| Method | 50% | 70% | 90% | ME | EM | RMSE |
|---|---|---|---|---|---|---|
| FPMBW_ RD | 1.772 | 3.122 | 4.68 | 10.201 | 2.372 | 1.78 |
| FPMBW_GPR | 1.935 | 3.122 | 4.215 | 6.85 | 2.312 | 1.58 |
| AFPM_GPR_ RD | 1.601 | 3.664 | 4.08 | 6.001 | 2.06 | 1.449 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, H.; Wang, Y.; Bi, J.; Qi, H. An Adaptive Bluetooth/Wi-Fi Fingerprint Positioning Method based on Gaussian Process Regression and Relative Distance. Sensors 2019, 19, 2784. https://doi.org/10.3390/s19122784
Cao H, Wang Y, Bi J, Qi H. An Adaptive Bluetooth/Wi-Fi Fingerprint Positioning Method based on Gaussian Process Regression and Relative Distance. Sensors. 2019; 19(12):2784. https://doi.org/10.3390/s19122784
Chicago/Turabian StyleCao, Hongji, Yunjia Wang, Jingxue Bi, and Hongxia Qi. 2019. "An Adaptive Bluetooth/Wi-Fi Fingerprint Positioning Method based on Gaussian Process Regression and Relative Distance" Sensors 19, no. 12: 2784. https://doi.org/10.3390/s19122784
APA StyleCao, H., Wang, Y., Bi, J., & Qi, H. (2019). An Adaptive Bluetooth/Wi-Fi Fingerprint Positioning Method based on Gaussian Process Regression and Relative Distance. Sensors, 19(12), 2784. https://doi.org/10.3390/s19122784





