Magnetic Induction Spectroscopy for Biomass Measurement: A Feasibility Study
Abstract
1. Introduction
2. Methods
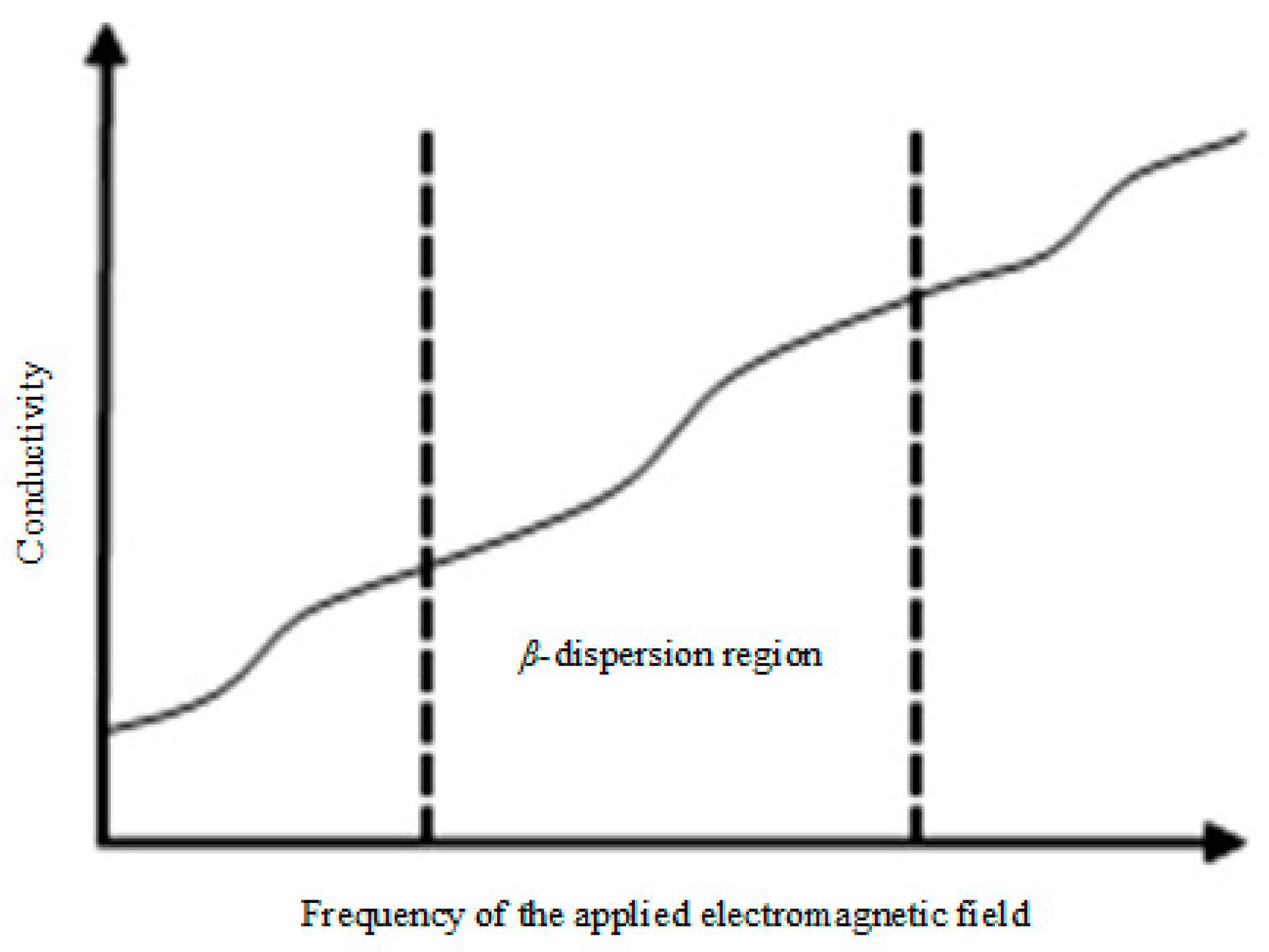
2.1. Description of the MIS Measurement Principle
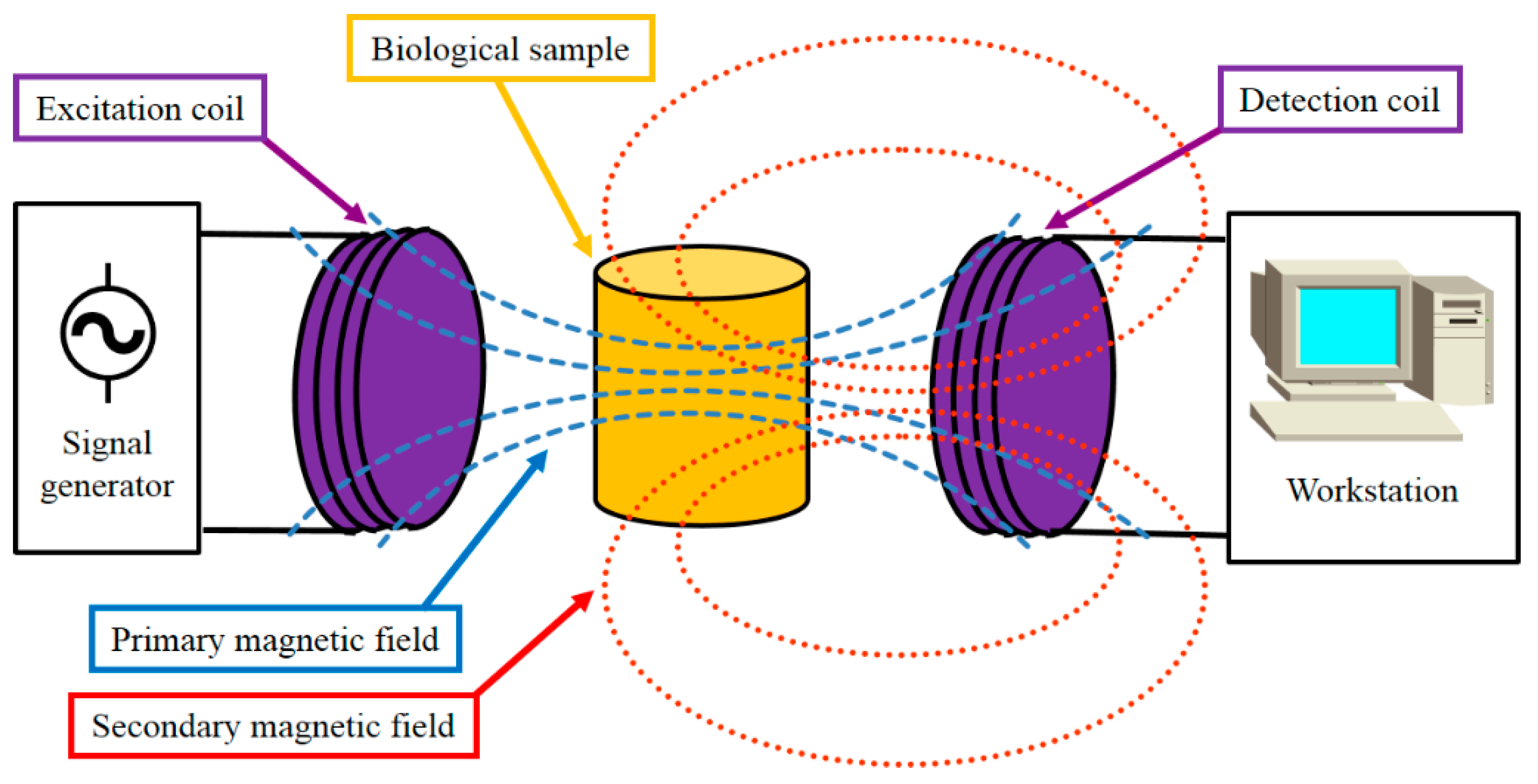
2.2. The South Wales MIS System
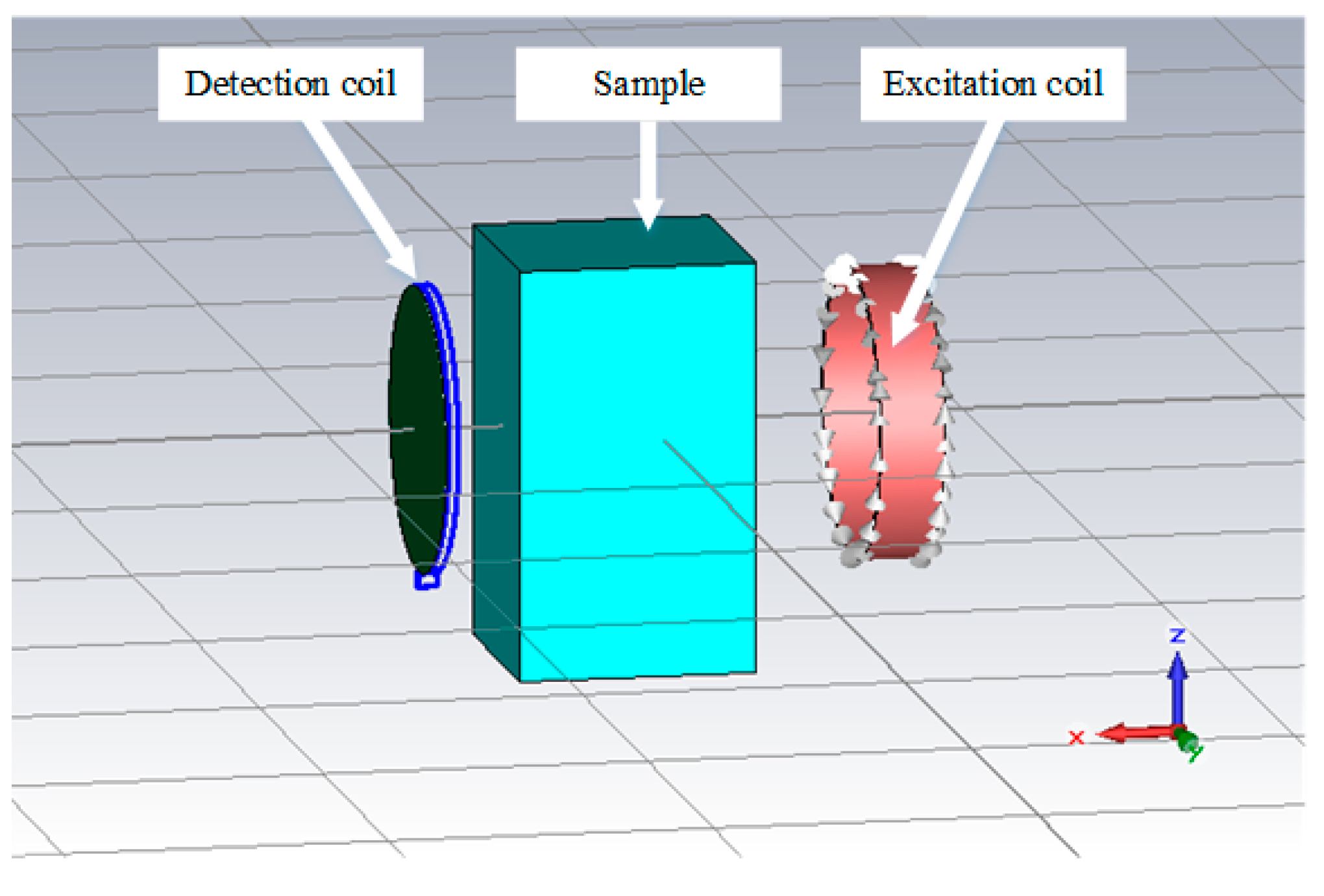
2.3. MIS Measurements and Simulations with Saline Solutions
2.4. Measurements with Yeast Suspensions
3. Results
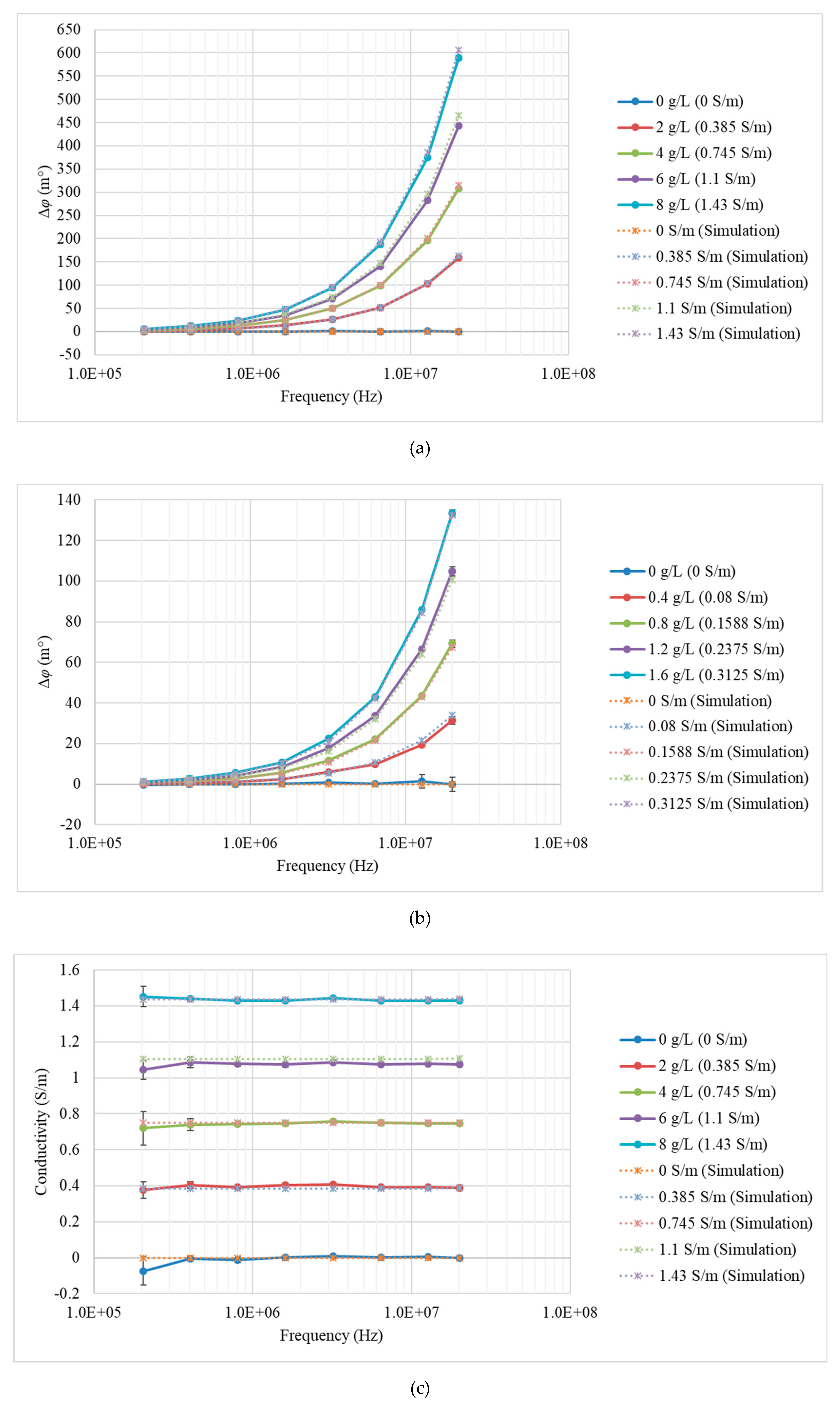
3.1. Measurements and Simulations with Saline Solutions
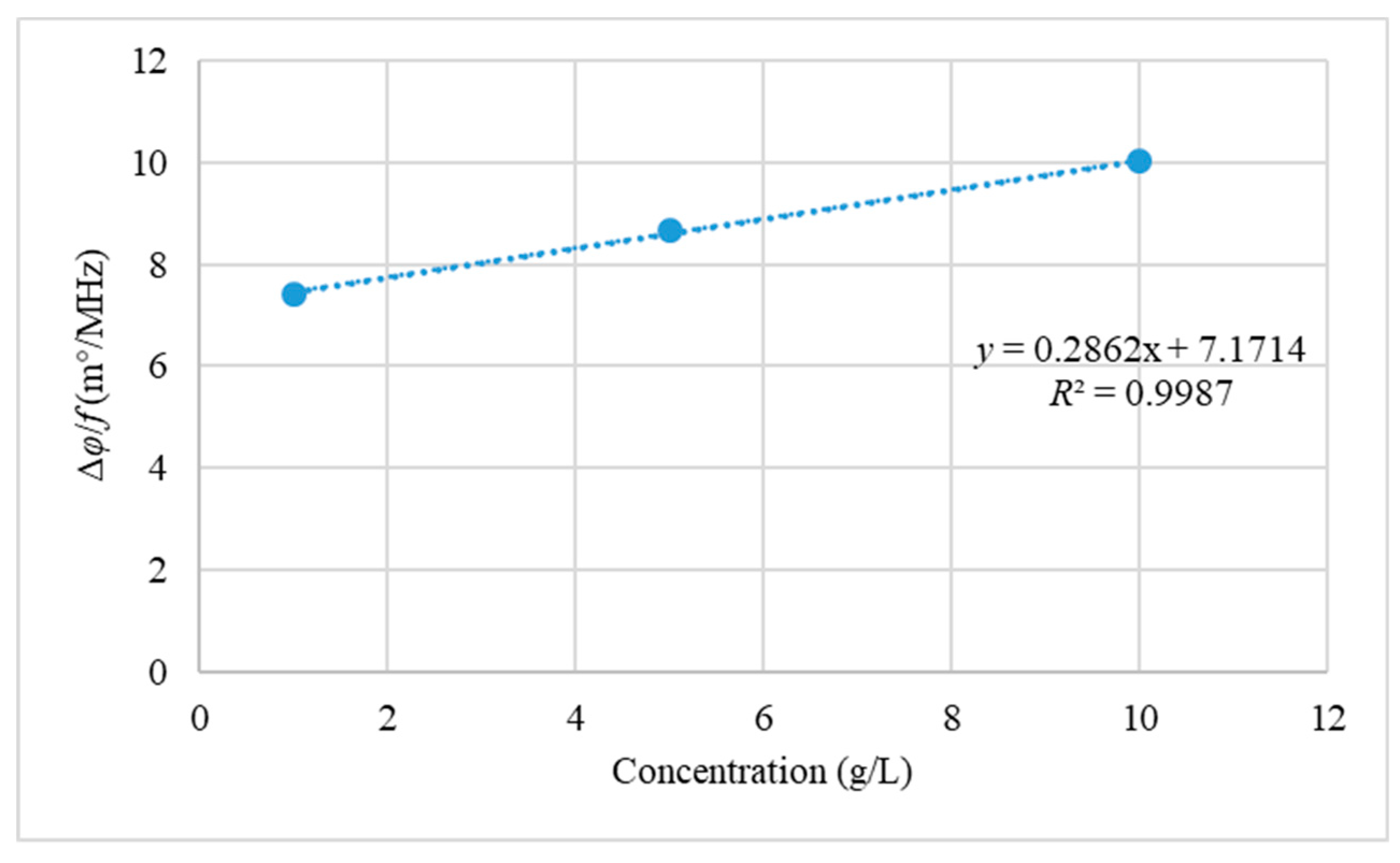
3.2. Measurements with Yeast Suspensions
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Grimnes, S.; Martinsen, O.G. Bioimpedance and Bioelectricity Basics, 3rd ed.; Academic Press: Cambridge, MA, USA, 2015; pp. 71–74. [Google Scholar]
- Pethig, R.; Kell, D.B. The passive electrical properties of biological systems: Their significance in physiology, biophysics and biotechnology. Phys. Med. Biol. 1987, 32, 933–970. [Google Scholar] [CrossRef] [PubMed]
- Foster, K.R.; Schwan, H.P. Dielectric properties of tissues and biological materials: A critical review. Crit. Rev. Biomed. Eng. 1989, 17, 25–104. [Google Scholar] [PubMed]
- Gabriel, C.; Gabriel, S.; Corthout, E. The dielectric properties of biological tissues: I. Literature survey. Phys. Med. Biol. 1996, 41, 2231–2249. [Google Scholar] [CrossRef] [PubMed]
- Heileman, K.; Daoud, J.; Tabrizian, M. Dielectric spectroscopy as a viable biosensing tool for cell and tissue characterization and analysis. Biosens. Bioelectron. 2013, 49, 348–359. [Google Scholar] [CrossRef] [PubMed]
- Traffano-Schiffo, M.V.; Castro-Giraldez, M.; Herrero, V.; Colom, R.J.; Fito, P.J. Development of a non-destructive detection system of Deep Pectoral Myopathy in poultry by dielectric spectroscopy. J. Food Eng. 2018, 237, 137–145. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, P.; Fan, L.; Zhou, Q.; Wang, Z.; Song, C.; Chai, Z.; Yue, Y.; Huang, L.; Wang, Z. Determination of water content and characteristic analysis in substrate root zone by electrical impedance spectroscopy. Comput. Electron. Agric. 2019, 156, 243–253. [Google Scholar] [CrossRef]
- Scharfetter, H.; Lackner, H.K.; Rosell, J. Magnetic induction tomography: Hardware for multi-frequency measurements in biological tissues. Physiol. Meas. 2001, 22, 131–146. [Google Scholar] [CrossRef]
- Scharfetter, H.; Casañas, R.; Rosell, J. Biological tissue characterization by magnetic induction spectroscopy (MIS): Requirements and limitations. IEEE Trans. Biomed. Eng. 2003, 50, 870–880. [Google Scholar] [CrossRef]
- González, C.A.; Villanueva, C.; Vera, C.; Flores, O.; Reyes, R.D.; Rubinsky, B. The detection of brain ischaemia in rats by inductive phase shift spectroscopy. Physiol. Meas. 2009, 30, 809–819. [Google Scholar] [CrossRef]
- Gonzalez-Diaz, C.A.; Uscanga-Carmona, M.C.; Lozano-Trenado, L.M.; Ortiz, J.L.; Gonzalez, J.A.; Guerrero-Robles, C.I. Clinical evaluation of inductive spectrometer to detect breast cancer. In IFMBE Proceedings; Springer: Singapore, 2017; Volume 60, pp. 678–681. [Google Scholar]
- O’Toole, M.D.; Marsh, L.A.; Davidson, J.L.; Tan, Y.M.; Armitage, D.W.; Peyton, A.J. Non-contact multi-frequency magnetic induction spectroscopy system for industrial-scale bio-impedance measurement. Meas. Sci. Technol. 2014, 26, 035102. [Google Scholar] [CrossRef]
- O’Toole, M.D.; Karimian, N.; Peyton, A.J. Classification of nonferrous metals using magnetic induction spectroscopy. IEEE Trans. Ind. Inform. 2018, 14, 3477–3485. [Google Scholar] [CrossRef]
- Li, G.; Sun, J.; Ma, L.; Yan, Q.; Zheng, X.; Qin, M.; Jin, G.; Ning, X.; Zhuang, W.; Feng, H.; et al. Construction of a cerebral hemorrhage test system operated in real-time. Sci. Rep. 2017, 7, 42842. [Google Scholar] [CrossRef] [PubMed]
- Yan, Q.; Jin, G.; Ma, K.; Qin, M.; Zhuang, W.; Sun, J. Magnetic inductive phase shift: A new method to differentiate hemorrhagic stroke from ischemic stroke on rabbit. Biomed. Eng. Online 2017, 16, 63. [Google Scholar] [CrossRef]
- Maimaitijiang, Y.; Roula., M.A.; Kahlert, J. Approaches for improving image quality in magnetic induction tomography. Physiol. Meas. 2010, 31, S147–S156. [Google Scholar] [CrossRef] [PubMed]
- Zakaria, Z.; Sarkawi, S.; Jalil, J.A.; Balkhis, I.; Rahim, M.A.A.; Mustafa, N.; Rahiman, M.H.F. Simulation of single channel magnetic induction spectroscopy for fetal hypoxia detection. J. Teknol. 2015, 73, 107–110. [Google Scholar] [CrossRef][Green Version]
- Wang, J.-Y.; Healey, T.; Barker, A.; Brown, B.; Monk, C.; Anumba, D. Magnetic induction spectroscopy (MIS)-probe design for cervical tissue measurements. Physiol. Meas. 2017, 38, 729–744. [Google Scholar] [CrossRef] [PubMed]
- Lyons, S.; Wei, K.; Soleimani, M. Wideband precision phase detection for magnetic induction spectroscopy. Measurement 2018, 115, 45–51. [Google Scholar] [CrossRef]
- Ma, L.; Soleimani, M. Magnetic induction spectroscopy for permeability imaging. Sci. Rep. 2018, 8, 7025. [Google Scholar] [CrossRef]
- Yardley, J.E.; Kell, D.B.; Barrett, J.; Davey, C.L. On-line, real-time measurements of cellular biomass using dielectric spectroscopy. Biotechnol. Genet. Eng. Rev. 2000, 17, 3–35. [Google Scholar] [CrossRef]
- Kiviharju, K.; Salonen, K.; Moilanen, U.; Eerikainen, T. Biomass measurement online: The performance of in situ measurements and software sensors. J. Ind. Microbiol. Biotechnol. 2008, 35, 657–665. [Google Scholar] [CrossRef]
- Ronnest, N.P.; Stocks, S.M.; Lantz, A.E.; Gernaey, K.V. Introducing process analytical technology (PAT) in filamentous cultivation process development: Comparison of advanced online sensors for biomass measurement. J. Ind. Microbiol. Biotechnol. 2011, 38, 1679–1690. [Google Scholar] [CrossRef] [PubMed]
- November, E.J.; Van Impe, J.F. Evaluation of on-line viable biomass measurements during fermentations of Candida utilis. Bioprocess Eng. 2000, 23, 473–477. [Google Scholar] [CrossRef]
- Treo, E.F.; Felice, C.J. Non-linear dielectric spectroscopy of microbiological suspensions. Biomed. Eng. Online 2009, 8, 19. [Google Scholar] [CrossRef] [PubMed]
- Fernandez, R.E.; Lebiga, E.; Koklu, A.; Sabuncu, A.C.; Beskok, A. Flexible Bioimpedance sensor for label-free detection of cell viability and biomass. IEEE Trans. Nanobiosci. 2015, 14, 700–706. [Google Scholar] [CrossRef] [PubMed]
- Barai, A.; Watson, S.; Griffiths, H.; Patz, R. Magnetic induction spectroscopy: Non-contact measurement of the electrical conductivity spectra of biological samples. Meas. Sci. Technol. 2012, 23, 085501. [Google Scholar] [CrossRef]
- Rao, R.N.; Prasad, K.G.; Naidu, C.G.; Maurya, P.K. Development of a validated liquid chromatographic method for determination of related substances of telmisartan in bulk drugs and formulations. J. Pharm. Biomed. Anal. 2011, 56, 471–478. [Google Scholar] [PubMed]

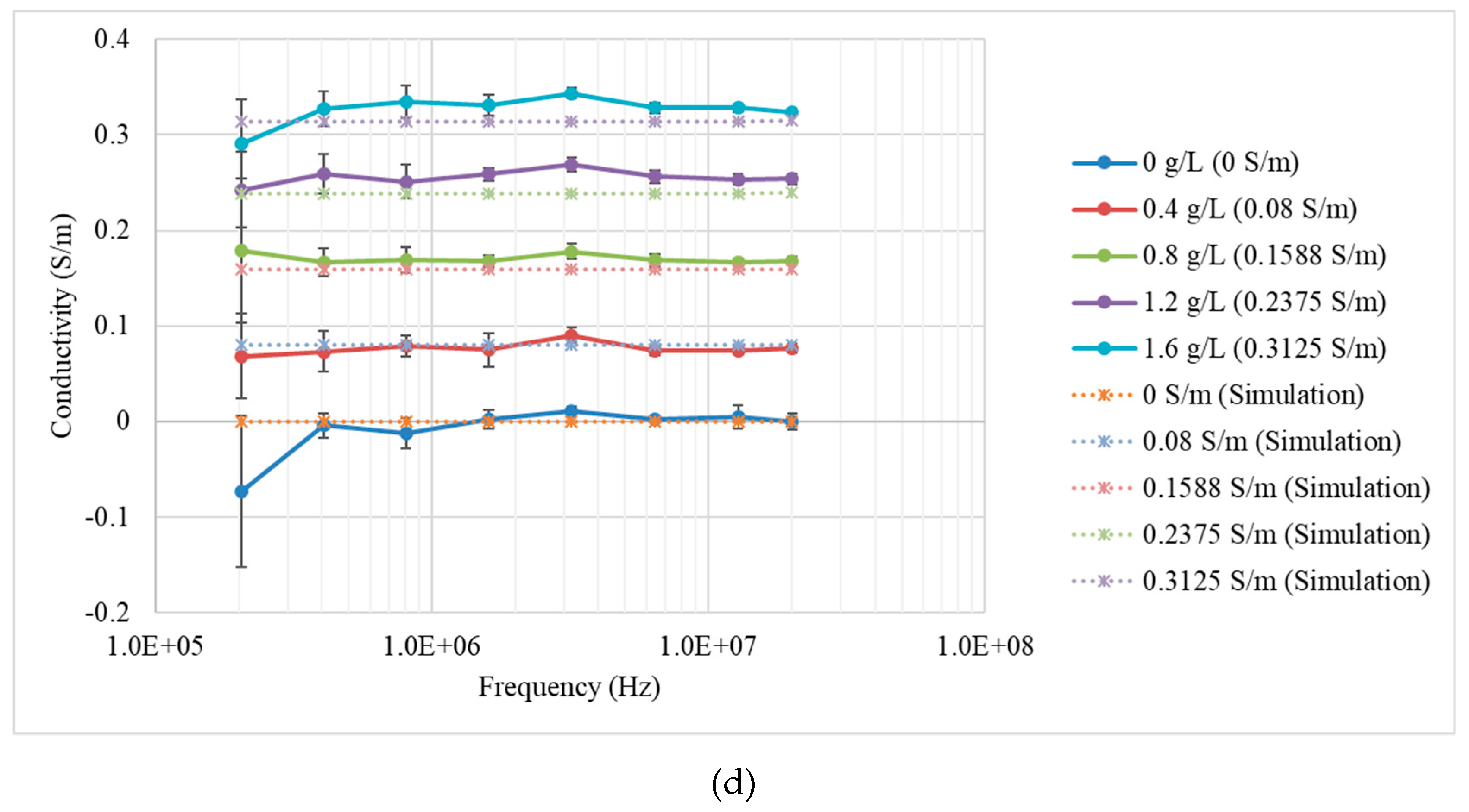
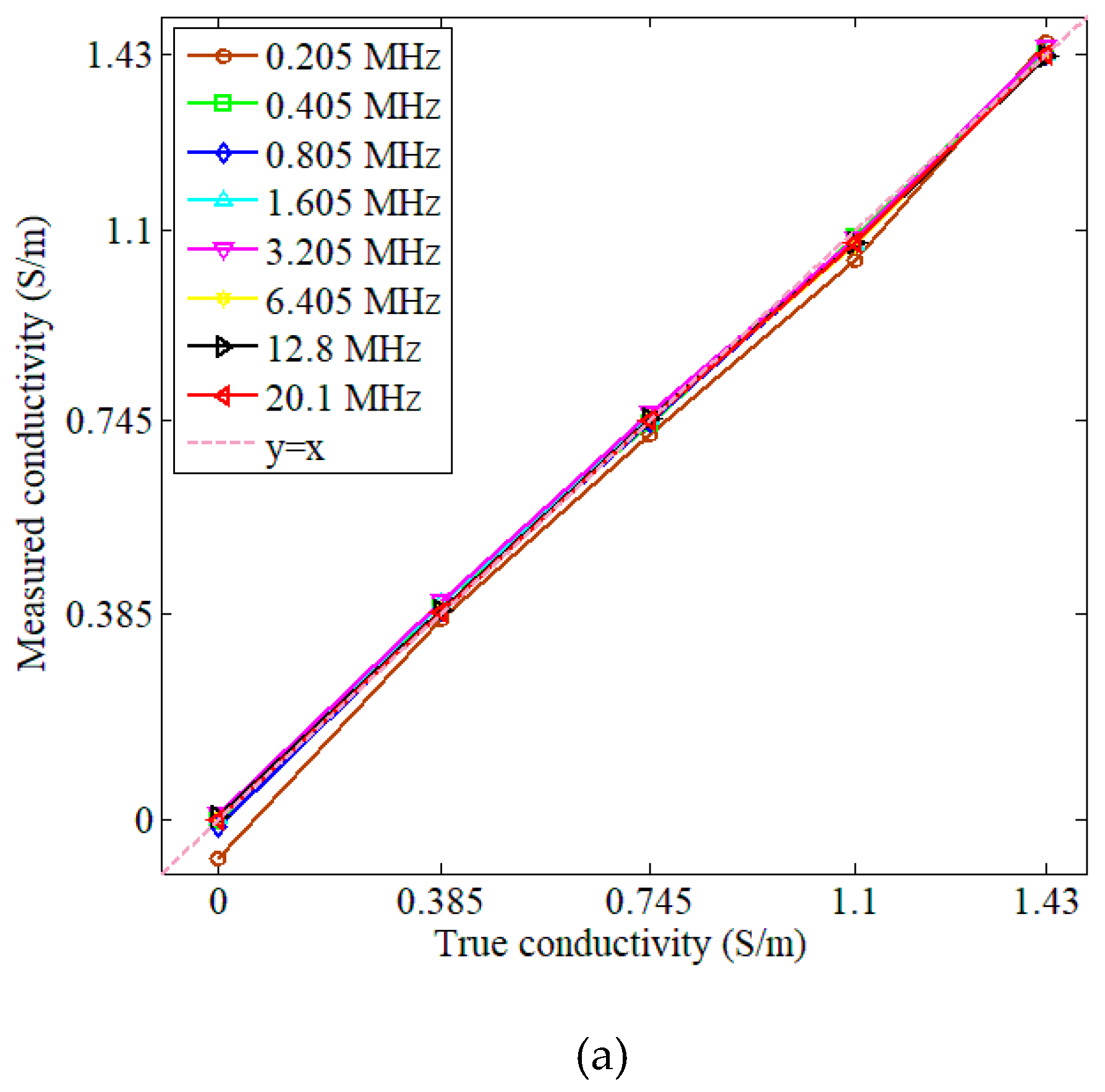
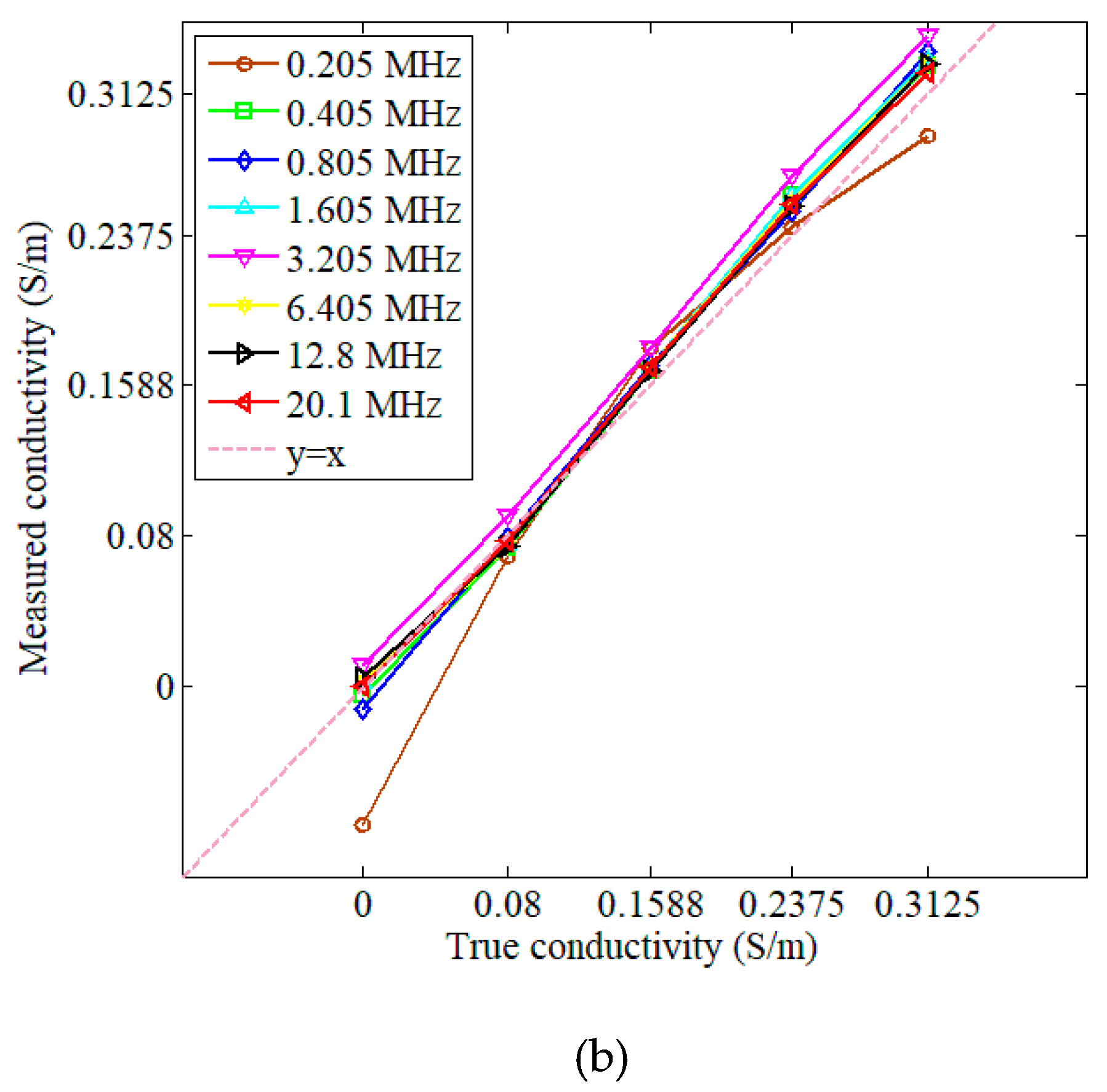
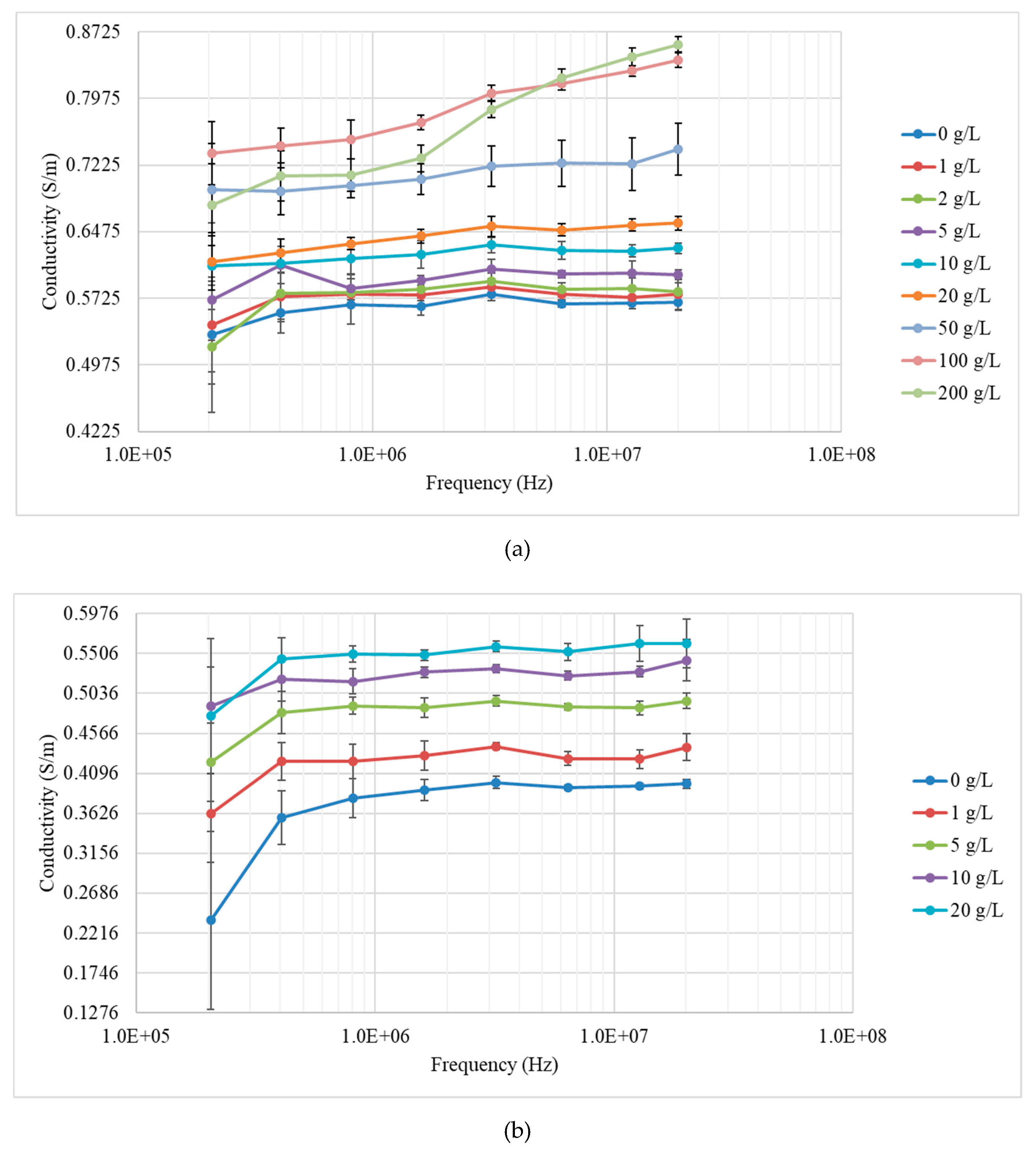
| Concentration (g/L) | Conductivity (S/m) |
|---|---|
| 0 | 0 |
| 0.4 | 0.08 |
| 0.8 | 0.1588 |
| 1.2 | 0.2375 |
| 1.6 | 0.3125 |
| 2 | 0.385 |
| 4 | 0.745 |
| 6 | 1.1 |
| 8 | 1.43 |
| Composition | Concentration (g/L) |
|---|---|
| Yeast extract | 10 |
| Peptone | 20 |
| Glucose | 20 |
| Frequency (MHz) | Step (i) | Step (ii) | ||
|---|---|---|---|---|
| Linear Correlation Coefficient | Norm of Residuals | Linear Correlation Coefficient | Norm of Residuals | |
| 0.205 | 0.9987 | 0.0601 | 0.9788 | 0.0597 |
| 0.405 | 0.9997 | 0.0254 | 0.9990 | 0.0119 |
| 0.805 | 0.9998 | 0.0223 | 0.9998 | 0.0046 |
| 1.605 | 0.9997 | 0.0282 | 0.9990 | 0.0118 |
| 3.205 | 0.9997 | 0.0266 | 0.9996 | 0.0073 |
| 6.405 | 0.9997 | 0.0245 | 0.9990 | 0.0119 |
| 12.8 | 0.9998 | 0.0192 | 0.9989 | 0.0118 |
| 20.1 | 0.9998 | 0.0204 | 0.9993 | 0.0095 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Roula, M.A.; Dinsdale, R. Magnetic Induction Spectroscopy for Biomass Measurement: A Feasibility Study. Sensors 2019, 19, 2765. https://doi.org/10.3390/s19122765
Zhang Z, Roula MA, Dinsdale R. Magnetic Induction Spectroscopy for Biomass Measurement: A Feasibility Study. Sensors. 2019; 19(12):2765. https://doi.org/10.3390/s19122765
Chicago/Turabian StyleZhang, Ziyi, Mohammed Ali Roula, and Richard Dinsdale. 2019. "Magnetic Induction Spectroscopy for Biomass Measurement: A Feasibility Study" Sensors 19, no. 12: 2765. https://doi.org/10.3390/s19122765
APA StyleZhang, Z., Roula, M. A., & Dinsdale, R. (2019). Magnetic Induction Spectroscopy for Biomass Measurement: A Feasibility Study. Sensors, 19(12), 2765. https://doi.org/10.3390/s19122765





