A Sensor-Driven Analysis of Distributed Direction Finding Systems Based on UAV Swarms
Abstract
1. Introduction
2. Problem Formulation
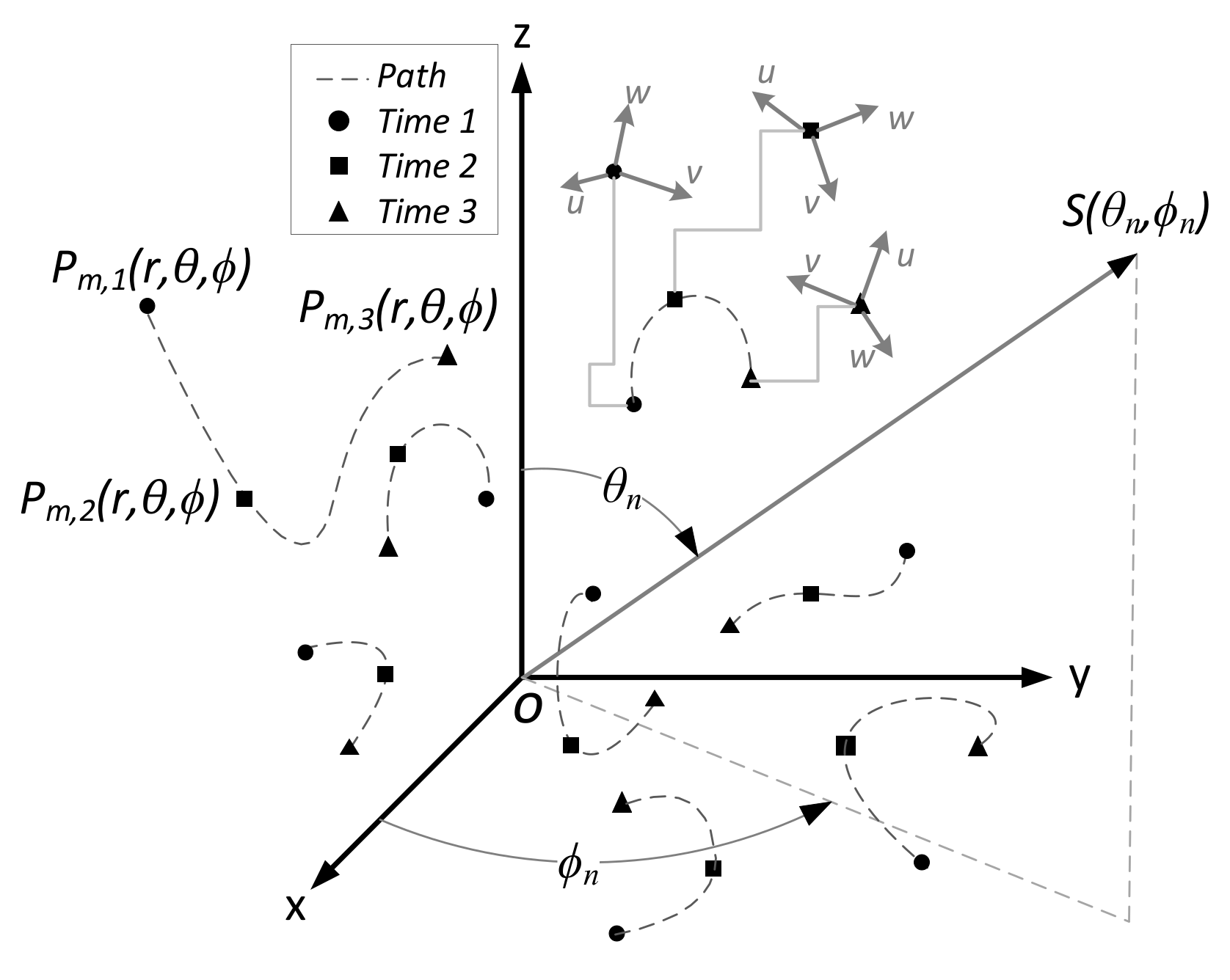
2.1. Swarming UAV Synthetic Aperture
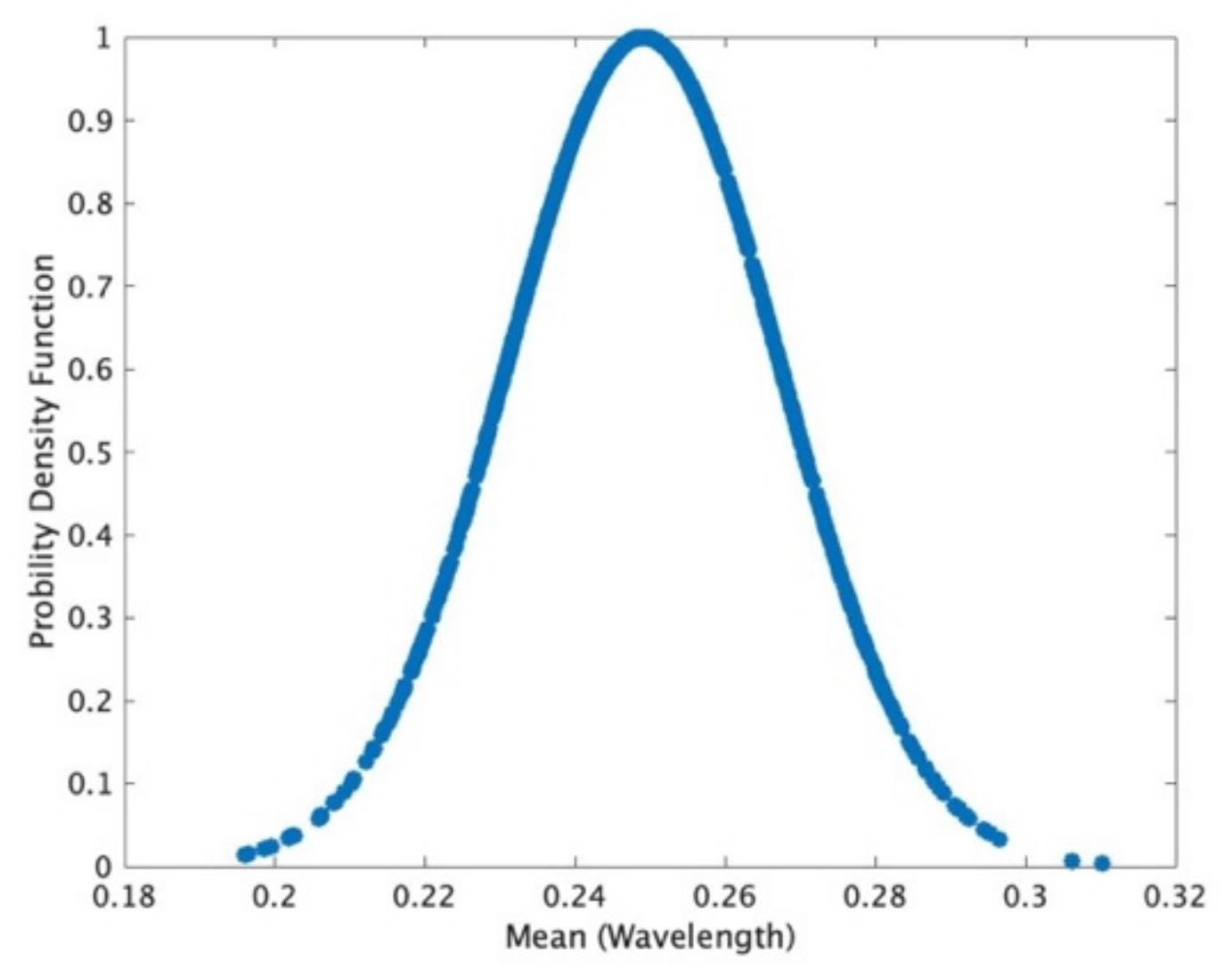
2.2. Signal Model
3. The CRB
3.1. Swarming UAV Synthetic Aperture
3.2. CRB for the UAV Swarming System
4. Analysis of Single-Emitter Case
5. The Algorithm
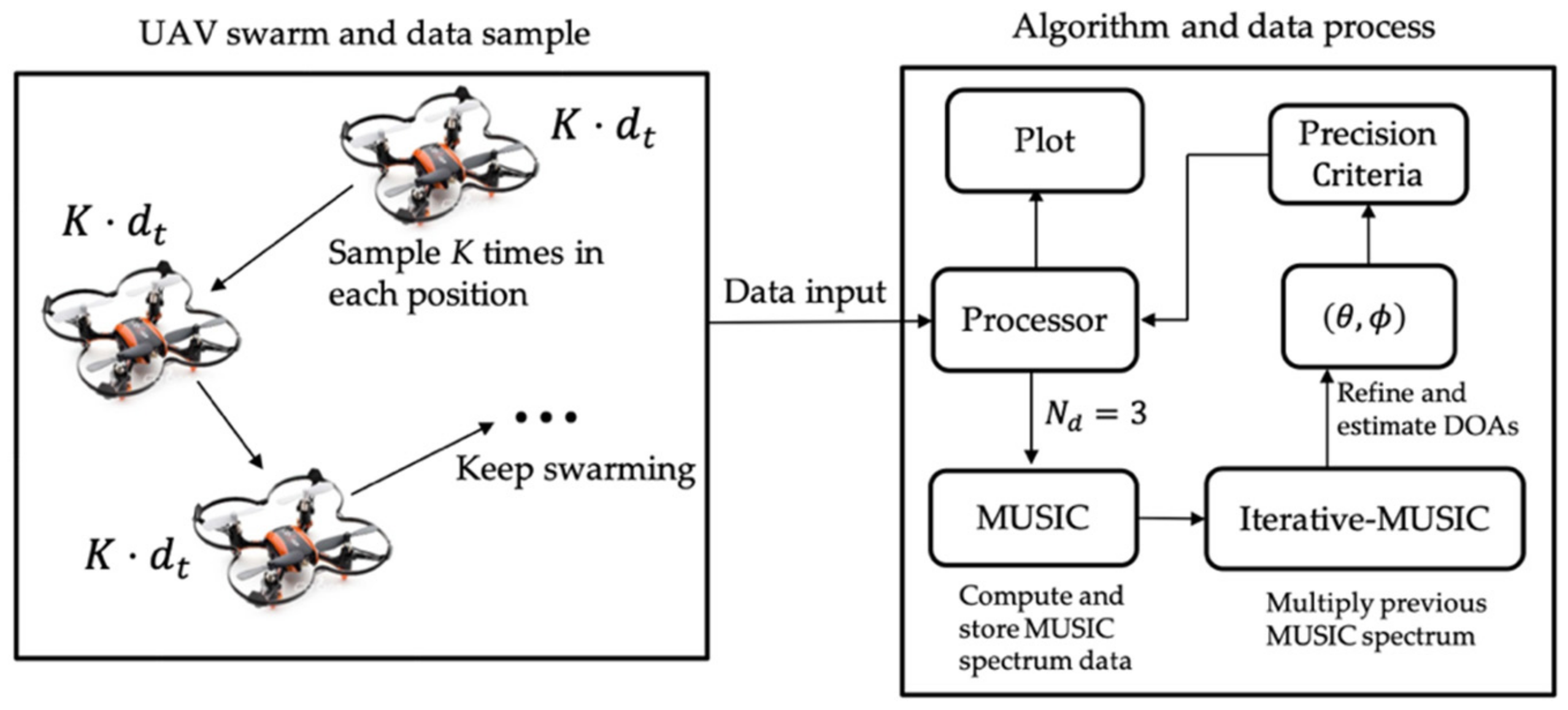
5.1. UAV Parameters
5.2. Data Processing and Algorithm
5.3. MUSIC Algorithm for MUSB Array
5.4. Convergence Check
5.5. Computational Complexity Analysis
6. Simulation and Measurement Results
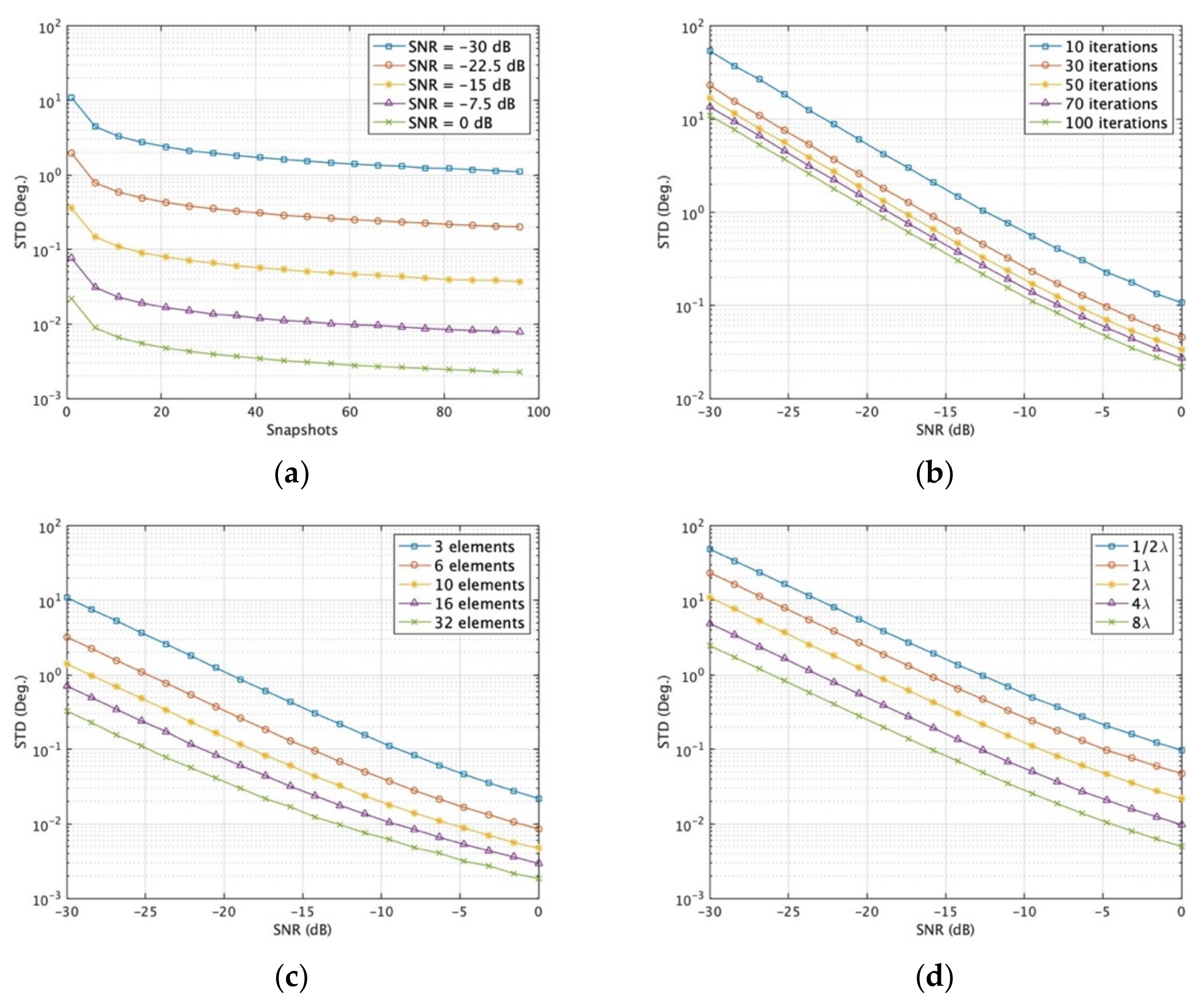
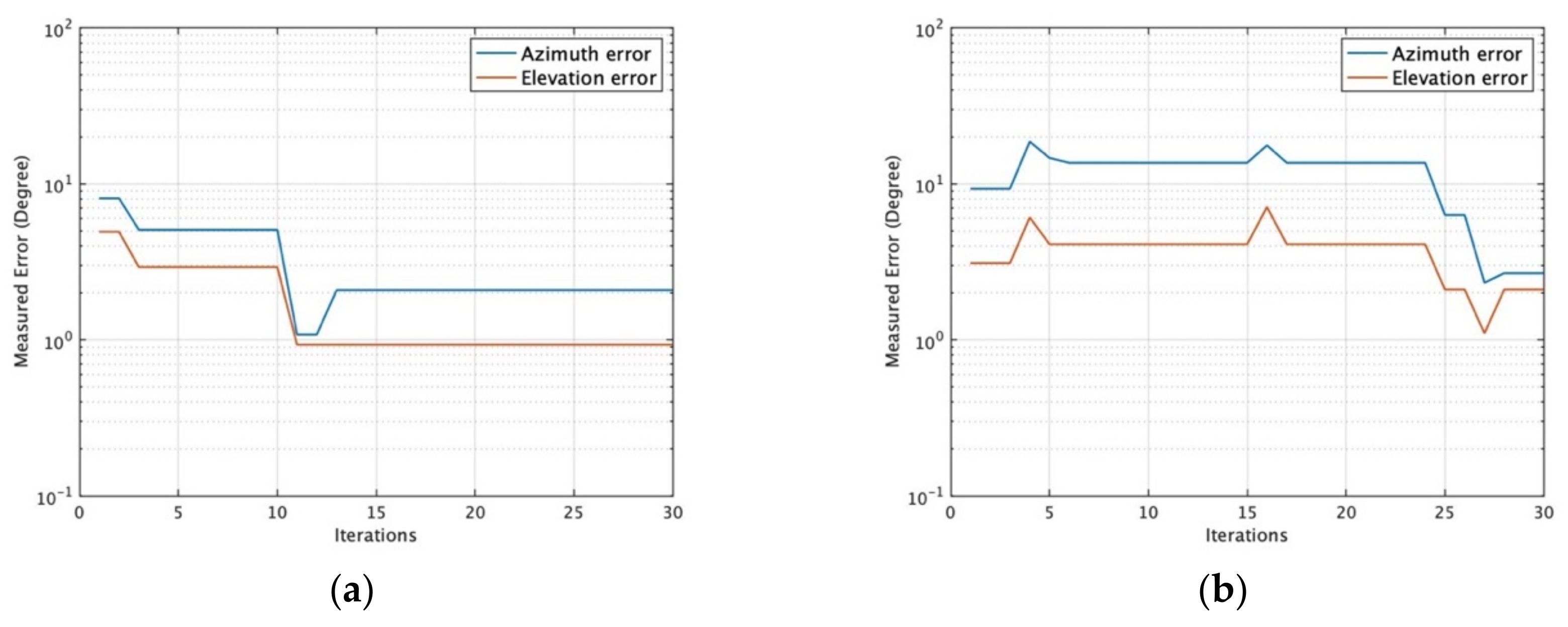
6.1. System Convergence
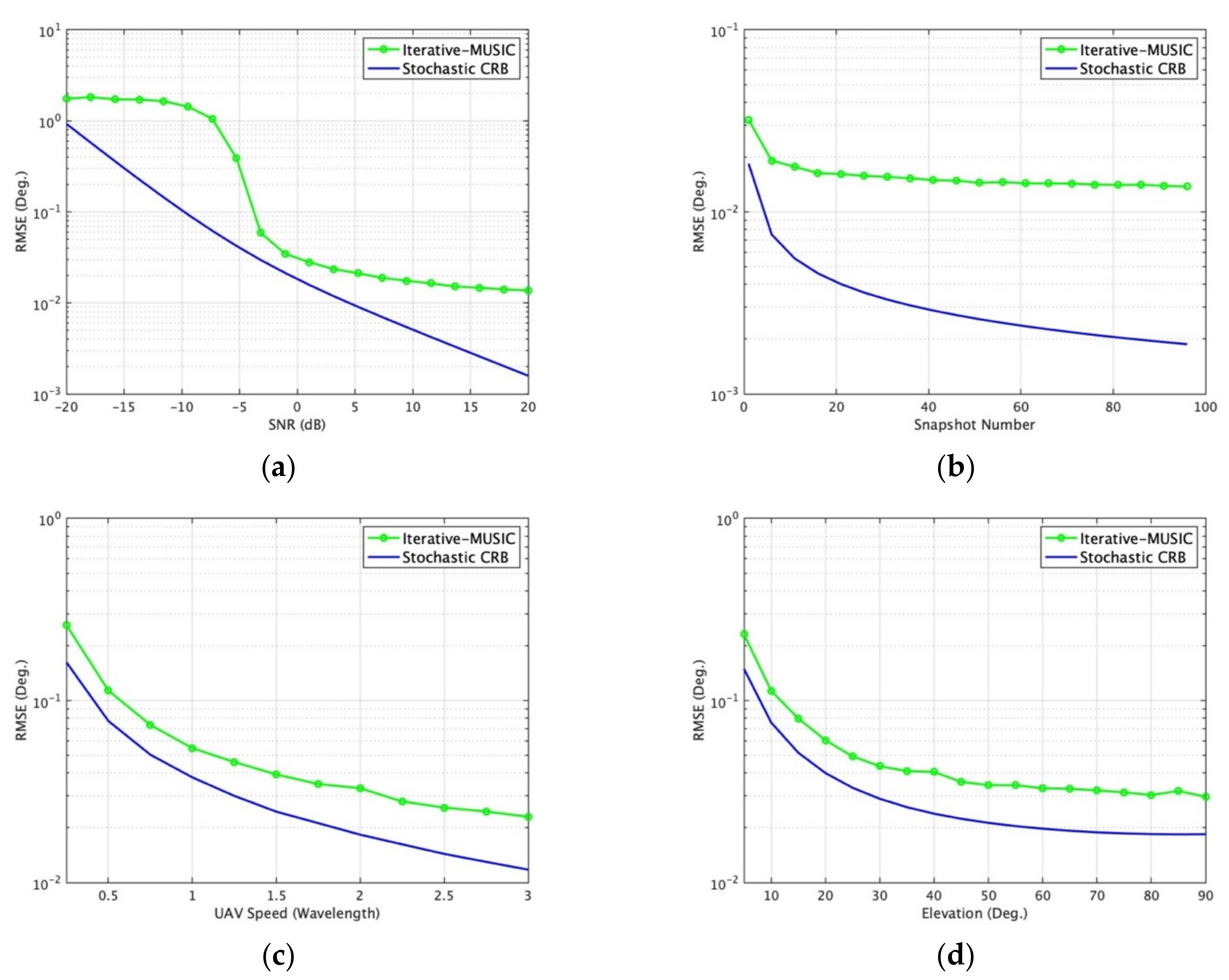
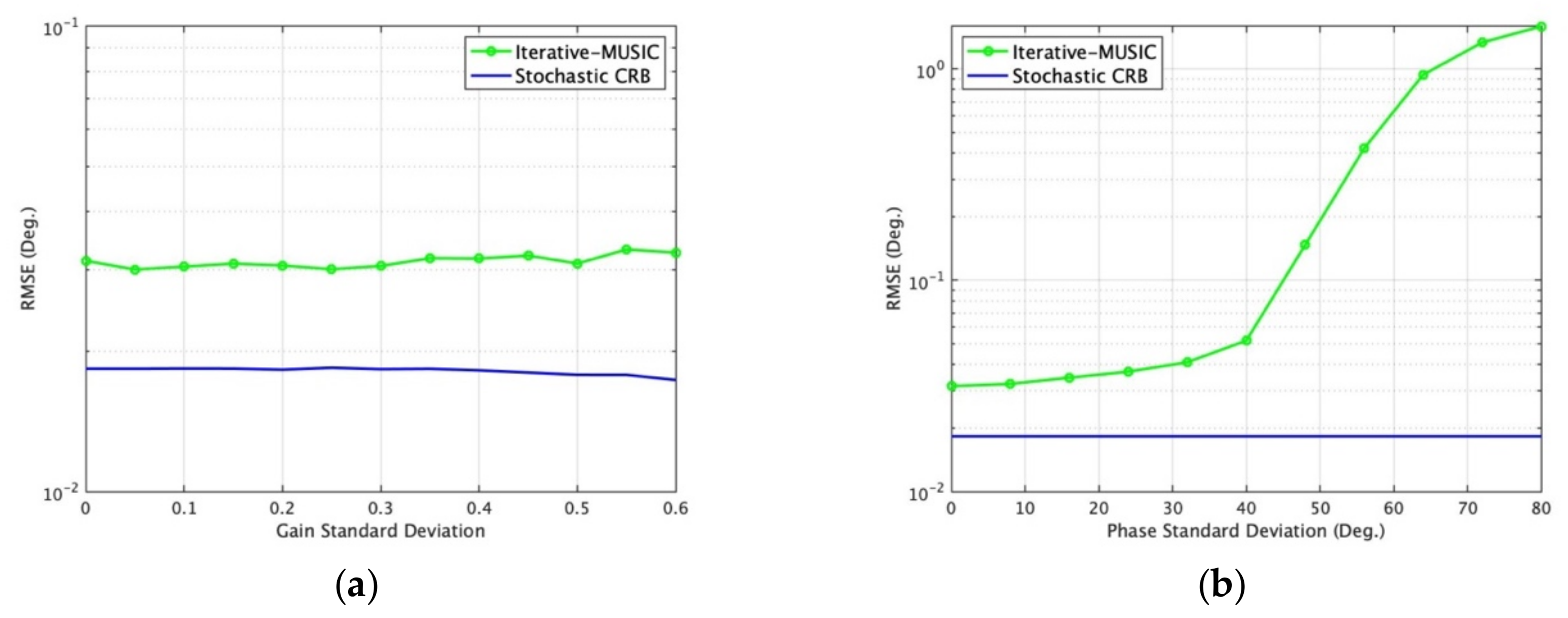
6.2. DOA Estimation Performance
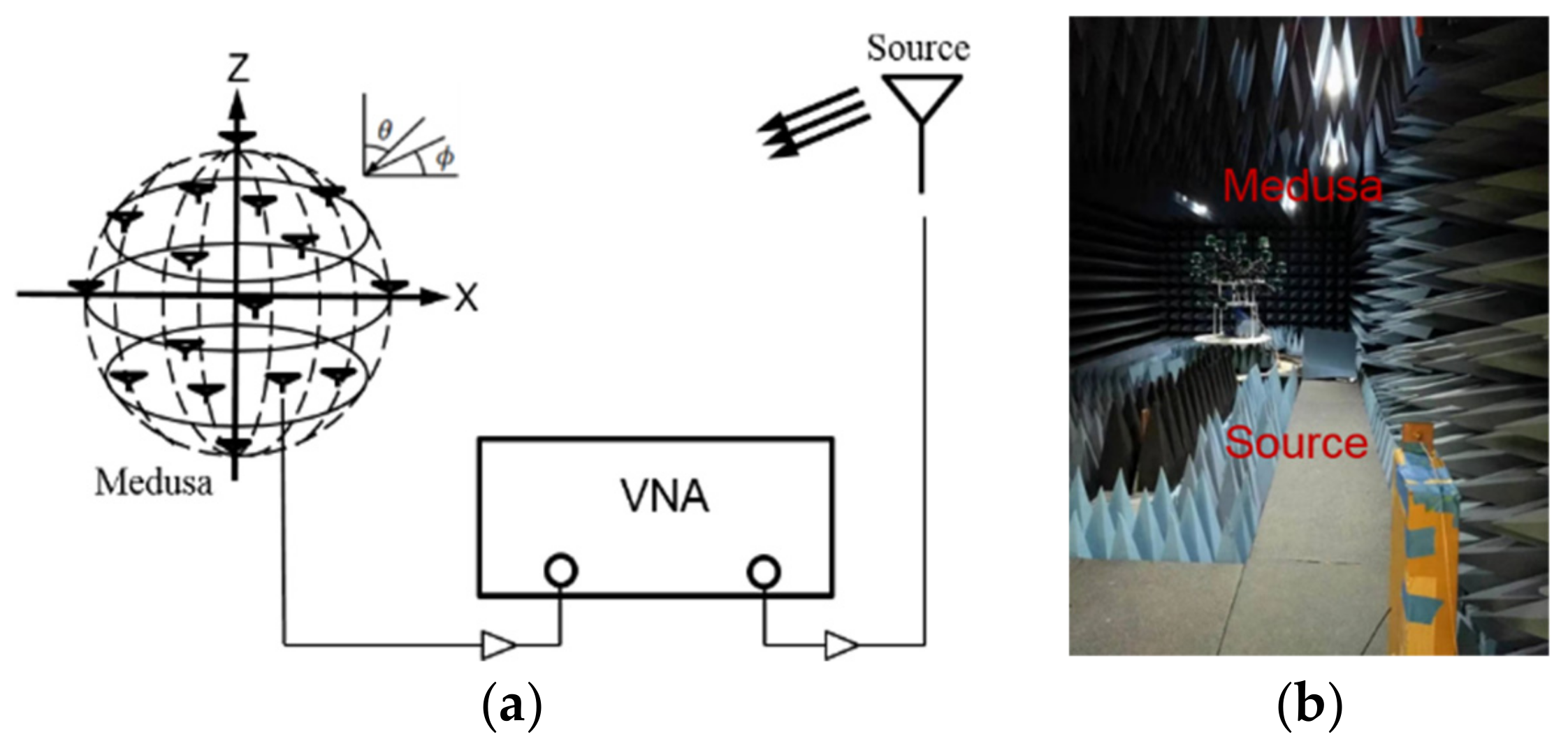
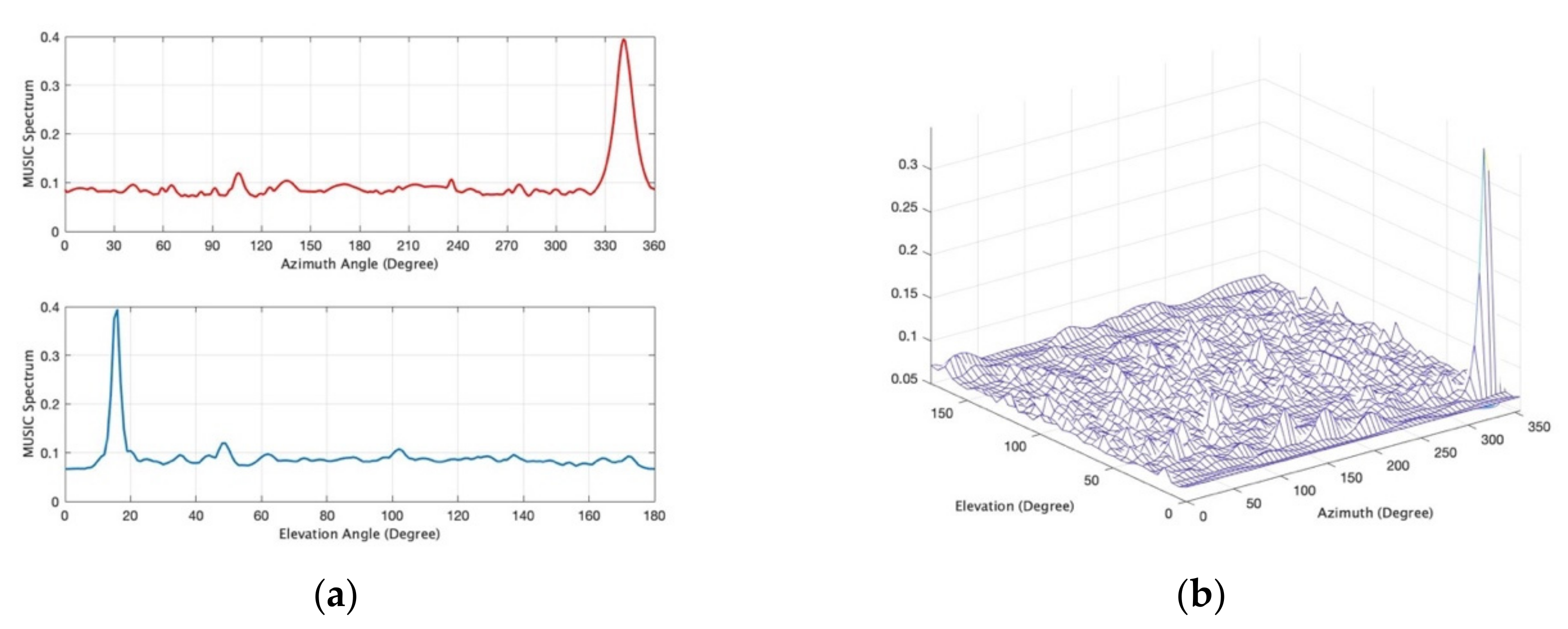
6.3. Measurement
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Bartlett, M.S. Smoothing periodograms from time series with continuous spectra. Nature 1948, 161, 686–687. [Google Scholar] [CrossRef]
- Bartlett, M.S. Periodogram analysis and continuous spectra. Biometrika 1950, 37, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Burg, J.P. Maximum Entropy Spectral Analysis. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1975. [Google Scholar]
- Gavish, M.; Weiss, A.J. Performance analysis of the VIA ESPRIT algorithm. IEE Proc. F-Radar Signal Process. 1993, 140, 123–128. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Dongarsane, C.R.; Jdhav, A.N. Simulation study on DOA estimation using MUSIC algorithm. Int. J. Technol. Eng. Syst. 2011, 2, 54–57. [Google Scholar]
- Tang, H. DOA Estimation Based on MUSIC Algorithm. Master’s Thesis, Linnaeus University, Kalmar, Sweden, May 2015. [Google Scholar]
- Oumar, O.A.; Siyau, M.F.; Sattar, T.P. Comparison between MUSIC and ESPRIT direction of arrival estimation algorithms for wireless communication systems. In Proceedings of the First International Conference on Future Generation Communication Technologies, London, UK, 12–14 December 2012. [Google Scholar]
- Stoica, P.; Nehorai, A. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1783–1795. [Google Scholar] [CrossRef]
- Lee, H.B. Resolution threshold beamspace MUSIC for two closely spaced emitters. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 723–738. [Google Scholar] [CrossRef]
- Barabell, A.J. Improving the resolution performance of eigenstructure-based direction-finding algorithms. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Boston, MA, USA, 14–16 April 1983. [Google Scholar]
- Rao, B.D.; Hari, K.V. Performance of analysis of root-MUSIC. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1939–1949. [Google Scholar] [CrossRef]
- Rubsamen, M.; Gershman, A.B. Direction-of-arrival estimation for nonuniform sensor arrays: From manifold separation to Fourier domain MUSIC methods. IEEE Trans. Signal Process. 2009, 57, 588–599. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H. Antenna array signal direction of arrival estimation in digital signal processing (DSP). Procedia Comput. Sci. 2015, 55, 782–791. [Google Scholar] [CrossRef][Green Version]
- Xie, Y.; Peng, C.; Jiang, X.; Shan, O. Hardware design and implementation of DOA estimation algorithms for spherical array antennas. In Proceedings of the 2014 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Guilin, China, 5–8 August 2014. [Google Scholar]
- Kim, M.; Ichige, K.; Arai, H. Implementation of FPGA based fast DOA estimator using unitary MUSIC algorithm. In Proceedings of the 2003 IEEE 58th Vehicular Technology Conference, Orlando, FL, USA, 6–9 October 2003. [Google Scholar]
- Abouda, A.A.; El-Sallabi, H.M.; Haggman, S.G. Impact of antenna array geometry on MIMO channel eigenvalues. In Proceedings of the 2005 IEEE 16th International Symposium on Personal, Indoor and Mobile Radio Communications, Berlin, Germany, 11–14 September 2005. [Google Scholar]
- Vu, D.; Renaux, R.B.; Marcos, S. Performance Analysis of 2D and 3D Antenna Arrays for Source Localization. In Proceedings of the 18th European Signal Processing Conference, Aalborg, Denmark, 23–27 August 2010. [Google Scholar]
- Hotta, H.; Teshima, M.; Amano, T. Estimation of radio propagation parameters using antennas arrayed 3-dimensional space. TEICE Tech. Rep. 2005, 105, 23–28. [Google Scholar]
- Godara, L.C.; Cantoni, A. Uniqueness and linear independence of steering vectors in array space. J. Acoust. Soc. Am. 1981, 70, 467–475. [Google Scholar] [CrossRef]
- Gazzah, H.; Karim, A.M. Optimum ambiguity-free directional and omnidirectional planar antenna arrays for DOA estimation. IEEE Trans. Signal Process. 2009, 57, 3942–3953. [Google Scholar] [CrossRef]
- Xia, Z.; Huff, G.H.; Chamberland, J.F.; Pfister, H.; Bhattacharya, R. Direction of arrival estimation using canonical and crystallographic volumetric element configurations. In Proceedings of the 2012 6th European Conference on Antennas and Propagation (EUCAP), Prague, Czech Republic, 26–30 March 201.
- Kiani, S.; Pezeshk, A.M. A Comparative Study of Several Array Geometries for 2D DOA Estimation. Procedia Comput. Sci. 2015, 58, 18–25. [Google Scholar] [CrossRef]
- Moriya, H. Cuboid array: A novel 3-d array configuration for high resolution 2-D DOA estimation. In Proceedings of the IEEE Workshop on Signal Processing Systems, Taipei City, Taiwan, 16–18 October 2013. [Google Scholar]
- Moriya, H. High-resolution 2-D DOA estimation by 3-D array configuration based on CRLB formulation. In Proceedings of the 2012 IEEE 11th International Conference on Signal Processing, Beijing, China, 21–25 October 2012. [Google Scholar]
- Poormohammad, S.; Farzaneh, F. Precision of direction of arrival (DOA) estimation using novel three-dimensional array geometries. Int. J. Electron. Commun. 2017, 75, 34–45. [Google Scholar] [CrossRef]
- Asgari, S. Theoretical and experimental study of DOA estimation using AML algorithm for an isotropic and non-isotropic 3D array. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 26–27 August 2007. [Google Scholar]
- Zhang, R.; Wang, S.; Lu, X.; Duan, W.; Cai, L. Two-dimensional DoA estimation for multipath propagation characterization using the array response of PN-sequences. IEEE Trans. Wirel. Commun. 2016, 15, 341–356. [Google Scholar] [CrossRef]
- Wan, L.; Liu, L.; Han, G.; Rodrigues, J.J. A low energy consumption DOA estimation approach for conformal array in ultra-wideband. Future Internet 2013, 5, 611–630. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, F.C. Azimuth and elevation estimation with rotating long-baseline interferometers. IEEE Trans. Signal Process. 2015, 63, 2405–2419. [Google Scholar] [CrossRef]
- Liu, Z. Direction-of-arrival estimation with time-varying arrays via Bayesian multitask learning. IEEE Trans. Veh. Technol. 2014, 63, 2405–2419. [Google Scholar] [CrossRef]
- Dvorkind, T.G.; Greenberg, E. DOA estimation and signal separation using antenna with time varying response. In Proceedings of the 2014 22nd European Signal Processing Conference (EUSIPCO), Lisbon, Portugal, 1–5 September 2014. [Google Scholar]
- Naaz, A.; Rao, R. DOA estimation-a comparative analysis. Int. J. Comp. Commun. 2014, 3, 141–144. [Google Scholar] [CrossRef]
- Demissie, B.; Oispuu, M.; Ruthotto, E. Localization of multiple sources with a moving array using subspace data fusion. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008. [Google Scholar]
- Kendra, J.R. Motion-extended array synthesis-part I: Theory and method. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2028–2044. [Google Scholar] [CrossRef]
- Corner, J.J.; Lamont, G.B. Parallel simulation of UAV swarm scenarios. In Proceedings of the 2004 Winter Simulation Conference, Washington, DC, USA, 5–8 December 2004. [Google Scholar]
- Saad, E.; Vian, J.; Clark, G.J.; Bieniawski, S. Vehicle swarm rapid prototyping testbed. In Proceedings of the IAAA Infotech at Aerospace Conference, Seattle, WA, DC, USA, 6–9 April 2009. [Google Scholar]
- Petko, J.S.; Werner, D.H. Positional tolerance analysis and error correction of micro-UAV swarm-based antenna arrays. In Proceedings of the 2009 IEEE Antennas and Propagation Society International Symposium, Charleston, SC, USA, 1–5 June 2009. [Google Scholar]
- Almeida, M.; Hildmann, H.; Solmaz, G. Distributed UAV-swarm-based real-time geomatic data collection under dynamically changing resolution requirements. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, W6, 5–12. [Google Scholar] [CrossRef]
- Namin, F.; Petko, J.S.; Werner, D.H. Design of robust aperiodic antenna array formations for micro-UAV swarms. In Proceedings of the 2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, CA, 11–17 July 2010. [Google Scholar]
- Namin, F.; Petko, J.S.; Werner, D.H. Analysis and design optimization of robust aperiodic micro-UAV swarm-based antenna arrays. IEEE Trans. Antennas Propag. 2012, 60, 2295–2308. [Google Scholar] [CrossRef]
- Goodman, N.R. Statistical analysis based on a certain multivariate complex distribution (an itroduction). Ann. Math. Stat. 1963, 34, 152–177. [Google Scholar] [CrossRef]
- Chen, Z.; Chamberland, J.F.; Huff, G.H. Impact of UAV swarm density and heterogeneity on synthetic aperture DoA convergence. In Proceedings of the IEEE USNC-URSI Radio Science Meeting (Joint with AP-S Symposium), San Diego, CA, USA, 9–14 July 2017. [Google Scholar]
- Friedlander, B.; Weiss, A.J. Direction finding in the presence of mutual coupling. IEEE Trans. Antennas Propag. 1991, 39, 273–284. [Google Scholar] [CrossRef]
- Hung, H.; Kaveh, M. On the statistical sufficiency of the coherently averaged covariance matrix for the estimation of the parameters of wide-band sources. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Dallas, TX, USA, 6–9 April 1987. [Google Scholar]
- Stoica, P.; Nehorai, A. MODE, maximum likelihood, and Cramer-Rao bound: Conditional and unconditional results. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Albuquerque, NM, USA, 3–6 April 1990. [Google Scholar]
- Zeira, A.; Friedlander, B. Direction finding with time-varying arrays. IEEE Trans. Signal Process. 1995, 43, 927–937. [Google Scholar] [CrossRef]
- Friedlander, B.; Weiss, A.J. Eigenstructure-based algorithms for direction finding with time-varying arrays. IEEE Trans. Aerosp. Electron. Syst. 1996, 39, 689–701. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. Performance study of conditional and unconditional direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 783–1795. [Google Scholar] [CrossRef]

| Algorithm | Primary Computations |
|---|---|
| Spectral MUSIC | |
| Iterative-MUSIC | for each iteration |
| Array Interpolation |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Yeh, S.; Chamberland, J.-F.; Huff, G.H. A Sensor-Driven Analysis of Distributed Direction Finding Systems Based on UAV Swarms. Sensors 2019, 19, 2659. https://doi.org/10.3390/s19122659
Chen Z, Yeh S, Chamberland J-F, Huff GH. A Sensor-Driven Analysis of Distributed Direction Finding Systems Based on UAV Swarms. Sensors. 2019; 19(12):2659. https://doi.org/10.3390/s19122659
Chicago/Turabian StyleChen, Zhong, Shihyuan Yeh, Jean-Francois Chamberland, and Gregory H. Huff. 2019. "A Sensor-Driven Analysis of Distributed Direction Finding Systems Based on UAV Swarms" Sensors 19, no. 12: 2659. https://doi.org/10.3390/s19122659
APA StyleChen, Z., Yeh, S., Chamberland, J.-F., & Huff, G. H. (2019). A Sensor-Driven Analysis of Distributed Direction Finding Systems Based on UAV Swarms. Sensors, 19(12), 2659. https://doi.org/10.3390/s19122659






