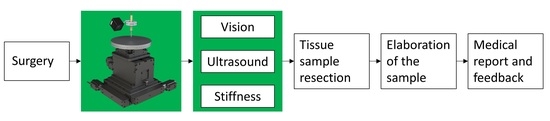
A Mechatronic Platform for Computer Aided Detection of Nodules in Anatomopathological Analyses via Stiffness and Ultrasound Measurements
Abstract
1. Introduction
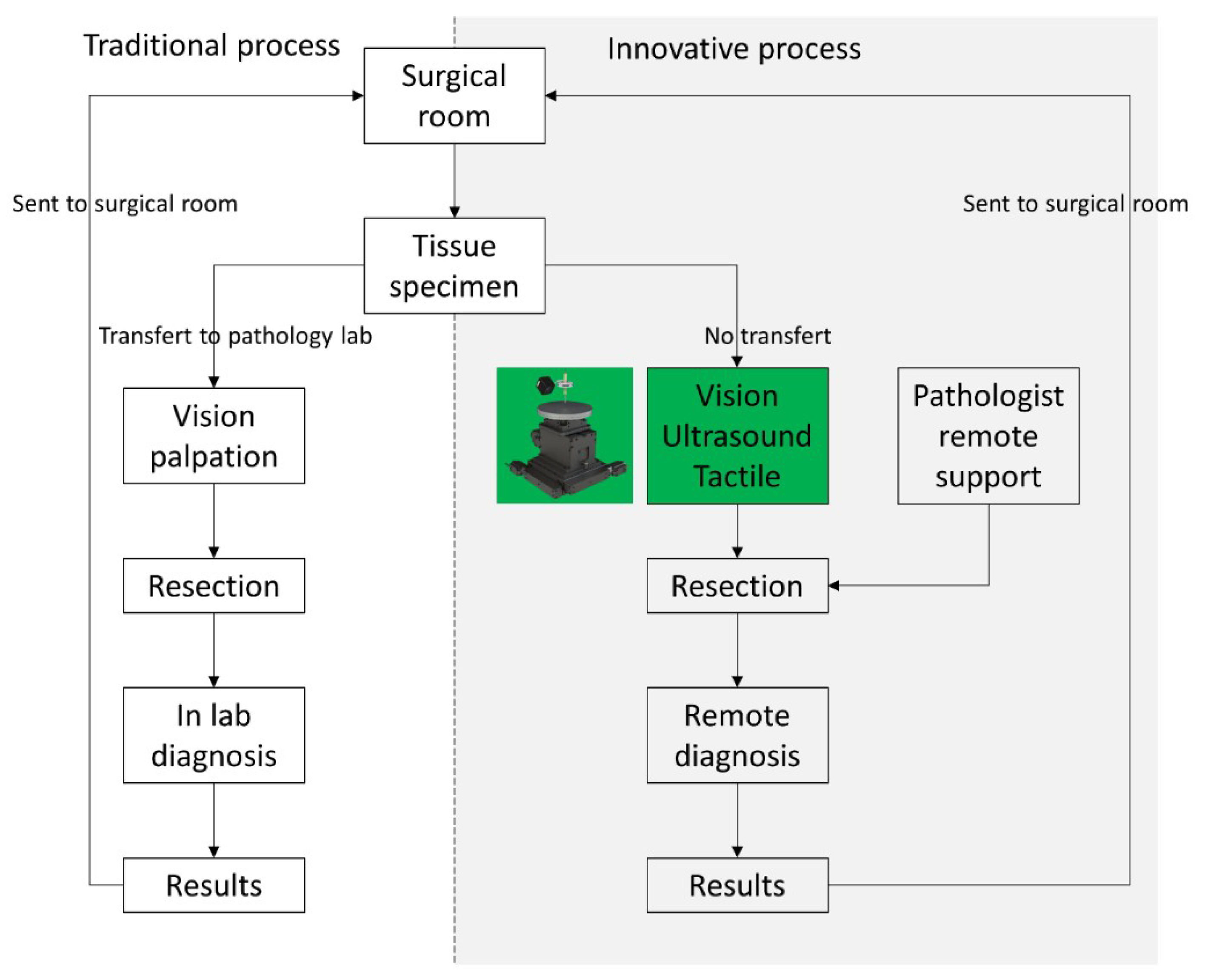
2. Materials and Methods
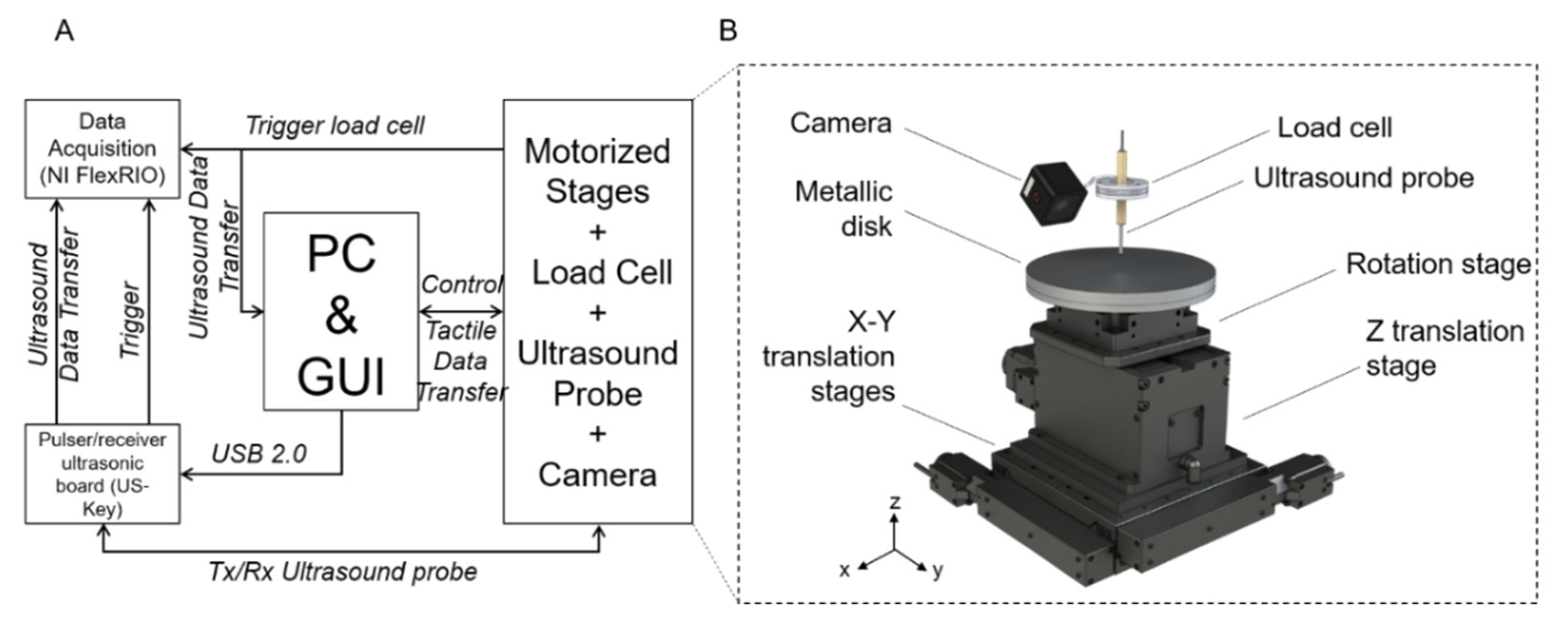
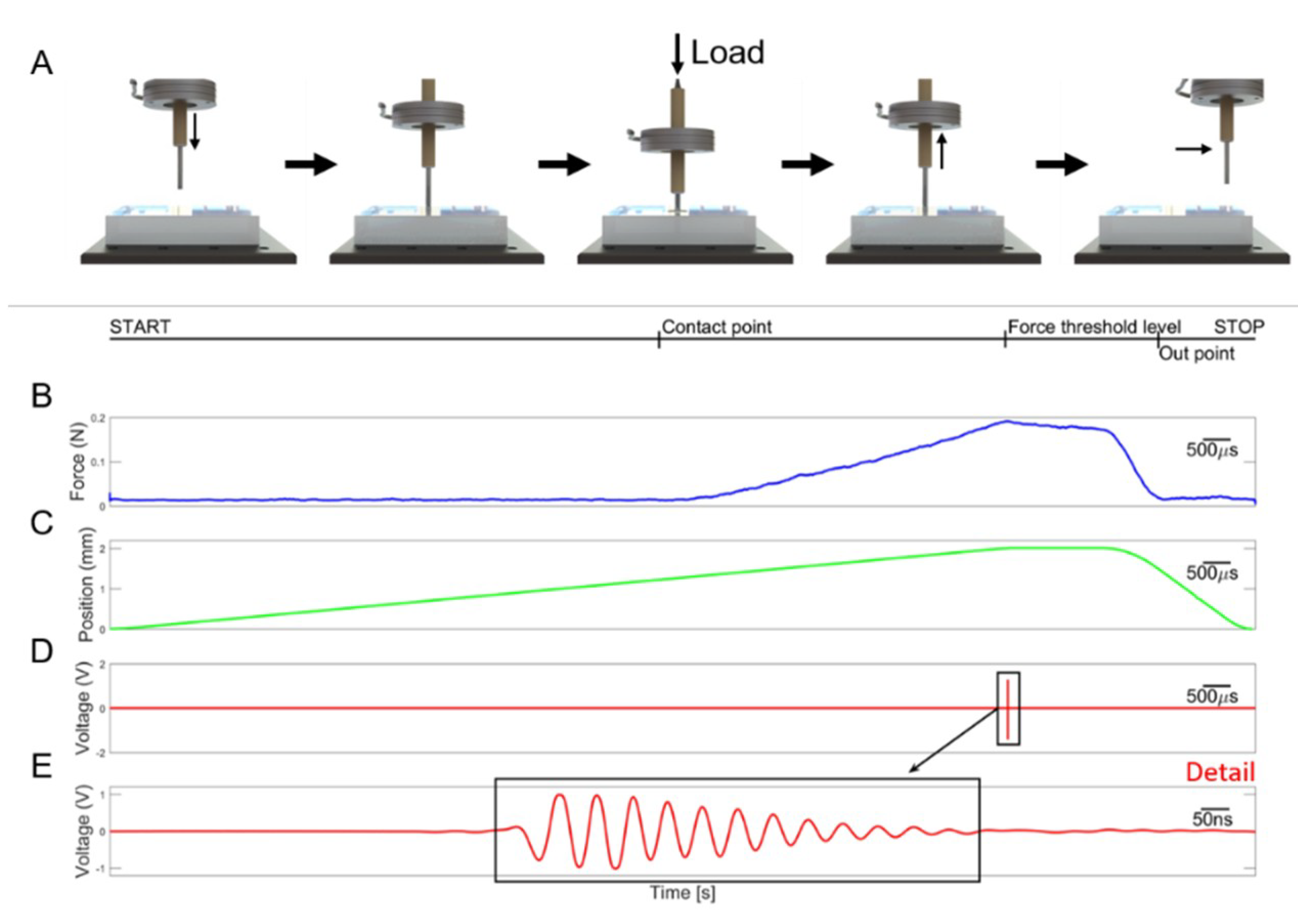
2.1. Platform Design
- (i)
- Three motorized translational stages and one rotational stage allowing to move the sample. A commercial stage (8MTF-102LS05, STANDA, Vilnius, Lithuania) with 10 cm of travel range and a resolution of 2.5 µm was used for the X and Y axes, while another translational stage (8MVT120-25-4247, STANDA, Vilnius, Lithuania) was used to indent the sample along the Z axis, having a travel range of 2.5 cm and a resolution of 5 µm. Additionally, a fourth stage was mounted on the mechatronic platform (8MR190-2-28, STANDA, Vilnius, Lithuania) in order to enable the rotation of the sample. Such stage had 360° rotation range with 0.01° resolution.
- (ii)
- An ultrasound probe (Sonomed, mod. 2014059, Warsaw, Poland) with 16 MHz central frequency and a fractional bandwidth equal to 0.25 at −6 dB used in pulse-echo mode. The needle-type probe, 3 mm in diameter, was selected for directly contacting and indenting the sample. A 30 Vpp pulsed excitation was delivered to the probe via a transmitter (US-Key, Lecoeur-Electronique, Chuelles, France) connected to a PC via USB2. The experimental setup was completed with the ultrasound data acquisition device, NI FlexRIO (National Instruments Corp., Austin, TX, USA), for acquisitions at high frequency (1.6 GHz).
- (iii)
- A load cell (Nano 43, ATI Industrial Automation, Apex, NC, USA) to collect interaction forces, up to 18 N with 0.004 N resolution along normal axis, arising at the interface between the ultrasound probe and the sample, also used in the control loop of the translation stages in order to operate force-controlled indentations. The developed software used this force data to calculate the stiffness and to trigger the high frequency US data collection at the threshold point of contact (0.2 N).
- (iv)
- A waterproof HD-camera (Hero5 Session, GoPro, San Mateo, CA, USA) with 10 MP and 4 K resolution, integrated to perform the sample shape recognition and to create a matrix of points to be indented.
- (v)
- A stainless-steel disk fixed on the top of the motorized stages for the positioning of the sample, but also to permit the reflection of the ultrasound signal back to the probe. The disk had a diameter of 16 cm and a thickness of 1 cm.
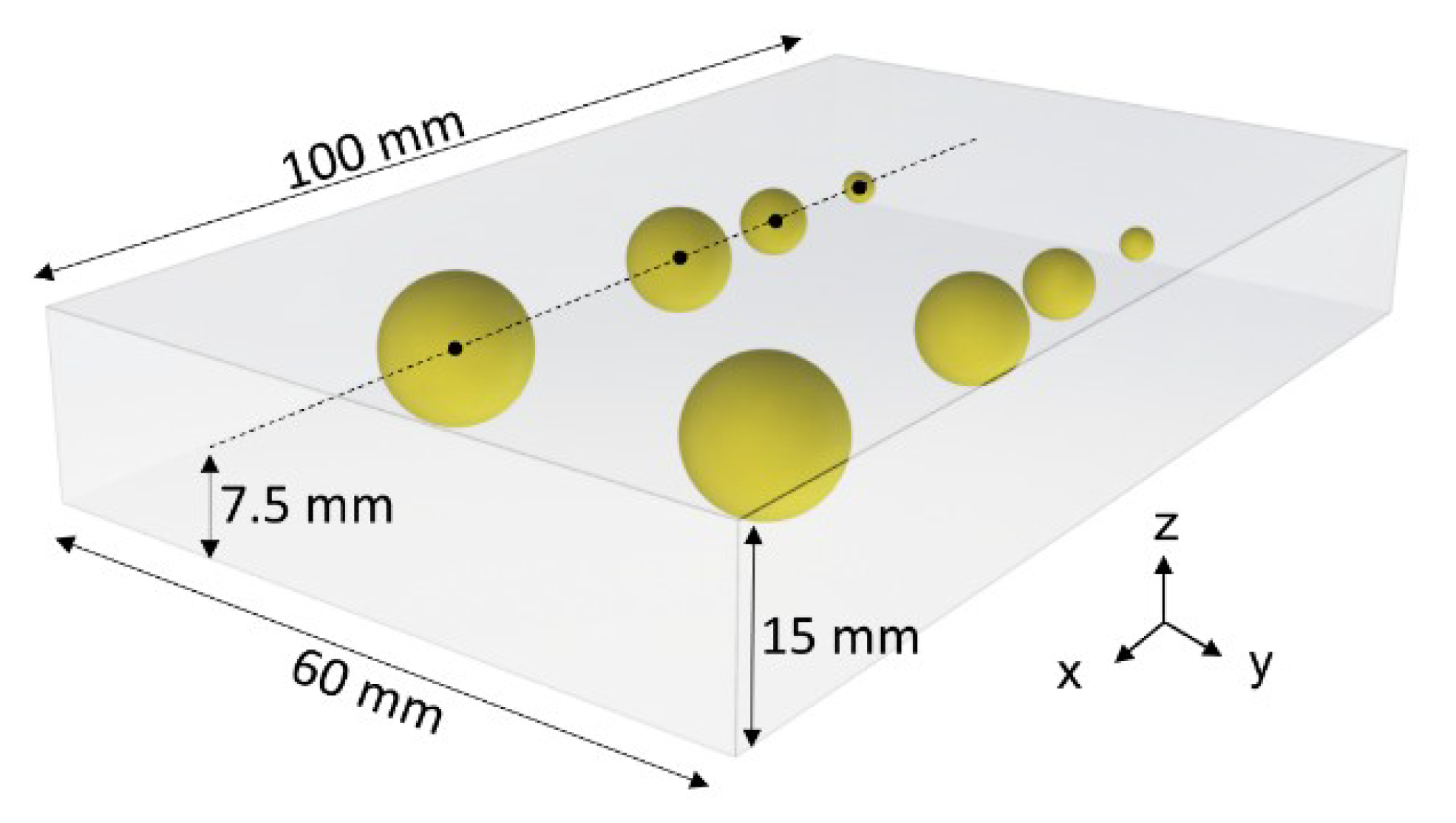
2.2. Phantom of Healthy Tissue and Inclusions
2.3. Experimental Protocol
- (i)
- Visual analysis;
- (ii)
- Stiffness and ultrasound analysis.
2.4. Data Analysis
3. Results
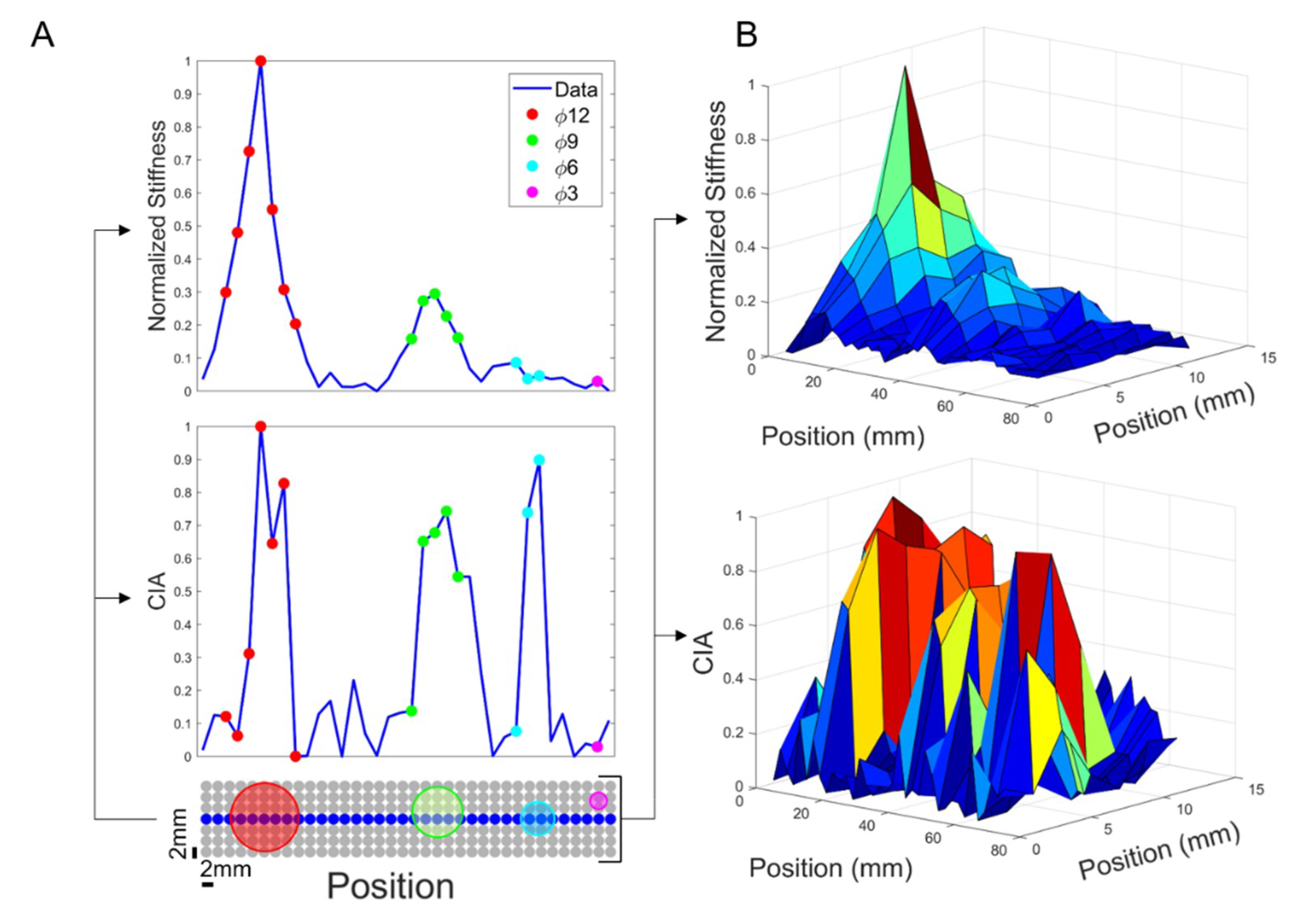
3.1. Results from Stiffness Measurements
3.2. Results from Ultrasound Measurements
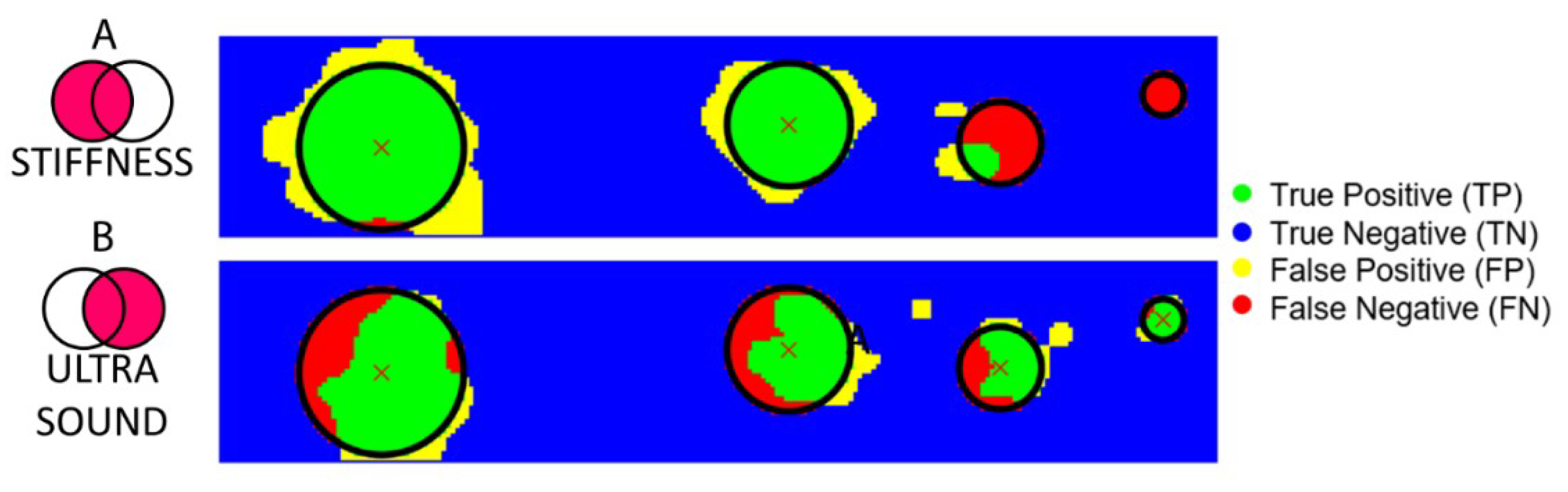
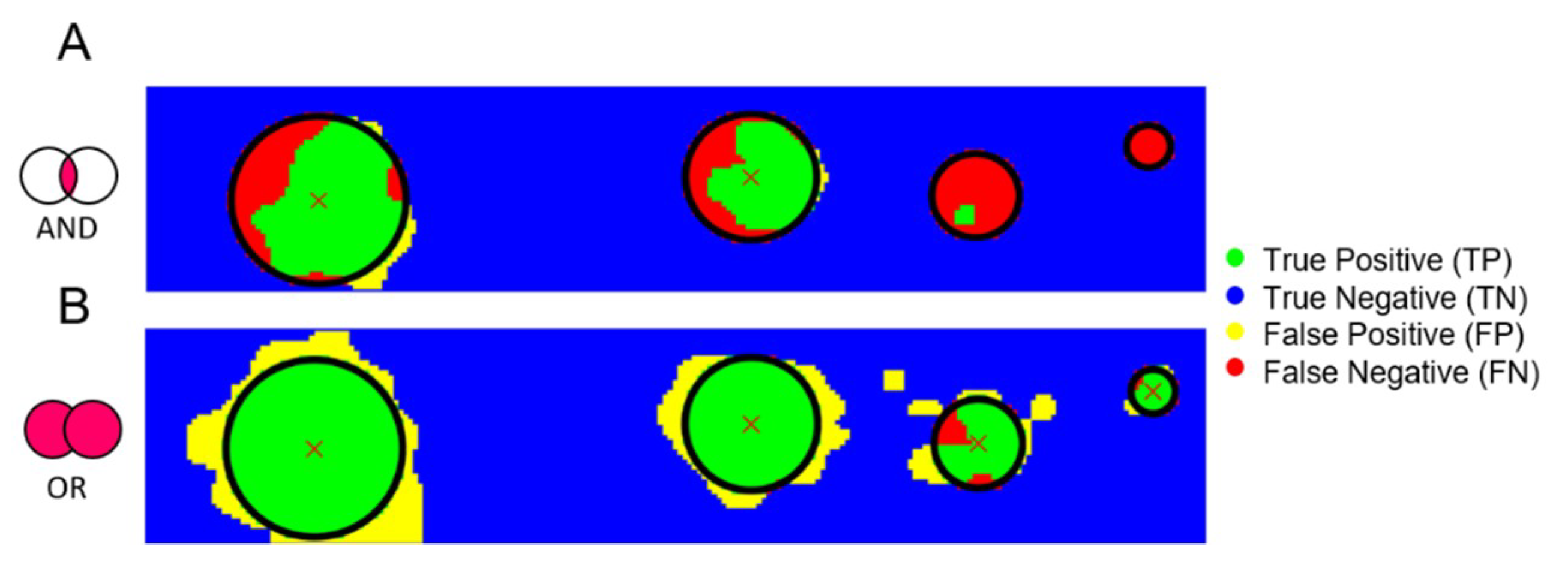
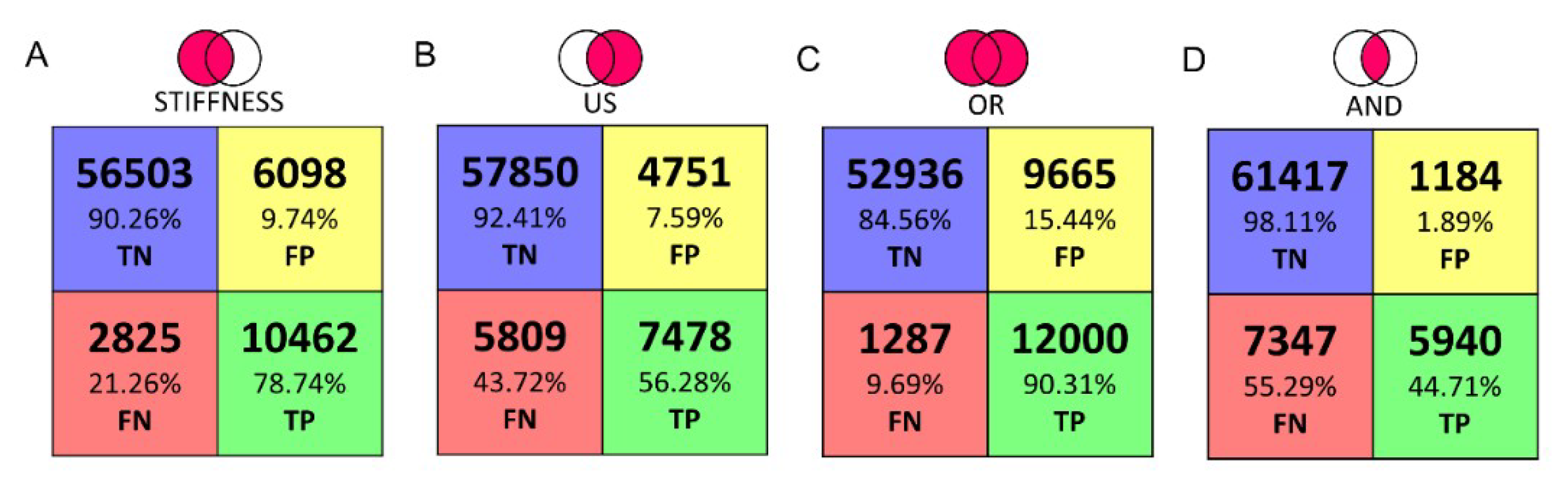
3.3. AND–OR Logics to Merge Stiffness and Ultrasound Measurements
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pierangelo, A.; Benali, A.; Antonelli, M.-R.; Novikova, T.; Validire, P.; Gayet, B.; Martino, A. De Ex-vivo characterization of human colon cancer by Mueller polarimetric imaging. Opt. Express 2011, 19, 1582. [Google Scholar] [CrossRef] [PubMed]
- Adam, R. Chemotherapy and surgery: New perspectives on the treatment of unresectable liver metastases. Ann. Oncol. 2003, 14, ii13–ii16. [Google Scholar] [CrossRef] [PubMed]
- Nagai, T.; Niikura, H.; Okamoto, S.; Nakabayashi, K.; Matoda, M.; Utsunomiya, H.; Nagase, S.; Watanabe, M.; Takeshima, N.; Yaegashi, N. A new diagnostic method for rapid detection of lymph node metastases using a one-step nucleic acid amplification (OSNA) assay in endometrial cancer. Ann. Surg. Oncol. 2015, 22, 980–986. [Google Scholar] [CrossRef] [PubMed]
- Candefjord, S.; Ramser, K.; Lindahl, O.A. Technologies for localization and diagnosis of prostate cancer. J. Med. Eng. Technol. 2009, 33, 585–603. [Google Scholar] [CrossRef] [PubMed]
- Krouskop, T.A.; Wheeler, T.M.; Kallel, F.; Garra, B.S.; Hall, T. Elastic moduli of breast and prostate tissues under compression. Ultrason. Imaging 1998, 20, 260–274. [Google Scholar] [CrossRef] [PubMed]
- Samani, A.; Zubovits, J.; Plewes, D. Elastic moduli of normal and pathological human breast tissues: An inversion-technique-based investigation of 169 samples. Phys. Med. Biol. 2007, 52, 1565. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Nigwekar, P.; Castaneda, B.; Hoyt, K.; Joseph, J.V.; di Sant’Agnese, A.; Messing, E.M.; Strang, J.G.; Rubens, D.J.; Parker, K.J. Quantitative characterization of viscoelastic properties of human prostate correlated with histology. Ultrasound Med. Biol. 2008, 34, 1033–1042. [Google Scholar] [CrossRef]
- Raveh Tilleman, T.; Tilleman, M.M.; Neumann, H.A.M. The elastic properties of cancerous skin: Poisson’s ratio and Young’s modulus. Isr. Med. J. 2004, 6, 753–755. [Google Scholar]
- Winstone, B.; Melhuish, C.; Pipe, T.; Callaway, M.; Dogramadzi, S. Toward Bio-Inspired Tactile Sensing Capsule Endoscopy for Detection of Submucosal Tumors. IEEE Sens. J. 2017, 17, 848–857. [Google Scholar] [CrossRef]
- Carter, F.J.; Frank, T.G.; Davies, P.J.; McLean, D.; Cuschieri, A. Measurements and modelling of the compliance of human and porcine organs. Med. Image Anal. 2001, 5, 231–236. [Google Scholar] [CrossRef]
- Konstantinova, J.; Li, M.; Mehra, G.; Dasgupta, P.; Althoefer, K.; Nanayakkara, T. Behavioral characteristics of manual palpation to localize hard nodules in soft tissues. IEEE Trans. Biomed. Eng. 2014, 61, 1651–1659. [Google Scholar] [CrossRef] [PubMed]
- Wells, P.N.T.; Liang, H.H.-D. Medical ultrasound: Imaging of soft tissue strain and elasticity. J. R. Soc. Interface 2011, 8, 1521–1549. [Google Scholar] [CrossRef] [PubMed]
- Carson, W.C.; Gerling, G.J.; Krupski, T.L.; Association Kowalik, C.G.; Harper, J.C.; Moskaluk, C.A. Material characterization of ex vivo prostate tissue via spherical indentation in the clinic. Med. Eng. Phys. 2011, 33, 302–309. [Google Scholar] [CrossRef] [PubMed]
- Gwilliam, J.C.; Yoshioka, T.; Okamura, A.M.; Hsiao, S.S. Neural coding of passive lump detection in compliant artificial tissue. J. Neurophysiol. 2014, 112, 1131–1141. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yau, J.M.; Kim, S.S.; Thakur, P.H.; Bensmaia, S.J. Feeling form: The neural basis of haptic shape perception. J. Neurophysiol. 2016, 115, 631–642. [Google Scholar] [CrossRef] [PubMed]
- Nam, K.; Rosado-Mendez, I.M.; Wirtzfeld, L.A.; Pawlicki, A.D.; Kumar, V.; Madsen, E.L.; Ghoshal, G.; Lavarello, R.J.; Oelze, M.L.; Bigelow, T.A. Ultrasonic attenuation and backscatter coefficient estimates of rodent-tumor-mimicking structures: Comparison of results among clinical scanners. Ultrason. Imaging 2011, 33, 233–250. [Google Scholar] [CrossRef]
- Hoch, G.; Croise-Laurent, V.; Germain, A.; Brunaud, L.; Bresler, L.; Ayav, A. Is intraoperative ultrasound still useful for the detection of colorectal cancer liver metastases? Int. Hepato Pancreato Biliary Assoc. 2015, 17, 514–519. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hata, S.; Imamura, H.; Aoki, T.; Hashimoto, T.; Akahane, M.; Hasegawa, K.; Bekku, Y.; Sugawara, Y.; Makuuchi, M.; Kokudo, N. Value of visual inspection, bimanual palpation, and intraoperative ultrasonography during hepatic resection for liver metastases of colorectal carcinoma. World J. Surg. 2011, 35, 2779–2787. [Google Scholar] [CrossRef]
- Ferrero, A.; Langella, S.; Giuliante, F.; Viganò, L.; Vellone, M.; Zimmitti, G.; Ardito, F.; Nuzzo, G.; Capussotti, L. Intraoperative liver ultrasound still affects surgical strategy for patients with colorectal metastases in the modern era. World J. Surg. 2013, 37, 2655–2663. [Google Scholar] [CrossRef] [PubMed]
- Chou, R.; Cuevas, C.; Fu, R.; Devine, B.; Wasson, N.; Ginsburg, A.; Zakher, B.; Pappas, M.; Graham, E.; Sullivan, S.D. Imaging techniques for the diagnosis of hepatocellular carcinoma: A systematic review and meta-analysis. Ann. Intern. Med. 2015, 162, 697–711. [Google Scholar] [CrossRef] [PubMed]
- Sigrist, R.M.S.; Liau, J.; El Kaffas, A.; Chammas, M.C.; Willmann, J.K. Ultrasound elastography: Review of techniques and clinical applications. Theranostics 2017, 7, 1303. [Google Scholar] [CrossRef] [PubMed]
- Baker, A.R.; Windsor, C.G. The classification of defects from ultrasonic data using neural networks: The Hopfield method. NDT Int. 1989, 22, 97–105. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Ahn, B.M.; Kim, J.; Ian, L.; Rha, K.H.; Kim, H.J. Mechanical property characterization of prostate cancer using a minimally motorized indenter in an ex vivo indentation experiment. Urology 2010, 76, 1007–1011. [Google Scholar] [CrossRef] [PubMed]
- Barr, R.G.; Ferraioli, G.; Palmeri, M.L.; Goodman, Z.D.; Garcia-Tsao, G.; Rubin, J.; Garra, B.; Myers, R.P.; Wilson, S.R.; Rubens, D. Elastography assessment of liver fibrosis: Society of radiologists in ultrasound consensus conference statement. Radiology 2015, 276, 845–861. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Belmont, B.; Greve, J.M.; Manders, A.B.; Downey, B.C.; Zhang, X.; Xu, Z.; Guo, D.; Shih, A. Polyvinyl chloride as a multimodal tissue-mimicking material with tuned mechanical and medical imaging properties. Med. Phys. 2016, 43, 5577–5592. [Google Scholar] [CrossRef]
- Culjat, M.O.; Goldenberg, D.; Tewari, P.; Singh, R.S. A review of tissue substitutes for ultrasound imaging. Ultrasound Med. Biol. 2010, 36, 861–873. [Google Scholar] [CrossRef] [PubMed]
- Cafarelli, A.; Verbeni, A.; Poliziani, A.; Dario, P.; Menciassi, A.; Ricotti, L. Tuning acoustic and mechanical properties of materials for ultrasound phantoms and smart substrates for cell cultures. Acta Biomater. 2017, 49, 368–378. [Google Scholar] [CrossRef] [PubMed]
- Cao, R.; Huang, Z.; Varghese, T.; Nabi, G. Tissue mimicking materials for the detection of prostate cancer using shear wave elastography: A validation study. Med. Phys. 2013, 40, 022903. [Google Scholar] [CrossRef] [PubMed]
- Manickam, K.; Machireddy, R.R.; Seshadri, S. Study of ultrasound stiffness imaging methods using tissue mimicking phantoms. Ultrasonics 2014, 54, 621–631. [Google Scholar] [CrossRef]
- Bamber, J.C.; Hill, C.R. Acoustic properties of normal and cancerous human liver—I. Dependence on pathological condition. Ultrasound Med. Biol. 1981, 7, 121–133. [Google Scholar] [CrossRef]
- Azhari, H. Basics of Biomedical Ultrasound for Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Bulletti, A.; Giannelli, P.; Calzolai, M.; Capineri, L. An integrated acousto/ultrasonic structural health monitoring system for composite pressure vessels. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 864–873. [Google Scholar] [CrossRef] [PubMed]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Sorgini, F.; Massari, L.; D’Abbraccio, J.; Palermo, E.; Menciassi, A.; Petrovic, P.; Mazzoni, A.; Carrozza, M.; Newell, F.; Oddo, C. Neuromorphic Vibrotactile Stimulation of Fingertips for Encoding Object Stiffness in Telepresence Sensory Substitution and Augmentation Applications. Sensors 2018, 18, 261. [Google Scholar] [CrossRef] [PubMed]
- Massari, L.; D’Abbraccio, J.; Baldini, L.; Sorgini, F.; Farulla, G.A.; Petrovic, P.; Palermo, E.; Oddo, C.M. Neuromorphic haptic glove and platform with gestural control for tactile sensory feedback in medical telepresence applications. In Proceedings of the 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rome, Italy, 11–13 June 2018; pp. 1–6. [Google Scholar]
- Sorgini, F.; Mazzoni, A.; Massari, L.; Caliò, R.; Galassi, C.; Kukreja, S.; Sinibaldi, E.; Carrozza, M.; Oddo, C. Encapsulation of Piezoelectric Transducers for Sensory Augmentation and Substitution with Wearable Haptic Devices. Micromachines 2017, 8, 270. [Google Scholar] [CrossRef] [PubMed]
- D’Abbraccio, J.; Massari, L.; Prasanna, S.; Baldini, L.; Sorgini, F.; Airò Farulla, G.; Bulletti, A.; Mazzoni, M.; Capineri, L.; Menciassi, A. Haptic Glove and Platform with Gestural Control For Neuromorphic Tactile Sensory Feedback In Medical Telepresence. Sensors 2019, 19, 641. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massari, L.; Bulletti, A.; Prasanna, S.; Mazzoni, M.; Frosini, F.; Vicari, E.; Pantano, M.; Staderini, F.; Ciuti, G.; Cianchi, F.; et al. A Mechatronic Platform for Computer Aided Detection of Nodules in Anatomopathological Analyses via Stiffness and Ultrasound Measurements. Sensors 2019, 19, 2512. https://doi.org/10.3390/s19112512
Massari L, Bulletti A, Prasanna S, Mazzoni M, Frosini F, Vicari E, Pantano M, Staderini F, Ciuti G, Cianchi F, et al. A Mechatronic Platform for Computer Aided Detection of Nodules in Anatomopathological Analyses via Stiffness and Ultrasound Measurements. Sensors. 2019; 19(11):2512. https://doi.org/10.3390/s19112512
Chicago/Turabian StyleMassari, Luca, Andrea Bulletti, Sahana Prasanna, Marina Mazzoni, Francesco Frosini, Elena Vicari, Marcello Pantano, Fabio Staderini, Gastone Ciuti, Fabio Cianchi, and et al. 2019. "A Mechatronic Platform for Computer Aided Detection of Nodules in Anatomopathological Analyses via Stiffness and Ultrasound Measurements" Sensors 19, no. 11: 2512. https://doi.org/10.3390/s19112512
APA StyleMassari, L., Bulletti, A., Prasanna, S., Mazzoni, M., Frosini, F., Vicari, E., Pantano, M., Staderini, F., Ciuti, G., Cianchi, F., Messerini, L., Capineri, L., Menciassi, A., & Oddo, C. M. (2019). A Mechatronic Platform for Computer Aided Detection of Nodules in Anatomopathological Analyses via Stiffness and Ultrasound Measurements. Sensors, 19(11), 2512. https://doi.org/10.3390/s19112512