1. Introduction
It is estimated that the number of Parkinson’s patients will outnumber those with Alzheimer’s disease by 2040, thus reaching pandemic proportions [
1]. Although Parkinson’s disease is currently the second most frequent neurodegenerative disorder, in 95% of the cases, it remains an idiopathic disease [
2]. Thus, there is a need for the medical and research community to understand its origin and to explore improved diagnostic methods and treatments that work better in the long term.
Parkinson’s symptomatology is diverse. Patients can experience tremor of the extremities at rest, the so-called
Resting Tremor (RT), muscle rigidity, slow motion (bradykinesia) or difficulty in carrying out precise movements (akinesia). The patients in this study were diagnosed with
benign tremulous Parkinsonism. This type of Parkinson’s is manifested by the following characteristics: (1) a noticeable RT; (2) symptoms not related to tremor have a confined incidence; (3) predominant lack of gait disorder; and (4) lack of impairments apart from tremor [
3].
Associated with this symptomatology, clinical states can be differentiated: the Non-Tremorous resting state (
NT), in which the patient does not experience tremor, and the Tremor state (
T), in which the patient suffers from tremor at rest. Among them, we can find a state called Tremor Onset (
TO), which is supposed to hold the key to understanding the transition between
NT and
T. A similar dynamical behaviour of the brain, transitioning between different states, can be found in other diseases. Such conditions are known as dynamical diseases [
4]. As a general definition, a dynamic disease causes abnormal dynamics in a physiological control system operating within a range of control parameters [
5]. Methods derived from non-linear dynamics analysis have been shown to be good at detecting key features of the different dynamical states, providing a formal understanding of how the emergence of the manifestations of dynamical diseases takes place [
4,
6].
An oral treatment, generally with dopaminergic effects, is usually the first option. Unfortunately, these patients have a high resistance to levodopa, even at doses above the tolerable levels [
3]. Furthermore, after a few years of use, the patients begin to suffer from the so-called ON-OFF effect: ON periods, in which the drug works, along with alternate OFF periods, in which despite the patient taking the drug as prescribed, it does not perform well and the patient continues suffering from the symptoms [
7]. Furthermore, the use of levodopa leads to dyskinesias (LID), causing involuntary movements that are often worse than the original PD’s symptomatology [
8,
9].
Deep Brain Stimulation (DBS) constitutes an alternative line of treatment in these cases. DBS consists of the surgical implantation of a neurostimulator. A neurostimulator is an Implantable Medical Device (IMD) made up of a pulse generator (IPG), and a set of electrodes, which provides High-Frequency Stimulation (HFS) to the target area, usually the Sub-Thalamic Nucleus (STN). Current neurostimulators work uninterruptedly after its implantation. As a consequence, several adverse effects have been reported in the literature, including paresthesia, cognitive or psychiatric dysfunction and even an increased risk of suicide [
10,
11]. Demand-driven deep brain stimulation strategies constitute an improved version of the current procedure, triggering stimulation only when necessary, which is believed to reduce the side effects [
12,
13,
14,
15]. Moreover, a closed-loop approach would extend the battery lifetime, as a result of the more efficient use of it.
The implementation of a demand-driven system requires an understanding of what features of the basal ganglia activity, the STN in the case of this study, change shortly before the symptoms appear. Understanding the tremor nature is paramount to decipher the behaviour of the STN nucleus in the different clinical states (NT, TO and T). However, this is challenging since STN-Local Field Potential (LFP) recordings in humans are generally acquired in 2–3 days after the surgical procedure, before the connection of the electrodes to the IPG, not being accessible any longer. Note that this procedure is carried out for research purposes. Otherwise, the electrodes are usually implanted during the surgery. Furthermore, we need to gather the neural activity when the patient (without medication and spontaneously) makes the transition from the NT to the T state. These two limitations make this type of recording difficult to obtain. In this work, we analyse four of them from our dataset, which fulfil these properties. The length of the four files studied ranged from 40 s–3.6 min (40 s, 2.13 min and 3.6 min). The objective is to characterise the dynamics of the different clinical states, with a particular interest in finding a fingerprint for the TO state, as this is the first step in preventing or suppressing the tremor with demand-driven DBS.
Local Field Potentials (LFPs) have been widely studied. While some researchers have explored the spectral power of the neural oscillations, usually assuming the existence of pathology when its range deviates from those present in control subjects [
16,
17], others have studied the connectivity between the neurons within the STN [
10,
18,
19]. However, the inherent dynamics and spatiotemporal profile of STN-LFPs have not been characterised for their application to a demand-driven DBS system. In the cases of dynamical diseases, algorithms from the non-linear dynamical analysis are particularly attractive to find biomarkers that differ between normal and pathological states of the disease [
20].
In this work, we apply time-series analysis methods derived from non-linear dynamics to the study of the STN activity under the different tremor states. A moving window Recurrence Network (RN) analysis is carried out to capture such rich dynamical behaviour. RNs are constructed based on the recurrences in the phase space. By applying network analysis methods, the dynamically-relevant structures of the time series data can be studied, extracting the geometrical properties of the attractor [
21]. The study of the topological structure of the RN allows us to infer the complexity of the dynamics associated with the STN-LFP time series.
Methods based on RN constitute an excellent approach to analyse the structural complexity of neural signals, as they can be applied to short and non-stationary data, since the network properties, such as global clustering coefficient, transitivity or assortativity, can still be reliably estimated. This makes RNs an ideal method for capturing the dynamical transitions in neural data. Previous works have demonstrated the applicability of this method in detecting the onset of epileptic seizures [
6,
22].
The present study aims to answer two main questions: (1) Do the dynamics of STN-LFPs have a permanent character or do they change depending on the movement state that the patient is in? (2) Would it be possible to characterise some feature in the neural signal, which can aid in predicting the onset of the tremor?
5. Moving Window -Recurrence Network Analysis
In this work, we used moving window -recurrence network analysis to compute the global measures . The time series was previously divided into two-second windows with 90% overlap. In order to get the temporal profile of global network measures, we assigned the global measure to the mid-point of each window. and m have been set on the first local minimum of the auto-mutual information and FNN method, respectively, and the recurrence rate RR was set to 0.03.
To determine whether it is possible to anticipate the beginning of a tremor episode, a moving median filter over the signals
was applied. This filtering allows one to smooth out short-term fluctuations and to highlight the real transients in the STN-LFP signal. The
and
standard deviations of the moving median filter were established to determine the statistical significance of the transients (peaks henceforth).
Figure 2 shows the results of the analysis of one of the recordings.
Clustering : We witnessed a low level of C during NT, which increased abruptly a few seconds before the onset of the TO . The peaks described an abrupt increase in the non-linearity in the system (for simplicity, we will talk about peaks instead of an increase in the non-linearity henceforth). Thereupon, the level of C decreased again, although it remained higher than its level during NT. A few seconds before the onset of the resting tremor T, we again detected an increase of C . During the T section, significant peaks were detected.
Transitivity : The levels of transitivity remain insignificant during NT. In both transition periods, we detected an increase in the level of T . During the tremor section, the amplitude of the peaks increased, surpassing in some cases the standard deviation.
Assortativity : A had the same behaviour as transitivity, in that its fluctuations remained insignificant during the entire NT period. However, it marked the transition windows by becoming significant and increasing in amplitude in TO and T.
Equivalent results were found for all files. Importantly, we found significant peaks before the transition of movement conditions for all the measures and files. These peaks were significant at the 99% and 95% levels, which implies that in all cases, the onset of the tremor can be predicted in advance by this method. Based on the obtained results, we can draw the following conclusions:
The trends of the different measures were quite similar since all of them exhibited a shift in their dynamics near the beginning of the TO episode and before the T episode. All measures detected the tremor efficiently before its appearance and therefore before the patient showed any physical symptoms. This fact made these measures good candidates for their application in a demand-driven DBS system.
During tremor episodes, T and A displayed a growing trend, while C exhibited the behaviour of shifting its dynamics more abruptly. The behaviour during NT and TO was similar across all the measures.
6. System
The objective of the system was to detect the tremor through the STN-LFP signal recorded by the electrodes, through the network features studied. The aim was to provide stimulation as soon as symptoms were detected, or ideally shortly before, and to stop stimulation as soon as atremorous instances were sensed. In this way, the system will be efficient concerning the treatment of symptomatology, as well as with the use of the battery.
As previously mentioned, it was within the section labelled as T when the patient began to experience physically appreciable tremor, as determined by clinicians with expertise in movement disorders.
From the moment a tremor window arrives until the system classifies it as such and orders the stimulation to begin, a few seconds may pass. Therefore, it would be interesting to detect within the STN signal some event that anticipates the tremor episode, i.e., the ideal solution would be to detect the tremor before the patient begins to experience it physically, using those seconds to turn on the stimulation. In other words, ideally, a demand-driven DBS system must detect the tremor when the patient is in a TO episode.
With this goal in mind, the dynamics of the STN signal have been studied following the methods presented in
Section 5, since as we have seen, the network measures have proven to be outstanding at capturing changes in the non-linearity of the system. These changes were especially noteworthy in the
TO state, detecting a peak that reached values of significance of
0.01 in all the studied recordings.
6.1. Start and Stop Stimulation Decision
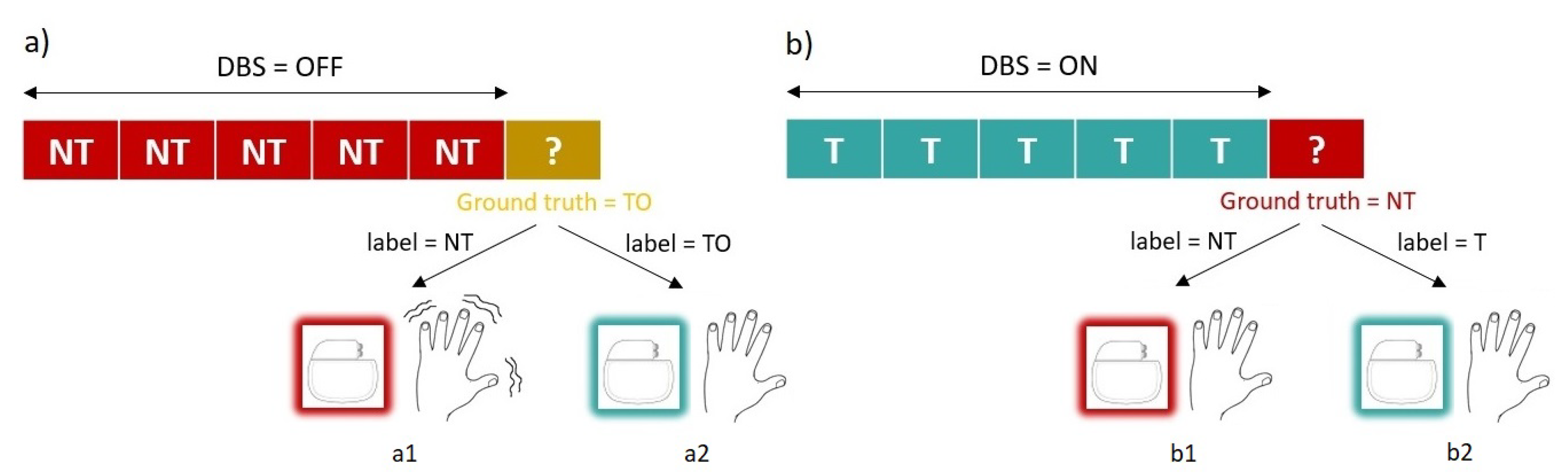
To be valid for its purpose, the system must be able to recognise two main conditions:
NT and
TO instances. Notice that we had three classes (
NT, TO and
T); however, the system only needed to learn the first two to be able to carry out the two instructions that the system performed: start and stop stimulation. Notice also that the accurate detection of
TO was more critical than the detection of
NT. This was because if a delay existed in stopping the stimulation as a consequence of not correctly classifying an instance of
NT, it would not have any effect on the symptomatology, going unnoticed by the patient. However, the same delay in detecting a tremor instance would lead to the patient experiencing tremor as many seconds as windows the system would need to perform a correct classification. The system has to avoid this situation, therefore, and give the accuracy shown detecting a peak of non-linearity within the
TO state, and the system will base the decision to start stimulation on the presence of that peak. These possible scenarios are depicted in
Figure 3.
However, this non-linearity peak did not occur when the patient transits from the
T to the
NT state, making a system based solely on this method not capable of detecting the stop condition. This would lead to a situation in which the IMD would stimulate in a continuous way (which is the current state that we were trying to improve). Therefore, to detect the stop condition, the system will made use of an SVM classifier trained per patient using ten-fold cross-validation. Support Vector Machines (SVM) are algorithms that create a non-linear discriminative classifier, determined by an optimal hyperplane that separates the instances of different classes, implicitly mapping the inputs into high-dimensional feature spaces (the well-known kernel trick) [
34]. Once the system has learned the mapping function, the new and unlabelled instances will be mapped into some of the created regions, adopting the label of that region.
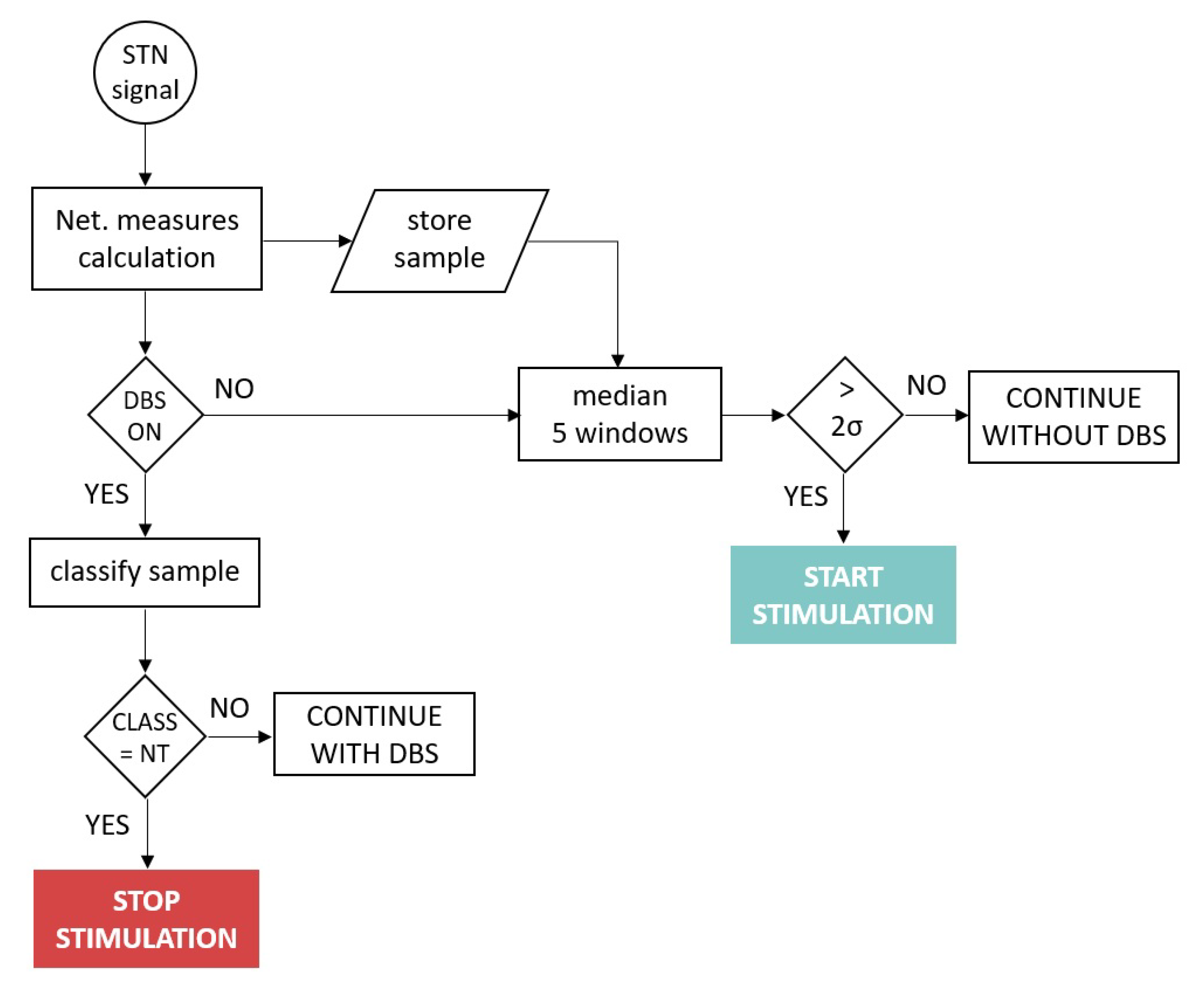
6.2. System Model
The system operated as follows: Assuming the system was running, at time
t, a new signal window arrived at the IMD. It preprocessed the signal as described in
Section 2, calculated the network measures as described in
Section 4 and
Section 5 and stored the results in memory. Notice that the system only maintained in memory the four windows before which it was evaluated. If DBS was OFF, the system had to decide if it would turn on the stimulation or continue just sensing the signal. For that, it averaged the current window with the four previous ones. Depending on the results: (a) If the result exceeded two standard deviations from the subject’s baseline, a non-linearity peak was detected, indicating that the patient was within the
TO state, and therefore, the decision made by the system would be to turn on the stimulation. (b) The system would continue in standby otherwise.
Nevertheless, if in time
t, the DBS was ON, the decision that the system must make was whether to turn off the stimulation. For this purpose, the trained SVM model would classify the sample. If it belonged to
NT, the IMD would order to stop the stimulation. It would continue stimulating otherwise. The flow diagram of the system operating mode is depicted in
Figure 4.
6.3. System Performance
This section discusses the validity of the proposed system. Validity reflects the accuracy of the system, and it is measured by sensitivity and specificity. Sensitivity is the proportion of true positives, and specificity is the proportion of true negatives that are correctly identified by the system. Besides, we were interested in measuring the False Positive (FPR) and False Negative Rates (FNR). FPR ( or type I error) measured the percentage of cases in which the null hypothesis was correct, but was rejected, while FNR ( or type II error) measured the percentage of cases in which the null hypothesis was false, but was accepted.
In a demand-driven DBS system, the two main actions to be taken are when to turn on and when to turn off the stimulation. The validity of the model in each of these actions is evaluated here.
Shut down the stimulation:
In this usage scenario, the system was stimulating (DBS ON), and it had to decide whether to stop the stimulation, i.e., the system was registering T samples (subthalamic signal associated with the tremor regarding the extracted features), but at a certain point, began to register NT samples (subthalamic signal associated with the atremorous state regarding the extracted features).
Sensitivity here is the ability of the system to classify a sample as T correctly, while specificity is the ability to classify a sample as NT correctly. A false positive in this scenario represents that the system classified an arriving sample as NT being T. While a false negative represents that an arriving sample was classified as T being NT.
The SVM module was trained to discriminate these two types of samples. Its performance is presented in
Table 1. In this scenario, we wanted the system to have a high degree of specificity and a low percentage of FPR.
In the case of Patient 2, there was a specificity of 100% and an FPR of zero. This is the ideal case. One hundred percent of the NT samples were identified without failure. Nevertheless, in the case of Patient 3, there was a 90.8 specificity and an FPR of 9.2. This means that about nine out of 10 NT samples were evaluated correctly, but one out of 10 were incorrectly classified as tremor.
Notice the implication that an FPR ≠ 0 has on this scenario: If the window being evaluated was incorrectly classified as tremorous, the system would continue stimulating, and it would evaluate the next window. Continued stimulating had no effect on the symptomatology and went unnoticed for the patient (as represented in
Figure 3b2). We were interested in having high specificity, but the fact of not reaching 100% was not critical.
Start up the stimulation:
Contrary to the previous use case, in this usage scenario, the system was in standby, sensing. For each incoming window, the system must decide whether to start stimulation, i.e, the system was recording NT samples, but at a certain point began to register TO samples.
Sensitivity here is the ability of the system to classify a sample as NT correctly, while specificity is the aptitude of correctly classifying a sample as TO. A false positive in this scenario represents that the system classified an arriving sample as TO being NT, while a false negative represents that an arriving sample was classified as NT being TO. Likewise, we wanted the system to return high values of specificity and a low percentage of FPR.
The proposed system based the detection of
TO on the existence of a non-linearity peak above 2
, as described in
Section 5. The reasons we opted for this solution were:
A peak above 3 was detected within the TO section of all subjects (specificity = 100%), indicating a clear pattern of sudden non-linearity increase in the neuronal signal of the subthalamic nucleus, just before the patient experienced physical tremor. This peak can be used as a trigger for the decision to begin stimulation by the system. It is a simple and effective system.
Notice that despite detecting a peak above 3 in all recordings, a conservative threshold was set at 2 (statistical significance of the peak p< 0.05) in order to ensure that the peak triggered the start of stimulation in unseen futures cases, which might perhaps present a less significant peak.
An SVM system was trained to distinguish
NT samples from
TO, obtaining worse results than in the previous usage scenario. This was the expected outcome since the classes to be classified were more similar between them. Remember in this regard that
TO is a transition state between
NT and
TO. Results are presented in
Table 2. As can be seen, the specificity did not reach 100% in any of the patients, obtaining higher values of FPR the previous use case. With the addition that in this case, the importance of correctly classifying a sample was more critical than in the previous usage case. If the window being evaluated was incorrectly classified as
NT, being a
TO sample, the system would continue in standby, not starting the stimulation. As soon as the patient left the
TO state and entered the
T state, he or she would begin to tremble (as represented in
Figure 3a1). It is crucial that the system does not leave the patient needing it without stimulation. This is a red line for the system.
7. Related Work
Closed-loop neurostimulation is an umbrella term that encompasses different advanced DBS strategies that apply various approaches to treat the symptoms. We can find the following families of closed-loop DBS strategies [
35]:
Adaptive DBS: These methods propose a real-time adaptation of HFS parameters (the frequency, duration and amplitude of a square-wave pulse train), which are currently determined by a clinician during the visit of the patient to the hospital every 3–12 months.
Demand-driven DBS: These strategies are based on detecting the fingerprints of pathological states and triggering the HFS as a result.
In our opinion, the combination of adaptive and demand-driven DBS approximations would provide a complete solution for an autonomous and intelligent DBS system, able to adapt the stimulation parameters by itself and also capable of start-up and shut-down by itself as required by the changing dynamics of the STN in real time.
Delayed DBS: These strategies consist of providing stimulation in a time-delayed manner, with the added possibility of doing it in different areas using several electrodes. The objective is to concentrate a beam of out-of-phase sinusoidal signals in the target area.
DBS based on proportional, derivative and integral feedback: These methods propose to design a stimulation signal following the LFP signal sensed in real time. This signal can be designed proportionally to the LFP activity or regarding integral or derivative LFP.
Optimal control strategies: These techniques base the control of the stimulation policy on finding the minimum of a defined cost function. This cost function would be adjusted to the DBS objectives, such as beta-band oscillation reduction or neuronal desynchronization.
Our study presented a proposal within the demand-driven DBS strategies. Focusing on this area, we compared the results obtained with those other studies in this sub-area that provided the level of accuracy of their systems. Wu et al. [
36] proposed a system using a radial basis function neural network based on particle swarm optimization trained with the STN-LFP signal. The system reached an 89.91% accuracy. In [
23], the authors examined several STN-LFP characteristics of both the time and frequency domain and characteristics based on information theory. After a feature selection process, they trained a feed-forward neural network classifier, obtaining 86% accuracy. Basu et al. [
37] proposed a system combining EMG and LFP signals making use of both spectral and non-linear properties of the signals, obtaining 80.2% accuracy. In [
38], the authors studied the spectral characteristics of the LFP signal, classifying it in the different states of tremor employing hidden Markov models. They obtained an accuracy level of 84%.
Finally, in two of our previous studies, we obtained a global accuracy level of 85.95% [
15] and 89.5% [
14], respectively. In the first one, we proposed a fuzzy inference system by using subthalamic-muscular synchronization features, whereas in the second, we designed a combined system that firstly classified the type of resting tremor presented by the patient and then trained a multi-layer perceptron with spectral features of the LFP-STN signal.
Systems that make use of both the muscle and the subthalamic signals have the disadvantage of needing an external device that senses the EMG signal for its operation. In this sense, systems that make use only of the STN-LFP signal are more functional, as they could be included in the existing DBS montage. In our opinion, this is an important characteristic to take into account.
8. Discussion
8.1. Preferred Network Measures
As discussed in
Section 5, the three network measures studied showed similar behaviour. However, our results showed that the clustering measure detected more abrupt changes in the non-linearity level of the subthalamic signal, which translated into more marked peaks. Thus, we would implement the trigger for starting up the DBS based on the clustering peaks.
8.2. Setting of the System Parameters
Since the actual mechanism of action of DBS is still unknown, there is not a standardised process to fix the stimulation parameters (rate, pulse width and voltage), which have to be fixed by the medical staff at the time of its implantation. The clinicians can later change these parameters during patient visits to the hospital to maximise the clinical improvement of the symptoms.
In order to use the proposed closed-loop DBS system, it will be necessary to calculate the parameters and m for each subject. There are two possibilities: (1) They can be fixed, as with the remainder of the parameters, at the time of implantation and reconsidered during the subsequent visits to the doctor or (2) they can be calculated from each window data in real time.
This decision will have to be made in the design phase of the IMD. The second option is more accurate, in so far as the value of the parameters is data-driven and performed in real time, and also entails a higher computation. This is inconvenient because neurostimulators, as with any other IMD, have restricted capabilities of energy, storage and computing power [
39].
Considering these restrictions, we would lean towards the first option. In this case, we need to test the robustness of the proposed method against the parameters and m. It is necessary to know to what extent these parameters affect the detection of the tremor states and transitively the detection of the tremor, i.e., the robustness of the proposed approach.
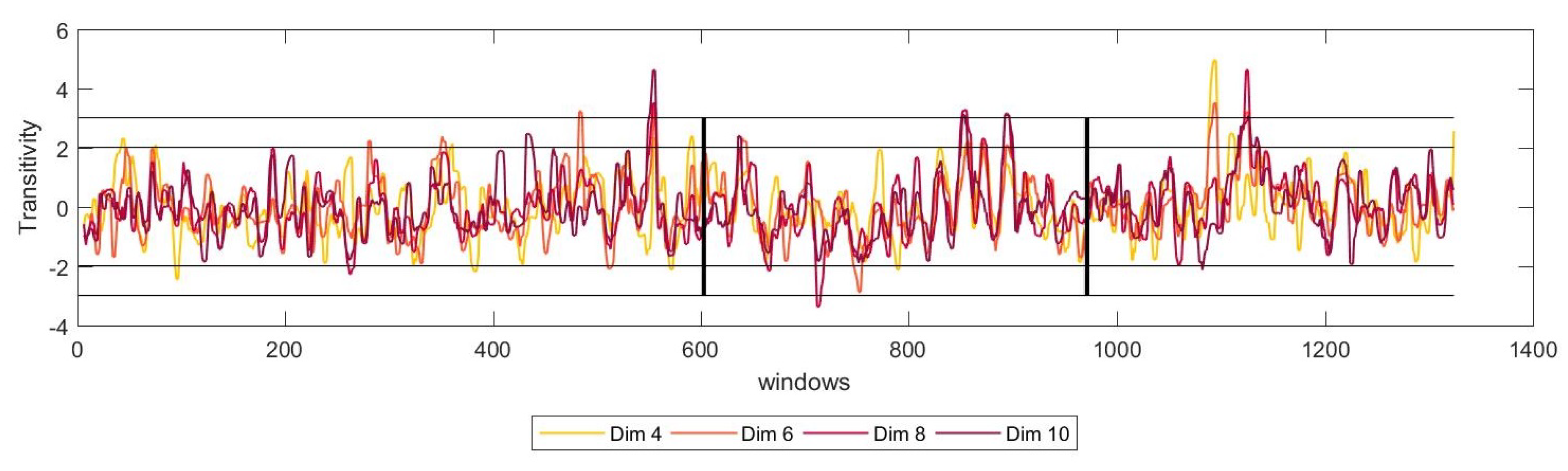
For that matter, we have studied the dynamics of the system for several numbers of dimensions,
m, of the reconstructed phase space. The results showed that for all the possible number of dimensions, the network measured show a similar trend, stabilising for higher values of
m.
Figure 5 shows these results for transitivity for one of the patients.
From these results, we can conclude that, even if the number of dimensions necessary to reconstruct the phase state change slightly, this would not affect the performance in the detection of the tremor. Nevertheless, more studies in this direction would be necessary.
For its part, the value of across windows has a very low variance, oscillating in a unit. For example, given a patient for which the optimal value of for most of the windows is , we could find some windows of this same patient with an optimal value of . In this case, we would set .
Nevertheless, we have found that the performance of the system was suitable across all the windows, and there was not an appreciable effect on the prediction of the peak before the onset of the tremor. Hence, we can conclude that the system was robust against the choice of the parameter , at least in our case, in which this parameter had a minimal variance.
8.3. Towards Future DBS Systems
DBS has proven to be an effective solution for the treatment of movement disorders, especially in cases where oral treatment is not enough. However, continued stimulation may induce adverse effects, while the device’s battery is not used efficiently. These two drawbacks of the DBS can be mitigated using new closed-loop strategies. In the case of demand-driven DBS strategies, the objective is to adapt the functioning of the device in real time in response to changes in clinical (motor) status experienced by the patient. Several studies, including significant device development companies, agree that closed-loop strategies will be the therapy implemented in future DBS systems. To this end, the new generation of DBS devices must be able to sense the electrical signal in the target area while simultaneously delivering therapy. These devices will be able to obtain artefact-free LFP recordings during stimulation. For this purpose, from the industry side, Medtronic developed the
Activa® PC+S neurostimulator, which is only available for research so far, but that points the way to future neurostimulation systems [
40].
9. Conclusions and Future Work
The behaviour of the STN becomes highly non-linear during tremor episodes, when compared with the basal state (
NT), making the geometry of the phase state more structured. We hypothesize that the witnessed increase in nonlinearity, as reflected by the shift in the network measures, could be attributed to the change in synchronization between the neurons during the tremor episode, as seen in a previous study [
19].
-recurrence network analysis is a suitable method to distinguish the transitions between movement conditions. Furthermore, the implemented method has the advantage of being able to deal with both short and non-stationary data, making it a good option for LFP data. These two facts make this procedure appropriate for its application to a closed-loop DBS system.
The setting of the parameters of the system, and m, can be taken at the time of the start-up of the device and adapted if necessary, during the visits of the patient to the clinician. This solution takes into consideration the inherent constraints of the IMD: energy, storage and computing power, making viable the implementation of the proposed solution.
Given the difficulty of getting STN recordings like those used in this work, only four patients have been studied. Despite having found very similar results in all of them, it would be necessary to consolidate these results in more patients. Our intention with this work is to propose that
-recurrence networks may be a useful tool in the design of systems that interact with brain signals, not only in PD [
6,
22], since all neural activity is a source of non-linear, non-stationary data.