As mentioned in the previous section, a challenge in calibrating an actual deployment in air pollution networks is that given a fixed data set of a few weeks, we will be able to provide calibrated ozone concentrations, i.e., good estimations of the test data set, regardless of time separation from the training data set. In this section we present a calibration model that we call multi-scale (MS) that corrects the bias produced in the ozone concentrations calibrated with respect to the model used in the previous section and that we called single-scale (SS).
6.1. Multi-Scale Calibration Using Multiple Linear Regression Correction with Exact Values
We call single-scale estimation (SS) to,
, the instant estimation on the test data set, i.e., using Equation (
3). Now, we call multi-scale estimation (MS),
, the corrected estimation on the value calculated by the single-scale model.
Now, taking expectation and variance in Equation (
10), we obtain expressions for constants
a and
a:
and
where
and
are the mean and standard deviation of the instantaneous testing data for the single-scale model,
, and
and
are the real mean and standard deviation of ozone concentrations in the period of the testing data for the multi-scale model,
.
Moreover, reformulating Equations (
7) and (
8) applying the linear correction and normalizing with respect to the reference standard deviation
we obtain:
and,
As it can be seen in Equations (
10)–(
12), to calculate
you need to know
,
,
and
. To estimate
,
,
and
a K-sample window has been taken. From now on we set this K window to the equivalent size in samples of a day or a week (multi-scale with daily/weekly averages correction). Then, the multi-scale calibration process consists of the following stages:
The biggest difficulty in applying the multi-scale correction is in estimating
and
(stage 3), since
and
can be obtained from
. Before proposing a way to estimate
and
let us check that if we knew the exact values of
and
, the linear correction improves the bias of the instant estimates. To do this, we are going to use the values of the mean and standard deviation of the ozone concentration values provided by the reference station when the node is placed with respect to that station. For this, we use the same data set as in
Section 5.2: Captor nodes 17013 (Manlleu), 17016 (Vic) and 17017 (Tona).
In the case of multi-scale calibration with exact correction,
=
and
=
(mean and standard deviation of the reference station data in the window interval [n−K, n]). Thus, Bias
= 0 and:
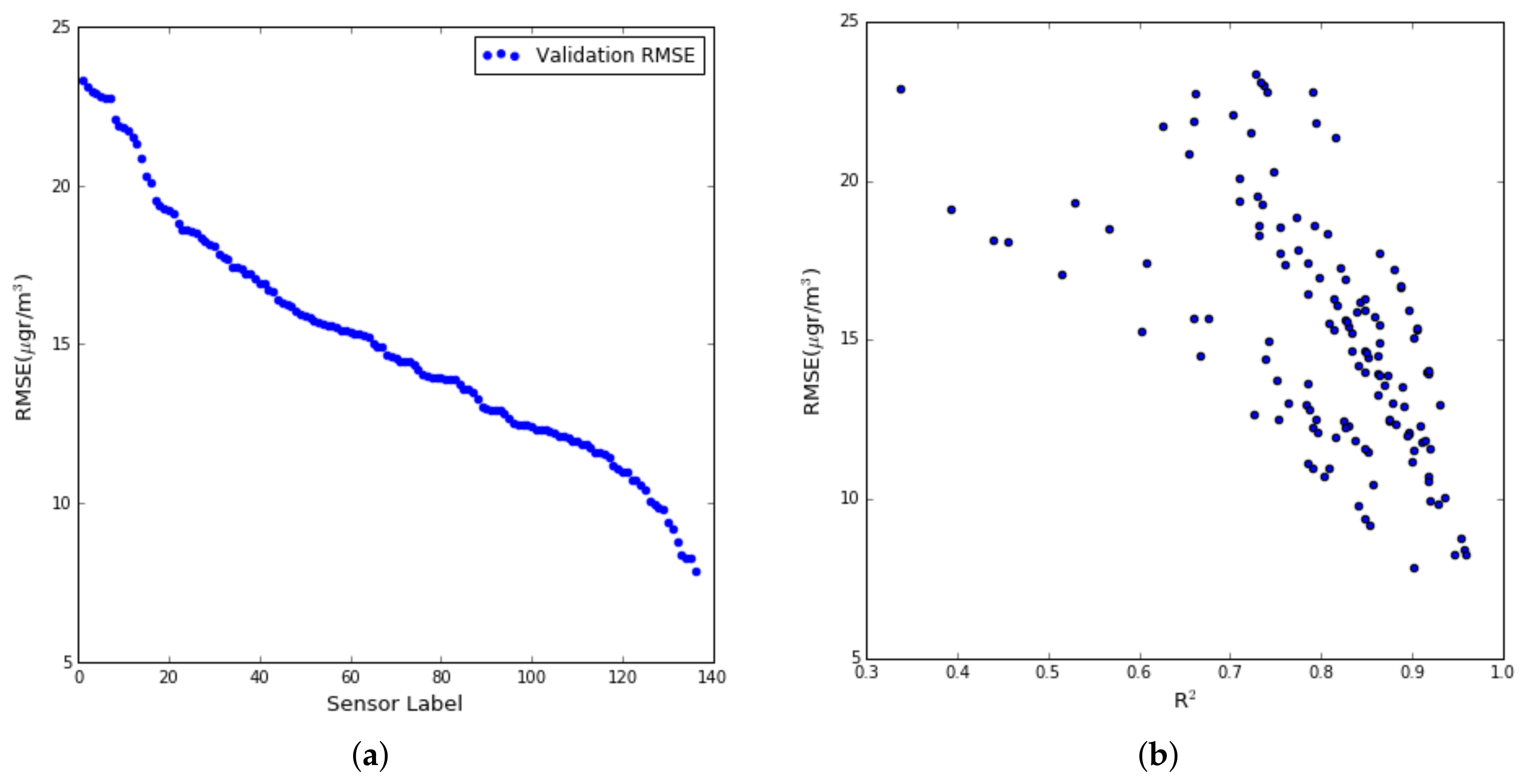
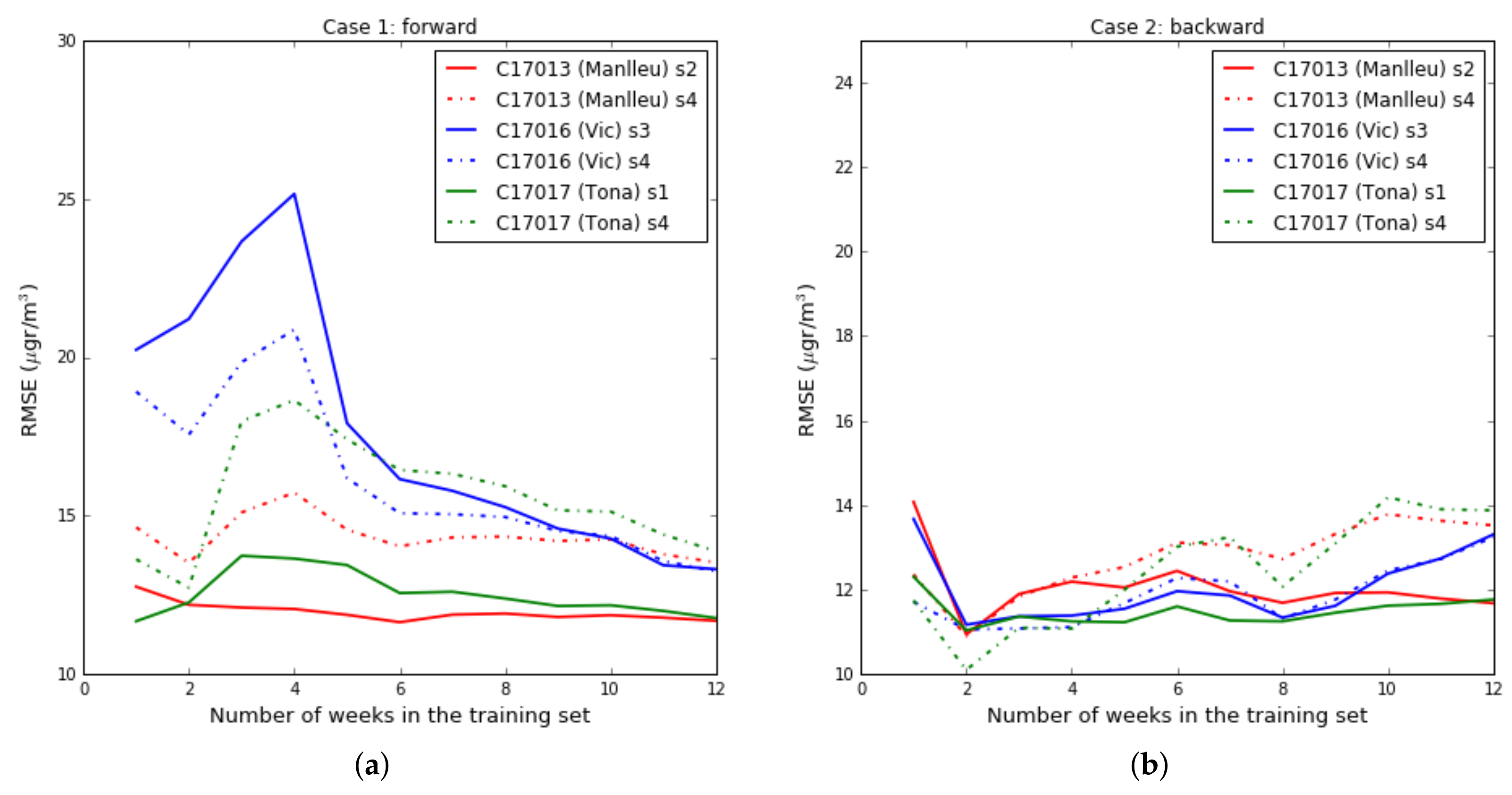
Figure 15a,b reproduces the results of
Figure 10a (
Section 5.2, case 3), where the RMSE of the test set is drawn day by day for the whole summer campaign. In this
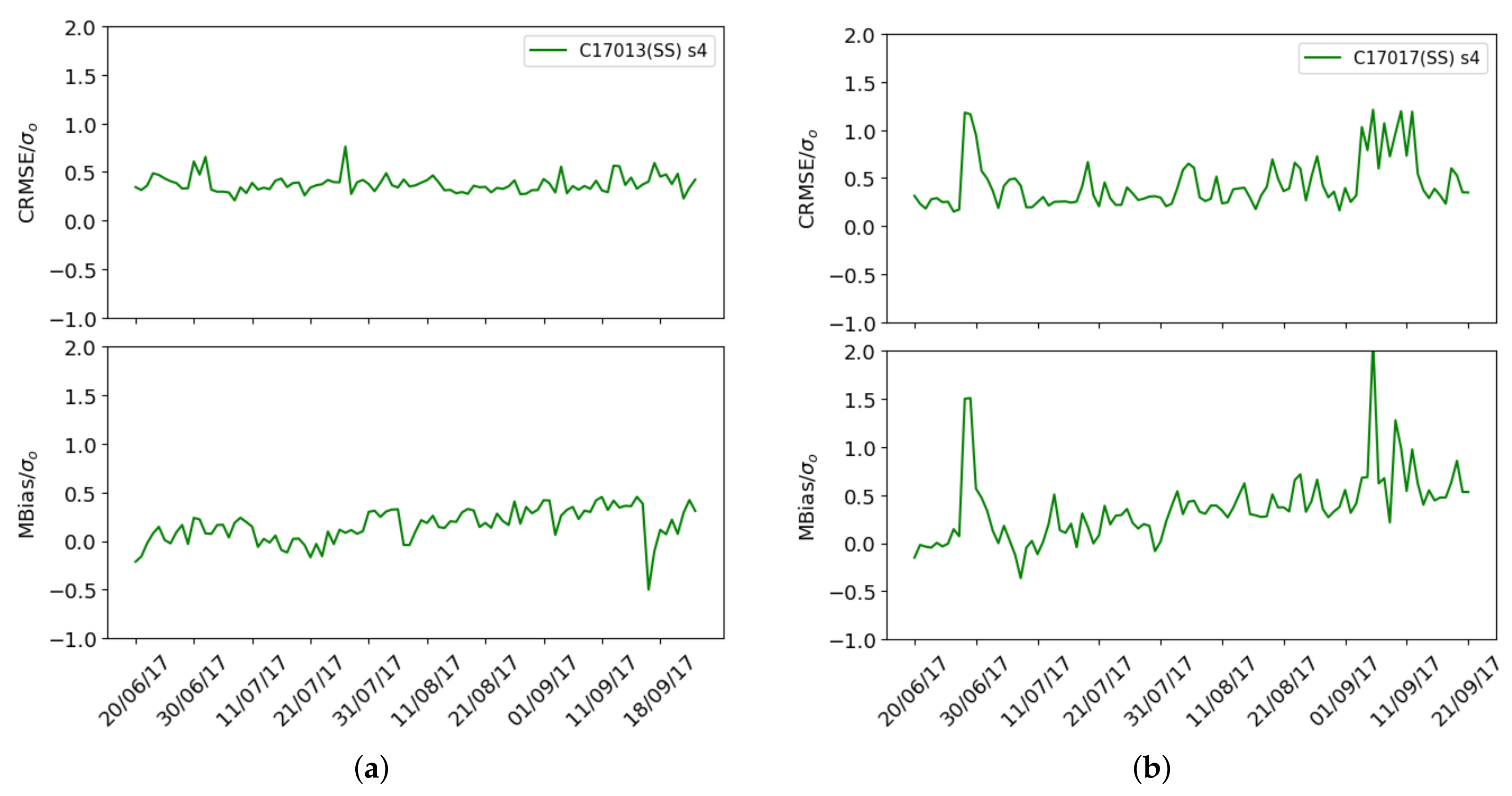
Figure 15, it can be observed that for the Captor nodes 17016 (Vic) and 17017 (Tona), the average per day is more stable, still with some peaks due to environmental conditions, but not with as high variability as observed in the single-scale case.
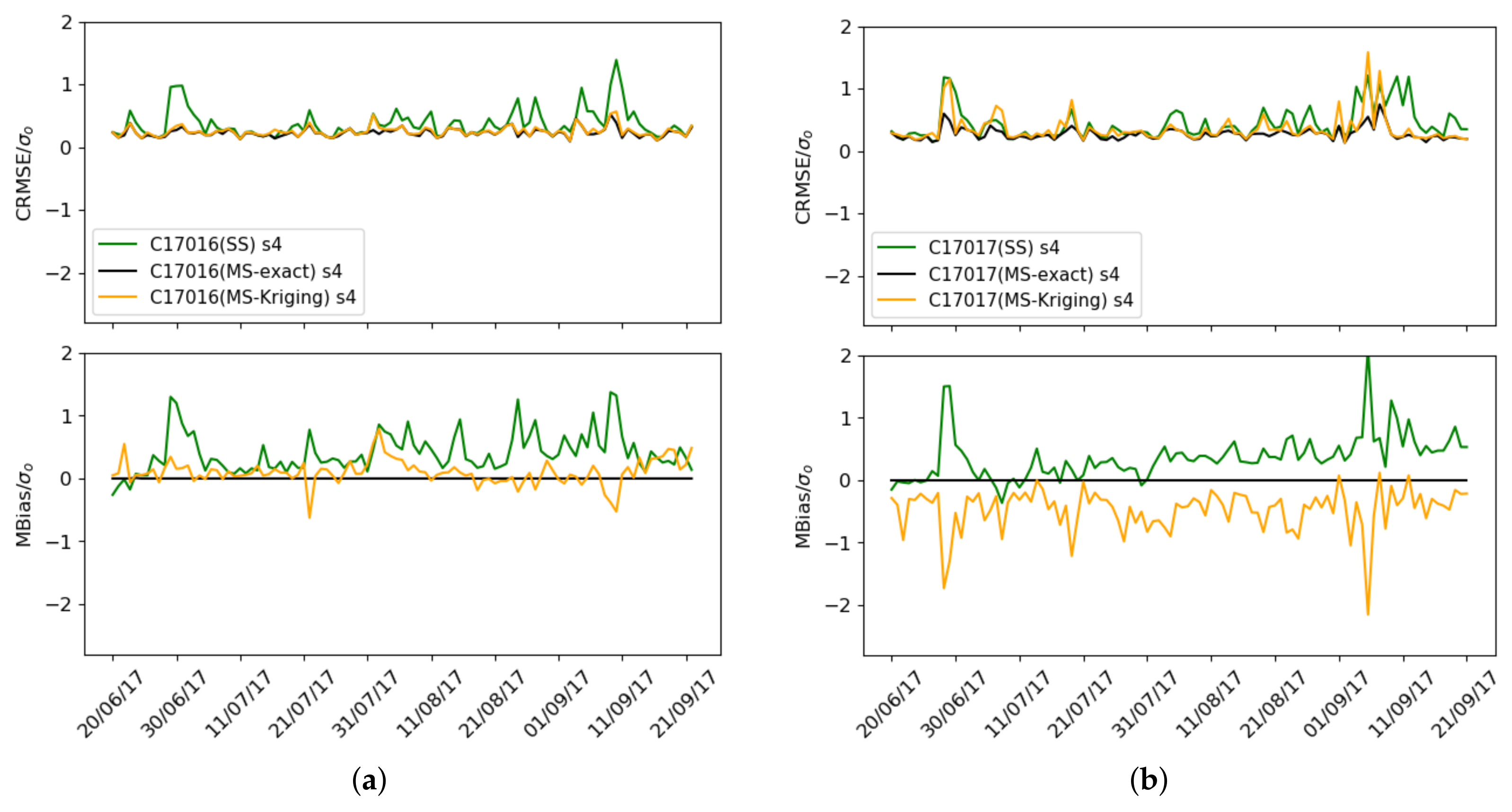
Figure 16a,b shows the mean normalized bias
and the normalized CRMSE
for the Captor 17016 and 17017 nodes. It can be seen that the mean normalized bias is zero and the normalized CRMSE
decreases with respect to the single-scale case (green) when exact correction (black) is used.
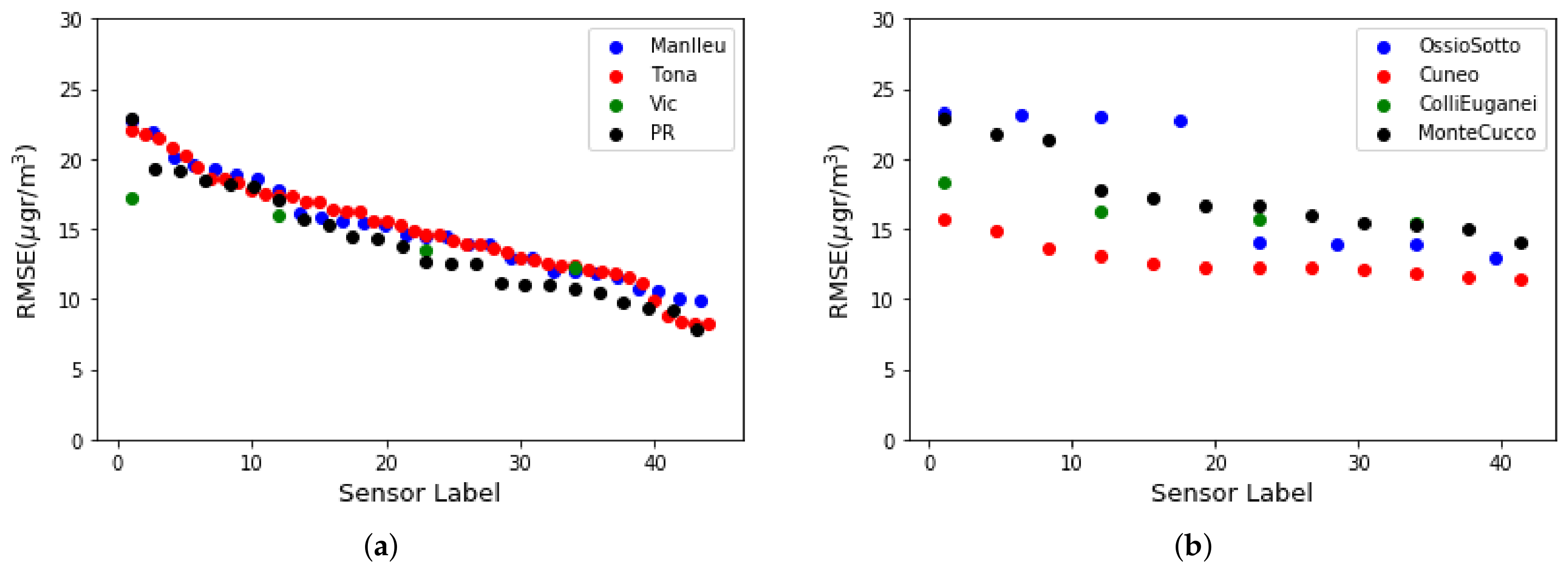
In addition,
Table 4 shows the values of the ozone concentrations before applying the correction, testing RMSE (SS), and after applying the correction, testing RMSE (MS), during the one hundred days of the campaign. For the correction we have considered two cases: (i) correction with mean and standard deviation with one day size K-window; and (ii) correction with mean and standard deviation with one week size K-window. It can be observed that the average RMSE decreases in all sensors when the values are daily, with reductions ranging from 25% to 75%. When the values are weekly, the reduction is smaller, although still considerable. The reason is that the estimation of the mean value and standard deviation of the ozone concentration is less accurate. These results show that it is possible to correct the bias presented by the sensors if we are able to find estimators of the mean and standard deviation. However, finding mechanisms that are capable of calculating such estimators is difficult, and if that is not possible, single-scale calibration is the best thing that can be done using MLR.
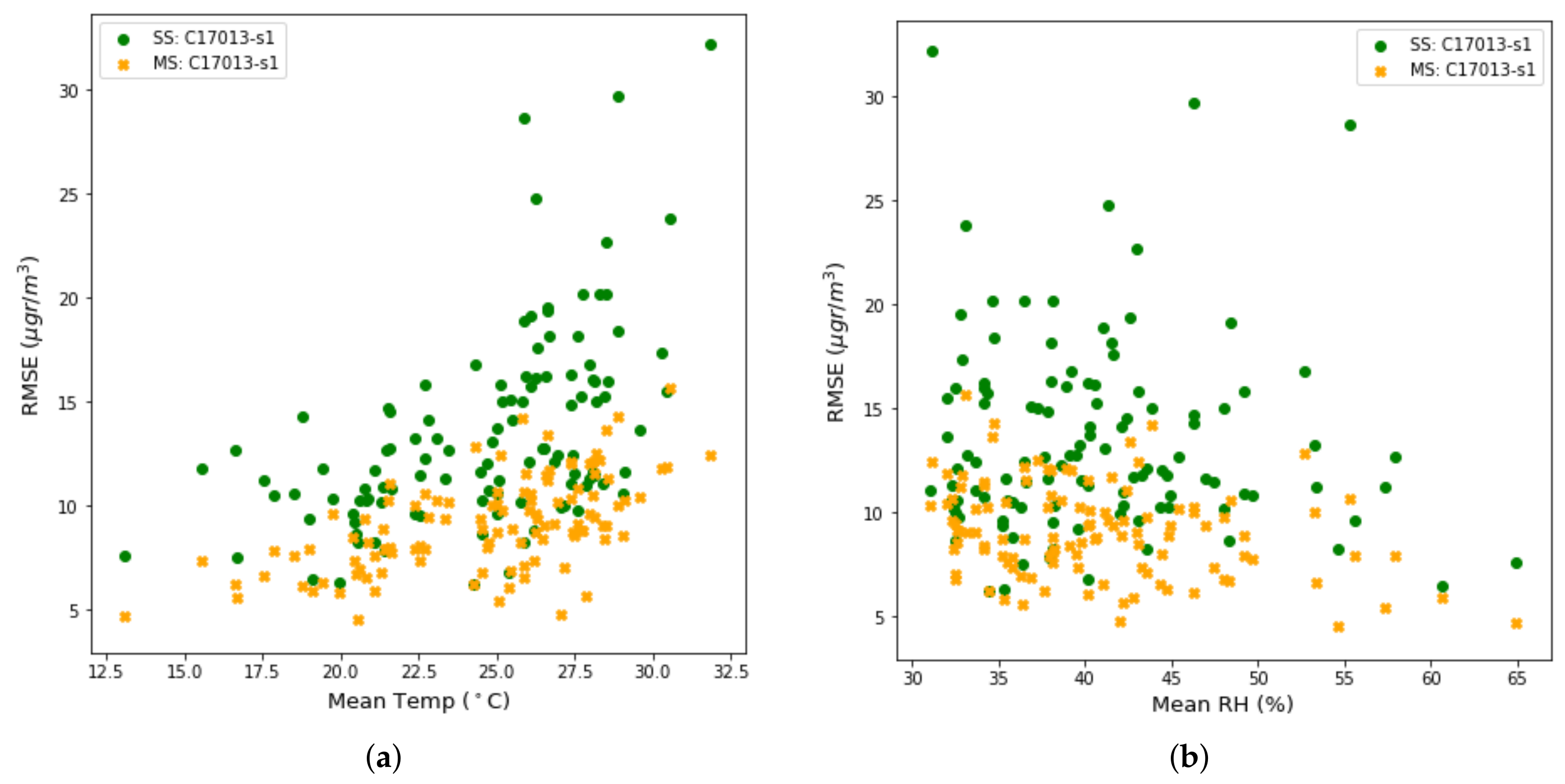
One of the effects of multi-scale correction is to mitigate the impact of environmental conditions, i.e., temperature and relative humidity, on the RMSE. By looking again at
Figure 13a,b, we can compare the effect of temperature and relative humidity in the RMSE for the single-scale case (green dots) and the multi-scale case (orange dots). You can see how the correction of mean and standard deviation softens the RMSE in all environmental conditions. In addition, we can observe that the reduction in the RMSE is greater when the RMSE is large, while the reduction is smaller when the RMSE is small. Examples are the reduction of an RMSE in the range of 28–34
g/m
to values in the range of 13–17
g/m
, while RMSE values in the range of 10–14
g/m
are reduced to values of 7–10
g/m
.
6.2. Multi-Scale Estimation Using Kriging
As the monitoring area is suburban/rural and the nodes have been deployed near reference stations, we propose to estimate the mean and standard deviation to correct the values obtained by the single-scale model using Kriging. Ozone concentrations in suburban/rural areas are known to show a relatively low spatial variability due to the secondary nature of this pollutant, which means that the Kriging approach could be adequate for this pollutant and type of area [
33]. This would not be the case for other pollutants such as NO
in urban areas, because of the high spatial variability of NO
emissions and ambient concentrations [
34]. In urban areas it would be necessary to use more sophisticated estimation models that would take into account the propagation of the pollutant in such areas.
Kriging is a technique used in geostatistical models that estimates the value of a function at a given point computing the weighted average of the known values of the function in the vicinity of the point. Although Kriging is not intended as a distributed mechanism, it allows estimating and therefore calibrating parameters at a localized point. In its distributed version, the nodes can gossip (Gossip is a type of routing mechanism for WSN that allows information to be communicated between nodes.) their values together with their GPS locations to the nodes participating in the Kriging mechanism. Kriging is closely related to regression analysis and is a particular case of the Gaussian process model [
35], where the domain is space. Kriging estimators interpolate the value of the random field at an unobserved location from observations of its values at nearby locations. The objective is to estimate the value at a localized point by a weighted average of the neighboring points to the location of the estimated target. In general, uniformly distributed dense data locations give good estimates, while sparse or clustered data locations can provide worse estimates.
In the CAPTOR project the set of neighbours is composed of other sensors already calibrated and reference stations. Since ozone is not necessarily constant and the neighboring nodes can be in an area of a few kilometers, we chose Universal Kriging with a Gaussian semivariogram model as an estimator of the mean
and the standard deviation
of ozone concentrations. We want to emphasize that we do not use Kriging to estimate the instantaneous value of ozone concentrations, but it is for the means and standard deviations that are used to correct the estimates of the single-scale model. Therefore, we estimate Kriging on the mean and standard deviation of 2-hop sensors using neighboring sensors that can be either pre-calibrated sensors or reference stations. Finally, we corrected the instantaneous ozone concentration values using Equation (
10), where a
and a
, Equations (
11) and (
12), are obtained using the Kriging estimates
and
.
To validate multi-scale calibration using linear correction with Kriging estimation, we calculated RMSE and R for target nodes 17013, 17016 and 17017. We use the same data set as in the previous section. As before, the training data set is three weeks. The test data set consists of one hundred days. Since these nodes are placed in reference stations, for the validation to be fair, we have to be careful that the reference stations where the target node is positioned do not participate in the Kriging process. All reference stations and Captor nodes in the Spanish geographical area participate in the final calibration of all nodes except baseline nodes 17013, 17016 and 17017 which have only been used to validate the model.
Table 5,
Table 6 and
Table 7 show the process of estimating the means and standard deviations for each of the three target nodes 17013, 17016 and 17017, using Kriging estimates. As an example, take node 17013, located in the Manlleu reference station, so this reference station does not participate in the algorithm in this case. To estimate its mean and standard deviation, the distributed algorithm consists of five steps,
Table 5: (1) we obtain the mean value and the standard deviation of the ozone concentrations in the Vic and Tona reference stations for the time window [n-K,n] and calculate with Kriging the value of
and
in the coordinates of nodes 17012 and 17023; (2) repeat the process in the coordinates of the node 17027, but now in the Kriging process participate the mean value and the standard deviation of the stations of Tona and Vic and the nodes 17012 and 17023; (3,4) the process is repeated with the rest of the nodes that participate in the calibration of the objective node 17013, and finally, in step (5) you get
and
in the coordinates of the objective node 17013 and you apply the multi-scale calibration process explained in
Section 6.1.
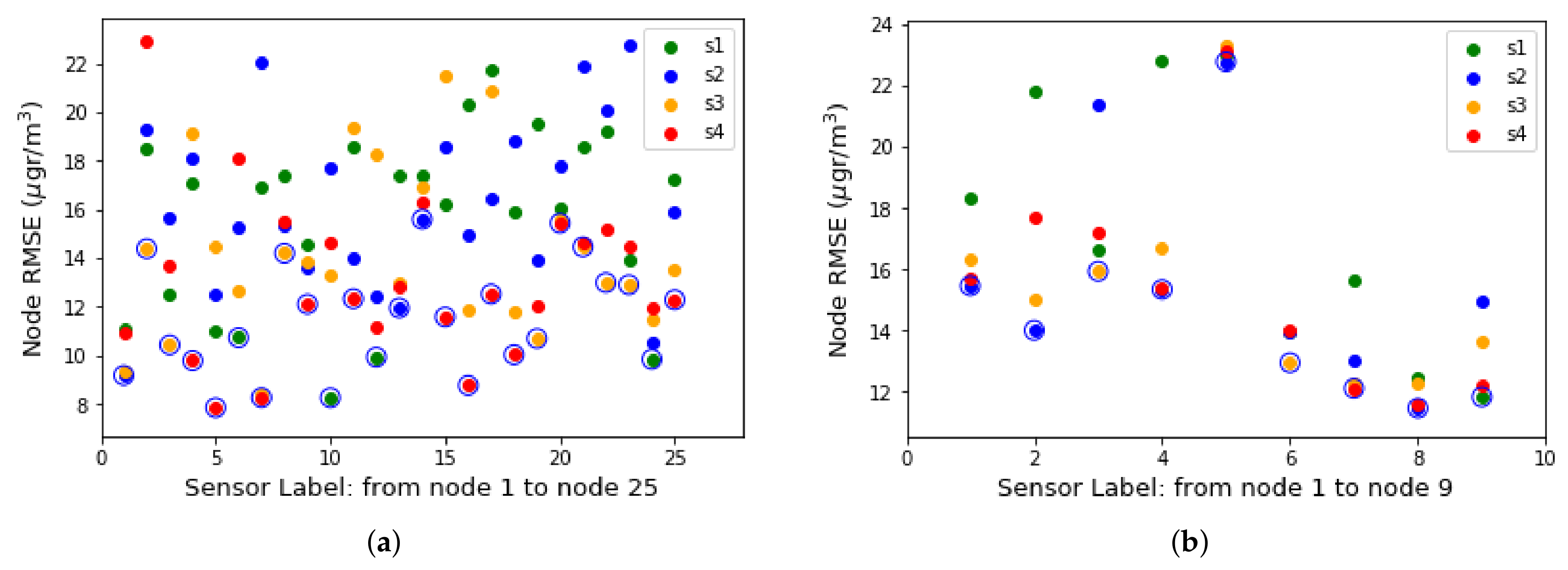
Looking at
Table 4, we can see: (i) the improvement using the multi-scale model with Kriging estimation with respect to the single-scale case; and (ii) how good is the multi-scale model with Kriging estimation with respect to the baseline estimation with exact values of the
Section 6.1. We can observe that the MS model with Kriging estimation has better performance in all sensors of node 17016 (Vic) for both daily and weekly averages and standard deviations. In the single-scale case, the lowest RMSE was 18.9
g/m
for the sensor s
and the highest was 35.4
g/m
for s
. With the estimate of Kriging MS, the RMSE for s
goes down to 11.2
g/m
(daily correction) and to 13.4
g/m
(weekly correction).
The values are worse than in the baseline case using the Vic reference station but close, showing an improvement over the single-scale case. In the case of node 17013 placed in the Manlleu reference station, the multi-scale model with mean correction and standard deviation with Kriging estimators improve the single-scale case, although not as much as in node 17016. The reason is that this node already had better RMSE values in the single-scale case than the 17016 node and therefore there is not as much room for improvement. Finally, for the 17017 node placed in the Tona reference station, the multi-scale model with daily or weekly averages correction with Kriging estimates works the same or even worse than the single-scale.
The case of nodes 17013 (Manlleu) and 17017 (Tona) are different from the case of node 17016 (Vic). The reason is that since node 17016 is in the center of the area studied,
Figure 5, two reference stations (Manlleu and Tona) participate in the estimation of the mean and standard deviation with Kriging. On the other hand, to calibrate node 17013, we only used one reference station (Vic), since we have excluded the Manlleu station for the validation of the results. The same occurs with the node 17017 in which we only used one reference station (Vic) in the calibration process.
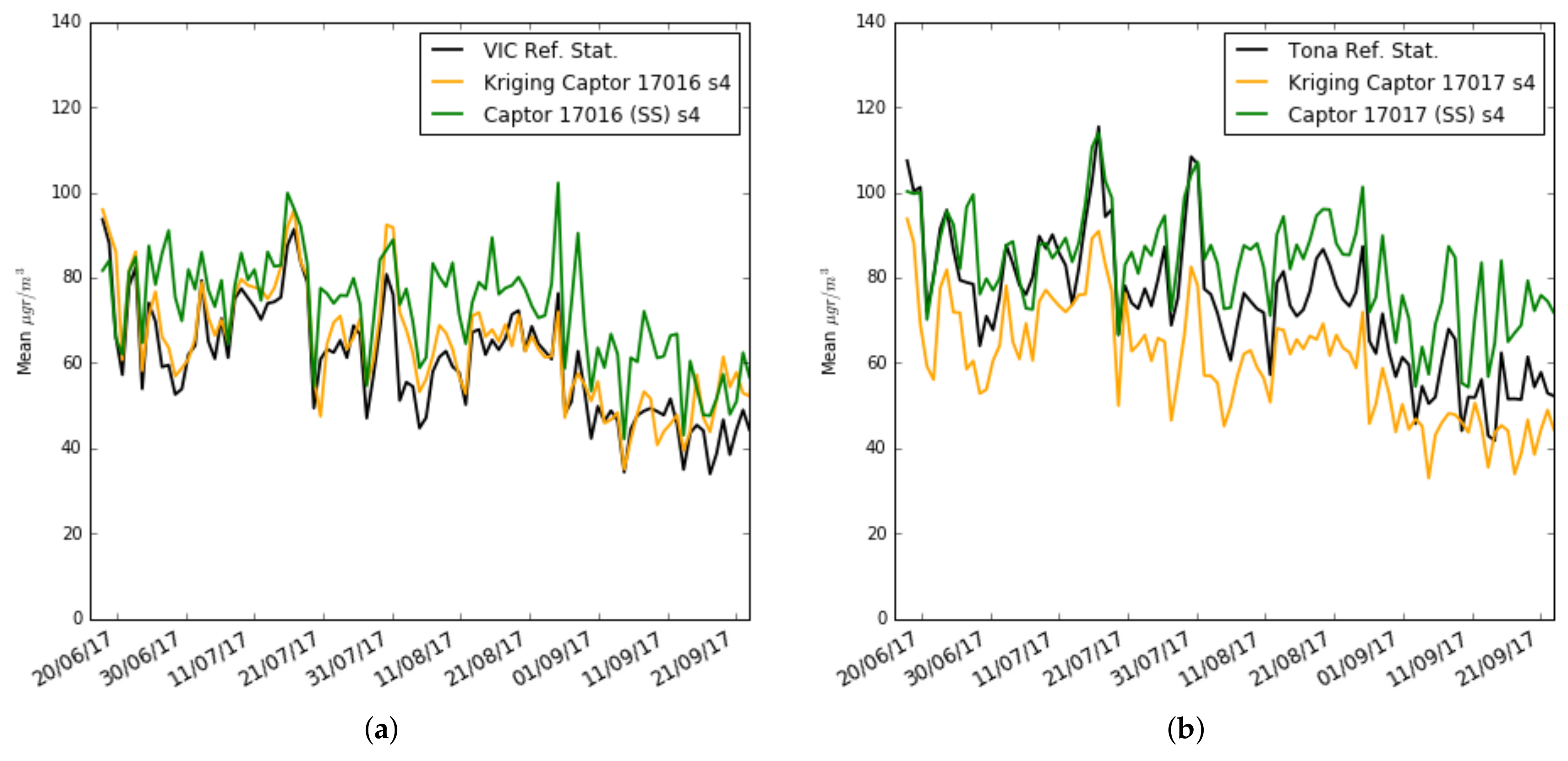
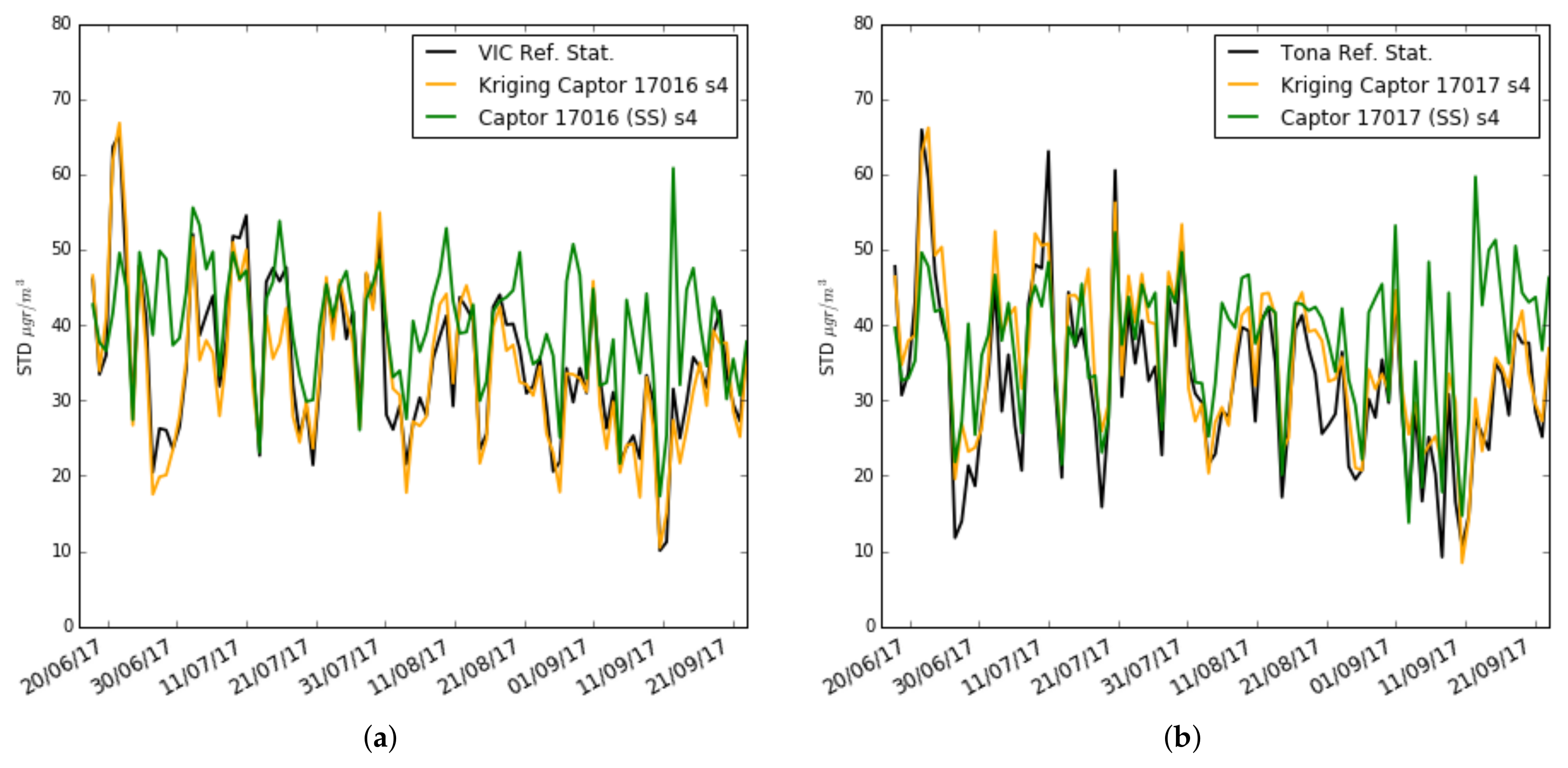
To better understand the causes of these results,
Figure 17a,b and
Figure 18a,b draw the daily estimates of the mean and standard deviation using Kriging estimators on nodes 17016 and 17017. We have chosen the s
sensor of node 17016 because the performance improvement between single-scale and multi-scale is big, and the s
sensor of node 17017 that has a worse performance in multi-scale compared to single-scale. One can observe the plot for the mean and standard deviation of the ozone concentration measured by: (i) the reference stations (black), (ii) the single-scale model (green), and (iii) the multi-scale models with Kriging estimators (orange). We can see that for the estimation of
and
, the sensor s
of the node 17016 estimates with little error the mean and the standard deviation, while the sensor s
of the node 17017 estimates with little error the standard deviation but underestimates the mean. The cause can be explained from
Figure 10b, where it is observed that the ozone concentration measurement in Tona is higher than in Vic and Manlleu. So, doing a Kriging using these stations that have lower averages underestimates the average. This shows the importance of having reference stations close to the nodes involved in the Kriging process for good results in estimating the mean and standard deviation.
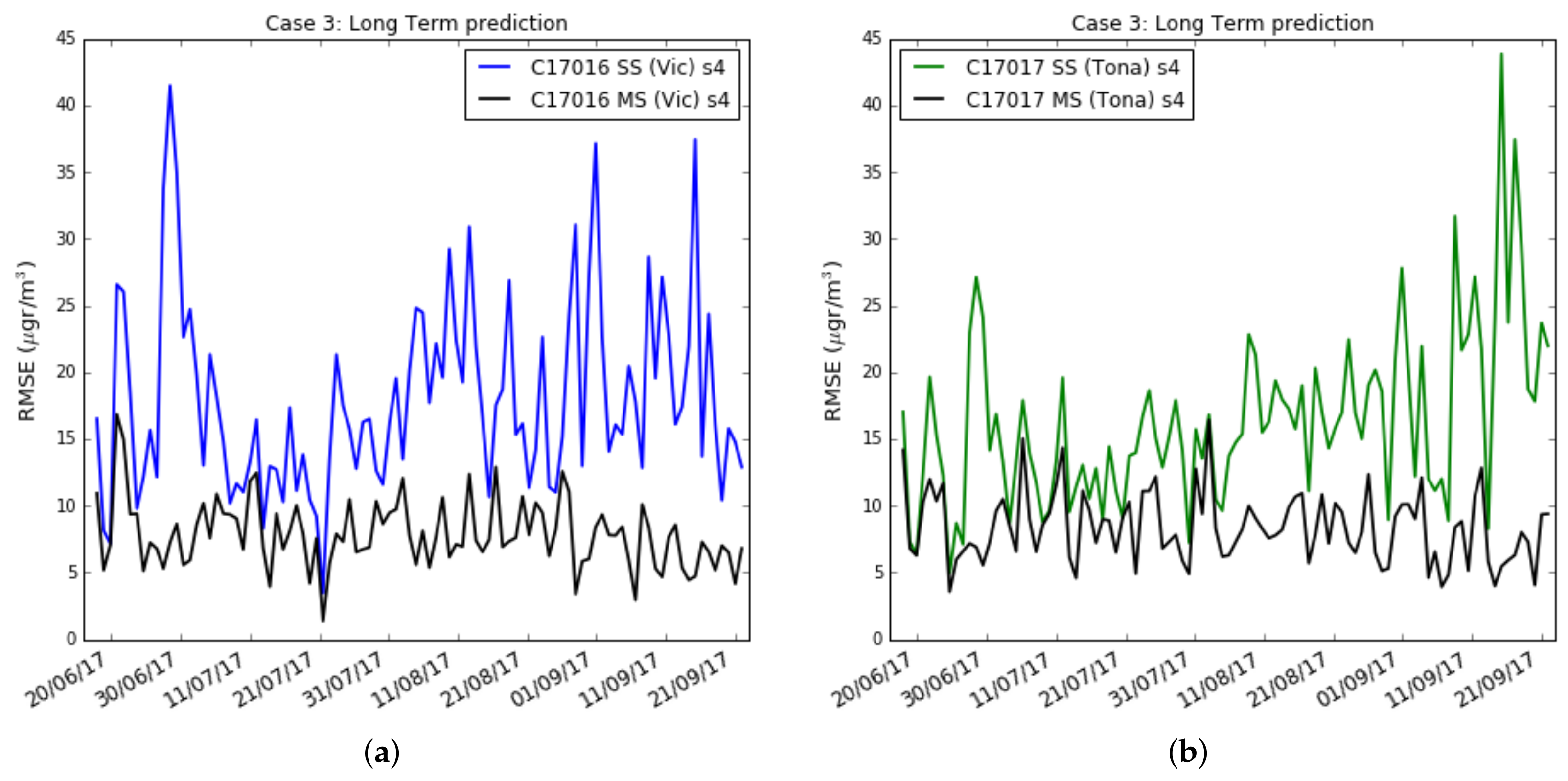
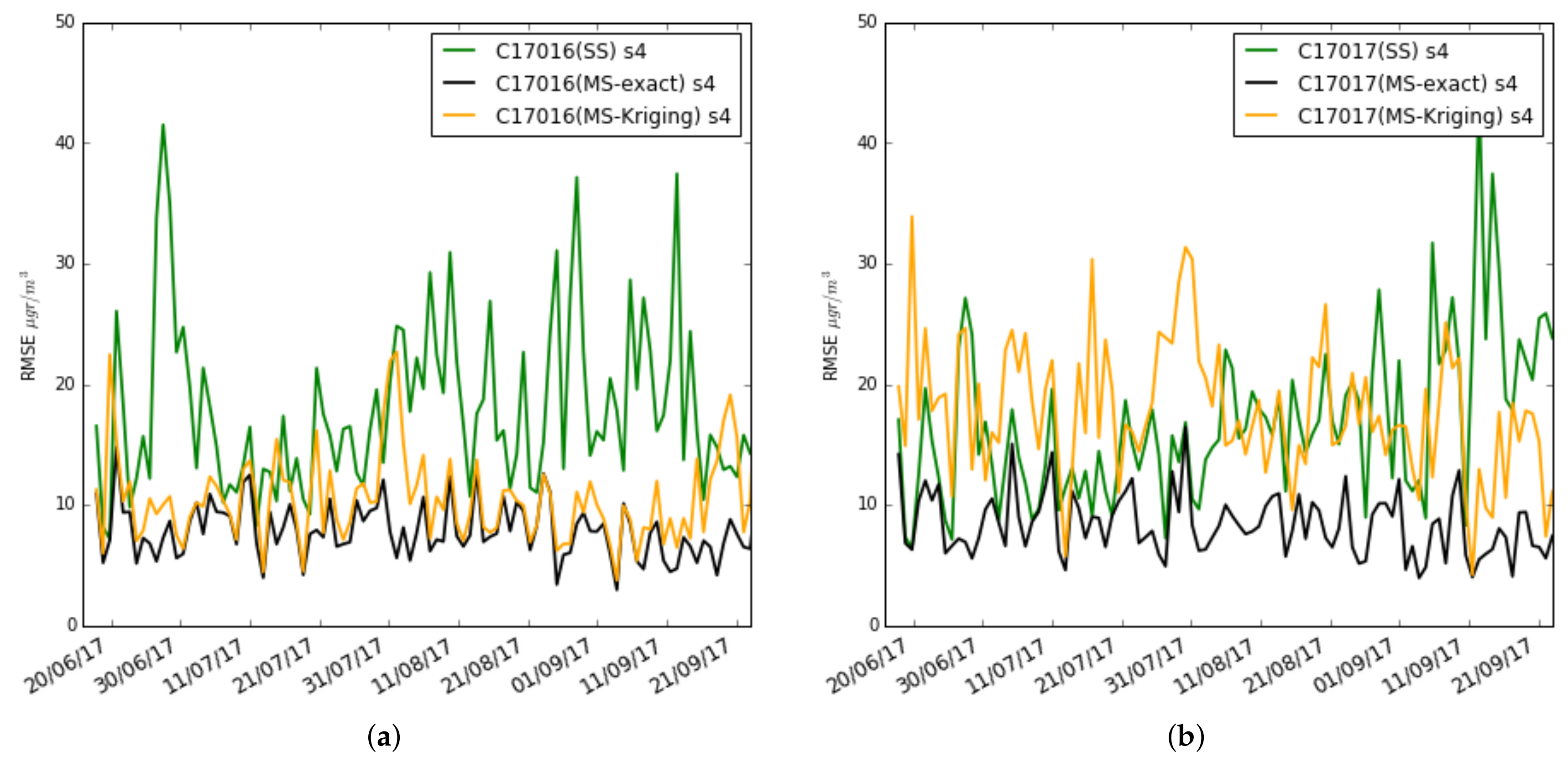
In
Figure 19, the average daily RMSE is drawn for the single-scale case (green), multi-scale with correction with exact values (black) and multi-scale with correction with Kriging estimators (orange) in the s
sensors of nodes 17016 and 17017. Observing the sensor s
of the node 17016—similar results were obtained in the other sensors of the nodes 17013 and 17016—it can be observed how the multi-scale model with correction with Kriging estimators has higher RMSE than with the correction with exact values but less than with the single-scale. This happens when the correction is made with daily and weekly values. On the other hand, for the reasons explained above, the sensors of node 17017 in general give worse performance in the multi-scale due to the underestimation of the mean in the Kriging method.
We can finally compare in
Figure 16a,b the mean bias for the Captor 17016 and 17017 nodes when using the single-scale and multi-scale case with exact values and with Kriging estimates of the mean and standard deviation. It is observed that for node 17016 the mean bias and the variance decrease, while for node 17017 the variance decreases slightly but underestimates the mean bias because it only uses one reference station, Vic, too far away and with a mean ozone concentration lower than in Tona.
The conclusions that can be drawn from this validation is as follows: (i) if there are no reference stations involved in the Kriging estimation process, it is best to use the single-scale case; (ii) if reference stations are available, an estimation of the mean and standard deviation and therefore a multi-scale correction can be made, provided that these reference stations have means of similar ozone concentrations and are close to the target node; (iii) if there are reference stations which, although close, have a very different mean ozone concentration, e.g., above or below, the Kriging estimate will overestimate or underestimate ozone concentrations, so in this case, it is best to use the single-scale model.