Perfusion Microfermentor Integrated into a Fiber Optic Quasi-Elastic Light Scattering Sensor for Fast Screening of Microbial Growth Parameters
Abstract
1. Introduction
2. Materials and Methods
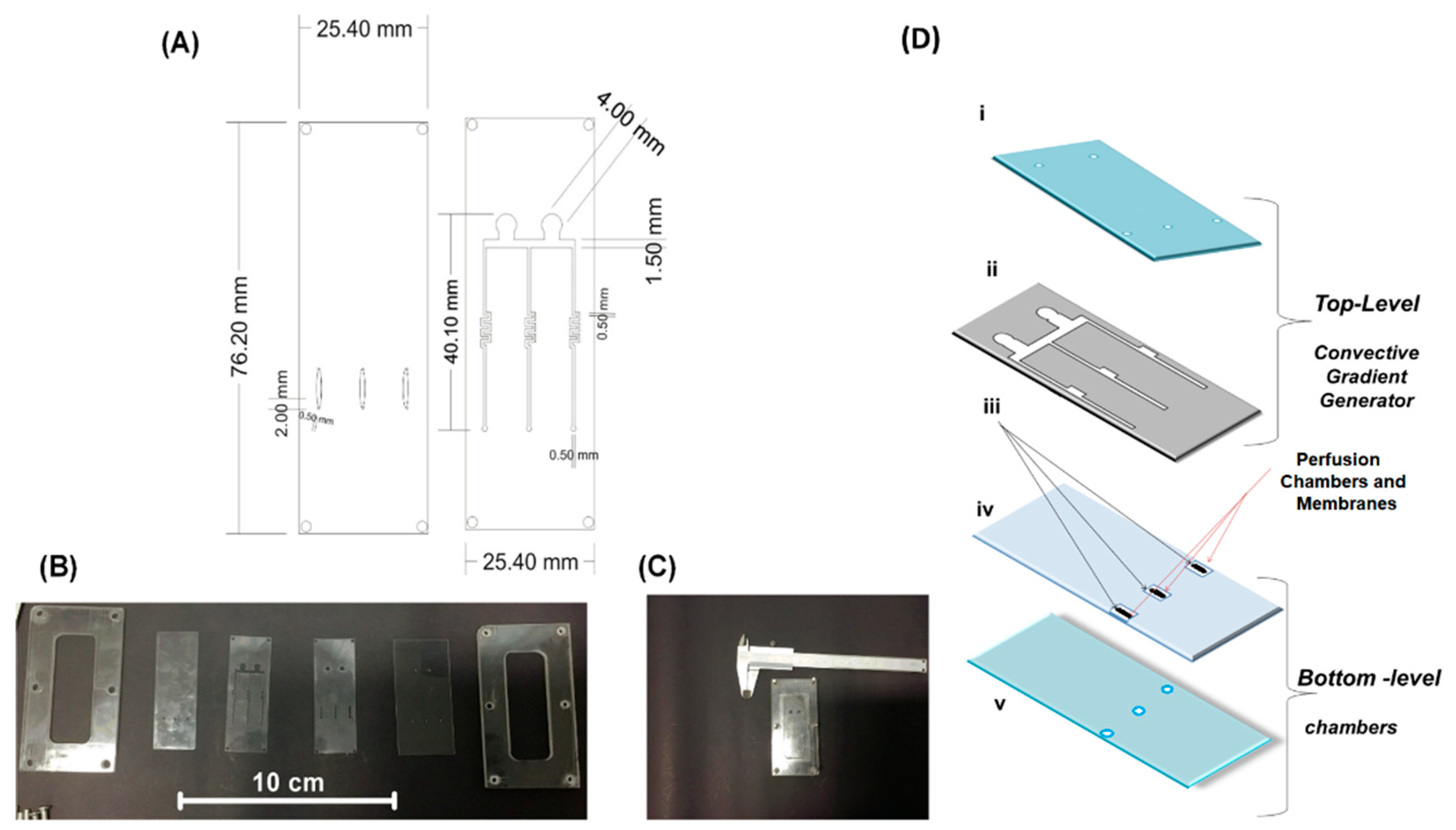
2.1. Microfermentor Design and Fabrication
2.2. Optical Fiber Sensor Design
2.3. Microbial Cultivation, Growth Kinetics, and Experimental Procedure
2.3.1. Definition of Experimental Conditions
2.3.2. Obtention of the Calibration Curve and the Batch Kinetics
2.3.3. Perfusion Microfermentor Tests
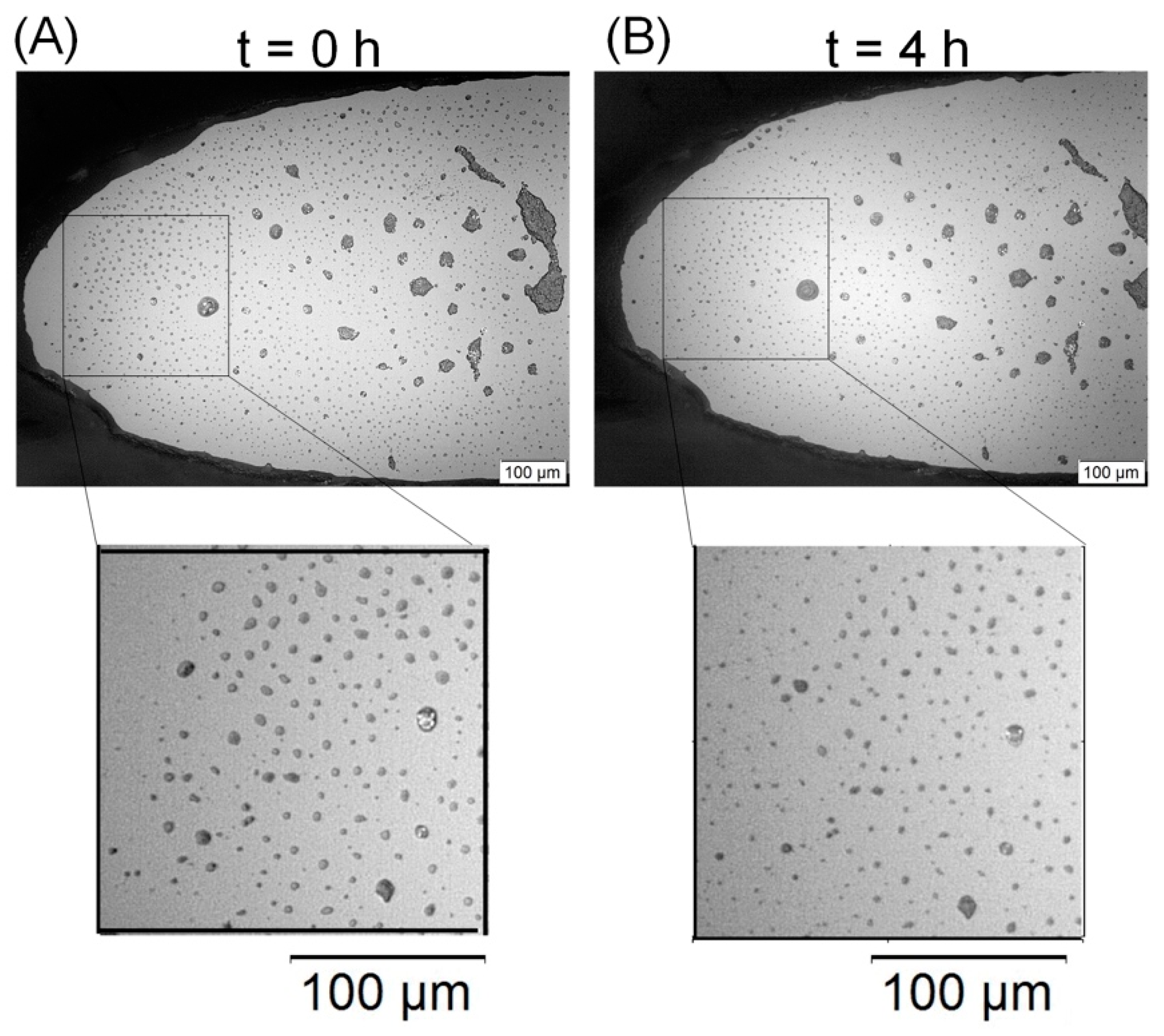
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bailey, J.; Ollis, D. Biochemical Engineering Fundamentals; McGraw-Hill: New York, NY, USA, 1986. [Google Scholar]
- Vit, F.F.; Oliveira, A.F.; Osório Rodríguez, D.A.; Carvalho, H.F.; Lancellotti, M.; de la Torre, L.G. Perfusion microbioreactor system with permeable membranes to monitor bacterial growth. J. Chem. Technol. Biotechnol. 2018, 94, 712–720. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical Reaction Engineering; John Wiley and Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Doran, P. Bioprocess Engineering Principles, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef]
- Mugo, S.M.; Zhang, Q. Nano-Sized Structured Platforms for Facile Solid-Phase Nanoextraction for Molecular Capture and (Bio) Chemical Analysis. In Nanomaterials Design for Sensing Applications; Zenkina, O.V., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 153–195. [Google Scholar]
- Lee, W.G.; Demirci, U.; Khademhosseini, A. Microscale electroporation: Challenges and perspectives for clinical applications. Int. Biol. 2009, 1, 242–251. [Google Scholar] [CrossRef] [PubMed]
- Szeto, G.L.; Egeren, D.V.; Worku, H.; Sharei, A.; Alejandro, B.; Park, C.; Frew, K.; Brefo, M.; Mao, S.; Heimann, M.; et al. Microfluidic squeezing for intracellular antigen loading in polyclonal B-cells as cellular vaccines. Sci. Rep. 2015, 5, 10276. [Google Scholar] [CrossRef]
- Psaltis, D.; Quake, S.R.; Yang, C. Developing optofluidic technology through the fusion of microfluidics and optics. Nature 2006, 442, 381–386. [Google Scholar] [CrossRef]
- Lien, V.; Vollmer, F. Microfluidic flow rate detection based on integrated optical fiber cantilever. Lab Chip 2007, 7, 1352–1356. [Google Scholar] [CrossRef]
- Zanzotto, A.; Szita, N.; Boccazzi, P.; Lessard, P.; Sinskey, A.; Jensen, K. Membrane-Aerated Microbioreactor for High-Throughput Bioprocessing. Biotechnol. Bioeng. 2004, 87, 243–254. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Nguyen, L.V.; Zhao, Y.; Ebendorff-Heidepriem, H.; Warren-Smith, S.C. High-sensitivity Sagnac-interferometer biosensor based on exposed core microstructured optical fiber. Sens. Act. B Chem. 2018, 269, 103–109. [Google Scholar] [CrossRef]
- Gong, C.; Gong, Y.; Chen, Q.; Rao, Y.-J.; Peng, G.-D.; Fan, X. Reproducible fiber optofluidic laser for disposable and array applications. Lab Chip 2017, 17, 3431–3436. [Google Scholar] [CrossRef] [PubMed]
- Gruber, P.; Marques, M.; Szita, N.; Mayr, T. Integration and application of optical chemical sensors in microbioreactors. Lab Chip 2017, 17, 2693–2712. [Google Scholar] [CrossRef]
- Choi, J.-W.; Pu, A.; Psaltis, D. Optical detection of asymmetric bacteria utilizing electro orientation. Opt. Exp. 2006, 14, 9780–9785. [Google Scholar] [CrossRef]
- Etcheverry, S.; Faridi, A.; Ramachandraiah, H.; Kumar, T.; Margulis, W.; Laurell, F.; Russom, A. High performance micro-flow cytometer based on optical fibres. Sci. Rep. 2017, 7, 5628. [Google Scholar] [CrossRef]
- Soares, M.C.P.; Fujiwara, E.; Gomes, M.K.; Mendes, B.F.; de la Torre, L.G.; Suzuki, C.K. Application of Optical Fiber Sensor on Fermentation Monitoring. OSA Tech. Digest OFS-26 2018, ThE39. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Pang, Y. Concentration gradient generation methods based on microfluidic systems. RSC Adv. 2017, 7, 29966–29984. [Google Scholar] [CrossRef]
- Karnik, R. Microfluidic Mixing. In Encyclopedia of Microfluidics and Nanofluidics, 2nd ed.; Li, D., Ed.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Fujiwara, E.; Ono, E.; Suzuki, C.K. Application of an Optical Fiber Sensor on the Determination of Sucrose and Ethanol Concentrations in Process Streams and Effluents of Sugarcane Bioethanol Industry. IEEE Sens. J. 2012, 12, 2839–2843. [Google Scholar] [CrossRef]
- Saleh, B.; Teich, M. Fundamentals of Photonics, 1st ed.; John Wiley and Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Finsy, R. Particle Sizing by Quasi-Elastic Light Scattering. Adv. Coll. Interf. Sci. 1994, 52, 79–143. [Google Scholar] [CrossRef]
- Berne, B.J.; Pecora, R. Dynamic Light Scattering with Applications to Chemistry, Biology and Physics; John Wiley and Sons: Hoboken, NJ, USA, 1976. [Google Scholar]
- Welty, J.; Wicks, C.; Wilson, R.; Rorrer, G. Fundamentals of Momentum, Heat, and Mass Transfer, 5th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Treco, D.; Lundblad, V. Preparation of Yeast Media. Curr. Protoc. Mol. Biol. 2001, 23, 13.1.1–13.1.7. [Google Scholar] [CrossRef] [PubMed]
- Andrade, R.R.; Rivera, E.C.; Atala, D.I.P.; Maciel Filho, R.; Maugieri Filho, F.; Costa, A.C. Study of kinetic parameters in a mechanistic model for bioethanol production through a screening technique and optimization. Bioprocess Biosyst. Eng. 2009, 32, 673–680. [Google Scholar] [CrossRef]
- Atala, D.I.P.; Costa, A.C.; Maciel Filho, R.; Maugieri Filho, F. Kinetics of ethanol fermentation with high biomass concentration considering the effect of temperature. Appl. Biochem. Biotechnol. 2001, 91–93, 353–364. [Google Scholar] [CrossRef]
- Lin, Y.; Tanaka, S. Ethanol fermentation from biomass resources: current state and prospects. Appl. Microbiol. Biotechnol. 2006, 69, 627–642. [Google Scholar] [CrossRef]
- Vallet, C.; Said, R.; Rabiller, C.; Martin, M.L. Natural abundance isotopic fractionation in the fermentation reaction: influence of the nature of the yeast. Bioorg. Chem. 1996, 24, 319–330. [Google Scholar] [CrossRef]
- Leticia, P.; Miguel, C.; Humberto, G.; Jaime, A.J. Fermentation parameters influencing higher alcohol production in the tequila process. Biotechnol. Lett. 1997, 19, 45–47. [Google Scholar]
- Todor, D.; Tsonka, U.D. Influence of the growth conditions on the resistance of Saccharomyces cerevisiae, strain NBIMCC 181, by freeze–drying. J. Cult. Collect. 2002, 3, 72–77. [Google Scholar]
- Ergun, M.; Mutlu, S.F. Application of a statistical technique to the production of ethanol from sugar beet molasses by Saccharomyces cerevisiae. Bioresour. Technol. 2000, 73, 251–255. [Google Scholar] [CrossRef]
- Siqueira, P.F.; Karp, S.G.; Carvalho, J.C.; Sturm, W.; Rodríguez-León, J.A.; Tholozan, J.-L.; Singhania, R.R.; Pandey, A.; Soccol, C.R. Production of bio-ethanol from soybean molasses by Saccharomyces cerevisiae at laboratory, pilot and industrial scales. Bioresour. Technol. 2008, 99, 8156–8163. [Google Scholar] [CrossRef]
- Celeromics. Cell Counting with Neubauer Chamber, Basic Hemocytometer Usage. Available online: http://www.celeromics.com/en/resources/docs/Articles/Cell-counting-Neubauer-chamber.pdf (accessed on 14 March 2018).
- Liu, J.Z.; Weng, L.P.; Zhang, Q.L.; Xu, H.; Ji, L.N. A mathematical model for gluconic acid fermentation by Aspergillus niger. Biochem. Eng. J. 2003, 14, 137–141. [Google Scholar] [CrossRef]
- Jain, K. Relationship between energy metabolism and growth. Archiv Mikrobiol. 1970, 72, 252–259. [Google Scholar] [CrossRef]
- Sonnleitner, B.; Käppeli, O. Growth of Saccharomyces cerevisiae is controlled by its limited respiratory capacity: formulation and verification of a hypothesis. Biotechnol. Bioeng. 1986, 28, 927–937. [Google Scholar] [CrossRef]
- Oliveira, A.F.; Pelegati, V.B.; Carvalho, C.; Cesar, C.L.; Bastos, R.G.; la Torre, L.G. Cultivation of yeast in diffusion-based microfluidic device. Biochem. Eng. J. 2016, 105, 288–295. [Google Scholar] [CrossRef]
- Koren, D.W.; Duvnjak, Z. Kinetics of the selective fermentation of glucose/frutose mixtures using Saccharomyces cerevisiae ATCC 36859. Acta Biotechnol. 1993, 35, 311–322. [Google Scholar] [CrossRef]
- Papagianni, M.; Boonpooh, Y.; Mattey, M.; Kristiansen, B. Substrate inhibition kinetics of Saccharomyces cerevisiae in fed-batch cultures operated at constant glucose and maltose concentration levels. J. Ind. Microbiol. Biotechnol. 2007, 34, 301–309. [Google Scholar] [CrossRef]
- Amillastre, E.; Aceves-Lara, C.-A.; Uribelarrea, J.-L.; Alfenore, S.; Guillouet, S.E. Dynamic model of temperature impact on cell viability and major product formation during fed-batch and continuous ethanolic fermentation in Saccharomyces cerevisiae. Bioresour. Technol. 2012, 117, 242–250. [Google Scholar] [CrossRef]
- Verduyn, C.; Postma, E.; Scheffers, W.A.; Van Dijken, J.P. Physiology of Saccharomyces cerevisiae in anerobic glucose-limited chemostats. J. Gen. Microbiol. 2015, 136, 395–403. [Google Scholar] [CrossRef]
- Postma, E.; Scheffers, W.A.; Van Dijken, J.P. Kinetics of growth and glucose transport in glucose-limited chemostat cultures of Saccharomyces cerevisiae CBS 8066. Yeast 2000, 5, 159–165. [Google Scholar] [CrossRef]



| Symbol | Meaning | Units |
|---|---|---|
| X | Concentration of Cells | (number of cells)·mL−1 |
| S | Concentration of Substrate (e.g., Sucrose) | g·L−1 |
| IR | Normalized Reflected Intensity Signal | - |
| I0 | Normalized Reference Signal | - |
| R | Power Reflectance | - |
| ni | Refractive Index of Medium “i” | - |
| G2 | Autocorrelation Function of IR | - |
| Γ | Decay Rate of the Autocorrelation | s−1 |
| t | Instant of the Measurement | s or h |
| τ | Arbitrary Delay Time | s |
| DAB | Diffusivity of Species “A” on Medium “B” | cm2·s−1 |
| q | Light Scattering Vector | cm−1 |
| α and β | Fitting Parameters | - |
| μ | Specific Growth Rate | h−1 |
| μm | Constant of Maximum Specific Growth Rate | h−1 |
| Km | Monod Constant | g·L−1 |
| μm (h−1) | KM (g/L) | Reference |
|---|---|---|
| 0.49 | 4.1 | (obtained with the microfermentor) |
| 0.50 | - | (obtained with the batch fermentation) |
| 0.42 | 4.1 | [27] |
| 0.50 | 0.187 | [36] |
| 0.17 | 0.5 | [37] |
| 0.32 | 0.27 | [38] |
| 0.24 | 4.56 | [39] |
| 0.40 | 1.51 | [40] |
| 0.42 | 0.50 | [41] |
| 0.31 | 0.099 | [42] |
| 0.49 | 3.6 | [43] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soares, M.C.P.; Vit, F.F.; Suzuki, C.K.; de la Torre, L.G.; Fujiwara, E. Perfusion Microfermentor Integrated into a Fiber Optic Quasi-Elastic Light Scattering Sensor for Fast Screening of Microbial Growth Parameters. Sensors 2019, 19, 2493. https://doi.org/10.3390/s19112493
Soares MCP, Vit FF, Suzuki CK, de la Torre LG, Fujiwara E. Perfusion Microfermentor Integrated into a Fiber Optic Quasi-Elastic Light Scattering Sensor for Fast Screening of Microbial Growth Parameters. Sensors. 2019; 19(11):2493. https://doi.org/10.3390/s19112493
Chicago/Turabian StyleSoares, Marco César Prado, Franciele Flores Vit, Carlos Kenichi Suzuki, Lucimara Gaziola de la Torre, and Eric Fujiwara. 2019. "Perfusion Microfermentor Integrated into a Fiber Optic Quasi-Elastic Light Scattering Sensor for Fast Screening of Microbial Growth Parameters" Sensors 19, no. 11: 2493. https://doi.org/10.3390/s19112493
APA StyleSoares, M. C. P., Vit, F. F., Suzuki, C. K., de la Torre, L. G., & Fujiwara, E. (2019). Perfusion Microfermentor Integrated into a Fiber Optic Quasi-Elastic Light Scattering Sensor for Fast Screening of Microbial Growth Parameters. Sensors, 19(11), 2493. https://doi.org/10.3390/s19112493






