Detecting Axial Ratio of Microwave Field with High Resolution Using NV Centers in Diamond
Abstract
1. Introduction
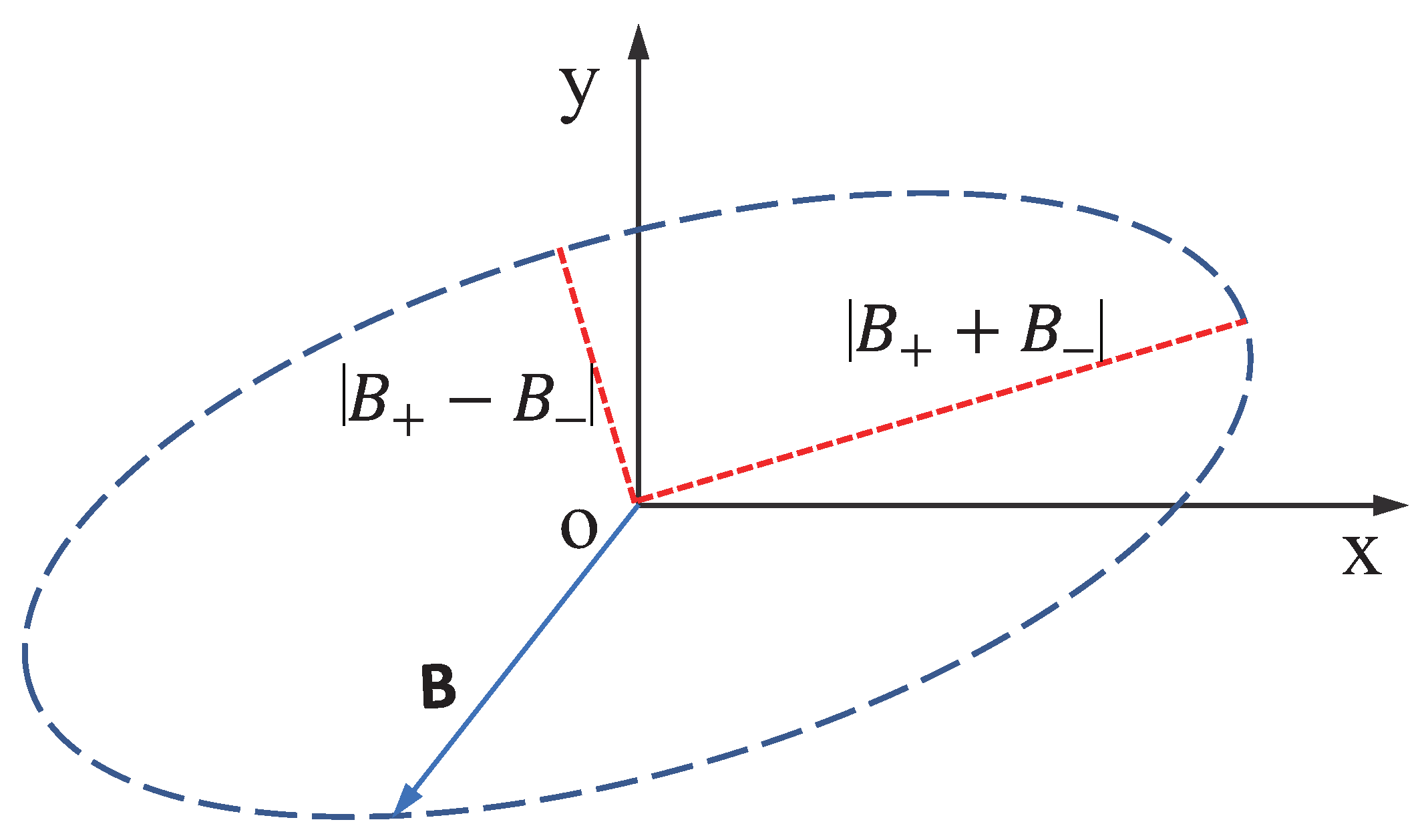
2. Principle
3. Experiments and Results
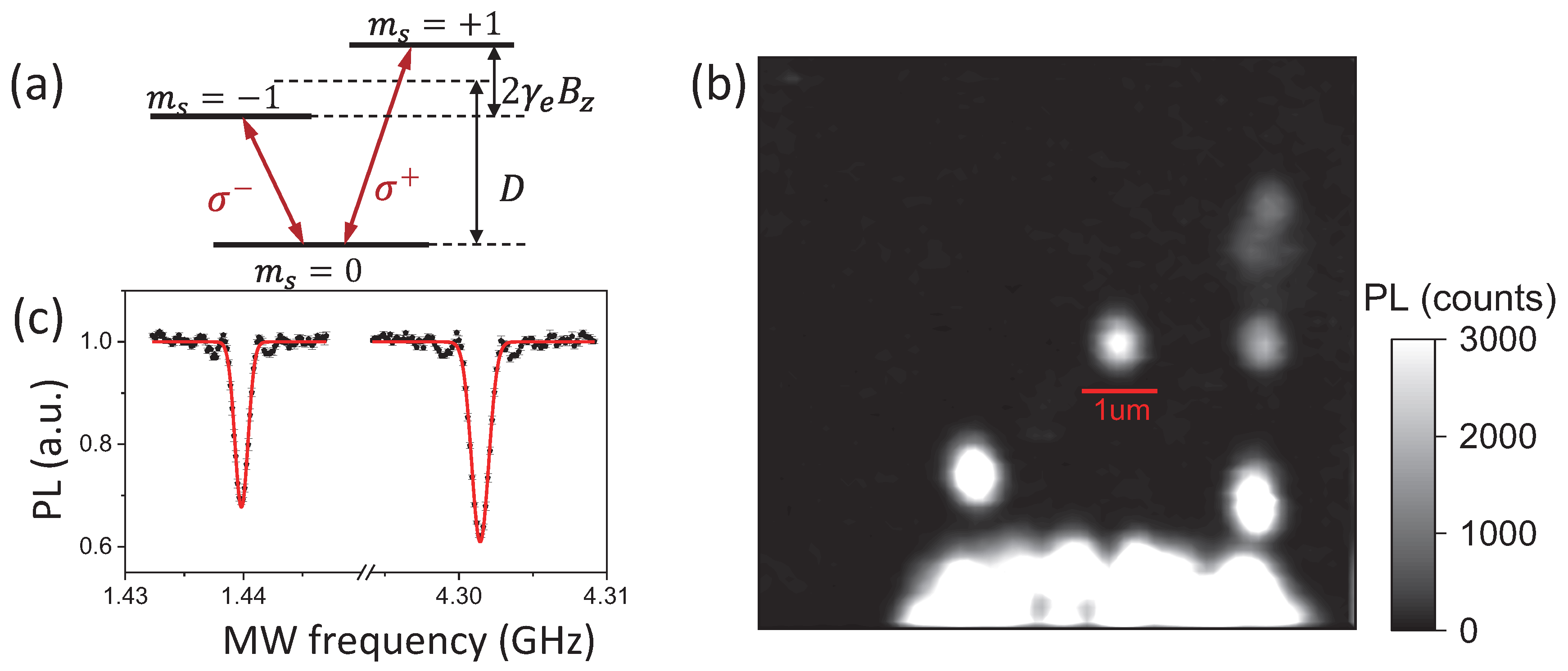
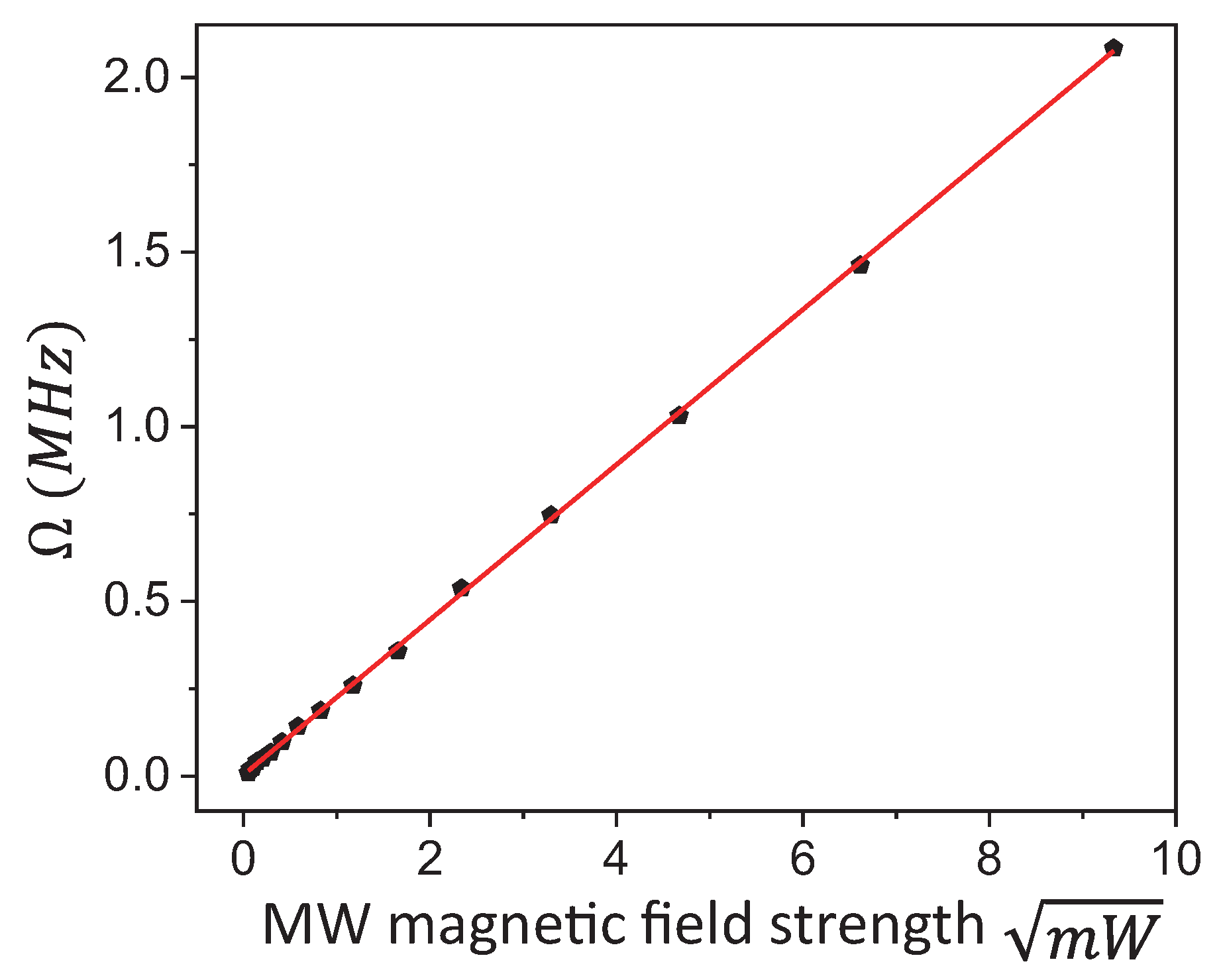
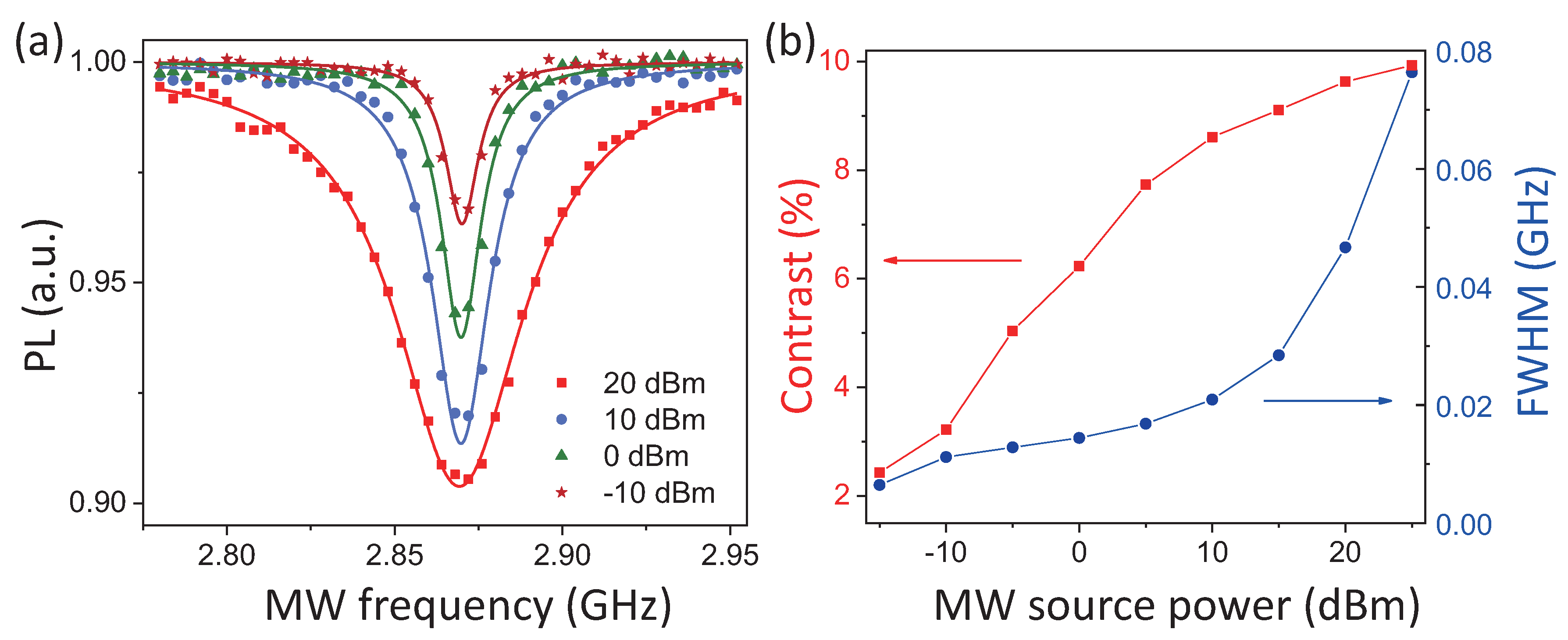
3.1. MW Magnetic Field Detection Using a Single NV Center in Diamond
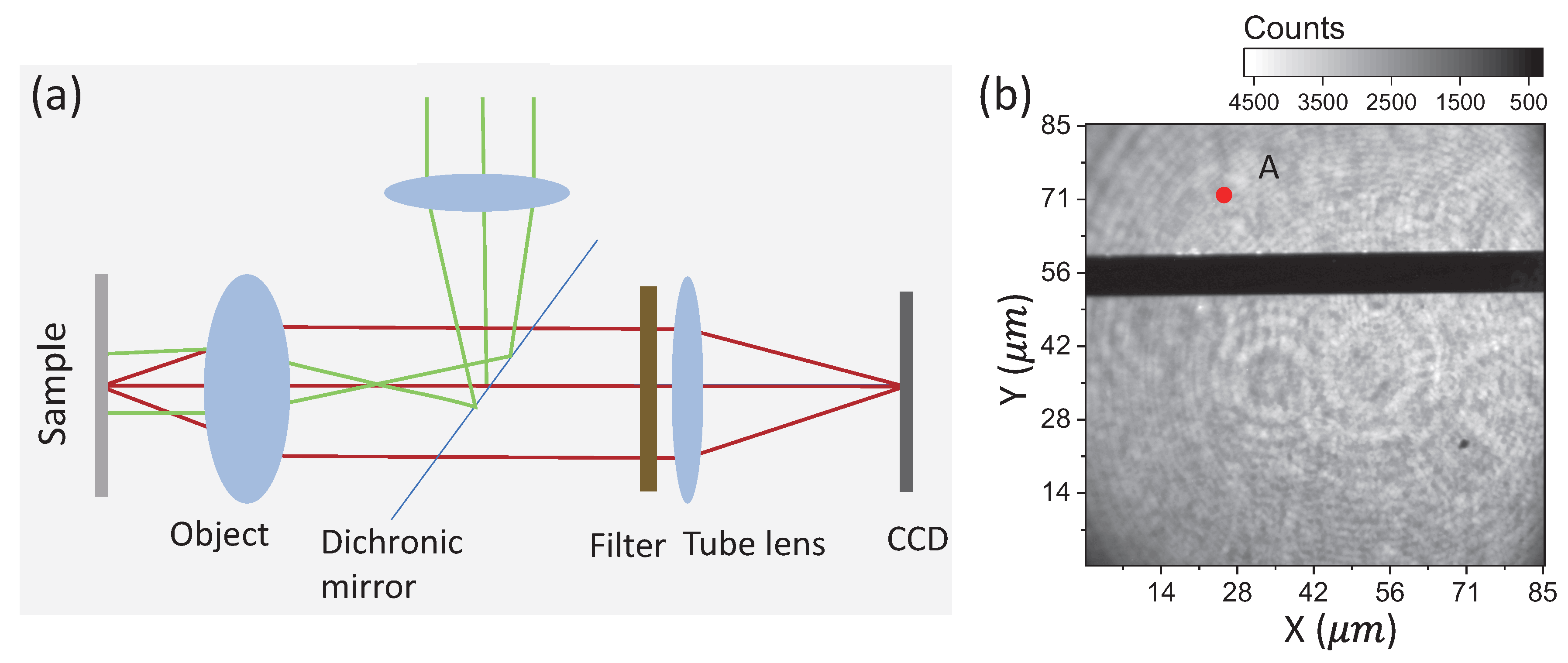
3.2. Wide-Field MW Magnetic Field Imaging with Ensemble NV Centers
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, M.; Meng, C.; Zhang, Q.; Duan, C.; Shi, F.; Du, J. Quantum metrology with single spins in diamond under ambient conditions. Natl. Sci. Rev. 2017, 5, 346–355. [Google Scholar] [CrossRef]
- Yasukawa, T.; Sigillito, A.; Rose, B.; Tyryshkin, A.; Lyon, S. Addressing spin transitions on Bi 209 donors in silicon using circularly polarized microwaves. Phys. Rev. B 2016, 93, 121306. [Google Scholar] [CrossRef]
- Iwasaki, H. A circularly polarized small-size microstrip antenna with a cross slot. IEEE Trans. Antennas Propag. 1996, 44, 1399–1401. [Google Scholar] [CrossRef]
- Wang, P.; Wen, G.; Li, J.; Huang, Y.; Yang, L.; Zhang, Q. Wideband circularly polarized UHF RFID reader antenna with high gain and wide axial ratio beamwidths. Prog. Electromagn. Res. 2012, 129, 365–385. [Google Scholar] [CrossRef]
- Li, C.; Zhang, F.S.; Zhang, F.; Yang, K. A Wideband Circularly Polarized Antenna with Wide Beamwidth for GNSS Applications. Prog. Electromagn. Res. 2018, 84, 189–200. [Google Scholar] [CrossRef]
- Anikeev, V. Calculation of calorimetric effect of thermo-field electron emission. IEEE Trans. Dielec. Electr. Insul. 1999, 6, 426–429. [Google Scholar] [CrossRef]
- Vremera, E.T.; Brunetti, L.; Oberto, L.; Sellone, M. Power sensor calibration by implementing true-twin microcalorimeter. IEEE Trans. Instrum. Meas. 2011, 60, 2335–2340. [Google Scholar] [CrossRef]
- Black, R.; Wellstood, F.; Dantsker, E.; Miklich, A.; Koelle, D.; Ludwig, F.; Clarke, J. Imaging radio-frequency fields using a scanning SQUID microscope. Appl. Phys. Lett. 1995, 66, 1267–1269. [Google Scholar] [CrossRef]
- Böhi, P.; Riedel, M.F.; Hänsch, T.W.; Treutlein, P. Imaging of microwave fields using ultracold atoms. Appl. Phys. Lett. 2010, 97, 051101. [Google Scholar] [CrossRef]
- Shi, H.; Ma, J.; Li, X.; Liu, J.; Li, C.; Zhang, S. A Quantum-Based Microwave Magnetic Field Sensor. Sensors 2018, 18, 3288. [Google Scholar] [CrossRef]
- Horsley, A.; Du, G.X.; Treutlein, P. Widefield microwave imaging in alkali vapor cells with sub-100 μm resolution. New J. Phys. 2015, 17, 112002. [Google Scholar] [CrossRef]
- Rondin, L.; Tetienne, J.; Hingant, T.; Roch, J.; Maletinsky, P.; Jacques, V. Magnetometry with nitrogen-vacancy defects in diamond. Rep. Prog. Phys. 2014, 77, 056503. [Google Scholar] [CrossRef]
- Wang, N.; Liu, G.Q.; Leong, W.H.; Zeng, H.; Feng, X.; Li, S.H.; Dolde, F.; Fedder, H.; Wrachtrup, J.; Cui, X.D.; et al. Magnetic Criticality Enhanced Hybrid Nanodiamond Thermometer under Ambient Conditions. Phys. Rev. X 2018, 8, 011042. [Google Scholar] [CrossRef]
- Gross, I.; Akhtar, W.; Garcia, V.; Martínez, L.; Chouaieb, S.; Garcia, K.; Carrétéro, C.; Barthélémy, A.; Appel, P.; Maletinsky, P.; et al. Real-space imaging of non-collinear antiferromagnetic order with a single-spin magnetometer. Nature 2017, 549, 252–256. [Google Scholar] [CrossRef]
- Kost, M.; Cai, J.; Plenio, M.B. Resolving single molecule structures with nitrogen-vacancy centers in diamond. Sci. Rep. 2015, 5, 11007. [Google Scholar] [CrossRef]
- Wang, P.; Yuan, Z.; Huang, P.; Rong, X.; Wang, M.; Xu, X.; Duan, C.; Ju, C.; Shi, F.; Du, J. High-resolution vector microwave magnetometry based on solid-state spins in diamond. Nat. Commun. 2015, 6, 6631. [Google Scholar] [CrossRef]
- Shao, L.; Liu, R.; Zhang, M.; Shneidman, A.V.; Audier, X.; Markham, M.; Dhillon, H.; Twitchen, D.J.; Xiao, Y.F.; Lončar, M. Wide-Field Optical Microscopy of Microwave Fields Using Nitrogen-Vacancy Centers in Diamonds. Adv. Opt. Mater. 2016, 4, 1075–1080. [Google Scholar] [CrossRef]
- Dréau, A.; Lesik, M.; Rondin, L.; Spinicelli, P.; Arcizet, O.; Roch, J.F.; Jacques, V. Avoiding power broadening in optically detected magnetic resonance of single NV defects for enhanced dc magnetic field sensitivity. Phys. Rev. B 2011, 84, 195204. [Google Scholar] [CrossRef]
- London, P.; Balasubramanian, P.; Naydenov, B.; McGuinness, L.; Jelezko, F. Strong driving of a single spin using arbitrarily polarized fields. Phys. Rev. A 2014, 90, 012302. [Google Scholar] [CrossRef]
- Alegre, T.P.M.; Santori, C.; Medeiros-Ribeiro, G.; Beausoleil, R.G. Polarization-selective excitation of nitrogen vacancy centers in diamond. Phys. Rev. B 2007, 76, 165205. [Google Scholar] [CrossRef]
- Herrmann, J.; Appleton, M.A.; Sasaki, K.; Monnai, Y.; Teraji, T.; Itoh, K.M.; Abe, E. Polarization-and frequency-tunable microwave circuit for selective excitation of nitrogen-vacancy spins in diamond. Appl. Phys. Lett. 2016, 109, 183111. [Google Scholar] [CrossRef]
- Goldman, M.L.; Doherty, M.; Sipahigil, A.; Yao, N.Y.; Bennett, S.; Manson, N.; Kubanek, A.; Lukin, M.D. State-selective intersystem crossing in nitrogen-vacancy centers. Phys. Rev. B 2015, 91, 165201. [Google Scholar] [CrossRef]
- Li, C.H.; Dong, Y.; Xu, J.Y.; Li, D.F.; Chen, X.D.; Du, A.; Ge, Y.S.; Guo, G.C.; Sun, F.W. Enhancing the sensitivity of a single electron spin sensor by multi-frequency control. Appl. Phys. Lett. 2018, 113, 072401. [Google Scholar] [CrossRef]
- Sipahigil, A.; Goldman, M.L.; Togan, E.; Chu, Y.; Markham, M.; Twitchen, D.J.; Zibrov, A.S.; Kubanek, A.; Lukin, M.D. Quantum interference of single photons from remote nitrogen-vacancy centers in diamond. Phys. Rev. Lett. 2012, 108, 143601. [Google Scholar] [CrossRef]
- Yahata, K.; Matsuzaki, Y.; Saito, S.; Watanabe, H.; Ishi-Hayase, J. Demonstration of vector magnetic field sensing by simultaneous control of nitrogen-vacancy centers in diamond using multi-frequency microwave pulses. Appl. Phys. Lett. 2019, 114, 022404. [Google Scholar] [CrossRef]
- Horsley, A.; Appel, P.; Wolters, J.; Achard, J.; Tallaire, A.; Maletinsky, P.; Treutlein, P. Microwave Device Characterization Using a Widefield Diamond Microscope. Phys. Rev. Appl. 2018, 10, 044039. [Google Scholar] [CrossRef]
- Horsley, A.; Du, G.X.; Pellaton, M.; Affolderbach, C.; Mileti, G.; Treutlein, P. Imaging of relaxation times and microwave field strength in a microfabricated vapor cell. Phys. Rev. A 2013, 88, 063407. [Google Scholar] [CrossRef]
- Dong, Y.; Zheng, Y.; Li, S.; Li, C.C.; Chen, X.D.; Guo, G.C.; Sun, F.W. Non-Markovianity-assisted high-fidelity Deutsch–Jozsa algorithm in diamond. NPJ Quantum Inf. 2018, 4, 3. [Google Scholar] [CrossRef]
- Jensen, K.; Leefer, N.; Jarmola, A.; Dumeige, Y.; Acosta, V.M.; Kehayias, P.; Patton, B.; Budker, D. Cavity-enhanced room-temperature magnetometry using absorption by nitrogen-vacancy centers in diamond. Phys. Rev. Lett. 2014, 112, 160802. [Google Scholar] [CrossRef]
- Wang, J.; Feng, F.; Zhang, J.; Chen, J.; Zheng, Z.; Guo, L.; Zhang, W.; Song, X.; Guo, G.; Fan, L.; et al. High-sensitivity temperature sensing using an implanted single nitrogen-vacancy center array in diamond. Phys. Rev. B 2015, 91, 155404. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.-H.; Li, D.-F.; Zheng, Y.; Sun, F.-W.; Du, A.M.; Ge, Y.-S. Detecting Axial Ratio of Microwave Field with High Resolution Using NV Centers in Diamond. Sensors 2019, 19, 2347. https://doi.org/10.3390/s19102347
Li C-H, Li D-F, Zheng Y, Sun F-W, Du AM, Ge Y-S. Detecting Axial Ratio of Microwave Field with High Resolution Using NV Centers in Diamond. Sensors. 2019; 19(10):2347. https://doi.org/10.3390/s19102347
Chicago/Turabian StyleLi, Cui-Hong, Deng-Feng Li, Yu Zheng, Fang-Wen Sun, A. M. Du, and Ya-Song Ge. 2019. "Detecting Axial Ratio of Microwave Field with High Resolution Using NV Centers in Diamond" Sensors 19, no. 10: 2347. https://doi.org/10.3390/s19102347
APA StyleLi, C.-H., Li, D.-F., Zheng, Y., Sun, F.-W., Du, A. M., & Ge, Y.-S. (2019). Detecting Axial Ratio of Microwave Field with High Resolution Using NV Centers in Diamond. Sensors, 19(10), 2347. https://doi.org/10.3390/s19102347



