Residual Motion Error Correction with Backprojection Multisquint Algorithm for Airborne Synthetic Aperture Radar Interferometry
Abstract
1. Introduction
- (1)
- The BP algorithm is firstly used to accurately focus InSAR image pairs, then the subapertures (also called sublooks in this paper) for MSQ differential interferometry is evenly split in the azimuth wavenumber domain. In contrast to the process of the subaperture differential interferometric phase integration in [2], the proposed BP-MSQ algorithm estimates polynomial parameters of RME by using the subaperture differential phase, while it analyzes the representation of RME in the azimuth time domain. In this manner, both high- and low-frequency error components of RME can be obtained precisely.
- (2)
- The second contribution of this work is that accurate analytic expressions of RME in BP InSAR image pairs from stripmap and spotlight SAR modes are derived separately. In addition, the characteristics of subaperture differential interferometry phase diagrams with linear and high-order types RME are analyzed, which makes the RME estimation more flexible and adjustable to multiple imaging modes.
- (3)
- In the framework of the improved BP-MSQ algorithm, linear RME estimation flowcharts for stripmap SAR and spotlight SAR are given differently. Meanwhile, a piecewise RME model is developed for the refined high-order RME compensation under spotlight mode. Avoiding the differential phase integration in RME estimation, the developed BP-MSQ outperforms the original MSQ in the case of strong noises.
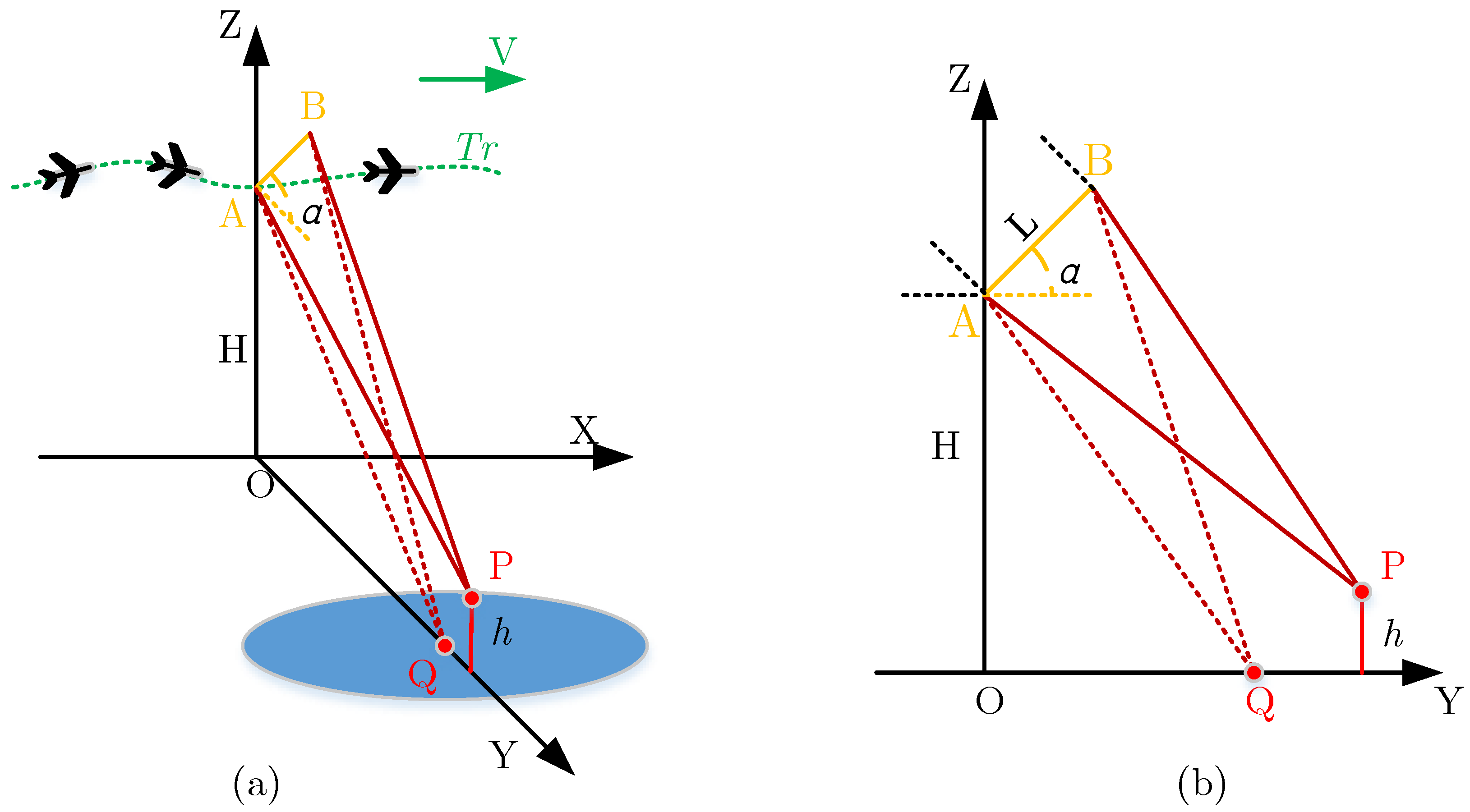
2. Airborne InSAR Focusing with Backprojection Imaging
3. RME Estimation Principle with the Polynomial Fitting MSQ
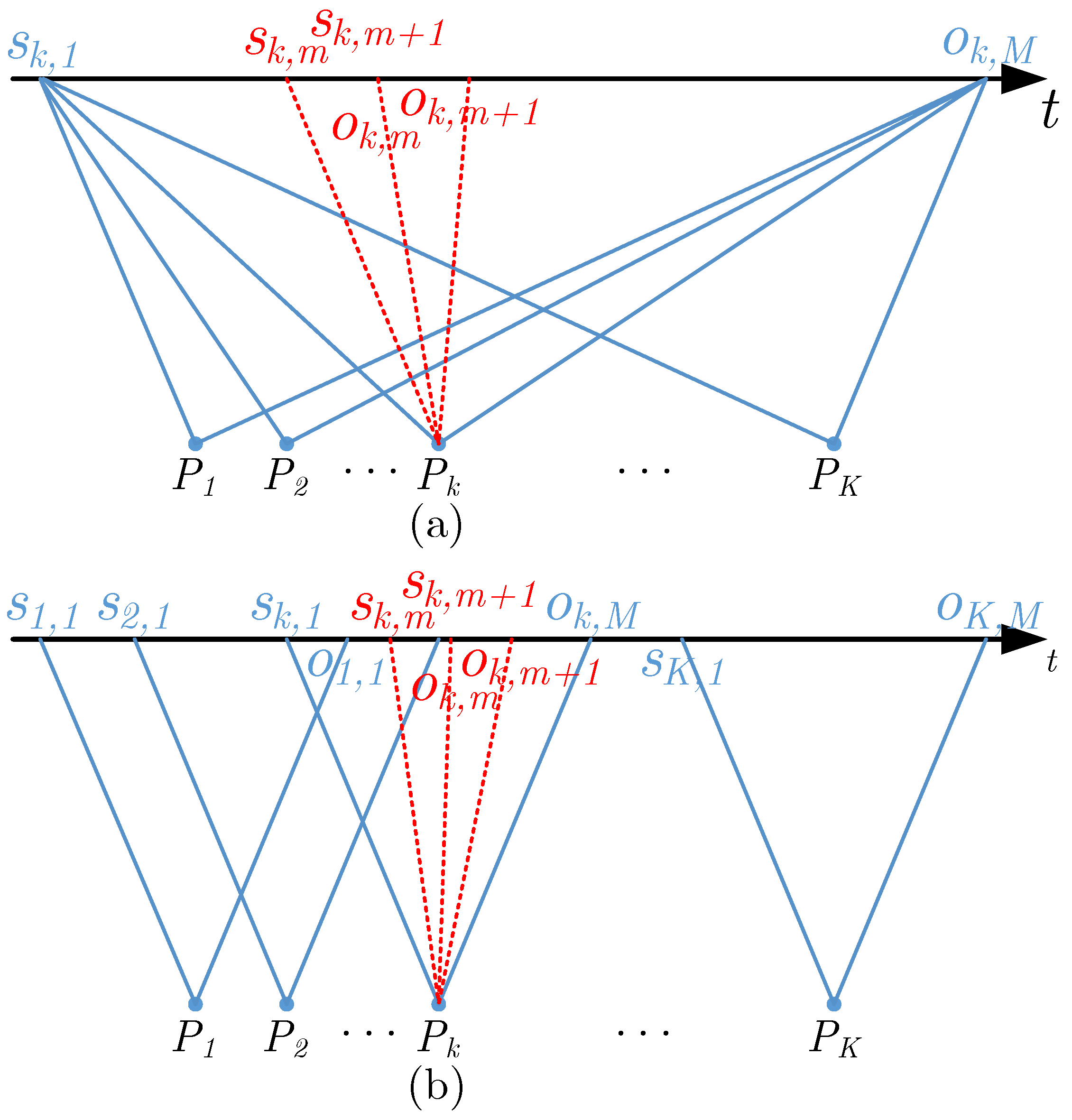
3.1. RME Estimation Principle with the BP-MSQ Algorithm
3.2. Investigation of RME Fitting Scheme in Stripmap and Spotlight SAR Modes
- (1)
- Assume InSAR works in spotlight mode and RME has a linear form, we haveIt can be illustrated that for the linear RME and SAR works in the spotlight mode, the differential phases of different scattering points in the same subaperture are the same, and the differential phase of the same scattering point in different subapertures is also the same. Therefore, the linear coefficient of the linear RME can be calculated by Equation (11), and the RME phase can be obtained by linear fitting.
- (2)
- Assume InSAR works in spotlight mode and RME has a high-order polynomial form, we haveIt can be illustrated that for the high-order RME and SAR works in the spotlight mode, the differential phases of the different scattering points in the same subaperture are the same, which is the same as in the Case (1). However, unlike Case (1), the differential phase of the same scattering point in different subapertures is generally different. Since the time intervals of the subapertures in spotlight SAR are independent of each other, when the subaperture number is sufficient, the RME in each subaperture can be considered to be linear. Therefore, the linear coefficient of the linear RME in each subaperture can be estimated by Equation (11), and the RME phase of the full imaging time is obtained by multi-linear high-order fitting.
- (3)
- Assume InSAR works in stripmap mode and RME has a linear form, we haveIt can be illustrated that for the strip mode, there is a partial coincidence interval in the imaging time interval of two adjacent scattering points and (the imaging time intervals are and , respectively). When the RME is linear, since the subaperture is divided in the azimuth Doppler domain, the RME differential phases of the different scattering points in the same subaperture are the same. At the same time, since the subaperture is evenly divided, the RME differential phase of the same scattering point in different subapertures is also the same. Therefore, the linear coefficient of the linear RME can be calculated by Equation (11) as in Case (1) and Case (2), and the linear RME phase can be obtained by linear fitting.
- (4)
- Assume InSAR works in stripmap mode and RME has a high-order polynomial form, we haveIn this case, the latter two equations in (15) no longer hold. When the high-order RME acts on the stripmap mode SAR, the interferometric phases of the azimuth-ordered scattering points in the same subaperture reflect the RME differential phases in different time intervals and are continuous in the time domain. Therefore, the RME differential phase still appears as a high-order form along the azimuth direction, and it is not feasible to estimate the linear coefficient through the RME differential phase. At the same time, since the imaging time corresponding to the adjacent subapertures is partially coincident, it is necessary to obtain the RME differential phase of the full imaging time by sub-image differential interferometric phase in a “sliding window” splicing manner, and then the full imaging time RME phase can be obtain through the RME differential phase interpolation and integration.
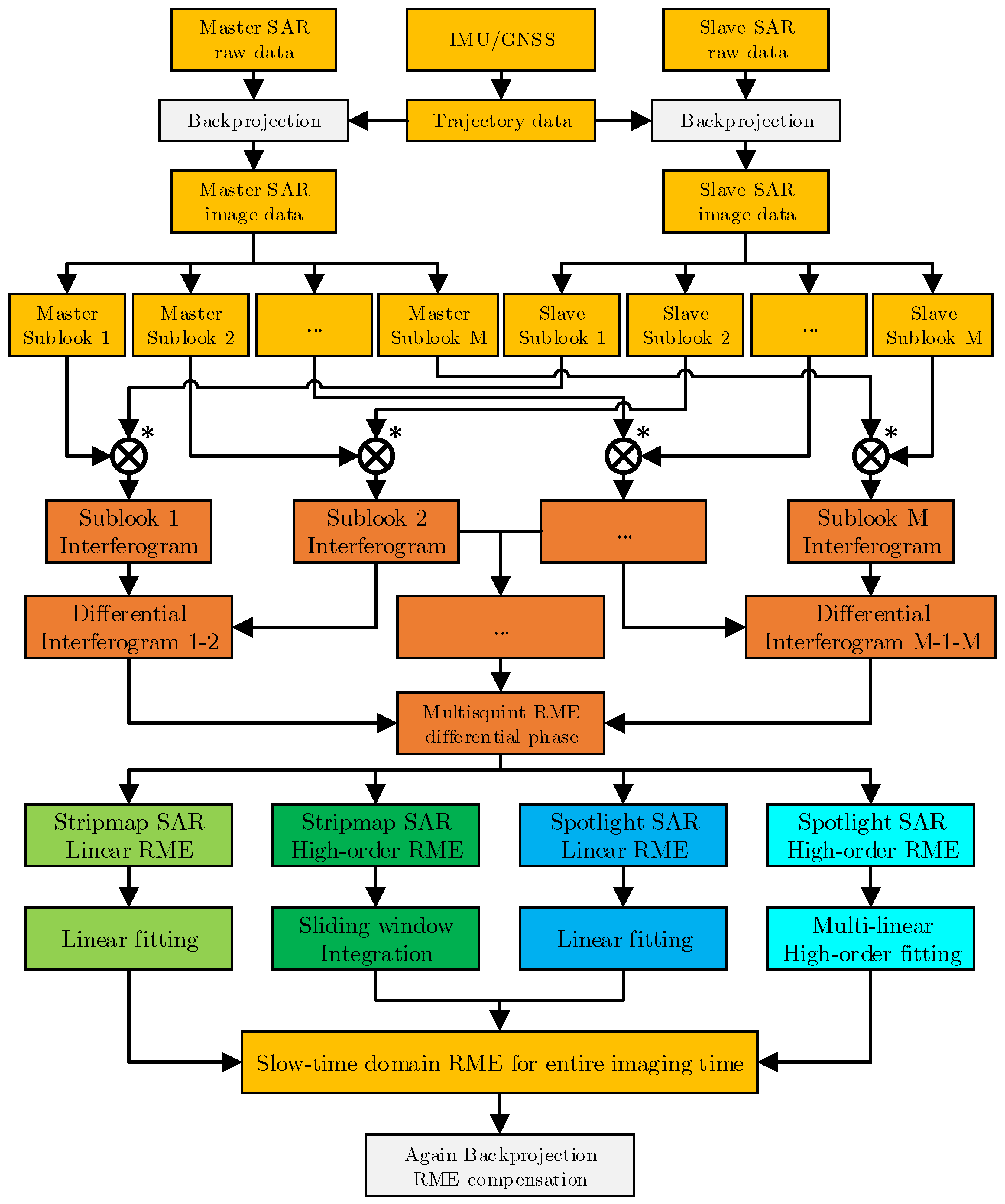
3.3. Detailed Algorithm Procedure
- Step (1)
- BP imaging using track information. Firstly, the track information can be extracted from IMU/GNSS. Then, the corresponding single-look complex image of each antenna can be obtained by BP algorithm from the echo data of the master antenna and the slave antenna.
- Step (2)
- Subapertures segmenting in azimuth Doppler domain. The Doppler spectrum of the single-look complex image of the master antenna and the slave antenna is uniformly divided into M frequency bands, and then multi-look images of the two antennas, i.e., a plurality of subaperture images are obtained.
- Step (3)
- Subaperture images differential interferometry. Firstly, the image of the subaperture with the same radar sight looking angle of the master antenna and the slave antenna is multiplied to obtain a subaperture interferogram. Then, the adjacent subaperture interferograms are multiplied by conjugate to obtain a subaperture differential interferogram.
- Step (4)
- RME estimation. The RME differential phase can be extracted from the subaperture differential interferogram, and then the corresponding strategy is adopted according to the SAR working mode and the RME type to estimate the value of the RME in the time domain over the entire imaging time.
- Step (5)
- BP imaging with RME compensation. BP algorithm was used to refocus the image and compensate RME at the same time to obtain the interferogram corrected by RME.
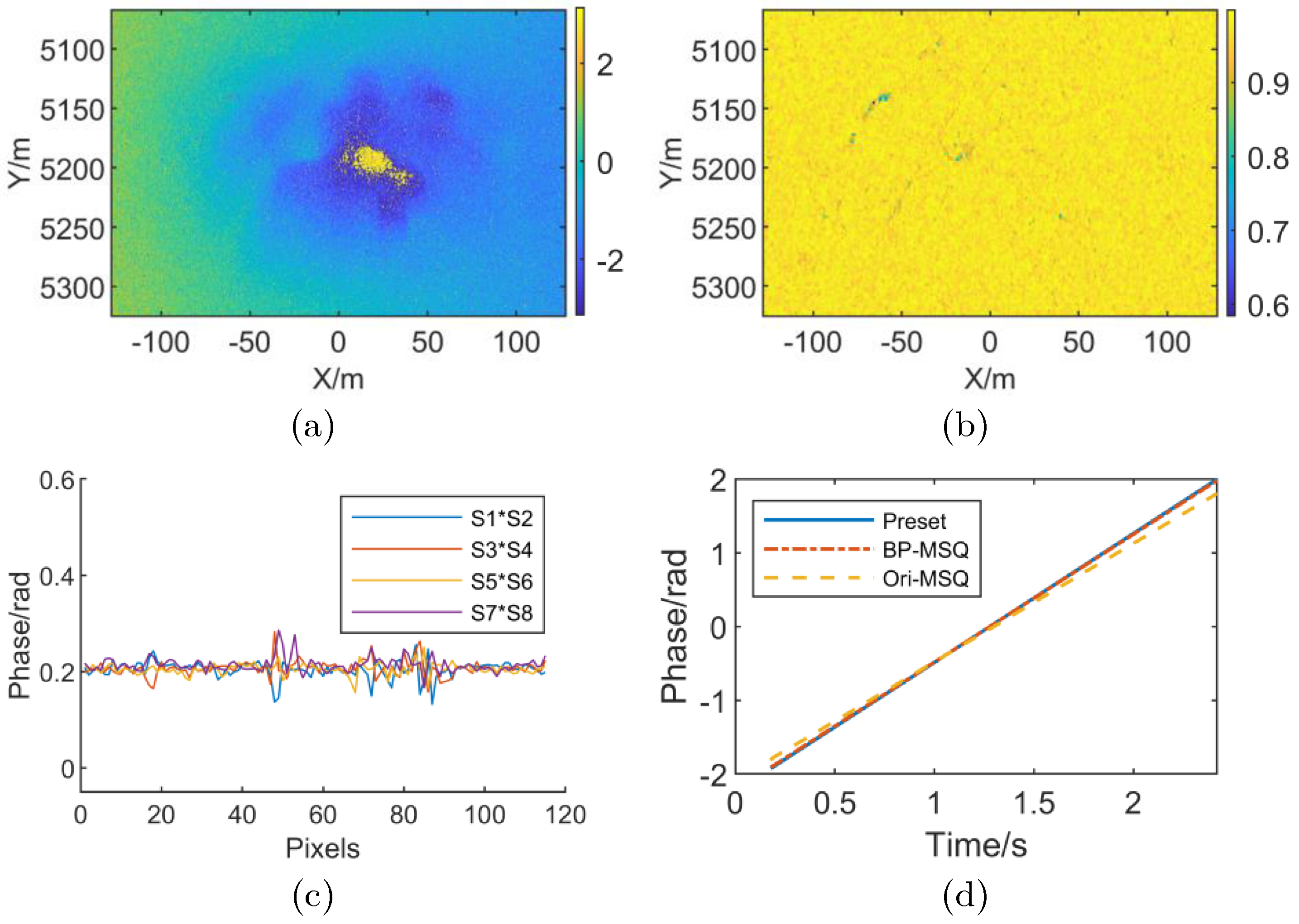
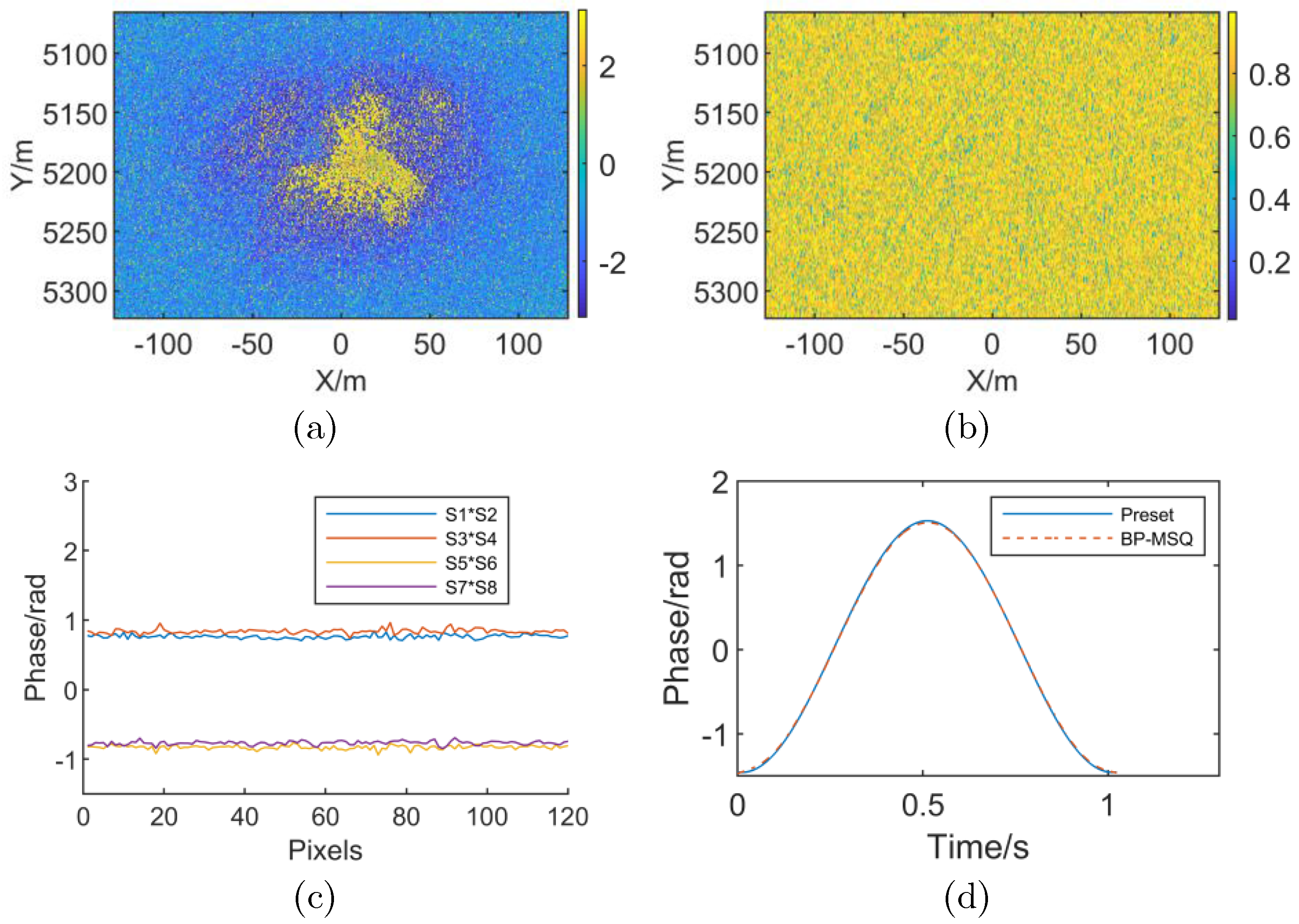
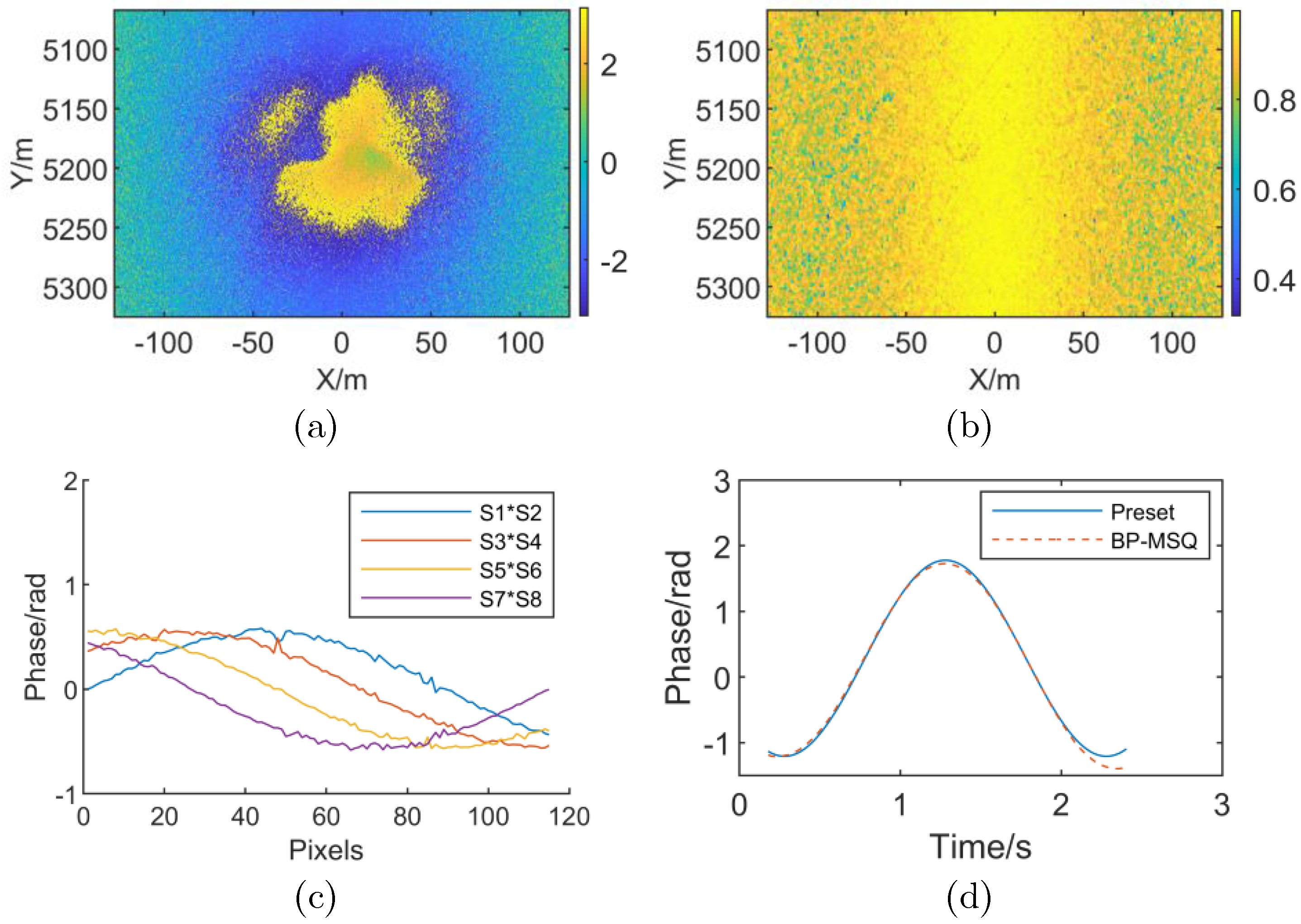
4. Experiments
4.1. Linear RME Simulation Experiment with Stripmap SAR
4.2. Simulation with High-Order RME
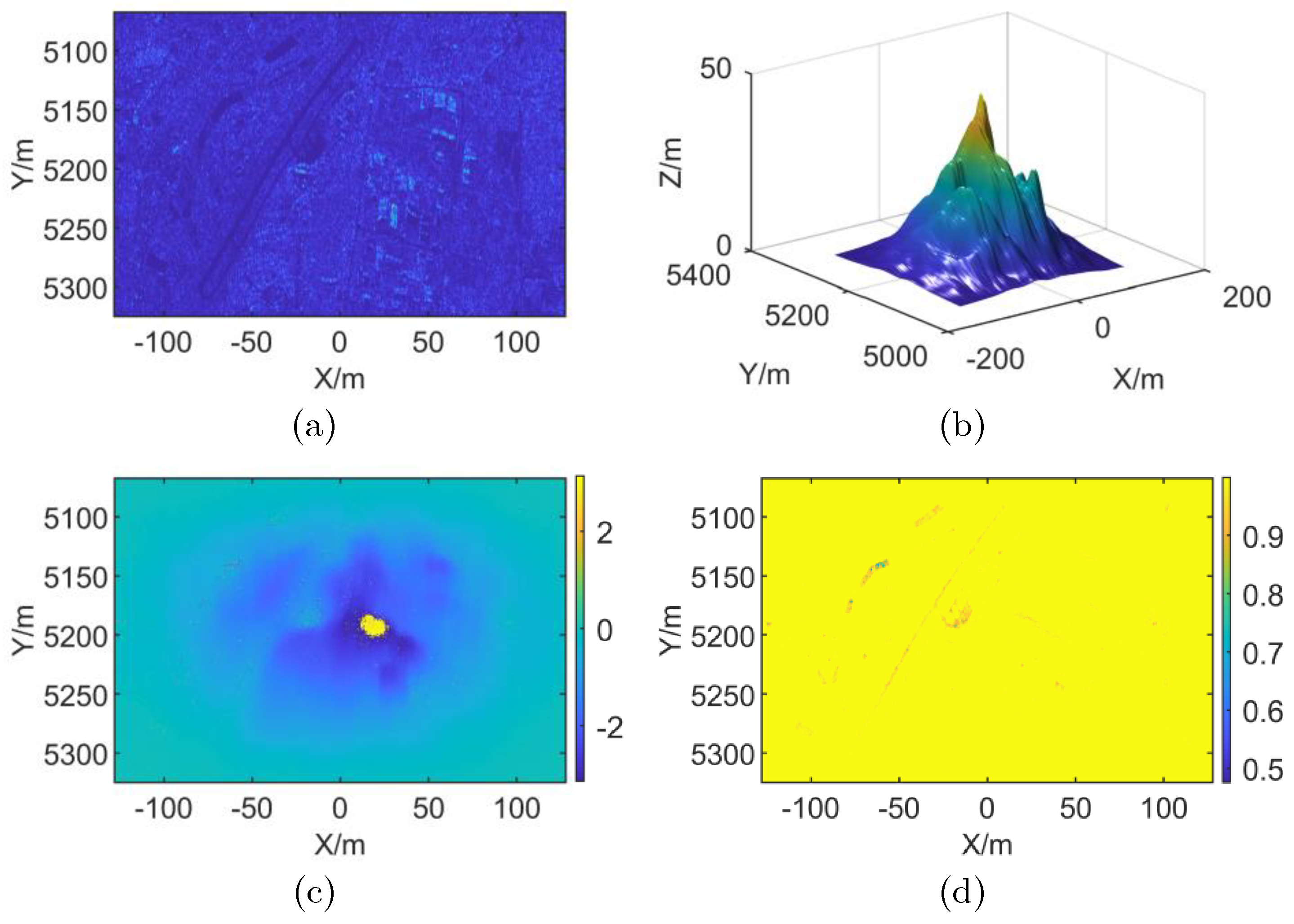
4.3. Actual InSAR System Data Processing
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- de Macedo, K.A.C.; Wimmer, C.; Moreira, J.R. Highly accurate and precise airborne single-pass interferometry for DEM generation over challenging terrain. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 394–397. [Google Scholar]
- Cao, N.; Lee, H.; Zaugg, E.; Shrestha, R.; Carter, W.E.; Glennie, G.; Lu, Z.; Yu, H. Estimation of Residual Motion Errors in Airborne SAR Interferometry Based on Time-Domain Backprojection and Multisquint Techniques. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2397–2407. [Google Scholar] [CrossRef]
- Ma, L.; Shi, J.; Wei, S.; Shi, D.; Xu, S. Ka-band InSAR data processing of BP method. In Proceedings of the 2014 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Guilin, China, 5–8 August 2014; pp. 316–320. [Google Scholar]
- Fornaro, G.; Franceschetti, G.; Perna, S. Motion Compensation Errors: Effects on the Accuracy of Airborne SAR Images. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1338–1352. [Google Scholar] [CrossRef]
- Yang, M.; Kong, F.; Zhu, D.; Yu, X. Efficient motion compensation approach with modified phase correction for airborne SAR. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1622–1625. [Google Scholar]
- Zhang, L.; Wang, G.; Qiao, Z.; Wang, H. Azimuth Motion Compensation With Improved Subaperture Algorithm for Airborne SAR Imaging. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 184–193. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, M.; Huang, Y.; Zhang, L.; Wang, F. Robust Two-Dimensional Spatial-Variant Map-Drift Algorithm for UAV SAR Autofocusing. Remote Sens. 2019, 11, 340. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, G.; Zhang, L. Precise Aperture-Dependent Motion Compensation with Frequency Domain Fast Back-Projection Algorithm. Sensors 2017, 17, 2454. [Google Scholar] [CrossRef] [PubMed]
- Frey, O.; Magnard, C.; Ruegg, M.; Meier, E. Focusing of Airborne Synthetic Aperture Radar Data From Highly Nonlinear Flight Tracks. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1844–1858. [Google Scholar] [CrossRef]
- Duersch, M.I.; Long, D.G. Analysis of time-domain back-projection for stripmap SAR. Int. J. Remote Sens. 2015, 36, 2010–2036. [Google Scholar] [CrossRef]
- Duersch, M.I.; Long, D.G. Backprojection SAR interferometry. Int. J. Remote Sens. 2015, 36, 979–999. [Google Scholar] [CrossRef]
- de Macedo, K.A.C.; Scheiber, R.; Moreira, A. An Autofocus Approach for Residual Motion Errors with Application to Airborne Repeat-Pass SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3151–3162. [Google Scholar] [CrossRef]
- Ran, L.; Liu, Z.; Zhang, L.; Li, T.; Xie, R. An Autofocus Algorithm for Estimating Residual Trajectory Deviations in Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3408–3425. [Google Scholar] [CrossRef]
- Fu, H.; Zhu, J.; Wang, C.; Wang, H.; Zhao, R. A Wavelet Decomposition and Polynomial Fitting-Based Method for the Estimation of Time-Varying Residual Motion Error in Airborne Interferometric SAR. IEEE Trans. Geosci. Remote Sens. 2018, 56, 49–59. [Google Scholar] [CrossRef]
- Prats, P.; Mallorqui, J.J. Estimation of Azimuth Phase Undulations With Multisquint Processing in Airborne Interferometric SAR Images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1530–1533. [Google Scholar] [CrossRef]
- Hensley, S.; Michel, T.; Simard, M.; Jones, C.; Muellerschoen, R.; Le, C.; Zebkery, H.; Chapman, B. Residual motion estimation for UAVSAR: Implications of an electronically scanned array. In Proceedings of the 2009 IEEE Radar Conference, Pasadena, CA, USA, 4–8 May 2009; pp. 1–5. [Google Scholar]
- Reigber, A.; Scheiber, R.; Jäger, M.; Prats-Iraola, P.; Jagdhuber, T.; Papathanassiou, K.P.; Nannini, M.; Aguilera, E.; Baumgartner, S.; Horn, R.; et al. Very-High-Resolution Airborne Synthetic Aperture Radar Imaging, Signal Processing and Applications. Proc. IEEE Inst. Electr. Electron. Eng. 2013, 101, 759–783. [Google Scholar] [CrossRef]
- Brancato, V.; Jäger, M.; Scheiber, R.; Hajnsek, I. A Motion Compensation Strategy for Airborne Repeat-Pass SAR Data. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1580–1584. [Google Scholar] [CrossRef]
- Scheiber, R.; Moreira, A. Coregistration of interferometric SAR images using spectral diversity. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2179–2191. [Google Scholar] [CrossRef]
- Prats, P.; de Macedo, K.A.C.; Reigber, A.; Scheiber, R.; Mallorqui, J.J. Comparison of Topography- and Aperture-Dependent Motion Compensation Algorithms for Airborne SAR. IEEE Geosci. Remote Sens. Lett. 2007, 4, 349–353. [Google Scholar] [CrossRef]
- Sun, B.; Fang, C.; Xu, H.; Gao, A. A New Synthetic Aperture Radar (SAR) Imaging Method Combining Match Filter Imaging and Image Edge Enhancement. Sensors 2018, 18, 4133. [Google Scholar] [CrossRef] [PubMed]


| Items | Symbol | Value |
|---|---|---|
| Wave Length | /(mm) | 18 |
| Band Width | B/(MHz) | 150 |
| Flight Speed | V/(m/s) | 200 |
| Pulse Repetition Frequency | PRF/(Hz) | 2000 |
| Flight Height | H/(m) | 3000 |
| Base Line | L/(m) | 1.21 |
| Baseline Obliquity | /() | 45 |
| Items | Symbol | Value |
|---|---|---|
| Wave Length | /(mm) | 8.57 |
| Band Width | B/(MHz) | 900 |
| Flight Speed | V/(m/s) | 100 |
| Pulse Repetition Frequency | PRF/(Hz) | 5000 |
| Flight Height | H/(m) | 3000 |
| Base Line | L/(m) | 0.087 |
| Baseline Obliquity | /() | 45 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, P.; Zhang, M.; Zhang, L.; Wang, G. Residual Motion Error Correction with Backprojection Multisquint Algorithm for Airborne Synthetic Aperture Radar Interferometry. Sensors 2019, 19, 2342. https://doi.org/10.3390/s19102342
Xie P, Zhang M, Zhang L, Wang G. Residual Motion Error Correction with Backprojection Multisquint Algorithm for Airborne Synthetic Aperture Radar Interferometry. Sensors. 2019; 19(10):2342. https://doi.org/10.3390/s19102342
Chicago/Turabian StyleXie, Pengfei, Man Zhang, Lei Zhang, and Guanyong Wang. 2019. "Residual Motion Error Correction with Backprojection Multisquint Algorithm for Airborne Synthetic Aperture Radar Interferometry" Sensors 19, no. 10: 2342. https://doi.org/10.3390/s19102342
APA StyleXie, P., Zhang, M., Zhang, L., & Wang, G. (2019). Residual Motion Error Correction with Backprojection Multisquint Algorithm for Airborne Synthetic Aperture Radar Interferometry. Sensors, 19(10), 2342. https://doi.org/10.3390/s19102342





