Fluid Sensing Using Quartz Tuning Forks—Measurement Technology and Applications
Abstract
1. Introduction
1.1. Benefits of Using Tuning Fork Sensors for Fluid Sensing
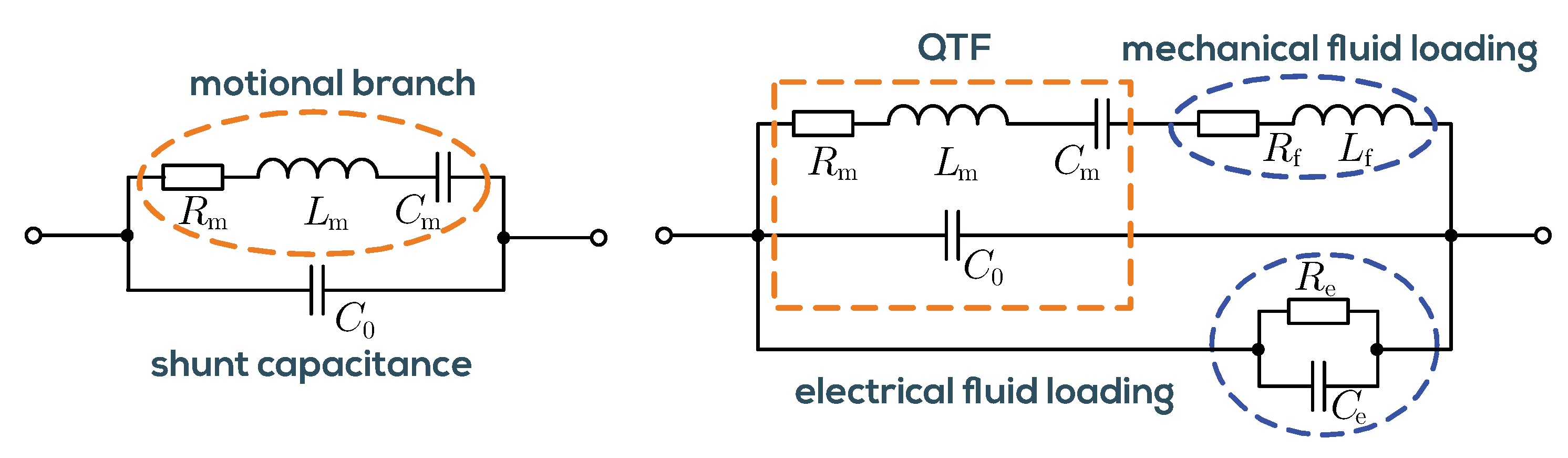
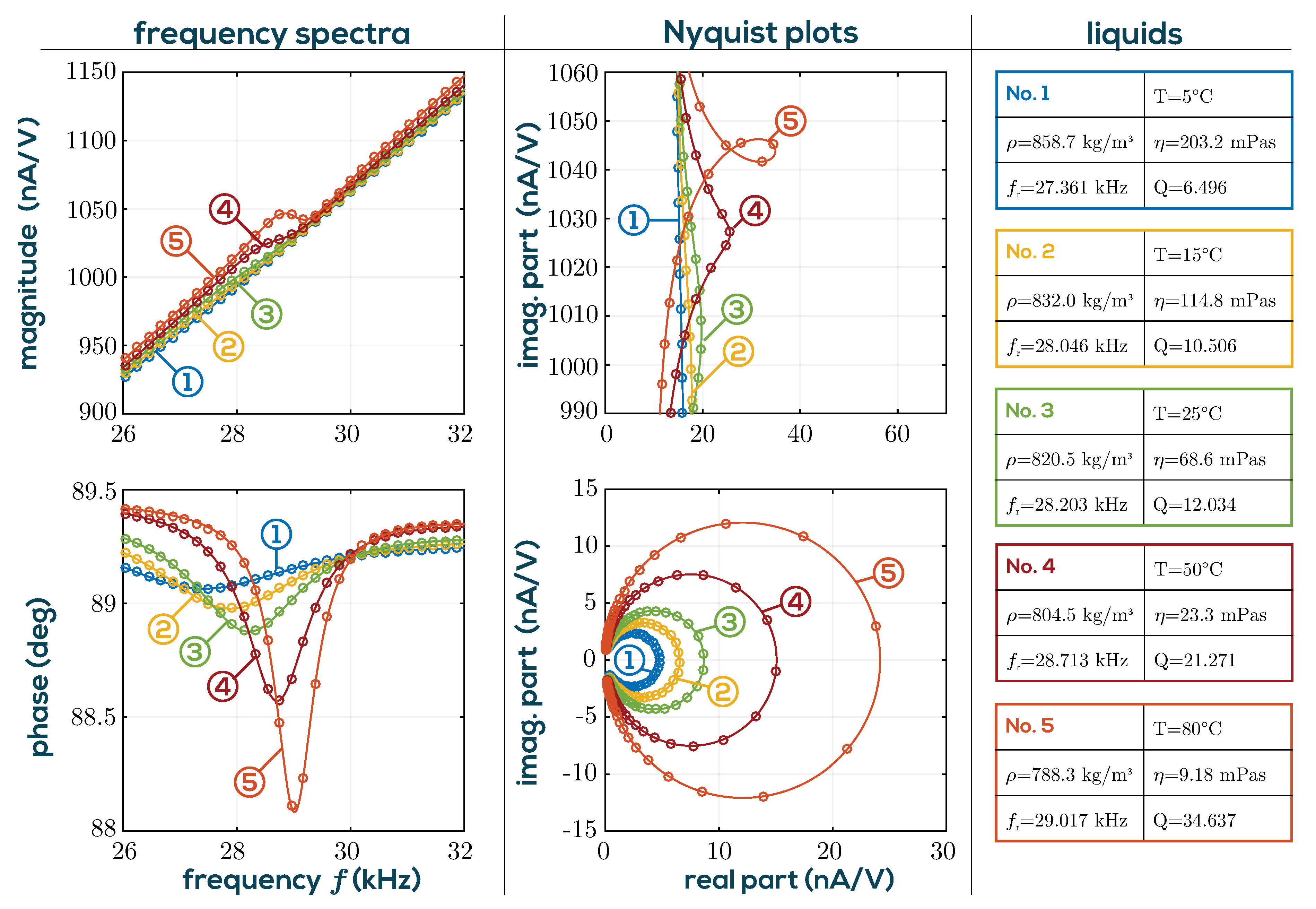
1.2. Viscosity and Density Sensing Using QTFs
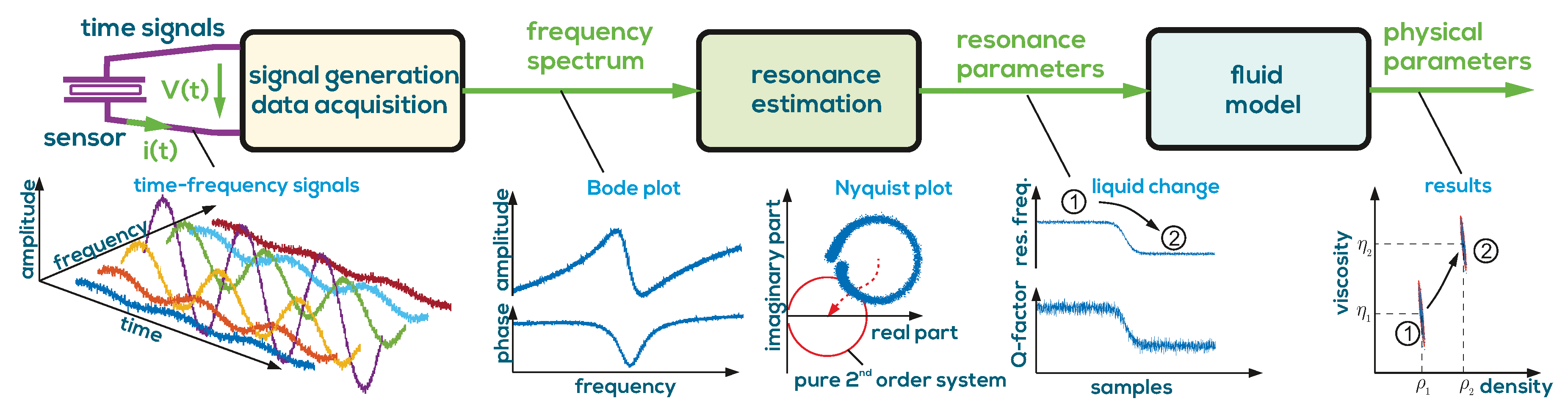
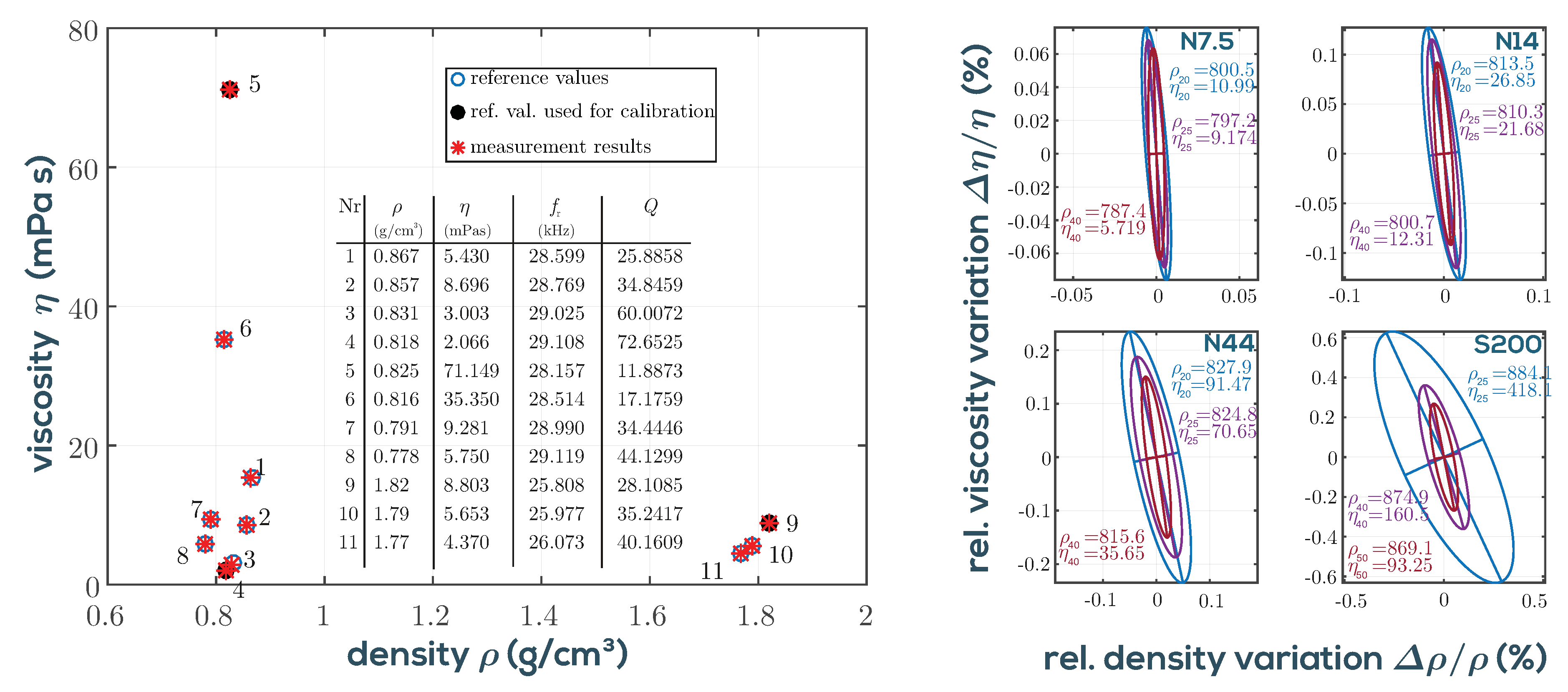
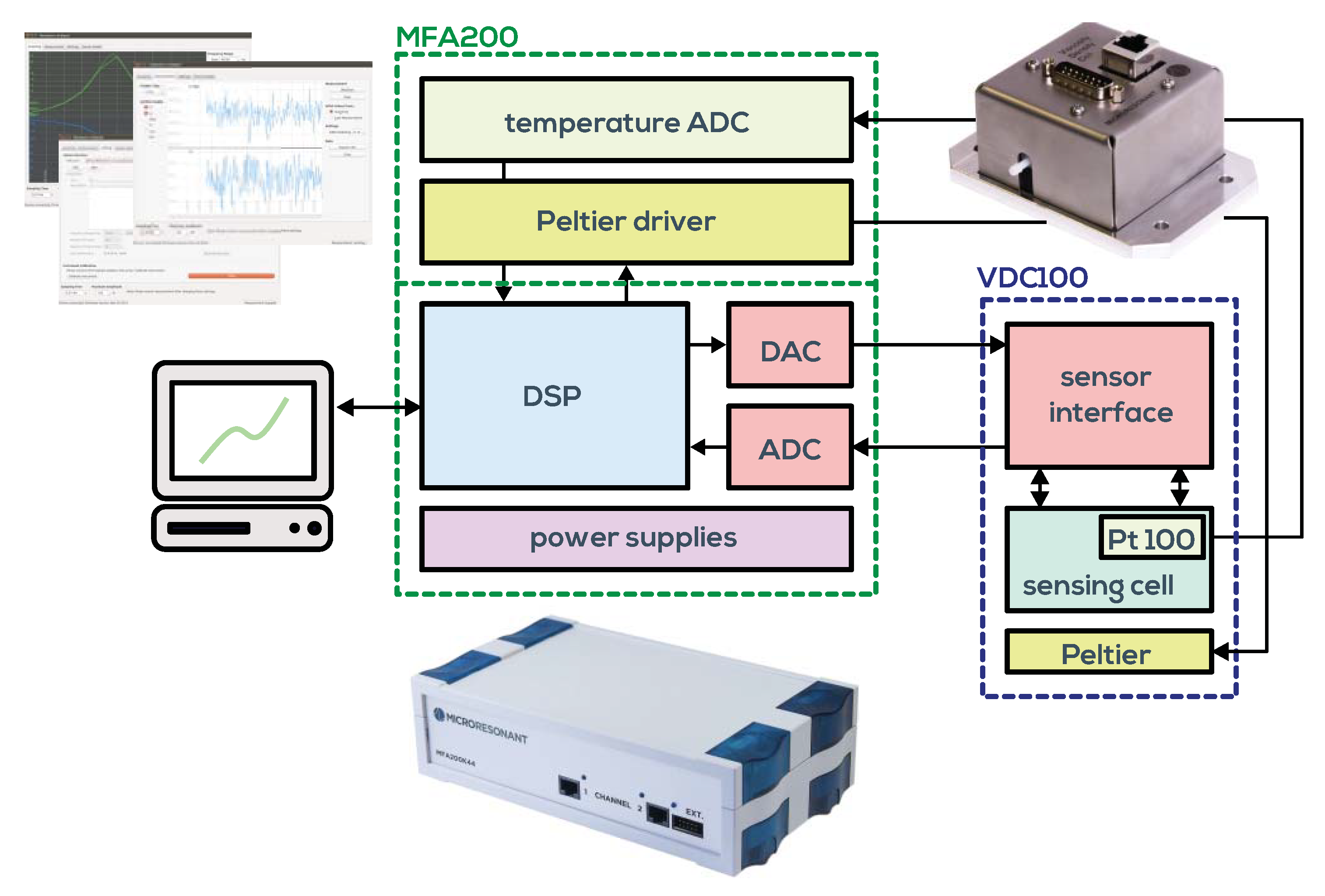
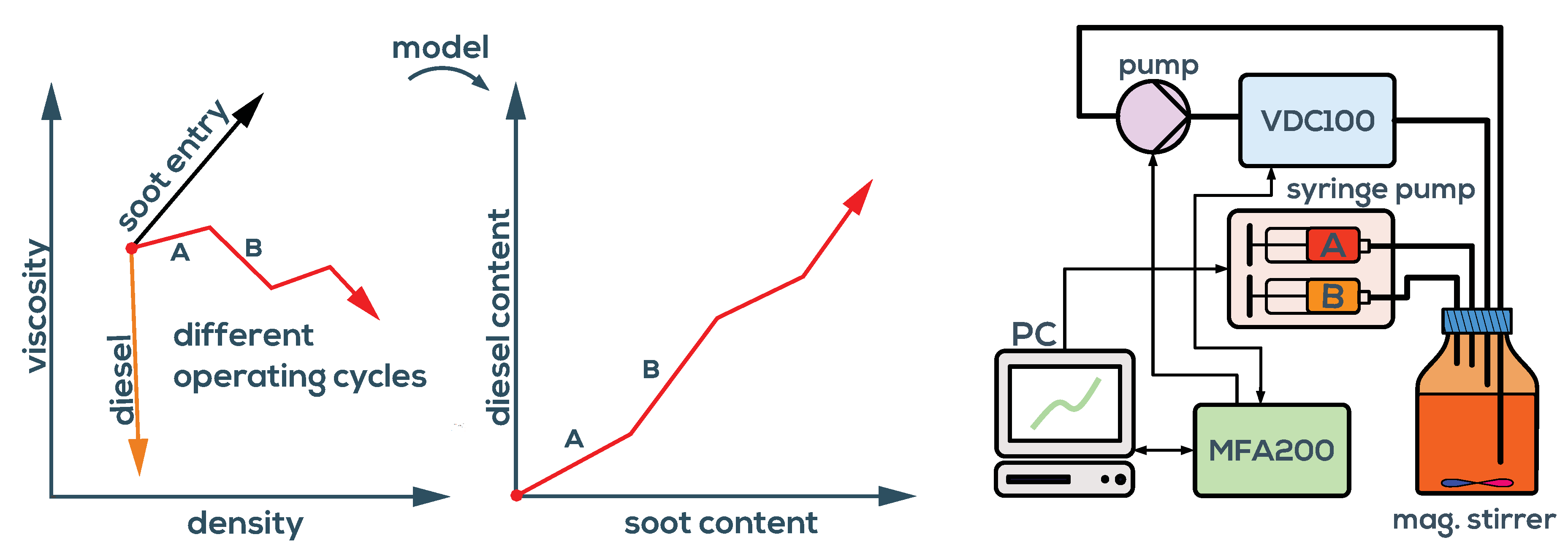
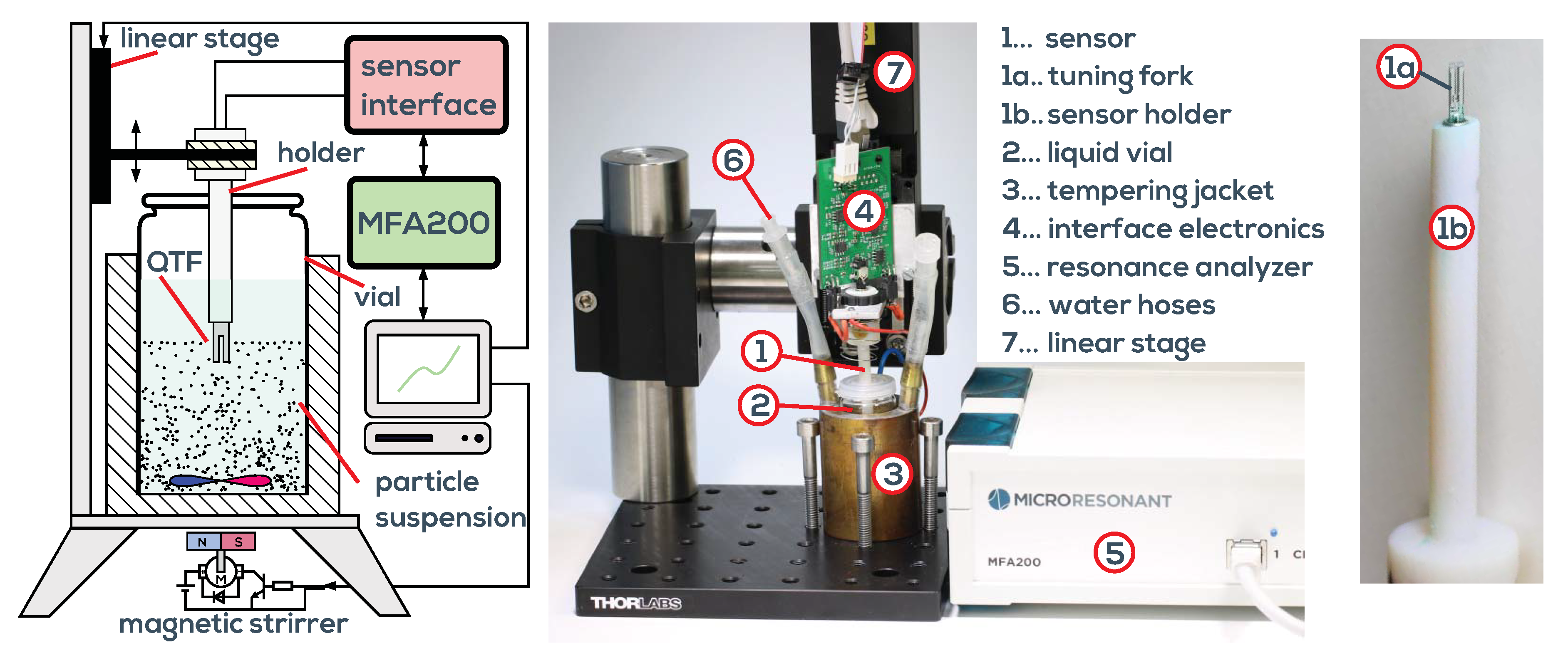
2. Measurement System
3. Applications
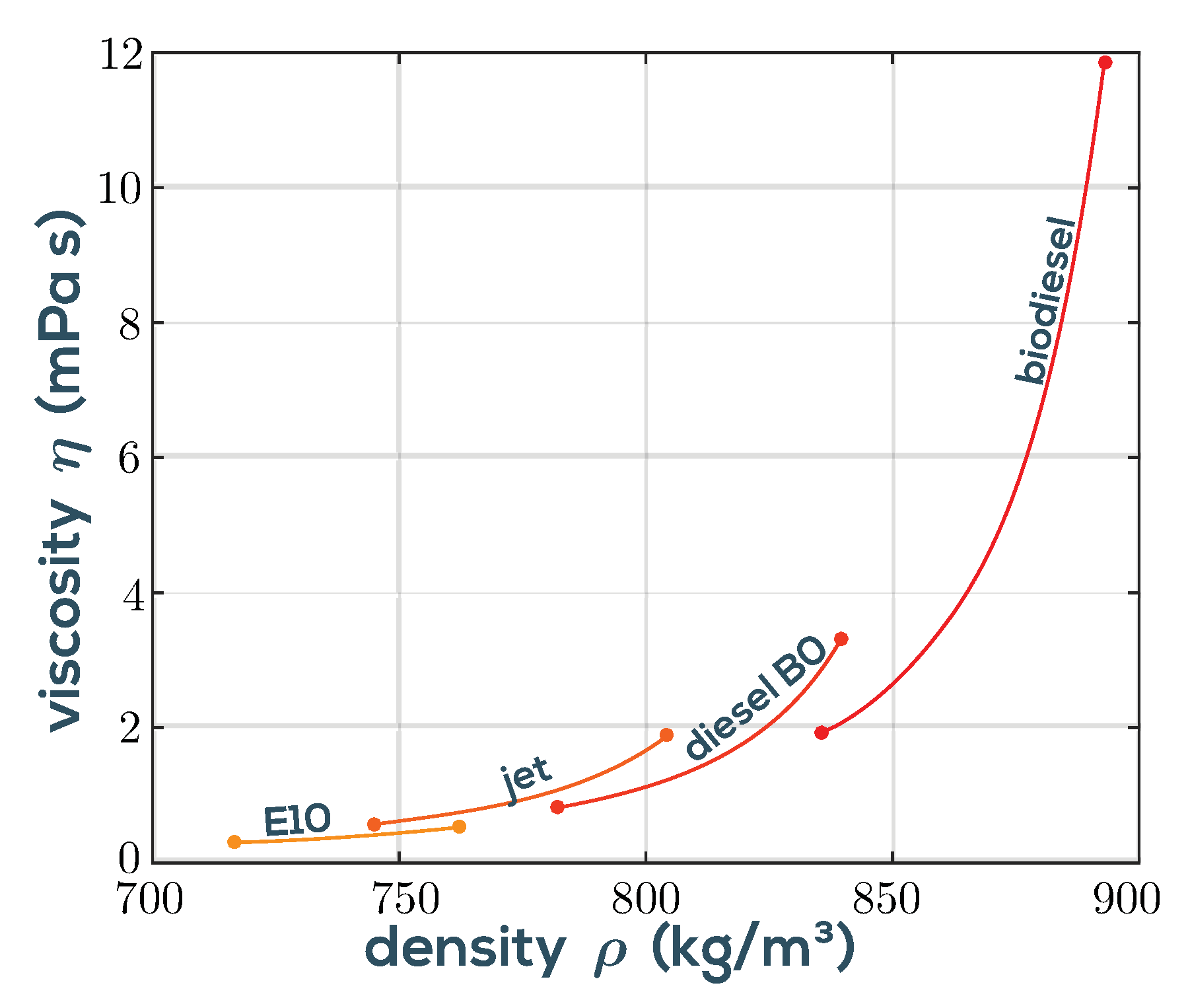
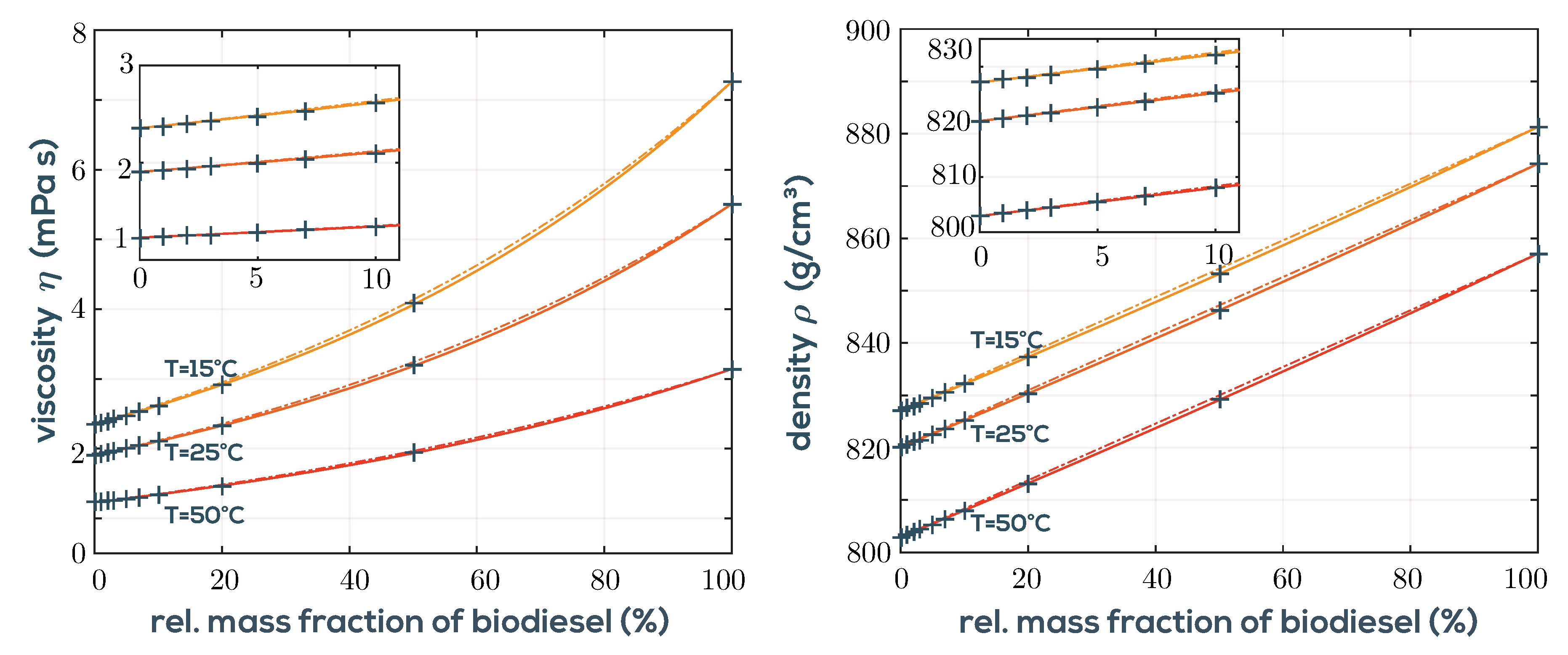
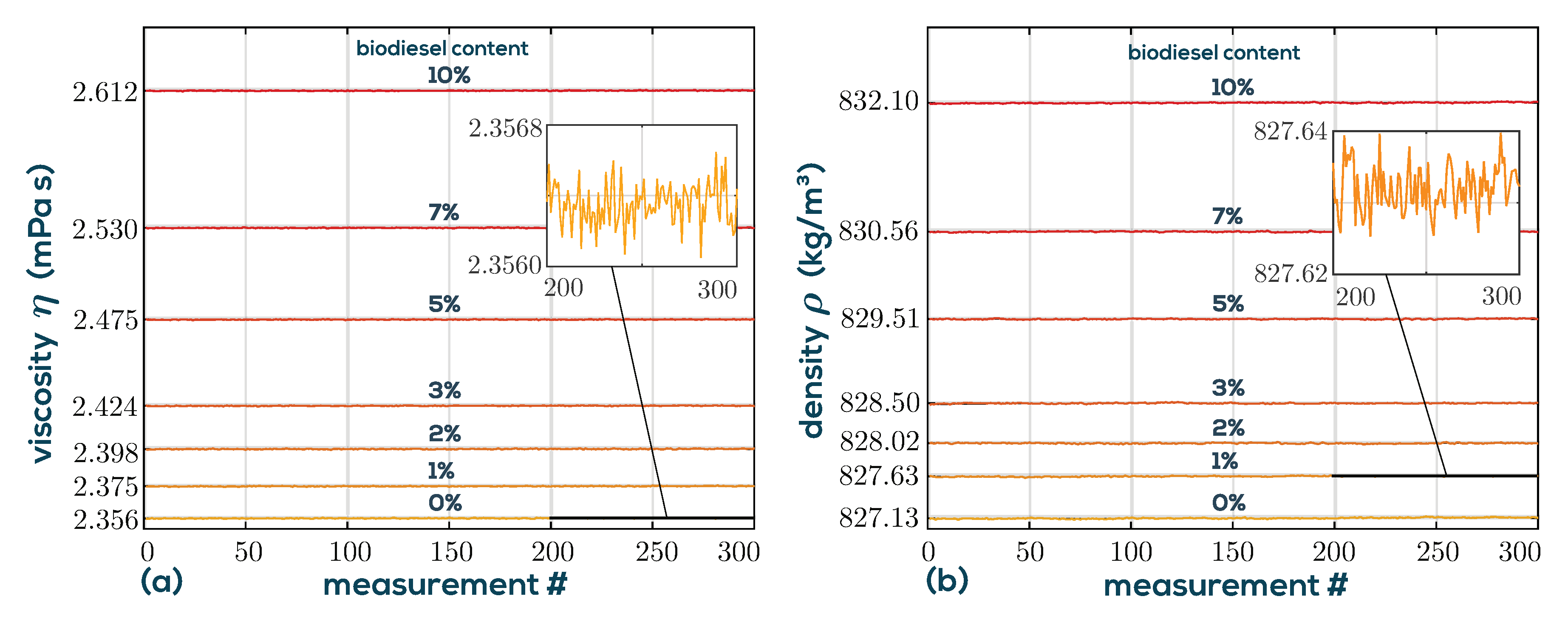
3.1. Real Time Monitoring of Biodiesel Content
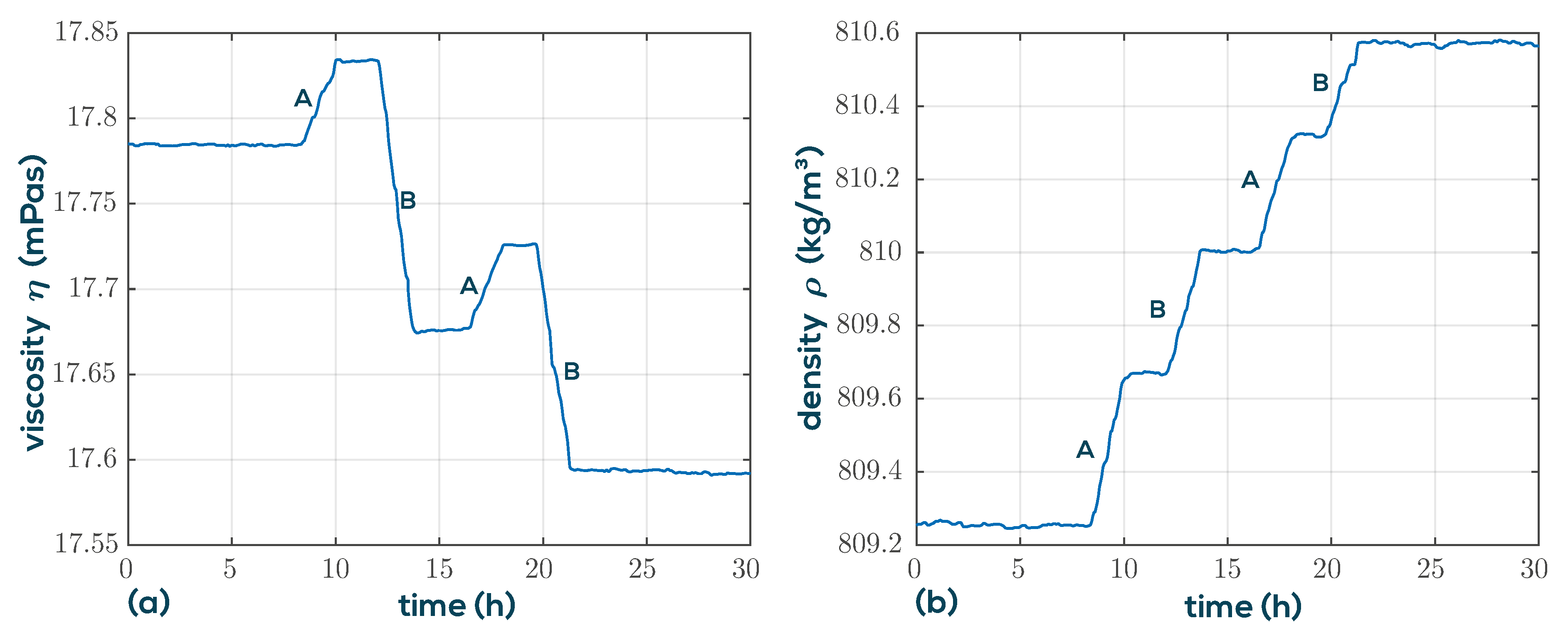
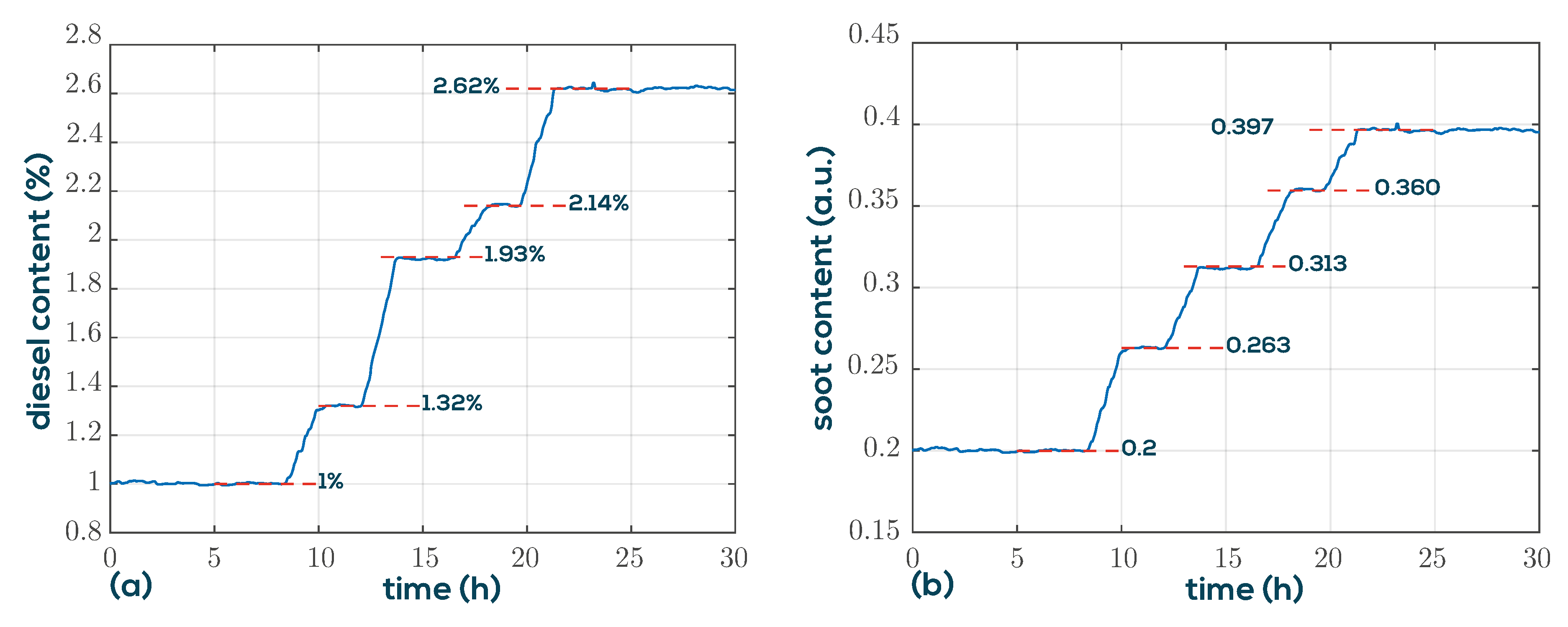
3.2. Diesel and Soot Determination in Engine Oil
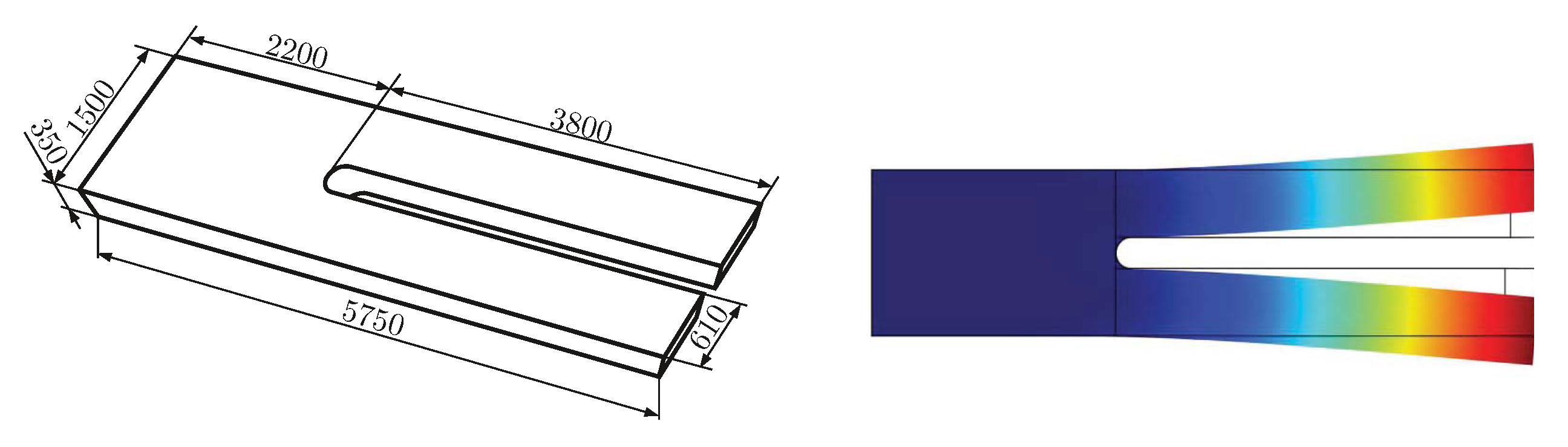
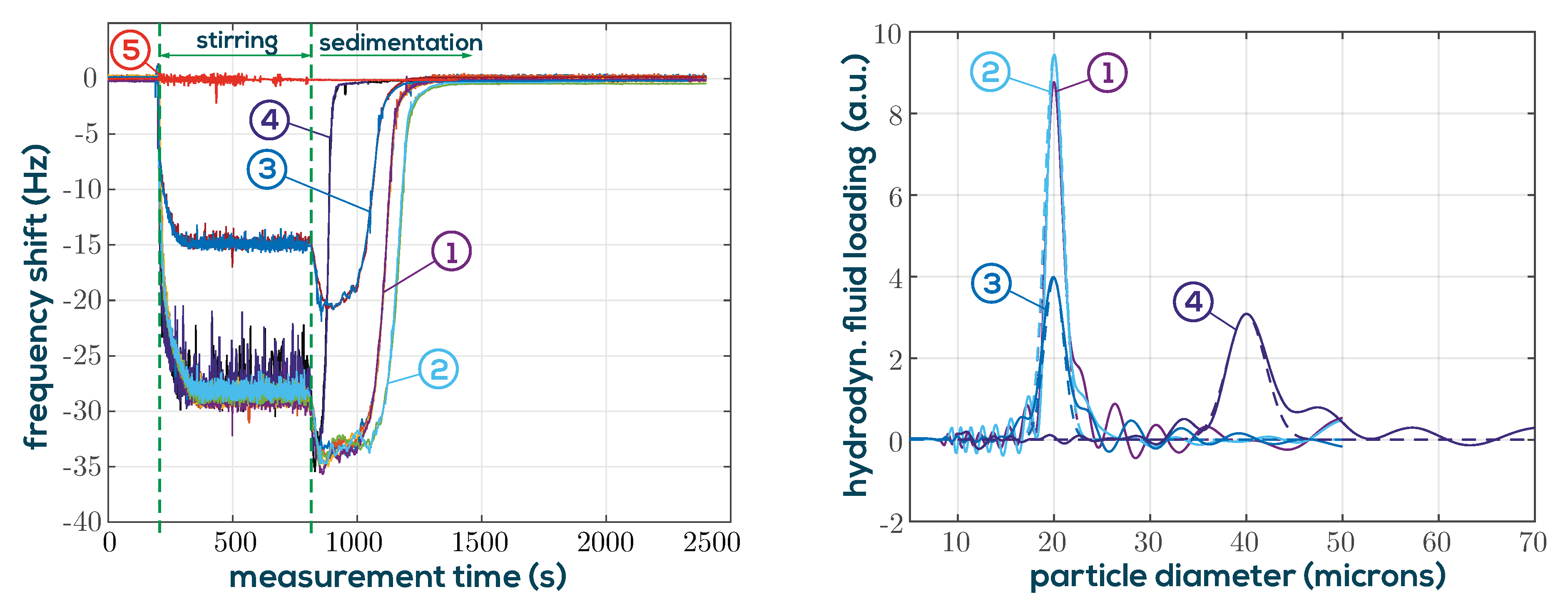
3.3. Particle Characterization by Monitored Sedimentation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arnau Vives, A. Piezoelectric Transducers and Applications; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Gautschi, G. Piezoelectric Sensors. In Piezoelectric Sensorics; Springer: Berlin/Heidelberg, Germany, 2002; pp. 73–91. [Google Scholar]
- Dufour, I.; Josse, F.; Heinrich, S.; Lucat, C.; Ayela, C.; Ménil, F.; Brand, O. Unconventional uses of cantilevers for chemical sensing in gas and liquid environments. Procedia Eng. 2010, 5, 1021–1026. [Google Scholar] [CrossRef]
- Patimisco, P.; Sampaolo, A.; Dong, L.; Giglio, M.; Scamarcio, G.; Tittel, F.; Spagnolo, V. Analysis of the electro-elastic properties of custom quartz tuning forks for optoacoustic gas sensing. Sens. Actuators Chem. 2016, 227, 539–546. [Google Scholar] [CrossRef]
- Padmasine, K.; Muruganand, S. Quartz Tuning Fork as Humidity Sensor. J. Nanomed. Nanotechnol. 2017, 8, 2. [Google Scholar]
- Vijaya, M. Piezoelectric Materials and Devices: Applications in Engineering and Medical Sciences; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- An, S.; Jhe, W. Nanopipette/Nanorod-Combined Quartz Tuning Fork–Atomic Force Microscope. Sensors 2019, 19, 1794. [Google Scholar] [CrossRef] [PubMed]
- Steinem, C.; Janshoff, A. Piezoelectric Sensors; Springer: Berlin/Heidelberg, Germany, 2007; Volume 5. [Google Scholar]
- Johannsmann, D. The Quartz Crystal Microbalance in Soft Matter Research: Fundamentals and Modeling; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Giessibl, F.J. High-speed force sensor for force microscopy and profilometry utilizing a quartz tuning fork. Appl. Phys. Lett. 1998, 73, 3956–3958. [Google Scholar] [CrossRef]
- Jakoby, B.; Beigelbeck, R.; Keplinger, F.; Lucklum, F.; Niedermayer, A.; Reichel, E.K.; Riesch, C.; Voglhuber-Brunnmaier, T.; Weiss, B. Miniaturized sensors for the viscosity and density of liquids-performance and issues. IEEE Trans. Ultrason. Ferr. 2010, 57, 111–120. [Google Scholar] [CrossRef]
- Waszczuk, K.; Piasecki, T.; Nitsch, K.; Gotszalk, T. Application of piezoelectric tuning forks in liquid viscosity and density measurements. Sens. Actuators Chem. 2011, 160, 517–523. [Google Scholar] [CrossRef]
- Toledo, J.; Manzaneque, T.; Hernando-García, J.; Vázquez, J.; Ababneh, A.; Seidel, H.; Lapuerta, M.; Sánchez-Rojas, J. Application of quartz tuning forks and extensional microresonators for viscosity and density measurements in oil/fuel mixtures. Microsyst. Technol. 2014, 20, 945–953. [Google Scholar] [CrossRef]
- Sell, J.K.; Niedermayer, A.O.; Babik, S.; Jakoby, B. Real-time monitoring of a high pressure reactor using a gas density sensor. Sens. Actuators Phys. 2010, 162, 215–219. [Google Scholar] [CrossRef]
- Voglhuber-Brunnmaier, T.; Heinisch, M.; Niedermayer, A.O.; Abdallah, A.; Beigelbeck, R.; Jakoby, B. Optimal Parameter Estimation Method for Different Types of Resonant Liquid Sensors. Proc. Eng. 2014, 87, 1581–1584. [Google Scholar] [CrossRef]
- Niedermayer, A.O.; Voglhuber-Brunnmaier, T.; Heinisch, M.; Jakoby, B. Accurate Determination of Viscosity and Mass Density of Fluids Using a Piezoelectric Tuning Fork Resonant Sensor. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=2ahUKEwjv2MTKvKviAhWKKqYKHcAdCKkQFjAAegQIAxAC&url=https%3A%2F%2Fwww.ama-science.org%2Fproceedings%2FgetFile%2FZGxkZt%3D%3D&usg=AOvVaw3tjSW-0UeZcXgjbRv2IboW (accessed on 20 April 2019).
- Voglhuber-Brunnmaier, T.; Niedermayer, A.; Heinisch, M.; Abdallah, A.; Reichel, E.; Jakoby, B.; Putz, V.; Beigelbeck, R. Modeling-free evaluation of resonant liquid sensors for measuring viscosity and density. In Proceedings of the 9th International Conference on Sensing Technology (IEEE (ICST), Auckland, New Zealand, 8–10 December 2015; pp. 300–305. [Google Scholar]
- Niedermayer, A.; Voglhuber-Brunnmaier, T.; Heinisch, M.; Feichtinger, F.; Jakoby, B. Monitoring of the dilution of motor oil with diesel using an advanced resonant sensor system. Procedia Eng. 2016, 168, 15–18. [Google Scholar] [CrossRef]
- Niedermayer, A.O.; Voglhuber-Brunnmaier, T.; Feichtinger, F.; Heinisch, M.; Jakoby, B. Online Condition Monitoring of Lubricating Oil based on Resonant Measurement of Fluid Properties. In Proceedings of the 19th ITG/GMA-Symposium on Sensors and Measuring Systems (VDE), Nuremberg, Germany, 26–27 June 2018; pp. 359–362. [Google Scholar]
- Voglhuber-Brunnmaier, T.; Niedermayer, A.O.; Feichtinger, F.; Heinisch, M.; Reichel, E.K.; Jakoby, B. High Precision Resonant Sensor Evaluation with Application to Fluid Sensing. In Proceedings of the 19th ITG/GMA-Symposium on Sensors and Measuring Systems (VDE), Nuremberg, Germany, 26–27 June 2018; pp. 355–358. [Google Scholar]
- Voglhuber-Brunnmaier, T.; Reichel, E.K.; Niedermayer, A.O.; Feichtinger, F.; Sell, J.K.; Jakoby, B. Determination of particle distributions from sedimentation measurements using a piezoelectric tuning fork sensor. Sens. Actuators Phys. 2018, 284, 266–275. [Google Scholar] [CrossRef]
- Voglhuber-Brunnmaier, T.; Niedermayer, A.O.; Feichtinger, F.; Jakoby, B. Precise Viscosity and Density Sensing in Industrial and Automotive Applications. In Proceedings of the 20th ITG/GMA-Symposium on Sensors and Measuring Systems (VDE), Nuremberg, Germany, 25–27 June 2019. [Google Scholar]
- Sauerbrey, G. Verwendung von Schwingquarzen Zur Wägung dünner Schichten und zur Mikrowägung. Z. Phys. 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Kanazawa, K.K.; Gordon, J.G. Frequency of a quartz microbalance in contact with liquid. Anal. Chem. 1985, 57, 1770–1771. [Google Scholar] [CrossRef]
- Matsiev, L.F. Application of flexural mechanical resonators to simultaneous measurements of liquid density and viscosity. In Proceedings of the IEEE Ultrasonics Symposium, Lake Tahoe, NV, USA, 17–20 October 1999; pp. 457–460. [Google Scholar]
- Matsiev, L.; Bennett, J.; McFarland, E. Application of low frequency mechanical resonators to liquid property measurements. In Proceedings of the 1998 IEEE Ultrasonics Symposium, Sendai, Japan, 5–8 October 1998; pp. 459–462. [Google Scholar]
- Reichel, E.K.; Riesch, C.; Keplinger, F.; Kirschhock, C.; Jakoby, B. Analysis and experimental verification of a metallic suspended plate resonator for viscosity sensing. Sens. Actuators Phys. 2010, 162, 418–424. [Google Scholar] [CrossRef]
- Jakoby, B.; Eisenschmid, H.; Herrmann, F. The potential of microacoustic SAW-and BAW-based sensors for automotive applications—A review. IEEE Sens. J. 2002, 2, 443–452. [Google Scholar] [CrossRef]
- Jakoby, B.; Vellekoop, M.J. Viscosity sensing using a Love-wave device. Sens. Actuators A Phys. 1998, 68, 275–281. [Google Scholar] [CrossRef]
- Jakoby, B.; Vellekoop, M.J. Physical sensors for water-in-oil emulsions. Sens. Actuators Phys. 2004, 110, 28–32. [Google Scholar] [CrossRef]
- Heinisch, M.; Voglhuber-Brunnmaier, T.; Reichel, E.; Dufour, I.; Jakoby, B. Application of resonant steel tuning forks with circular and rectangular cross sections for precise mass density and viscosity measurements. Sens. Actuators Phys. 2015, 226, 163–174. [Google Scholar] [CrossRef]
- Brumley, D.R.; Willcox, M.; Sader, J.E. Oscillation of cylinders of rectangular cross section immersed in fluid. Phys. Fluids 2010, 22, 052001. [Google Scholar] [CrossRef]
- Lighthill, M.; Rosenhead, L. Laminar Boundary Layers; Clarendon Press: Oxford, UK, 1963. [Google Scholar]
- Ahmed, N.; Nino, D.F.; Moy, V.T. Measurement of solution viscosity by atomic force microscopy. Rev. Sci. Instrum. 2001, 72, 2731–2734. [Google Scholar] [CrossRef]
- Bergaud, C.; Nicu, L. Viscosity measurements based on experimental investigations of composite cantilever beam eigenfrequencies in viscous media. Rev. Sci. Instrum. 2000, 71, 2487–2491. [Google Scholar] [CrossRef]
- Sader, J.E.; Chon, J.W.; Mulvaney, P. Calibration of rectangular atomic force microscope cantilevers. Rev. Sci. Instrum. 1999, 70, 3967–3969. [Google Scholar] [CrossRef]
- Slattery, A.D.; Quinton, J.S.; Gibson, C.T. Atomic force microscope cantilever calibration using a focused ion beam. Nanotechnology 2012, 23, 285704. [Google Scholar] [CrossRef] [PubMed]
- Photiadis, D.M.; Judge, J.A. Attachment losses of high Q oscillators. Appl. Phys. Lett. 2004, 85, 482–484. [Google Scholar] [CrossRef]
- Tuck, E. Calculation of unsteady flows due to small motions of cylinders in a viscous fluid. J. Eng. Math. 1969, 3, 29–44. [Google Scholar] [CrossRef]
- Heinisch, M.; Voglhuber-Brunnmaier, T.; Reichel, E.; Dufour, I.; Jakoby, B. Reduced Order Models for Resonant Viscosity and Mass Density Sensors. Sens. Actuators Phys. 2014, 220, 76–84. [Google Scholar] [CrossRef]
- Voglhuber-Brunnmaier, T.; Niedermayer, A.; Beigelbeck, R.; Jakoby, B. Resonance parameter estimation from spectral data: Cramér–Rao lower bound and stable algorithms with application to liquid sensors. Meas. Sci. Technol. 2014, 25, 105303–105313. [Google Scholar] [CrossRef]
- Reynolds, O. IV. On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. 1886, 1, 157–234. [Google Scholar]
- Heinisch, M. Mechanical Resonators for Liquid Viscosity and Mass Density Sensing. PhD Thesis, Université de Bordeaux, Bordeaux, France, August 2015. [Google Scholar]
- Matsiev, L. Application of flexural mechanical resonators to high throughput liquid characterization. In Proceedings of the 2000 IEEE Ultrasonics Symposium, San Juan, Puerto Rico, 22–25 October 2000; pp. 427–434. [Google Scholar]
- Niedermayer, A.; Voglhuber-Brunnmaier, T.; Sell, J.; Jakoby, B. Evaluating the Robustness of an Algorithm Determining Key Parameters of Resonant Sensors. Procedia Eng. 2012, 47, 330–333. [Google Scholar] [CrossRef]
- Kim, B.; Jahng, J.; Khan, R.M.; Park, S.; Potma, E.O. Eigenmodes of a quartz tuning fork and their application to photoinduced force microscopy. Phys. Rev. 2017, 95, 075440. [Google Scholar] [CrossRef]
- Micro Resonant OG. Available online: http://www.micro-resonant.at/cms (accessed on 25 October 2018).
- Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998, 84, 64–76. [Google Scholar] [CrossRef]
- Grunberg, L.; Nissan, A.H. Mixture law for viscosity. Nature 1949, 164, 799. [Google Scholar] [CrossRef]
- Genzale, C.L.; Pickett, L.M.; Kook, S. Liquid penetration of diesel and biodiesel sprays at late-cycle post-injection conditions. SAE Int. J. Eng. 2010, 3, 479–495. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voglhuber-Brunnmaier, T.; Niedermayer, A.O.; Feichtinger, F.; Jakoby, B. Fluid Sensing Using Quartz Tuning Forks—Measurement Technology and Applications. Sensors 2019, 19, 2336. https://doi.org/10.3390/s19102336
Voglhuber-Brunnmaier T, Niedermayer AO, Feichtinger F, Jakoby B. Fluid Sensing Using Quartz Tuning Forks—Measurement Technology and Applications. Sensors. 2019; 19(10):2336. https://doi.org/10.3390/s19102336
Chicago/Turabian StyleVoglhuber-Brunnmaier, Thomas, Alexander O. Niedermayer, Friedrich Feichtinger, and Bernhard Jakoby. 2019. "Fluid Sensing Using Quartz Tuning Forks—Measurement Technology and Applications" Sensors 19, no. 10: 2336. https://doi.org/10.3390/s19102336
APA StyleVoglhuber-Brunnmaier, T., Niedermayer, A. O., Feichtinger, F., & Jakoby, B. (2019). Fluid Sensing Using Quartz Tuning Forks—Measurement Technology and Applications. Sensors, 19(10), 2336. https://doi.org/10.3390/s19102336




