3.1. High-Level Flight Control Strategy
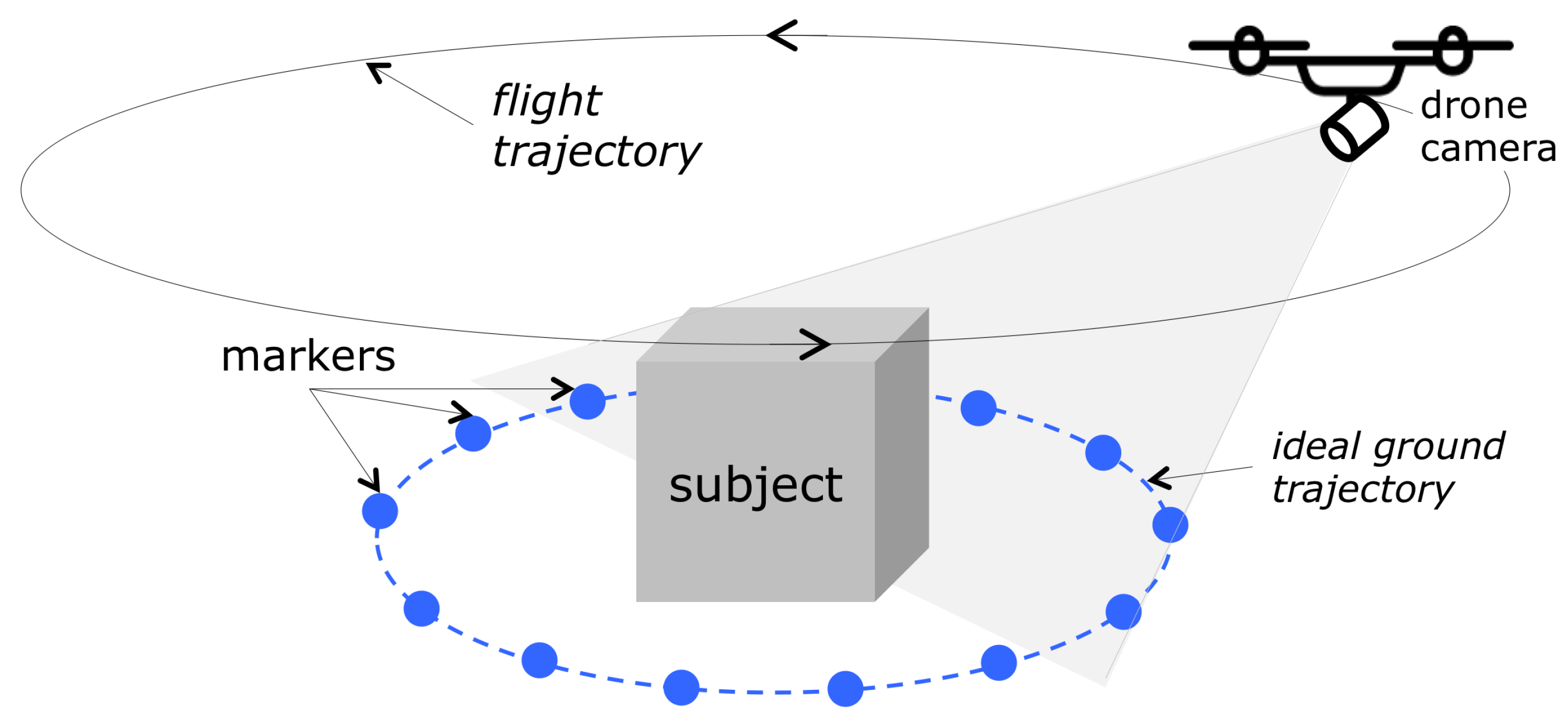
Aim of the mission control algorithm is to drive the drone approximately one round along the closed trajectory, as it is defined by the markers, while: (a) keeping the object to reconstruct approximately in the image center, and (b) keeping approximately the same horizontal distance from the trajectory. Due to the constraints imposed by the drone’s flight control interface [
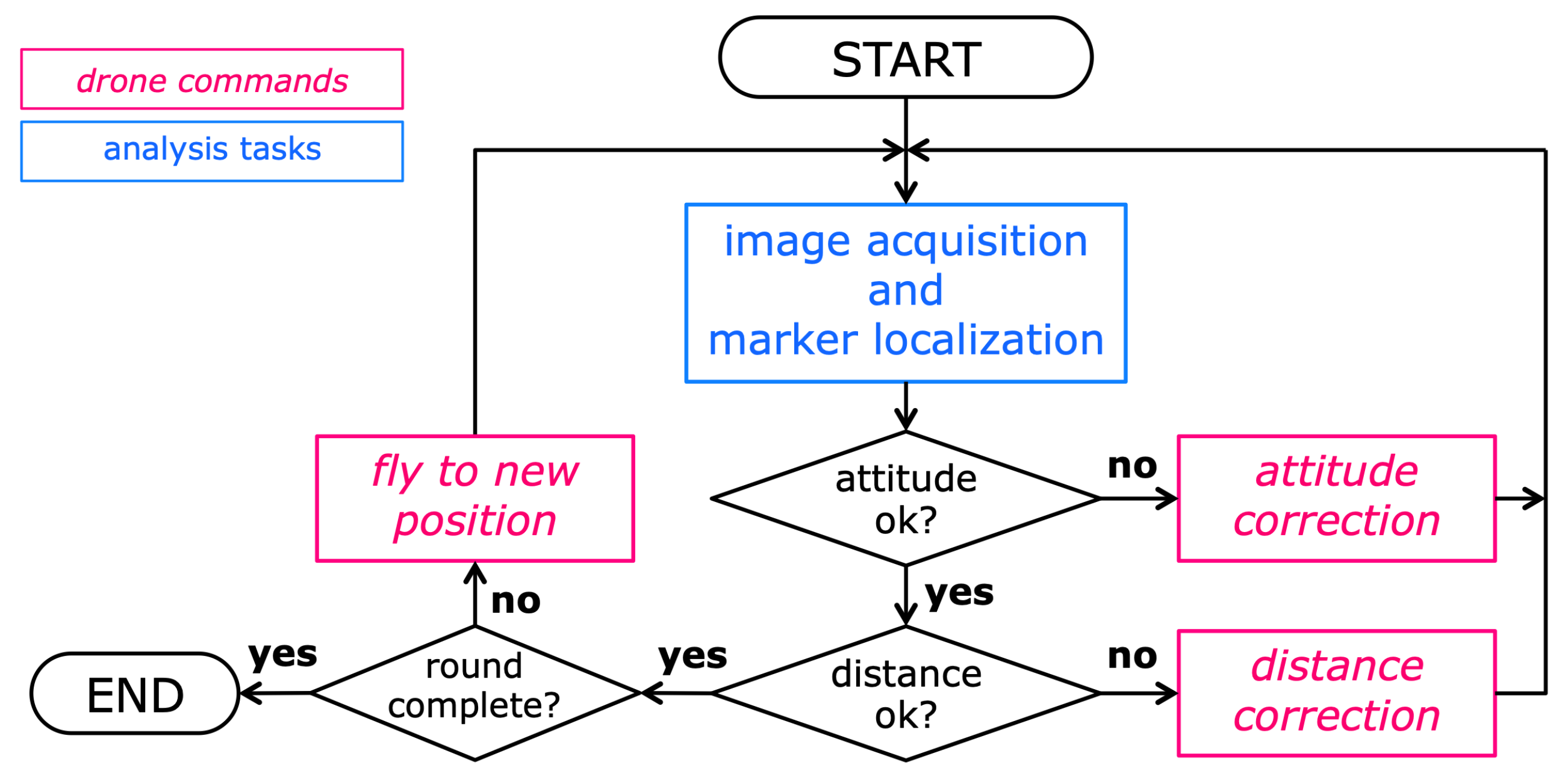
14], the most efficient solution was to split the control into two separate correction phases. This is accomplished by the proposed algorithm, whose high-level structure is shown in the flowchart of
Figure 2. The structure of the algorithm is a control loop, aimed at controlling the drone flight and the image acquisition in real time. As
Figure 2 shows, the loop alternates image analysis tasks, in which the acquired photograph is analyzed by the application and all visible markers are localized, and flight control tasks, in which the application, according to the measured marker positions, issues motion commands to the drone (through the functions of the drone API [
14]). A loop iteration takes approximately 6
; on average, half of this time is taken by the image analysis tasks, and the remaining time is taken by the drone to adjust its position (when necessary) and move to the next viewpoint. Considering the average lifetime of a battery pack on the adopted drone (a
DJI Phantom 4), the proposed procedure enables therefore to carry out acquisitions of up to 250 images with a single flight.
3.1.1. Attitude Correction
After the acquisition of a camera frame, the system performs the
attitude analysis of the acquired image, consisting of the estimation of the camera attitude from the positions of the localized trajectory markers. The details of this task are described in
Section 3.1.1. If the attitude relative to the subject needs a correction, a corresponding command is given to the flight controller (a
yaw rotation, corresponding to a rotation around the vertical axis) and the test is carried out again (see
Figure 3). This cycle is repeated until the correct attitude is reached (corresponding to a centered subject in the image).
3.1.2. Distance Correction
Once the drone has reached the correct attitude, a
distance analysis is performed on the last acquired image, in order to evaluate the horizontal distance from the defined trajectory. The details of this task are described in
Section 3.1.2. If the estimated distance is outside the validity range, a correction command is given, consisting of a horizontal translation of the drone along the same direction of the camera axis, in order to reach the desired distance (see
Figure 4), then the distance test is repeated. Also this cycle is repeated as long as a valid distance is reached. Each of the two above correction tasks is composed of three subsequent steps:
A new image is acquired and a sphere detection algorithm detects the visible spherical markers and localizes them accurately by estimating the centroids of the circular marker images.
Using the centroid coordinates as input data, the attitude analysis and distance analysis algorithms, respectively, compute the necessary corrections.
The system gives the computed attitude/distance flight correction command to the drone and waits for command execution.
These detection and analysis algorithms are now described in details.
3.2. Efficient Spherical Marker Localization
There is plenty of algorithms for circle detection and accurate localization in literature [
15,
16]. In this particular application, however, the most crucial aspect is the computational efficiency, as the algorithm runs in real time on a platform with limited computing power (a tablet running Android), so longer computation times necessarily lead to longer idle times during the drone flight. For this reason, a fast algorithm is of primary importance in this application.
Each time the drone acquires an image and the Android device receives it through the radio link, the application starts the marker detection algorithm, which is composed of the following three processing steps: color segmentation, shape selection, and centroid localization.
3.2.1. Color Segmentation
This step is carried out by thresholding the image in the RGB color space. Different color spaces, like YUV and HSV, have been also considered for this thresholding and tested on the real images, but RGB has been finally chosen for its robustness against the high variance of the illumination, typically occurring in daylight-illuminated images. The HSV space is really not well suited for clustering constant-color regions in outdoor scenes because, rather counter-intuitively, the imaged hue of a constant color changes significantly going from sunlight to shadow, as demonstrated in [
17].
Moreover, the strongly varying illumination, typical in outdoor scenes, makes it difficult to achieve a correct clustering by thresholding with an a-priori fixed threshold. For this reason, we developed an adaptive approach in which the threshold values are adapted to the current acquisition session. In order also to account for the ease-of-use design requirement, the application asks the user to take a picture of one of the deployed trajectory markers just before starting the acquisition flight. The application then extracts from this image all the pixels belonging to the well visible marker and their color coordinates are averaged, thus yielding a robust estimate of the mean marker color , defined as vector in the RGB space. The color segmentation criterion, applied to all subsequently acquired images, is then defined as follows: each pixel i of color belongs to the color subspace of the markers if
The threshold factors
and
have been determined experimentally, aiming at the most accurate color segmentation results in daylight illumination conditions. The segmentation produces a binary image, in which the ‘white’ pixels denote pixels whose color satisfies the color similarity criterion defined in (
1).
3.2.2. Shape Selection
In the binary image resulting from segmentation, all white connected regions are localized using a computationally efficient region-growing algorithm. All regions then undergo a shape selection process in which a region is recognized as a valid marker if all the following criteria are satisfied:
3.2.3. Centroid Localization
For each region recognized in the previous step as the image of a spherical marker, the circle center is estimated by simply computing the geometrical barycenter of the region. More sophisticated estimation techniques, like the estimation of the least-squares circumference on the region perimeter, have been also tested, but they did not provided significant accuracy improvements, while requiring significantly more computation time compared to the computationally efficient barycenter estimation. Due to the prioritary processing speed requirements, we therefore stuck to the more efficient technique.
3.3. Estimation and Control of the Camera Attitude
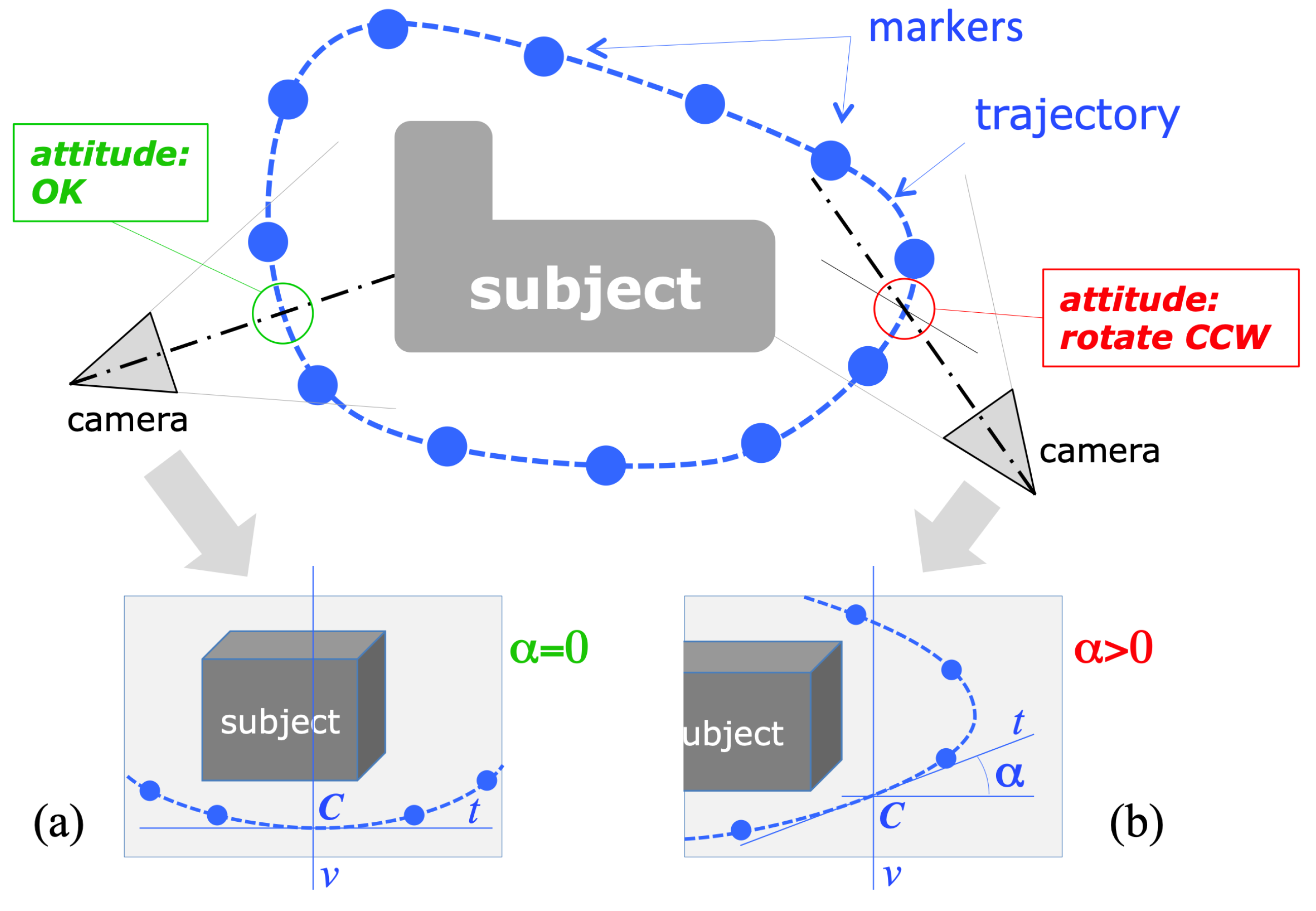
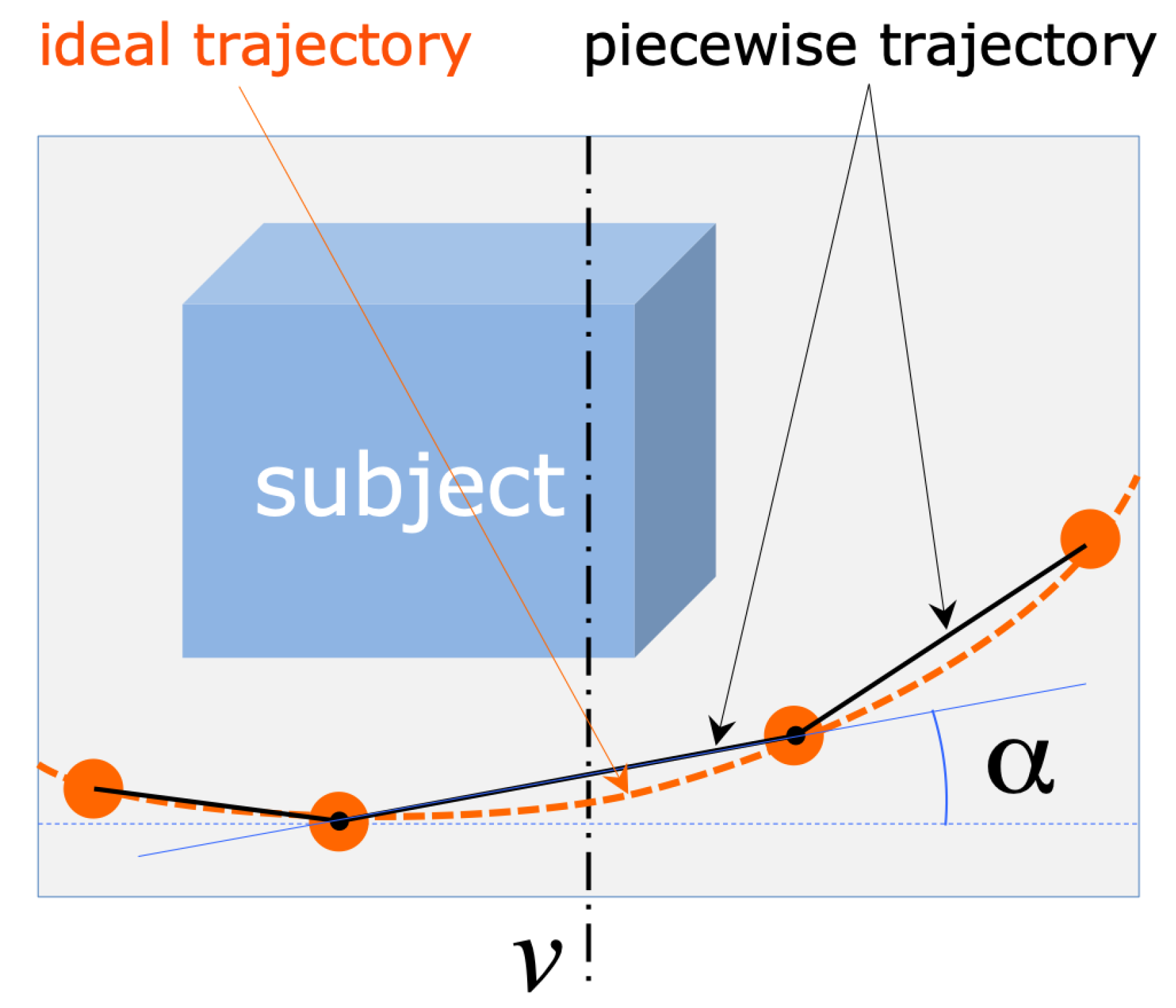
The image coordinates of the detected marker centers are the input for the module computing the drone camera attitude, that is, the direction of the camera axis with respect to the current trajectory and, consequently, to the subject to reconstruct. The geometrical schematization of the problem is represented in
Figure 3. If we consider the projection of the camera’s optical axis on the trajectory plane (assumed to be horizontal), the camera attitude is considered correct if the axis projection is orthogonal to the trajectory curve in their intersection point
C, the one closer to the camera. The image of this point of intersection, in the acquired frame, corresponds to the intersection of the imaged trajectory, which can be defined as the smooth curve passing through the visible markers, with the vertical mid-line
v passing through the image of the optical center. In fact,
v corresponds to the intersection of the image plane with the vertical plane containing the optical axis, as the image’s horizontal axis is parallel to the horizontal plane (the camera is held horizontal by the drone active gimbal).
Under the described geometric assumptions, the local direction of the imaged trajectory in its intersection with
v gives a direct measure of the angular deviation from the correct attitude. Referring to
Figure 3, calling
the angle formed by the tangent
t to the trajectory in the intersection point, with the image horizontal axis,
(
t is horizontal) in case of correct attitude, whereas
(line
t rising, from left to right) when the camera should be rotated to the left and, vice versa, rotated to the right for
(line
t falling).
The estimation of
would require the estimation of the interpolating curve passing through all the visible markers, whose number is significantly variable from image to image. Experiments with different interpolation models have shown that the varying number of interpolation points leads to position instabilities in case of higher-order fitting curves. For this reason, and also considering the need for fast and efficient algorithms, we adopted the simplest interpolation model, consisting of a trajectory curve defined as the piece-wise line connecting adjacent markers. According to this simplified model,
is simply and efficiently computed as the slope of the linear segment connecting the two nearest markers to the middle line
v, on the bottom part of the trajectory, as schematized in
Figure 5.
Based on the estimated value of
, the algorithm issues a yaw rotation command to the drone, in order to reach the correct attitude. For
, a counter-clockwise
yaw rotation of the drone is necessary, clockwise for
. The amplitude of the yaw angle is computed as a function of
. An experimental search for the best function relating the determined deviation angle
to the requested yaw rotation angle
resulted in the observation that a simple proportional action, despite its simplicity, is one of the most effective correction strategies. Moreover, for low values of
there is no need to apply a correction, as the measured attitude allows anyway a valid image acquisition. For these reasons we adopted the following correction strategy:
where
therefore represents the threshold angle for a correcting action: an attitude correction is triggered only when
exceeds
. The best value for
has been also determined experimentally, by searching for the value giving the minimum occurrence of corrections (and therefore the shortest overall acquisition time) without affecting the quality of the final 3D point cloud. For the adopted drone/camera setup, the best value resulted in being
. The best value for
has been obtained experimentally as well, searching for the value giving the quickest correction without incurring into oscillating behaviors in the flight dynamics due to overcorrections of the yaw angle. For this drone, the best results were obtained with
.
3.4. Estimation and Control of the Subject-Camera Distance
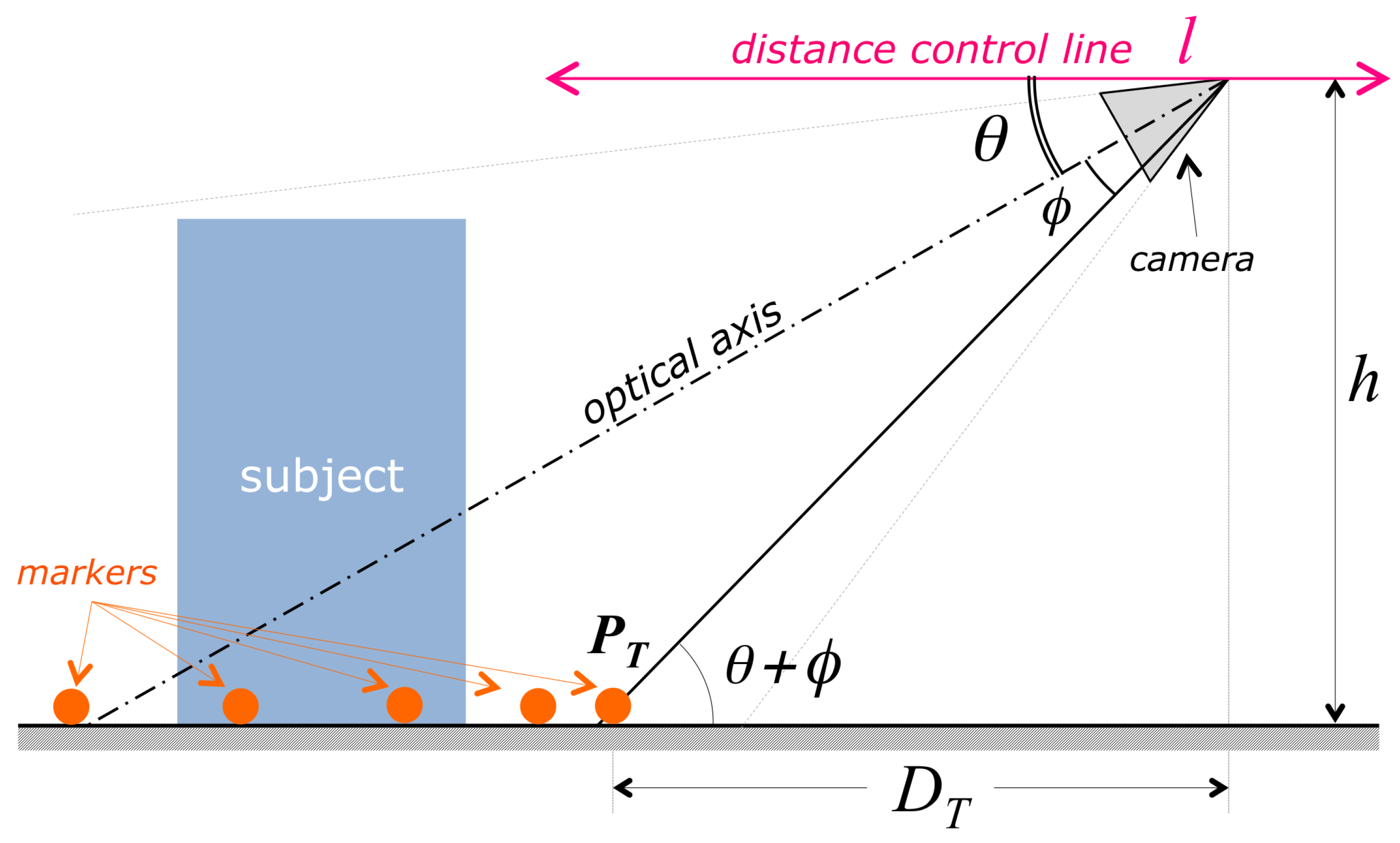
The correct camera attitude ensures that the subject is horizontally centered in the field of view, but gives no guarantee that the vertical extent of the subject is entirely contained in the image. A successful acquisition, for any vertical extent of the subject, is guaranteed as follows: the acquisition procedure requires the user to place the drone in an initial position, in which the vertical extent of the subject is entirely contained in the image field. After then, the automatic acquisition procedure keeps the distance and the camera pitch (the angular vertical elevation of the optical axis, corresponding to
in
Figure 4) constant, thereby ensuring that the vertical extent of the subject in the image will be kept contained in the image field.
Operatively, the constancy of the camera pitch is automatically obtained by keeping the drone in steady flight (also called
hovering) when an image is shot. A constant distance from the subject, conversely, is achieved by keeping the vertical height of the lowest trajectory point in the image plane constant. As
Figure 4 shows, if the camera pitch
is constant, then the distance of the drone from the nearest point along the trajectory (and consequently from the subject) is
where
h is the drone height with respect to the ground plane and
is the vertical angular coordinate of the visual ray corresponding to the nearest trajectory point,
. Since we need a constant value for
, we need
h,
and
to be constant: the procedure holds
h constant by commanding constant height to the drone flight controller (the drone is equipped with sensors measuring the distance from ground);
corresponds to the vertical inclination of the camera gimbal, that is held fixed, so
is constant during hovering;
is constant as long as the vertical image coordinate
(see
Figure 6) of the lowest trajectory point
is constant.
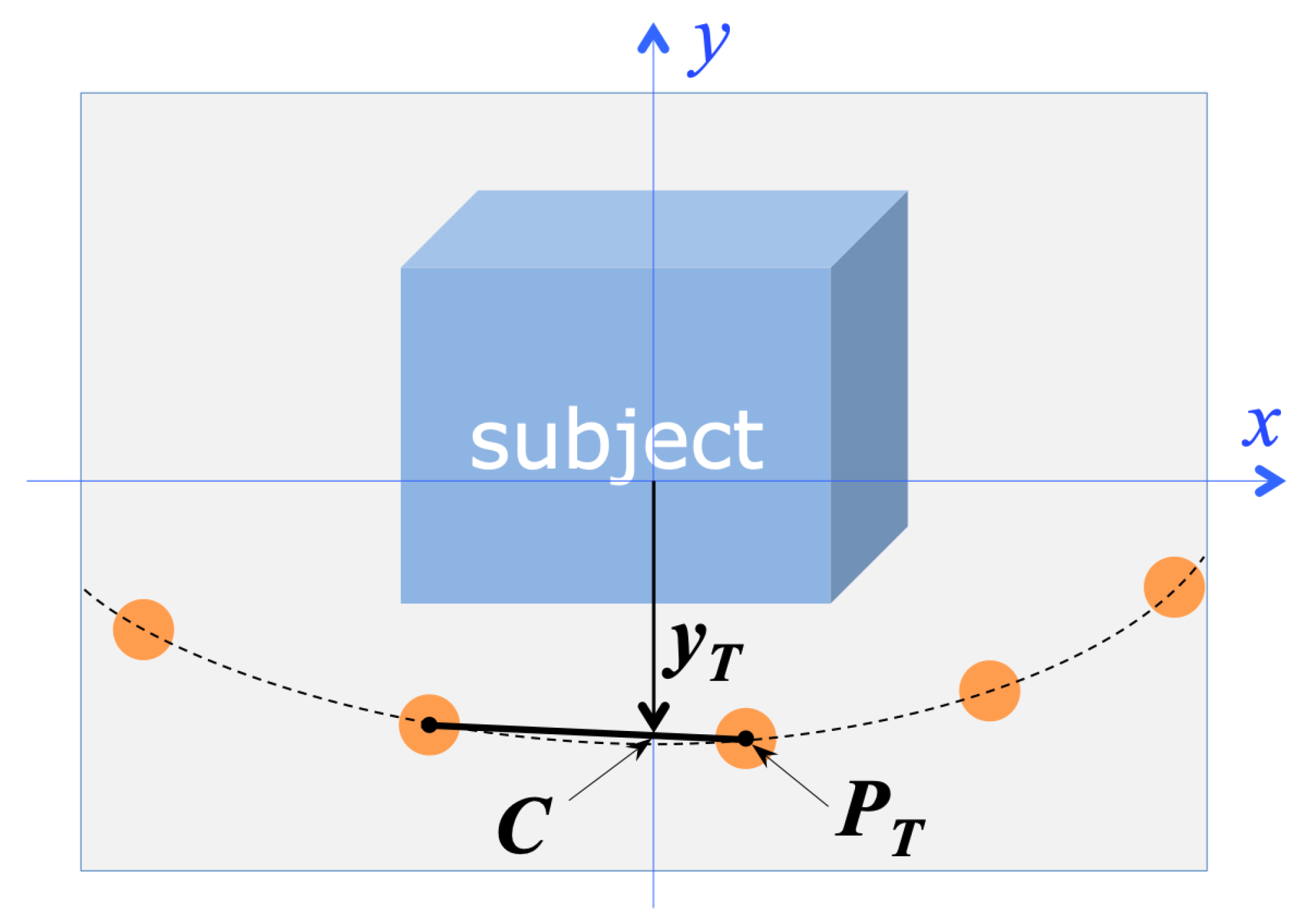
Referring to the acquisition geometry represented in
Figure 4 and
Figure 6, it is possible to control the value of
without changing
h and
, by translating the drone along the
distance control linel (see
Figure 4), defined as the intersection between the horizontal plane and the vertical plane containing the optical axis of the camera. The distance estimation and control algorithm works therefore as follows:
The algorithm selects the two centermost markers among those provided by marker detection; since this step occurs just after attitude correction, the two markers likely describe the bottommost section of the imaged trajectory. As
Figure 6 shows,
is estimated as the
y-coordinate of the intersection of the segment connecting the two centermost markers with the
y axis of the image reference frame.
Depending on the amplitude of the deviation from the initial value, , the algorithm decides, as correcting action, a translation along the distance control line l.
Similarly as for the attitude control, the implemented correction strategy is a function relating the translation amplitude
to the measured deviation
:
that is, a correcting action is undertaken when
is exceeded. Similarly as for the attitude, the best values for
and
have been determined experimentally, by finding the value giving the minimum occurrence of corrections without affecting the quality of the final 3D point cloud. For the adopted drone/camera system, the best value for
was
of the total image height, while
.
3.5. Drone Flight Control
As the flowchart in
Figure 2 shows, there are three different situations in which commands are issued to the drone for controlling its flight and its position: the correction of the attitude, the correction of the subject-camera distance, and the move to the next viewpoint for a shoot. To accomplish these tasks, it is necessary to access the flight control software interface, available to the application by means of the drone’s API, provided by the drone manufacturer through a Software Development Kit for mobile devices [
14]. The main tool provided by the API for flight control is the function call:
sendVirtualStickFlightControlData(pitch, roll, yaw, throttle, time), which simulates the corresponding actions on the controller sticks. The provided argument values (
,
,
, and
) define the entity of the actions on each virtual stick, while
time defines the duration of these actions. After that time, the actions are terminated and the drone returns to a steady hovering flight. Having such API call as interface, it is necessary to define all the motion tasks requested by our procedure, in terms of proper combination of arguments for the call.
Actually, for a given requested motion, the set of arguments leading to that motion is not unique: for instance, a change in the attitude
A should be the result of the product
, as
defines the angular velocity around the vertical axis. The preferred solution would then be the fastest, i.e.,
, but we experienced that more intense actions lead to bigger uncertainties in the resulting motion. For this reason we carried out “tuning” experiments, to find the best combination of arguments for each of the motion tasks, leading to the best trade-off between motion speed and motion accuracy. Each of the three motion tasks has been therefore implemented as a call to
sendVirtualStickFlightControlData, with the arguments specified in
Table 1, where
,
,
, and
are the optimal arguments and
A,
D and
L represent the desired attitude correction, the distance correction and the lateral shift, respectively.
Concerning the desired correction parameters, A, D, and L, it is important to notice that while A and D result from the computation of the necessary correction, the amount of lateral motion L is arbitrarily set by the user, according to the desired inter-distance between subsequent image shots. The total amount of acquired images varies according to this parameter.
3.6. User Interface
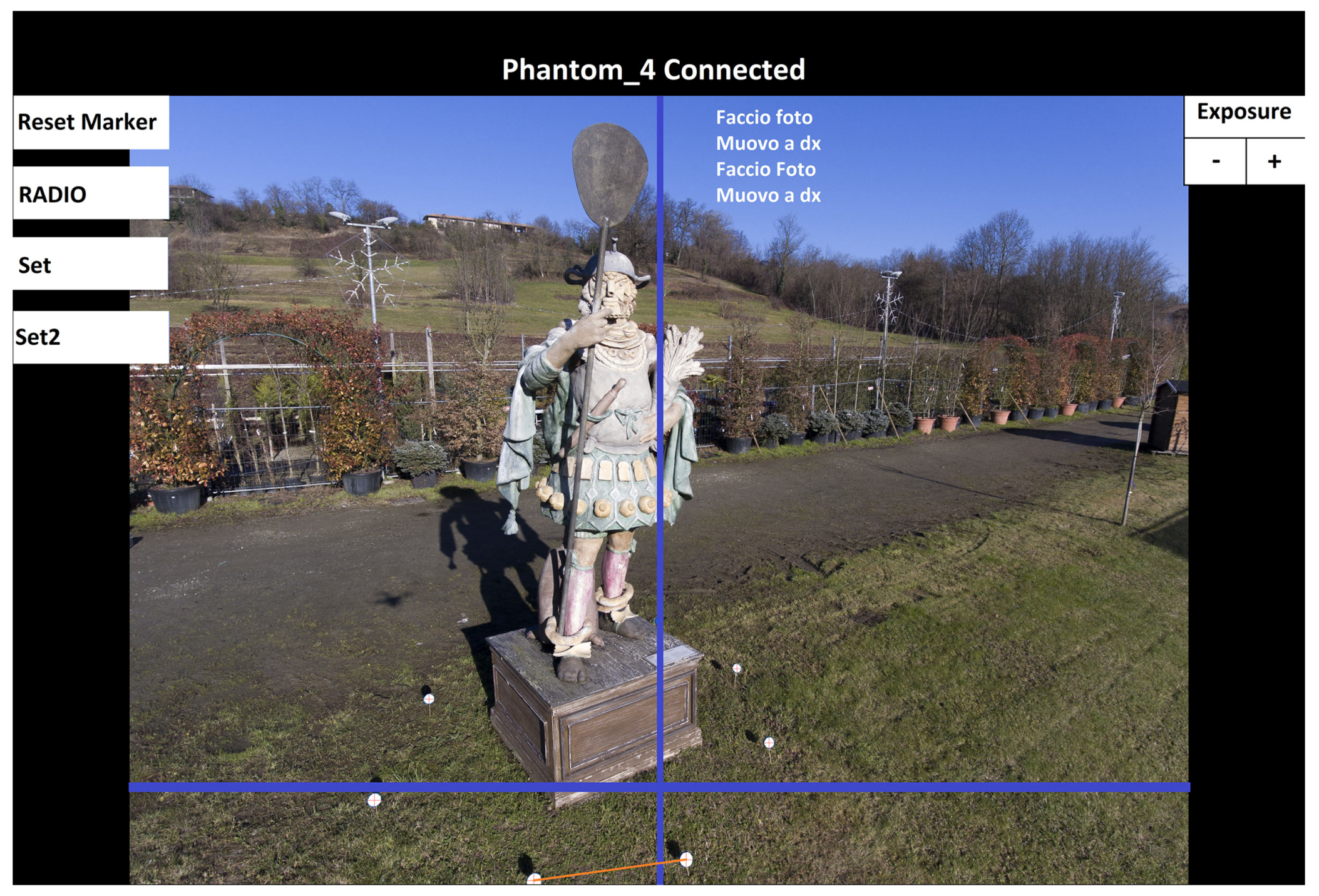
The most important role played by the user interface of this application is to provide the user with exhaustive real-time information about the progress of the on-going acquisition procedure, thus allowing the user to supervise the whole process. A screenshot of this interface is shown in
Figure 7. The interface presents a dashboard showing the video stream currently acquired by the camera and, superimposed to the image frames: (a) a vertical line representing the position of the
axis, as shown in
Figure 3 and
Figure 5; (b) a horizontal line representing the line:
in the image plane. As schematized in
Figure 6, this is the line defining the target “height” of the lowest trajectory marker
; (c) a red segment connecting the two bottommost trajectory markers selected for attitude/distance correction; (d) the list of the latest flight commands given by the control application to the drone.
The provided information, updated in real time, allows the user to supervise the flight and to evaluate the quality of the images taken during the whole acquisition process. Through this interface, for instance, it is clearly visible how many corrections of the trajectory are needed, or whether a trajectory marker is not visible or not recognized.