Colour Constancy for Image of Non-Uniformly Lit Scenes †
Abstract
1. Introduction
Related Work
2. Image Colour Constancy Adjustment by Fusion of Image Segments’ Initial Colour Correction Factors
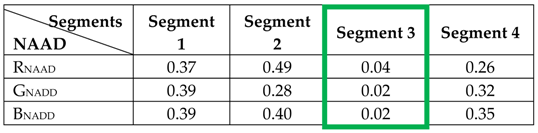
2.1. Automatic Image Segmentation
2.2. Segments’ Selection and Calculation of Initial Colour Constancy Weighting Factors for each Segment
2.3. Calculation of the Colour Adjustment Factors for each Pixel
3. Experimental Results and Evaluation
3.1. Evaluation Procedure
3.2. Example of Image Segmentation and Segment Selection
3.3. Experimental Results
3.3.1. Subjective Result
3.3.2. Objective Result
4. Execution Time
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bowdle, D. Background Science for Colour Imaging and CCDs, Faulkes Telescope Project. Available online: http://www.euhou.net/docupload/files/euhou_colour_images_ccds.pdf. (accessed on 12 February 2019).
- Urbaniak, A. “Monochroming” a Colour Sensor and Colour Photography with the Monochrom. Wilddog. 2017. Available online: https://wilddogdesign.co.uk/blog/monochroming-colour-sensor-colour-photography-monochrom. (accessed on 8 February 2019).
- Applications, E. Inc.; Edmund Optics Inc. and E. Inc. “Imaging Electronics 101: Understanding Camera Sensors for Machine Vision Applications”, Edmundoptics.com, 2019. Available online: https://www.edmundoptics.com/resources/application-notes/imaging/understanding-camera-sensors-for-machine-vision-applications/ (accessed on 22 March 2019).
- Oliver, S.; Peter, S.L. A True-Color Sensor and Suitable Evaluation Algorithm for Plant Recognition. Sensors 2017, 17, 1823. [Google Scholar] [CrossRef]
- Woo, S.M.; Lee, S.H.; Yoo, J.S.; Kim, J.O. Improving Color Constancy in an Ambient Light Environment Using the Phong Reflection Model. IEEE Trans. Image Process. 2018, 27, 1862–1877. [Google Scholar] [CrossRef] [PubMed]
- Tai, S.; Liao, T.; Chang, C.Y. Automatic White Balance algorithm through the average equalization and threshold. In Proceedings of the 8th International Conference on Information Science and Digital Content Technology, Jeju, Korea, 26–28 June 2012; pp. 571–576. [Google Scholar]
- Teng, S.J.J. Robust Algorithm for Computational Color Constancy. In Proceedings of the 2014 International Conference on Technologies and Applications of Artificial Intelligence, Hsinchu, Taiwan, 18–20 November 2010; pp. 1–8. [Google Scholar]
- Banic, N.; Lončarić, S. Improving the white patch method by subsampling. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 605–609. [Google Scholar]
- Banić, N.; Lončarić, S. Color Cat: Remembering Colors for Illumination Estimation. IEEE Signal Process. Lett. 2013, 22, 651–655. [Google Scholar] [CrossRef]
- Joze, H.R.V.; Drew, M.S. White Patch Gamut Mapping Colour Constancy. In Proceedings of the 2012 19th IEEE International Conference on Image Processing (ICIP 2012), Orlando, FL, USA, 30 September–3 October 2012; pp. 801–804. [Google Scholar]
- Simão, J.; Schneebeli, H.J.A.; Vassallo, R.F. An Iterative Approach for Colour Constancy. In Proceedings of the 2014 Joint Conference on Robotics: SBR-LARS Robotics Symposium and Robocontrol, Sao Carlos, Sao Paolo, Brazil, 18–23 October 2014; pp. 130–135. [Google Scholar]
- Gijsenij, A.; Gevers, T.; Van de Weijer, J. Computational Colour Constancy: Survey and Experiments. IEEE Trans. Image Process. 2011, 20, 2475–2489. [Google Scholar] [CrossRef]
- Aytekin, C.; Nikkanen, J.; Gabbouj, M. Deep multi-resolution color constancy. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3735–3739. [Google Scholar]
- Lam, E.Y. Combining gray world and retinex theory for automatic white balance in digital photography. In Proceedings of the Ninth International Symposium on Consumer Electronics, ISCE 2005, Macau, China, 14–16 June 2005; pp. 134–139. [Google Scholar]
- Zhang, B.; Batur, A.U. A real-time auto white balance algorithm for mobile phone cameras. In Proceedings of the 2012 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 13–16 January 2012; pp. 1–4. [Google Scholar]
- Buchsbaum, G. A spatial processor model for object colour perception. J. Frankl. Inst. 1980, 32, 1–26. [Google Scholar] [CrossRef]
- Land, E. The retinex theory of colour vision. Sci. Am. 1977, 237, 28–128. [Google Scholar] [CrossRef]
- Finlayson, G.D.; Trezzi, E. Shades of Grey and Colour Constancy; Society for Imaging Science and Technology: Scottsdale, AZ, USA, 2004; pp. 37–41. [Google Scholar]
- Van de Weijer, J.; Gevers, T.; Gijsenij, A. Edge-based colour constancy. IEEE Trans Image Process. 2007, 16, 2207–2217. [Google Scholar] [CrossRef]
- Gijsenij, A.; Gevers, T.; Van de Weijer, J. Improving Colour Constancy by Photometric Edge Weighting. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 918–929. [Google Scholar] [CrossRef]
- Finlayson, G.D. Corrected-Moment Illuminant Estimation. 2013 IEEE Int. Conf. Comput. Vis. 2013. [Google Scholar] [CrossRef]
- Forsyth, D.A. A novel algorithm for color constancy. Int. J. Comput. Vis. 1990, 5, 5–35. [Google Scholar] [CrossRef]
- Gijsenij, A.; Gevers, T.; Van de Weijer, J. Generalized gamut mapping using image derivative structures for color constancy. Int. J. Comput. Vis. 2010, 86, 127–139. [Google Scholar] [CrossRef]
- Finlayson, G.; Hordley, S.; Xu, R. Convex programming colour constancy with a diagonal-offset model. IEEE Int. Conf. Image Process. 2005, 3, 948–951. [Google Scholar]
- Barron, J.T. Convolutional Color Constancy. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 13–16 December 2015; pp. 379–387. [Google Scholar]
- Bianco, S.; Cusano, C.; Schettini, R. Color constancy using CNNs. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Boston, MA, USA, 7–12 June 2015; pp. 81–89. [Google Scholar]
- Fourure, D.; Emonet, R.; Fromont, E.; Muselet, D.; Trémeau, A.; Wolf, C. Mixed pooling neural networks for colour constancy. In Proceedings of the IEEE International Conference on Image Processing, Phoenix, AZ, USA, 25–28 September 2016; pp. 3997–4001. [Google Scholar]
- Bianco, S.; Cusano, C.; Schettini, R. Single and Multiple Illuminant Estimation Using Convolutional Neural Networks. IEEE Trans. Image Process. 2017, 26, 4347–4362. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.; Chen, K.; Nikkanen, J.; Kämäräinen, J.; Matas, J. Recurrent Color Constancy. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 5459–5467. [Google Scholar]
- Riess, C.; Eibenberger, E.; Angelopoulou, E. Illuminant color estimation for real-world mixed-illuminant scenes. In Proceedings of the 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 6–13 November 2011; pp. 782–7813. [Google Scholar]
- Bleier, M.; Riess, C.; Beigpour, S.; Eibenberger, E.; Angelopoulou, E.; Tröger, T.; Kaup, A.M. Color constancy and non-uniform illumination: Can existing algorithms work? In Proceedings of the 2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 6–13 November 2011; pp. 774–781. [Google Scholar]
- Gijsenij, A.; Lu, R.; Gevers, T. Color Constancy for Multiple Light Sources. IEEE Trans. Image. Process. 2012, 21, 697–707. [Google Scholar] [CrossRef]
- Beigpour, S.; Riess, C.; Van De Weijer, J.; Angelopoulou, E. Multi-Illuminant Estimation with Conditional Random Fields. IEEE Trans. Image Process. 2014, 23, 83–96. [Google Scholar] [CrossRef] [PubMed]
- Mazin, B.; Delon, J.; Gousseau, Y. Estimation of Illuminants from Projections on the Planckian Locus. IEEE Trans. Image Process. 2013, 24, 11344–11355. [Google Scholar]
- Bianco, S.; Schettini, R. Adaptive Color Constancy Using Faces. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1505–1518. [Google Scholar] [CrossRef] [PubMed]
- ElFiky, N.; Gevers, T.; Gijsenij, A.; Gonzàlez, J. Color Constancy Using 3D Scene Geometry Derived from a Single Image. IEEE Trans. Image Process. 2014, 23, 3855–3868. [Google Scholar] [CrossRef]
- Cheng, D.; Price, B.; Cohen, S.; Brown, M.S. Beyond White: Ground Truth Colors for Color Constancy Correction. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013; pp. 2138–2306. [Google Scholar]
- Cheng, D.; Kamel, A.; Price, B.; Cohen, S.; Brown, M.S. Two Illuminant Estimation and User Correction Preference. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, LV, USA, 26 June–1 July 2016; pp. 469–477. [Google Scholar]
- Gao, S.B.; Yang, K.F.; Li, C.Y.; Li, Y.J. Color Constancy Using Double-Opponency. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 37, 11373–11385. [Google Scholar] [CrossRef]
- Zhang, X.S.; Gao, S.B.; Li, R.X.; Du, X.Y.; Li, C.Y.; Li, Y.J. A Retinal Mechanism Inspired Color Constancy Model. IEEE Trans. Image Process. 2016, 25, 1219–1232. [Google Scholar] [CrossRef] [PubMed]
- Akbarinia, A.; Parraga, C.A. Color Constancy Beyond the Classical Receptive Field. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 14, 1–14. [Google Scholar]
- Yang, K.F.; Gao, S.B.; Li, Y.J. Efficient illuminant estimation for colour constancy using grey pixels. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 2254–2263. [Google Scholar]
- Joze, H.R.V.; Drew, M.S. Exemplar-Based Color Constancy and Multiple Illumination. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 860–873. [Google Scholar] [CrossRef]
- Males, M.; Hedi, A.; Grgic, M. Color balancing using sclera color. IET Image Process. 2018, 12, 416–421. [Google Scholar] [CrossRef]
- Hussain, M.A.; Sheikh Akbari, A. Colour Constancy for Image of Non-Uniformly Lit Scenes. In Proceedings of the IEEE International Conference on Imaging Systems and Techniques (IST 2018), Kraków, Poland, 16–18 October 2018. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. K-means++: The Advantages of Careful Seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA ’07), Louisiana, USA, 7–9 January, 2007; pp. 227–235. [Google Scholar]
- Von Kries, J. Influence of Adaptation on the Effects Produced by Luminous Stimuli. Sources of Colour Vision; MacAdam, D., Ed.; MIT Press: Cambridge, MA, USA, 1970; pp. 29–119. [Google Scholar]
- Gehler, P.; Rother, C.; Blake, A.; Sharp, T.; Minka, T. Bayesian colour constancy revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 24–26 June 2008; pp. 1–8. [Google Scholar]
- Ciurea, F.; Funt, B. A Large Image Database for Colour Constancy Research. In Proceedings of the Imaging Science and Technology Eleventh Colour Imaging Conference, Scottsdale, AZ, USA, 3 November 2003; pp. 160–164. [Google Scholar]
- Tkačik, G.; Garrigan, P.; Ratliff, C.; Milčinski, G.; Klein, J.M.; Seyfarth, L.H.; Sterling, P.; Brainard, D.H.; Balasubramanian, V. Natural Images from the Birthplace of the Human Eye. PLoS ONE 2011, 6, e20409. [Google Scholar] [CrossRef]
- Hordley, S.D.; Finlayson, G.D. Re-evaluating color constancy algorithms. In Proceedings of the 17th International Conference on Pattern Recognition, ICPR 2004, Cambridge, UK, 23–26 August 2004; pp. 76–79. [Google Scholar]
- Finlayson, G.D.; Zakizadeh, R.; Gijsenij, A. The Reproduction Angular Error for Evaluating the Performance of Illuminant Estimation Algorithms. IEEE Trans. Pattern. Anal. Mach. Intell. 2017, 39, 1482–1488. [Google Scholar] [CrossRef]
- Gijsenij, A.; Gevers, T.; Lucassen, M.P. Perceptual Analysis of Distance Measures for Colour Constancy Algorithms. J. Optical Soc. Am. A 2009, 26, 2243–2256. [Google Scholar] [CrossRef]
- Shi, L.; Xiong, W.; Funt, B. Illumination estimation via thin-plate spline interpolation. J. Opt. Soc. A 2011, 28, 940. [Google Scholar] [CrossRef]
- Hussain, M.A.; Akbari, A.S. Color Constancy Algorithm for Mixed-Illuminant Scene Images. IEEE Access 2018, 6, 8964–8976. [Google Scholar] [CrossRef]






| Dataset (Number of Images) | Method | ||||
|---|---|---|---|---|---|
| WGE | Gisenji et al. | MIRF | Cheng et al. | Proposed CCAFIS | |
| MLS (9 outdoor) | 3.25 | 4.20 | 4.04 | 3.69 | 4.22 |
| MIMO (78) | 3.71 | 3.80 | 4.18 | 4.12 | 4.24 |
| Grey Ball (200) | 4.00 | 3.25 | 3.88 | 3.94 | 4.36 |
| Colour Checker (100) | 3.80 | 3.76 | 3.91 | 3.79 | 4.29 |
| UPenn (57) | 3.92 | 3.85 | 4.09 | 3.94 | 4.12 |
| Method | Recovery Error | Reproduction Error | ||
|---|---|---|---|---|
| Mean | Median | Mean | Median | |
| Statistics-based methods | ||||
| Gray World | 7.1° | 7.0° | 10.1° | 7.5° |
| Max-RGB | 6.8° | 5.3° | 9.7° | 7.5° |
| Shades of Gray | 6.1° | 5.3° | 6.9° | 3.9° |
| Gray Edge-1 | 5.1° | 4.7° | 6.3° | 3.6° |
| Gray Edge-2 | 6.1° | 4.1° | 5.8° | 3.6° |
| Proposed CCAFIS | 3.9° | 4.0° | 4.1° | 2.6° |
| Learning-based methods | ||||
| Exemplar-based | 4.4° | 3.4° | 4.8° | 3.7° |
| Gray Pixel (std) | 4.6° | 6.2° | - | - |
| Deep Learning | 4.8° | 3.7° | - | - |
| Natural Image Statistics | 5.2° | 3.9° | 5.5° | 4.3° |
| Spectral Statistics | 10.3° | 8.9° | - | - |
| ASM | 4.7° | 3.8° | 5.2° | 2.3° |
| Method | Recovery Error | Reproduction Error | ||
|---|---|---|---|---|
| Mean | Median | Mean | Median | |
| Statistics-based methods | ||||
| Gray World | 9.8° | 7.4° | ||
| Max-RGB | 8.1° | 6.0° | ||
| Shades of Gray | 7.0° | 5.3° | ||
| Gray Edge-1 | 5.2° | 5.5° | 4.9 | |
| Gray Edge-2 | 7.0° | 5.0° | ||
| Proposed CCAFIS | ||||
| Learning-based methods | ||||
| Exemplar-based | 2.6 | |||
| Gray Pixel (std) | 4.7 | - | - | |
| ASM | ||||
| AAC | - | - | ||
| HLVI BU | . | - | - | |
| HLVI BU & TD | - | - | ||
| CCDL | - | - | ||
| EB | - | - | ||
| BDP | - | - | ||
| CM | - | - | ||
| FB+GM | - | - | ||
| PCL | - | - | ||
| SF | - | - | ||
| CCP | - | - | ||
| CCC | - | - | ||
| AlexNet+SVR | - | - | ||
| CNN-Per patch | - | - | ||
| CNN average--pooling | - | - | ||
| CNN median-pooling | - | - | ||
| CNN fine-tuned | - | - | ||
| CNN + SVR | - | - | ||
| Method | MIMO (real) | MIMO (lab) | ||
|---|---|---|---|---|
| Mean | Median | Mean | Median | |
| Statistical methods | ||||
| Grey world | 4.2° | 5.2° | 3.2° | 2.9° |
| Max-RGB | 5.6° | 6.8° | 7.8° | 7.6° |
| Grey Edge-1 | 3.9° | 5.3° | 3.1° | 2.8° |
| Grey Edge-2 | 4.7° | 6.0° | 3.2° | 2.9° |
| MIRF | 4.1° | 3.3° | 2.6° | 2.6° |
| Grey Pixel | 5.7° | 3.2° | 2.5° | 3.1° |
| Proposed CCAFIS | 4.2° | 4.3° | 2.1° | |
| Learning-based methods | ||||
| MLS + GW | 4.3 | |||
| MLS + WP | 4.2 | |||
| MIRF + GW | ||||
| MIRF + WP | ||||
| MIRF + IEbV | 4.5 | |||
| Method | Median Error |
|---|---|
| Max-RGB | 7.8° |
| Grey World | 8.9° |
| Grey Edge-1 | 6.4° |
| Grey Edge-2 | 5.0° |
| Gisenji et al. | 5.1° |
| Proposed CCAFIS | 2.6° |
| Method | Time (s) |
|---|---|
| Statistics-Based Methods | |
| Gray World | 2.01 |
| Max-RGB (White Patch) | 2.21 |
| Gray Edge-1 | 23.67 |
| Gray Edge-2 | 24.21 |
| Proposed CCAFIS | 26.37 |
| Learning-Nased Methods | |
| Exemplar-based | 2827 |
| Gray Pixel (std) | 1165 |
| ASM | 2500 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, M.A.; Sheikh-Akbari, A.; Mporas, I. Colour Constancy for Image of Non-Uniformly Lit Scenes. Sensors 2019, 19, 2242. https://doi.org/10.3390/s19102242
Hussain MA, Sheikh-Akbari A, Mporas I. Colour Constancy for Image of Non-Uniformly Lit Scenes. Sensors. 2019; 19(10):2242. https://doi.org/10.3390/s19102242
Chicago/Turabian StyleHussain, Md Akmol, Akbar Sheikh-Akbari, and Iosif Mporas. 2019. "Colour Constancy for Image of Non-Uniformly Lit Scenes" Sensors 19, no. 10: 2242. https://doi.org/10.3390/s19102242
APA StyleHussain, M. A., Sheikh-Akbari, A., & Mporas, I. (2019). Colour Constancy for Image of Non-Uniformly Lit Scenes. Sensors, 19(10), 2242. https://doi.org/10.3390/s19102242






