Numerical Simulation and Experimental Study of a Simplified Force-Displacement Relationship in Superelastic SMA Helical Springs
Abstract
:1. Introduction
2. Mechanical Model of a Superelastic SMA Helical Spring
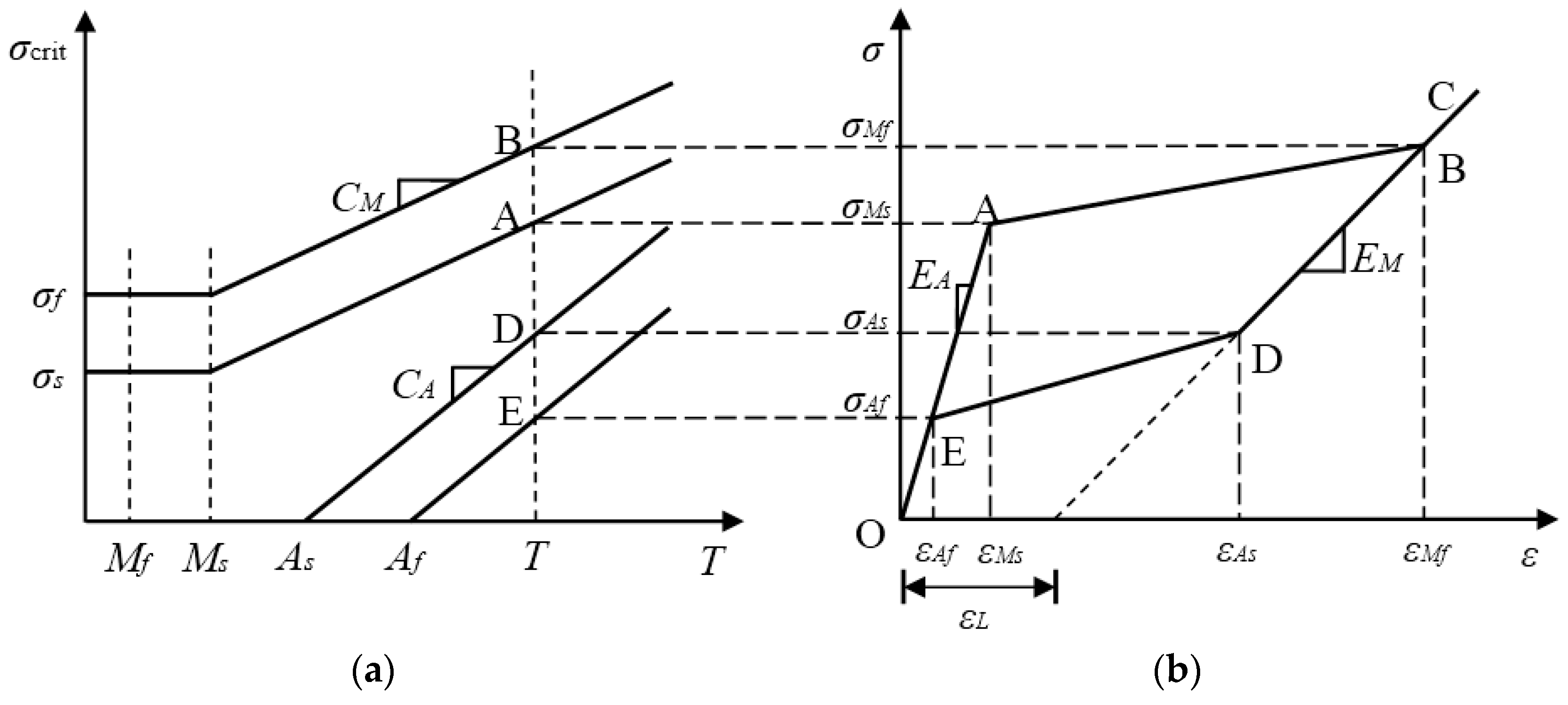
2.1. Multilinear Constitutive Model of SMA Material
2.1.1. Major Loop
2.1.2. Subloops
2.2. Constitutive Model of an SMA Helical Spring
3. Experiments and Results
3.1. Tension Tests of SMA Helical Springs
3.2. Testing Results
3.2.1. Cyclic Loading with Variable Amplitudes
3.2.2. Complex Single-Cycle Loading
3.3. Comparison of the Numerical and Experimental Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hartl, D.; Lagoudas, D.C. Aerospace applications of shape memory alloys. Proc. Inst. Mech. Eng. Part G–J Aerosp. Eng. 2007, 221, 535–552. [Google Scholar] [CrossRef] [Green Version]
- Bundhoo, V.; Haslam, E.; Birch, B.; Park, E.J. A shape memory alloy-based tendon-driven actuation system for biomimetic artificial fingers, part I: Design and evaluation. Robotica 2009, 27, 131–146. [Google Scholar] [CrossRef]
- Jani, J.M.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Song, G.; Ma, N.; Penney, N.; Barr, T.; Lee, H.J.; Arnold, S. Design and Control of a Proof-of-Concept Active Jet Engine Intake Using Shape Memory Alloy Actuators. Smart. Struct. Syst. 2004, 7, 1–13. [Google Scholar] [CrossRef]
- Patil, D.; Song, G. Shape memory alloy actuated accumulator for ultra-deepwater oil and gas exploration. Smart Mater. Struct. 2016, 25, 045012. [Google Scholar] [CrossRef]
- Saadat, S.; Salichs, J.; Noori, M.; Hou, Z.; Davoodi, H.; Bar-On, I.; Suzuki, Y.; Masuda, A. An overview of vibration and seismic applications of NiTi shape memory alloy. Smart Mater. Struct. 2002, 11, 218–229. [Google Scholar] [CrossRef]
- Ren, W.-J.; Li, H.-N.; Song, G. A one-dimensional strain-rate-dependent constitutive model for superelastic shape memory alloys. Smart Mater. Struct. 2007, 16, 191–197. [Google Scholar] [CrossRef]
- Ren, W.-J.; Li, H.-N.; Song, G. Phenomenological modeling of the cyclic behavior of superelastic shape memory alloys. Smart Mater. Struct. 2007, 16, 1083–1089. [Google Scholar] [CrossRef]
- Liu, M.; Li, H.-N.; Song, G.; Ou, J. Investigation of vibration mitigation of stay cables incorporated with superelastic shape memory alloy dampers. Smart Mater. Struct. 2007, 16, 2202–2213. [Google Scholar] [CrossRef]
- Song, G.; Ma, N.; Li, H.-N. Applications of shape memory alloys in civil structures. Eng. Struct. 2006, 28, 1266–1274. [Google Scholar] [CrossRef]
- Ozbulut, O.E.; Hurlebaus, S.; Desroches, R. Seismic Response Control Using Shape Memory Alloys: A Review. J. Intell. Mater. Syst. Struct. 2011, 22, 1531–1549. [Google Scholar] [CrossRef]
- Wilde, K.; Gardoni, P.; Fujino, Y. Base isolation system with shape memory alloy device for elevated highway bridges. Eng. Struct. 2000, 22, 222–229. [Google Scholar] [CrossRef]
- Qian, H.; Li, H.-N.; Song, G. Experimental investigations of building structure with a superelastic shape memory alloy friction damper subject to seismic loads. Smart Mater. Struct. 2016, 25, 125026. [Google Scholar] [CrossRef]
- Qiu, C.-X.; Zhu, S.-Y. Shake table test and numerical study of self-centering steel frame with SMA braces. Earthq. Eng. Struct. Dyn. 2017, 46, 117–137. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, M.; Li, H.; Song, G. Experimental investigations on seismic control of cable-stayed bridges using shape memory alloy self-centering dampers. Struct. Control Health Monit. 2018, 25, e2180. [Google Scholar] [CrossRef]
- Li, H.-N.; Liu, M.-M.; Fu, X. An innovative re-centering SMA-lead damper and its application to steel frame structures. Smart Mater. Struct. 2018, 27, 075029. [Google Scholar] [CrossRef] [Green Version]
- Song, G.; Mo, Y.L.; Otero, K.; Gu, H. Health monitoring and rehabilitation of a concrete structure using intelligent materials. Smart Mater. Struct. 2006, 15, 309–314. [Google Scholar] [CrossRef]
- Li, X.; Li, M.; Song, G. Energy-dissipating and self-repairing SMA-ECC composite material system. Smart Mater. Struct. 2015, 24, 025024. [Google Scholar] [CrossRef]
- Speicher, M.; Hodgson, D.E.; Desroches, R.; Leon, R.T. Shape Memory Alloy Tension/Compression Device for Seismic Retrofit of Buildings. J. Mater. Eng. Perform. 2009, 18, 746–753. [Google Scholar] [CrossRef]
- Attanasi, G.; Auricchio, F. Innovative superelastic isolation device. J. Earthqu. Eng. 2011, 15, 72–89. [Google Scholar] [CrossRef]
- Mishra, S.K.; Gur, S.; Chakraborty, S. An improved tuned mass damper (SMA-TMD) assisted by a shape memory alloy spring. Smart Mater. Struct. 2013, 22, 095016. [Google Scholar] [CrossRef]
- Huang, B.; Zhang, H.-Y.; Wang, H.; Song, G. Passive base isolation with superelastic nitinol SMA helical springs. Smart Mater. Struct. 2014, 23, 065009. [Google Scholar] [CrossRef]
- Zhuang, P.; Xue, S.-D.; Nie, P.; Wang, W. Experimental and numerical study on hysteretic performance of SMA spring-friction bearings. Earthq. Eng. Eng. Vib. 2016, 15, 597–609. [Google Scholar] [CrossRef]
- Ruth, D.J.S.; Dhanalakshmi, K.; Nakshatharan, S.S. Bidirectional angular control of an integrated sensor/actuator shape memory alloy based system. Measurement. 2015, 69, 210–221. [Google Scholar] [CrossRef]
- Cui, D.; Song, G.; Li, H.-N. Modeling of the electrical resistance of shape memory alloy wires. Smart Mater. Struct. 2010, 19, 055019. [Google Scholar] [CrossRef]
- Kim, H.; Han, Y.; Lee, D.; Ha, J.I.; Cho, K.J. Sensorless displacement estimation of a shape memory alloy coil spring actuator using inductance. Smart Mater. Struct. 2012, 22, 025001. [Google Scholar] [CrossRef]
- Song, G.; Ma, N.; Lee, H.J. Position estimation and control of SMA actuators based on electrical resistance measurement. Smart. Struct. Syst. 2007, 3, 189–200. [Google Scholar] [CrossRef]
- Wang, T.-M.; Shi, Z.-Y.; Liu, D.; Ma, C.; Zhang, Z.H. An accurately controlled antagonistic shape memory alloy actuator with selfsensing. Sensors 2012, 12, 7682–7700. [Google Scholar] [CrossRef]
- Liu, S.-H.; Huang, T.-S.; Yen, J.-Y. Tracking Control of Shape-Memory-Alloy Actuators Based on Self-Sensing Feedback and Inverse Hysteresis Compensation. Sensors 2010, 10, 112–127. [Google Scholar] [CrossRef]
- Zhang, J.-J.; Yin, Y.-H.; Zhu, J.-Y. Electrical Resistivity-Based Study of Self-Sensing Properties for Shape Memory Alloy-Actuated Artificial Muscle. Sensors 2013, 13, 12958–12974. [Google Scholar] [CrossRef] [Green Version]
- Tobushi, H.; Tanaka, K. Deformation of a shape memory alloy helical spring:analysis based on stress-strain-temperature relation. JSME Int. J. Ser. I 1991, 34, 83–89. [Google Scholar]
- Tanaka, K. A Thermomechanical sketch of shape memory effect:one-dimensional tensile behavior. Res. Mech. 1986, 18, 251–263. [Google Scholar]
- Liang, C.; Rogers, C.A. Design of shape memory alloy springs with applications in vibration control. J. Intell. Mater. Syst. Struct. 1997, 8, 314–322. [Google Scholar] [CrossRef]
- Liang, C.; Rogers, C.A. One-dimensional thermomechanical constitutive relations for shape memory materials. J. Intell. Mater. Syst. Struct. 1990, 1, 207–234. [Google Scholar] [CrossRef]
- Toi, Y.; Lee, J.B.; Taya, M. Finite element analysis of superelastic, large deformation behavior of shape memory alloy helical springs. Comput. Struct. 2004, 82, 1685–1693. [Google Scholar] [CrossRef]
- Brinson, L.C. One-dimensional constitutive behavior of shape memory alloys:thermomechanical derivation with non-constant material functions and redefined martensite internal variable. J. Intell. Mater. Syst. Struct. 1993, 4, 229–242. [Google Scholar] [CrossRef]
- Aguiar, R.A.A.; Savi, M.A.; Pacheco, P.M.C.L. Experimental and numerical investigations of shape memory alloy helical springs. Smart Mater. Struct. 2010, 19, 025008. [Google Scholar] [CrossRef]
- Paiva, A.; Savi, M.A.; Braga, A.M.B.; Pacheco, P.M.C.L. A constitutive model for shape memory alloys considering tensile–compressive asymmetry and plasticity. Int. J. Solids Struct. 2005, 42, 3439–3457. [Google Scholar] [CrossRef]
- Mirzaeifar, R.; Desroches, R.; Yavari, A. A combined analytical, numerical, and experimental study of shape-memory-alloy helical springs. Int. J. Solids Struct. 2011, 48, 611–624. [Google Scholar] [CrossRef]
- Mirzaeifar, R.; Shakeri, M.; Sadighi, M. Nonlinear finite element formulation for analyzing shape memory alloy cylindrical panels. Smart Mater. Struct. 2009, 18, 035002. [Google Scholar] [CrossRef]
- Mirzaeifar, R.; Desroches, R.; Yavari, A. Exact solutions for pure torsion of shape memory alloy circular bars. Mech. Mater. 2010, 42, 797–806. [Google Scholar] [CrossRef]
- Thiebaud, F.; Zineb, B.T. Experimental and finite element analysis of superelastic, behaviour of shape memory alloy for damping applications. Mech. Ind. 2014, 15, 371–376. [Google Scholar] [CrossRef]
- Chemisky, Y.; Duval, A.; Patoor, E.; Zineb, T.B. Constitutive model for shape memory alloys including phase transformation, martensitic reorientation and twins accommodation. Mech. Mater. 2011, 43, 361–376. [Google Scholar] [CrossRef]
- Enemark, S.; Savi, M.A.; Santos, I.F. Nonlinear dynamics of a pseudoelastic shape memory alloy system-theory and experiment. Smart Mater. Struct. 2014, 23, 085018. [Google Scholar] [CrossRef]
- Savi, M.A.; Pacheco, P.M.C.L.; Garcia, M.S.; Aguiar, R.A.; De Souza, L.F.G.; Da Hora, R.B. Nonlinear geometric influence on the mechanical behavior of shape memory alloy helical springs. Smart Mater. Struct. 2015, 24, 035012. [Google Scholar] [CrossRef]
- Auricchio, F.; Taylor, R.L.; Lubliner, J. Shape-memory alloys: Macromodelling and numerical simulations of the superelastic behavior. Comput. Meth. Appl. Mech. Eng. 1997, 146, 281–312. [Google Scholar] [CrossRef]
- Mehrabi, R.; Ravari, M.R.K. Simulation of superelastic SMA helical springs. Smart. Struct. Syst. 2015, 16, 183–194. [Google Scholar] [CrossRef]
- Mehrabi, R.; Kadkhodaei, M.; Elahinia, M. A thermodynamically-consistent microplane model for shape memory alloys. Int. J. Solids Struct. 2014, 51, 2666–2675. [Google Scholar] [CrossRef]
- Motahari, S.A.; Ghassemieh, M. Multilinear one-dimensional shape memory material model for use in structural engineering applications. Eng. Struct. 2007, 29, 904–913. [Google Scholar] [CrossRef]
- Lagoudas, D.; Hartl, D.; Chemisky, Y.; Machado, L.; Popov, P. Constitutive model for the numerical analysis of phase transformation in polycrystalline shape memory alloys. Int. J. Plast. 2012, 32–33, 155–183. [Google Scholar] [CrossRef]
- Brinson, L.C.; Huang, M.S. Simplifications and Comparisons of Shape Memory Alloy Constitutive Models. J. Intell. Mater. Syst. Struct. 1996, 7, 108–114. [Google Scholar] [CrossRef]
- Lagoudas, D.C.; Mayes, J.J.; Khan, M.M. Simplified shape memory alloy (SMA) material model for vibration isolation. In Proceedings of the Smart Structures and Materials 2001 Conference, Newport Beach, CA, USA, 5–8 March 2001; Volume 4326, pp. 452–461. [Google Scholar]
- Bekker, A.; Brinson, L.C. Phase diagram based description of the hysteresis behavior of shape memory alloys. Acta Mater. 1998, 46, 3649–3665. [Google Scholar] [CrossRef]
- Doraiswamy, S.; Rao, A.; Srinivasa, A.R. Combining thermodynamic principles with Preisach models for superelastic shape memory alloy wires. Smart Mater. Struct. 2011, 20, 085032. [Google Scholar] [CrossRef]
- Heintze, O.; Seelecke, S. A coupled thermomechanical model for shape memory alloys-From single crystal to polycrystal. Mater. Sci. Eng. A 2008, 481, 389–394. [Google Scholar] [CrossRef]
- Sitnikova, E.; Pavlovskaia, E.; Ing, J.; Wiercigroch, M. Suppressing nonlinear resonances in an impact oscillator using SMAs. Smart Mater. Struct. 2012, 21, 075028. [Google Scholar] [CrossRef]
- Manach, P.Y.; Favier, D. Shear and tensile thermomechanical behavior of near equiatomic NiTi alloy. Mater. Sci. Eng. A 1997, 222, 45–57. [Google Scholar] [CrossRef]
- Zhou, X.; You, Z. Theoretical analysis of superelastic SMA helical structures subjected to axial and torsional loads. Smart. Struct. Syst. 2015, 15, 1271–1291. [Google Scholar] [CrossRef]
- Enemark, S.; Santos, I.F.; Savi, M.A. Modelling, characterisation and uncertainties of stabilised pseudoelastic shape memory alloy helical springs. J. Intell. Mater. Syst. Struct. 2016, 27, 2721–2743. [Google Scholar] [CrossRef]
- Wahl, A.M. Mechanical Springs, 1st ed.; Penton Publishing Co.: Cleveland, OH, USA, 1944. [Google Scholar]
- Sedlák, P.; Frost, M.; Kruisová, A.; Hiřmanová, K.; Heller, L.; Šittner, P. Simulations of Mechanical Response of Superelastic NiTi Helical Spring and its Relation to Fatigue Resistance. J. Mater. Eng. Perform. 2014, 23, 2591–2598. [Google Scholar] [CrossRef]
- Mehrabi, R.; Kadkhodaei, M.; Elahinia, M. Constitutive modeling of tension-torsion coupling and tensioncompression asymmetry in NiTi shape memory alloys. Smart Mater. Struct. 2014, 23, 075021. [Google Scholar] [CrossRef]
- Song, Y. Experimental and Numerical Study of Vibration Control of Frame Structure with SMAS-TMD System. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2017. [Google Scholar]



















| Calculation Formula | Parameter |
|---|---|
| GA = EA/2(1 + ν) | Shear modulus of austenite |
| GM = EM/2(1 + ν) | Shear modulus of martensite |
| τMs = σMs/ | Starting shear stress of the martensitic transformation |
| τMf = σMf/ | Final shear stress of the martensitic transformation |
| τAs = σAs/ | Starting shear stress of the austenitic transformation |
| τAf = σAf/ | Final shear stress of the austenitic transformation |
| γL = εL | Maximum residual shear strain |
| Specimen | R0 (mm) | r (mm) | L0 (mm) | N |
|---|---|---|---|---|
| SMA-S1 | 6.4 | 0.5 | 22 | 7 |
| SMA-S2 | 6.1 | 0.4 | 19 | 7 |
| SMA-S3 | 5.5 | 0.5 | 12 | 7 |
| SMA-S4 | 5.6 | 0.4 | 13 | 7 |
| Specimen | EA (GPa) | EM (GPa) | CA (MPa/K) | CM (MPa/K) | MS (K) | As (K) | Af (K) | σs (MPa) | σf (MPa) | εL |
|---|---|---|---|---|---|---|---|---|---|---|
| SMA-S1 | 72 | 60 | 11.0 | 6.8 | 269 | 280 | 290 | 99 | 527 | 0.037 |
| SMA-S2 | 72 | 64 | 11.0 | 7.6 | 268 | 278 | 288 | 96 | 582 | 0.032 |
| SMA-S3 | 72 | 60 | 11.0 | 6.8 | 269 | 280 | 290 | 99 | 527 | 0.037 |
| SMA-S4 | 72 | 64 | 11.0 | 7.6 | 268 | 278 | 288 | 96 | 582 | 0.032 |
| Case | Displacement Amplitudes (mm) | Loading History |
|---|---|---|
| I | 60, 70, 80, 90 and 100 |  |
| II | 100, 90, 80, 70 and 60 |  |
| III | 60, 30, 100, 50 and 80 |  |
| IV | 80, 30, 70, 40, 60, 50, 100, 60, 90, 65 and 85 |  |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, B.; Lv, H.; Song, Y. Numerical Simulation and Experimental Study of a Simplified Force-Displacement Relationship in Superelastic SMA Helical Springs. Sensors 2019, 19, 50. https://doi.org/10.3390/s19010050
Huang B, Lv H, Song Y. Numerical Simulation and Experimental Study of a Simplified Force-Displacement Relationship in Superelastic SMA Helical Springs. Sensors. 2019; 19(1):50. https://doi.org/10.3390/s19010050
Chicago/Turabian StyleHuang, Bin, Hongwang Lv, and Yang Song. 2019. "Numerical Simulation and Experimental Study of a Simplified Force-Displacement Relationship in Superelastic SMA Helical Springs" Sensors 19, no. 1: 50. https://doi.org/10.3390/s19010050
APA StyleHuang, B., Lv, H., & Song, Y. (2019). Numerical Simulation and Experimental Study of a Simplified Force-Displacement Relationship in Superelastic SMA Helical Springs. Sensors, 19(1), 50. https://doi.org/10.3390/s19010050




