Novel Fuzzy PID-Type Iterative Learning Control for Quadrotor UAV
Abstract
1. Introduction
2. Model for The Quadrotor UAV
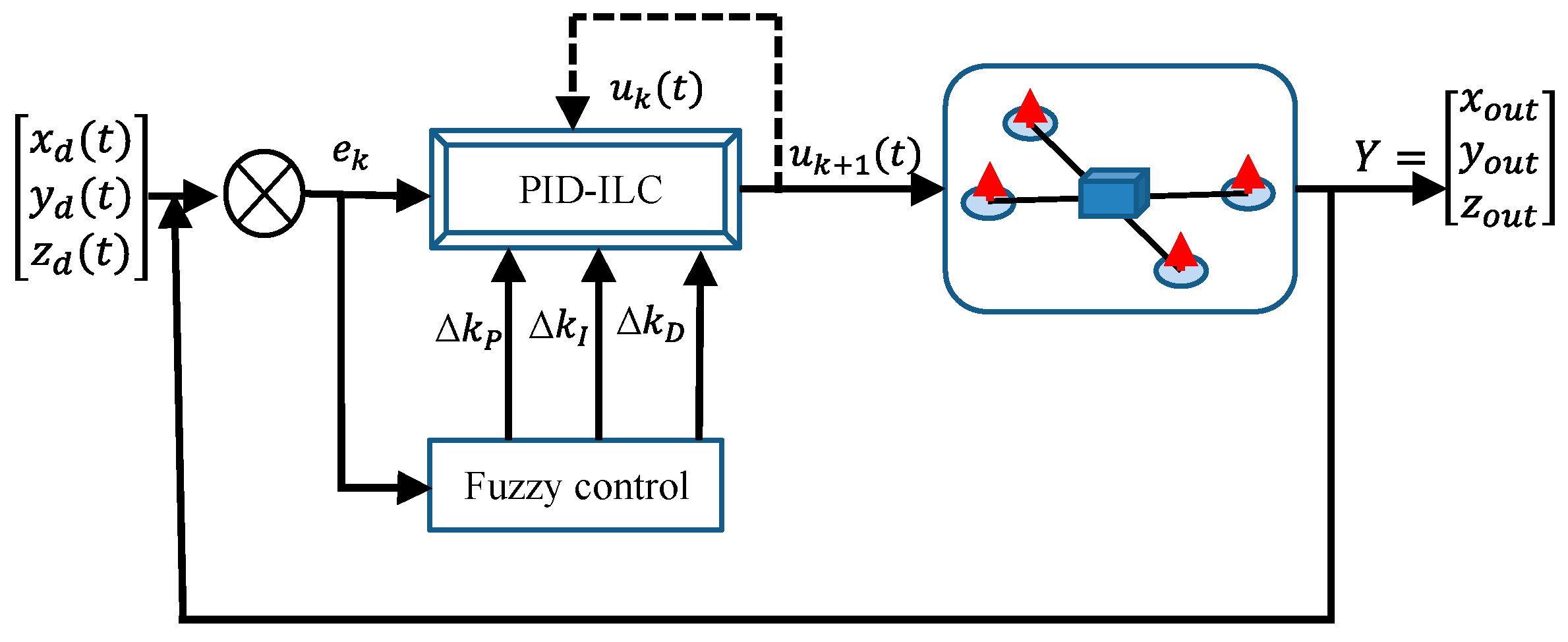
3. Controller Design for Quadrotor UAV
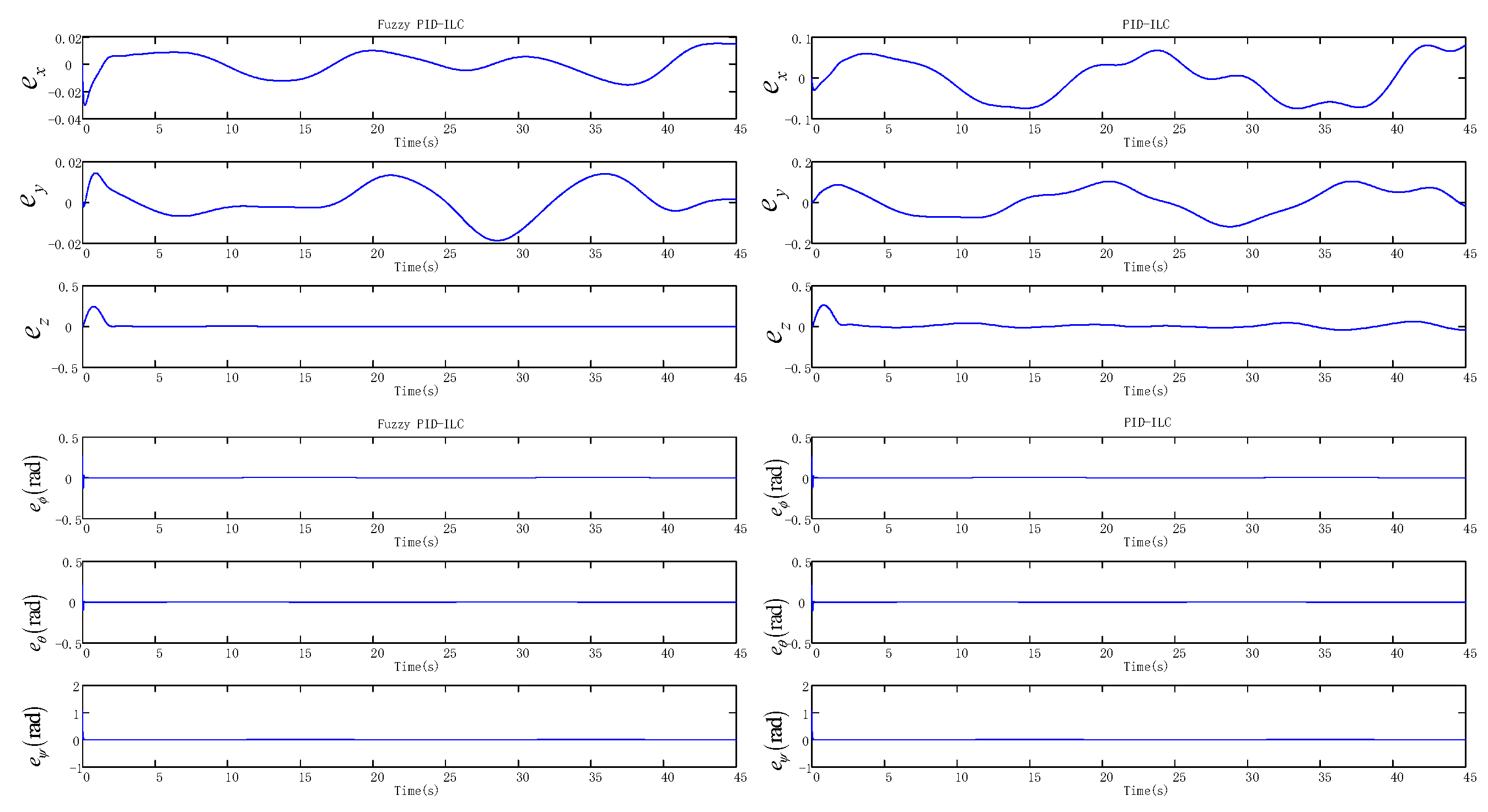
4. Convergence Analysis
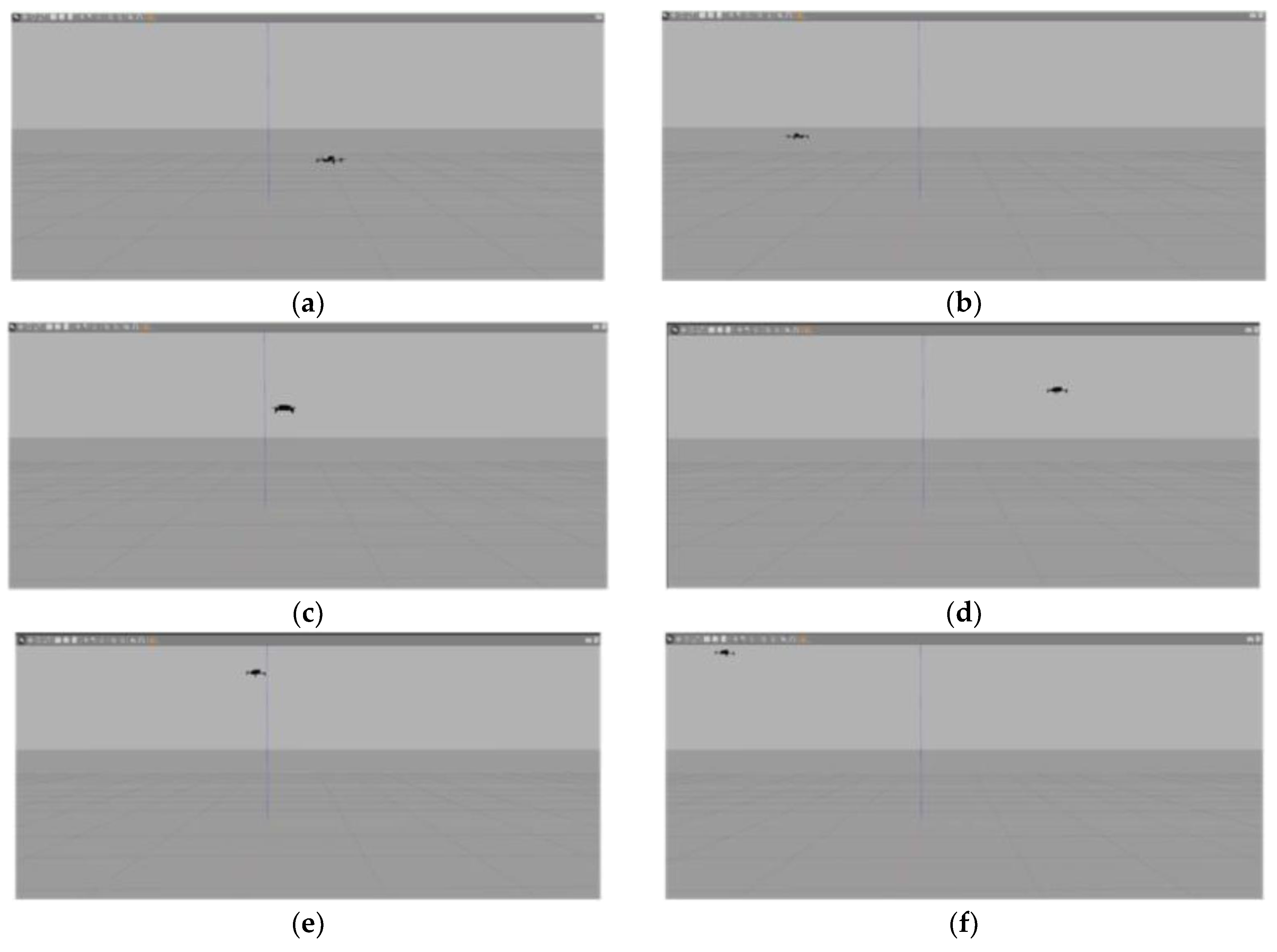
5. Gazebo Environment Simulation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xia, D.; Cheng, L.; Yao, Y. A Robust Inner and Outer Loop Control Method for Trajectory Tracking of a Quadrotor. Sensors 2017, 9, 2147. [Google Scholar] [CrossRef] [PubMed]
- Ryll, M.; Buelthoff, H.H.; Giordano, P.R. A Novel Overactuated Quadrotor Unmanned Aerial Vehicle: Modeling, Control, and Experimental Validation. IEEE Trans. Control Syst. Technol. 2015, 23, 540–556. [Google Scholar] [CrossRef]
- Park, J.; Kim, Y.; Kim, S. Landing Site Searching and Selection Algorithm Development Using Vision System and Its Application to Quadrotor. IEEE Trans. Control Syst. Technol. 2015, 23, 488–503. [Google Scholar] [CrossRef]
- Abdolhosseini, M.; Zhang, Y.M.; Rabbath, C.A. An Efficient Model Predictive Control Scheme for an Unmanned Quadrotor Helicopter. J. Intell. Robot. Syst. Theory Appl. 2013, 70, 27–38. [Google Scholar] [CrossRef]
- Alexis, K.; Nikolakopoulos, G.; Tzes, A. On trajectory tracking model predictive control of an unmanned quadrotor helicopter subject to aerodynamic disturbances. Asian J. Control 2014, 16, 209–224. [Google Scholar] [CrossRef]
- Kostas, A.; George, N.; Anthony, T. Switching model predictive attitude control for a quadrotor helicopter subject to atmospheric disturbances. Control Eng. Pract. 2011, 19, 1195–1207. [Google Scholar]
- Jaffery, M.H.; Shead, L.; Forshaw, J.L. Experimental quadrotor flight performance using computationally efficient and recursively feasible linear model predictive control. Int. J. Control 2013, 86, 2189–2202. [Google Scholar] [CrossRef]
- Moreno-Valenzuela, J.; Pérez-Alcocer, R.; Guerrero-Medina, M.; Dzul, A. Nonlinear PID-Type Controller for Quadrotor Trajectory Tracking. IEEE/ASME Trans. Mechatron. 2018, 23, 2436–2447. [Google Scholar] [CrossRef]
- Zhao, B.; Xian, B.; Zhang, Y. Nonlinear Robust Adaptive Tracking Control of a Quadrotor UAV Via Immersion and Invariance Methodology. IEEE Trans. Ind. Electron. 2015, 62, 2891–2902. [Google Scholar] [CrossRef]
- Basri, M.A.M.; Husain, A.R.; Danapalasingam, K.A. A hybrid optimal backstepping and adaptive fuzzy control for autonomous quadrotor helicopter with time-varying disturbance. Proceedings of the Institution of Mechanical Engineers, Part G. J. Aerosp. Eng. 2015, 229, 2178–2195. [Google Scholar]
- Basri, M.A.M.; Husain, A.R.; Danapalasingam, K.A. GSA-based optimal backstepping controller with a fuzzy compensator for robust control of an autonomous quadrotor UAV. Aircr. Eng. Aerosp. Technol. 2015, 87, 493–505. [Google Scholar] [CrossRef]
- Tnunay, H.; Abdurrohman, M.Q.; Nugroho, Y. Auto-tuning quadcopter using Loop Shaping. In Proceedings of the 2013 International Conference on Computer, Control, Informatics and Its Applications (IC3INA), Jakarta, Indonesia, 19–21 November 2013; pp. 111–115. [Google Scholar]
- Bouadi, H.; Bouchoucha, M.; Tadjine, M. Sliding m ode control based on backstep pin g approach for an UAV type-quadrotor. Int. J. Appl. Math. Comput. Sci. 2008, 4, 12. [Google Scholar]
- Shakev, N.G.; Topalov, A.V.; Kaynak, O. Comparative Results on Stabilization of the Quad-rotor Rotorcraft Using Bounded Feedback Controllers. J. Intell. Robot. Syst. 2012, 65, 389–408. [Google Scholar] [CrossRef]
- Courbon, J.; Mezouar, Y.; Guénard, N. Vision-based navigation of unmanned aerial vehicles. Control Eng. Pract. 2010, 18, 789–799. [Google Scholar] [CrossRef]
- Bolder, J.; Oomen, T. Rational Basis Functions in Iterative Learning Control-With Experimental Verification on a Motion System. IEEE Trans. Control Syst. Technol. 2015, 23, 722–729. [Google Scholar] [CrossRef]
- De Best, J.; Liu, L.; van de Molengraft, R. Second-Order Iterative Learning Control for Scaled Setpoints. IEEE Trans. Control Syst. Technol. 2015, 23, 805–812. [Google Scholar] [CrossRef]
- Zhu, Q.; Hu, G.-D.; Liu, W.-Q. Iterative learning control design method for linear discrete-time uncertain systems with iteratively periodic factors. IET Control Theory Appl. 2015, 9, 2305–2311. [Google Scholar] [CrossRef]
- Schoellig, A.P.; Mueller, F.L.; D’Andrea, R. Optimization-based iterative learning for precise quadrocopter trajectory tracking. Auton. Robot. 2012, 33, 103–127. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, T.; Shen, L.; Kong, W.; Zhao, B.; Yao, K. An Iterative Learning Controller for Quadrotor UAV Path Following at a Constant Altitude. In Proceedings of the 34th Chinese Control Conference, Tokyo, Japan, 28–30 July 2015; pp. 4406–4411. [Google Scholar]
- Chen, Y.; He, Y.; Zhou, M. Decentralized PID neural network control for a quadrotor helicopter subjected to wind disturbance. J. Cent. South Univ. 2015, 22, 168–179. [Google Scholar] [CrossRef]
- Tao, Y.; Xie, G.; Chen, Y. A PID and fuzzy logic based method for Quadrotor aircraft control motion. J. Intel. Fuzzy Syst. Appl. Eng. Technol. 2016, 31, 2975–2983. [Google Scholar] [CrossRef]
- Qiao, J.; Liu, Z.; Zhang, Y. Modeling and GS-PID Control of the Quad-Rotor UAV. In Proceedings of the 2018 10th International Conference on Computer and Automation Engineering, Brisbane, Australia, 24–26 February 2018; pp. 221–226. [Google Scholar]
- Ortiz, J.P.; Minchala, L.I.; Reinoso, M.J. Nonlinear Robust H-Infinity PID Controller for the Multivariable System Quadrotor. IEEE Lat. Am. Trans. 2016, 14, 1176–1183. [Google Scholar] [CrossRef]
- Ermeydan, A.; Kiyak, E. Fault tolerant control against actuator faults based on enhanced PID controller for a quadrotor. Aircr. Eng. Aerosp. Technol. 2017, 89, 468–476. [Google Scholar] [CrossRef]
- Chang, W.-J.; Chen, P.-H.; Ku, C.-C. Mixed sliding mode fuzzy control for discrete-time non-linear stochastic systems subject to variance and passivity constraints. IET Control Theory Appl. 2015, 9, 2369–2376. [Google Scholar] [CrossRef]
- Jafari, R.; Yu, W. Fuzzy control for uncertainty nonlinear systems with dual fuzzy equations. J. Intell. Fuzzy Syst. Appl. Eng. Technol. 2015, 29, 1229–1240. [Google Scholar] [CrossRef]
- Cherrat, N.; Boubertakh, H.; Arioui, H. Adaptive fuzzy PID control for a quadrotor stabilisation. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Bangkok, Thailand, 24–26 February 2018. [Google Scholar]





| Parameter | Description | Value | Unit |
|---|---|---|---|
| m | Total quadrotor mass | 1 | kg |
| l | Quadrotor radius length | 0.25 | m |
| Ix | Moment of inertia about X-axis | 4 × 10−3 | Kg·m2 |
| Iy | Moment of inertia about Y-axis | 4 × 10−3 | kg·m2 |
| Iz | Moment of inertia about Z-axis | 8 × 10−3 | kg·m2 |
| ωmax | Maximum rotor speed | 200 | rad/s |
| g | Gravitational acceleration | 9.81 | ms2 |
| e | ||||
|---|---|---|---|---|
| NB | ZO | PB | ||
| NB | PB/PS/PM | PB/PS/PS | PB/PS/PS | |
| ZO | PM/PM/PB | PS/PB/PM | PM/PM/PB | |
| PB | PB/PS/PS | PB/PS/PS | PB/PS/PM | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; He, B. Novel Fuzzy PID-Type Iterative Learning Control for Quadrotor UAV. Sensors 2019, 19, 24. https://doi.org/10.3390/s19010024
Dong J, He B. Novel Fuzzy PID-Type Iterative Learning Control for Quadrotor UAV. Sensors. 2019; 19(1):24. https://doi.org/10.3390/s19010024
Chicago/Turabian StyleDong, Jian, and Bin He. 2019. "Novel Fuzzy PID-Type Iterative Learning Control for Quadrotor UAV" Sensors 19, no. 1: 24. https://doi.org/10.3390/s19010024
APA StyleDong, J., & He, B. (2019). Novel Fuzzy PID-Type Iterative Learning Control for Quadrotor UAV. Sensors, 19(1), 24. https://doi.org/10.3390/s19010024




