Implicit Calibration Using Probable Fixation Targets
Abstract
1. Introduction
1.1. Calibration
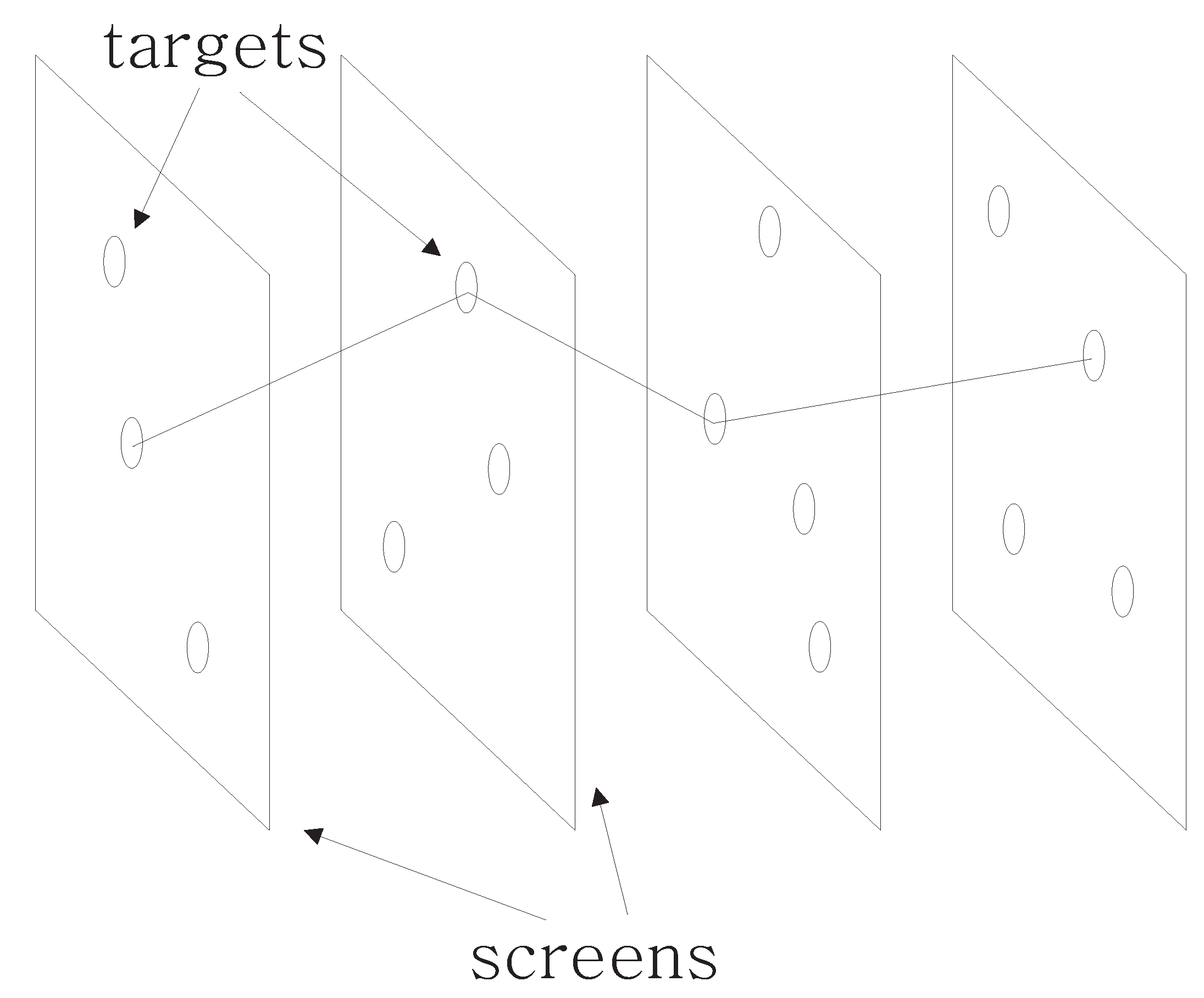
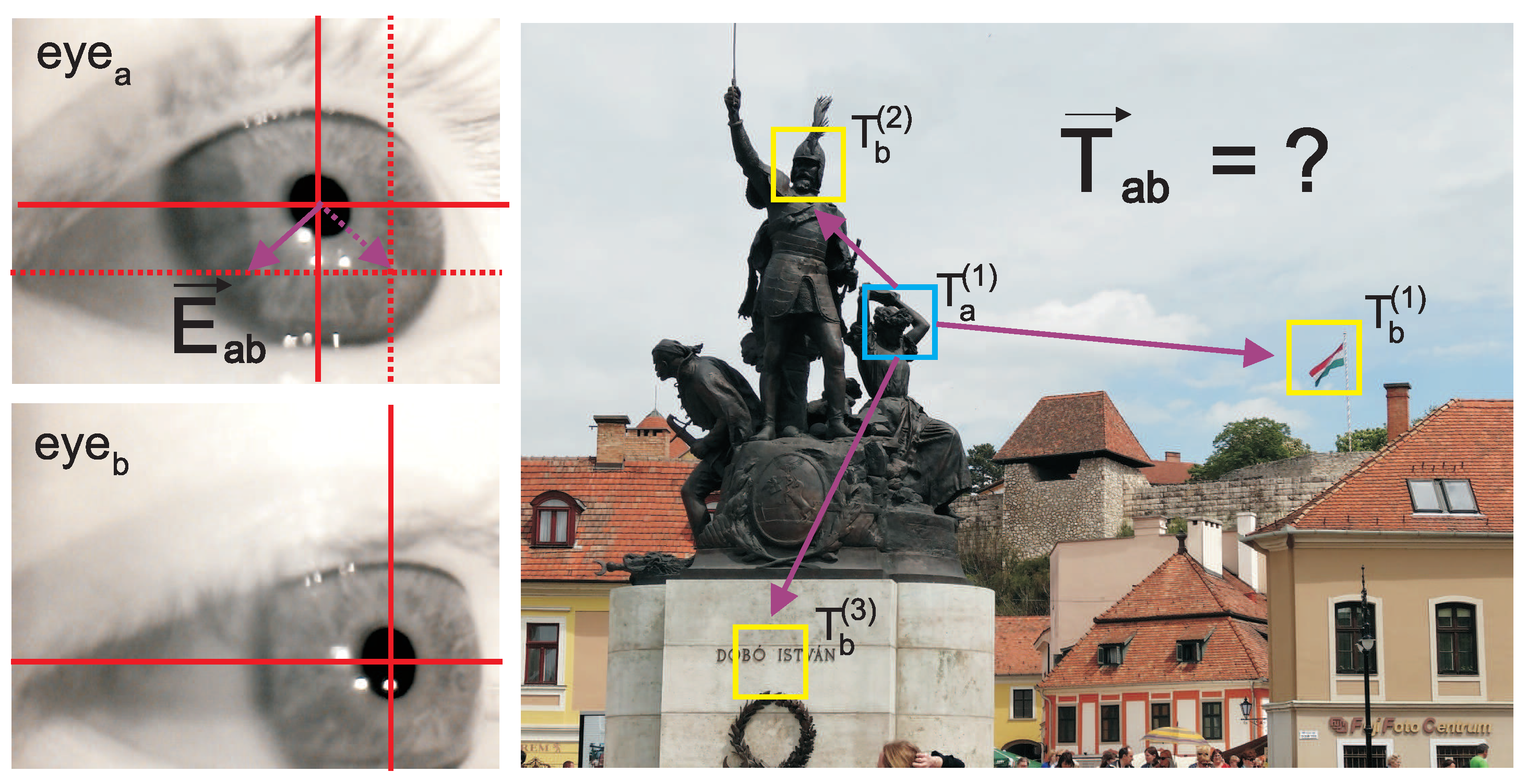
1.2. Implicit Calibration
1.3. The State of the Art
1.4. Paper’s Contribution
- saliency maps prediction,
- conversion of saliency maps to lists of PFTs,
- choosing a mapping (a set of PFTs) using miscellaneous criteria and heuristic algorithms,
- using the chosen PFT mapping to build a calibration model.
- Analyses of algorithms for PFT (targets) creation using saliency maps.
- Introduction of new mapping comparison functions.
- More extensive analyses of results and possible algorithms’ parameters.
- Introduction of two new datasets.
- Implementation of all presented algorithms in a publicly available new version of the ETCAL library which has been created for calibration purposes and is available at GitHub [30].
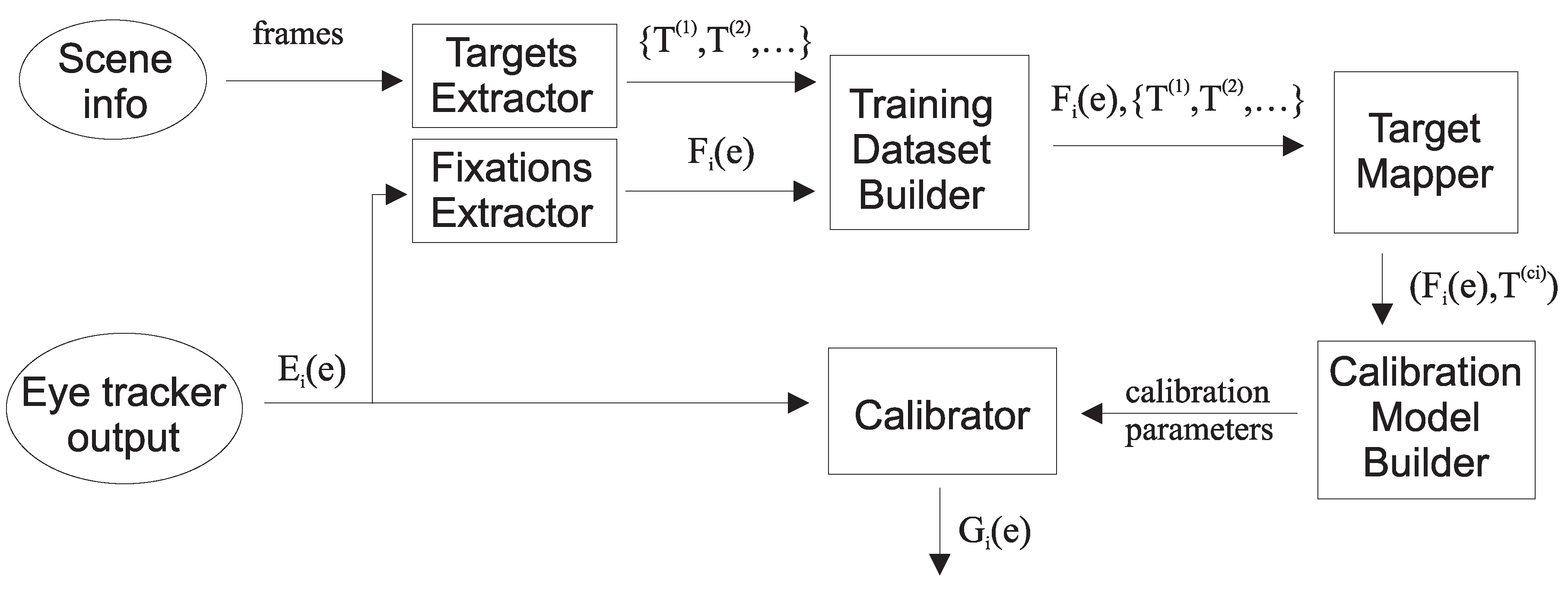
2. Methods and Materials
- Extraction of targets (PFTs) from saliency information.
- Choosing the mappings comparison function (MCF).
- Developing heuristic algorithms for searching the mapping space (genetic and incremental)
- Building a calibration model using the ETCAL library ([30]).
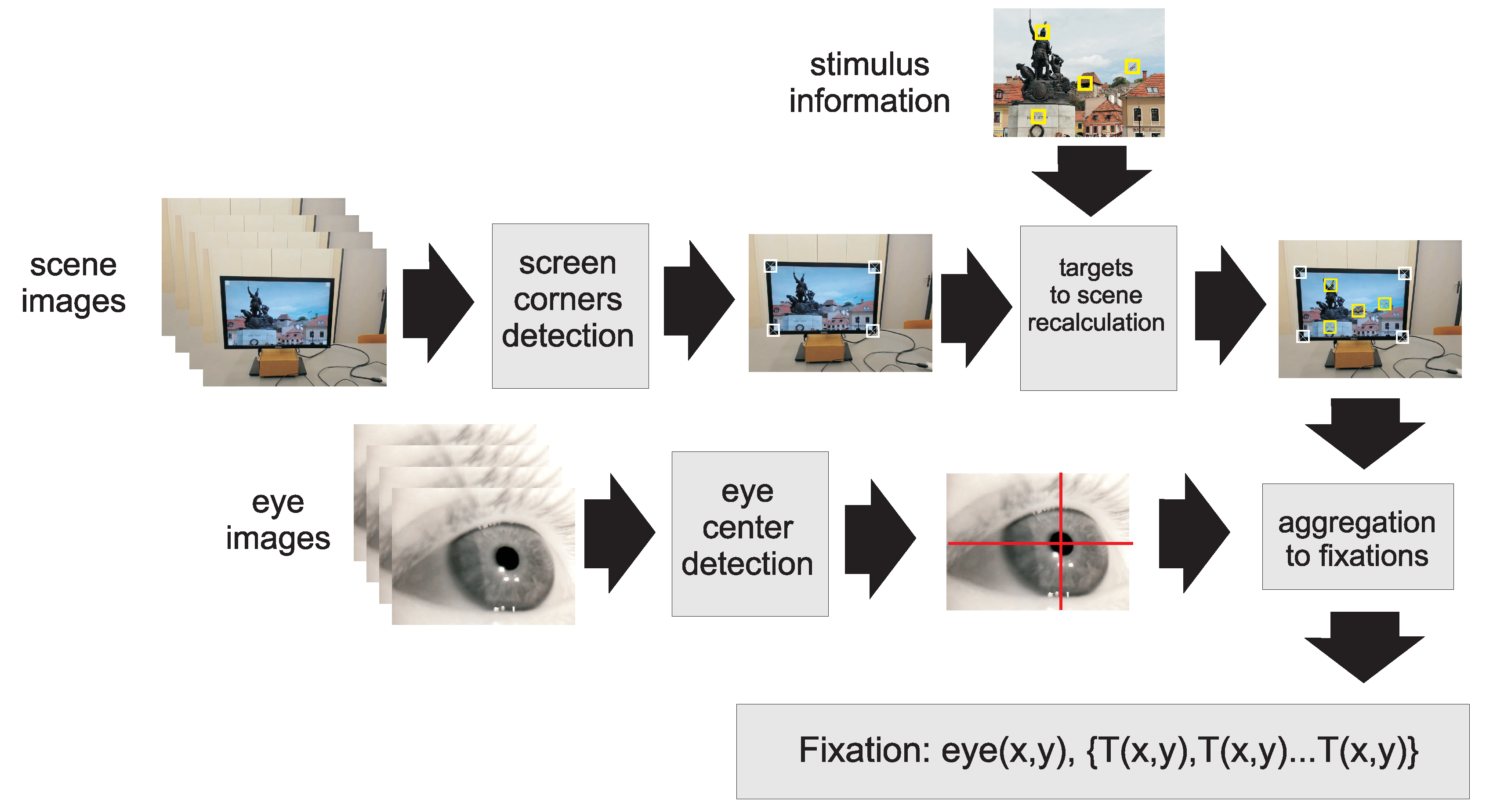
2.1. Extraction of Targets (PFTs) from Saliency Information
- BMS—Boolean maps saliency [36]—a graphical model based on a series of thresholds and sophisticated mathematical morphology,
- CovSal [37]—based on the innovation introduced in a certain area when compared to its neighborhood in image, using covariance as a measure,
- FES [38]—Bayesian bi-variate modelling of saliency based on the center-surround model at multiple scales.
- GBVS—the graph-based visual saliency model by Harel et al. [23], location vectors dissimilarity used as graph edge values,
- IttiKoch—a biologically plausible model, based on modelling of the underlying processes [21],
- LDS—Learning Discriminative Subspaces [39]—based on the image segments projection onto pre-trained dictionary patches of PCA reduced visual features.
- RARE2012 [40]—based on the multiscale innovation (rarity) in location, identified with Gabor filters and information theoretic measure self-information.
- SR-PQFT—a spectral residual (SR) model (as proposed by Hou and Zhang in [41]), but in a variant that was developed by Schauerte and Stiefelhagen [42] for color images, where color values are quaternion encoded in opponent color space and the quaternion formula of Fourier transform is employed (PQFT),
- SWD [43]—spatially weighted dissimilarity—saliency model also based on the difference from the surrounding area, where outlying segments are identified in PCA reduced feature space.
- GT—users’ fixation maps created using eye-tracking information gathered during genuine observations undertaken by several participants.
- EXP—additionally, we also tested if PFTs may be set manually, by the ‘fixation expert’. One of the co-authors of the paper manually defined PFTs for each image, based on his experience (before seeing any saliency map).
2.2. Choosing the Best Mappings Comparison Function (MCF)
2.2.1. Regression Based Mappings Comparison Function
2.2.2. Mapping Comparison Function Based on Relative Distances
2.2.3. MCF Based on Correlation between Distances
2.2.4. MCF Based on Direction
2.2.5. Fusion of More than One MCF
2.3. Heuristic Algorithms for Searching the Mapping Space
2.3.1. Genetic Algorithm
| Algorithm 1 Heuristic genetic algorithm searching for the best mapping |
|
2.3.2. Incremental Mapping
| Algorithm 2 Iterative algorithm finding best mappings after adding a new fixation with to mappings created so far |
|
2.4. Removing Irrelevant Fixations
2.5. Classic Calibration Using ETCAL Library
3. Experiments
3.1. Head-Mounted Eye Tracker
- Initial classic nine points calibration
- Reference screen 1
- 34 images—two seconds per image
- Reference screen 2
- 34 images—two seconds per image
- Reference screen 3
3.2. Remote Eye Tracker
- Initial 9-point calibration
- 6 images observations (3 s each)
- Reference screen—user clicks 9 points looking at them
- 6 images observations (3 s each)
- Final 9-point calibration
3.3. Movie Experiment
- Initial 9-point calibration
- Movie watching
- Reference screen—user clicks 9 points looking at them
4. Results
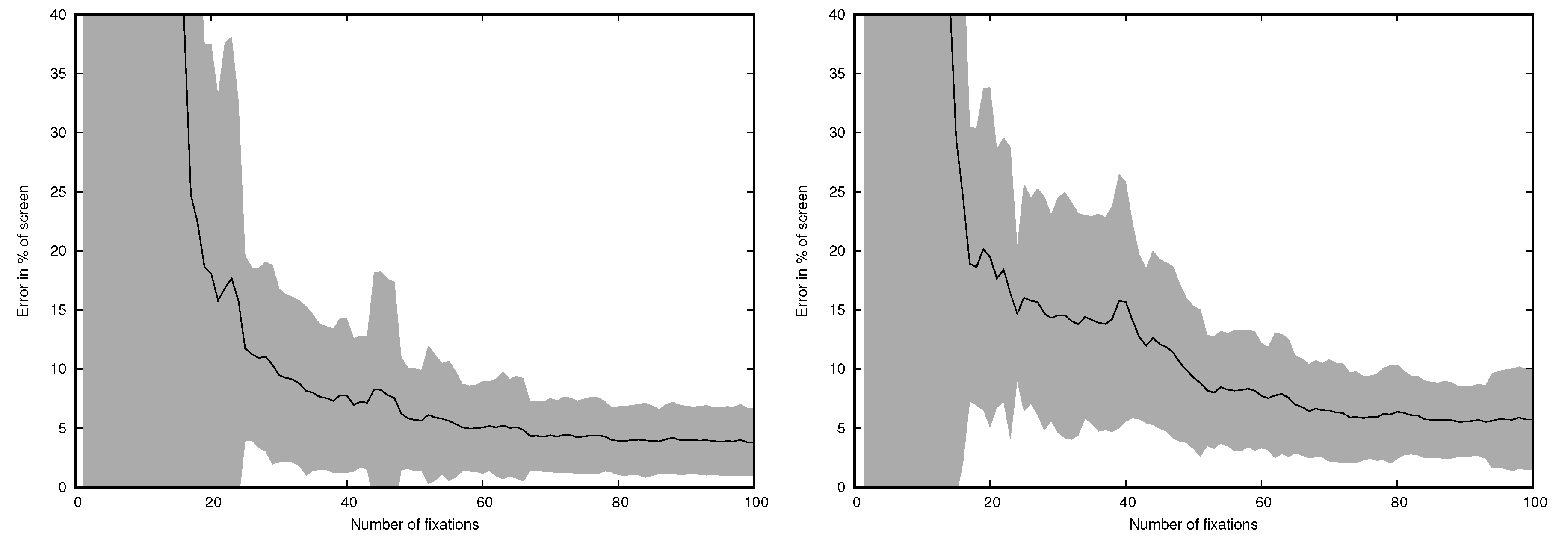
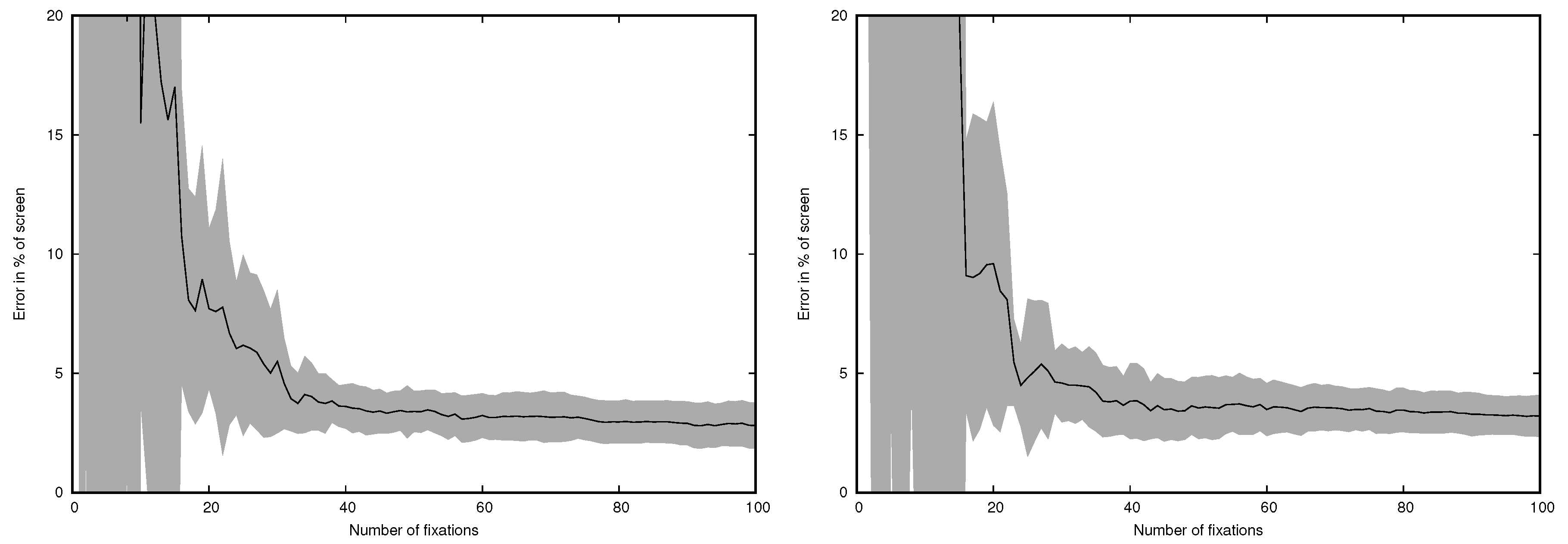
4.1. Head-Mounted Eye Tracker
4.2. Remote Eye Tracker
4.3. Movie Experiment
- The models do not take into account the contents of the previous frames, while such information may be important to estimate points of interest correctly.
- All models used in this research were prepared for real-world images (for instance photographs of nature or people), so their performance during the animated movie with artificial and sharp contours may be far from optimal.
4.4. Time Analysis
5. Discussion
- Data processing is easier and faster, which makes a ‘real-time’ calibration feasible.
- It is more universal as it may be used with any stimulus: static images, movies—but also with computer interfaces (e.g., with buttons or labels as targets) or games (e.g., with avatars as targets as was proposed in [6]).
- Creating a short list of potential targets could be faster than the creation of a full saliency map. For example a face extractor using fast Haar cascades may be used to define each face as a potential target.
- Definition of targets may be easily done manually, by a human expert (which was checked experimentally) while the creation of a saliency map requires special algorithms.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PFT | Probable Fixation Target |
| MCF | Mapping Comparison Function |
References
- Funke, G.; Greenlee, E.; Carter, M.; Dukes, A.; Brown, R.; Menke, L. Which Eye Tracker Is Right for Your Research? Performance Evaluation of Several Cost Variant Eye Trackers. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting, Washington, DC, USA, 19–23 September 2016; SAGE Publications Sage CA: Los Angeles, CA, USA, 2016; Volume 60, pp. 1240–1244. [Google Scholar]
- Dalmaijer, E. Is the Low-Cost EyeTribe Eye Tracker Any Good for Research? PeerJ PrePrints 2014, 2, e585v1. [Google Scholar]
- Mannaru, P.; Balasingam, B.; Pattipati, K.; Sibley, C.; Coyne, J.T. Performance Evaluation of the Gazepoint GP3 Eye Tracking Device Based on Pupil Dilation. In Proceedings of the International Conference on Augmented Cognition, Vancoucer, BC, Canada, 9–14 July 2017; Springer: New York, NY, USA, 2017; pp. 166–175. [Google Scholar]
- Gibaldi, A.; Vanegas, M.; Bex, P.J.; Maiello, G. Evaluation of the Tobii EyeX Eye tracking controller and Matlab toolkit for research. Behav. Res. Methods 2017, 49, 923–946. [Google Scholar] [CrossRef] [PubMed]
- Hornof, A.J.; Halverson, T. Cleaning up systematic error in eye-tracking data by using required fixation locations. Behav. Res. Methods Instrum. Comput. 2002, 34, 592–604. [Google Scholar] [CrossRef] [PubMed]
- Kasprowski, P.; Harezlak, K. Implicit calibration using predicted gaze targets. In Proceedings of the Ninth Biennial ACM Symposium on Eye Tracking Research & Applications, Charleston, SC, USA, 14–17 March 2016; ACM: New York, NY, USA, 2016; pp. 245–248. [Google Scholar]
- Sugano, Y.; Matsushita, Y.; Sato, Y. Calibration-free gaze sensing using saliency maps. In Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010; pp. 2667–2674. [Google Scholar]
- Wang, K.; Wang, S.; Ji, Q. Deep eye fixation map learning for calibration-free eye gaze tracking. In Proceedings of the Ninth Biennial ACM Symposium on Eye Tracking Research & Applications, Charleston, SC, USA, 14–17 March 2016; ACM: New York, NY, USA, 2016; pp. 47–55. [Google Scholar]
- Maiello, G.; Harrison, W.J.; Bex, P.J. Monocular and binocular contributions to oculomotor plasticity. Sci. Rep. 2016, 6, 31861. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Song, M.; Liu, Z.; Sun, M.T. Real-Time Gaze Estimation with Online Calibration. IEEE MultiMed. 2014, 21, 28–37. [Google Scholar] [CrossRef]
- Canessa, A.; Gibaldi, A.; Chessa, M.; Sabatini, S.P.; Solari, F. The perspective geometry of the eye: Toward image-based eye-tracking. In Human-Centric Machine Vision; InTech: Vienna, Austria, 2012. [Google Scholar]
- Kasprowski, P.; Harezlak, K.; Stasch, M. Guidelines for the eye tracker calibration using points of regard. Inf. Technol. Biomed. 2014, 4, 225–236. [Google Scholar]
- Vadillo, M.A.; Street, C.N.; Beesley, T.; Shanks, D.R. A simple algorithm for the offline recalibration of eye-tracking data through best-fitting linear transformation. Behav. Res. Methods 2015, 47, 1365–1376. [Google Scholar] [CrossRef]
- Kasprowski, P.; Harezlak, K. Study on participant-controlled eye tracker calibration procedure. In Proceedings of the 7th Workshop on Eye Gaze in Intelligent Human Machine Interaction: Eye-Gaze & Multimodality, Istanbul, Turkey, 12–16 November 2014; ACM: New York, NY, USA, 2014; pp. 39–41. [Google Scholar]
- Pfeuffer, K.; Vidal, M.; Turner, J.; Bulling, A.; Gellersen, H. Pursuit calibration: Making gaze calibration less tedious and more flexible. In Proceedings of the 26th Annual ACM Symposium on User Interface Software and Technology, Scotland, UK, 8–11 October 2013; ACM: New York, NY, USA, 2013; pp. 261–270. [Google Scholar]
- Hirvonen, T.; Aalto, H.; Juhola, M.; Pyykkö, I. A comparison of static and dynamic calibration techniques for the vestibulo-ocular reflex signal. Int. J. Clin. Monit. Comput. 1995, 12, 97–102. [Google Scholar] [CrossRef]
- Chen, J.; Ji, Q. A probabilistic approach to online eye gaze tracking without explicit personal calibration. IEEE Trans. Image Process. 2015, 24, 1076–1086. [Google Scholar] [CrossRef]
- Perra, D.; Gupta, R.K.; Frahm, J.M. Adaptive eye-camera calibration for head-worn devices. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4146–4155. [Google Scholar]
- Zhang, Y.; Hornof, A.J. Easy post-hoc spatial recalibration of eye tracking data. In Proceedings of the Symposium on Eye Tracking Research And Applications, Safety Harbor, FL, USA, 26–28 March 2014; ACM: New York, NY, USA, 2014; pp. 95–98. [Google Scholar]
- Sugano, Y.; Matsushita, Y.; Sato, Y.; Koike, H. An incremental learning method for unconstrained gaze estimation. In Proceedings of the 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008; Springer: New York, NY, USA, 2008; pp. 656–667. [Google Scholar]
- Itti, L.; Koch, C.; Niebur, E. A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1254–1259. [Google Scholar] [CrossRef]
- Sugano, Y.; Matsushita, Y.; Sato, Y. Appearance-based gaze estimation using visual saliency. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 329–341. [Google Scholar] [CrossRef] [PubMed]
- Harel, J.; Koch, C.; Perona, P. Graph-Based Visual Saliency. In Proceedings of the Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 4–7 December 2006. [Google Scholar]
- Alnajar, F.; Gevers, T.; Valenti, R.; Ghebreab, S. Auto-Calibrated Gaze Estimation Using Human Gaze Patterns. Int. J. Comput. Vis. 2017, 124, 223–236. [Google Scholar] [CrossRef]
- Nguyen, P.; Fleureau, J.; Chamaret, C.; Guillotel, P. Calibration-free gaze tracking using particle filter. In Proceedings of the 2013 IEEE International Conference on Multimedia and Expo (ICME), San Jose, CA, USA, 15–19 July 2013; pp. 1–6. [Google Scholar]
- Wang, K.; Ji, Q. 3D gaze estimation without explicit personal calibration. Pattern Recognit. 2018, 79, 216–227. [Google Scholar] [CrossRef]
- Kasprowski, P. Mining of eye movement data to discover people intentions. In Proceedings of the International Conference: Beyond Databases, Architectures and Structures, Ustron, Poland, 27–30 May 2014; Springer: New York, NY, USA, 2014; pp. 355–363. [Google Scholar]
- Sugano, Y.; Bulling, A. Self-calibrating head-mounted eye trackers using egocentric visual saliency. In Proceedings of the 28th Annual ACM Symposium on User Interface Software & Technology, Charlotte, NC, USA, 11–15 November 2015; ACM: New York, NY, USA, 2015; pp. 363–372. [Google Scholar]
- Kasprowski, P.; Harezlak, K. Comparison of mapping algorithms for implicit calibration using probable fixation targets. In Proceedings of the 10th Biennial ACM Symposium on Eye Tracking Research & Applications, Warsaw, Poland, 14–17 June 2018; ACM: New York, NY, USA, 2018. [Google Scholar]
- Kasprowski, P.; Harezlak, K. ETCAL—A versatile and extendable library for eye tracker calibration. Dig. Signal Process. 2018, 77, 222–232. [Google Scholar] [CrossRef]
- Judd, T.; Ehinger, K.; Durand, F.; Torralba, A. Learning to predict where humans look. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2106–2113. [Google Scholar] [CrossRef]
- Koch, C.; Ullman, S. Shifts in selective visual attention: Towards the underlying neural circuitry. Hum. Neurobiol. 1985, 4, 219–227. [Google Scholar]
- Harezlak, K.; Kasprowski, P. Chaotic Nature of Eye Movement Signal. In Proceedings of the International Conference on Intelligent Decision Technologies, Sorrento, Italy, 17–19 June 2017; Springer: New York, NY, USA, 2017; pp. 120–129. [Google Scholar]
- Judd, T.; Durand, F.; Torralba, A. A Benchmark of Computational Models of Saliency to Predict Human Fixations; MIT: Cambridge, MA, USA, 2012. [Google Scholar]
- Le Meur, O.; Liu, Z. Saccadic model of eye movements for free-viewing condition. Vis. Res. 2015, 116, 152–164. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Sclaroff, S. Exploiting Surroundedness for Saliency Detection: A Boolean Map Approach. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 889–902. [Google Scholar] [CrossRef]
- Erdem, E.; Erdem, A. Visual saliency estimation by nonlinearly integrating features using region covariances. J. Vis. 2013, 13, 11. [Google Scholar] [CrossRef]
- Tavakoli, H.R.; Rahtu, E.; Heikkila, J. Fast and Efficient Saliency Detection Using Sparse Sampling and Kernel Density Estimation. In Image Analysis; Springer: Berlin/Heidelberg, Germany, 2011; pp. 666–675. [Google Scholar] [CrossRef]
- Fang, S.; Li, J.; Tian, Y.; Huang, T.; Chen, X. Learning Discriminative Subspaces on Random Contrasts for Image Saliency Analysis. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 1095–1108. [Google Scholar] [CrossRef]
- Riche, N.; Mancas, M.; Duvinage, M.; Mibulumukini, M.; Gosselin, B.; Dutoit, T. RARE2012: A multi-scale rarity-based saliency detection with its comparative statistical analysis. Signal Process. Image Commun. 2013, 28, 642–658. [Google Scholar] [CrossRef]
- Hou, X.; Zhang, L. Saliency Detection: A Spectral Residual Approach. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Schauerte, B.; Stiefelhagen, R. Quaternion-Based Spectral Saliency Detection for Eye Fixation Prediction. In Proceedings of the Computer Vision—ECCV, Florence, Italy, 7–13 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 116–129. [Google Scholar] [CrossRef]
- Duan, L.; Wu, C.; Miao, J.; Qing, L.; Fu, Y. Visual saliency detection by spatially weighted dissimilarity. In Proceedings of the CVPR, Colorado Springs, CO, USA, 20–25 June 2011; pp. 473–480. [Google Scholar] [CrossRef]
- Bradski, G.; Kaehler, A. Learning OpenCV: Computer Vision with the OpenCV Library; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2008. [Google Scholar]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Suzuki, S. Topological structural analysis of digitized binary images by border following. Comput. Vis. Gr. Image Process. 1985, 30, 32–46. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: New York, NY, USA, 1978; pp. 105–116. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. In Readings in Computer Vision; Elsevier: Amsterdam, The Netherlands, 1987; pp. 726–740. [Google Scholar]
- Kasprowski, P. Implicit Calibration ETRA. 2018. Available online: https://youtu.be/CLtNx0IVWmU (accessed on 12 December 2018).
- Kar, A.; Corcoran, P. Performance Evaluation Strategies for Eye Gaze Estimation Systems with Quantitative Metrics and Visualizations. Sensors 2018, 18, 3151. [Google Scholar] [CrossRef] [PubMed]
- Kasprowski, P. Implicit Calibration For Video. Available online: https://youtu.be/kj3sNrc02MA (accessed on 12 December 2018).




| Removal Percent | Error X (%) | Error Y (%) | Avg Error (%) |
|---|---|---|---|
| 0 | 8.52 | 7.17 | 7.84 |
| 10 | 8.11 | 7.06 | 7.59 |
| 20 | 8.06 | 7.03 | 7.55 |
| 30 | 8.12 | 7.08 | 7.60 |
| 40 | 8.13 | 7.23 | 7.68 |
| MCF | Algorithm | Saliency Model | Error X (%) | Error Y (%) | Avg Error (%) |
|---|---|---|---|---|---|
| CALIB | 2.49 | 2.02 | 2.26 | ||
| DIR | G | GT | 2.36 | 2.82 | 2.59 |
| DIR | I | GT | 2.40 | 3.15 | 2.77 |
| DIR | I | EXP | 2.65 | 2.97 | 2.81 |
| DIR | G | EXP | 2.71 | 2.94 | 2.83 |
| REG | G | EXP | 5.76 | 6.92 | 6.34 |
| DIST | I | GT | 7.72 | 5.63 | 6.68 |
| REG | I | EXP | 8.09 | 7.19 | 7.64 |
| DIST | I | EXP | 9.69 | 5.74 | 7.71 |
| DC | G | EXP | 8.76 | 7.33 | 8.05 |
| DIST | G | EXP | 9.54 | 6.94 | 8.24 |
| DISTC | I | EXP | 9.00 | 7.55 | 8.28 |
| DISTC | I | GT | 8.28 | 8.52 | 8.40 |
| DC | G | GT | 9.02 | 8.58 | 8.80 |
| DIST | G | GT | 10.64 | 8.80 | 9.72 |
| REG | G | GT | 11.53 | 9.06 | 10.30 |
| REG | I | GT | 12.49 | 9.72 | 11.11 |
| CENTER | 12.41 | 10.03 | 11.22 |
| Saliency Model | Error X (%) | Error Y (%) | Avg Error (%) | Number of Targets |
|---|---|---|---|---|
| GT | 2.36 | 2.82 | 2.59 | 10.38 |
| EXP | 2.71 | 2.94 | 2.83 | 3.47 |
| RARE2012 | 3.18 | 3.36 | 3.27 | 4.79 |
| SWD | 3.48 | 3.68 | 3.58 | 9.25 |
| GBVS | 3.05 | 4.21 | 3.63 | 3.47 |
| BMS | 4.03 | 3.52 | 3.78 | 5.12 |
| SR-PQFT | 4.99 | 3.64 | 4.31 | 4.12 |
| IttiKoch | 4.12 | 4.98 | 4.55 | 4.24 |
| LDS | 7.95 | 7.10 | 7.52 | 1.78 |
| FES | 8.07 | 7.91 | 7.99 | 1.74 |
| CovSal | 10.63 | 8.91 | 9.77 | 1.49 |
| GT | EXP | RARE2012 | GBVS | SWD | BMS | SR-PQFT | IttiKoch | LDS | FES | CovSal | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| GT | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ||||
| EXP | ∗ | ∗ | ∗ | ∗ | ∗ | ||||||
| RARE2012 | ∗ | ∗ | ∗ | ||||||||
| GBVS | ∗ | ∗ | ∗ | ||||||||
| SWD | ∗ | ∗ | ∗ | ∗ | |||||||
| BMS | ∗ | ∗ | ∗ | ∗ | |||||||
| SR-PQFT | ∗ | ∗ | ∗ | ∗ | ∗ | ||||||
| IttiKoch | ∗ | ∗ | ∗ | ∗ | ∗ | ||||||
| LDS | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ||
| FES | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | |||
| CovSal | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ |
| MCF | Algorithm | Error X (%) | Error Y (%) | Avg Error (%) |
|---|---|---|---|---|
| G | 2.24 | 2.62 | 2.43 | |
| G | 2.17 | 2.69 | 2.43 | |
| G | 2.24 | 2.69 | 2.47 | |
| G | 2.29 | 2.66 | 2.47 | |
| G | 2.29 | 2.71 | 2.50 | |
| G | 2.34 | 2.71 | 2.53 |
| Removal Percent | Error X (%) | Error Y (%) | Avg Error (%) |
|---|---|---|---|
| 0 | 14.81 | 12.51 | 13.66 |
| 10 | 14.16 | 11.80 | 12.98 |
| 20 | 13.97 | 11.35 | 12.66 |
| 30 | 14.05 | 11.43 | 12.74 |
| 40 | 14.42 | 11.48 | 12.95 |
| MCF Type | Algorithm | Saliency | Error X (%) | Error Y (%) | Avg Error (%) |
|---|---|---|---|---|---|
| CAL2 | 3.04 | 4.21 | 3.63 | ||
| CAL1 | 3.04 | 4.59 | 3.82 | ||
| DIR | G | EXP | 3.44 | 5.37 | 4.41 |
| DIR | I | EXP | 3.44 | 5.77 | 4.60 |
| DIR | G | GT | 4.85 | 6.50 | 5.68 |
| DIR | I | GT | 5.35 | 6.41 | 5.88 |
| REG | G | EXP | 8.44 | 7.70 | 8.07 |
| REG | G | GT | 10.15 | 11.41 | 10.78 |
| REG | I | EXP | 12.65 | 9.51 | 11.08 |
| DIST | I | GT | 13.64 | 12.16 | 12.90 |
| DIST | I | EXP | 16.42 | 10.38 | 13.40 |
| DISTC | G | EXP | 16.91 | 13.23 | 15.07 |
| DIST | G | GT | 19.88 | 11.53 | 15.70 |
| DISTC | I | EXP | 17.94 | 14.08 | 16.01 |
| DISTC | G | GT | 19.48 | 12.69 | 16.08 |
| DISTC | I | GT | 18.28 | 14.87 | 16.58 |
| REG | I | GT | 20.33 | 15.33 | 17.83 |
| DIST | G | EXP | 22.27 | 15.35 | 18.81 |
| CENTER | 21.37 | 18.41 | 19.89 |
| MCF Type | Error X (%) | Error Y (%) | Average Error | Number of Targets |
|---|---|---|---|---|
| EXP | 3.44 | 5.37 | 4.41 | 3.07 |
| GT | 4.85 | 6.50 | 5.68 | 4.62 |
| SR-PQFT | 5.89 | 7.78 | 6.84 | 3.71 |
| BMS | 4.87 | 9.53 | 7.20 | 4.79 |
| GBVS | 5.94 | 10.19 | 8.07 | 4.43 |
| RARE2012 | 4.77 | 12.29 | 8.53 | 5.43 |
| IttiKoch | 9.18 | 8.21 | 8.70 | 5.36 |
| SWD | 8.90 | 8.51 | 8.71 | 9.71 |
| LDS | 12.91 | 11.46 | 12.18 | 2.29 |
| CovSal | 19.18 | 18.37 | 18.78 | 1.36 |
| FES | 20.83 | 17.20 | 19.02 | 1.36 |
| EXP | GT | SP-PQFT | BMS | GBVS | RARE2012 | IttiKoch | SWD | LDS | CovSal | FES | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| EXP | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | |||
| GT | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | |||||
| SP-PQFT | ∗ | ∗ | ∗ | ∗ | |||||||
| BMS | ∗ | ∗ | ∗ | ∗ | ∗ | ||||||
| GBVS | ∗ | ∗ | ∗ | ∗ | |||||||
| RARE2012 | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ||||
| IttiKoch | ∗ | ∗ | ∗ | ∗ | ∗ | ||||||
| SWD | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | |||
| LDS | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ||
| CovSal | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ||
| FES | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ | ∗ |
| MCF Type | Algorithm | Number of Trials | Error X (%) | Error Y (%) | Average Error |
|---|---|---|---|---|---|
| G | 29 | 3.00 | 4.83 | 3.91 | |
| G | 29 | 2.97 | 4.86 | 3.91 | |
| G | 29 | 2.93 | 5.03 | 3.98 | |
| G | 29 | 3.07 | 5.00 | 4.03 | |
| G | 29 | 2.93 | 5.14 | 4.03 | |
| G | 29 | 2.79 | 5.28 | 4.03 | |
| G | 29 | 2.93 | 5.14 | 4.03 | |
| G | 29 | 3.00 | 5.14 | 4.07 |
| MCF Type | Error X (%) | Error Y (%) | Average Error | Number of Targets |
|---|---|---|---|---|
| CAL | 3.44 | 3.90 | 3.67 | 3.35 |
| RARE2012 | 7.38 | 11.51 | 9.45 | 4.35 |
| IttiKoch | 10.22 | 9.48 | 9.85 | 2.46 |
| GT | 12.92 | 9.76 | 11.34 | 1.38 |
| GBVS | 9.00 | 15.16 | 12.08 | 2.14 |
| SR-PQFT | 12.06 | 14.32 | 13.19 | 3.62 |
| BMS | 13.27 | 14.13 | 13.70 | 6.29 |
| FES | 14.31 | 13.24 | 13.77 | 2.13 |
| SWD | 17.59 | 15.75 | 16.67 | 1.74 |
| LDS | 19.71 | 15.80 | 17.75 | 1.38 |
| CovSal | 19.82 | 17.35 | 18.58 | 1.62 |
| Saliency Map | Implementation | Average Execution Time (s) |
|---|---|---|
| FES | MATLAB | 0.170 |
| BMS | exe (binary) | 0.196 |
| SWD | MATLAB | 0.242 |
| Itti-Koch | MATLAB | 0.328 |
| SR-PQFT | MATLAB | 0.388 |
| LDS | MATLAB | 0.511 |
| RARE2012 | MATLAB | 0.746 |
| GBVS | MATLAB | 0.921 |
| CovSal | MATLAB | 21.4 |
| MCF Type | Incremental Time (s) | Genetic Time (s) |
|---|---|---|
| DISTC | 0.10 | 2.32 |
| DIR | 3.78 | 9.52 |
| REG | 26.86 | 62.24 |
| DIST | 127.64 | 492.41 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kasprowski, P.; Harȩżlak, K.; Skurowski, P. Implicit Calibration Using Probable Fixation Targets. Sensors 2019, 19, 216. https://doi.org/10.3390/s19010216
Kasprowski P, Harȩżlak K, Skurowski P. Implicit Calibration Using Probable Fixation Targets. Sensors. 2019; 19(1):216. https://doi.org/10.3390/s19010216
Chicago/Turabian StyleKasprowski, Pawel, Katarzyna Harȩżlak, and Przemysław Skurowski. 2019. "Implicit Calibration Using Probable Fixation Targets" Sensors 19, no. 1: 216. https://doi.org/10.3390/s19010216
APA StyleKasprowski, P., Harȩżlak, K., & Skurowski, P. (2019). Implicit Calibration Using Probable Fixation Targets. Sensors, 19(1), 216. https://doi.org/10.3390/s19010216





