Validating Deep Neural Networks for Online Decoding of Motor Imagery Movements from EEG Signals
Abstract
1. Introduction
2. Related Work
2.1. Recurrent Neural Networks (RNN)
2.1.1. Elman Neural Network
2.1.2. Long-Short Term Memory (LSTM)
2.2. Convolutional Neural Networks (CNN)
2.3. Recurrent Convolutional Neural Networks (RCNN)
3. Methods
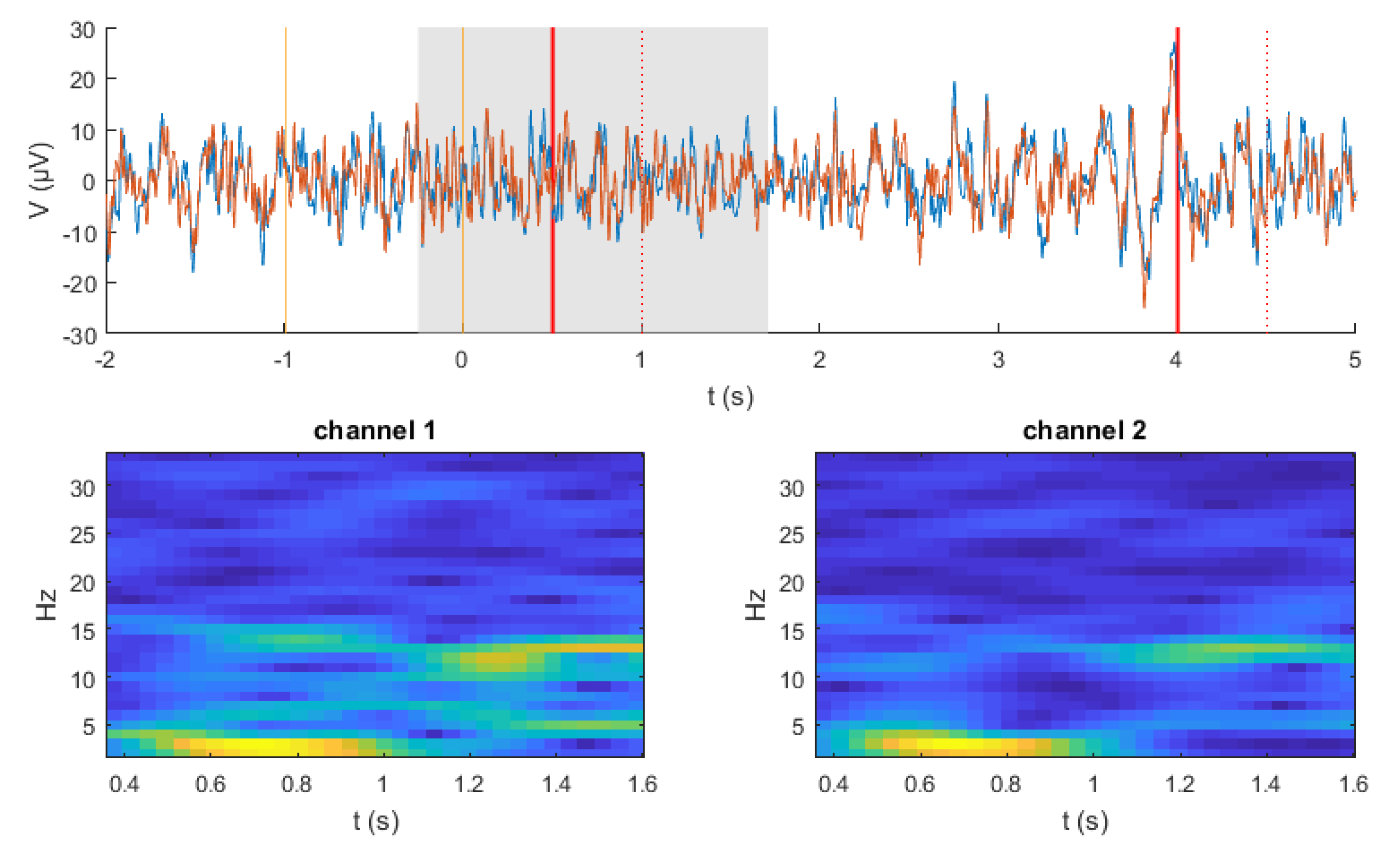
3.1. EEG Signals Recording
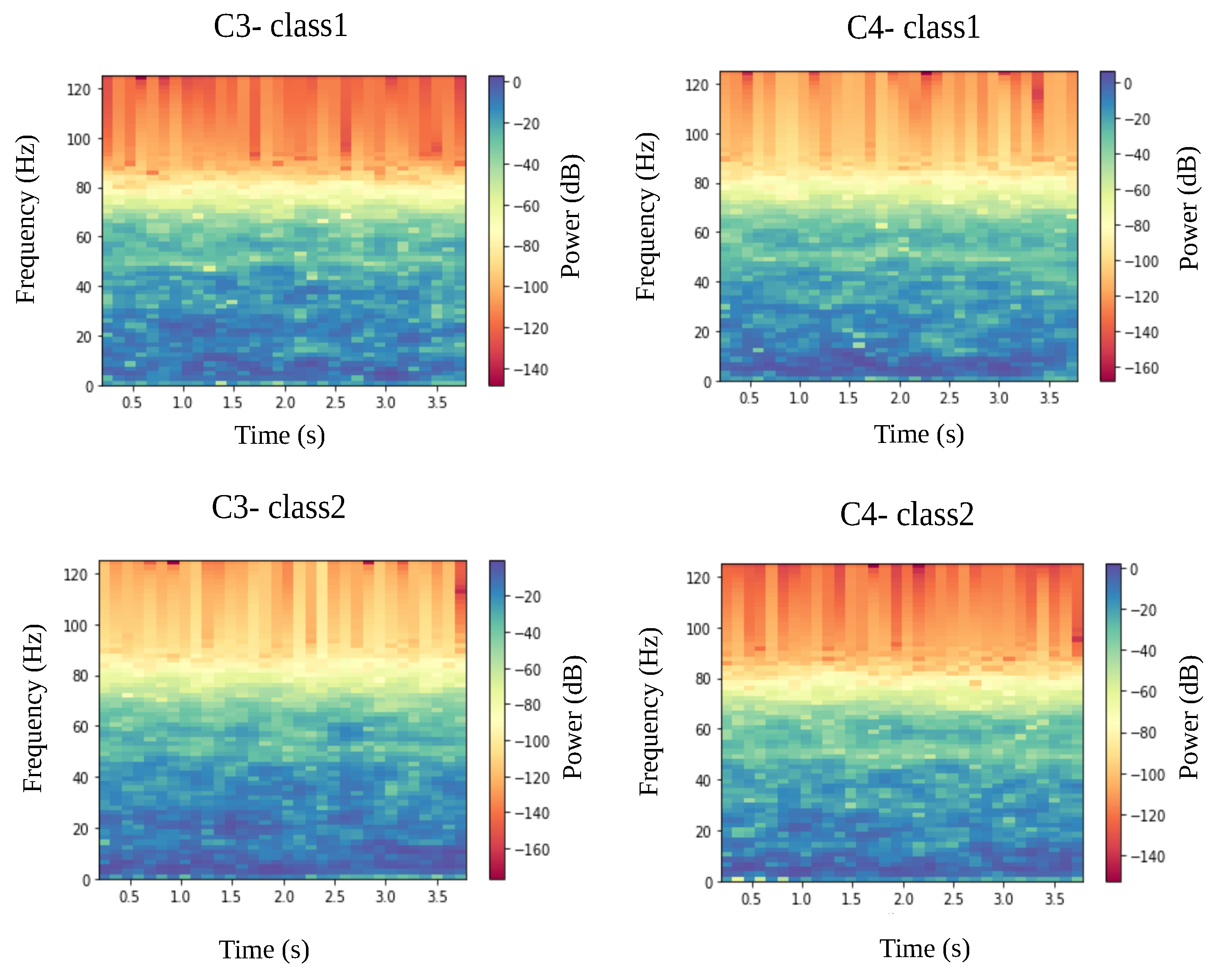
3.2. Data Preprocessing
3.3. Decoding Methods
3.3.1. LSTM Model
3.3.2. The Pragmatic CNN Model (pCNN)
3.3.3. RCNN Model
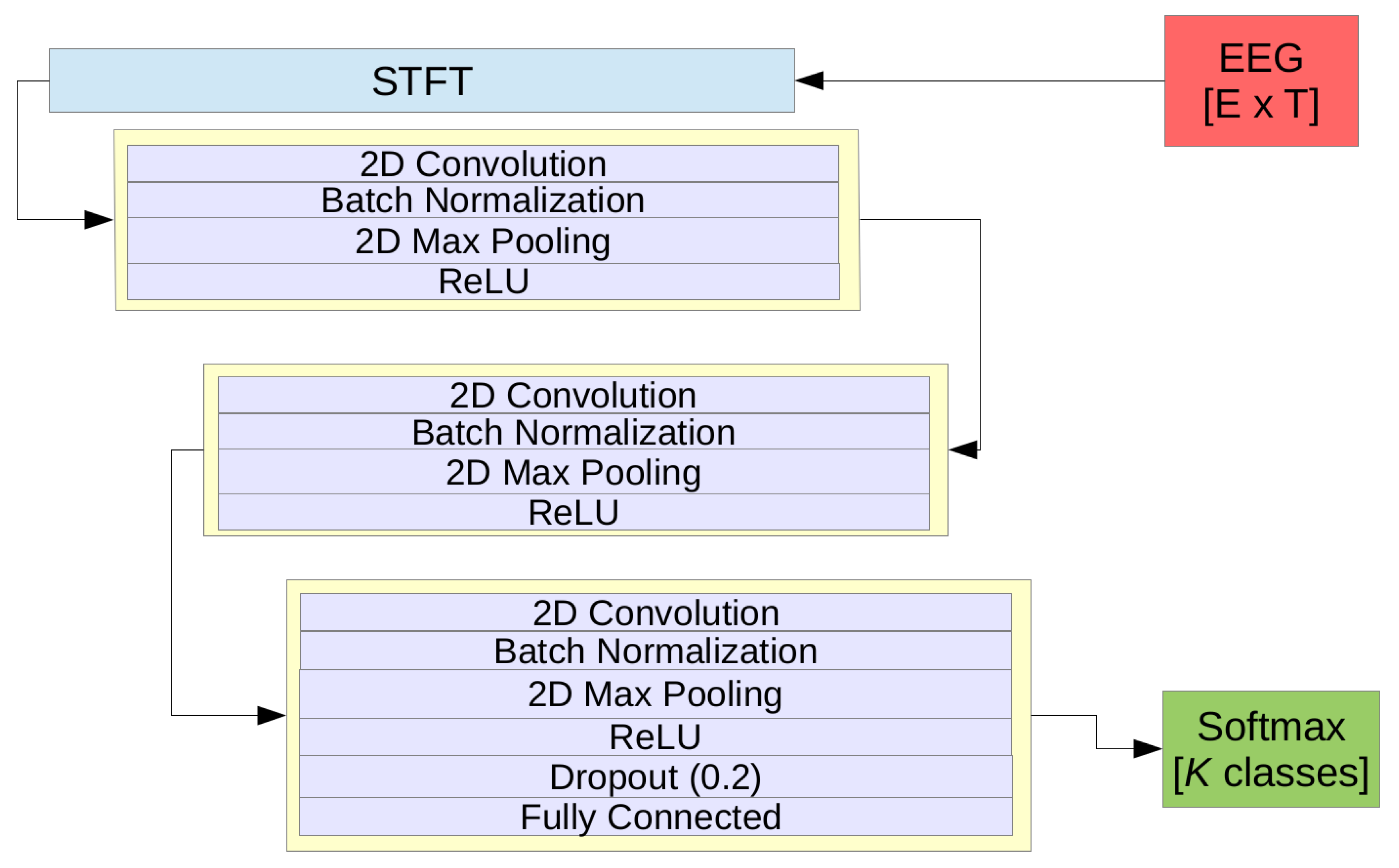
3.3.4. Shallow-CNN (sCNN) and deep-CNN (dCNN)
3.3.5. Traditional Machine Learning Approaches
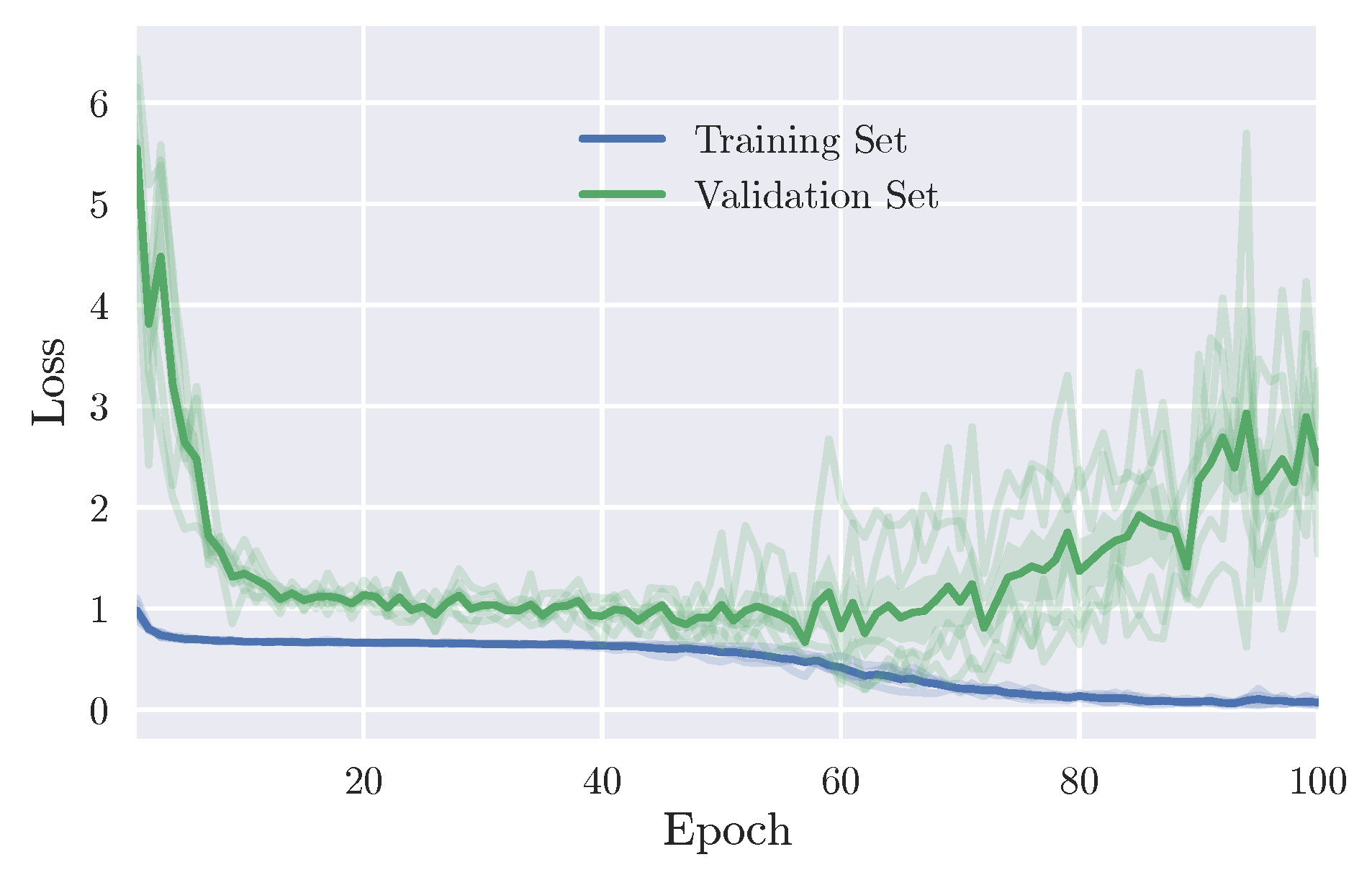
4. Results
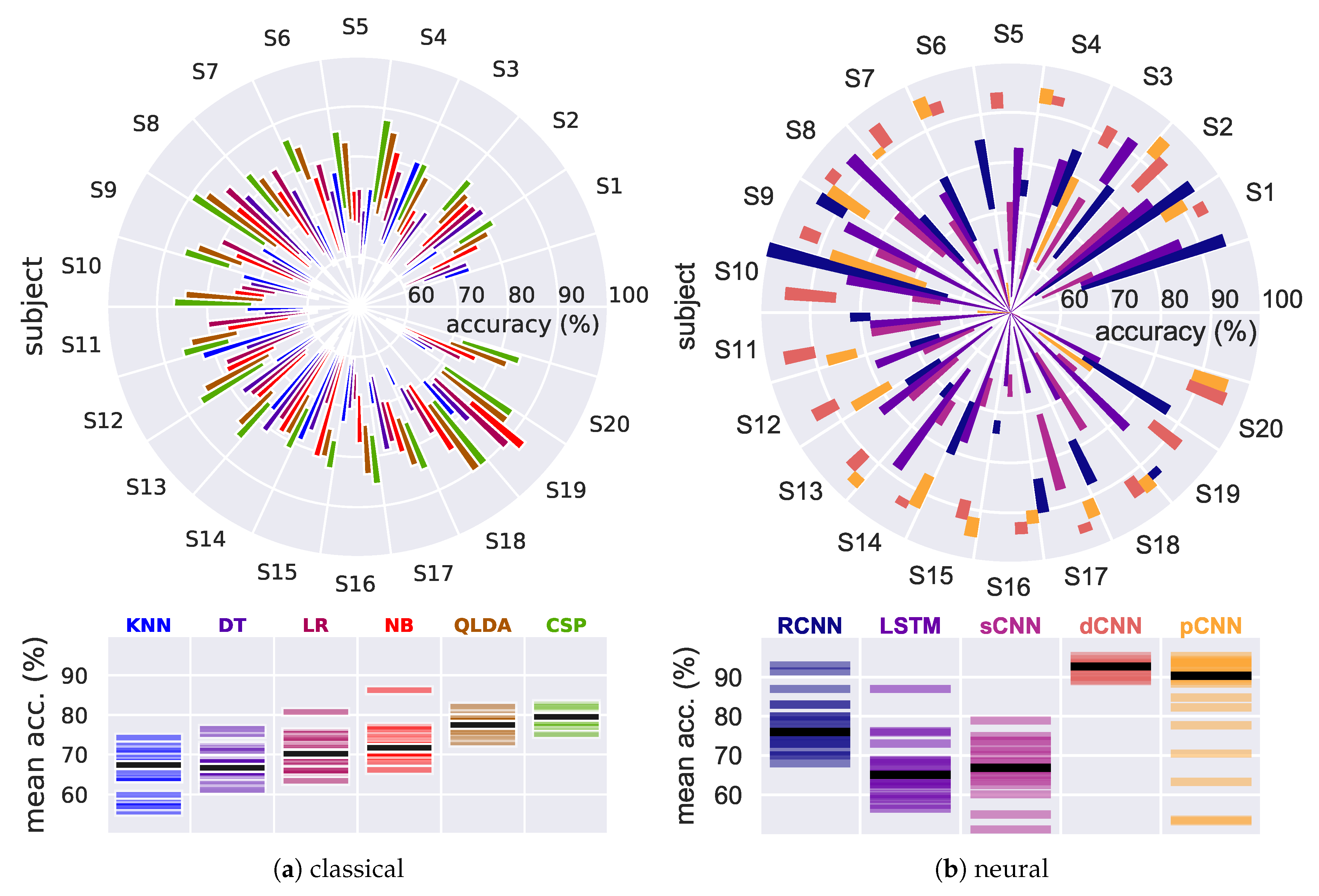
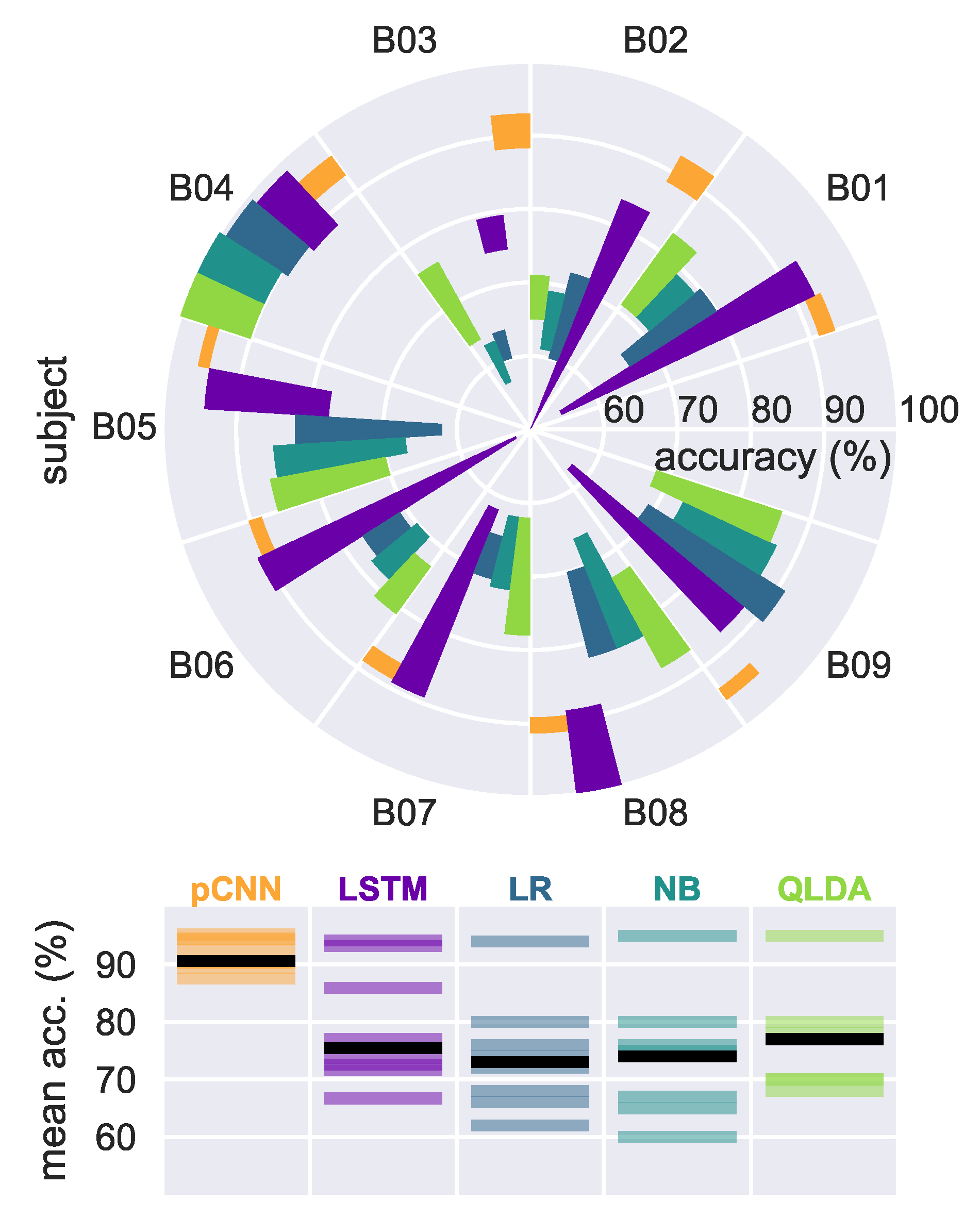
4.1. Results on Our EEG Recorded Dataset
4.1.1. Traditional, Baseline Classifiers
4.1.2. Neural Models
LSTM Model
CNN Models
RCNN Model
4.2. Results on EEG Graz Dataset
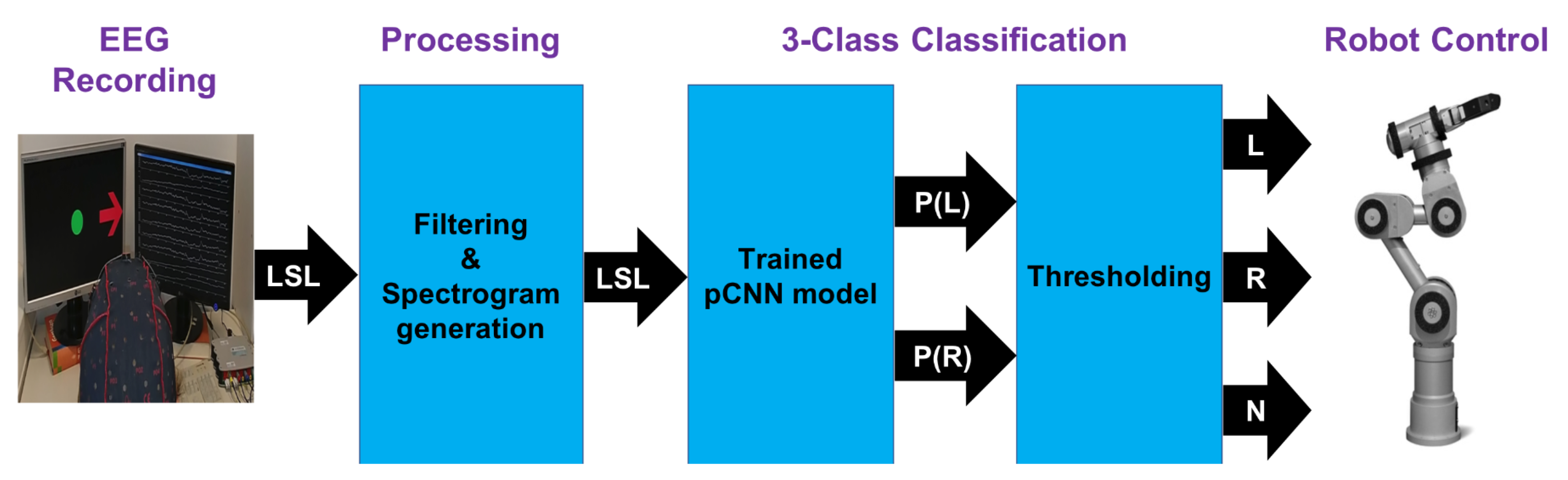
5. Real-Time Control of a Robot Arm
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Layer | Input | Operation | Output | Parameters |
|---|---|---|---|---|
| 1 | STFT | - | ||
| 2 | 10,392 | |||
| BatchNorm | 260 | |||
| MaxPool2D | - | |||
| ReLU | - | |||
| 2 | 73,776 | |||
| BatchNorm | 128 | |||
| MaxPool2D | - | |||
| ReLU | - | |||
| 3 | 73,824 | |||
| BatchNorm | 64 | |||
| MaxPool2D () | - | |||
| ReLU | - | |||
| Dropout () | - | |||
| 4 | Flatten | 6144 | - | |
| 6144 | Softmax | K | 12,290 | |
| Total |
| Layer | Input | Operation | Output | Parameters |
|---|---|---|---|---|
| 1 | () | 275 | ||
| 2 | Reshape | - | ||
| () | 1900 | |||
| BatchNorm | 100 | |||
| ELU | - | |||
| MaxPool2D () | - | |||
| Dropout (0.5) | - | |||
| 3 | () | 12,550 | ||
| BatchNorm | 200 | |||
| ELU | - | |||
| MaxPool2D () | - | |||
| Dropout (0.5) | - | |||
| 4 | Reshape | - | ||
| () | 50,100 | |||
| BatchNorm | 400 | |||
| ELU | - | |||
| MaxPool2D | - | |||
| Dropout (0.5) | - | |||
| 5 | Reshape | - | ||
| () | 200,200 | |||
| BatchNorm | 800 | |||
| ELU | - | |||
| MaxPool2D () | - | |||
| 6 | Flatten | 1600 | - | |
| 1600 | Softmax | K | 3202 | |
| Total |
| Layer | Input | Operation | Output | Parameters |
|---|---|---|---|---|
| 1 | () | 1040 | ||
| Dropout (0.5) | - | |||
| 2 | Reshape | - | ||
| () | 4840 | |||
| BatchNorm | 160 | |||
| -Activation | - | |||
| Dropout (0.5) | - | |||
| 3 | Reshape | - | ||
| AvgPool2d () | - | |||
| -Activation | - | |||
| 4 | Flatten | 2480 | - | |
| 6144 | Softmax | K | 4962 | |
| Total |
References
- Meng, J.; Zhang, S.; Bekyo, A.; Olsoe, J.; Baxter, B.; He, B. Noninvasive Electroencephalogram Based Control of a Robotic Arm for Reach and Grasp Tasks. Sci. Rep. 2016, 6, 2045–2322. [Google Scholar] [CrossRef] [PubMed]
- Carlson, T.; del, R.; Millan, J. Brain-Controlled Wheelchairs: A Robotic Architecture. IEEE Robot. Autom. Mag. 2013, 20, 65–73. [Google Scholar] [CrossRef]
- Lebedev, M.A.; Nicolelis, M.A.L. Brain-Machine Interfaces: From Basic Science to Neuroprostheses and Neurorehabilitation. Physiol. Rev. 2017, 97, 767–837. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Tabar, Y.R.; Halici, U. A novel deep learning approach for classification of EEG motor imagery signals. J. Neural Eng. 2016, 14, 016003. [Google Scholar] [CrossRef] [PubMed]
- Thomas, J.; Maszczyk, T.; Sinha, N.; Kluge, T.; Dauwels, J. Deep learning-based classification for brain-computer interfaces. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 234–239. [Google Scholar]
- Sakhavi, S.; Guan, C.; Yan, S. Learning Temporal Information for Brain-Computer Interface Using Convolutional Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5619–5629. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, C.; Gong, X. Deep convolutional neural network for decoding motor imagery based brain computer interface. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–5. [Google Scholar]
- Leeb, R.; Brunner, C.; Mueller-Put, G.; Schloegl, A.; Pfurtscheller, G. BCI Competition 2008-Graz Data Set b; Graz University of Technology: Graz, Austria, 2008. [Google Scholar]
- Greaves, A.S. Classification of EEG with Recurrent Neural Networks. Available online: https://cs224d.stanford.edu/reports/GreavesAlex.pdf (accessed on 12 March 2018).
- Forney, E.M.; Anderson, C.W. Classification of EEG during imagined mental tasks by forecasting with Elman Recurrent Neural Networks. In Proceedings of the The 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 2749–2755. [Google Scholar]
- Hema, C.R.; Paulraj, M.P.; Yaacob, S.; Adom, A.H.; Nagarajan, R. Recognition of motor imagery of hand movements for a BMI using PCA features. In Proceedings of the 2008 International Conference on Electronic Design, Penang, Malaysia, 1–3 December 2008; pp. 1–4. [Google Scholar]
- Zhang, X.; Yao, L.; Huang, C.; Sheng, Q.Z.; Wang, X. Enhancing mind controlled smart living through recurrent neural networks. arXiv, 2017; arXiv:1702.06830. [Google Scholar]
- Goldberger, A.L.; Amaral, L.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.; Peng, C.; Stanley, H. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, 215–220. [Google Scholar] [CrossRef]
- An, J.; Cho, S. Hand motion identification of grasp-and-lift task from electroencephalography recordings using recurrent neural networks. In Proceedings of the 2016 International Conference on Big Data and Smart Computing (BigComp), Hong Kong, China, 18–20 January 2016; pp. 427–429. [Google Scholar]
- Cho, K.; Merrienboer, B.V.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. arXiv, 2014; arXiv:1409.1259. [Google Scholar]
- Schirrmeister, R.T.; Springenberg, J.T.; Fiederer, L.D.J.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Hum. Brain Mapp. 2017, 38, 5391–5420. [Google Scholar] [CrossRef] [PubMed]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGnet: A compact convolutional network for EEG-based brain-computer interfaces. arXiv, 2016; arXiv:1611.08024. [Google Scholar] [CrossRef] [PubMed]
- Bashivan, P.; Rish, I.; Yeasin, M.; Codella, N. Learning representations from EEG with deep recurrent-convolutional neural networks. arXiv, 2015; arXiv:1511.06448. [Google Scholar]
- Popov, E.; Fomenkov, S. Classification of hand motions in EEG signals using recurrent neural networks. In Proceedings of the 2016 2nd International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Chelyabinsk, Russia, 19–20 May 2016; pp. 1–4. [Google Scholar]
- Guger Technologies. 2017. Available online: http://www.gtec.at/ (accessed on 12 March 2018).
- Tayeb, Z.; Waniek, N.; Fedjaev, J.; Ghaboosi, N.; Rychly, L.; Widderich, C.; Richter, C.; Braun, J.; Saveriano, M.; Cheng, G.; et al. Gumpy: A Python toolbox suitable for hybrid brain–computer interfaces. J. Neural Eng. 2018, 15, 065003. [Google Scholar] [CrossRef] [PubMed]
- Nolan, H.; Whelan, R.; Reilly, R. FASTER: Fully Automated Statistical Thresholding for EEG artifact Rejection. J. Neurosci. Methods 2010, 192, 152–162. [Google Scholar] [CrossRef] [PubMed]
- Team, T.T.D. Theano: A Python framework for fast computation of mathematical expressions. arXiv, 2016; arXiv:1605.02688. [Google Scholar]
- Chollet, F. Keras, 2015. Available online: https://github.com/fchollet/keras (accessed on 4 April 2018).
- Erhan, D.; Bengio, Y.; Courville, A.; Manzagol, P.A.; Vincent, P.; Bengio, S. Why Does Unsupervised Pre-training Help Deep Learning? J. Mach. Learn. 2010, 11, 625–660. [Google Scholar]
- Sun, D.L.; Smith, J.O., III. Estimating a Signal from a Magnitude Spectrogram via Convex Optimization. arXiv. 2012. Available online: https://arxiv.org/pdf/1209.2076.pdf (accessed on 26 March 2018).
- Pfurtscheller, G.; da Silva, F.H.L. Event-related EEG/MEG synchronization and desynchronization: Basic principles. Clin. Neurophysiol. 1999, 110, 1842–1857. [Google Scholar] [CrossRef]
- loffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv, 2015; arXiv:1502.03167. [Google Scholar]
- Ioffe, S.; Szegedy, C. Adam: A method for stochastic optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- Liang, M.; Hu, X. Recurrent convolutional neural network for object recognition. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3367–3375. [Google Scholar]
- Grosse-Wentrup, M.; Buss, M. Multiclass Common Spatial Patterns and Information Theoretic Feature Extraction. IEEE Trans. Biomed. Eng. 2008, 8, 1991–2000. [Google Scholar] [CrossRef] [PubMed]
- Brodu, N.; Lotte, F.; Lecuyer, A. Comparative study of band-power extraction techniques for Motor Imagery classification. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence, Cognitive Algorithms, Mind, and Brain (CCMB), Paris, France, 11–15 April 2011; pp. 1–6. [Google Scholar]
- Gerking, J.M.; Pfurtscheller, G.; Flyvbjerg, H. Designing optimal spatial filters for single-trial EEG classification in a movement task. Clin. Neurophysiol. 1999, 110, 787–798. [Google Scholar] [CrossRef]
- Sherwani, F.; Shanta, S.; Ibrahim, B.S.K.K.; Huq, M.S. Wavelet based feature extraction for classification of motor imagery signals. In Proceedings of the 2016 IEEE EMBS Conference on Biomedical Engineering and Sciences (IECBES), Kuala Lumpur, Malaysia, 4–8 December 2016; pp. 360–364. [Google Scholar]
- Pudil, P.; Novovicova, J.; Kittler, J. Floating search methods in feature selection. Pattern Recognit. Lett. 2008, 15, 1119–1125. [Google Scholar] [CrossRef]
- Lab Streaming Layer. Available online: https://github.com/sccn/labstreaminglayer (accessed on 15 April 2018).
- Hessel, M.; Soyer, H.; Espeholt, L.; Czarnecki, W.; Schmitt, S.; van Hasselt, H. Multi-task deep reinforcement learning with popart. arXiv, 2018; arXiv:1809.04474. [Google Scholar]
- Li, Z.; Wang, Y.; Zhi, T.; Chen, T. A survey of neural network accelerators. Front. Comput. Sci. 2017, 11, 746–761. [Google Scholar] [CrossRef]
- Merolla, P.V.; Arthur, J.V.; Alvarez-Icaza, R.; Cassidy, A.S.; Sawada, J.; Akopyan, F.; Jackson, B.L.; Imam, N.; Guo, C.; Nakamura, Y.; et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 2014, 345, 668–673. [Google Scholar] [CrossRef] [PubMed]

| Layer Type | Size | Output Shape |
|---|---|---|
| Convolutional | filters | (144,1,1280,256) |
| Max pooling | Pool size 4, stride 4 | (144,1,1280,256) |
| RCL | 256 filters (), 256 filters (), three iterations | (144,1,1280,256) |
| Max pooling | Pool size 4, stride 4 | (144,1,320,256) |
| RCL | 256 filters (), 256 filters (), three iterations | (144,1,320,256) |
| Max pooling | Pool size 4, stride 4 | (144,1,80,256) |
| RCL | 256 filters (), 256 filters (), three iterations | (144,1,20,256) |
| Max pooling | Pool size 4, stride 4 | (144,1,5,256) |
| RCL | 256 filters (), 256 filters (), three iterations | (144,1,20,256) |
| Max pooling | Pool size 4, stride 4 | (144,1,5,256) |
| Fully connected | (144,2) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tayeb, Z.; Fedjaev, J.; Ghaboosi, N.; Richter, C.; Everding, L.; Qu, X.; Wu, Y.; Cheng, G.; Conradt, J. Validating Deep Neural Networks for Online Decoding of Motor Imagery Movements from EEG Signals. Sensors 2019, 19, 210. https://doi.org/10.3390/s19010210
Tayeb Z, Fedjaev J, Ghaboosi N, Richter C, Everding L, Qu X, Wu Y, Cheng G, Conradt J. Validating Deep Neural Networks for Online Decoding of Motor Imagery Movements from EEG Signals. Sensors. 2019; 19(1):210. https://doi.org/10.3390/s19010210
Chicago/Turabian StyleTayeb, Zied, Juri Fedjaev, Nejla Ghaboosi, Christoph Richter, Lukas Everding, Xingwei Qu, Yingyu Wu, Gordon Cheng, and Jörg Conradt. 2019. "Validating Deep Neural Networks for Online Decoding of Motor Imagery Movements from EEG Signals" Sensors 19, no. 1: 210. https://doi.org/10.3390/s19010210
APA StyleTayeb, Z., Fedjaev, J., Ghaboosi, N., Richter, C., Everding, L., Qu, X., Wu, Y., Cheng, G., & Conradt, J. (2019). Validating Deep Neural Networks for Online Decoding of Motor Imagery Movements from EEG Signals. Sensors, 19(1), 210. https://doi.org/10.3390/s19010210





