A Tangible Solution for Hand Motion Tracking in Clinical Applications
Abstract
1. Introduction
1.1. Motivation
1.2. Previous Approaches to Hand Motion Tracking
1.3. The Proposed Approach
2. Materials and Methods
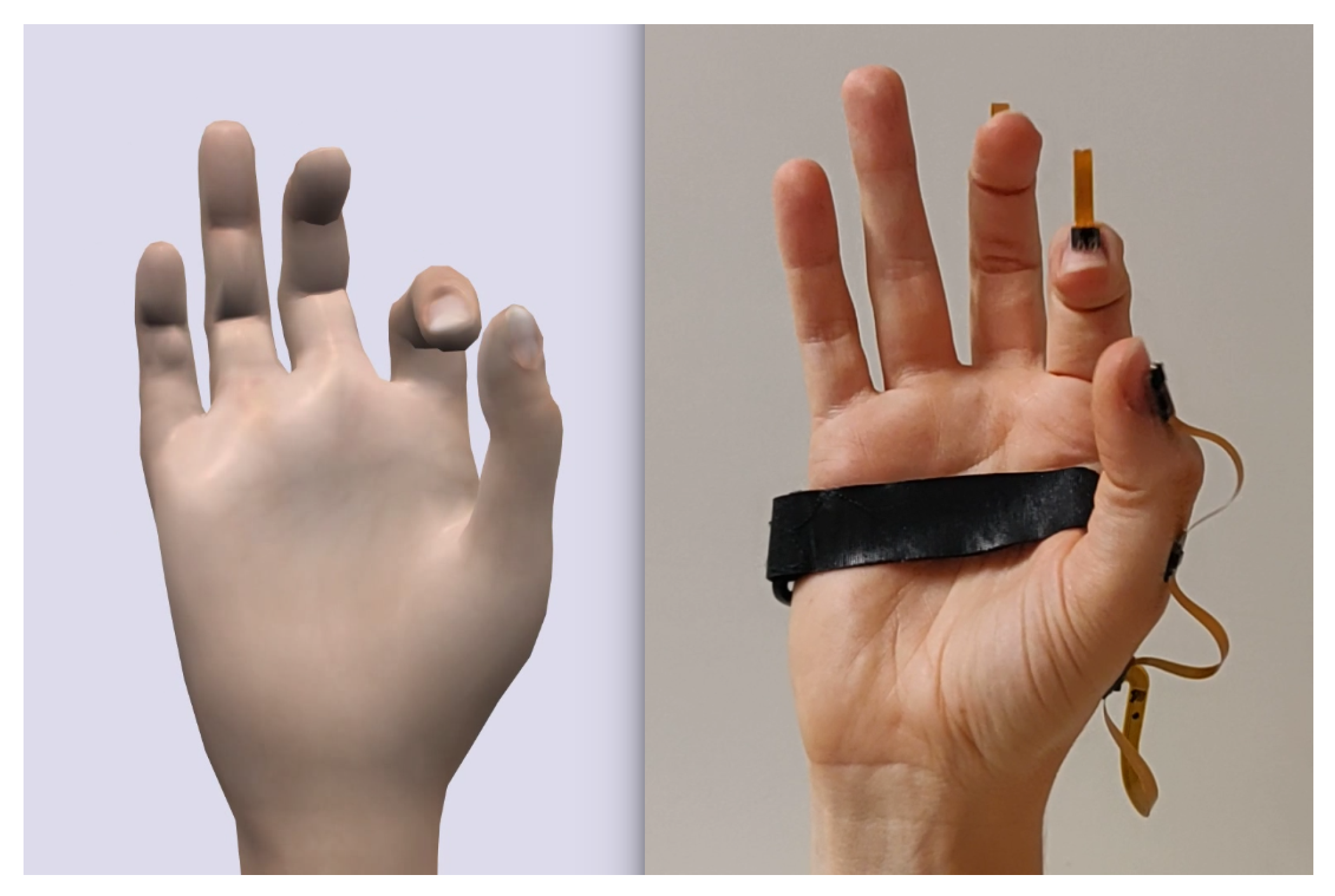
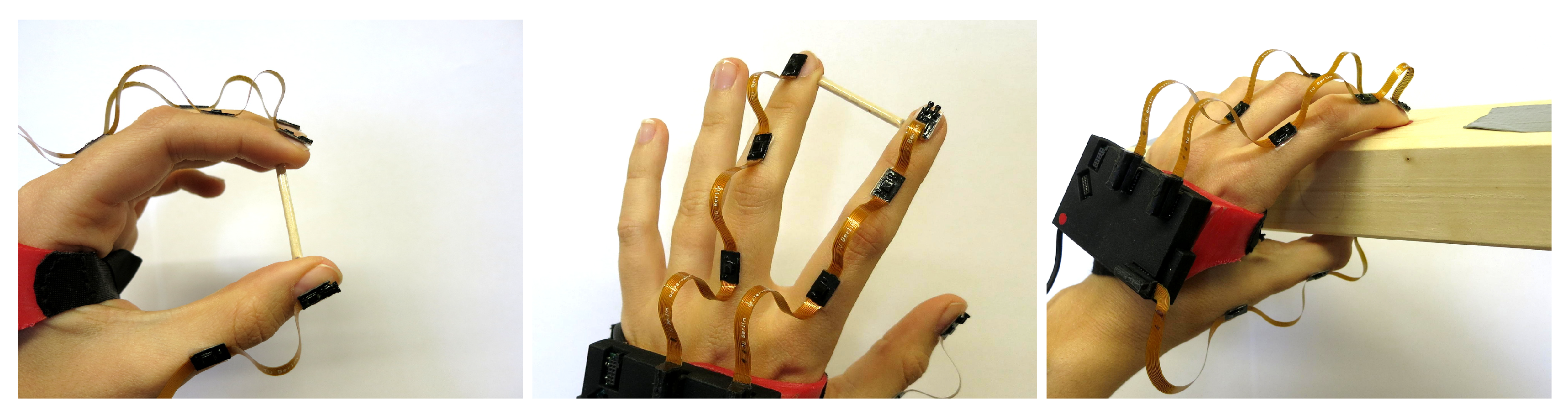
2.1. Hand Sensor System Hardware
2.2. Biomechanical Hand Model
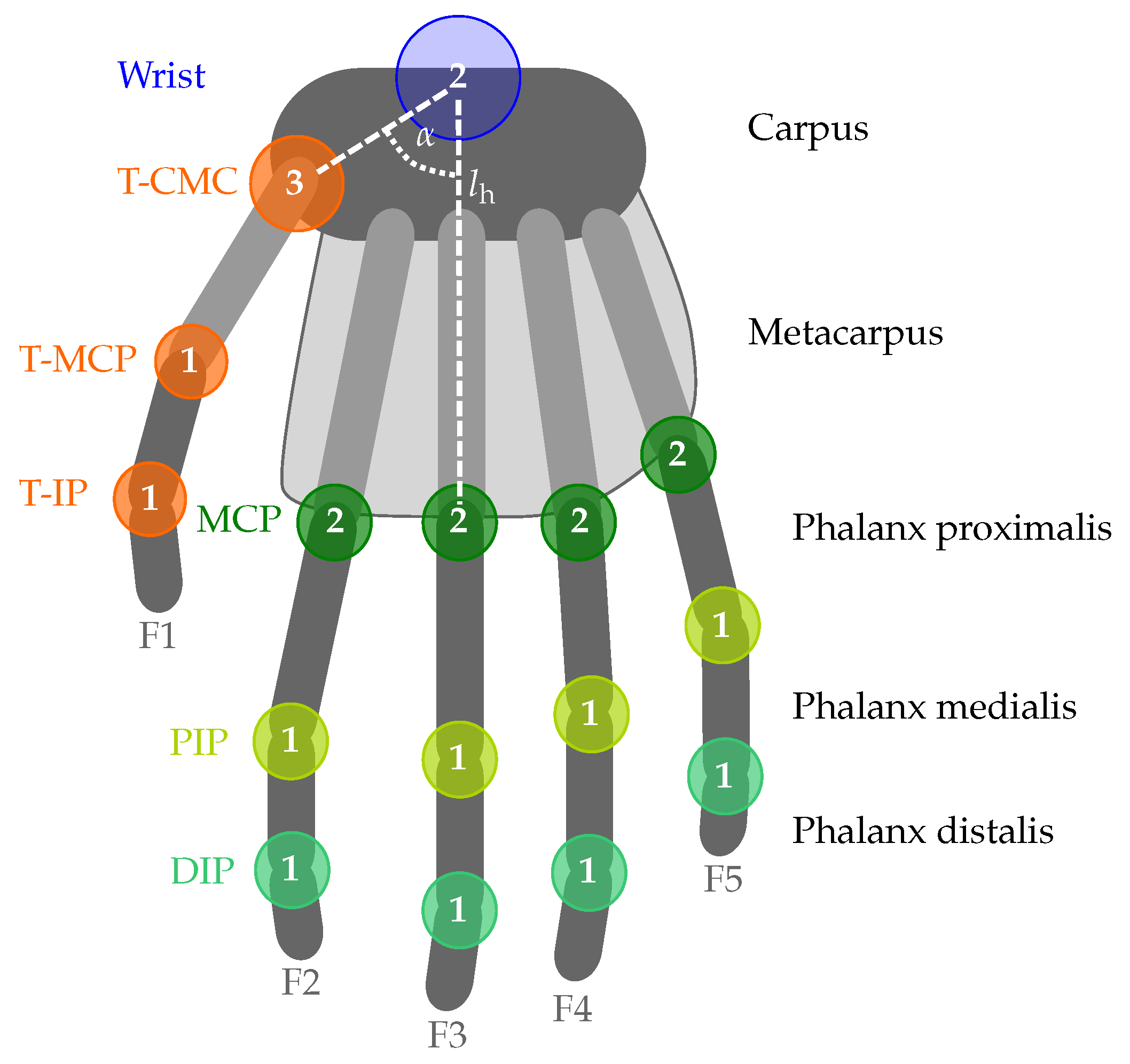
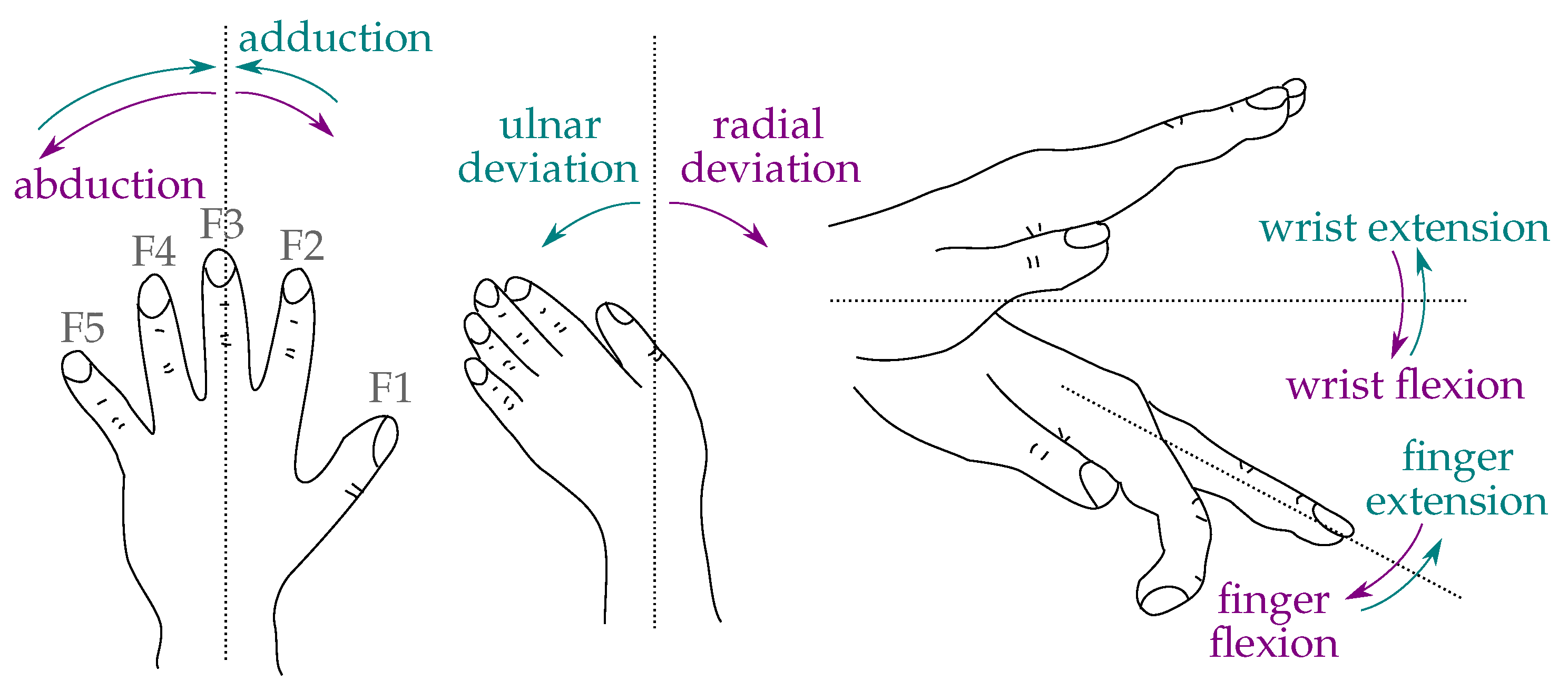
2.2.1. Anatomy of the Hand
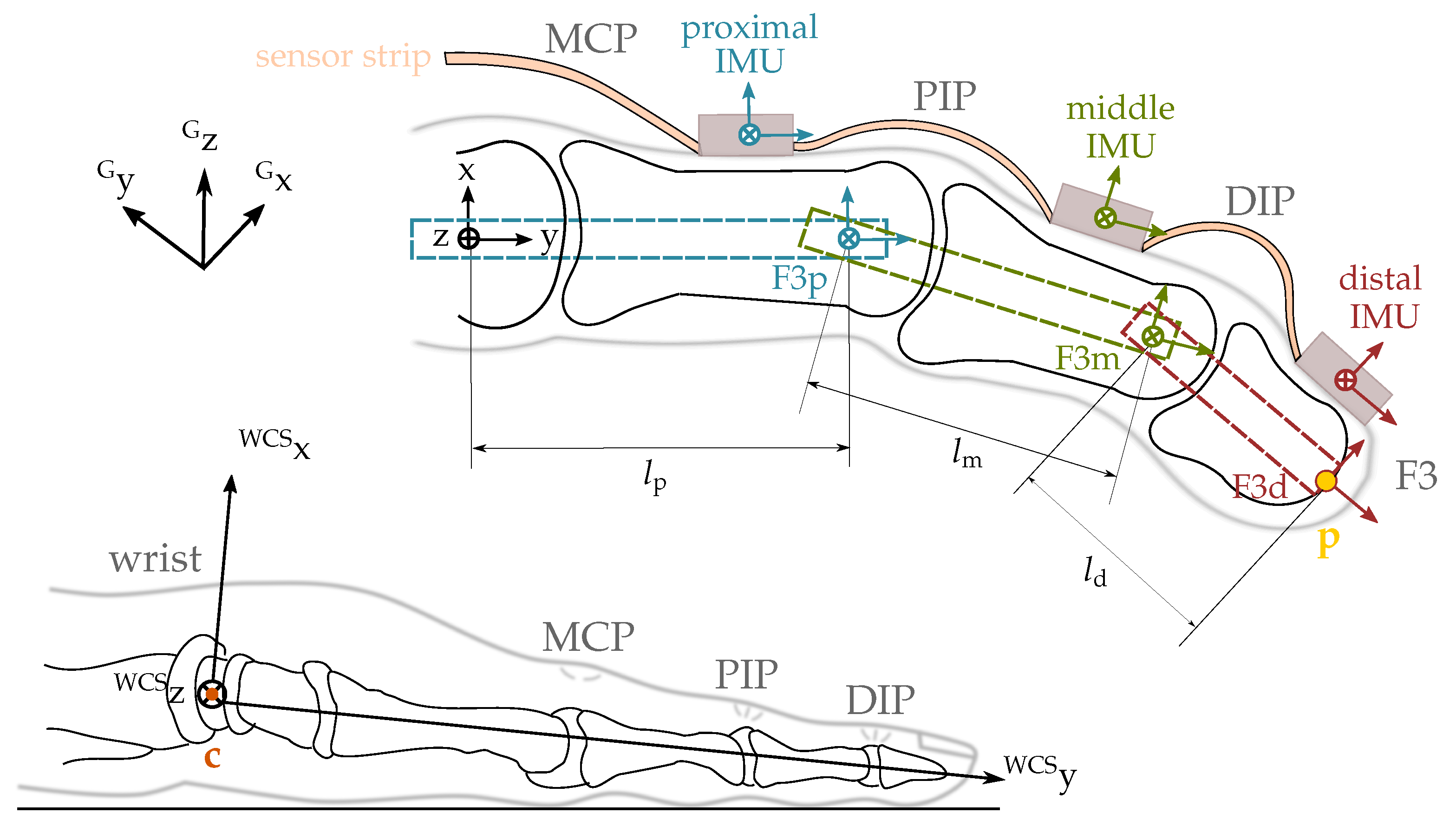
2.2.2. Definition of Local Coordinate Systems
2.2.3. Lengths of the Phalanges
2.3. Introduction to Quaternions and Dual Quaternions
2.3.1. Definitions
2.3.2. Describing Rotations and Translations with Dual Quaternions
2.4. The Hand Sensor System Algorithm
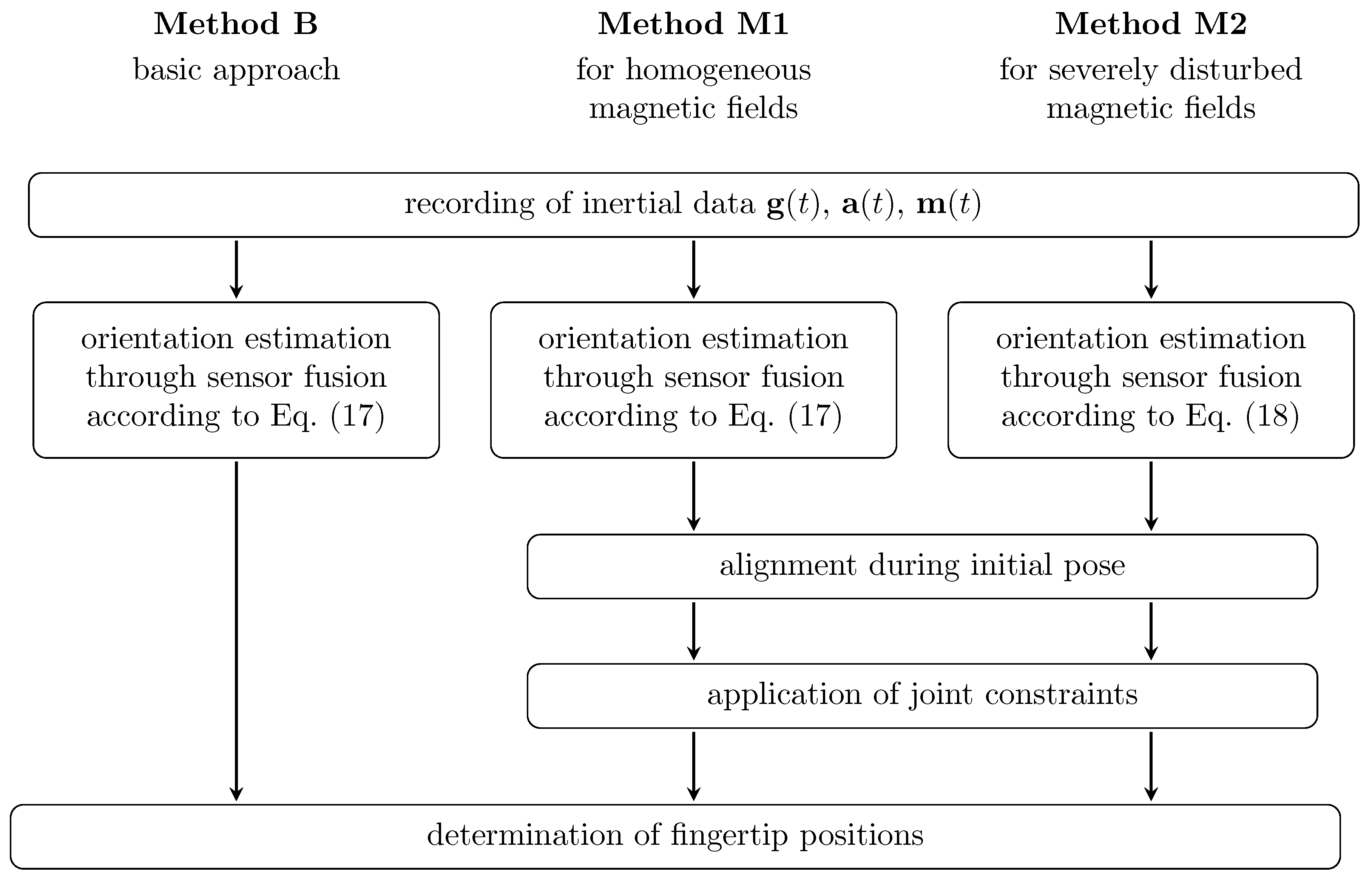
2.4.1. Data Recording and Sensor Fusion (B, M1, M2)
2.4.2. Initial Pose Alignment (M1, M2)
2.4.3. Application of Joint Constraints (M1, M2)
2.4.4. Determination of the Fingertip Positions (B, M1, M2)
3. Experimental Validation
3.1. Idealistic Setting with Optical Reference System (Setting 1)
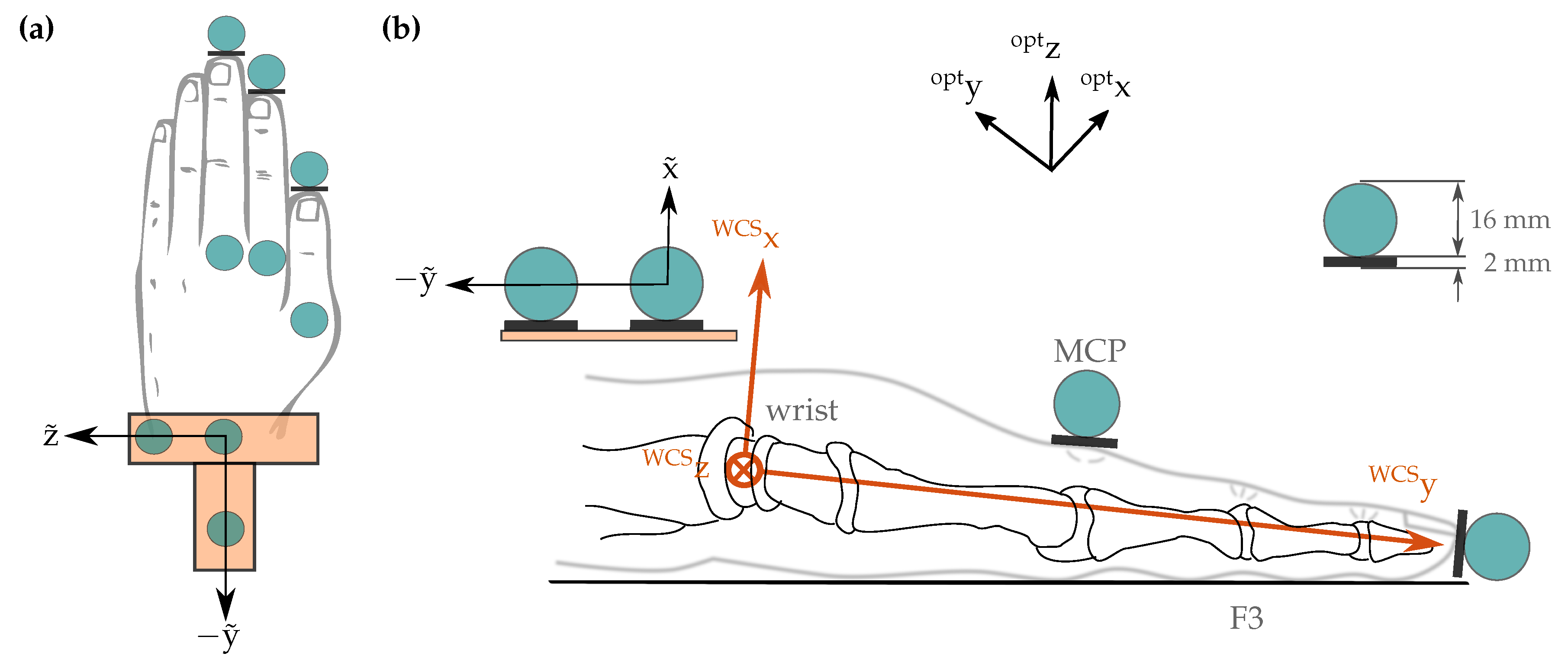
3.1.1. Setup
3.1.2. Alignment of the Coordinate Frames between IMUs and Optical System
3.1.3. Conducted Experiments
3.2. Evaluation under Realistic Conditions Exploiting Characteristic Hand Poses (Setting 2)
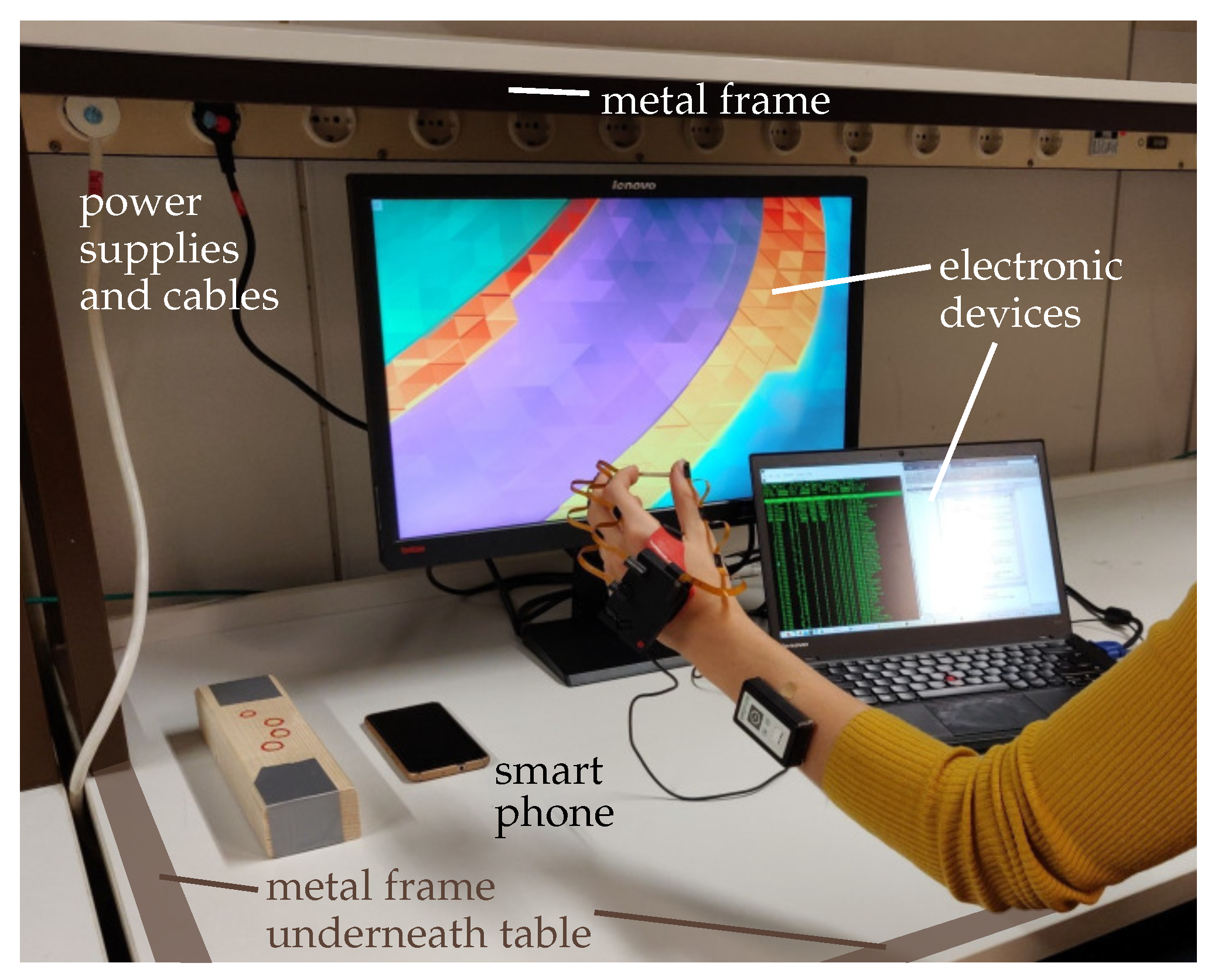
3.2.1. Setup
3.2.2. Conducted Experiments
4. Results
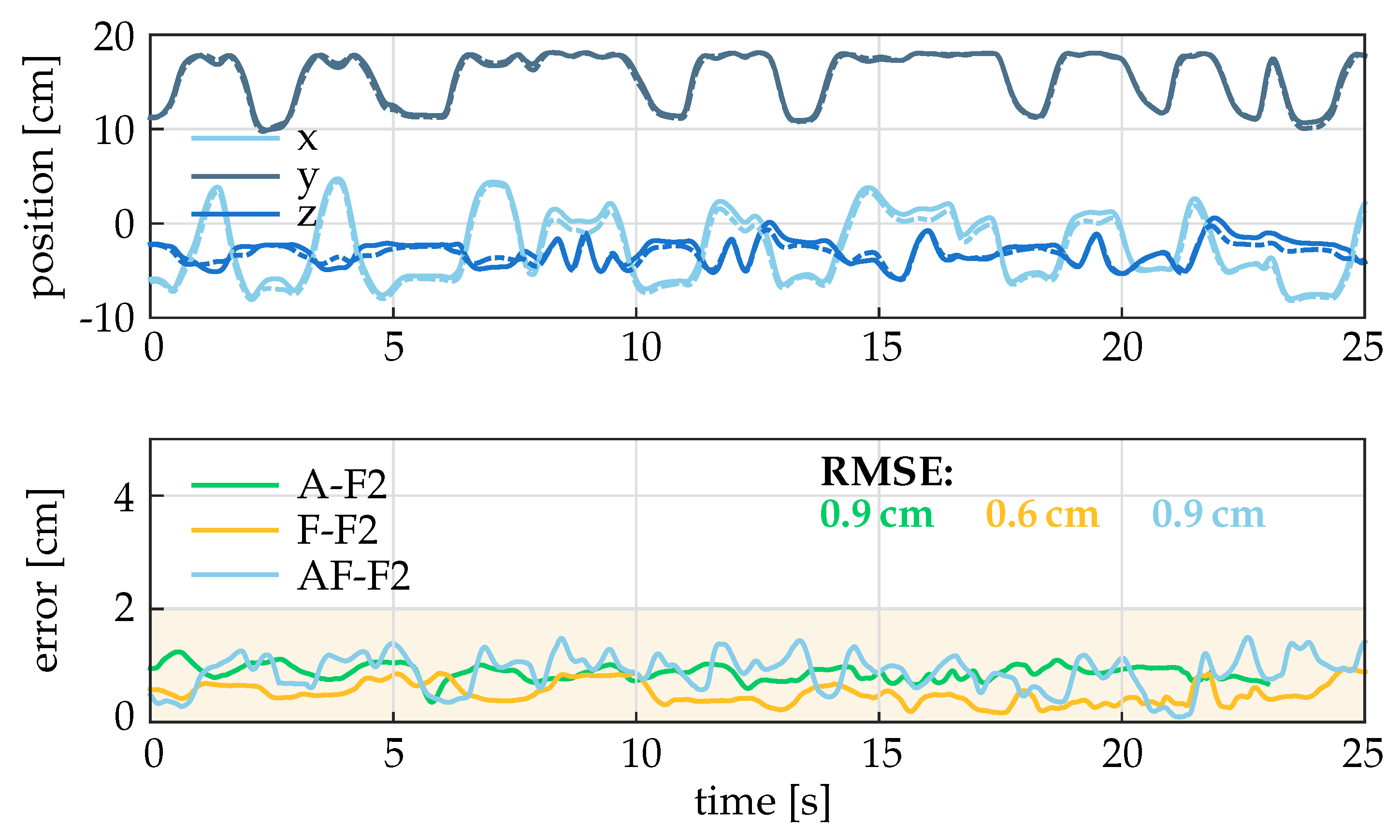
4.1. Results under Idealistic Conditions (Setting 1)
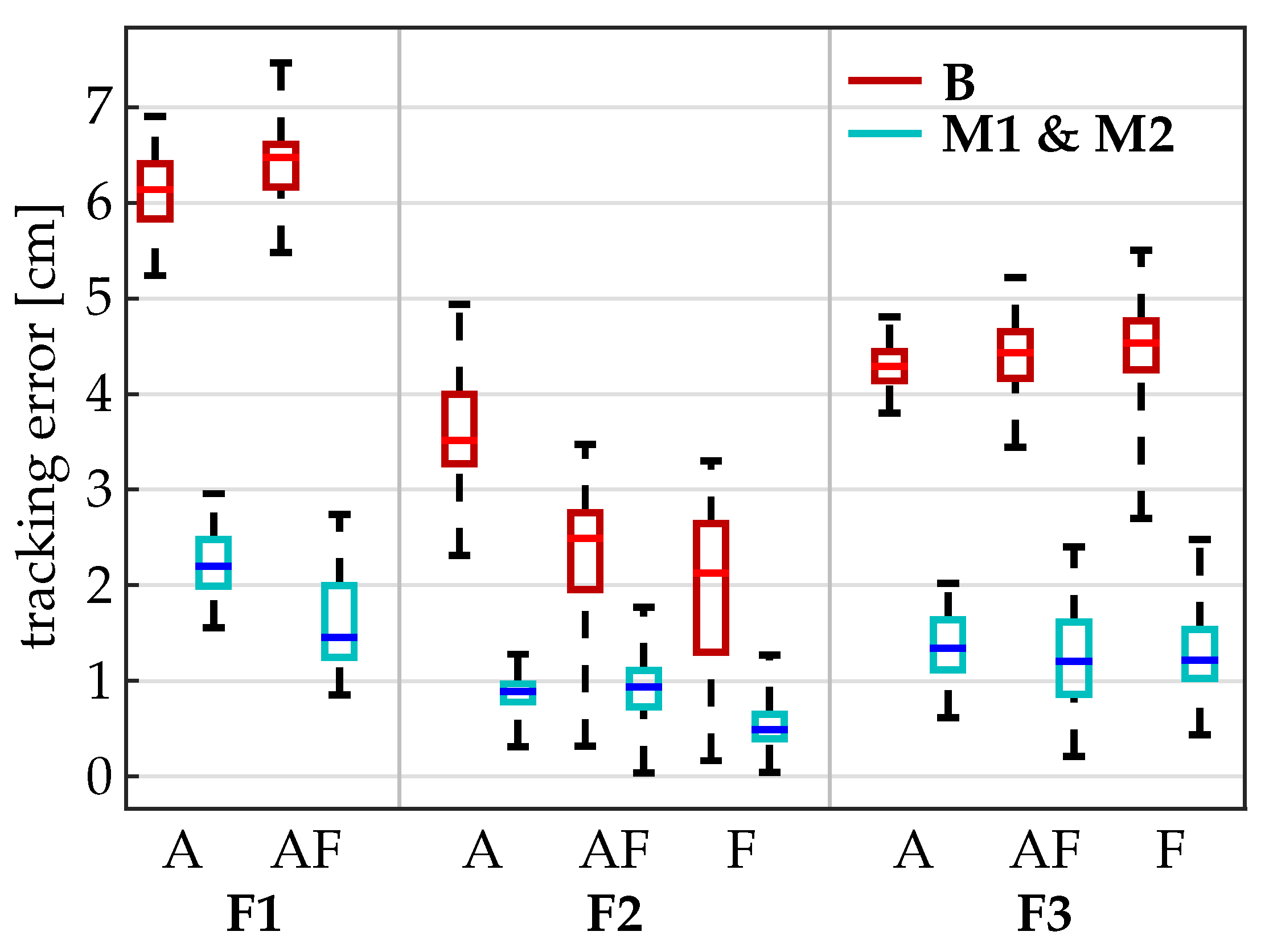
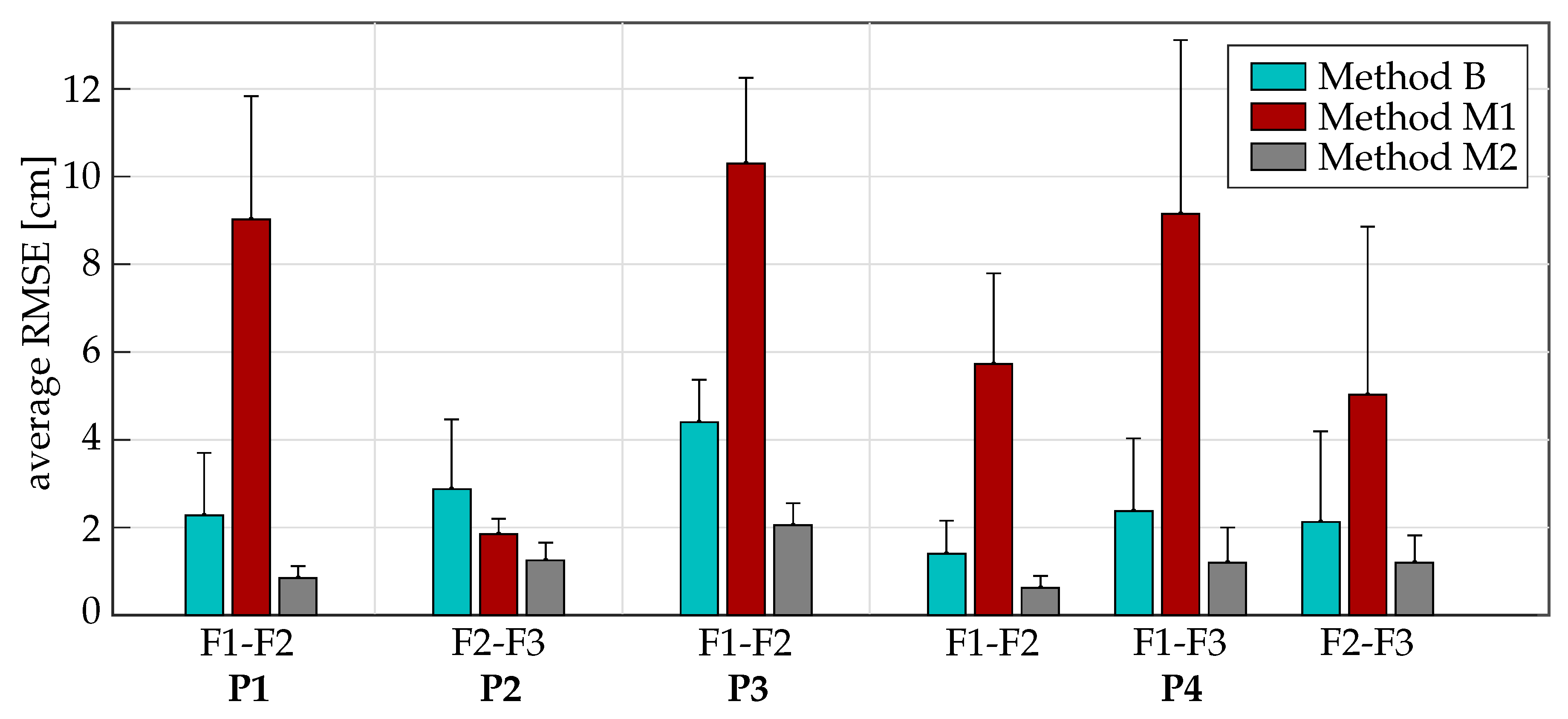
4.2. Results under Realistic Conditions (Setting 2)
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| A | Abduction |
| CI | Confidence interval |
| DIP | Distal interphalangeal joint |
| DoF | Degrees of freedom |
| F | Flexion |
| F1 | Finger no. 1 (thumb) |
| F2 | Finger no. 2 (index) |
| F3 | Finger no. 3 (middle) |
| F4 | Finger no. 4 (ring) |
| F5 | Finger no. 5 (little) |
| FES | Functional electrical stimulation |
| IMU | Inertial measurement unit |
| ipa | Initial pose aligned |
| ISB | International Society of Biomechanics |
| MCP | Metacarpal-phalangeal joints |
| P1…4 | Experiments P1 to P4 in setting 2 |
| PIP | Proximal interphalangeal joint |
| RMSE | Root mean square error |
| SCI | Spinal cord injury |
| std | Standard deviation |
| T-CMC | Thumb-carpo-metacarpal joint |
| T-IP | Thumb-interphalangeal joint |
| T-MCP | Thumb-metacarpal-phalangeal joint |
| WCS | Wrist coordinate system |
References
- Peckham, P.H.; Knutson, J.S. Functional Electrical Stimulation for Neuromuscular Applications. Annu. Rev. Biomed. Eng. 2005, 7, 327–360. [Google Scholar] [CrossRef] [PubMed]
- Soska, A.; Freeman, C.; Rogers, E. ILC for FES-based Stroke Rehabilitation of Hand and Wrist. In Proceedings of the 2012 IEEE International Symposium on Intelligent Control, Dubrovnik, Croatia, 3–5 October 2012; pp. 1267–1272. [Google Scholar]
- Schauer, T. Sensing motion and muscle activity for feedback control of functional electrical stimulation: Ten years of experience in Berlin. Annu. Rev. Control 2017, 44, 355–374. [Google Scholar] [CrossRef]
- Valtin, M.; Seel, T.; Raisch, J.; Schauer, T. Iterative learning control of drop foot stimulation with array electrodes for selective muscle activation. In Proceedings of the Preprints 19th WC IFAC, Cape Town, South Africa, 24–29 August 2014; pp. 6586–6592. [Google Scholar] [CrossRef]
- Müller, P.; Balligand, C.; Seel, T.; Schauer, T. Iterative Learning Control and System Identification of the Antagonistic Knee Muscle Complex During Gait Using Functional Electrical Stimulation. IFAC-PapersOnLine 2017, 50, 8786–8791. [Google Scholar] [CrossRef]
- Freeman, C.; Hughes, A.M.; Burridge, J.; Chappell, P.; Lewin, P.; Rogers, E. Iterative learning control of FES applied to the upper extremity for rehabilitation. Control Eng. Pract. 2009, 17, 368–381. [Google Scholar] [CrossRef]
- Freeman, C. Control System Design for Electrical Stimulation in Upper Limb Rehabilitation: Modelling, Identification and Robust Performance; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Passon, A.; Seel, T.; Massmann, J.; Freeman, C.; Schauer, T. Iterative learning vector field for FES-supported cyclic upper limb movements in combination with robotic weight compensation. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Popovic, M.R.; Popovic, D.B.; Keller, T. Neuroprostheses for grasping. Neurol. Res. 2002, 24, 443–452. [Google Scholar] [CrossRef]
- Koutsou, A.D.; Moreno, J.C.; del Ama, A.J.; Rocon, E.; Pons, J.L. Advances in selective activation of muscles for non-invasive motor neuroprostheses. J. Neuroeng. Rehabil. 2016, 13, 56. [Google Scholar] [CrossRef]
- Salchow-Hömmen, C.; Jankowski, N.; Valtin, M.; Schönijahn, L.; Böttcher, S.; Dähne, F.; Schauer, T. User-centered practicability analysis of two identification strategies in electrode arrays for FES induced hand motion in early stroke rehabilitation. J. Neuroeng. Rehabil. 2018, 15, 123. [Google Scholar] [CrossRef]
- Colombo, R.; Sanguineti, V. Rehabilitation Robotics: Technology and Application; Elsevier Science: Amsterdam, The Netherlands, 2018. [Google Scholar]
- De Vries, W.H.; Veeger, H.E.; Baten, C.T.; van der Helm, F.C. Magnetic distortion in motion labs, implications for validating inertial magnetic sensors. Gait Posture 2009, 29, 535–541. [Google Scholar] [CrossRef]
- Seel, T.; Ruppin, S. Eliminating the Effect of Magnetic Disturbances on the Inclination Estimates of Inertial Sensors. IFAC-PapersOnLine 2017, 50, 8798–8803. [Google Scholar] [CrossRef]
- Erol, A.; Bebis, G.; Nicolescu, M.; Boyle, R.D.; Twombly, X. Vision-based hand pose estimation: A review. Comput. Vis. Image Underst. 2007, 108, 52–73. [Google Scholar] [CrossRef]
- Dipietro, L.; Sabatini, A.M.; Dario, P. A survey of glove-based systems and their applications. IEEE Trans. Syst. Man Cybern. C 2008, 38, 461–482. [Google Scholar] [CrossRef]
- Fahn, C.S.; Sun, H. Development of a Fingertip Glove Equipped with Magnetic Tracking Sensors. Sensors 2010, 10, 1119–1140. [Google Scholar] [CrossRef] [PubMed]
- Saggio, G.; Bocchetti, S.; Pinto, C.A.; Orengo, G.; Giannini, F. A novel application method for wearable bend sensors. In Proceedings of the 2nd International Symposium on Applied Sciences in Biomedical and Communication Technologies, Bratislava, Slovakia, 24–27 November 2009; pp. 1–3. [Google Scholar] [CrossRef]
- Kortier, H.G.; Sluiter, V.I.; Roetenberg, D.; Veltink, P.H. Assessment of hand kinematics using inertial and magnetic sensors. J. Neuroeng. Rehabil. 2014, 11, 70. [Google Scholar] [CrossRef] [PubMed]
- Van den Noort, J.C.; Kortier, H.G.; van Beek, N.; Veeger, D.H.E.J.; Veltink, P.H.; Bensmaia, S.J. Measuring 3D Hand and Finger Kinematics—A Comparison between Inertial Sensing and an Opto-Electronic Marker System. PLoS ONE 2016, 11, e0164889. [Google Scholar] [CrossRef] [PubMed]
- Westerveld, A.J.; Kuck, A.; Schouten, A.C.; Veltink, P.H.; van der Kooij, H. Grasp and release with surface functional electrical stimulation using a Model Predictive Control approach. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012. [Google Scholar] [CrossRef]
- Kim, Y.S.; Soh, B.S.; Lee, S.G. A new wearable input device: SCURRY. IEEE Trans. Ind. Electron. 2005, 52, 1490–1499. [Google Scholar] [CrossRef]
- Connolly, J.; Condell, J.; O’Flynn, B.; Sanchez, J.T.; Gardiner, P. IMU Sensor-Based Electronic Goniometric Glove for Clinical Finger Movement Analysis. IEEE Sens. J. 2018, 18, 1273–1281. [Google Scholar] [CrossRef]
- Choi, Y.; Yoo, K.; Kang, S.J.; Seo, B.; Kim, S.K. Development of a low-cost wearable sensing glove with multiple inertial sensors and a light and fast orientation estimation algorithm. J. Supercomput. 2018, 74, 3639–3652. [Google Scholar] [CrossRef]
- Lin, B.S.; Lee, I.; Yang, S.Y.; Lo, Y.C.; Lee, J.; Chen, J.L. Design of an Inertial-Sensor-Based Data Glove for Hand Function Evaluation. Sensors 2018, 18, 1545. [Google Scholar] [CrossRef]
- Salchow, C.; Valtin, M.; Seel, T.; Schauer, T. Development of a Feedback-Controlled Hand Neuroprosthesis: FES-Supported Mirror Training. In Proceedings of the AUTOMED Workshop, Wismar, Germany, 22–23 September 2016. [Google Scholar]
- Valtin, M.; Salchow, C.; Seel, T.; Laidig, D.; Schauer, T. Modular finger and hand motion capturing system based on inertial and magnetic sensors. Curr. Dir. Biomed. Eng. 2017, 3, 19–23. [Google Scholar] [CrossRef]
- Salchow-Hömmen, C.; Thomas, T.; Valtin, M.; Schauer, T. Automatic control of grasping strength for functional electrical stimulation in forearm movements via electrode arrays. at-Autom 2018, 66, 1027–1036. [Google Scholar] [CrossRef]
- Clauser, C.E.; McConville, J.T.; Young, J.W. Weight, Volume, and Center of Mass of Segments of the Human Body (AMRL TR 69-70); Technical Report; Antioch College: Yellow Springs, OH, USA, 1969. [Google Scholar]
- Zhang, R.; Hoflinger, F.; Reind, L.M. Calibration of an IMU using 3-D rotation platform. IEEE Sens. J. 2014, 14, 1778–1787. [Google Scholar] [CrossRef]
- Winter, D.A. Biomechanics and Motor Control of Human Movement, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Cobos, S.; Ferre, M.; Uran, M.S.; Ortego, J.; Pena, C. Efficient human hand kinematics for manipulation tasks. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008. [Google Scholar] [CrossRef]
- Cobos, S.; Ferre, M.; Aracil, R.; Ortego, J.; Angel, M. Simplified Human Hand Models for Manipulation Tasks. In Cutting Edge Robotics 2010; InTech: London, UK, 2010. [Google Scholar] [CrossRef]
- Cocchiarella, D.M.; Kociolek, A.M.; Tse, C.T.F.; Keir, P.J. Toward a realistic optoelectronic-based kinematic model of the hand: Representing the transverse metacarpal arch reduces accessory rotations of the metacarpophalangeal joints. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 639–647. [Google Scholar] [CrossRef] [PubMed]
- Keir, P.; Cocciarella, D.; Kociolek, A. Development of a kinematic hand model with a realistic representation of the metacarpal arch. In Proceedings of the 24th ISB Congress, Natal, Brazil, 4–9 August 2013. [Google Scholar]
- Wu, G.; van der Helm, F.C.; Veeger, H.; Makhsous, M.; van Roy, P.; Anglin, C.; Nagels, J.; Karduna, A.R.; McQuade, K.; Wang, X.; et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion–Part II: Shoulder, elbow, wrist and hand. J. Biomech. 2005, 38, 981–992. [Google Scholar] [CrossRef] [PubMed]
- Goislard de Monsabert, B.; Visser, J.; Vigouroux, L.; van der Helm, F.; Veeger, H. Comparison of three local frame definitions for the kinematic analysis of the fingers and the wrist. J. Biomech. 2014, 47, 2590–2597. [Google Scholar] [CrossRef] [PubMed]
- Gustus, A.; Stillfried, G.; Visser, J.; Jörntell, H.; van der Smagt, P. Human hand modelling: Kinematics, dynamics, applications. Biol. Cybernet. 2012, 106, 741–755. [Google Scholar] [CrossRef] [PubMed]
- Buchholz, B.; Armstrong, T.J.; Goldstein, S.A. Anthropometric data for describing the kinematics of the human hand. Ergonomics 1992, 35, 261–273. [Google Scholar] [CrossRef]
- Hamilton, R.; Dunsmuir, R.A. Radiographic Assessment of the Relative Lengths of the Bones of the Fingers of the Human Hand. J. Hand. Surg. Eur. 2002, 27, 546–548. [Google Scholar] [CrossRef]
- Park, A.E.; Fernandez, J.J.; Schmedders, K.; Cohen, M.S. The fibonacci sequence: Relationship to the human hand. J. Hand. Surg. Am. 2003, 28, 157–160. [Google Scholar] [CrossRef] [PubMed]
- Buryanov, A.; Kotiuk, V. Proportions of Hand Segments. Int. J. Morphol. 2010, 28, 755–758. [Google Scholar] [CrossRef]
- Radavelli, L.; Simoni, R.; De Pieri, E.R.; Martins, D. A Comparative Study of the Kinematics of Robots Manipulators by Denavit-Hartenberg and Dual Quaternion. Mecánica Comput. Multi-Body Syst. 2012, 31, 2833–2848. [Google Scholar]
- Leclercq, G.; Lefèvre, P.; Blohm, G. 3D kinematics using dual quaternions: Theory and applications in neuroscience. Front. Behav. Neurosci. 2013, 7, 7. [Google Scholar] [CrossRef]
- Hamilton, W.R. II. On quaternions; Or on a new system of imaginaries in algebra. Philos. Mag. Ser. 3 1844, 25. [Google Scholar] [CrossRef]
- Kenwright, B. A beginners guide to dual-quaternions: What they are, how they work, and how to use them for 3D character hierarchies. In Proceedings of the 20th WSCG International Conference on Computer Graphics, Visualization and Computer Vision 2012, Plzeň, Czech Republic, 25–28 June 2012; pp. 1–13. [Google Scholar]
- Aumüller, G.; Aust, G.; Doll, A.; Engele, J.; Kirsch, J.; Mense, S.; Reißig, D.; Salvetter, J.; Schmidt, W.; Schmitz, F.; et al. Anatomie, 1st ed.; Duale Reihe, Thieme: Stuttgart, Germany, 2007. [Google Scholar]
- Kutlu, M.; Freeman, C.; Hughes, A.M.; Spraggs, M. A Home-based FES System for Upper-limb Stroke Rehabilitation with Iterative Learning Control. IFAC-PapersOnLine 2017, 50, 12089–12094. [Google Scholar] [CrossRef]
- Kok, M.; Hol, J.D.; Schön, T.B. An optimization-based approach to human body motion capture using inertial sensors. In Proceedings of the 19th IFAC World Congress, Cape Town, South Africa, 24–29 August 2014; Volume 47, pp. 79–85. [Google Scholar] [CrossRef]
- Müller, P.; Bégin, M.A.; Schauer, T.; Seel, T. Alignment-Free, Self-Calibrating Elbow Angles Measurement using Inertial Sensors. IEEE J. Biomed. Health Inform. 2017, 21, 312–319. [Google Scholar] [CrossRef] [PubMed]
- Laidig, D.; Schauer, T.; Seel, T. Exploiting Kinematic Constraints to Compensate Magnetic Disturbances when Calculating Joint Angles of Approximate Hinge Joints from Orientation Estimates of Inertial Sensors. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 971–976. [Google Scholar] [CrossRef]
- Teufl, W.; Miezal, M.; Taetz, B.; Fröhlich, M.; Bleser, G. Validity, Test-Retest Reliability and Long-Term Stability of Magnetometer Free Inertial Sensor Based 3D Joint Kinematics. Sensors 2018, 18, 1980. [Google Scholar] [CrossRef] [PubMed]
- Kortier, H.G.; Schepers, H.M.; Veltink, P.H. Identification of Object Dynamics Using Hand Worn Motion and Force Sensors. Sensors 2016, 16, 2005. [Google Scholar] [CrossRef] [PubMed]
- Laidig, D.; Trimpe, S.; Seel, T. Event-Based Sampling for Reducing Communication Load in Realtime Human Motion Analysis by Wireless Inertial Sensor Networks. Curr. Dir. Biomed. Eng. 2016, 2, 711–714. [Google Scholar] [CrossRef]


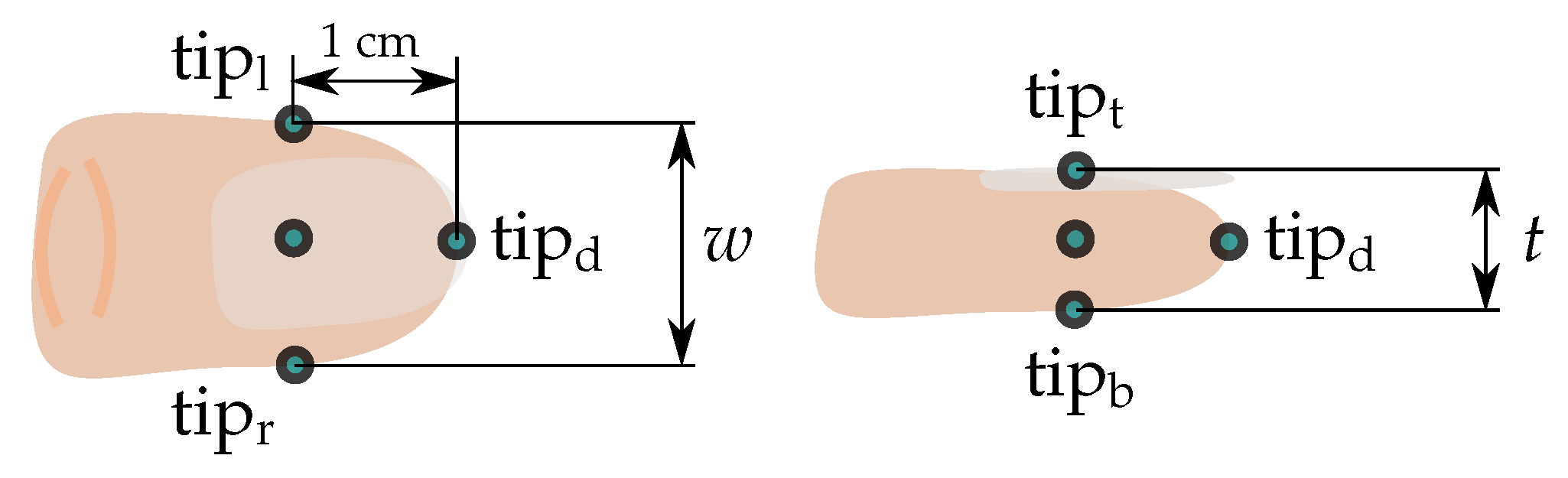

| System Type | Examples | Advantages and Disadvantages |
|---|---|---|
| Optical systems with markers | Vicon (Vicon Motion Systems Ltd., Oxford, UK) | (+) accurate (–) extensive setup by expert, expensive, line-of-sight restriction, stationary |
| Optical systems without markers | Kinect V2 (Microsoft, Redmond, WA, USA), Leap Motion (Leap Motion, San Francisco, CA, USA) | (+) contactless, affordable (–) limited accuracy, line-of-sight restriction |
| Sensor gloves with bend sensors | 5DT Data Glove Ultra (5DT Inc., Orlando, FL, USA), Cyperglove III (CyberGlove Systems Inc. LLC, San Jose, CA, USA) | (+) quick setup (–) less sense of touch, glove not suitable for spastic hand, hygienically problematic, measures only angles (no accelerations/ velocities/positions) |
| Sensor gloves with IMUs | IGS Cobra Glove (Synertial, Lewes, UK), PowerGlove [19,20] | (+) quick setup, detailed measurements (–) less sense of touch, glove not suitable for spastic hand, hygienically problematic, uses magnetometers and calibration motions |
| F1 | F2 | F3 | F4 | F5 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Ratios | 0.98 | 1.86 | 1.24 | 1.72 | 1.36 | 1.70 | 1.29 | 1.91 | 1.06 |
| 95% CI | 0.018 | 0.018 | 0.013 | 0.016 | 0.016 | 0.016 | 0.022 | 0.022 | |
| F1 | F2 | F3 | F4 | F5 |
|---|---|---|---|---|
| Experiment ID | Description |
|---|---|
| A-F1, A-F2, A-F3 | Pure abduction motion of F1, F2, F3 |
| F-F2, F-F3 | Pure flexion motion of F2 and F3 |
| AF-F1, AF-F2, AF-F3 | Combined abduction and flexion motion of F1, F2, F3 |
| Experiment ID | Description |
|---|---|
| P1 | Spacer with length between F1 and F2 |
| P2 | Spacer with length between F2 and F3 |
| P3 | F1 tip and F2 tip in contact, distance |
| P4 | All fingers fixed on a wooden block that is moved in space, distance predefined for each pair of fingers (, , ) |
| Experiment ID | Method B | Method M1 | Method M2 | |||
|---|---|---|---|---|---|---|
| MeanStd(E) | RMSE | MeanStd(E) | RMSE | MeanStd(E) | RMSE | |
| A-F1 | 6.00.60 | 6.1 | 2.20.36 | 2.2 | 1.80.18 | 1.8 |
| A-F2 | 3.60.47 | 3.6 | 0.90.14 | 0.9 | 0.90.19 | 1.0 |
| A-F3 | 4.20.44 | 4.3 | 1.30.26 | 1.4 | 0.60.17 | 0.7 |
| AF-F1 | 6.30.52 | 6.3 | 1.60.45 | 1.6 | 2.00.52 | 2.1 |
| AF-F2 | 2.20.63 | 2.3 | 0.90.30 | 0.9 | 0.90.49 | 1.0 |
| AF-F3 | 4.30.48 | 4.4 | 1.20.45 | 1.3 | 0.90.45 | 1.0 |
| F-F2 | 2.00.75 | 2.1 | 0.50.20 | 0.6 | 0.60.19 | 0.6 |
| F-F3 | 4.30.76 | 4.4 | 1.20.34 | 1.3 | 0.80.34 | 0.8 |
| Experiment | Fingers | Subject | Method B | Method M1 | Method M2 | |||
|---|---|---|---|---|---|---|---|---|
| ID | MeanStd(E) | RMSE | MeanStd(E) | RMSE | MeanStd(E) | RMSE | ||
| P1 | F1–F2 | #1 | 3.31.51 | 3.7 | 6.71.85 | 7.0 | 0.80.57 | 1.0 |
| #2 | 3.51.14 | 3.7 | 12.61.24 | 12.7 | 0.40.25 | 0.5 | ||
| #3 | 0.80.47 | 0.9 | 10.61.74 | 10.7 | 1.20.24 | 1.2 | ||
| #4 | 0.70.45 | 0.8 | 5.12.67 | 5.7 | 0.60.35 | 0.7 | ||
| Average | 2.10.89 | 2.3 | 8.81.88 | 9.0 | 0.80.35 | 0.9 | ||
| P2 | F2–F3 | #1 | 4.91.97 | 5.3 | 1.81.27 | 2.2 | 1.70.65 | 1.8 |
| #2 | 0.90.68 | 1.1 | 1.11.36 | 1.8 | 0.60.27 | 0.7 | ||
| #3 | 3.01.14 | 3.2 | 1.81.22 | 2.1 | 1.00.39 | 1.1 | ||
| #4 | 1.80.45 | 1.9 | 1.10.59 | 1.3 | 1.40.44 | 1.4 | ||
| Average | 2.71.06 | 2.9 | 1.51.11 | 1.9 | 1.20.44 | 1.3 | ||
| P3 | F1–F2 | #1 | 4.53.17 | 5.5 | 11.02.61 | 11.3 | 1.40.55 | 1.5 |
| #2 | 4.11.19 | 4.3 | 12.52.83 | 12.8 | 1.60.42 | 1.6 | ||
| #3 | 4.61.47 | 4.9 | 9.22.34 | 9.5 | 2.60.41 | 2.6 | ||
| #4 | 2.71.05 | 2.9 | 7.12.69 | 7.6 | 2.50.44 | 2.5 | ||
| Average | 4.01.72 | 4.4 | 10.02.62 | 10.3 | 2.00.46 | 2.0 | ||
| P4 | F1–F2 | #1 | 1.91.59 | 2.5 | 4.02.51 | 4.7 | 0.70.39 | 0.8 |
| #2 | 0.50.40 | 0.7 | 8.03.48 | 8.8 | 0.20.14 | 0.2 | ||
| #3 | 0.50.39 | 0.7 | 5.52.73 | 6.2 | 0.50.32 | 0.6 | ||
| #4 | 1.60.56 | 1.7 | 2.91.28 | 3.2 | 0.90.24 | 0.9 | ||
| Average | 1.10.74 | 1.4 | 5.12.5 | 5.7 | 0.60.27 | 0.6 | ||
| P4 | F1–F3 | #1 | 4.81.97 | 5.2 | 15.02.52 | 15.2 | 0.40.23 | 0.4 |
| #2 | 0.90.51 | 1.0 | 9.33.28 | 9.9 | 1.90.26 | 2.0 | ||
| #3 | 1.20.85 | 1.5 | 8.63.59 | 9.4 | 2.00.32 | 2.0 | ||
| #4 | 1.50.89 | 1.8 | 3.81.66 | 4.1 | 0.40.19 | 0.4 | ||
| Average | 2.11.06 | 2.4 | 9.22.76 | 9.7 | 1.20.25 | 1.2 | ||
| P4 | F2–F3 | #1 | 5.51.55 | 5.7 | 11.02.47 | 11.3 | 0.40.40 | 0.6 |
| #2 | 0.50.48 | 0.7 | 3.91.54 | 4.2 | 1.90.47 | 2.0 | ||
| #3 | 0.90.54 | 1.0 | 2.82.48 | 3.7 | 1.60.48 | 1.6 | ||
| #4 | 0.90.60 | 1.1 | 0.80.43 | 0.9 | 0.50.32 | 0.6 | ||
| Average | 2.00.79 | 2.1 | 4.61.73 | 5.0 | 1.10.42 | 1.2 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salchow-Hömmen, C.; Callies, L.; Laidig, D.; Valtin, M.; Schauer, T.; Seel, T. A Tangible Solution for Hand Motion Tracking in Clinical Applications. Sensors 2019, 19, 208. https://doi.org/10.3390/s19010208
Salchow-Hömmen C, Callies L, Laidig D, Valtin M, Schauer T, Seel T. A Tangible Solution for Hand Motion Tracking in Clinical Applications. Sensors. 2019; 19(1):208. https://doi.org/10.3390/s19010208
Chicago/Turabian StyleSalchow-Hömmen, Christina, Leonie Callies, Daniel Laidig, Markus Valtin, Thomas Schauer, and Thomas Seel. 2019. "A Tangible Solution for Hand Motion Tracking in Clinical Applications" Sensors 19, no. 1: 208. https://doi.org/10.3390/s19010208
APA StyleSalchow-Hömmen, C., Callies, L., Laidig, D., Valtin, M., Schauer, T., & Seel, T. (2019). A Tangible Solution for Hand Motion Tracking in Clinical Applications. Sensors, 19(1), 208. https://doi.org/10.3390/s19010208





