A Multiscale Denoising Framework Using Detection Theory with Application to Images from CMOS/CCD Sensors
Abstract
1. Introduction
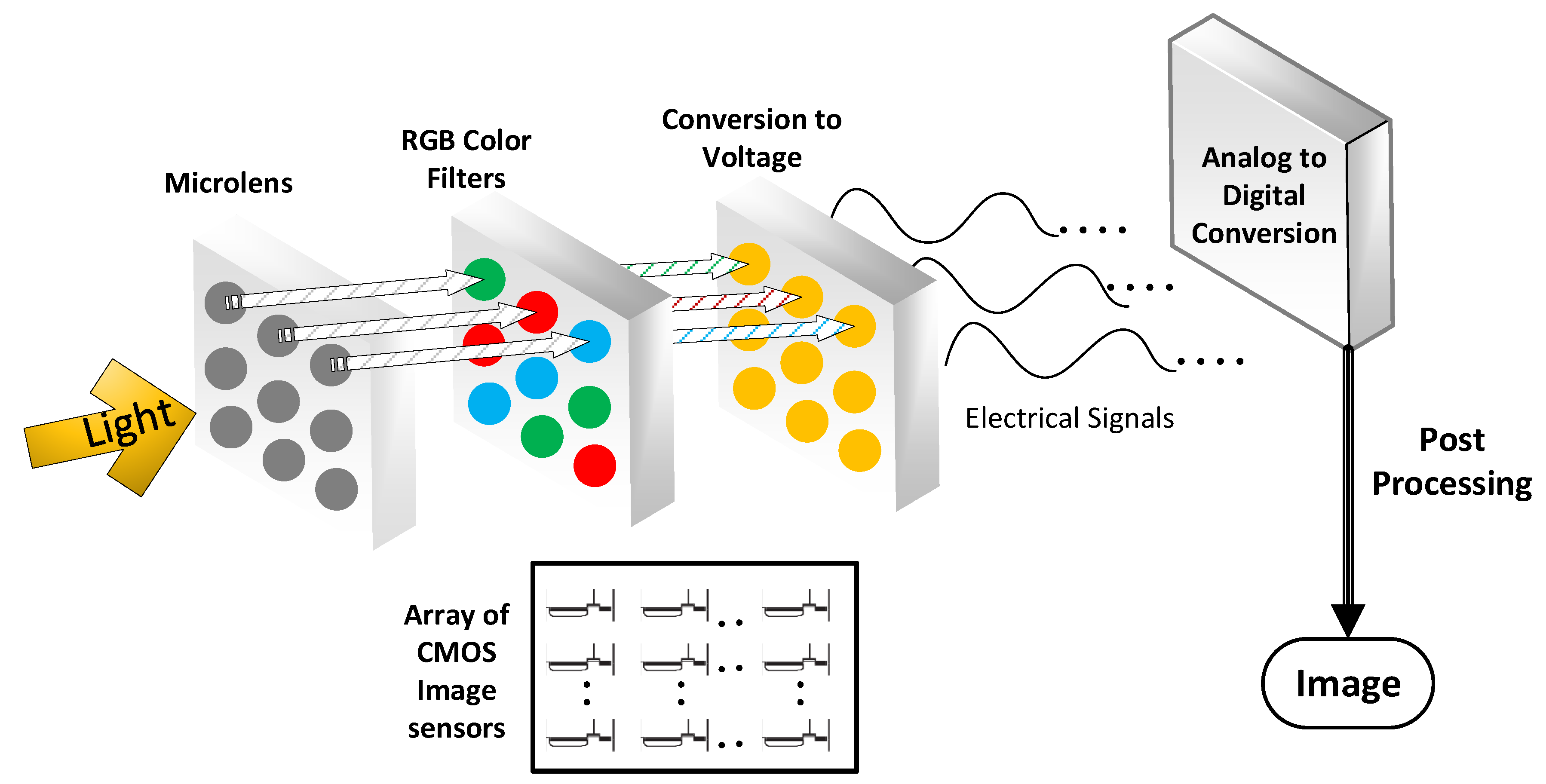
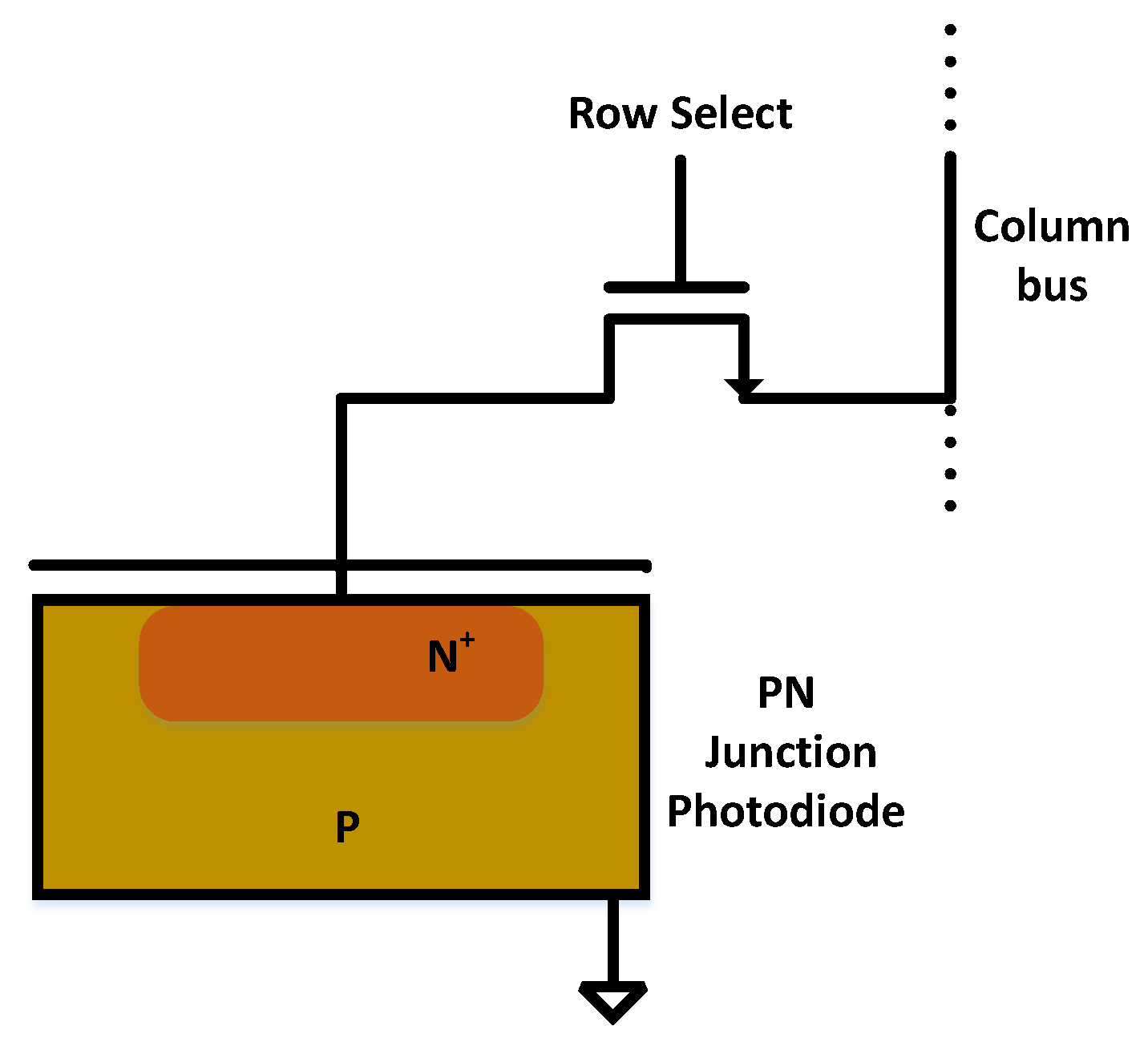
2. CMOS Imaging and Sources of Noise
3. Statement of Problem
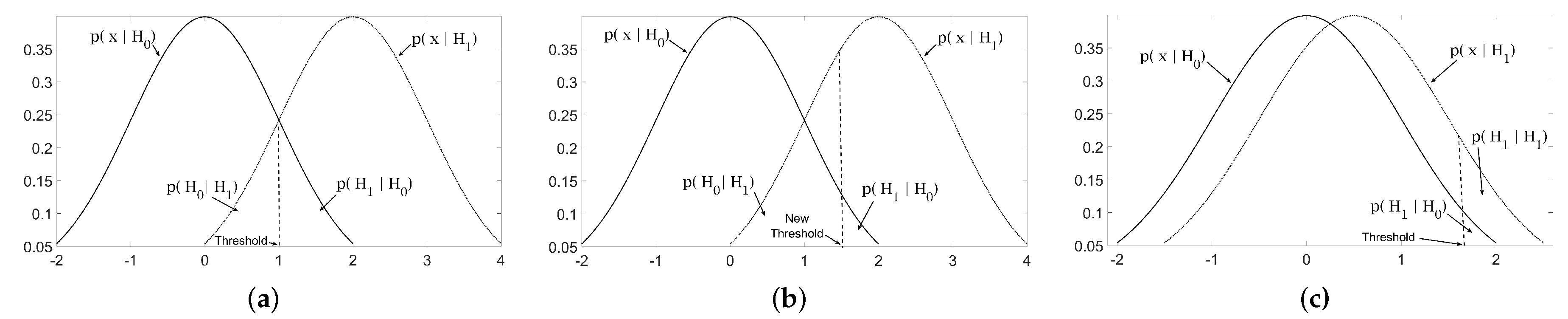
4. Preliminaries: Introduction to Hypothesis Testing in Detection Theory
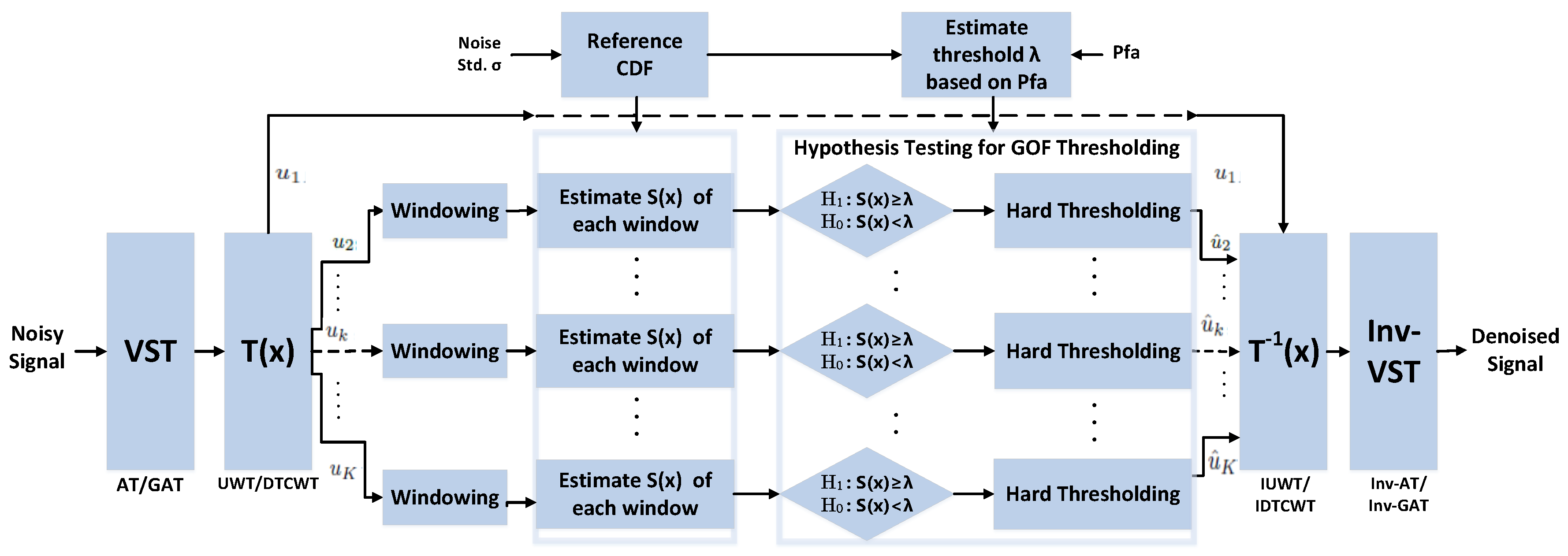
5. Proposed Denoising Framework Using Detection Theory
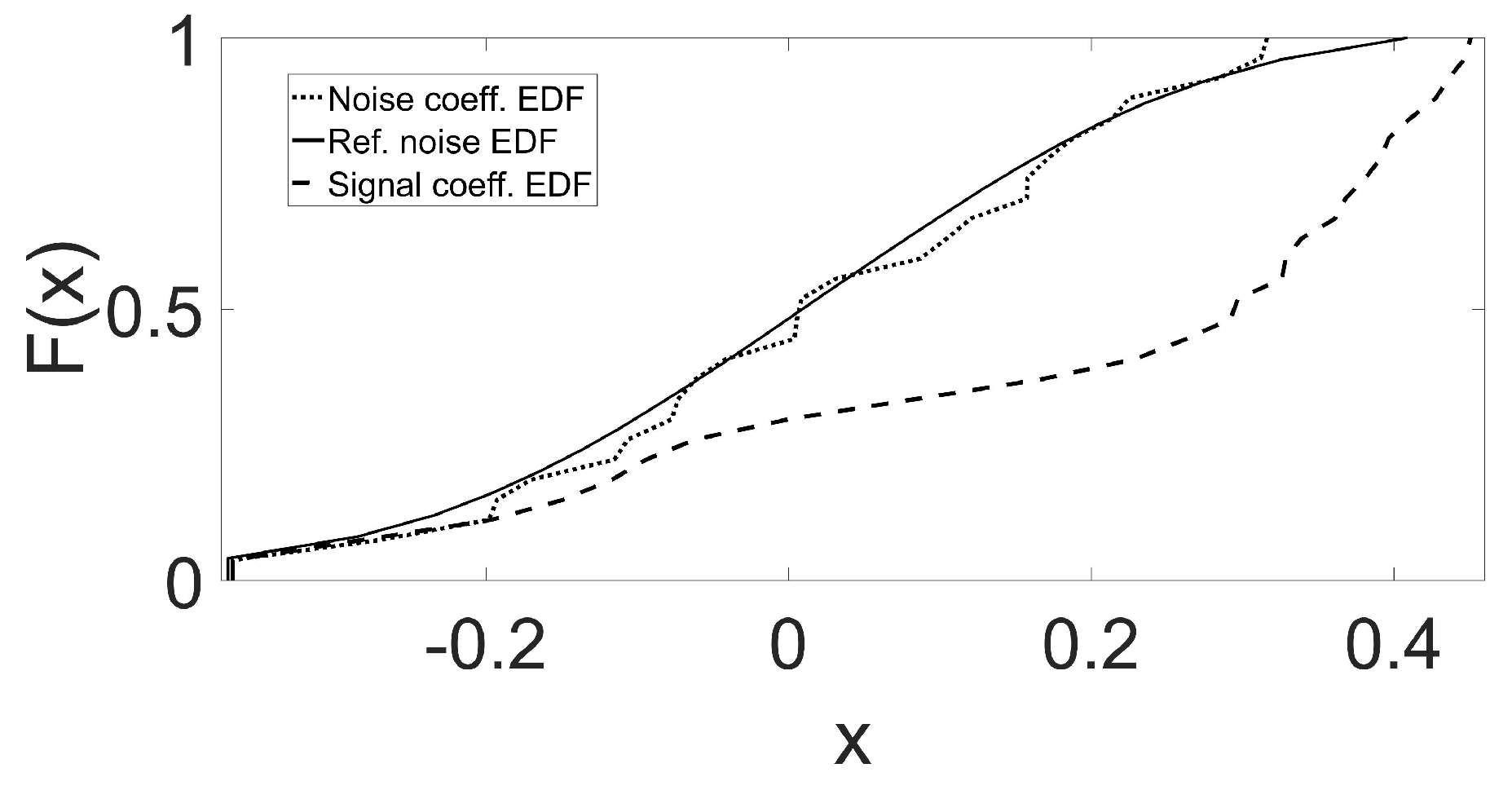
- To ensure the preservation of spatio-temporal characteristics of multiscale coefficients of noisy image, two dimensional (2D) windows of size are considered around the coefficient for local hypothesis testing.
- Two dimensional EDFs are not unique and are computationally expensive [49], therefore, their use for GoF testing on 2D data is not suitable. Consequently, in our work, we list the coefficients in the windows as 1D vectors followed by the computation of their unique (1D) EDF. Note that listing of 2D segments as 1D vectors is a common practice in image denoising methods whereby multivariate statistical distributions are used to model multiscale dependencies [50].
5.1. Variance Stability Transform (VST)
5.2. Multiscale Local Hypothesis Testing Based on EDF
- must decompose a signal across multiple scales.
- Across each scale, signal and noise must be distributed among separate coefficients/values.
5.3. Estimation of Threshold
5.4. Multiscale GoF Statistics Estimation
5.5. Multiscale Thresholding Based on Hypothesis Testing
5.6. Inverse VST
6. Experimental Results
6.1. Poisson Denoising
6.2. Poisson–Gaussian denoising
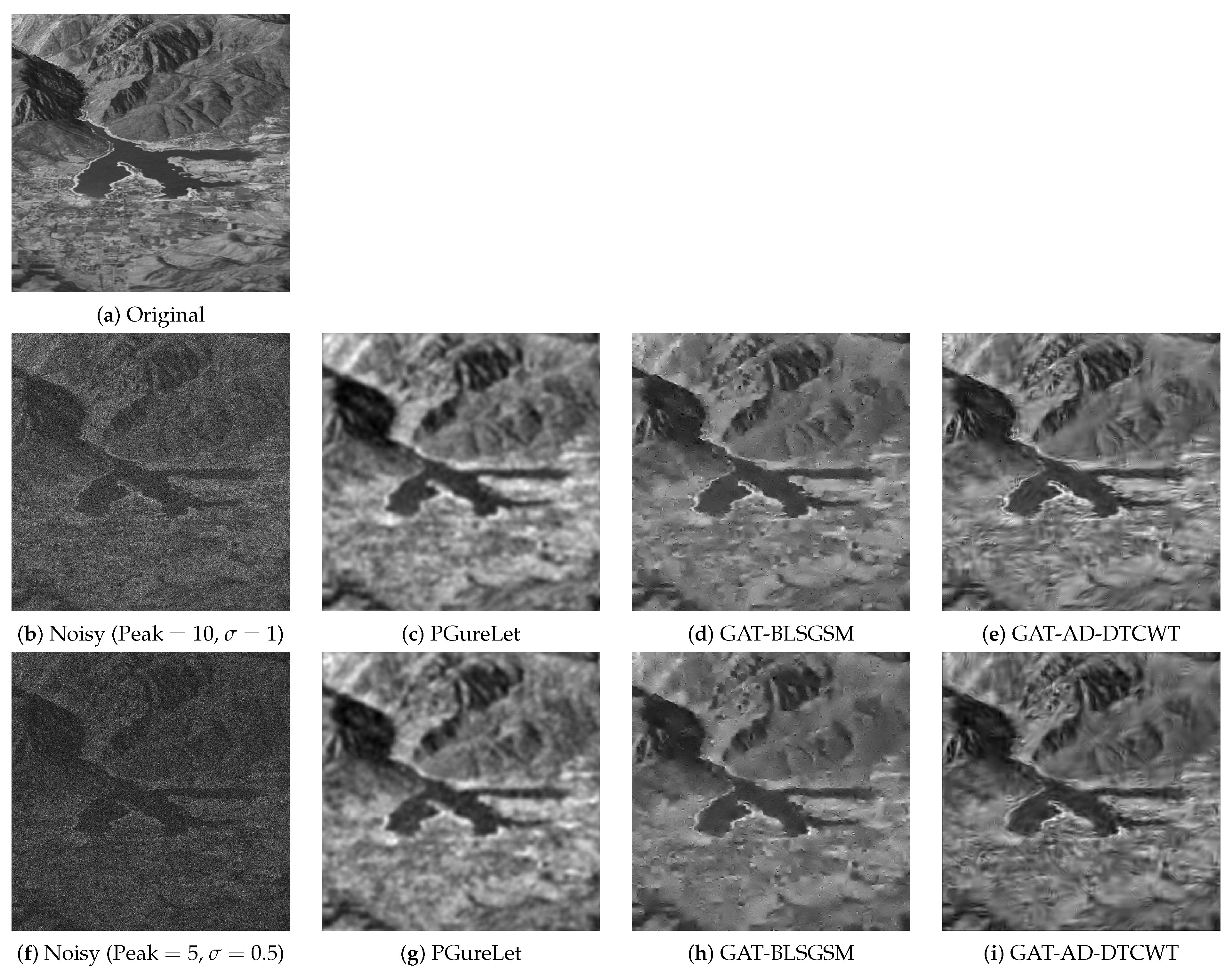
6.3. A Denoising Example of an Image Obtained from CMOS Sensor
7. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kawai, N.; Kawahito, S. Noise analysis of high-gain, low-noise column readout circuits for CMOS image sensors. IEEE Trans. Electron Devices 2004, 51, 185–194. [Google Scholar] [CrossRef]
- Cho, M.; Javidi, B. Three-dimensional photon counting imaging with axially distributed sensing. Sensors 2016, 16, 1184. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, K.H. Noise Sources in Bulk CMOS. Unpublished Paper. 2002. Available online: www.mit.edu/~klund/papers/UNP_noise.pdf (accessed on 8 December 2018).
- Foi, A.; Trimeche, M.; Katkovnik, V.; Egiazarian, K. Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data. IEEE Trans. Image Process. 2008, 17, 1737–1754. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Maik, V.; Jang, J.; Shin, J.; Paik, J. Noise-adaptive spatio-temporal filter for real-time noise removal in low light level images. IEEE Trans. Consum. Electron. 2005, 51, 648–653. [Google Scholar]
- Kolaczyk, E.D. Nonparametric estimation of intensity maps using Haar wavelets and Poisson noise characteristics. Astrophys. J. 2000, 534, 490–505. [Google Scholar] [CrossRef]
- Zhang, Y.; Guangyi, W.; Xu, J. Parameter estimation of signal-dependent random noise in CMOS/CCD image sensor based on numerical characteristic of mixed Poisson noise samples. Sensors 2018, 18, 2276. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Lee, M.S.; Kang, M.G. Poisson–Gaussian Noise Analysis and Estimation for Low-Dose X-ray Images in the NSCT Domain. Sensors 2018, 18, 1019. [Google Scholar]
- Zhang, J.; Hirakawa, K. Improved denoising via Poisson mixture modeling of image sensor noise. IEEE Trans. Image Process. 2017, 26, 1565–1578. [Google Scholar] [CrossRef]
- Li, D.; Sun, C.; Yang, J.; Liu, H.; Peng, J.; Zhang, L. Robust multi-frame adaptive optics image restoration algorithm using maximum likelihood estimation with poisson statistics. Sensors 2017, 17, 785. [Google Scholar] [CrossRef]
- Gao, Q.; Eck, S.; Matthias, J.; Chung, I.; Engelhardt, J.; Rippe, K.; Rohr, K. Bayesian joint super-resolution, deconvolution, and denoising of images with Poisson–Gaussian noise. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; pp. 938–942. [Google Scholar]
- Niknejad, M.; Figueiredo, M.A. Poisson Image Denoising Using Best Linear Prediction: A Post-Processing Framework. arXiv, 2018; arXiv:1803.00389. [Google Scholar]
- Donoho, D.L.; Johnstone, I.M. Adapting to unknown smoothness via wavelet shrinkage. J. Am. Stat. Assoc. 1995, 90, 1200–1224. [Google Scholar] [CrossRef]
- Luisier, F.; Vonesch, C.; Blu, T.; Unser, M. Fast interscale wavelet denoising of Poisson-corrupted images. Signal Process. 2010, 90, 415–427. [Google Scholar] [CrossRef]
- Luisier, F.; Blu, T.; Unser, M. Image denoising in mixed Poisson–Gaussian noise. IEEE Trans. Image Process. 2011, 20, 696–708. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Luisier, F.; Blu, T. PURE-LET image deconvolution. IEEE Trans. Image Process. 2018, 27, 92–105. [Google Scholar] [CrossRef] [PubMed]
- Deledalle, C.A.; Tupin, F.; Denis, L. Poisson NL means: Unsupervised non local means for Poisson noise. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Hong Kong, China, 26–29 September 2010; pp. 801–804. [Google Scholar]
- Salmon, J.; Harmany, Z.; Deledalle, C.A. Willett, R. Poisson noise reduction with non-local PCA. J. Math. Imaging Vis. 2014, 48, 279–294. [Google Scholar] [CrossRef]
- Donoho, D.L. Nonlinear wavelet methods for recovery of signals, densities and spectra from indirect and noisy data. In Proceedings of Symposia in Applied Mathematics: Different Perspectives on Wavelets; American Mathematical Society: Providence, RI, USA, 1993; Volume 47, pp. 173–205. [Google Scholar]
- Anscombe, F.J. The transformation of Poisson, binomial and negative- binomial data. Biometrika 1948, 35, 246–254. [Google Scholar] [CrossRef]
- Makitalo, M.; Foi, A. On the inversion of the Anscombe transformation in low-count Poisson image denoising. In Proceedings of the IEEE International Workshop on Local and Non-Local Approximation in Image Processing, Tuusula, Finland, 19–21 August 2009; pp. 26–32. [Google Scholar]
- Makitalo, M.; Foi, A. Optimal inversion of the Anscombe transformation in low-count Poisson image denoising. IEEE Trans. Image Process. 2011, 20, 99–109. [Google Scholar] [CrossRef] [PubMed]
- Azzari, L.; Foi, A. Variance Stabilization for Noisy+ Estimate Combination in Iterative Poisson Denoising. IEEE Signal Process. Lett. 2016, 23, 1086–1090. [Google Scholar] [CrossRef]
- Makitalo, M.; Foi, A. Optimal inversion of the generalized Anscombe transformation for Poisson–Gaussian noise. IEEE Trans. Image Process. 2013, 22, 91–103. [Google Scholar] [CrossRef]
- Starck, J.L.; Murtagh, F.; Bijaoui, A. Image Processing and Data Analysis; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Portilla, J.; Strela, V.; Wainwright, M.J.; Simoncelli, E.P. Image denoising using scale mixtures of Gaussians in the wavelet domain. IEEE Trans. Image Process. 2003, 12, 1338–1351. [Google Scholar] [CrossRef]
- Zhang, B.; Fadili, M.J.; Starck, J.L.; Olivo-Marin, J.C. Multiscale variance-stabilizing transform for mixed-Poisson–Gaussian processes and its applications in bioimaging. In Proceedings of the IEEE International Conference on Image Processing (ICIP), San Antonio, TX, USA, 16 September–19 October 2007; Volume 6, pp. VI–233. [Google Scholar]
- Zhang, B.; Fadili, J.M.; Starck, J.L. Wavelets, ridgelets, and curvelets for Poisson noise removal. IEEE Trans. Image Process. 2008, 17, 1093–1108. [Google Scholar] [CrossRef]
- Zhang, B.; Fadili, J.M.; Starck, J.L.; Digel, S.W. Fast Poisson noise removal by biorthogonal Haar domain hypothesis testing. Stat. Methodol. 2008, 5, 387–396. [Google Scholar] [CrossRef]
- Charles, C.; Rasson, J.P. Wavelet denoising of Poisson-distributed data and applications. Comput. Stat. Data Anal. 2003, 43, 139–148. [Google Scholar] [CrossRef]
- ur Rehman, N.; Abbas, S.Z.; Asif, A.; Javed, A.; Naveed, K.; Mandic, D.P. Translation invariant multi-scale signal denoising based on goodness-of-fit tests. Signal Process. 2017, 131, 220–234. [Google Scholar] [CrossRef]
- Naveed, K.; Shaukat, B.; ur Rehman, N. Dual tree complex wavelet transform-based signal denoising method exploiting neighbourhood dependencies and goodness-of-fit test. R. Soc. Open Sci. 2017, 5, 180436. [Google Scholar] [CrossRef]
- Naveed, K.; Shaukat, B.; ur Rehman, N. Signal denoising based on dual tree complex wavelet transform and goodness of fit test. In Proceedings of the IEEE International Conference on Digital Signal Processing (DSP), London, UK, 23–25 August 2017; pp. 1–5. [Google Scholar]
- ur Rehman, N.; Naveed, K.; Ehsan, S.; McDonald-Maier, K. Multi-scale image denoising based on goodness-of-fit tests. In Proceedings of the European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 29 August–2 September 2016; pp. 1548–1552. [Google Scholar]
- Naveed, K.; Shaukat, B.; Ehsan, S.; McDonald-Maier, K.; ur Rehman, N. Multiscale image denoising using goodness-of-fit test based on EDF statistics. PLOS ONE 2018. submitted. [Google Scholar]
- Nakamura, J. Image Sensors and Signal Processing for Digital Still Cameras; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Chiabrando, F.; Chiabrando, R.; Piatti, D.; Rinaudo, F. Sensors for 3D imaging: Metric evaluation and calibration of a CCD/CMOS time-of-flight camera. Sensors 2009, 9, 10080–10096. [Google Scholar] [CrossRef] [PubMed]
- Gamal, A.E.; Eltoukhy, H. CMOS image sensors. IEEE Circuits Devices Mag. 2005, 21, 6–20. [Google Scholar] [CrossRef]
- Rizzolo, S.; Goiffon, V.; Estribeau, M.; Paillet, P.; Marcandella, C.; Durnez, C.; Magnan, P. Total-Ionizing Dose Effects on Charge Transfer Efficiency and Image Lag in Pinned Photodiode CMOS Image Sensors. IEEE Trans. Nucl. Sci. 2018, 65, 84–91. [Google Scholar] [CrossRef]
- Yeh, S.F.; Chou, K.Y.; Tu, H.Y.; Chao, C.Y.P.; Hsueh, F.L. A 0.66 e rms-Temporal-Readout-Noise 3-D-Stacked CMOS Image Sensor With Conditional Correlated Multiple Sampling Technique. IEEE J. Solid-State Circuits 2018, 53, 527–537. [Google Scholar] [CrossRef]
- Theuwissen, A.J. CMOS image sensors: State-of-the-art. Solid-State Electron. 2008, 52, 1401–1406. [Google Scholar] [CrossRef]
- Gow, R.D.; Renshaw, D.; Findlater, K.; Grant, L.; McLeod, S.J.; Hart, J.; Nicol, R.L. A comprehensive tool for modeling CMOS image-sensor-noise performance. IEEE Trans. Electron Devices 2007, 54, 1321–1329. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Detection Thery; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1993; Volume II. [Google Scholar]
- Reich, E.; Swerling, P. Detection of a sine wave in Gaussian noise. J. Appl. Phys 1953, 24, 289–296. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. A Test of Goodness-of-Fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Cramr, H. On the composition of elementary errors. Scand. Actuar. J. 1928, 11, 141–180. [Google Scholar] [CrossRef]
- Lei, S.; Wang, H.; Shen, L. Spectrum sensing based on goodness-of-fit tests. In Proceedings of the IEEE International Conference on Electronics, Communications and Control, Ningbo, China, 9–11 September 2011; pp. 485–489. [Google Scholar]
- Wang, H.; Yang, E.; Zhao, Z.; Zhang, W. Spectrum Sensing in Cognitive Radio Using goodness-of-fit Testing. IEEE Trans. Wirel. Commun. 2009, 8, 5427–5430. [Google Scholar] [CrossRef]
- Peacock, J.A. Two-dimensional goodness-of-fit testing in astronomy. Mon. Not. R. Astron. Soc. 1983, 202, 615–627. [Google Scholar] [CrossRef]
- Cho, D.; Bui, T.D. Multivariate statistical modeling for image denoising using wavelet transforms. Signal Process. Image Commun. 2005, 20, 77–89. [Google Scholar] [CrossRef]
- Selesnick, I.W. The double density DWT. In Wavelets in Signal and Image Analysis; Springer: Dordrecht, The Netherlands, 2001; pp. 39–66. [Google Scholar]
- Selesnick, I.W.; Ivan, W.; Baraniuk, R.G.; Kingsbury, N.C. The dual-tree complex wavelet transform. IEEE Signal Process. Mag. 2005, 22, 123–151. [Google Scholar] [CrossRef]
- Starck, J.L.; Fadili, J.; Murtagh, F. The undecimated wavelet decomposition and its reconstruction. IEEE Trans. Image Process. 2007, 16, 297–309. [Google Scholar] [CrossRef]
- Singh, R.; Mohanty, S.R.; Kishor, N.; Thakur, A. Real-Time Implementation of Signal Processing Techniques for Disturbances Detection. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Kumar, A.; Rastogi, P.; Srivastava, P. Design and FPGA Implementation of DWT, Image Text Extraction Technique. Procedia Comput. Sci. 2015, 57, 1015–1025. [Google Scholar] [CrossRef]
- Zhang, J.; Chow, P.; Liu, H. FPGA implementation of low-power and high-PSNR DCT/IDCT architecture based on adaptive recoding CORDIC. In Proceedings of the IEEE International Conference on Field Programmable Technology (FPT), Queenstown, New Zealand, 7–9 December 2015; pp. 128–135. [Google Scholar]
- Siddiqui, M.F.; Reza, A.W.; Kanesan, J.; Ramiah, H. Investigation of a novel common subexpression elimination method for low power and area efficient DCT architecture. Sci. World J. 2014, 2014, 620868. [Google Scholar] [CrossRef] [PubMed]
- Anaya, J.; Barbu, A. RENOIR–A dataset for real low-light image noise reduction. J. Vis. Commun. Image Represent. 2018, 51, 144–154. [Google Scholar] [CrossRef]





| Peaks | Inp. | MS- | NL- | Pure- | Pois- | AT-AD | AT-AD | Inp. | MS | NL | Pure- | Pois- | AT-AD | AT-AD |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | VST | PCA | Let | NLM | UWT | DTCWT | PSNR | VST | PCA | Let | NLM | UWT | DTCWT | |
| Lena | Plane | |||||||||||||
| 1 | 2.93 | 17.19 | 20.67 | 22.08 | 19.73 | 21.65 | 22.22 | 1.11 | 14.62 | 19.06 | 20.53 | 17.33 | 19.80 | 20.45 |
| 2 | 5.96 | 17.70 | 20.87 | 23.31 | 21.40 | 23.02 | 23.26 | 4.15 | 14.61 | 19.09 | 21.68 | 19.34 | 21.34 | 21.70 |
| 3 | 7.73 | 17.86 | 20.74 | 23.98 | 22.64 | 23.85 | 23.87 | 5.90 | 14.86 | 19.18 | 22.56 | 20.71 | 22.41 | 22.77 |
| 4 | 8.95 | 18.04 | 20.77 | 24.51 | 23.57 | 24.73 | 24.86 | 7.16 | 15.43 | 19.19 | 23.07 | 21.65 | 23.02 | 23.32 |
| 5 | 9.95 | 18.44 | 20.78 | 24.89 | 24.28 | 25.67 | 25.43 | 8.13 | 15.94 | 19.15 | 23.54 | 22.40 | 23.58 | 23.96 |
| 10 | 12.97 | 20.23 | 20.49 | 26.27 | 26.39 | 26.79 | 27.18 | 11.13 | 18.09 | 19.07 | 24.90 | 24.44 | 25.21 | 25.58 |
| 20 | 15.97 | 22.39 | 20.32 | 27.75 | 27.54 | 28.47 | 28.84 | 14.13 | 20.48 | 18.84 | 26.42 | 25.59 | 26.86 | 27.29 |
| 50 | 19.91 | 25.45 | 17.98 | 29.58 | 30.15 | 30.48 | 30.75 | 18.12 | 23.65 | 18.44 | 28.48 | 28.20 | 29.09 | 29.49 |
| 100 | 22.95 | 27.78 | 19.53 | 31.28 | 32.23 | 32.07 | 32.32 | 21.13 | 26.04 | 18.73 | 30.14 | 30.42 | 30.74 | 31.23 |
| Peppers | Boat | |||||||||||||
| 1 | 2.73 | 16.61 | 18.82 | 21.45 | 19.28 | 20.96 | 21.44 | 2.96 | 16.83 | 20.17 | 21.28 | 19.06 | 20.72 | 21.36 |
| 2 | 5.76 | 17.00 | 18.94 | 22.80 | 21.12 | 22.58 | 22.80 | 5.96 | 17.43 | 20.22 | 22.22 | 20.48 | 21.89 | 22.24 |
| 3 | 7.54 | 17.25 | 18.81 | 23.55 | 22.40 | 23.26 | 23.39 | 7.72 | 17.47 | 20.29 | 22.77 | 21.56 | 22.63 | 22.74 |
| 4 | 8.80 | 17.58 | 18.87 | 24.17 | 23.36 | 24.22 | 24.18 | 8.94 | 17.59 | 20.31 | 23.27 | 22.39 | 23.11 | 23.44 |
| 5 | 9.72 | 17.96 | 18.74 | 24.49 | 24.04 | 24.85 | 24.89 | 9.93 | 17.92 | 20.20 | 23.69 | 22.98 | 23.62 | 23.86 |
| 10 | 12.75 | 19.83 | 18.36 | 25.75 | 26.01 | 26.34 | 26.38 | 12.94 | 19.72 | 20.21 | 24.90 | 24.77 | 24.88 | 25.23 |
| 20 | 15.79 | 22.05 | 18.44 | 27.15 | 27.00 | 27.73 | 27.81 | 15.94 | 21.79 | 20.09 | 26.19 | 25.80 | 26.28 | 26.72 |
| 50 | 19.72 | 24.81 | 16.67 | 29.01 | 29.07 | 29.37 | 29.51 | 19.90 | 24.71 | 19.99 | 28.06 | 28.09 | 28.14 | 28.67 |
| 100 | 22.76 | 26.87 | 16.63 | 30.33 | 30.61 | 30.35 | 30.55 | 22.96 | 26.85 | 19.81 | 29.78 | 30.07 | 29.66 | 30.22 |
| Padma River | Ogden Valley | |||||||||||||
| 1 | 3.27 | 16.71 | 19.63 | 19.91 | 18.66 | 19.48 | 19.58 | 4.01 | 18.12 | 20.81 | 21.78 | 20.13 | 21.54 | 21.68 |
| 2 | 6.26 | 17.53 | 19.77 | 20.66 | 19.90 | 20.44 | 20.70 | 7.05 | 18.75 | 20.83 | 22.66 | 21.18 | 22.54 | 22.42 |
| 3 | 7.97 | 17.53 | 19.77 | 21.15 | 20.75 | 21.07 | 21.17 | 8.82 | 18.88 | 20.79 | 23.09 | 22.01 | 23.16 | 22.97 |
| 4 | 9.29 | 17.50 | 19.80 | 21.58 | 21.43 | 21.47 | 21.61 | 10.06 | 18.92 | 20.90 | 23.60 | 22.64 | 23.61 | 23.44 |
| 5 | 10.25 | 17.75 | 19.81 | 21.86 | 21.80 | 21.74 | 21.90 | 11.01 | 19.18 | 20.87 | 23.91 | 23.10 | 23.96 | 23.81 |
| 10 | 13.29 | 19.11 | 19.82 | 22.91 | 23.11 | 22.73 | 22.97 | 14.02 | 20.42 | 20.90 | 25.04 | 24.50 | 25.06 | 25.15 |
| 20 | 16.30 | 20.87 | 19.71 | 24.06 | 23.81 | 23.79 | 24.10 | 17.00 | 22.40 | 20.82 | 26.26 | 25.33 | 26.28 | 26.58 |
| 50 | 20.24 | 23.42 | 19.44 | 25.92 | 25.35 | 25.13 | 25.54 | 20.99 | 25.12 | 20.75 | 28.10 | 27.43 | 28.07 | 28.63 |
| 100 | 23.29 | 25.43 | 19.61 | 27.56 | 26.78 | 26.21 | 26.73 | 24.01 | 27.34 | 20.60 | 29.70 | 29.66 | 29.62 | 30.28 |
| Peaks | Noise | Inp. | MSVST | GAT-BL | PGure- | GAT-AD | Inp. | MSVST | GAT-BL | PGure- | GAT-AD | Inp. | MSVST | GAT-BL | PGure- | GAT-AD |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| std. | PSNR | MPG | SGSM | Let | DTCWT | PSNR | MPG | SGSM | Let | DTCWT | PSNR | MPG | SGSM | Let | DTCWT | |
| Lena | Plane | Lena | ||||||||||||||
| 1 | 0.1 | 2.87 | 17.06 | 18.63 | 21.98 | 22.09 | 1.07 | 14.28 | 19.98 | 20.10 | 20.63 | 2.69 | 16.47 | 17.27 | 21.45 | 21.30 |
| 2 | 0.2 | 5.79 | 16.70 | 23.10 | 23.12 | 23.30 | 4.03 | 13.90 | 21.69 | 21.18 | 21.71 | 5.63 | 16.23 | 21.16 | 22.59 | 22.82 |
| 3 | 0.3 | 7.48 | 16.41 | 24.57 | 23.65 | 24.00 | 5.71 | 13.97 | 22.43 | 21.69 | 22.64 | 7.30 | 16.04 | 23.26 | 23.12 | 23.53 |
| 4 | 0.4 | 8.63 | 16.64 | 24.96 | 23.97 | 24.64 | 6.92 | 14.66 | 23.17 | 21.95 | 23.23 | 8.48 | 16.48 | 24.21 | 23.39 | 24.25 |
| 5 | 0.5 | 9.53 | 17.17 | 25.16 | 24.13 | 25.08 | 7.48 | 15.36 | 23.54 | 22.11 | 23.68 | 9.37 | 16.98 | 24.91 | 23.56 | 24.86 |
| 10 | 1 | 12.17 | 19.21 | 26.51 | 24.52 | 26.58 | 10.6 | 17.46 | 25.43 | 22.45 | 25.51 | 12.00 | 18.84 | 26.53 | 23.83 | 26.02 |
| Boat | Padma River | Ogden Valley | ||||||||||||||
| 1 | 0.1 | 2.84 | 16.64 | 18.32 | 21.10 | 21.31 | 3.21 | 16.80 | 18.86 | 19.90 | 19.71 | 3.90 | 17.96 | 19.16 | 21.84 | 21.62 |
| 2 | 0.2 | 5.78 | 16.45 | 21.22 | 21.93 | 22.27 | 6.09 | 16.36 | 20.57 | 20.44 | 20.69 | 6.79 | 17.82 | 22.41 | 22.54 | 22.56 |
| 3 | 0.3 | 7.47 | 16.14 | 22.58 | 22.27 | 22.86 | 7.79 | 16.00 | 21.28 | 20.72 | 20.97 | 8.48 | 17.29 | 23.06 | 23.01 | 22.86 |
| 4 | 0.4 | 8.63 | 16.38 | 23.24 | 22.46 | 23.29 | 8.93 | 16.20 | 21.27 | 20.84 | 21.39 | 9.62 | 17.26 | 23.21 | 23.13 | 23.23 |
| 5 | 0.5 | 9.52 | 16.91 | 23.61 | 22.60 | 23.69 | 9.83 | 16.64 | 21.85 | 20.91 | 21.93 | 10.48 | 17.61 | 23.65 | 23.35 | 23.54 |
| 10 | 1 | 12.15 | 18.69 | 25.12 | 22.86 | 24.88 | 12.43 | 18.14 | 23.02 | 21.04 | 22.59 | 13.04 | 19.31 | 24.52 | 23.62 | 24.64 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naveed, K.; Ehsan, S.; McDonald-Maier, K.D.; Ur Rehman, N. A Multiscale Denoising Framework Using Detection Theory with Application to Images from CMOS/CCD Sensors. Sensors 2019, 19, 206. https://doi.org/10.3390/s19010206
Naveed K, Ehsan S, McDonald-Maier KD, Ur Rehman N. A Multiscale Denoising Framework Using Detection Theory with Application to Images from CMOS/CCD Sensors. Sensors. 2019; 19(1):206. https://doi.org/10.3390/s19010206
Chicago/Turabian StyleNaveed, Khuram, Shoaib Ehsan, Klaus D. McDonald-Maier, and Naveed Ur Rehman. 2019. "A Multiscale Denoising Framework Using Detection Theory with Application to Images from CMOS/CCD Sensors" Sensors 19, no. 1: 206. https://doi.org/10.3390/s19010206
APA StyleNaveed, K., Ehsan, S., McDonald-Maier, K. D., & Ur Rehman, N. (2019). A Multiscale Denoising Framework Using Detection Theory with Application to Images from CMOS/CCD Sensors. Sensors, 19(1), 206. https://doi.org/10.3390/s19010206







