Wireless Sensor Networks Intrusion Detection Based on SMOTE and the Random Forest Algorithm
Abstract
1. Introduction
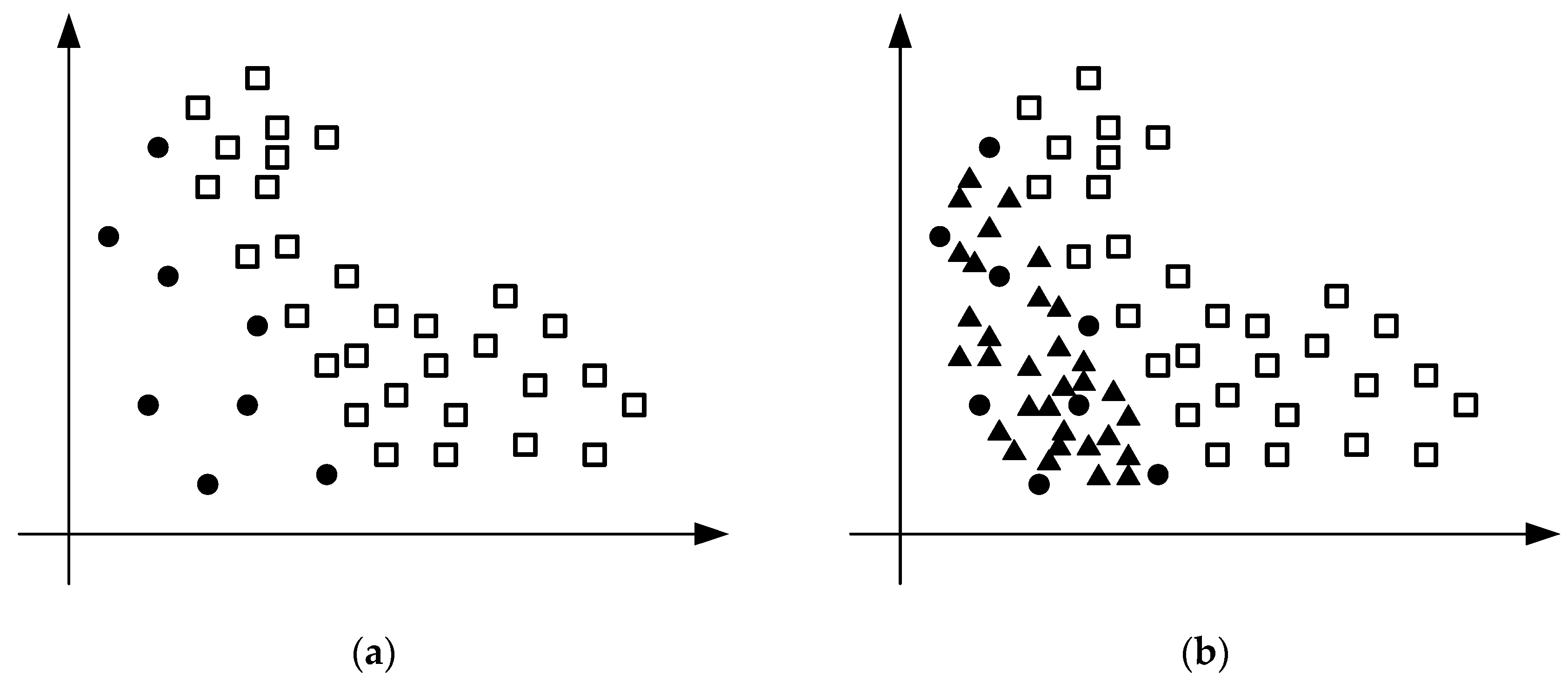
2. Principle of SMOTE
3. Random Forest Algorithm
- The method of random repeated sampling is applied to randomly extract K samples from the original training set as self- service sample set, and then K classification regression trees are generated.
- Assuming that the original training set has n features, m features are randomly selected at each node of each tree . By calculating the amount of information contained in each feature, a feature with the most classification ability is selected among the m features for node splitting.
- Every tree grows to its maximum without any cutting.
- The generated trees are composed of random forest, and the new data is classified by random forest. The classification results are determined by the number of votes of the tree classifiers.
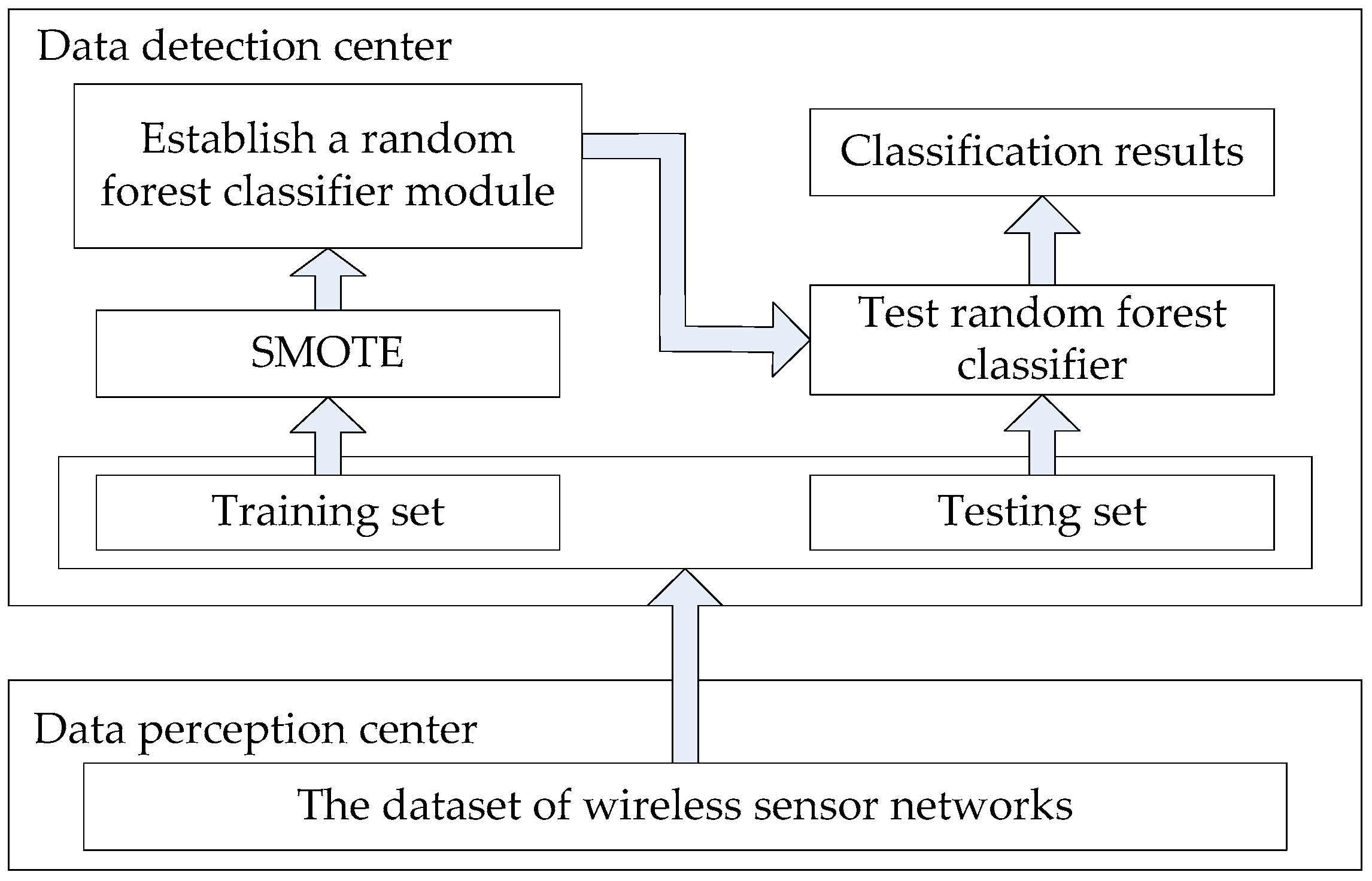
4. Intrusion Detection Technology Combined with SMOTE and Random Forest
- Suppose that the sample space of attack data of wireless sensor networks is P and the sample space of normal data is Q. P consists of n samples of attack data, and represents the features of the th attack data. Thus, P can be represented as . For each sample, there are f features, recorded as .
- For each sample in the attack data set, the Euclidean distance is used to calculate the distance from it to all other samples in P, and its K nearest neighbors are obtained.
- The sampling magnification N is set according to the ratio of the number of attack data samples P to the number of normal data samples Q. N neighbors are randomly selected from the K nearest neighbors of each attack data sample , recorded as , where .
- Each randomly-selected neighbor sample B constructs a new attack data sample with attack data sample D according to Equation (12). The represents a random number of the interval [0,1]:
- Combine the constructed new samples with the normal data samples Q to generate a new data sample space R.
- Assuming represents the th data sample, then . For each sample, there are f features, which are recorded as . Select the decision tree and use it as the base classifier.
- A new training set is generated by sampling from the data sample space R using the method of Bootstrap, and a decision tree is constructed by .
- The k features are randomly extracted from the nodes of each decision tree. By calculating the amount of information contained in each feature, a feature with the most classification ability is selected among the k features to split the nodes until the tree grows to the maximum.
- Repeat steps 7 and 8 for m times to train m decision trees.
- The generated decision trees are composed of random forest, and the new data is classified by the random forest. The classification results are determined by the number of votes of the tree classifiers.
5. Experimental Results and Analysis
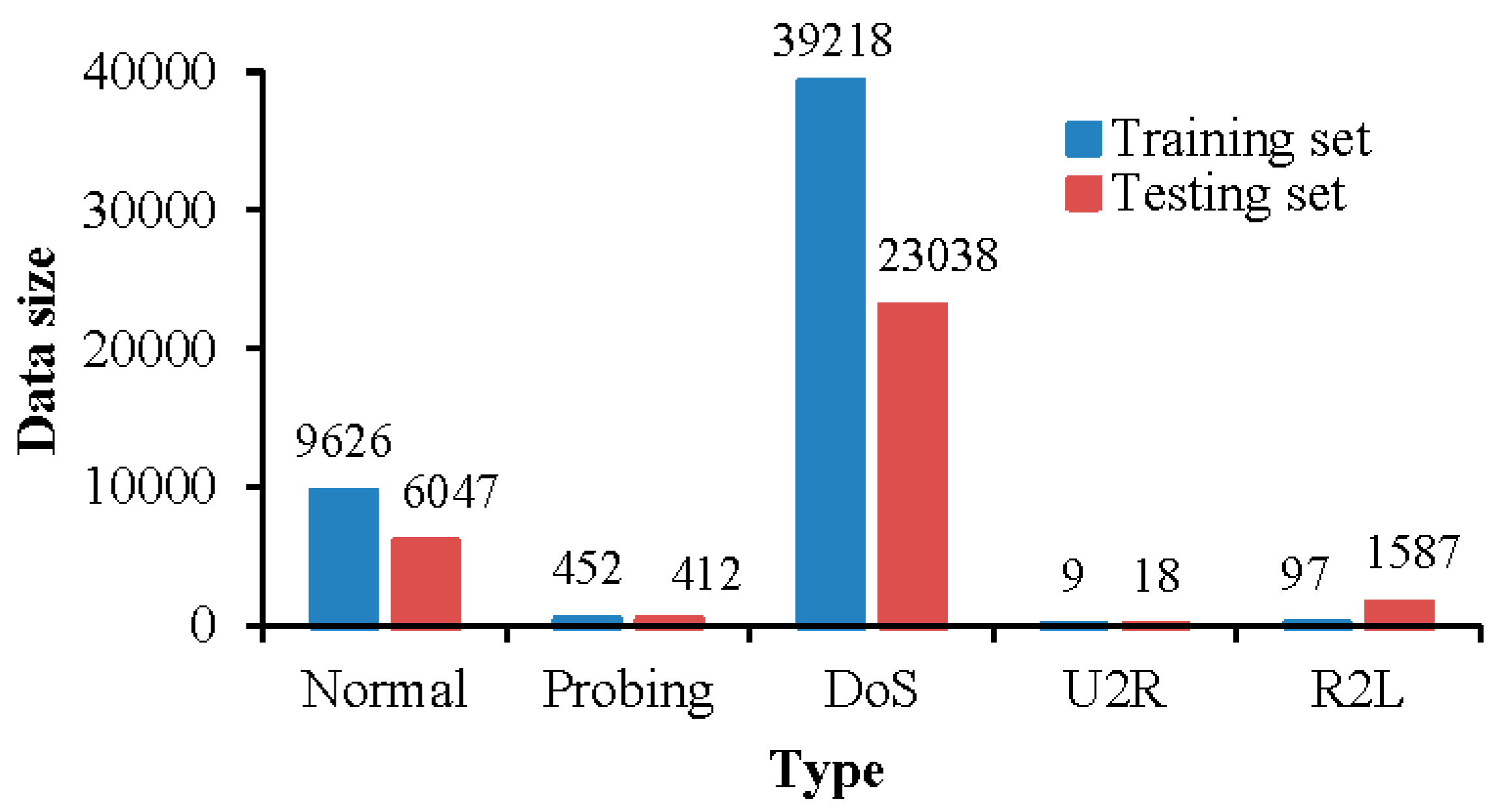
5.1. Dataset and Evaluation Indicators
5.2. Results and Comparison
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Z.; Glaser, S.; Bales, R.; Conklin, M.; Rice, R.; Marks, D. Technical report: The design and evaluation of a basin-scale wireless sensor network for mountain hydrology. Water Resour. Res. 2017, 53, 4487–4498. [Google Scholar] [CrossRef]
- Victor, G.F.; Carles, G.; Helena, R.P. A Comparative Study of Anomaly Detection Techniques for Smart City Wireless Sensor Networks. Sensors 2016, 16, 868–887. [Google Scholar]
- Lu, T.; Liu, G.; Chang, S. Energy-efficient data sensing and routing in unreliable energy-harvesting wireless sensor network. Wirel. Netw. 2018, 24, 611–625. [Google Scholar] [CrossRef]
- Fang, X.; Nan, L.; Jiang, Z.; Chen, L. Fingerprint localisation algorithm for noisy wireless sensor network based on multi-objective evolutionary model. IET Commun. 2017, 11, 1297–1304. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, S.; Fapojuwo, A.O. A Protocol Layer Trust-Based Intrusion Detection Scheme for Wireless Sensor Networks. Sensors 2017, 17, 1227. [Google Scholar] [CrossRef] [PubMed]
- Ferng, H.W.; Khoa, N.M. On security of wireless sensor networks: A data authentication protocol using digital signature. Wirel. Netw. 2017, 23, 1113–1131. [Google Scholar] [CrossRef]
- Ismail, B.; In-Ho, R.; Ravi, S. An Intrusion Detection System Based on Multi-Level Clustering for Hierarchical Wireless Sensor Networks. Sensors 2015, 15, 28960–28978. [Google Scholar]
- Li, M.; Lou, W.; Ren, K. Data security and privacy in wireless body area networks. IEEE Wirel. Commun. 2016, 17, 51–58. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, Y.; Zhang, K.; Shen, X. Adaptive and Channel-Aware Detection of Selective Forwarding Attacks in Wireless Sensor Networks. IEEE Trans. Wirel. Commun. 2016, 15, 3718–3731. [Google Scholar] [CrossRef]
- Wang, J.; Wang, F.; Cao, Z.; Lin, F.; Wu, J. Sink location privacy protection under direction attack in wireless sensor networks. Wirel. Netw. 2017, 23, 579–591. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, R. Study of Immune-Based Intrusion Detection Technology in Wireless Sensor Networks. Arab. J. Sci. Eng. 2017, 42, 3159–3174. [Google Scholar] [CrossRef]
- Yan, J.; Li, X.; Luo, X.; Guan, X. Virtual-Lattice Based Intrusion Detection Algorithm over Actuator-Assisted Underwater Wireless Sensor Networks. Sensors 2017, 17, 1168. [Google Scholar] [CrossRef] [PubMed]
- Kalnoor, G.; Agarkhed, J. Detection of Intruder using KMP Pattern Matching Technique in Wireless Sensor Networks. Proc. Comput. Sci. 2018, 125, 187–193. [Google Scholar] [CrossRef]
- Osanaiye, O.A.; Alfa, A.S.; Hancke, G.P. Denial of Service Defence for Resource Availability in Wireless Sensor Networks. IEEE Access 2018, 6, 6975–7004. [Google Scholar] [CrossRef]
- Ma, T.; Wang, F.; Cheng, J.; Yu, Y.; Chen, X. A Hybrid Spectral Clustering and Deep Neural Network Ensemble Algorithm for Intrusion Detection in Sensor Networks. Sensors 2016, 16, 1701. [Google Scholar] [CrossRef] [PubMed]
- Wazid, M.; Das, A. An Efficient Hybrid Anomaly Detection Scheme Using K-Means Clustering for Wireless Sensor Networks. Wirel. Pers. Commun. 2016, 90, 1971–2000. [Google Scholar] [CrossRef]
- Belavagi, M.C.; Muniyal, B. Performance Evaluation of Supervised Machine Learning Algorithms for Intrusion Detection. Proc. Comput. Sci. 2016, 89, 117–123. [Google Scholar] [CrossRef]
- Lu, N.; Sun, Y.; Liu, H.; Li, S. Intrusion Detection System Based on Evolving Rules for Wireless Sensor Networks. J. Sens. 2018, 2018, 1–8. [Google Scholar] [CrossRef]
- Singh, R.; Singh, J.; Singh, R. Fuzzy Based Advanced Hybrid Intrusion Detection System to Detect Malicious Nodes in Wireless Sensor Networks. Wirel. Commun. Mob. Comput. 2017, 2017, 1–14. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, Y.; Liang, G.; Zhou, Z. An Intrusion Detection Model for Wireless Sensor Networks with an Improved V-Detector Algorithm. IEEE Sens. J. 2018, 18, 1971–1984. [Google Scholar] [CrossRef]
- Tajbakhsh, A.; Rahmati, M.; Mirzaei, A. Intrusion detection using fuzzy association rules. Appl. Soft. Comput. 2009, 9, 462–469. [Google Scholar] [CrossRef]
- Xie, M.; Hu, J.; Guo, S.; Zomaya, A.Y. Distributed Segment-Based Anomaly Detection with Kullback–Leibler Divergence in Wireless Sensor Networks. IEEE Trans. Inf. Forensic Secur. 2017, 12, 101–110. [Google Scholar] [CrossRef]
- Xie, M.; Hu, J.; Guo, S. Segment-based anomaly detection with approximated sample covariance matrix in wireless sensor networks. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 574–583. [Google Scholar] [CrossRef]
- Haider, W.; Hu, J.; Slay, J.; Turnbull, B.P.; Xie, Y. Generating realistic intrusion detection system dataset based on fuzzy qualitative modeling. J. Netw. Comput. Appl. 2017, 87, 185–192. [Google Scholar] [CrossRef]
- Ye, Y.; Li, T.; Adjeroh, D.; Iyengar, S.S. A survey on malware detection using data mining techniques. ACM Comput. Surv. 2017, 50, 41. [Google Scholar] [CrossRef]
- Kumar, M.; Hanumanthappa, M. Intrusion detection system using stream data mining and drift detection method. Res. Vet. Sci. 2013, 93, 168–171. [Google Scholar]
- Khorshidpour, Z.; Hashemi, S.; Hamzeh, A. Evaluation of random forest classifier in security domain. Appl. Intell. 2017, 47, 558–569. [Google Scholar] [CrossRef]
- Paul, A.; Mukherjee, D.P.; Das, P.; Gangopadhyay, A.; Chintha, A.R.; Kundu, S. Improved Random Forest for Classification. IEEE Trans. Image Process. 2018, 27, 4012–4024. [Google Scholar] [CrossRef]
- Lee, S.M.; Kim, D.S.; Park, J.S. A Hybrid Approach for Real-Time Network Intrusion Detection Systems. IEEE Trans. Veh. Technol. 2011, 60, 457–472. [Google Scholar]
- Singh, K.; Guntuku, S.C.; Thakur, A.; Hota, C. Big Data Analytics framework for Peer-to-Peer Botnet detection using Random Forests. Inf. Sci. 2014, 278, 488–497. [Google Scholar] [CrossRef]
- Ronao, C.A.; Cho, S.B. Anomalous query access detection in RBAC-administered databases with random forest and PCA. Inf. Sci. 2016, 369, 238–250. [Google Scholar] [CrossRef]
- Taft, L.M.; Evans, R.S.; Shyu, C.R.; Egger, M.J.; Chawla, N.; Mitchell, J.A.; Thornton, S.N.; Bray, B.; Varner, M. Countering imbalanced datasets to improve adverse drug event predictive models in labor and delivery. J. Biomed. Inform. 2009, 42, 356–364. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Shang, Z.; Li, H. Imbalance-oriented SVM methods for financial distress prediction: A comparative study among the new SB-SVM-ensemble method and traditional methods. J. Oper. Res. Soc. 2014, 65, 1905–1919. [Google Scholar] [CrossRef]
- Santos, M.S.; Abreu, P.H.; García-Laencina, P.J.; Simão, A.; Carvalho, A. A new cluster-based oversampling method for improving survival prediction of hepatocellular carcinoma patients. J. Biomed. Inform. 2015, 58, 49–59. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Lusa, L. SMOTE for high-dimensional class-imbalanced data. BMC Bioinform. 2013, 14, 106. [Google Scholar]
- Jeatrakul, P.; Wong, K.W.; Fung, C.C. Classification of imbalanced data by combining the complementary neural network and SMOTE algorithm. In Proceedings of the International Conference on Neural Information Processing, Sydney, Australia, 22–25 November 2010; pp. 152–159. [Google Scholar]
- Wang, J.; Xu, M.; Wang, H.; Zhang, J. Classification of imbalanced data by using the SMOTE algorithm and locally linear embedding. In Proceedings of the International Conference on Signal Processing, Beijing, China, 16–20 November 2006. [Google Scholar]
- Blagus, R.; Lusa, L. Evaluation of smote for high-dimensional class-imbalanced microarray data. In Proceedings of the International Conference on Machine Learning and Applications, Boca Raton, FL, USA, 12–15 December 2012; pp. 89–94. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Hasan, M.A.; Nasser, M.; Ahmad, S.; Molla, M.K. Feature Selection for Intrusion Detection Using Random Forest. J. Inf. Secur. 2016, 7, 129–140. [Google Scholar] [CrossRef]
- Farnaaz, N.; Jabbar, M.A. Random forest modeling for network intrusion detection system. Proc. Comput. Sci. 2016, 89, 213–217. [Google Scholar] [CrossRef]
- Yi, Y.A.; Min, M.M. An analysis of random forest algorithm based network intrusion detection system. In Proceedings of the International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing, Kanazawa, Japan, 26–28 June 2017; pp. 127–132. [Google Scholar]
- KDD Cup 1999 Data. Available online: http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html (accessed on 20 September 2018).
- Liu, Y.; Xiang, C.; Wang, H. Optimization of feature selection based on mutual information in intrusion detection. J. Northwest. Univ. 2017, 47, 666–673. [Google Scholar]
- Yan, J.H. Optimization Boosting Classification Based on Metrics of Imbalanced Data. Comput. Eng. Appl. 2018, 54, 1–6. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Sahu, S.; Mehtre, B.M. Network intrusion detection system using J48 Decision Tree. In Proceedings of the International Conference on Advances in Computing, Communications and Informatics, Kochi, India, 10–13 August 2015. [Google Scholar]
- Amor, N.B.; Benferhat, S.; Elouedi, Z. Naive Bayes vs decision trees in intrusion detection systems. In Proceedings of the ACM Symposium on Applied Computing, Nicosia, Cyprus, 14–17 March 2004; pp. 420–424. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Gaikwad, D.P.; Thool, R.C. Intrusion Detection System Using Bagging Ensemble Method of Machine Learning. In Proceedings of the International Conference on Computing Communication Control & Automation, Pune, India, 26–27 February 2015. [Google Scholar]
- Cortes, E.A.; Martinez, M.G.; Rubio, N.G. Multiclass corporate failure prediction by Adaboost.M1. Int. Adv. Econ. Res. 2007, 13, 301–312. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
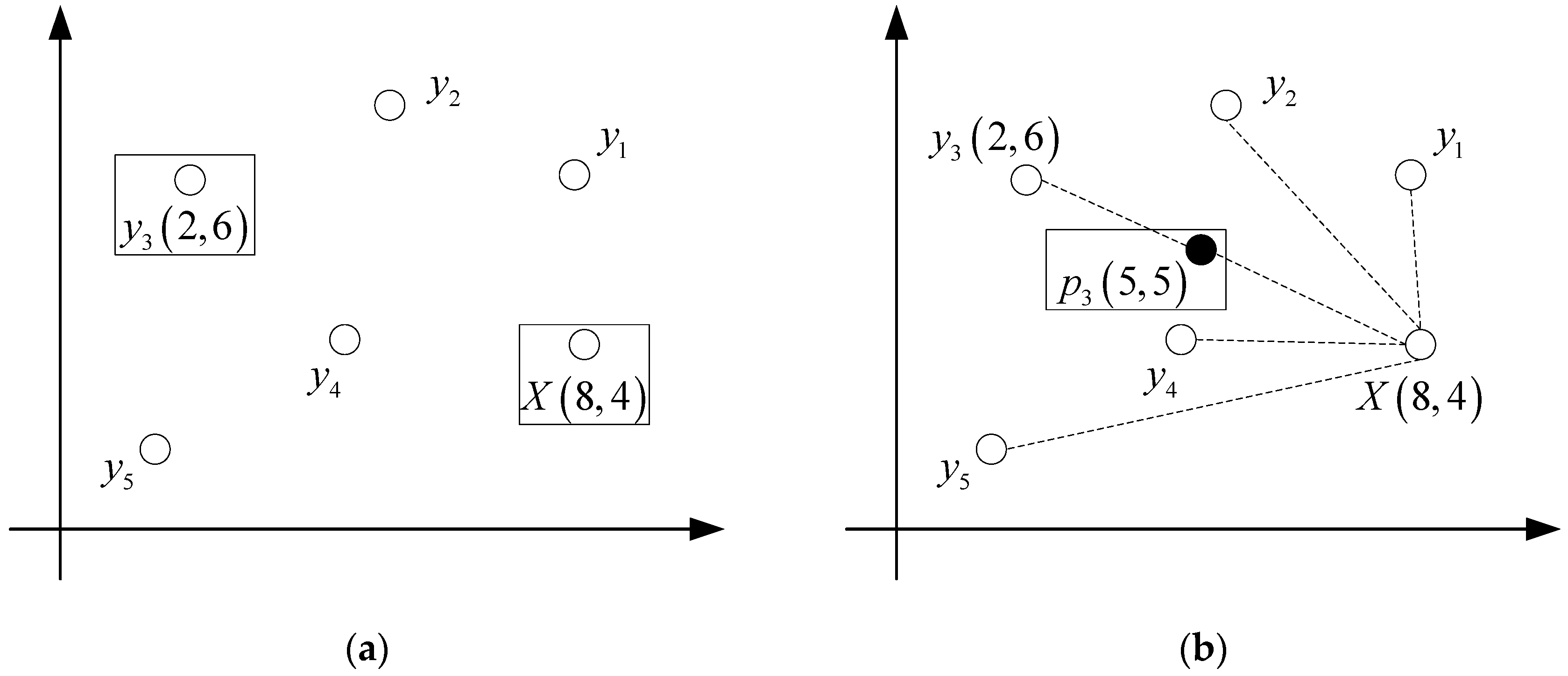
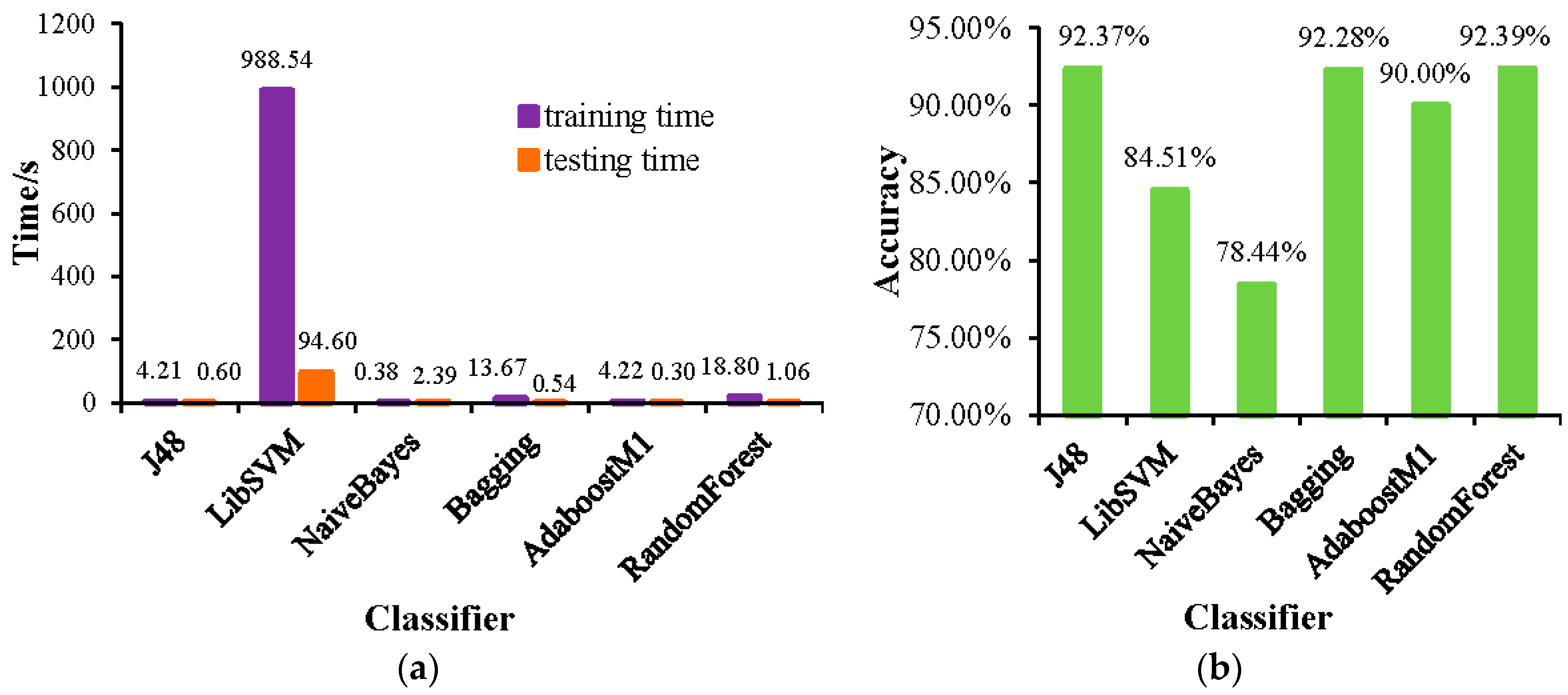
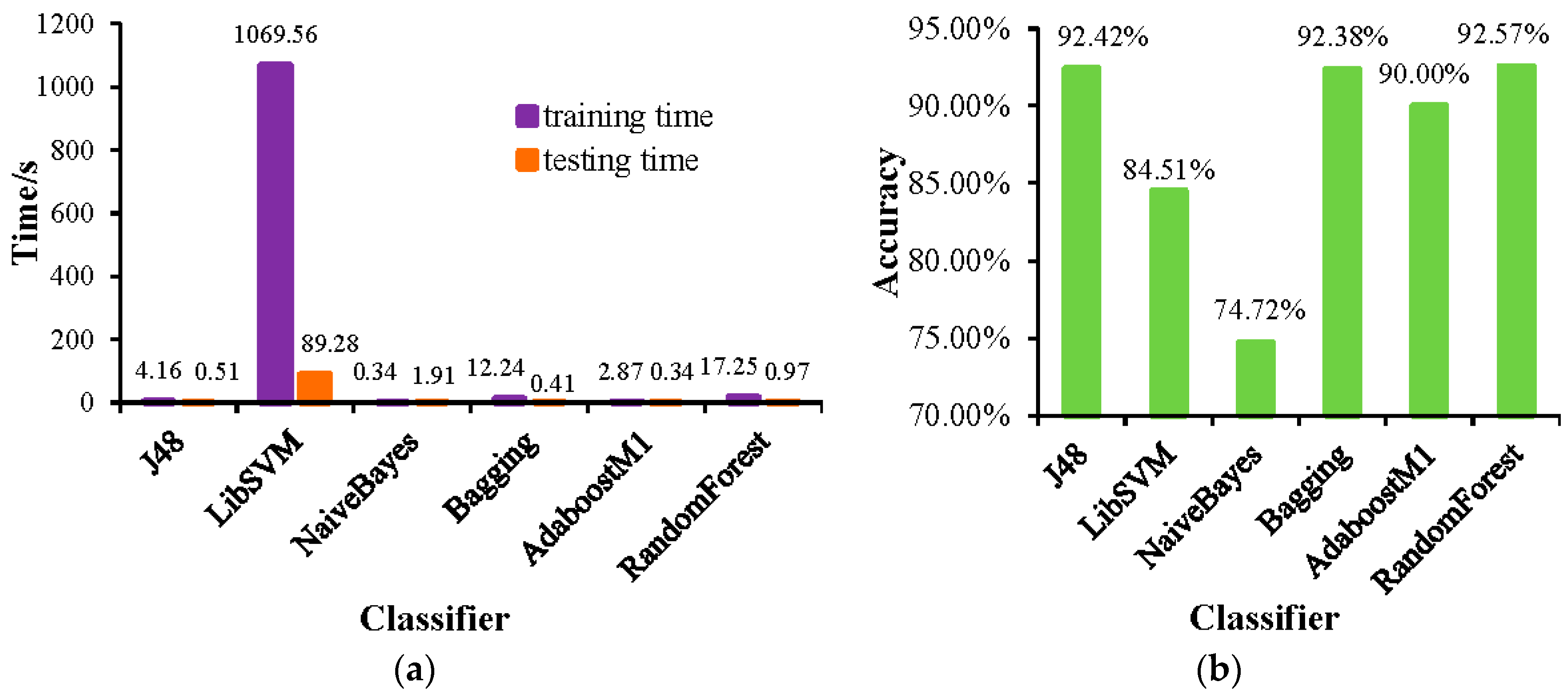
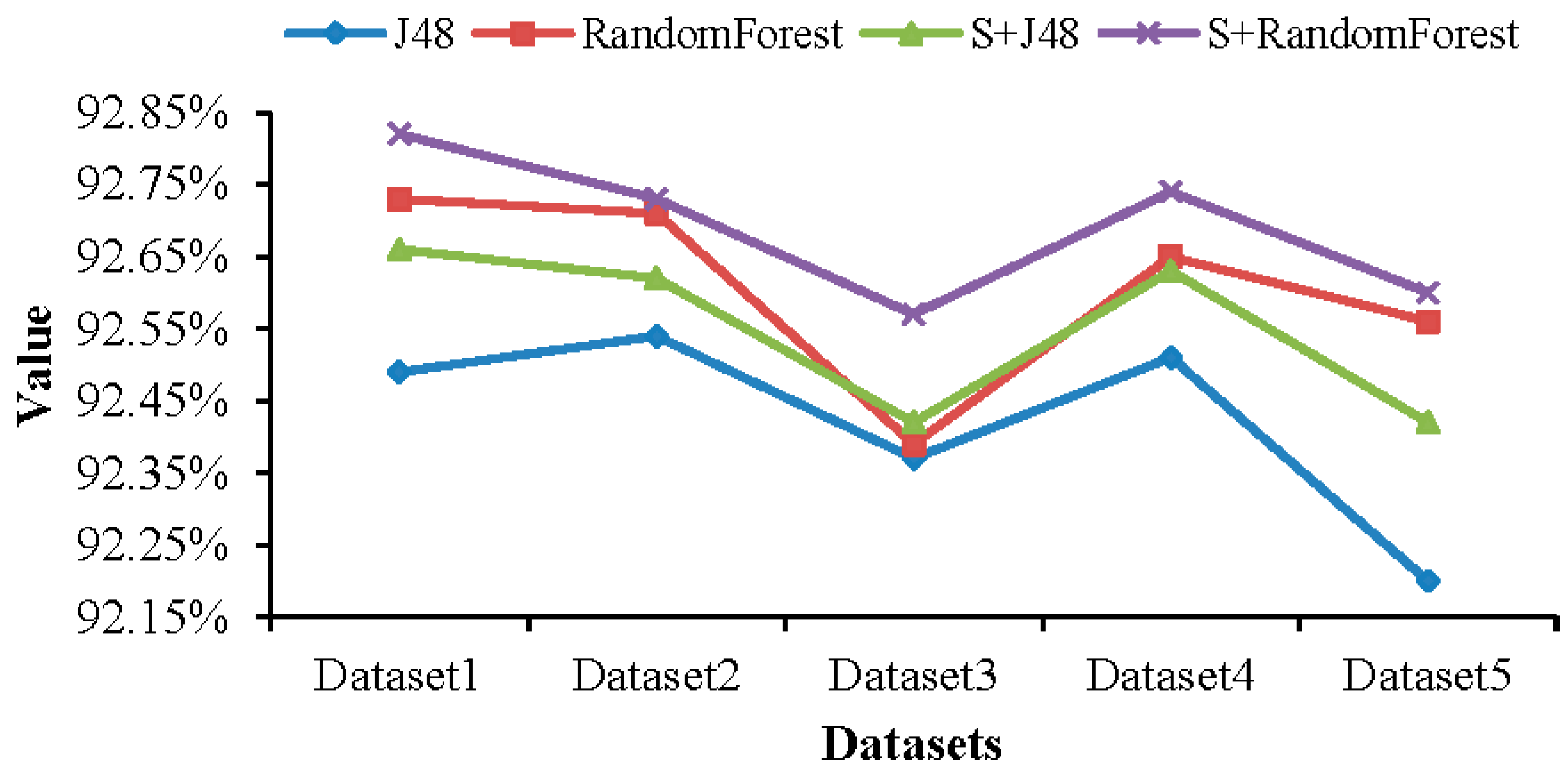
| Type\Classifier | J48 | LibSVM | NaiveBayes | Bagging | AdaboostM1 | RandomForest |
|---|---|---|---|---|---|---|
| Normal | 0.728 | 0.562 | 0.730 | 0.758 | 0.682 | 0.728 |
| Probing | 0.808 | 0.697 | 0.083 | 0.890 | 0.000 | 0.896 |
| DoS | 0.998 | 0.997 | 0.992 | 0.982 | 0.984 | 0.995 |
| U2R | 0.000 | 0.000 | 0.049 | 0.000 | 0.000 | 1.000 |
| R2L | 0.983 | 0.000 | 0.771 | 0.680 | 0.000 | 0.990 |
| Type\Classifier | J48 | LibSVM | NaiveBayes | Bagging | AdaboostM1 | RandomForest |
|---|---|---|---|---|---|---|
| Normal | 0.951 | 0.904 | 0.970 | 0.979 | 0.950 | 0.974 |
| Probing | 0.890 | 0.686 | 0.978 | 0.924 | 0.919 | 0.993 |
| DoS | 0.980 | 0.933 | 0.896 | 0.995 | 0.971 | 0.990 |
| U2R | 0.644 | 0.500 | 0.519 | 0.908 | 0.928 | 0.935 |
| R2L | 0.804 | 0.500 | 0.949 | 0.567 | 0.888 | 0.669 |
| Type\Classifier | J48 | LibSVM | NaiveBayes | Bagging | AdaboostM1 | RandomForest |
|---|---|---|---|---|---|---|
| Normal | 0.725 | 0.562 | 0.809 | 0.759 | 0.682 | 0.728 |
| Probing | 0.904 | 0.697 | 0.086 | 0.453 | 0.000 | 0.901 |
| DoS | 0.998 | 0.997 | 0.886 | 0.994 | 0.984 | 0.999 |
| U2R | 0.375 | 0.000 | 0.044 | 0.200 | 0.000 | 0.333 |
| R2L | 0.941 | 0.000 | 0.717 | 0.944 | 0.000 | 0.981 |
| Type\Classifier | J48 | LibSVM | NaiveBayes | Bagging | AdaboostM1 | RandomForest |
|---|---|---|---|---|---|---|
| Normal | 0.949 | 0.904 | 0.970 | 0.974 | 0.943 | 0.976 |
| Probing | 0.891 | 0.686 | 0.981 | 0.868 | 0.774 | 0.995 |
| DoS | 0.982 | 0.933 | 0.892 | 0.987 | 0.970 | 0.986 |
| U2R | 0.720 | 0.500 | 0.542 | 0.856 | 0.869 | 0.995 |
| R2L | 0.519 | 0.500 | 0.949 | 0.571 | 0.921 | 0.677 |
| Type\Dataset | Dataset1 | Dataset2 | Dataset3 | Dataset4 | Dataset5 |
|---|---|---|---|---|---|
| Training data | 24,701 | 37,051 | 49,402 | 61,752 | 74,103 |
| testing data | 15,551 | 23,327 | 31,102 | 38,878 | 46,654 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, X.; Su, S.; Huang, Z.; Guo, X.; Zuo, Z.; Sun, X.; Li, L. Wireless Sensor Networks Intrusion Detection Based on SMOTE and the Random Forest Algorithm. Sensors 2019, 19, 203. https://doi.org/10.3390/s19010203
Tan X, Su S, Huang Z, Guo X, Zuo Z, Sun X, Li L. Wireless Sensor Networks Intrusion Detection Based on SMOTE and the Random Forest Algorithm. Sensors. 2019; 19(1):203. https://doi.org/10.3390/s19010203
Chicago/Turabian StyleTan, Xiaopeng, Shaojing Su, Zhiping Huang, Xiaojun Guo, Zhen Zuo, Xiaoyong Sun, and Longqing Li. 2019. "Wireless Sensor Networks Intrusion Detection Based on SMOTE and the Random Forest Algorithm" Sensors 19, no. 1: 203. https://doi.org/10.3390/s19010203
APA StyleTan, X., Su, S., Huang, Z., Guo, X., Zuo, Z., Sun, X., & Li, L. (2019). Wireless Sensor Networks Intrusion Detection Based on SMOTE and the Random Forest Algorithm. Sensors, 19(1), 203. https://doi.org/10.3390/s19010203




