Reinforcement Strains in Reinforced Concrete Tensile Members Recorded by Strain Gauges and FBG Sensors: Experimental and Numerical Analysis
Abstract
:1. Introduction
2. Testing Methods
2.1. Specimens
2.2. Material Properties
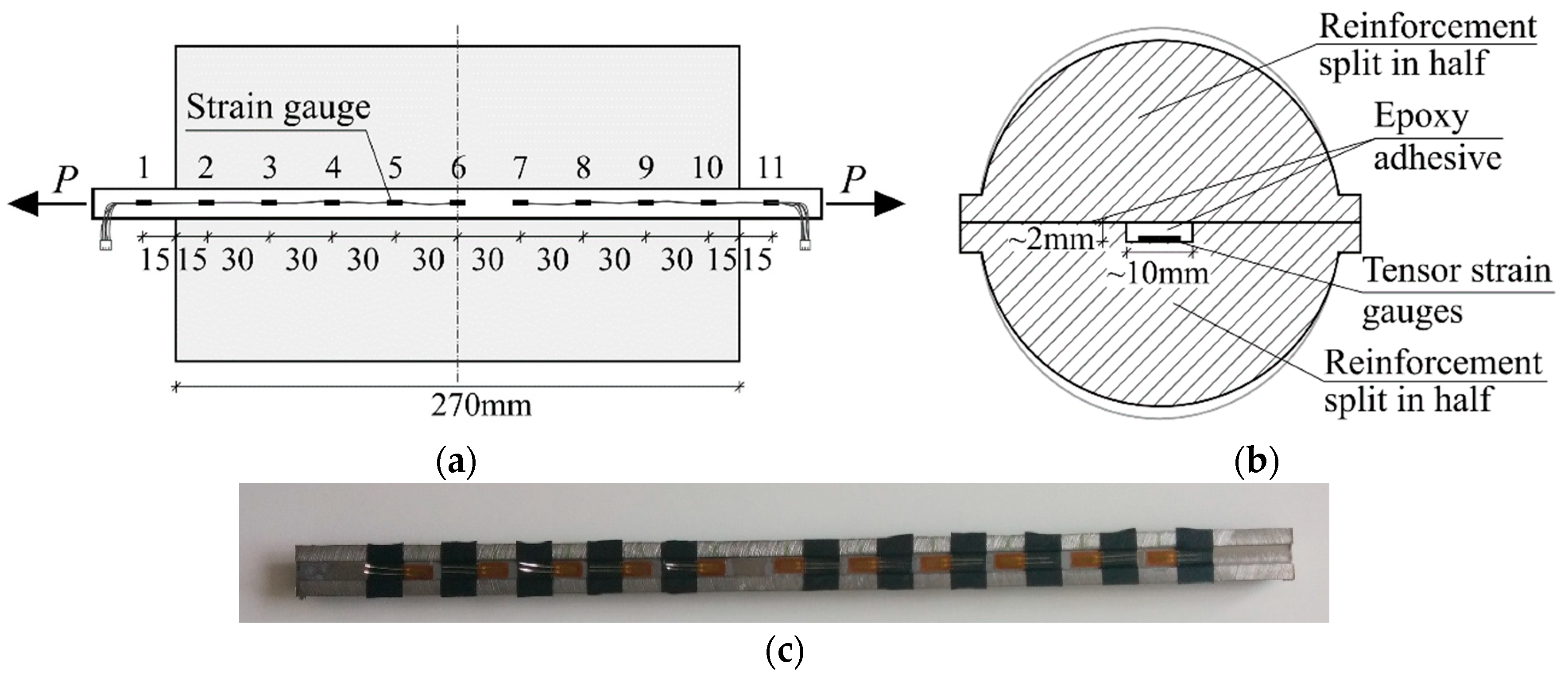
2.3. Strain Guage Experimental Setup
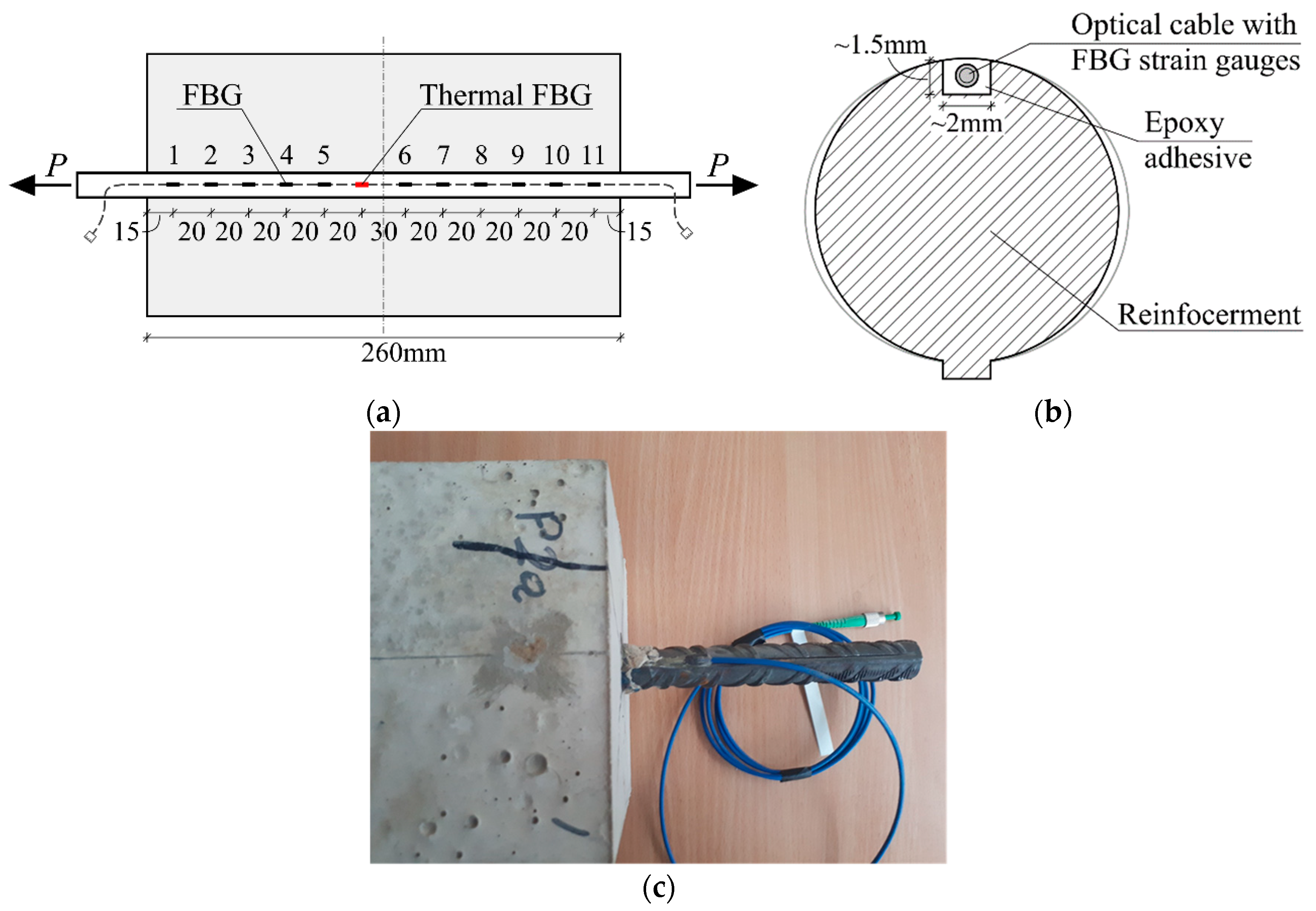
2.4. Fiber Bragg Grating Experimental Setup
2.5. Testing Procedure
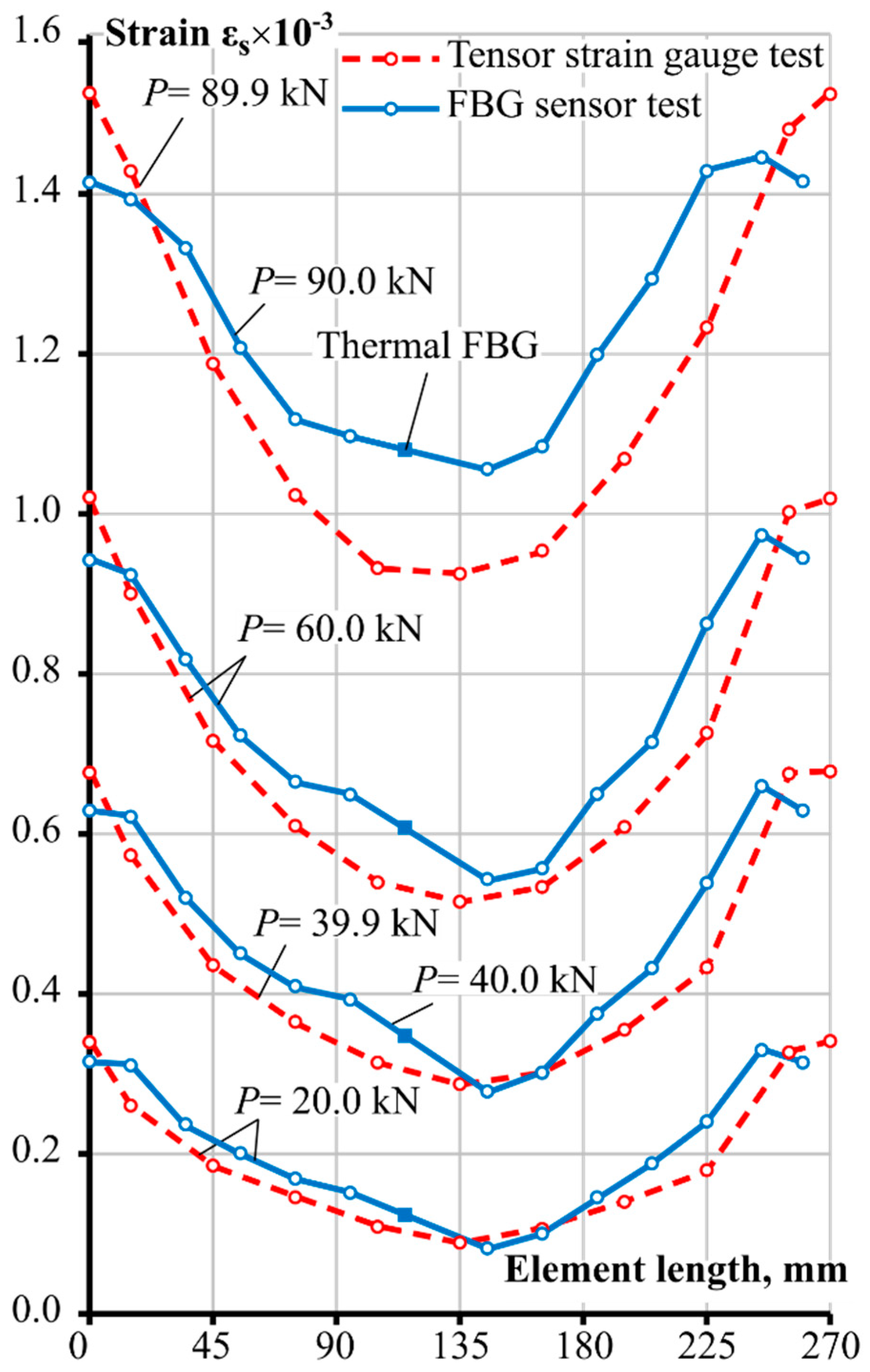
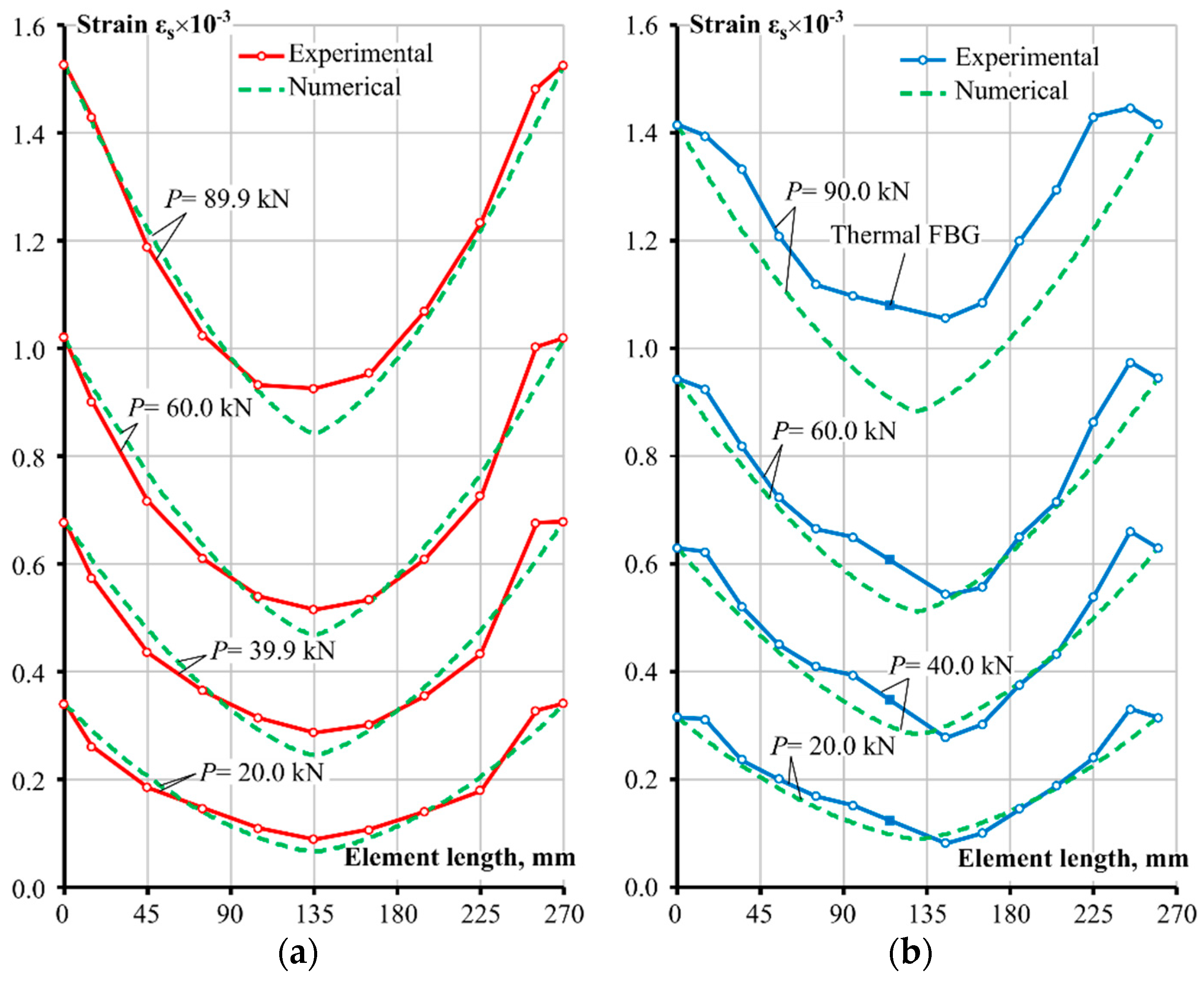
3. Results of the Experiments
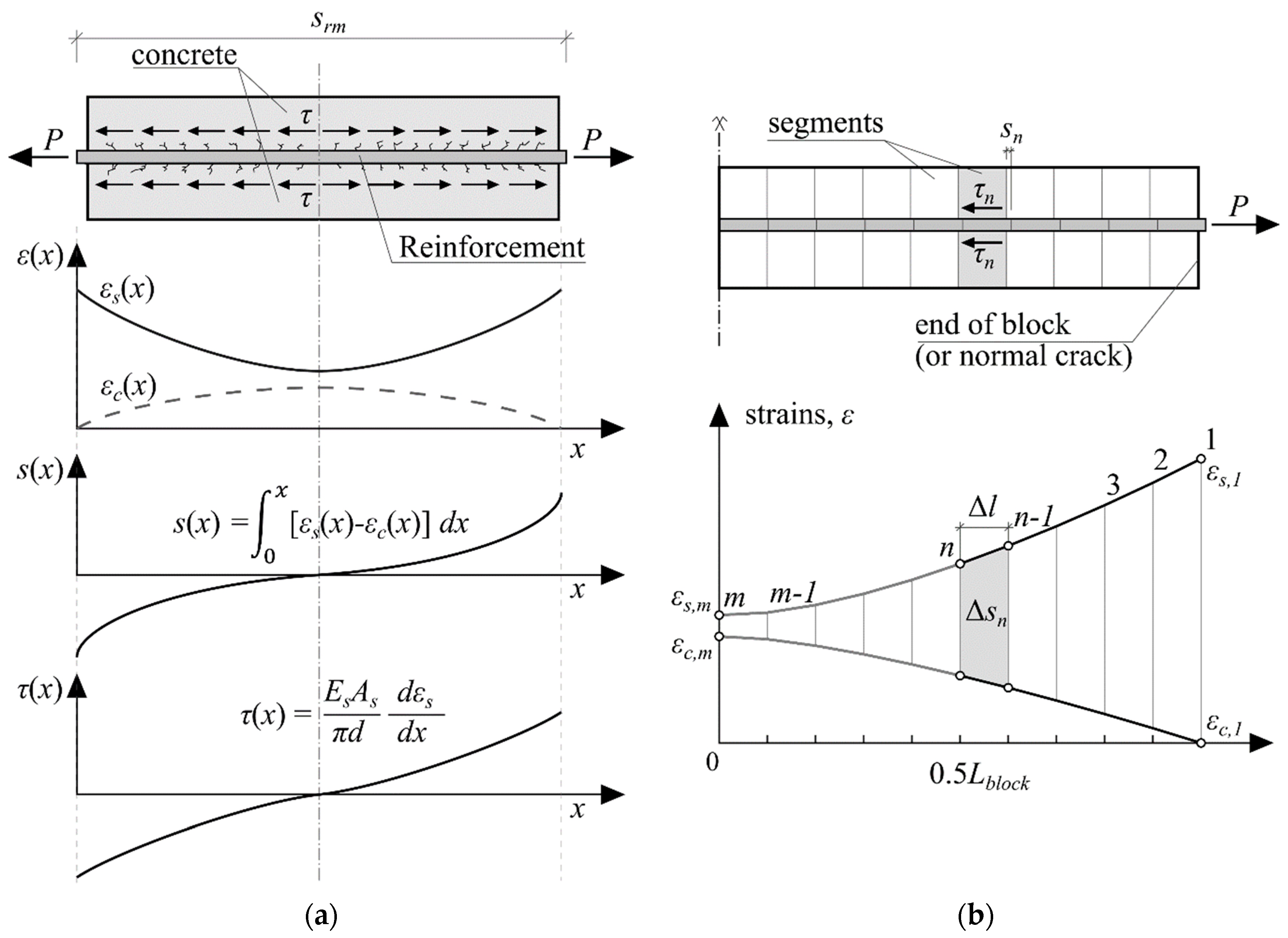
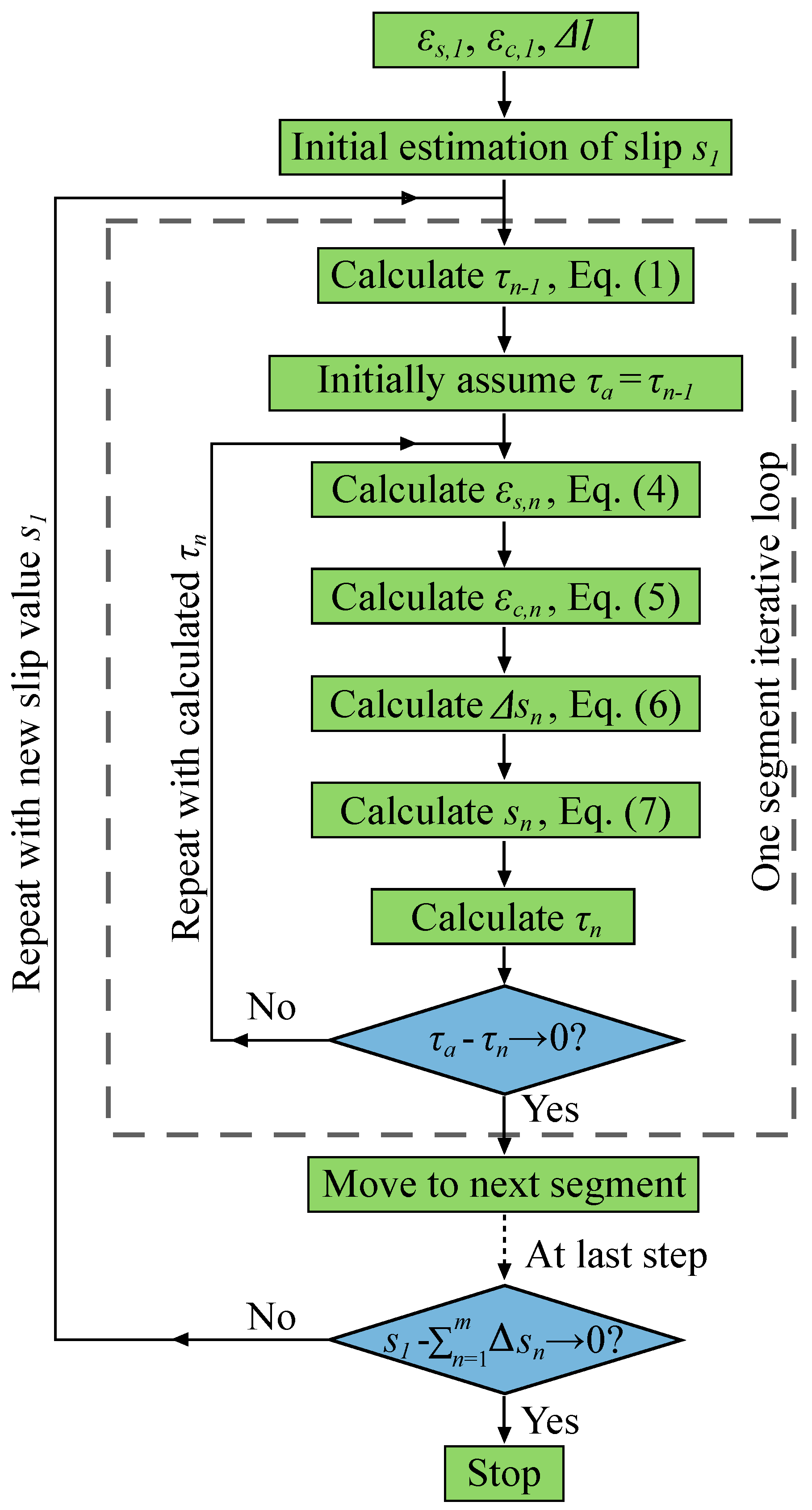
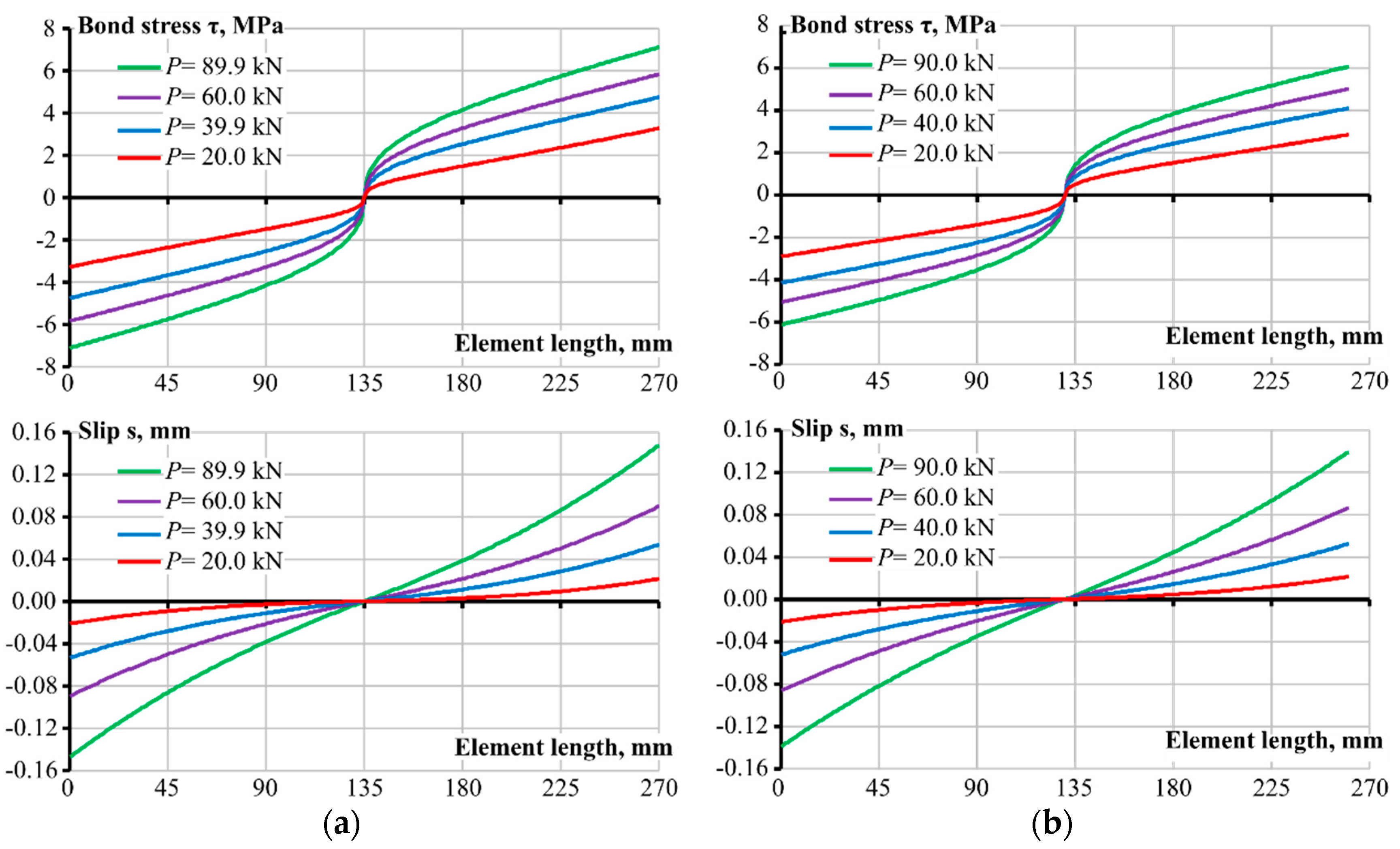
4. Numerical Analysis and Discussion
5. Conclusions
- The experimental techniques provided strain variations along the steel bar with reasonable accuracy and smoothness, however, the specimen strain results of the fibre Bragg grating optical gauge test displayed anomalies, particularly near the end of the specimen. The measured strains were larger than the strain value estimated for a bare bar assuming the experimental value of the modulus of elasticity of the bar. In addition, the FBG recordings were lacking consistency regarding the symmetry condition of the left and the right side of the member. However, the FBG approach is far less complex in preparing the specimen, as opposed to the tensor strain gauge experimental setup, which required careful milling, installation of gauges, and fastening of the bars back together. Moreover, the FBG technique can be used for smaller diameter bars, which would not be possible with the strain gauge approach due to a significant loss of section and lack of remaining sectional area to glue the two halves of the bar together. An option of a finer spacing of the sensors is another advantage of the FGB technique over the strain gauge approach.
- The observed behaviour in the strain profiles towards the ends of the reinforced concrete elements demands further investigation. Due to fluctuations in the strain values recorded by FBG sensors and the rather rare spacing between the sensors, it cannot be firmly asserted whether the phenomenon was related to the debonding effect proposed in previous research by the authors. The effect implies altered bond behaviour between the reinforcement and the concrete material surrounding it around the location of the cracks or elements’ ends.
- A comparison of the numerical results with appropriate experimental strain curves of the steel reinforcement showed that the Model Code 2010 bond-slip equation could provide sufficiently accurate results when coupled with the stress transfer approach for the Ø20 mm specimens. However, additional tests with different diameter bars and reinforcement ratios would help either affirm or negate the findings. Some discrepancy in numerical and experimental strain comparison appeared at the highest loading of the FBG specimen. The overall observed behaviour was parabolic, with steeper strain gradients at higher loading stages.
- The stress transfer approach can provide very comprehensive results of reinforcement and concrete strains, the bond stress and slip values over the entire distribution of the element, provided the implemented bond-slip model is accurate.
Author Contributions
Funding
Conflicts of Interest
References
- Balázs, G.L.; Bisch, P.; Borosnyói, A.; Burdet, O.; Burns, C.; Ceroni, F.; Cervenka, V.; Chiorino, M.A.; Debernardi, P.; Eckfeldt, L.; et al. Design for SLS according to fib Model Code 2010. Struct. Concr. 2013, 14, 99–123. [Google Scholar] [CrossRef]
- Farra, B.; Jaccoud, J.P. Bond behaviour, tension stiffening and crack prediction of high strength concrete. In Proceedings of the International Symposium Bond in Concrete, Riga, Latvia, 15–17 October 1992. [Google Scholar]
- Beeby, A.W. The influence of the parameter ϕ/ρeff on crack widths. Struct. Concr. 2004, 5, 71–83. [Google Scholar] [CrossRef]
- Borosnyói, A.; Balázs, G.L. Models for flexural cracking in concrete: The state of the art. Struct. Concr. 2005, 6, 53–62. [Google Scholar] [CrossRef]
- Broms, B.B. Crack width and crack spacing in reinforced concrete members. ACI J. 1965, 62, 1237–1256. [Google Scholar]
- Clark, A.P. Cracking in reinforced concrete flexural members. J. Proc. 1956, 52, 851–862. [Google Scholar]
- Saliger, R. High grade steel in reinforced concrete. In Proceedings of the 2nd Congress of IABSE, Berlin/Munich, Germany, 1–11 October 1936; IABSE Publications: Munich/Berlin, Germany, 1936. [Google Scholar]
- Somayaji, S.; Shah, S.P. Bond stress versus slip relationship and cracking response of tension members. J. Proc. 1981, 78, 217–225. [Google Scholar]
- Balazs, G.L. Cracking analysis based on slip and bond stresses. Mat. J. 1993, 90, 340–348. [Google Scholar]
- Comité Européen de Normalisation (CEN). Eurocode 2: Design of Concrete Structures: Part 1-1: General Rules and Rules for Buildings; EN 1992-1-1; Comité Européen de Normalisation: Brussels, Belgium, 2004. [Google Scholar]
- Fédération Internationale du Béton (FIB). Model Code 2010; International Federation for Structural Concrete: Lausanne, Switzerland, 2010. [Google Scholar]
- Du Béton, F.I. Bond of Reinforcement in Concrete: State-of-Art Report; Bulletin: Lausanne, Switzerland, 2000. [Google Scholar]
- Scott, R.H.; Gill, P.A. Short-term distributions of strain and bond stress along tension reinforcement. Struct. Eng. 1987, 65, 39–43. [Google Scholar]
- Mains, R.M. Measurement of the distribution of tensile and bond stresses along reinforcing bars. J. Proc. ACI J. 1951, 48, 225–252. [Google Scholar]
- Bresler, B.; Bertero, V. Behavior of reinforced concrete under repeated load. J. Struct. Div. 1968, 94, 1567–1592. [Google Scholar]
- Houde, J. Study of Force-Displacement Relationships for the Finite-Element Analysis of Reinforced Concrete. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 1974. [Google Scholar]
- Kankam, C.K. Relationship of bond stress, steel stress, and slip in reinforced concrete. J. Struct. Eng. 1997, 123, 79–85. [Google Scholar] [CrossRef]
- Wenkenbach, I. Tension Stiffening in Reinforced Concrete Members with Large Diameter Reinforcement. Ph.D. Thesis, Durham University, Durham, UK, 2011. [Google Scholar]
- Masukawa, J. Degradation of Shear Performance of Beams due to Bond Deterioration and Longitudinal bar Cutoffs. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2012. [Google Scholar]
- Davis, M.A.; Bellemore, D.G.; Kersey, A.D. Distributed fibre Bragg grating strain sensing in reinforced concrete structural components. Cem. Concr. Compos. 1997, 19, 45–57. [Google Scholar] [CrossRef]
- Kenel, A.; Nellen, P.; Frank, A.; Marti, P. Reinforcing steel strains measured by Bragg grating sensors. J. Mater. Civ. Eng. 2005, 17, 423–431. [Google Scholar] [CrossRef]
- Kaklauskas, G.; Ramanauskas, R.; Jakubovskis, R. Mean crack spacing modelling for RC tension elements. Eng. Struct. 2017, 150, 843–851. [Google Scholar] [CrossRef]
- Li, W.; Xu, C.; Ho, S.C.M.; Wang, B.; Song, G. Monitoring Concrete Deterioration Due to Reinforcement Corrosion by Integrating Acoustic Emission and FBG Strain Measurements. Sensors 2017, 17, 657. [Google Scholar] [CrossRef]
- Kaklauskas, G. Crack model for RC members based on compatibility of stress-transfer and mean-strain approaches. J. Struct. Eng. 2017, 143, 04017105. [Google Scholar] [CrossRef]
- Kim, S.-W.; Park, W.-S.; Jang, Y.-I.; Jang, S.-J.; Yun, H.-D. Bonding Behavior of Deformed Steel Rebars in Sustainable Concrete Containing both Fine and Coarse Recycled Aggregates. Materials 2017, 10, 1082. [Google Scholar] [CrossRef]
- Bouazaoui, L.; Li, A. Analysis of steel/concrete interfacial shear stress by means of pull out test. Int. J. Adhes. Adhes. 2008, 28, 101–108. [Google Scholar] [CrossRef]
- Dang, C.N.; Murray, C.D.; Floyd, R.W.; Hale, W.M.; Marti-Vargas, J.R. Analysis of bond stress distribution for prestressing strand by Standard Test for Strand Bond. Eng. Struct. 2014, 72, 152–159. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R.; Barrias, A. Performance of Rayleigh-Based Distributed Optical Fiber Sensors Bonded to Reinforcing Bars in Bending. Sensors 2018, 18, 3125. [Google Scholar] [CrossRef]
- Ding, Z.; Wang, C.; Liu, K.; Jiang, J.; Yang, D.; Pan, G.; Pu, Z.; Liu, T. Distributed Optical Fiber Sensors Based on Optical Frequency Domain Reflectometry: A review. Sensors 2018, 18, 1072. [Google Scholar] [CrossRef] [PubMed]
- Barrias, A.; Casas, J.R.; Villalba, S. Application study of embedded Rayleigh based Distributed Optical Fiber Sensors in concrete beams. Proc. Eng. 2017, 199, 2014–2019. [Google Scholar] [CrossRef]
- Henault, J.M.; Quiertant, M.; Delepine-Lesoille, S.; Salin, J.; Moreau, G.; Taillade, F.; Benzarti, K. Quantitative strain measurement and crack detection in RC structures using a truly distributed fiber optic sensing system. Constr. Build. Mater. 2012, 37, 916–923. [Google Scholar] [CrossRef]

| Test Setup | H × B × L, mm | Bar Diameter, mm | As,ef, cm2 | fy, MPa | Es, GPa | fcm, MPa | Ecm, GPa |
|---|---|---|---|---|---|---|---|
| Strain gauge | 150 × 150 × 270 | Ø20 | 2.90 | 527 | 204 | 45.5 | 34.6 |
| FBG sensor | 150 × 150 × 260 | Ø20 | 3.11 | 527 | 204 | 36.8 | 32.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaklauskas, G.; Sokolov, A.; Ramanauskas, R.; Jakubovskis, R. Reinforcement Strains in Reinforced Concrete Tensile Members Recorded by Strain Gauges and FBG Sensors: Experimental and Numerical Analysis. Sensors 2019, 19, 200. https://doi.org/10.3390/s19010200
Kaklauskas G, Sokolov A, Ramanauskas R, Jakubovskis R. Reinforcement Strains in Reinforced Concrete Tensile Members Recorded by Strain Gauges and FBG Sensors: Experimental and Numerical Analysis. Sensors. 2019; 19(1):200. https://doi.org/10.3390/s19010200
Chicago/Turabian StyleKaklauskas, Gintaris, Aleksandr Sokolov, Regimantas Ramanauskas, and Ronaldas Jakubovskis. 2019. "Reinforcement Strains in Reinforced Concrete Tensile Members Recorded by Strain Gauges and FBG Sensors: Experimental and Numerical Analysis" Sensors 19, no. 1: 200. https://doi.org/10.3390/s19010200
APA StyleKaklauskas, G., Sokolov, A., Ramanauskas, R., & Jakubovskis, R. (2019). Reinforcement Strains in Reinforced Concrete Tensile Members Recorded by Strain Gauges and FBG Sensors: Experimental and Numerical Analysis. Sensors, 19(1), 200. https://doi.org/10.3390/s19010200





