Multiple Wire-Mesh Sensors Applied to the Characterization of Two-Phase Flow inside a Cyclonic Flow Distribution System †
Abstract
1. Introduction
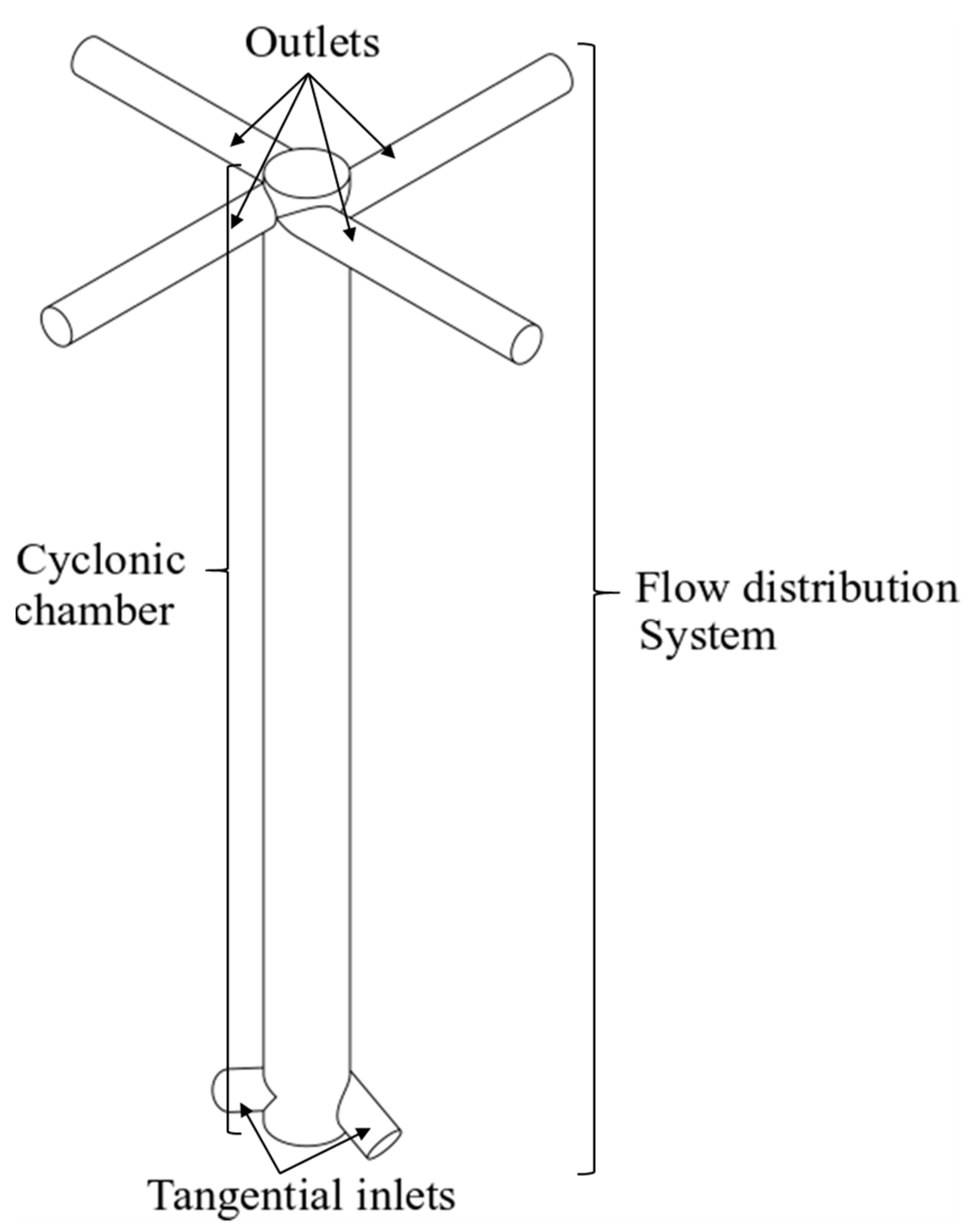
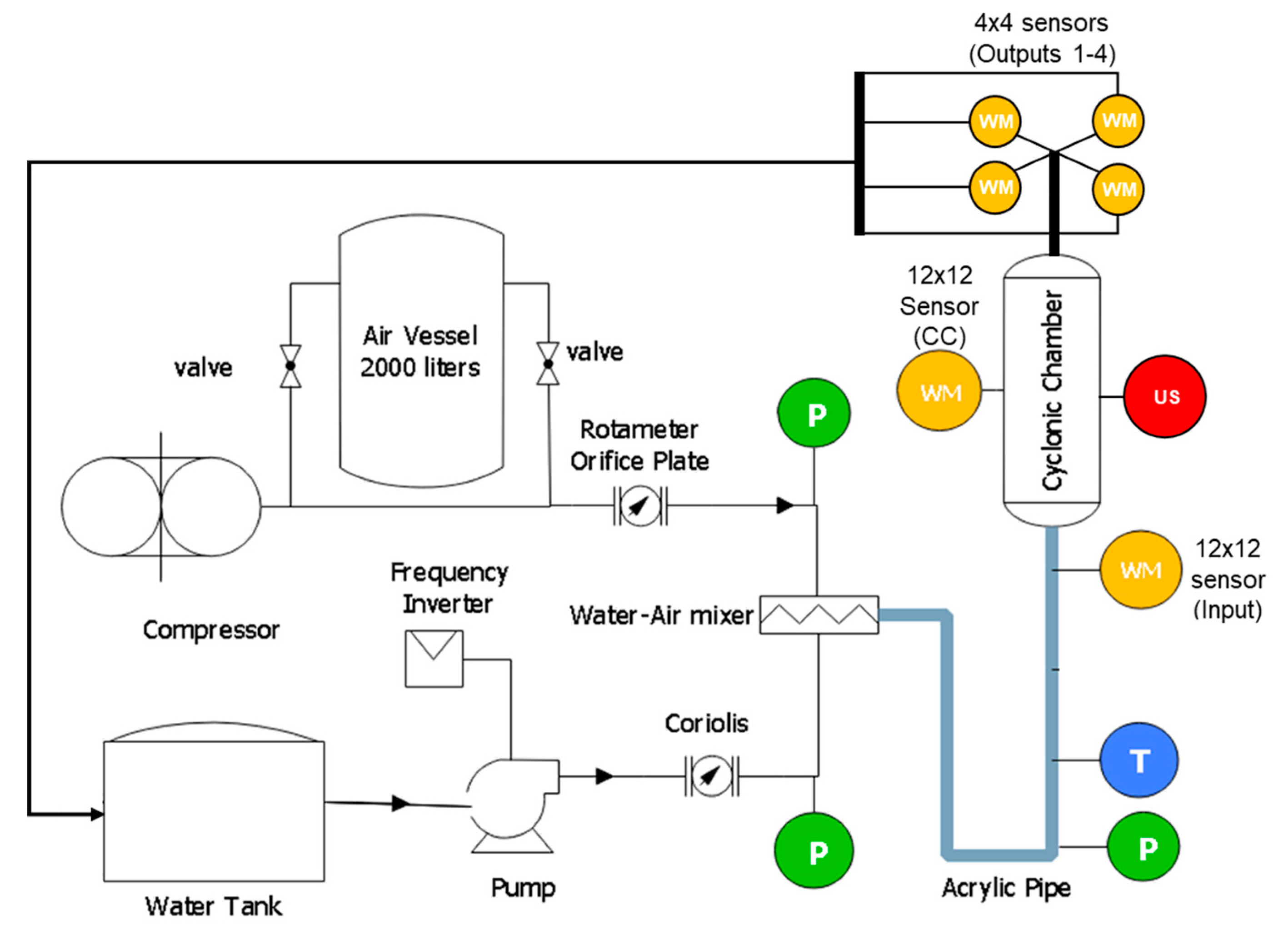
2. Experimental Setup
3. Results and Discussion
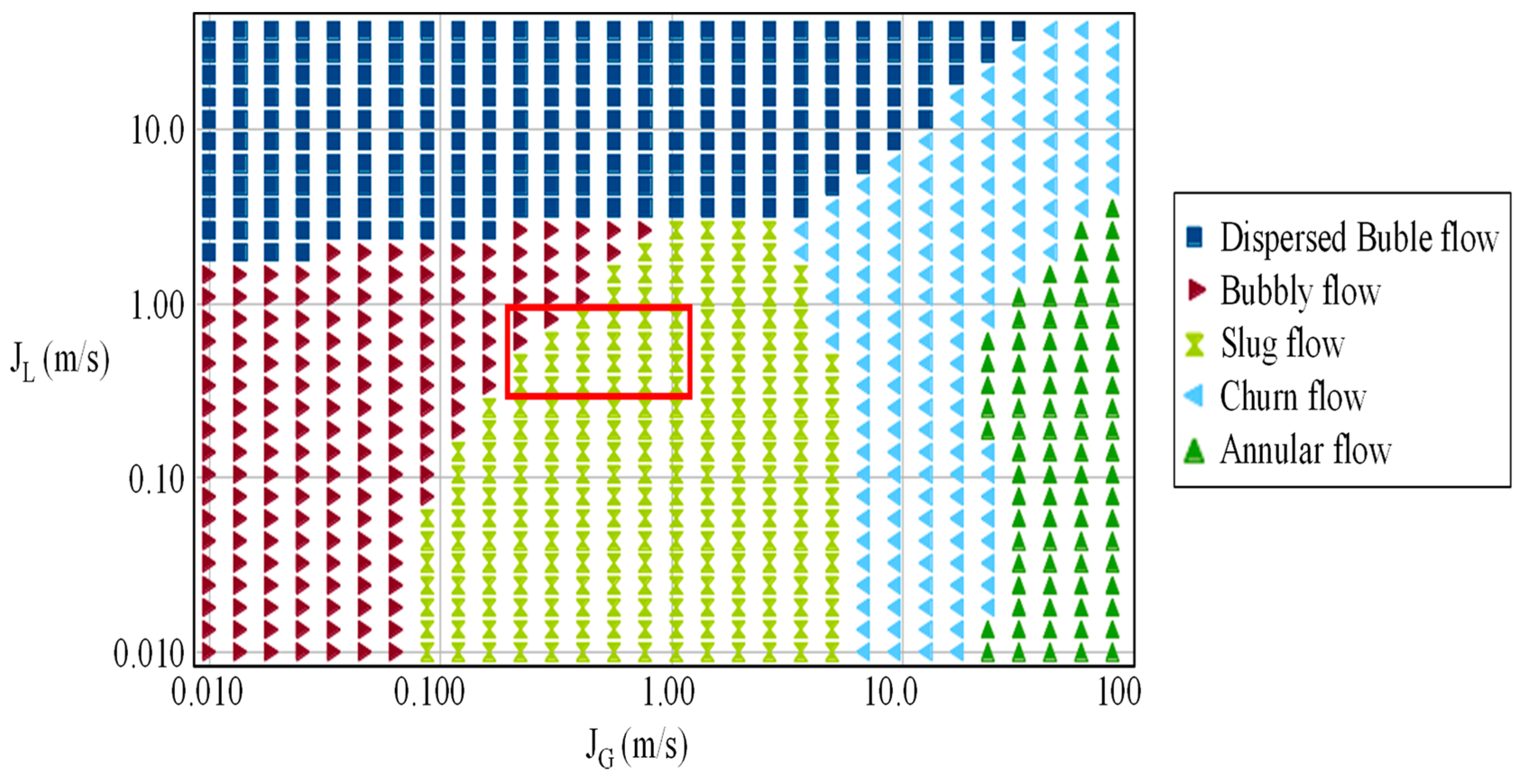
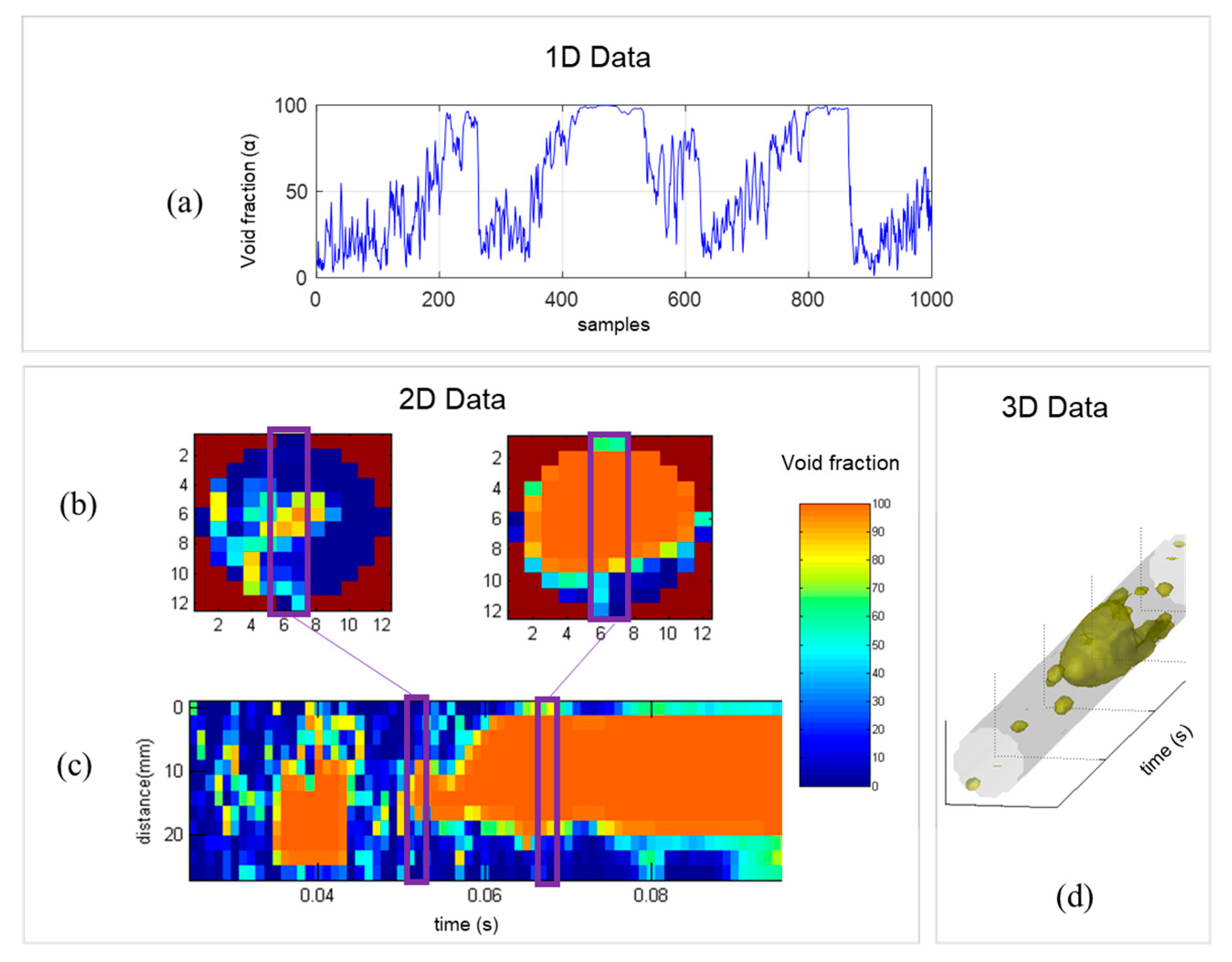
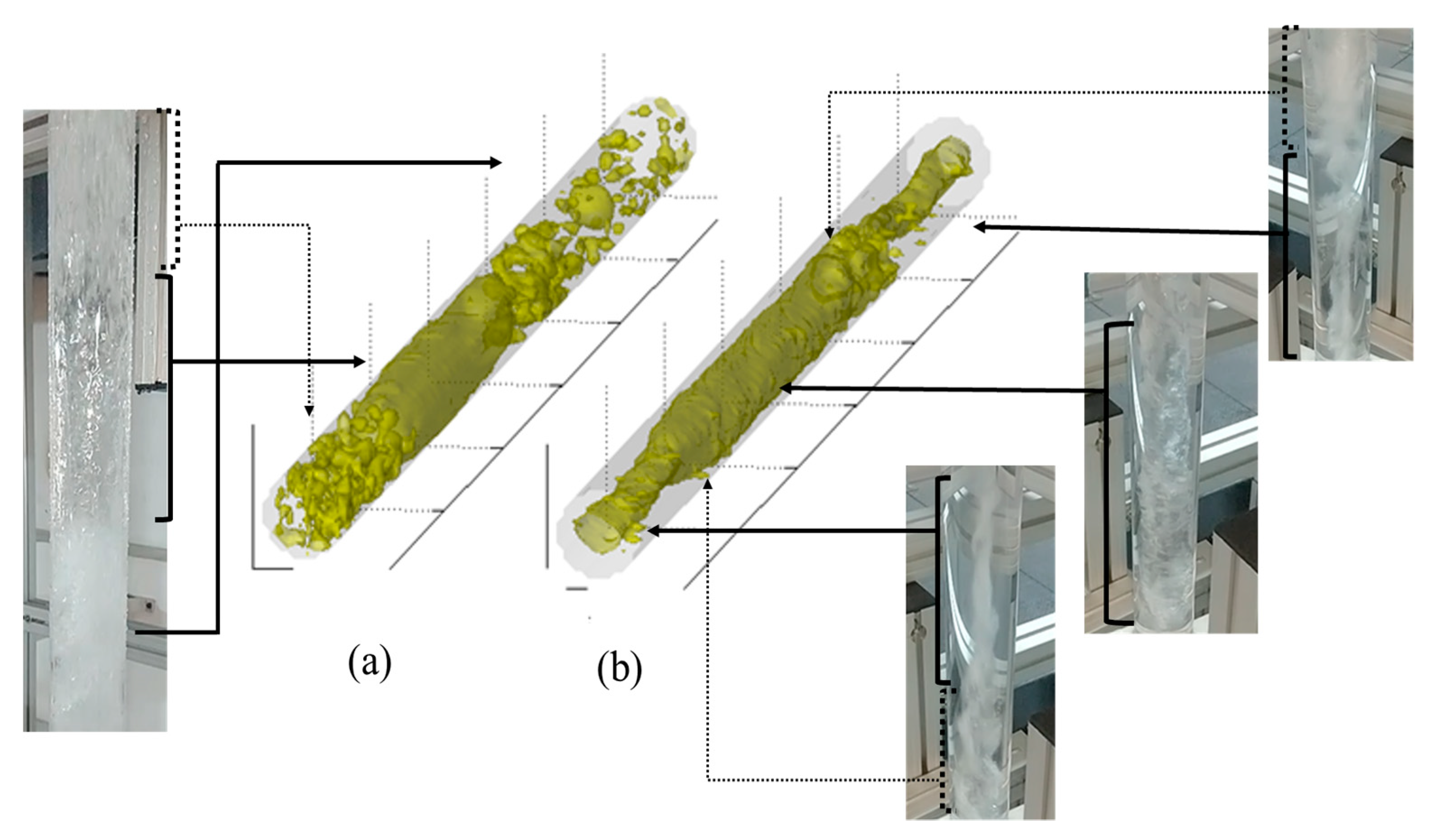
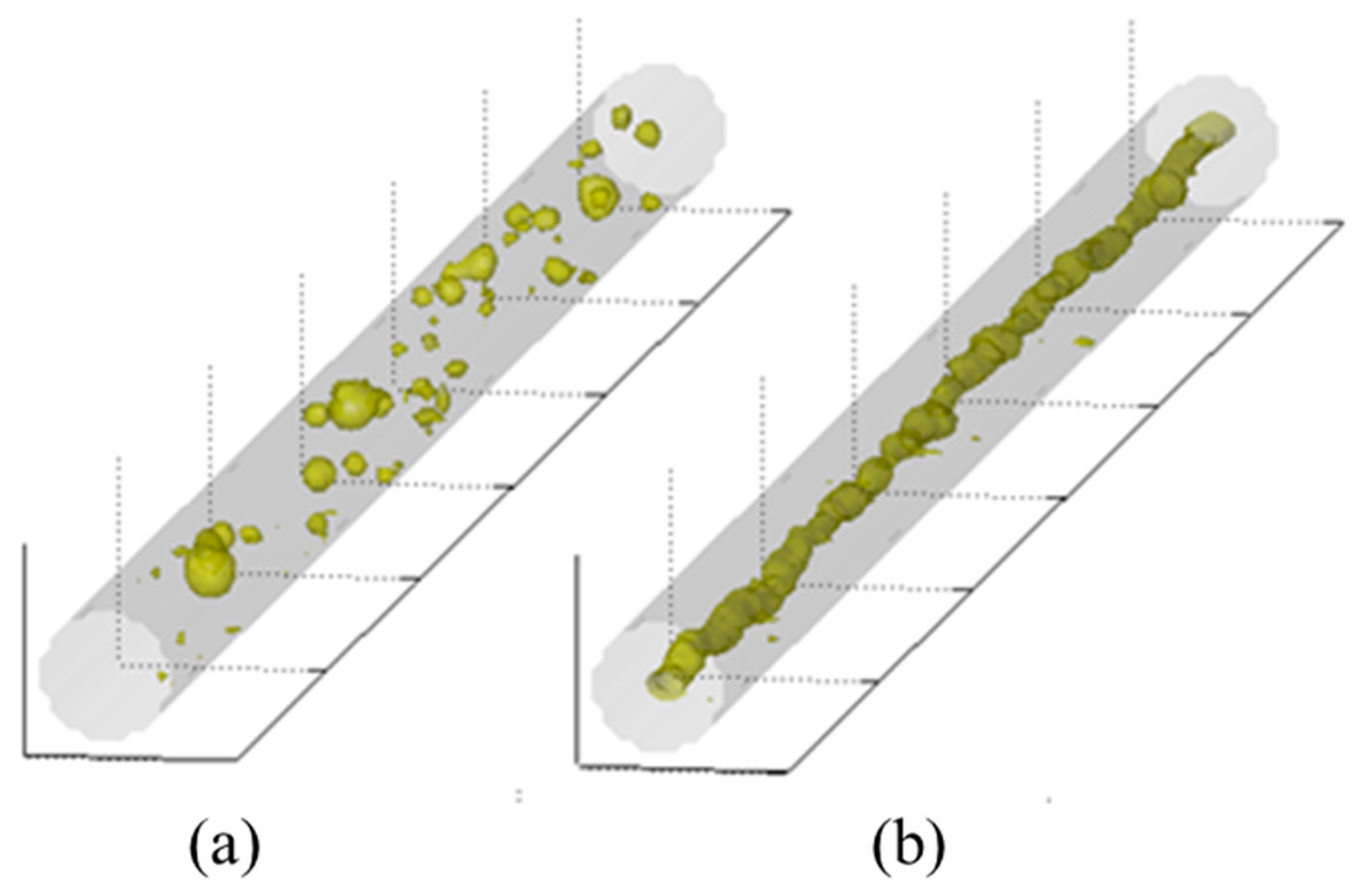
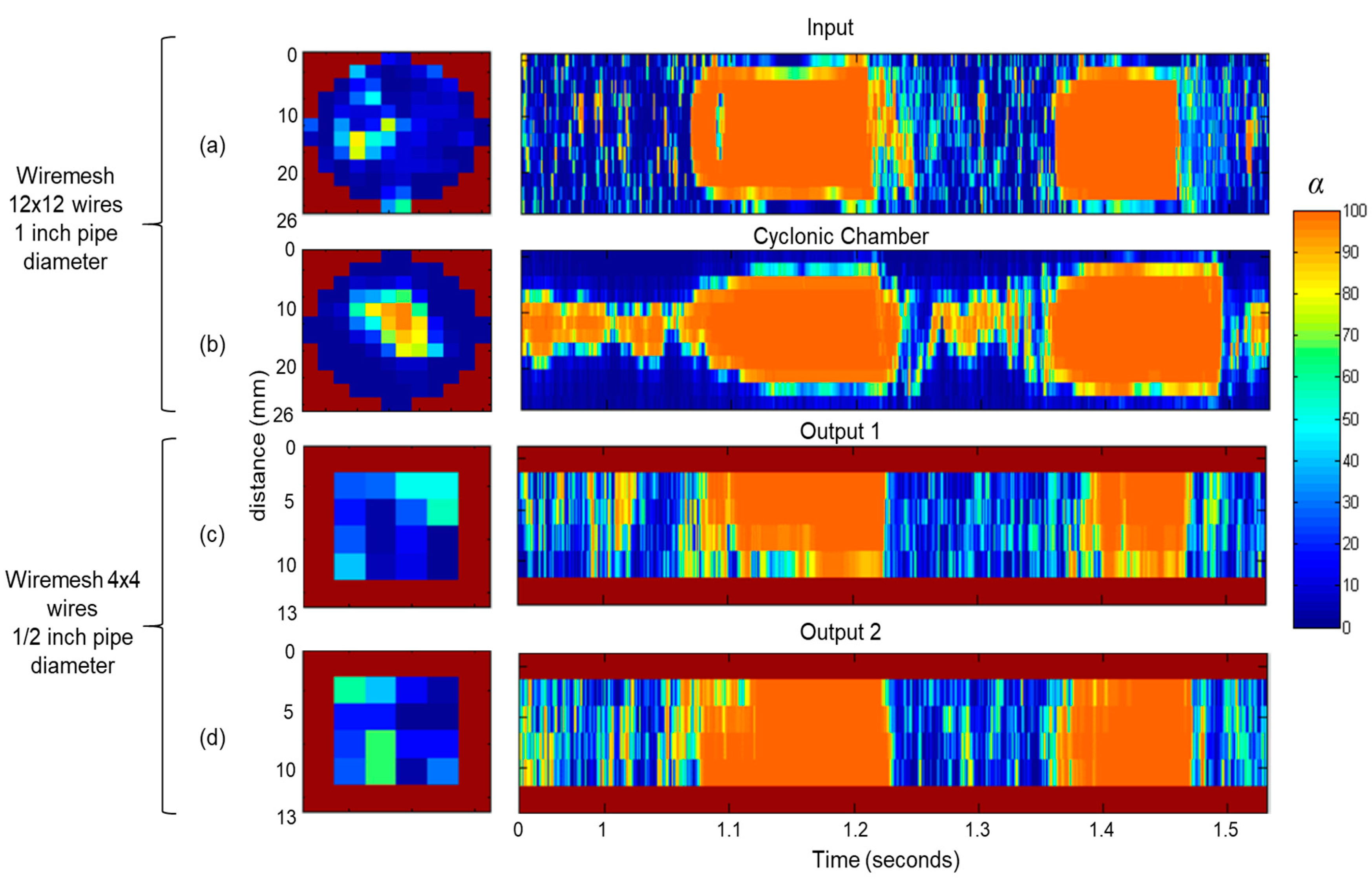
3.1. Flow Pattern Analysis
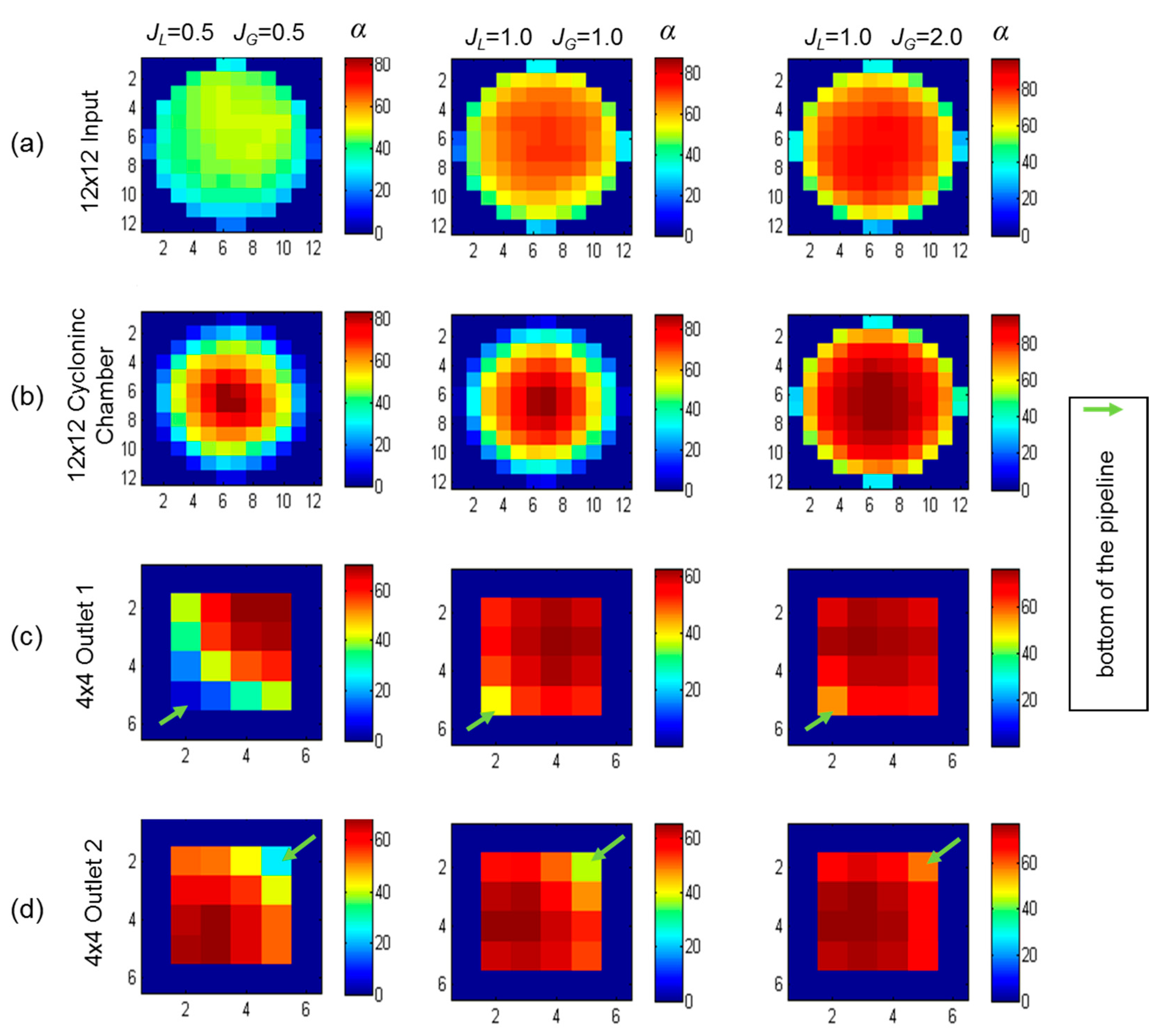
3.2. Flow Distribution Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Prasser, H.M. Novel experimental measuring techniques required to provide data for CFD validation. Nucl. Eng. Des. 2008, 238, 744–770. [Google Scholar] [CrossRef]
- Hernandez-Perez, V.; Azzopardi, B.; Kaji, R.; da Silva, M.J. Wisp-like Structures in Vertical Gas-Liquid Pipe Flow Revealed by Wire Mesh Sensor Studies. Int. J. Multiph. Flow 2010, 36, 908–915. [Google Scholar] [CrossRef]
- Da Silva, M.J.; Hampel, U.; Arruda, L.V.R.; Amaral, C.E.F.D.; Morales, R.E.M. Experimental Investigation of Horizontal Gas-Liquid Slug Flow by Means of Wire-Mesh Sensor. J. Braz. Soc. Mech. Sci. Eng. 2011, 33, 237–242. [Google Scholar]
- Tat, T.; Kikura, H.; Murakawa, H.; Tsuzuki, N. Measurement of Bubbly Two-Phase Flow in Vertical Pipe Using Multiwave Ultrasonic Pulsed Dopller Method and Wire Mesh Tomography. Energy Procedia 2015, 71, 337–351. [Google Scholar] [CrossRef]
- KRagna, I.; Brito, R.; Scheicher, E.; Hampel, U. Developments for the Application of the Wire-Mesh Sensor in Industries. Int. J. Multiph. Flow 2016, 85, 86–95. [Google Scholar] [CrossRef]
- Ragna, K.; Kryk, H.; Schleicher, E.; Gustke, M.; Hampel, U. Application of a Wire-Mesh Sensor for the Study of Chemical Species Conversion in a Bubble Column. Chem. Eng. Technol. 2017, 40, 1425–1433. [Google Scholar]
- Jaworski Artur, J.; Meng, G. On-Line Measurement of Separation Dynamics in Primary Gas/Oil/Water Separators: Challenges and Technical Solutions—A Review. J. Pet. Sci. Eng. 2009, 68, 47–59. [Google Scholar] [CrossRef]
- Prescott, N.; Mantha, A.; Kundu, T.; Swenson, J. Subsea Separation—Advanced Subsea Processing with Linear Pipe Separators. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2016. [Google Scholar]
- Orlowski, R. Marlim 3 Phase Subsea Separation System—Challenges and Solutions for the Subsea Separation Station to Cope with Process Requirements. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 2012. [Google Scholar]
- Ninahuanca, H.E.M.; Stel, H.; Morales, R.E.M.; Ofuchi, C.; da Silva, M.J.; Neves, F., Jr. Characterization of the Liquid Film Flow in a Centrifugal Separator. AIChE J. 2016, 62, 2213–2226. [Google Scholar] [CrossRef]
- Rosa, E.S.; França, F.A.; Ribeiro, G.S. The Cyclone Gas-Liquid Separator: Operation and Mechanistic Modeling. J. Pet. Sci. Eng. 2001, 32, 87–101. [Google Scholar] [CrossRef]
- Sunday, K.; Yeung, H.; Lao, L. Study of Phase Distribution in Pipe Cyclonic Compact Separator Using Wire Mesh Sensor. Flow Meas. Instrum. 2017, 53, 154–160. [Google Scholar]
- Kouba, G.E.; Shoham, O. A Review of Gas-Liquid Cylindrical Cyclone (GlCC) Technology. In Proceedings of the Production Separation System International Conference, Aberdeen, UK, 23–24 April 1996. [Google Scholar]
- Kouba, G.; Wang, S.; Gomez, L.; Mohan, R. Review of the State-of-the-Art Gas/Liquid Cylindrical Cyclone (GLCC) Technology—Field Applications. In Proceedings of the 2006 SPE International Oil & Gas Conference and Exhibition, Beijing, China, 1–9 December 2006. [Google Scholar]
- Huang, L.; Deng, S.; Chen, Z.; Guan, J.; Chen, M. Numerical Analysis of a Novel Gas-Liquid Pre-Separation Cyclone. Sep. Purif. Technol. 2018, 194, 470–479. [Google Scholar] [CrossRef]
- Abrand, S.; Bonissel, M.; Roberto, D.S.V.; Raymond, H. Liquid Gas Separation Device and Method, in Particular for Crude Oil Liquid and Gaseous Phases. Patent US2010/0116128 A1, 2010. [Google Scholar]
- Barnea, D. A Unified Model for Predicting Flow-Pattern Transitions for the Whole Range of Pipe Inclinations. Int. J. Multiph. Flow 1987, 13, 1–12. [Google Scholar] [CrossRef]
- Prasser, H. A New Electrode-Mesh Tomograph for Gas–liquid Flows. Flow Meas. Instrum. 1998, 9, 111–119. [Google Scholar] [CrossRef]
- Da Silva, M.J.; Schleicher, E.; Hampel, U. Capacitance Wire-Mesh Sensor for Fast Measurement of Phase Fraction Distributions. Meas. Sci. Technol. 2007, 18, 2245–2251. [Google Scholar] [CrossRef]
- Ali, P.L.; Svrcek, W.Y.; Monnery, W. Computational Fluid Dynamics-Based Study of an Oilfield Separator—Part II: An Optimum Design. Oil Gas. Facil. 2013, 2. [Google Scholar] [CrossRef]
- Casey, T.; Prasser, H.M.; Corradini, M. Wire-Mesh Sensors: A Review of Methods and Uncertainty in Multiphase Flows Relative to other Measurement Techniques. Nucl. Eng. Des. 2018, 337, 205–220. [Google Scholar] [CrossRef]

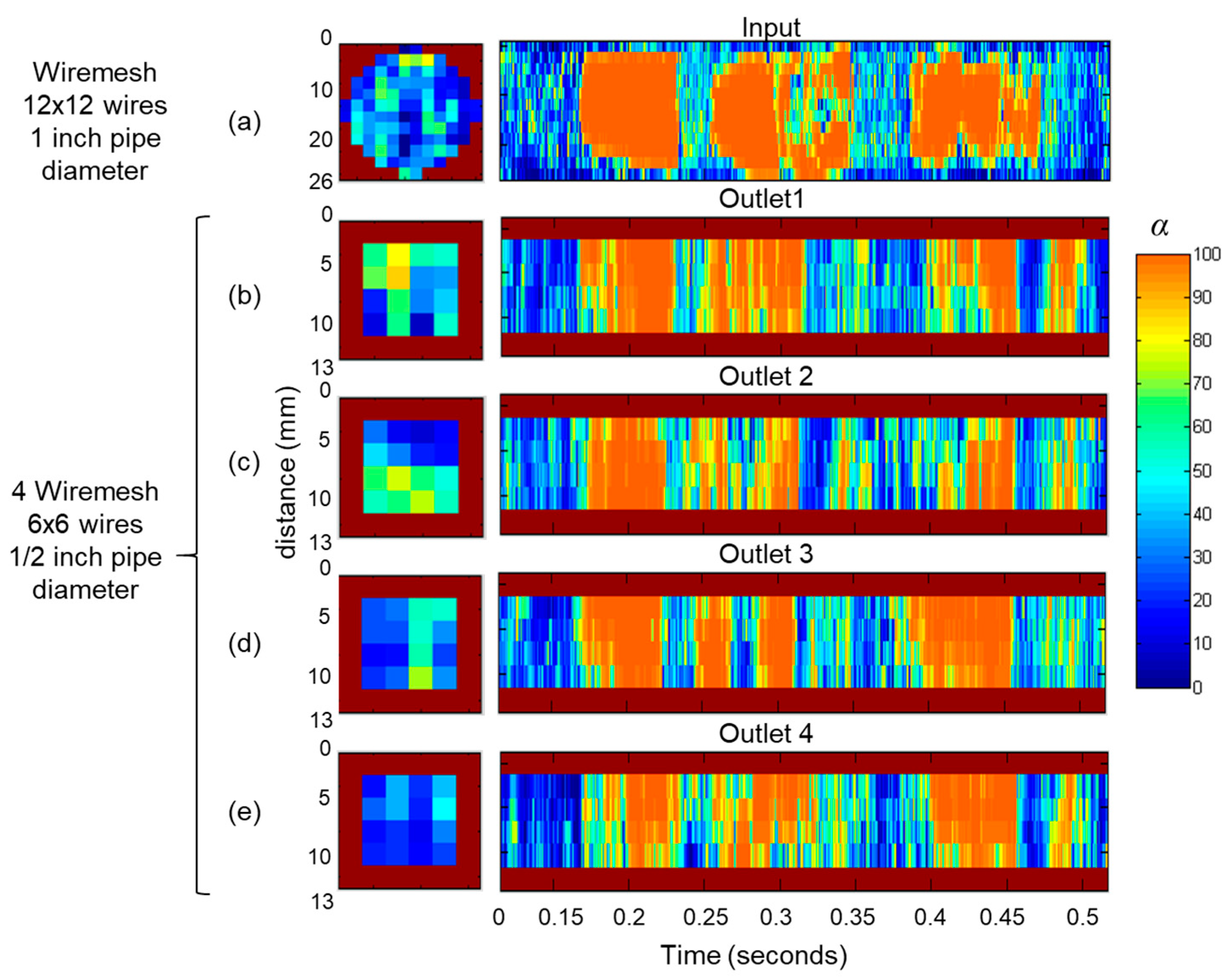
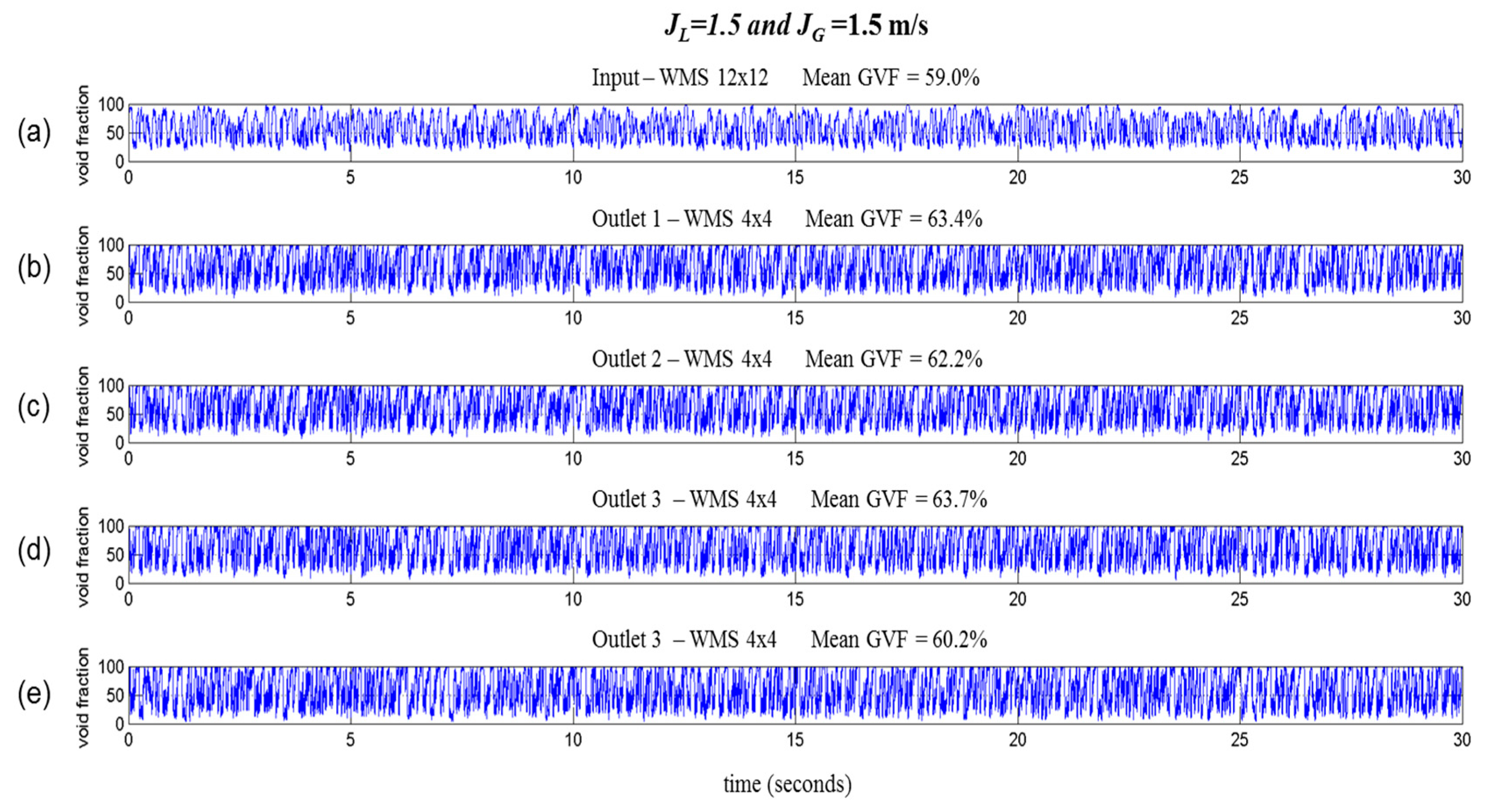
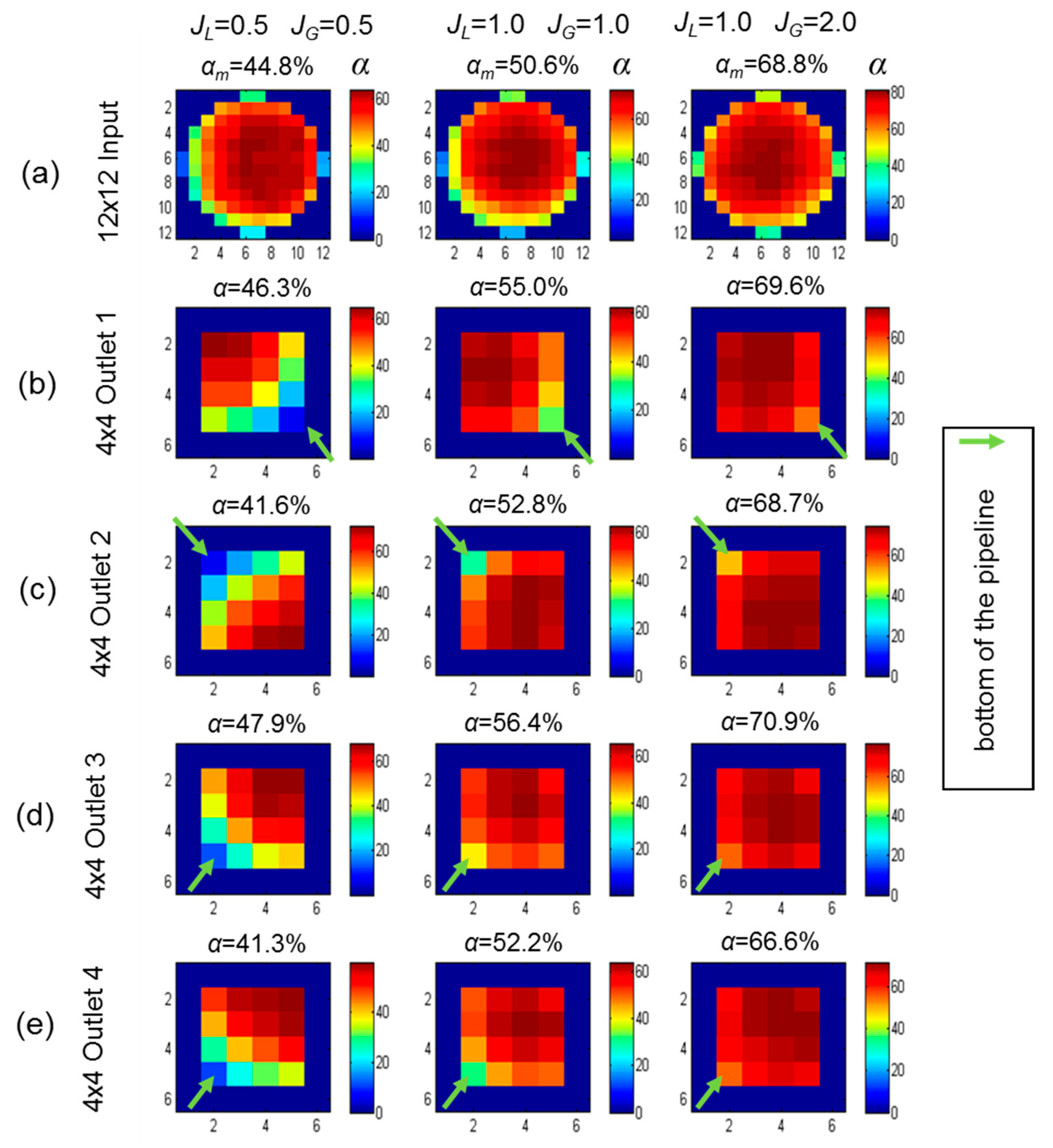
| Test | Input | Cyclonic Chamber | Outlet |
|---|---|---|---|
| Flow pattern analysis | 12 × 12 | 12 × 12 | Two 4 × 4 |
| Flow distribution analysis | 12 × 12 | -- | Four 4 × 4 |
| JL (m/s) | JG (m/s) | Void Fraction (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Input | Outlet 1 | Outlet 2 | Outlet 3 | Outlet 4 | Mean | Worst Case Difference | |||
| 12 × 12 | 4 × 4 | 4 × 4 | 4 × 4 | 4 × 4 | Outlets | Value | % | ||
| 0.5 | 0.5 | 44.84 | 46.30 | 41.63 | 47.91 | 41.34 | 44.29 | 3.61 | 8.2 |
| 0.5 | 1.0 | 60.18 | 64.22 | 60.23 | 65.66 | 58.17 | 62.07 | 3.90 | 6.3 |
| 1.0 | 0.5 | 33.08 | 40.68 | 38.67 | 42.01 | 37.78 | 39.79 | 2.22 | 5.6 |
| 1.0 | 1.0 | 50.59 | 55.04 | 52.82 | 56.47 | 52.29 | 54.15 | 2.32 | 4.3 |
| 1.0 | 1.5 | 62.03 | 63.63 | 62.27 | 65.20 | 60.54 | 62.91 | 2.38 | 3.8 |
| 1.0 | 2.0 | 68.83 | 69.62 | 68.70 | 70.93 | 66.67 | 68.98 | 2.31 | 3.3 |
| 1.5 | 0.5 | 29.93 | 40.63 | 38.41 | 41.44 | 37.88 | 39.59 | 1.85 | 4.7 |
| 1.5 | 1.0 | 47.69 | 53.48 | 52.59 | 54.96 | 50.44 | 52.87 | 2.42 | 4.6 |
| 1.5 | 1.5 | 59.00 | 63.41 | 62.19 | 63.79 | 60.21 | 62.40 | 3.20 | 5.1 |
| 2.0 | 0.5 | 30.80 | 44.14 | 44.32 | 46.14 | 41.93 | 44.13 | 2.20 | 5.0 |
| 2.0 | 1.0 | 45.49 | 56.99 | 55.71 | 57.80 | 54.73 | 56.31 | 1.58 | 2.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ofuchi, C.Y.; Eidt, H.K.; Rodrigues, C.C.; Dos Santos, E.N.; Dos Santos, P.H.D.; Da Silva, M.J.; Neves, F., Jr.; Domingos, P.V.S.R.; Morales, R.E.M. Multiple Wire-Mesh Sensors Applied to the Characterization of Two-Phase Flow inside a Cyclonic Flow Distribution System. Sensors 2019, 19, 193. https://doi.org/10.3390/s19010193
Ofuchi CY, Eidt HK, Rodrigues CC, Dos Santos EN, Dos Santos PHD, Da Silva MJ, Neves F Jr., Domingos PVSR, Morales REM. Multiple Wire-Mesh Sensors Applied to the Characterization of Two-Phase Flow inside a Cyclonic Flow Distribution System. Sensors. 2019; 19(1):193. https://doi.org/10.3390/s19010193
Chicago/Turabian StyleOfuchi, César Y., Henrique K. Eidt, Carolina C. Rodrigues, Eduardo N. Dos Santos, Paulo H. D. Dos Santos, Marco J. Da Silva, Flávio Neves, Jr., Paulo Vinicius S. R. Domingos, and Rigoberto E. M. Morales. 2019. "Multiple Wire-Mesh Sensors Applied to the Characterization of Two-Phase Flow inside a Cyclonic Flow Distribution System" Sensors 19, no. 1: 193. https://doi.org/10.3390/s19010193
APA StyleOfuchi, C. Y., Eidt, H. K., Rodrigues, C. C., Dos Santos, E. N., Dos Santos, P. H. D., Da Silva, M. J., Neves, F., Jr., Domingos, P. V. S. R., & Morales, R. E. M. (2019). Multiple Wire-Mesh Sensors Applied to the Characterization of Two-Phase Flow inside a Cyclonic Flow Distribution System. Sensors, 19(1), 193. https://doi.org/10.3390/s19010193






