Left-Handed Metamaterial-Inspired Unit Cell for S-Band Glucose Sensing Application
Abstract
1. Introduction
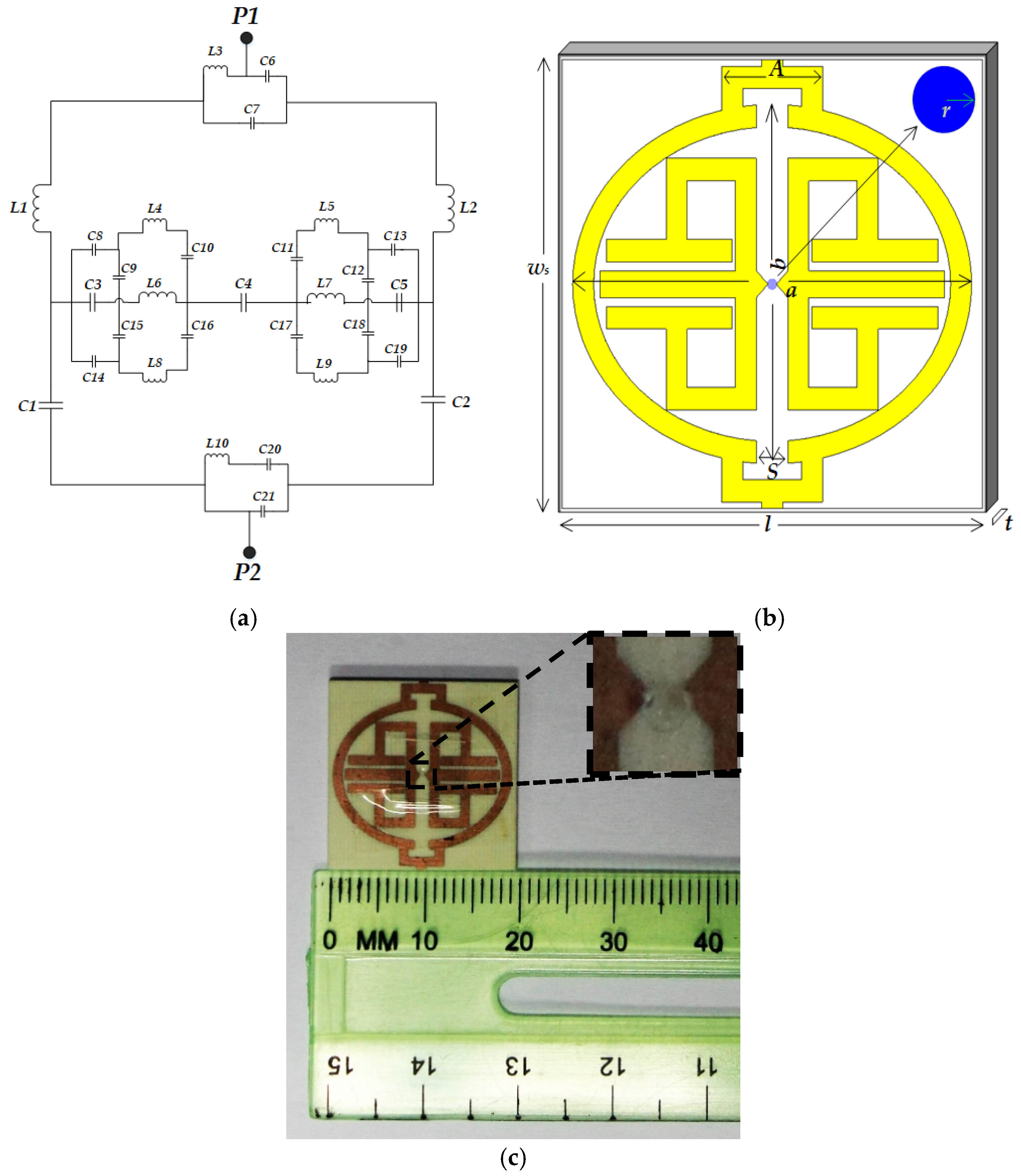
2. Design Methodology
- a = major axis length
- b = minor axis length
- l = length of the micro strip line
- w = width of the micro strip line
- t = thickness of the microstrip line
- = dielectric constant of dielectric film
- d = average distance between mutual striplines
- correction factor =
- ws = substrate width
- = substrate thickness
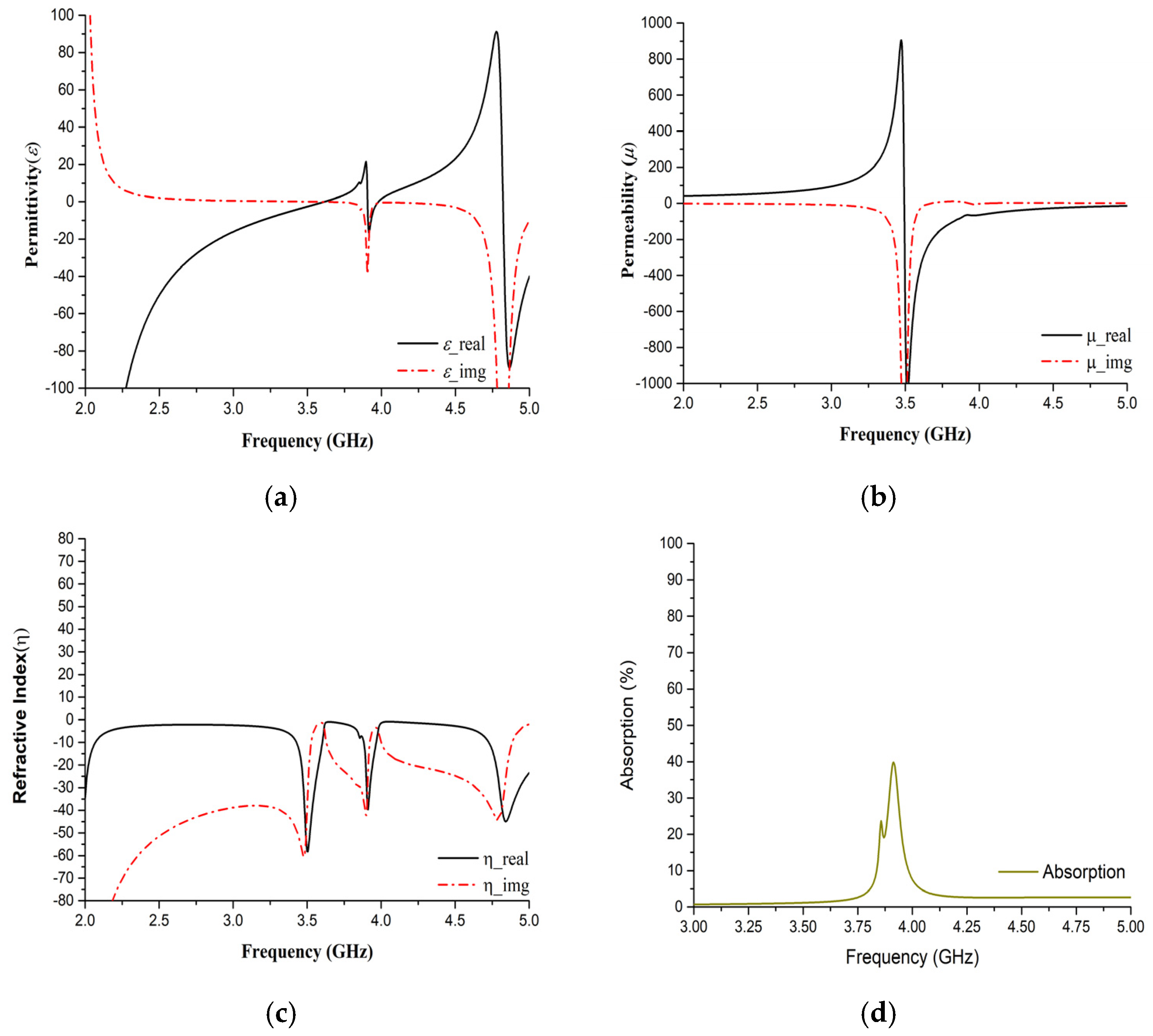
3. Results and Discussion
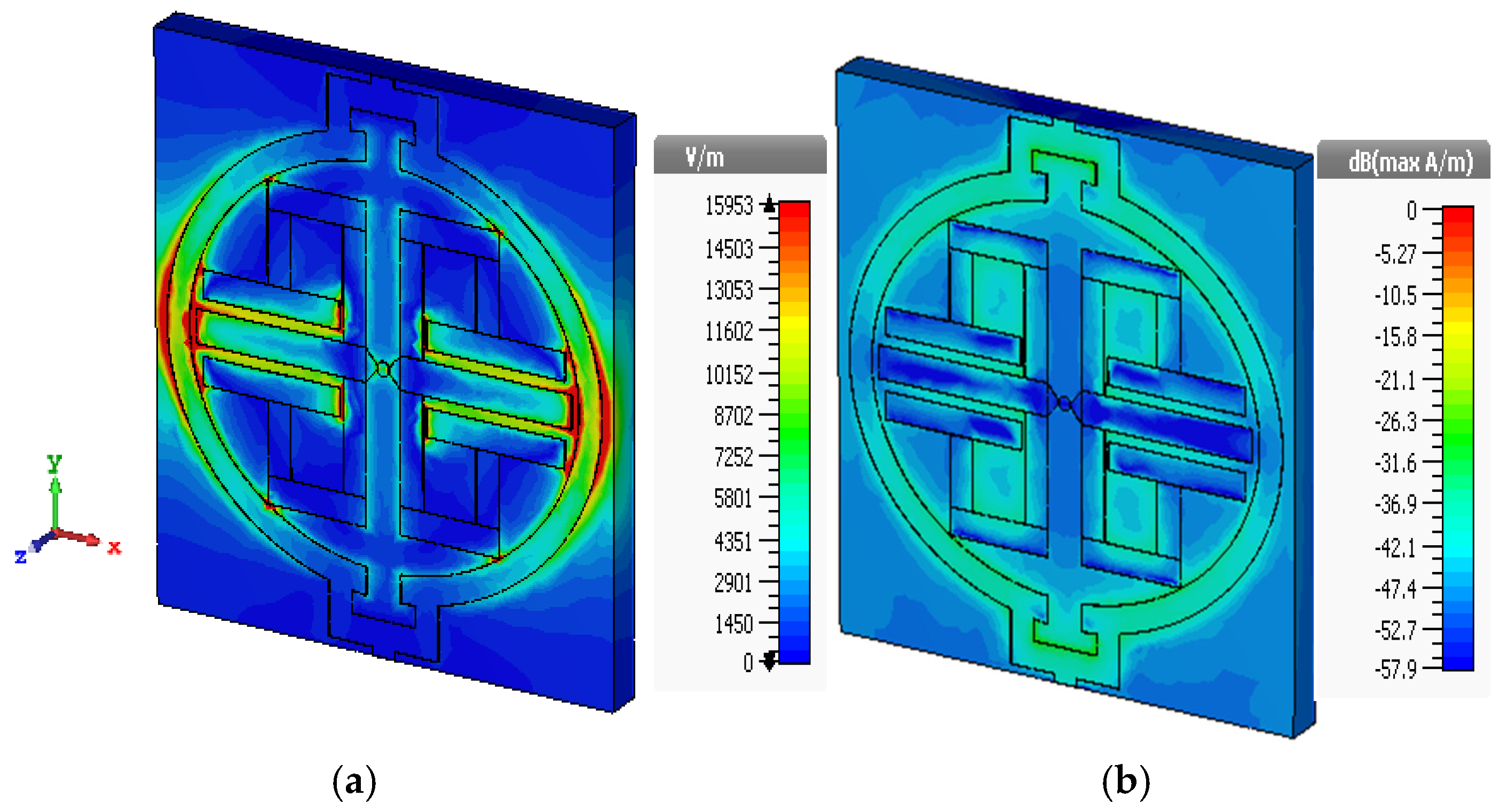
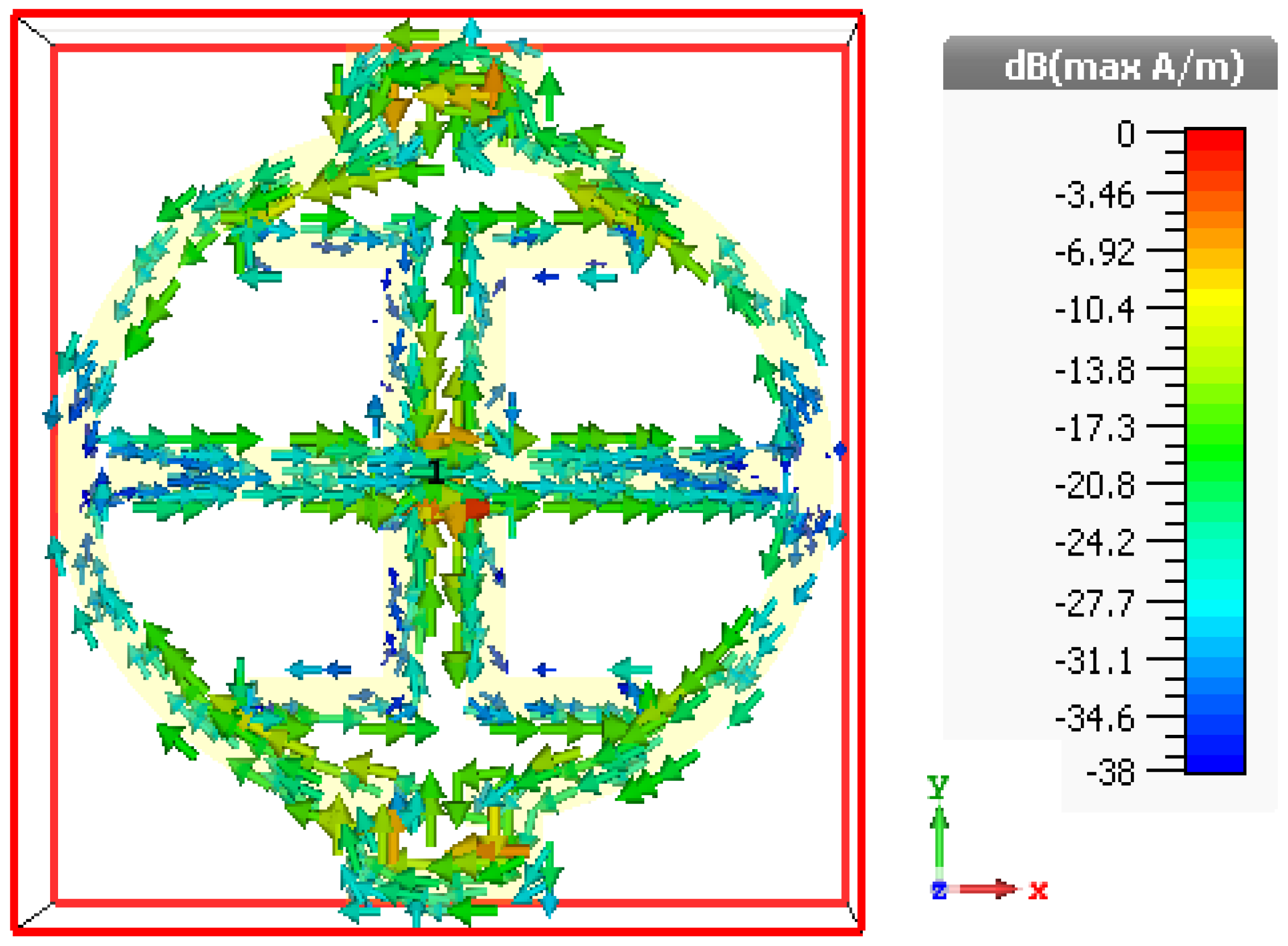
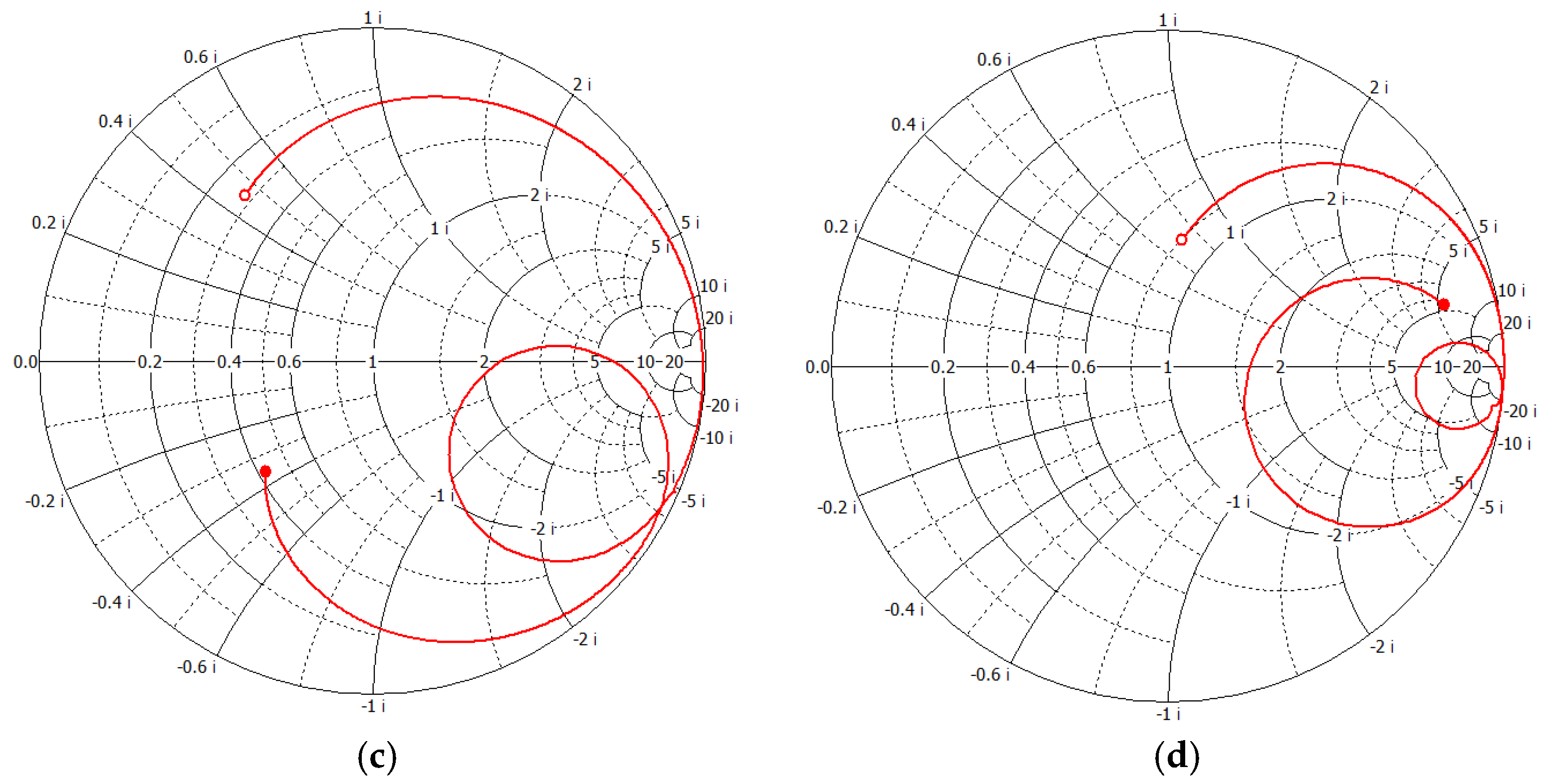
3.1. E-Field, H-Field and Surface Current Analysis
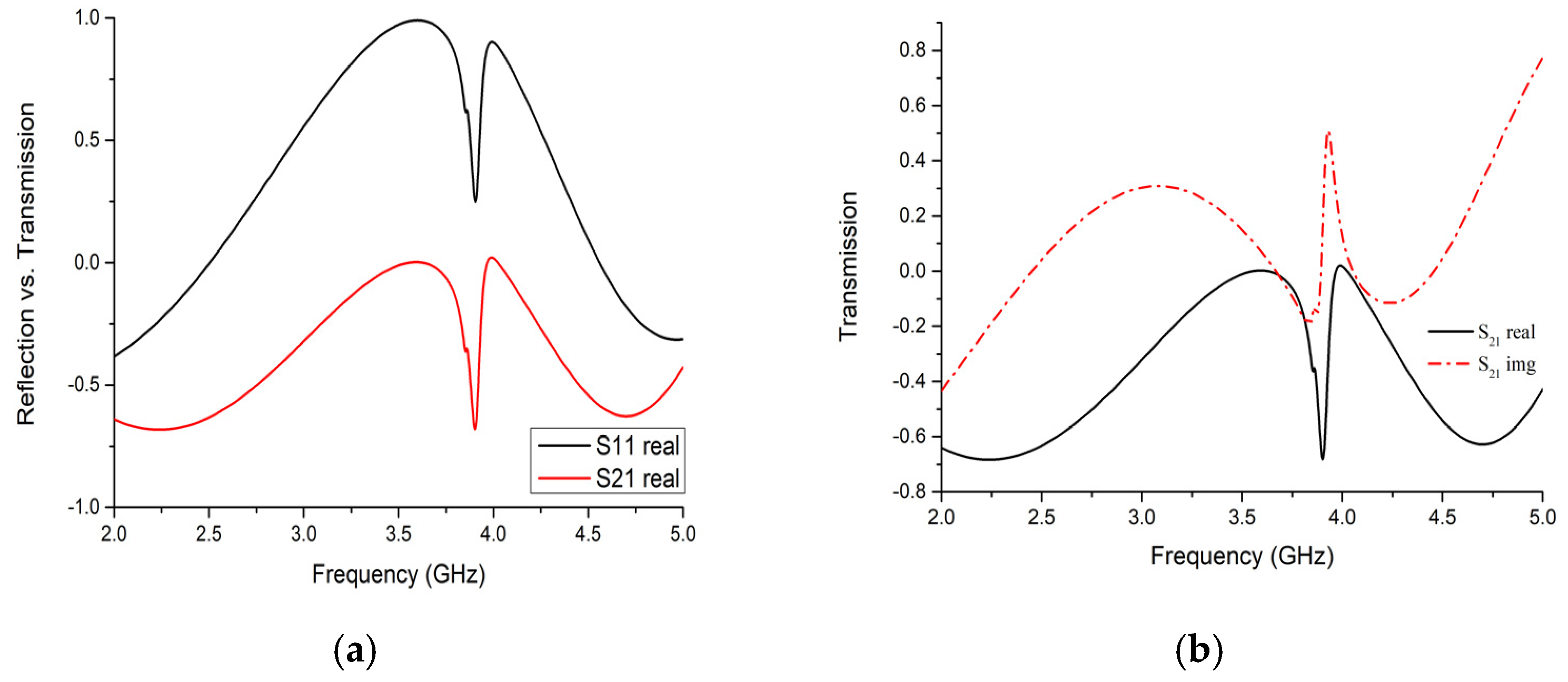
3.2. Transmission and Reflection Performance
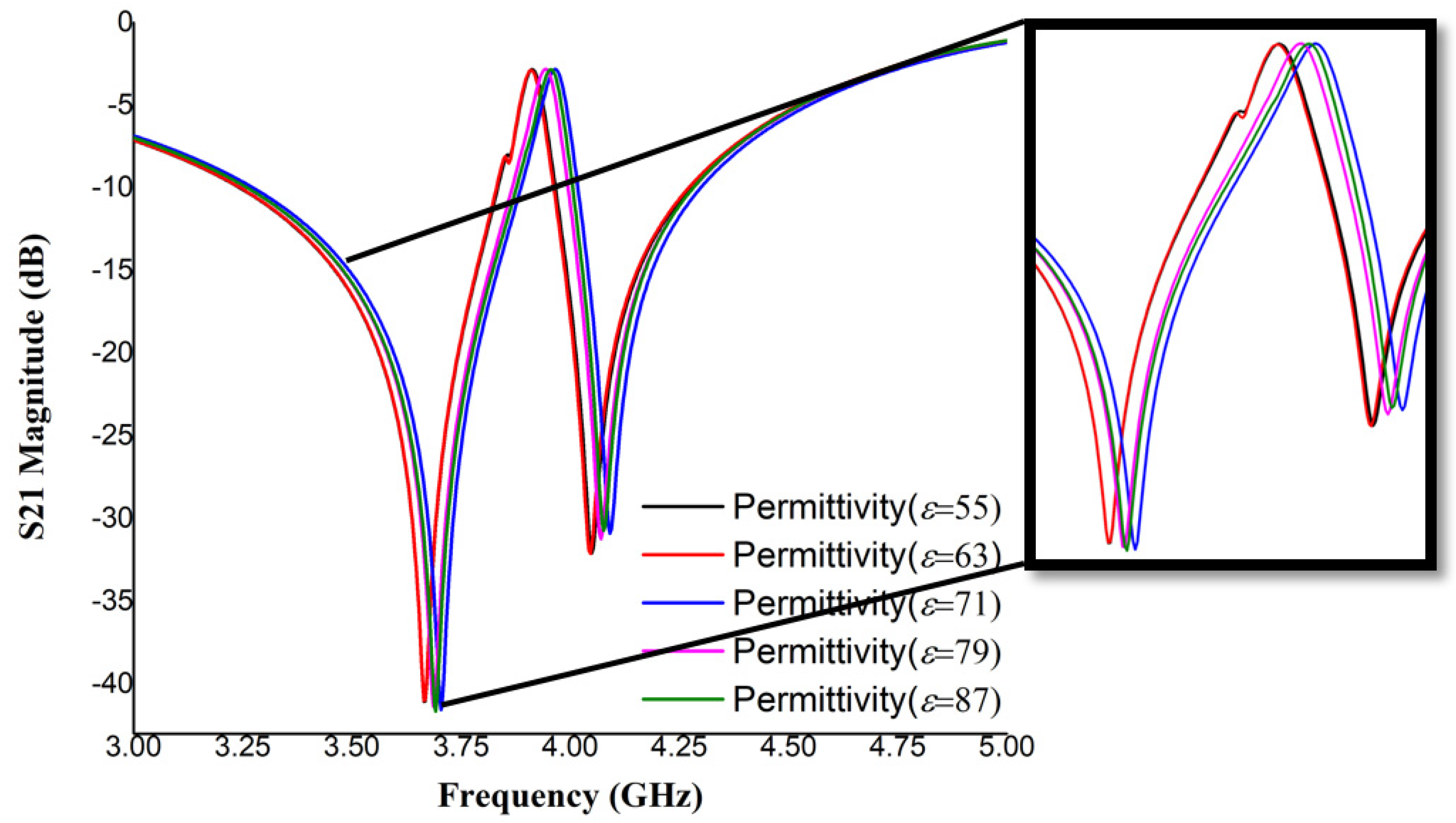
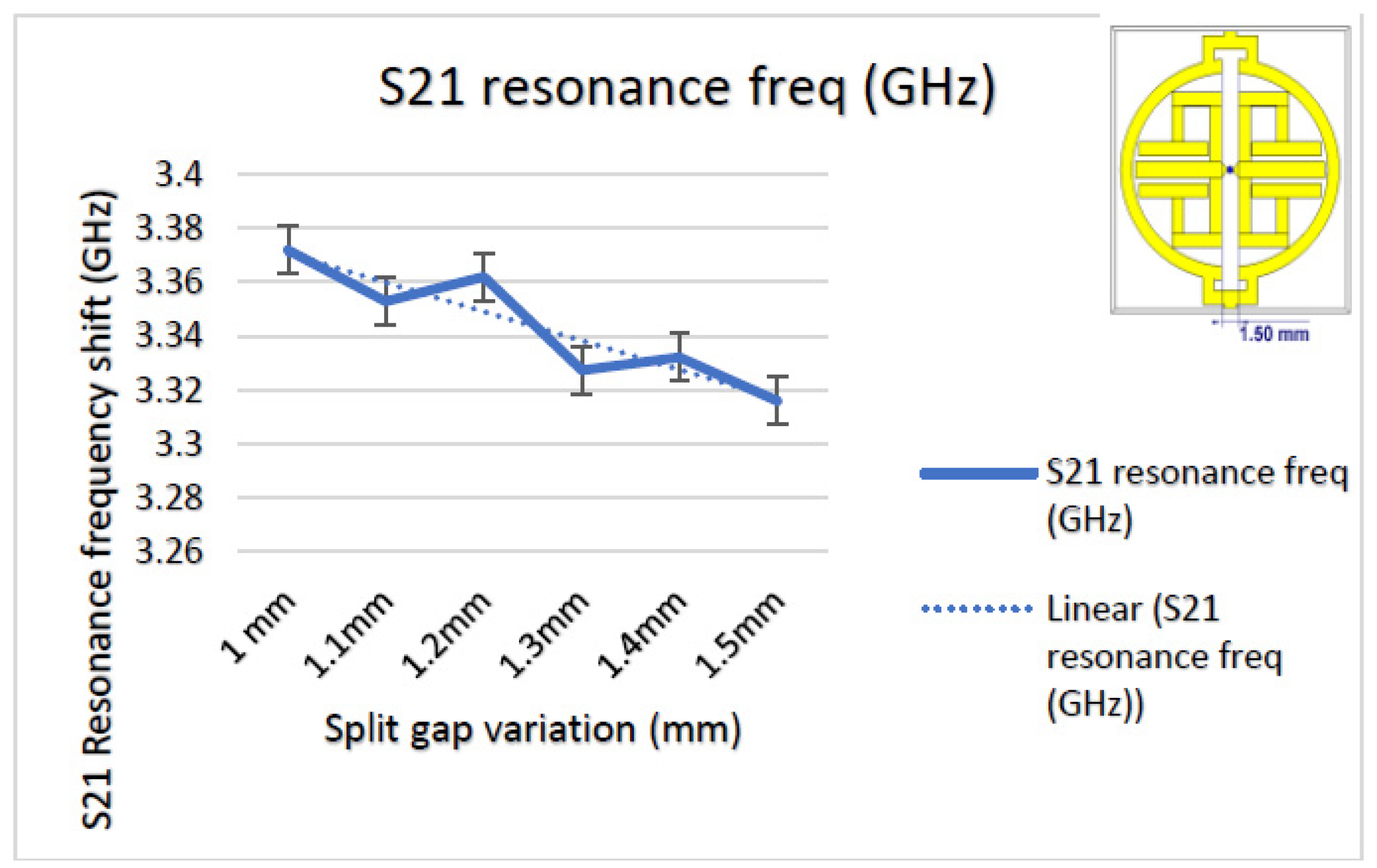
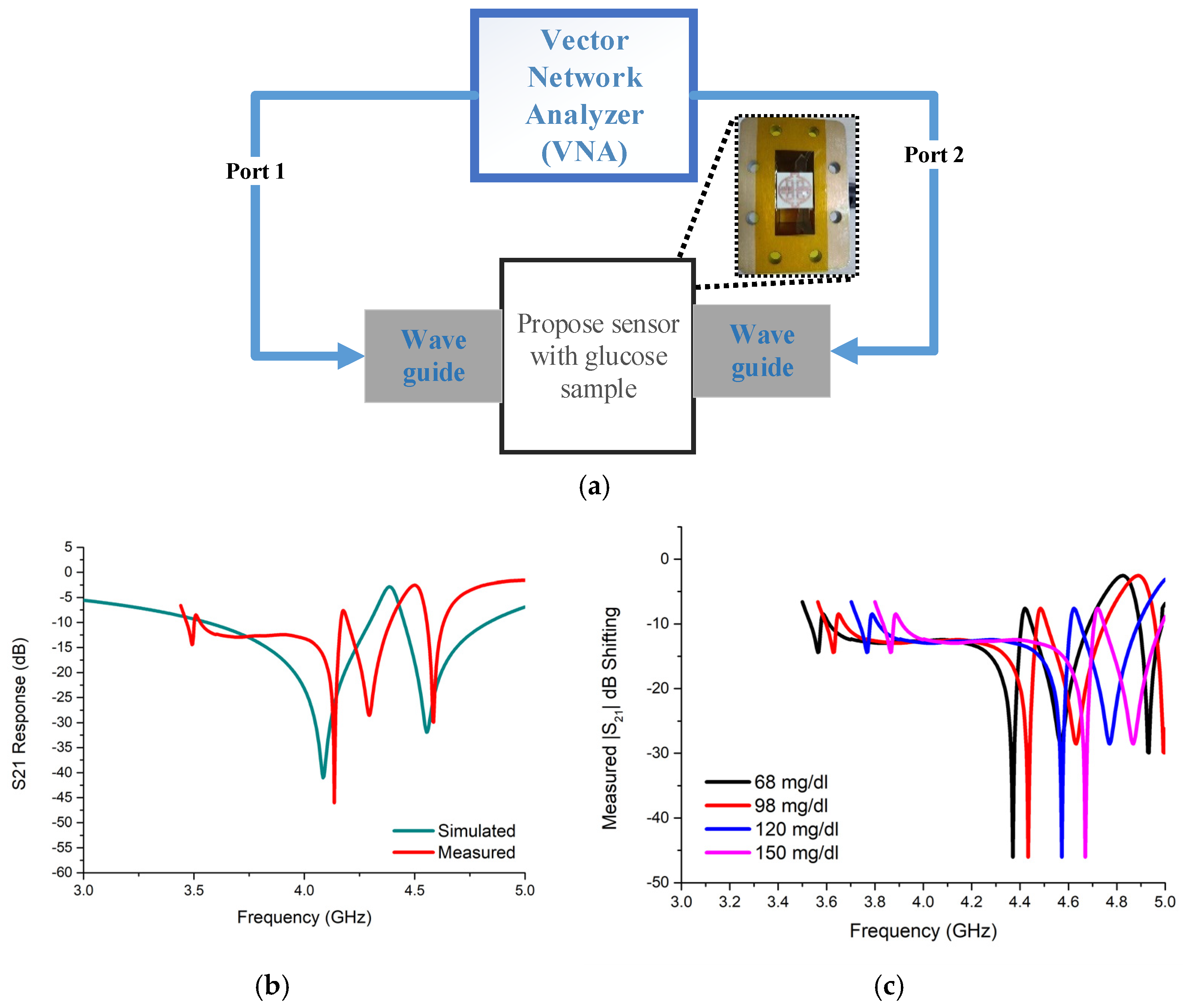
3.3. Sensitvity in the Experimental Setup
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- World Health Organization (WHO). World Health Organization Diabetes Fact Sheet; WHO: Geneva, Switzerland, 2011. [Google Scholar]
- Zhang, R.; Qu, Z.; Jin, H.; Liu, S.; Luo, Y.; Zheng, Y. Noninvasive glucose measurement by microwave biosensor with accuracy enhancement. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–4. [Google Scholar]
- Diabetes Control and Complications Trial Research Group. The effect of intensive treatment of diabetes on the development and progression of long-term complications in insulin-dependent diabetes mellitus. N. Engl. J. Med. 1993, 329, 977–986. [Google Scholar] [CrossRef] [PubMed]
- Hönes, J.; Müller, P.; Surridge, N. The technology behind glucose meters: Test strips. Diabetes Technol. Ther. 2008, 10, S10–S26. [Google Scholar] [CrossRef]
- Clarke, R.; Gregory, A.; Cannell, D.; Patrick, M.; Wylie, S.; Youngs, I.; Hill, G. A Guide to the Characterisation of Dielectric Materials at RF and Microwave Frequencies; NPL: London, UK, 2003. [Google Scholar]
- Marsland, T.; Evans, S. Dielectric measurements with an open-ended coaxial probe. IEE Proc. H Microw. Antennas Propag. 1987, 134, 341–349. [Google Scholar] [CrossRef]
- Chretiennot, T.; Dubuc, D.; Grenier, K. Optimized electromagnetic interaction microwave resonator/microfluidic channel for enhanced liquid bio-sensor. In Proceedings of the 2013 European Microwave Conference (EuMC), Nuremberg, Germany, 6–11 October 2013; pp. 464–467. [Google Scholar]
- Kapilevich, B.; Litvak, B. Microwave sensor for accurate measurements of water solution concentrations. In Proceedings of the 2007 Asia-Pacific Microwave Conference (APMC 2007), Bangkok, Thailand, 11–14 December 2007; pp. 1–4. [Google Scholar]
- Li, L.; Uttamchandani, D. A microwave dielectric biosensor based on suspended distributed mems transmission lines. IEEE Sens. J. 2009, 9, 1825–1830. [Google Scholar] [CrossRef]
- Gennarelli, G.; Romeo, S.; Scarfi, M.R.; Soldovieri, F. A microwave resonant sensor for concentration measurements of liquid solutions. IEEE Sens. J. 2013, 13, 1857–1864. [Google Scholar] [CrossRef]
- Shaforost, E.; Klein, N.; Vitusevich, S.; Barannik, A.; Cherpak, N. High sensitivity microwave characterization of organic molecule solutions of nanoliter volume. Appl. Phys. Lett. 2009, 94, 112901. [Google Scholar] [CrossRef]
- Kim, J.; Babajanyan, A.; Hovsepyan, A.; Lee, K.; Friedman, B. Microwave dielectric resonator biosensor for aqueous glucose solution. Rev. Sci. Instrum. 2008, 79, 086107. [Google Scholar] [CrossRef] [PubMed]
- Guarin, A.; Hofmann, M.; Weigel, R.; Fischer, G.; Kissinger, D. Determination of sugar concentration in aqueous solutions using ultra-wideband microwave impedance spectroscopy. In Proceedings of the 2013 IEEE MTT-S International Microwave Symposium Digest (IMS), Seattle, WA, USA, 2–7 June 2013; pp. 1–4. [Google Scholar]
- Schwerthoeffer, U.; Weigel, R.; Kissinger, D. A highly sensitive glucose biosensor based on a microstrip ring resonator. In Proceedings of the 2013 IEEE MTT-S International Microwave Workshop Series on RF and Wireless Technologies for Biomedical and Healthcare Applications (IMWS-BIO), Singapore, 9–11 December 2013; pp. 1–3. [Google Scholar]
- Navau, C.; Mach-Batlle, R.; Parra, A.; Prat-Camps, J.; Laut, S.; Del-Valle, N.; Sanchez, A. Enhancing the sensitivity of magnetic sensors by 3d metamaterial shells. Sci. Rep. 2017, 7, 44762. [Google Scholar] [CrossRef] [PubMed]
- Dhakal, R.; Wang, C.; Kim, E.-S.; Kim, N.-Y. Complex permittivity characterization of serum with an air-bridge enhanced capacitor for quantifiable detection of glucose. Appl. Phys. Lett. 2015, 106, 073702. [Google Scholar] [CrossRef]
- Kim, N.-Y.; Adhikari, K.K.; Dhakal, R.; Chuluunbaatar, Z.; Wang, C.; Kim, E.-S. Rapid, sensitive, and reusable detection of glucose by a robust radiofrequency integrated passive device biosensor chip. Sci. Rep. 2015, 5, 7807. [Google Scholar] [CrossRef] [PubMed]
- RoyChoudhury, S.; Rawat, V.; Jalal, A.H.; Kale, S.; Bhansali, S. Recent advances in metamaterial split-ring-resonator circuits as biosensors and therapeutic agents. Biosens. Bioelectron. 2016, 86, 595–608. [Google Scholar] [CrossRef] [PubMed]
- Bahl, I.J. Lumped Elements for RF and Microwave Circuits; Artech house: Norwood, MA, USA, 2003. [Google Scholar]
- Terman, F.E. Radio Engineers’ Handbook; The McGraw-Hill Companies, Inc.: New York, NY, USA, 1943. [Google Scholar]
- Islam, S.S.; Faruque, M.R.I.; Islam, M.T. A new direct retrieval method of refractive index for the metamaterial. Curr. Sci. 2015, 109, 337–341. [Google Scholar]
- Yang, J.J.; Huang, M.; Sun, J. Double negative metamaterial sensor based on microring resonator. IEEE Sens. J. 2011, 11, 2254–2259. [Google Scholar] [CrossRef]
- Sethi, K.K.; Palai, G.; Sarkar, P. Realization of accurate blood glucose sensor using photonics based metamaterial. Optik 2018, 168, 296–301. [Google Scholar] [CrossRef]
- Vrba, J.; Vrba, D. A microwave metamaterial inspired sensor for non-invasive blood glucose monitoring. Radioengineering 2015, 24, 877–884. [Google Scholar] [CrossRef]
- Chretiennot, T.; Dubuc, D.; Grenier, K. Microwave-based microfluidic sensor for non-destructive and quantitative glucose monitoring in aqueous solution. Sensors 2016, 16, 1733. [Google Scholar] [CrossRef] [PubMed]
- Sathyanath, D.; Jayakrishnan, M.; Thushara, H.; Mridula, S.; Mohanan, P. Microwave based biosensor for blood glucose monitoring. In Proceedings of the 2015 Fifth International Conference on Advances in Computing and Communications (ICACC), Kochi, India, 2–4 September 2015; pp. 362–365. [Google Scholar]
- Kumari, R.; Patel, P.N.; Yadav, R. An eng resonator-based microwave sensor for the characterization of aqueous glucose. J. Phys. D Appl. Phys. 2018, 51, 075601. [Google Scholar] [CrossRef]
- Parsamyan, H.; Babajanyan, A.Z.; Arakelyan, S.K.; Lee, K. Determination of glucose concentration in aqueous solution by using modified hilbert shaped microwave metamaterial sensor. Proc. YSU Phys. Math. 2018, 52, 144–148. [Google Scholar]
- Sharafadinzadeh, N.; Abdolrazzaghi, M.; Daneshmand, M. Highly sensitive microwave split ring resonator sensor using gap extension for glucose sensing. In Proceedings of the 2017 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Pavia, Italy, 20–22 September 2017; pp. 1–3. [Google Scholar]
| Parameter | l | ws | a | b | r | S | A |
|---|---|---|---|---|---|---|---|
| Size (mm) | 20 | 20 | 19 | 16 | 0.25 | 1.5 | 4.80 |
| Resonance Frequency (GHz) | Permittivity, ε | Permeability, µ | Reflection Co-efficient, η |
|---|---|---|---|
| 3.914 | −16.55 | −65.40 | −38.12 |
| Ref. # | Size (mm) | Substrate Material | Operating Frequency (GHz) | Application Procedure | Sensitivity | Remarks |
|---|---|---|---|---|---|---|
| [24] | 20 × 5.55 | GML 1000 | 1–2 | Non-invasive | 10 mmol/L | Artificial transmission line used for monitoring |
| [2] | 75 × 50 | Inductive coil based | 1–2 | Non-invasive | 400 mg/dL | Data fusion prediction and accuracy enhancement |
| [25] | Sensor unit (20 × 15) | SU-8 | 0–55 | Non-destructive and Quantitative | 7.6 × 10−3 dB/(g/L) | Thin film microstrip technique |
| [26] | 80 × 2.4485 | Rogers RT 5880 | 0–2.4 | Non/minimally invasive | −40 dB/2.5 mL | High Q sensor |
| [27] | 40 × 20 | FR-4 | 1–3 | Invasive | Range 20–100 mg/mL | Microwave filter as Sensor device |
| [28] | 20 × 40 | Al2O3 | 1–6 | Non-invasive | 21 dB shift/(50 mg/dL) | Modified Hilbert curve |
| [29] | 20 × 15 | Rogers RT 5880 | 1–2 | Glucose Sensing | 1.6 MHz shift/(1–15 g/dL) | SRR resonator without metamaterial |
| Proposed Sensor | 20 × 20 | Rogers RO4350B | 2–5 | Non-invasive | 0.037 GHz shift/(30 mg/dL) | Sensing capacity with DNG property & Minimally absorption |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, M.T.; Hoque, A.; Almutairi, A.F.; Amin, N. Left-Handed Metamaterial-Inspired Unit Cell for S-Band Glucose Sensing Application. Sensors 2019, 19, 169. https://doi.org/10.3390/s19010169
Islam MT, Hoque A, Almutairi AF, Amin N. Left-Handed Metamaterial-Inspired Unit Cell for S-Band Glucose Sensing Application. Sensors. 2019; 19(1):169. https://doi.org/10.3390/s19010169
Chicago/Turabian StyleIslam, Mohammad Tariqul, Ahasanul Hoque, Ali F. Almutairi, and Nowshad Amin. 2019. "Left-Handed Metamaterial-Inspired Unit Cell for S-Band Glucose Sensing Application" Sensors 19, no. 1: 169. https://doi.org/10.3390/s19010169
APA StyleIslam, M. T., Hoque, A., Almutairi, A. F., & Amin, N. (2019). Left-Handed Metamaterial-Inspired Unit Cell for S-Band Glucose Sensing Application. Sensors, 19(1), 169. https://doi.org/10.3390/s19010169







