Vibration Mitigation Effect Investigation of a New Slab Track Plate Design
Abstract
:1. Introduction
2. Theoretical Background
2.1. Modal Analysis Using PolyMAX
2.2. Structural Characteristics for Slabs
3. Design of the Novel Track Damping Plate
3.1. The Raw Material and the Recipe
3.2. Test Specimen Design and Mechanical Properties Testing Procedure
3.3. Mechanical Properties Analysis
4. Modal Analysis for the Novel Track Damping Plate
4.1. The New Designed Vibration Mitigation Slab Track Plate Casting
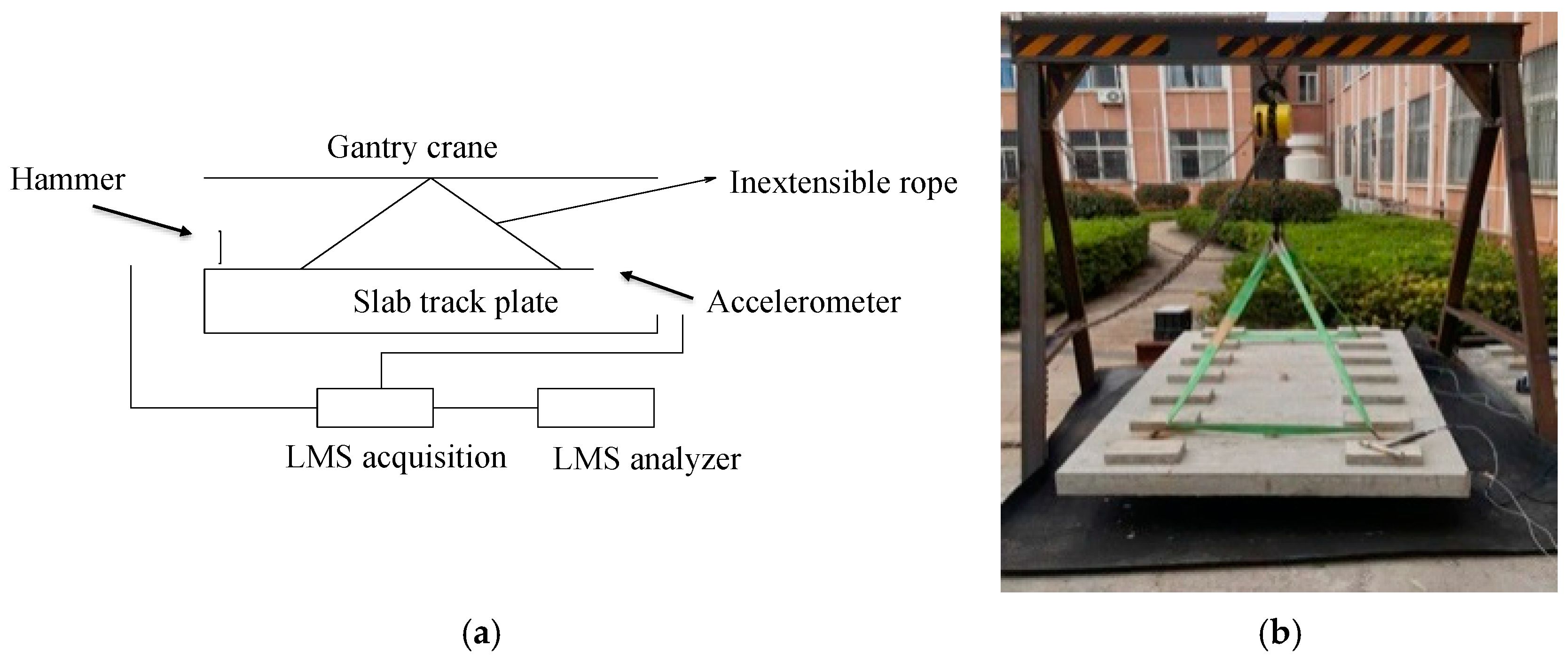
4.2. Test Instrumentation
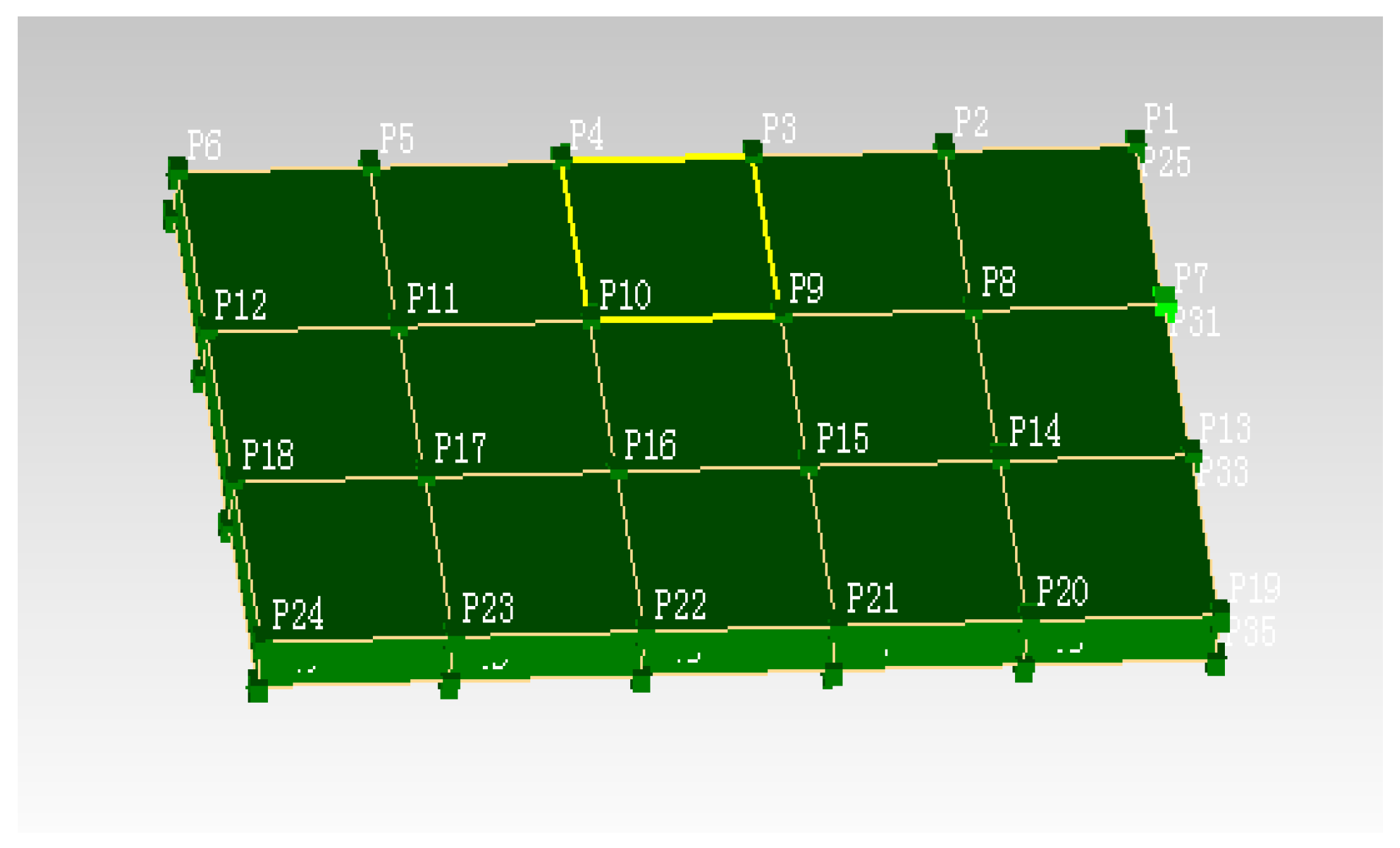
4.3. Modal Testing Setup
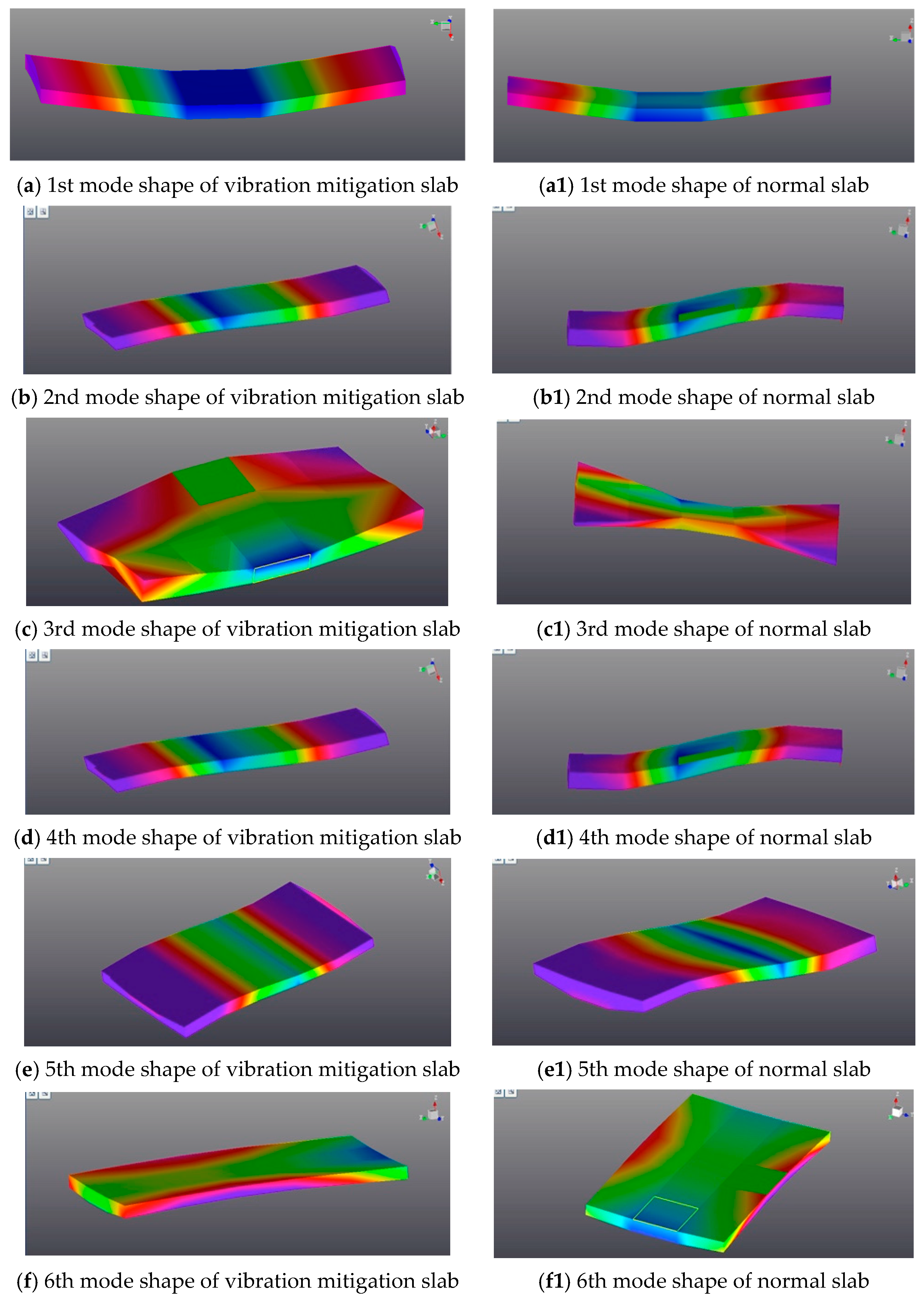
4.4. Modal Analysis
5. Vibration Mitigation Analysis for the New Designed Track Damping Plate
5.1. Testing Setup
5.2. Tests and Results Analysis
6. Conclusions
- (1)
- The introduction of silicon rubber could promote the damping ratio of the new vibration mitigation slab track plate but reduces its strength, but the coupling agent can compensate the strength at certain amount. For the purpose of balancing the mechanical properties and damping characteristic, it is indispensable to keep the r/c to be 6%, and adding 1.5% by of coupling agent.
- (2)
- Under the same constraint conditions and structural style, the mode shapes of the newly designed vibration mitigation slab track plate overall agreed with those of the normal slab track plates, but each resonant frequency for the vibration mitigation slab track plate is less than that for the normal slab track plate; each modal damping for the vibration mitigation slab track plate is higher than that for the normal slab track plate. This means that the dynamic characteristics and damping properties are all enhanced.
- (3)
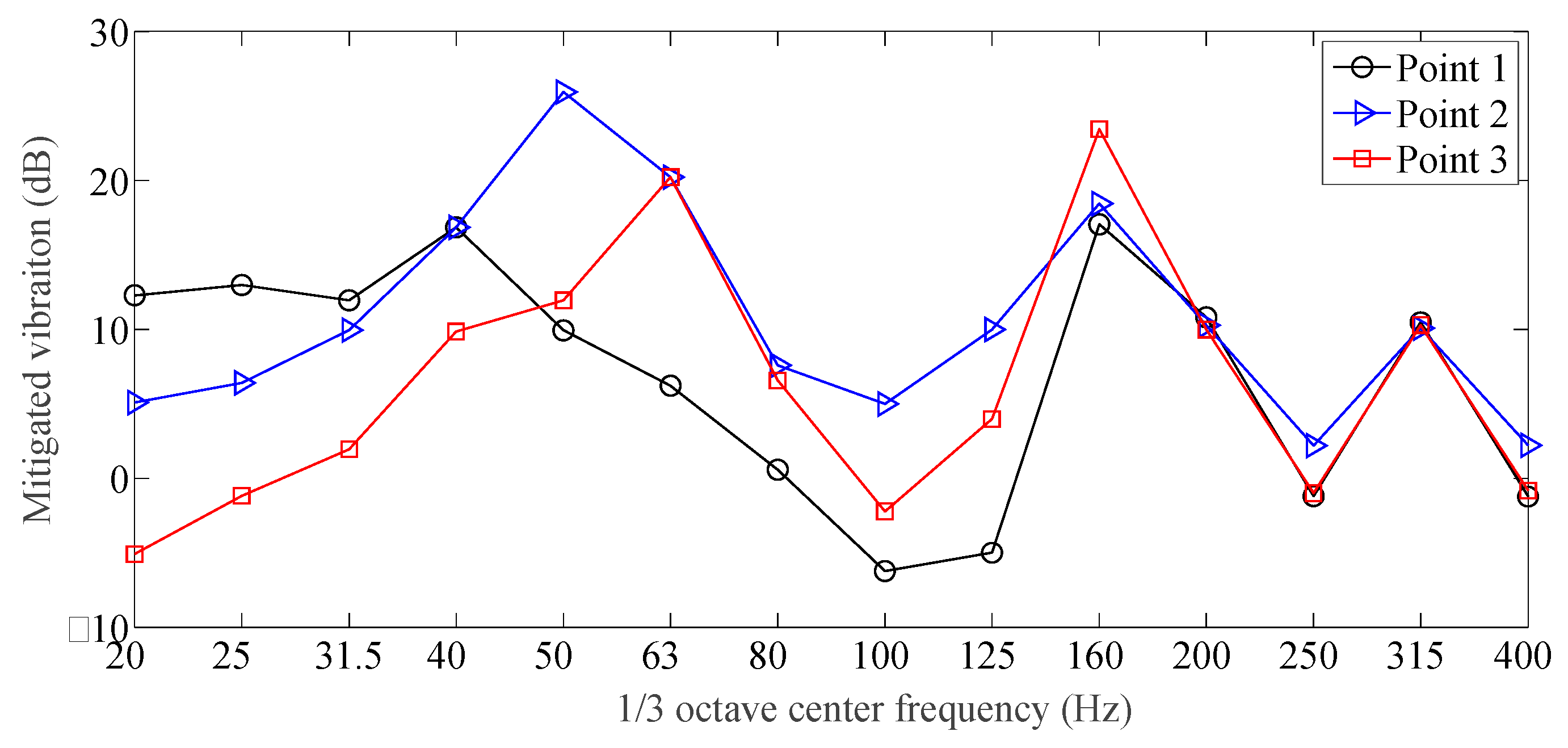
- In laboratory testing, under excitation loading, the new vibration mitigation slab track plate has better vibration mitigation performance, with a maximum vibration mitigation of 26.8 dB, and an average vibration mitigation of 8.9 dB, which implies the newly designed slab track plate has better vibration mitigation capacity. The vibration mitigation performance for this newly designed slab track plate under real rail transit lines needs further investigation.
Author Contributions
Funding
Conflicts of Interest
References
- Maia, N.M.M.; Silva, J.M.M. Theoretical and Experimental Modal Analysis (Mechanical Engineering Research Studies: Engineering Dynamics Series); Wiley-Blackwell: Hoboken, NJ, USA; ISBN1 0863802087. ISBN2 978-0863802089.
- Zhou, Y.; Maia, N.M.M.; Sampaio, R.; Wahab, M.A. Structural damage detection using transmissibility together with hierarchical clustering analysis and similarity measure. Struct. Health Monit. Int. J. 2017, 16, 711–731. [Google Scholar] [CrossRef]
- Zhou, Y.; Wahab, M.A. Cosine based extended transmissibility damage indicators for structural damage detection. Eng. Struct. 2017, 141, 175–183. [Google Scholar] [CrossRef]
- Gupta, S.; Stanus, Y.; Lombaert, G.; Degrande, G. Influence of tunnel and soil parameters on vibrations from underground railways. J. Sound Vib. 2009, 327, 70–91. [Google Scholar] [CrossRef]
- Liu, H.P.; Wu, T.X.; Li, Z.G. Theoretical modelling and effectiveness study of rail vibration absorber for noise control. J. Sound Vib. 2009, 323, 594–608. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, J.; Zhao, Y.; Howson, W.P.; Williams, F.W. Symplectic random vibration analysis of a vehicle moving on an infinitely long periodic track. J. Sound Vib. 2010, 329, 4440–4454. [Google Scholar] [CrossRef]
- Galvin, P.; Romero, A.; Dominguez, J. Vibrations induced by HST passage on ballast and non-ballast tracks. Soil Dyn. Earthq. Eng. 2010, 30, 862–873. [Google Scholar] [CrossRef] [Green Version]
- Feng, H. Design of Rubber Concrete Monolithic Track Bed and Study on its Damping Performance. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2015. [Google Scholar]
- Kuo, K.A.; Hunt, H.E.M.; Hussein, M.F.M. The effect of a twin tunnel on the propagation of ground-borne vibration from an underground railway. J. Sound Vib. 2011, 330, 6203–6222. [Google Scholar] [CrossRef]
- Çalım, F.F. Forced vibration of curved beams on two-parameter elastic foundation. Appl. Math. Model. 2012, 36, 964–973. [Google Scholar] [CrossRef]
- Koroma, S.G.; Hussein, M.F.M.; Owen, J.S. Vibration of a beam on continuous elastic foundation with nonhomogeneous stiffness and damping under a harmonically excited mass. J. Sound Vib. 2014, 333, 2571–2587. [Google Scholar] [CrossRef] [Green Version]
- Connolly, D.; Giannopoulos, A.; Forde, M.C. Numerical modelling of ground borne vibrations from high speed rail lines on embankments. Soil Dyn. Earthq. Eng. 2013, 46, 13–19. [Google Scholar] [CrossRef] [Green Version]
- Yaseri, M.H.; Bazyar, N. Hataf 3D coupled scaled boundary finite-element/finite-element analysis of ground vibrations induced by underground train movement. Comput. Geotech. 2014, 60, 1–8. [Google Scholar] [CrossRef]
- Attar, M.; Karrech, A.; Regenauer-Lieb, K. Free vibration analysis of a cracked shear deformable beam on a two-parameter elastic foundation using a lattice spring model. J. Sound Vib. 2014, 333, 2359–2377. [Google Scholar] [CrossRef]
- Lopes, P.; Costa, P.A.; Ferraz, M.; Calçada, R.; Cardoso, A.S. Numerical modeling of vibrations induced by railway traffic in tunnels: From the source to the nearby buildings. Soil Dyn. Earthq. Eng. 2014, 61–62, 269–285. [Google Scholar] [CrossRef]
- Lombaert, G.; Galvín, P.; François, S.; Degrande, G. Quantification of uncertainty in the prediction of railway induced ground vibration due to the use of statistical track unevenness data. J. Sound Vib. 2014, 333, 4232–4253. [Google Scholar] [CrossRef] [Green Version]
- Kouroussis, G.; van Parys, L.; Conti, C.; Verlinden, O. Using three-dimensional finite element analysis in time domain to model railway-induced ground vibrations. Adv. Eng. Softw. 2014, 70, 63–76. [Google Scholar] [CrossRef]
- Amado-Mendes, P.; Costa, P.A.; Godinho, L.M.C.; Lopes, P. 2.5D MFS–FEM model for the prediction of vibrations due to underground railway traffic. Eng. Struct. 2015, 104, 141–154. [Google Scholar] [CrossRef]
- Paneiro, G.; Durão, F.O.; Silva, M.C.E.; Neves, P.F. Prediction of ground vibration amplitudes due to urban railway traffic using quantitative and qualitative field data. Transp. Res. Part D 2015, 40, 1–13. [Google Scholar] [CrossRef]
- Xu, Q.; Ou, X.; Au, F.T.K.; Lou, P.; Xiao, Z. Effects of track irregularities on environmental vibration caused by underground railway. Eur. J. Mech. A Solids 2016, 59, 280–293. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhao, Y.; Xu, W.; Yu, Z.; Chen, Li.; Lou, P. Random vibration analysis of train–bridge under track irregularities and traveling seismic waves using train–slab track–bridge interaction model. J. Sound Vib. 2015, 342, 22–43. [Google Scholar] [CrossRef]
- El Kacimi, A.; Woodward, P.K.; Laghrouche, O.; Medero, G. Time domain 3D finite element modelling of train-induced vibration at high speed. Comput. Struct. 2013, 118, 66–73. [Google Scholar] [CrossRef]
- Zeng, Z.; Liu, F.; Lou, P.; Zhao, Y.; Peng, L. Formulation of three-dimensional equations of motion for train–slab track–bridge interaction system and its application to random vibration analysis. Appl. Math. Model. 2016, 40, 5891–5929. [Google Scholar] [CrossRef]
- Kouroussis, G.; Vogiatzis, K.E.; Connolly, D.P. A combined numerical/experimental prediction method for urban railway vibration. Soil Dyn. Earthq. Eng. 2017, 97, 377–386. [Google Scholar] [CrossRef]
- Costa, P.A.; Calcada, R.; Cardoso, A.S. Ballast mats for the reduction of railway traffic vibrations. Numerical study. Soil Dyn. Earthq. Eng. 2012, 42, 137–150. [Google Scholar] [CrossRef]
- Zhu, S.; Yang, J.; Yan, H.; Zhang, L.; Cai, C. Low-frequency vibration control of floating slab tracks using dynamic vibration absorbers. Veh. Syst. Dyn. 2015, 53, 1296–1314. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, J.; Cai, C.; Wang, K.; Zhai, W. Development of a Vibration Attenuation Track at Low Frequencies for Urban Rail Transit. Comput.-Aided Civ. Infrastruct. Eng. 2017, 32, 713–726. [Google Scholar] [CrossRef]
- Kefei, L.; Weining, L.; Xiaojing, S.; Deyun, D.; Yang, Y. Field test and analysis of vibration reduction measures for underground lines of Beijing Metro Line 5. Railway Trans. 2011, 33, 112–118. [Google Scholar]
- Linfeng, L.; Meng, M.; Weining, L.; Linlin, D. Study on the damping effect of steel spring floating slab track under different excitation. Eng. Mech. 2018, 35, 253–258. (In Chinese) [Google Scholar]
- Wei, Z.; Boogaard, A.; Núñez, A.; Li, Z.; Dollevoet, R. An integrated approach for characterizing the dynamic behaviour of wheel-rail interaction at crossings. IEEE Trans. Instrum. Meas. 2018, 67, 2332–2344. [Google Scholar] [CrossRef]
- Jamshidi, A.; Faghih-Roohi, S.; Hajizadeh, S.; Núñez, A.; Babuska, R.; Dollevoet, R.; Li, Z.; De Schutter, B. A big data analysis approach for rail failure risk assessment. Risk Anal. 2017, 37, 1495–1507. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Núñez, A.; Dollevoet, R. Entropy-based local irregularity detection for high-speed railway catenaries with frequent inspections. IEEE Trans. Instrum. Meas. 2018, accepted. [Google Scholar] [CrossRef]
- Marin, L.; Cruz, N.; Saez, D.; Sumner, M.; Núñez, A. Prediction interval methodology based on fuzzy numbers and its extension to fuzzy systems and neural networks. Expert Syst. Appl. 2019, 119, 128–141. [Google Scholar] [CrossRef]
- Zhou, Yu.; Maia, N.M.M.; Wahab, M.A. Damage detection using transmissibility compressed by principal component analysis enhanced with distance measure. J. Vib. Control 2016, 2001–2019. [Google Scholar] [CrossRef]
- Zhou, Y.; Qian, X.; Birnie, A.; Zhao, X. A reference free ultrasonic phased array to identify surface cracks in welded steel pipes based on transmissibility. Int. J. Press. Vessel. Pip. 2018, 168, 66–78. [Google Scholar] [CrossRef]
- Montalvao, D.; Maia, N.M.M.; Ribeiro, A.M.R. A review of vibration-based structural health monitoring with special emphasis on composite materials. Shock Vib. Dig. 2006, 38, 295–324. [Google Scholar] [CrossRef]
- Qin, S.; Reynders, E.; He, L.; Bui, T.T.; de Roeck, G. Effects of initial conditions in operational modal analysis. Struct. Control Health Monit. 2014, 21, 557–573. [Google Scholar] [CrossRef]
- Lv, Z.; Yang, C.; Tang, L. Research progress of multi-point excitation modal parameter identification methods. Vib. Impact 2011, 30, 197–203. [Google Scholar]
- Ma, D. Noise and Vibration Control Engineering Handbook; Machinery Industry Press: Beijing, China, 2002; ISBN 9787111108306. [Google Scholar]
- Yan, L.; Jenkins, C.H.; Pendleton, R.L. Polyolefin fiber-reinforced concrete composites, Part I: Damping and frequency characteristics. Cem. Concr. Res. 2000, 30, 391. [Google Scholar] [CrossRef]
- Ministry of Construction of the People's Republic of China. GB/T50081-2002 Standard for Test Methods of Mechanical Properties of Ordinary Concrete; China Construction Industry Press: Beijing, China, 2004.
- Ke, G.; Guo, C.; Hu, S.; Chen, Z.; Shi, J.; Sun, D.; Chen, J. Study on damping ratio of concrete. J. Mater. 2004, 1, 35–40. [Google Scholar]
- Wan, Z.; Liu, P.; Shi, W. Experimental study and damping mechanism of high damping concrete. Concrete 2007, 07, 37–40. [Google Scholar]
- Zhou, Y.; He, S.; Song, Y.; Zhao, X.; Yang, Y. Dynamic test of curved continuous rigid frame model bridge based on hammering method. Vib. Test. Diagn. 2007, 3, 212–215, 258. [Google Scholar]
- Zhang, H.; Song, G.; Zhang, Z.; Kong, X.J. Application of modal separation method in dynamic loading test of arch bridge. Highw. Traffic Sci. Technol. 2005, 1, 66–68. [Google Scholar]
- Wang, H.; Qiu, T.-S. A unified classification method for non-stationary deterministic signals and non-stationary random signals. J. Commun. 2015, 36, 1–10. [Google Scholar]






| Concrete Recipe | w/c Ratio | r/c Ratio/% | Cement Weight (kg) | Silicon Rubber Weight (kg) | Coupling Agent/% |
|---|---|---|---|---|---|
| #1 | 0.6 | - | 308 | 0 | - |
| #2 | 0.6 | 3 | 308 | 10 | - |
| #3 | 0.6 | 3 | 308 | 10 | 1.5 |
| #4 | 0.6 | 6 | 308 | 20 | - |
| #5 | 0.6 | 6 | 308 | 20 | 1.5 |
| #6 | 0.6 | 9 | 308 | 40 | - |
| #7 | 0.6 | 9 | 308 | 40 | 1.5 |
| #8 | 0.6 | 12 | 308 | 80 | - |
| #9 | 0.6 | 12 | 308 | 80 | 1.5 |
| Concrete Specimen | Tensile Strength/MPa | Young’s Modulus/GPa | Damping Ratio/% |
|---|---|---|---|
| #1 | 46.5 | 35.9 | 2.05 |
| #2 | 43.5 | 31.9 | 2.55 |
| #3 | 44.8 | 31.4 | 2.57 |
| #4 | 38.4 | 30.2 | 3.31 |
| #5 | 42.2 | 29.8 | 3.44 |
| #6 | 31.2 | 27.5 | 3.92 |
| #7 | 36.7 | 27.9 | 4.06 |
| #8 | 23.3 | 26.4 | 4.39 |
| #9 | 29.1 | 26.2 | 4.52 |
| Order | Vibration Mitigation Slab Plate | Normal Slab Plate | ||||||
|---|---|---|---|---|---|---|---|---|
| Resonant Frequency/Hz | Damping Ratio/% | Resonant Frequency/Hz | Damping Ratio/% | |||||
| Test | FEA | Error/% | Test | FEA | Error/% | |||
| 1 | 65.771 | 64.940 | 1.19 | 0.89 | 85.084 | 84.530 | 0.66 | 0.42 |
| 2 | 75.211 | 73.290 | 2.62 | 0.87 | 97.297 | 96.020 | 1.33 | 0.48 |
| 3 | 161.115 | 160.250 | 0.54 | 0.98 | 208.435 | 204.83 | 1.76 | 0.45 |
| 4 | 179.393 | 175.680 | 2.11 | 0.91 | 231.004 | 229.79 | 0.53 | 0.47 |
| 5 | 201.462 | 199.450 | 1.01 | 0.85 | 266.271 | 268.360 | 0.78 | 0.49 |
| 6 | 248.508 | 250.420 | 0.76 | 1.04 | 327.284 | 330.910 | 1.10 | 0.56 |
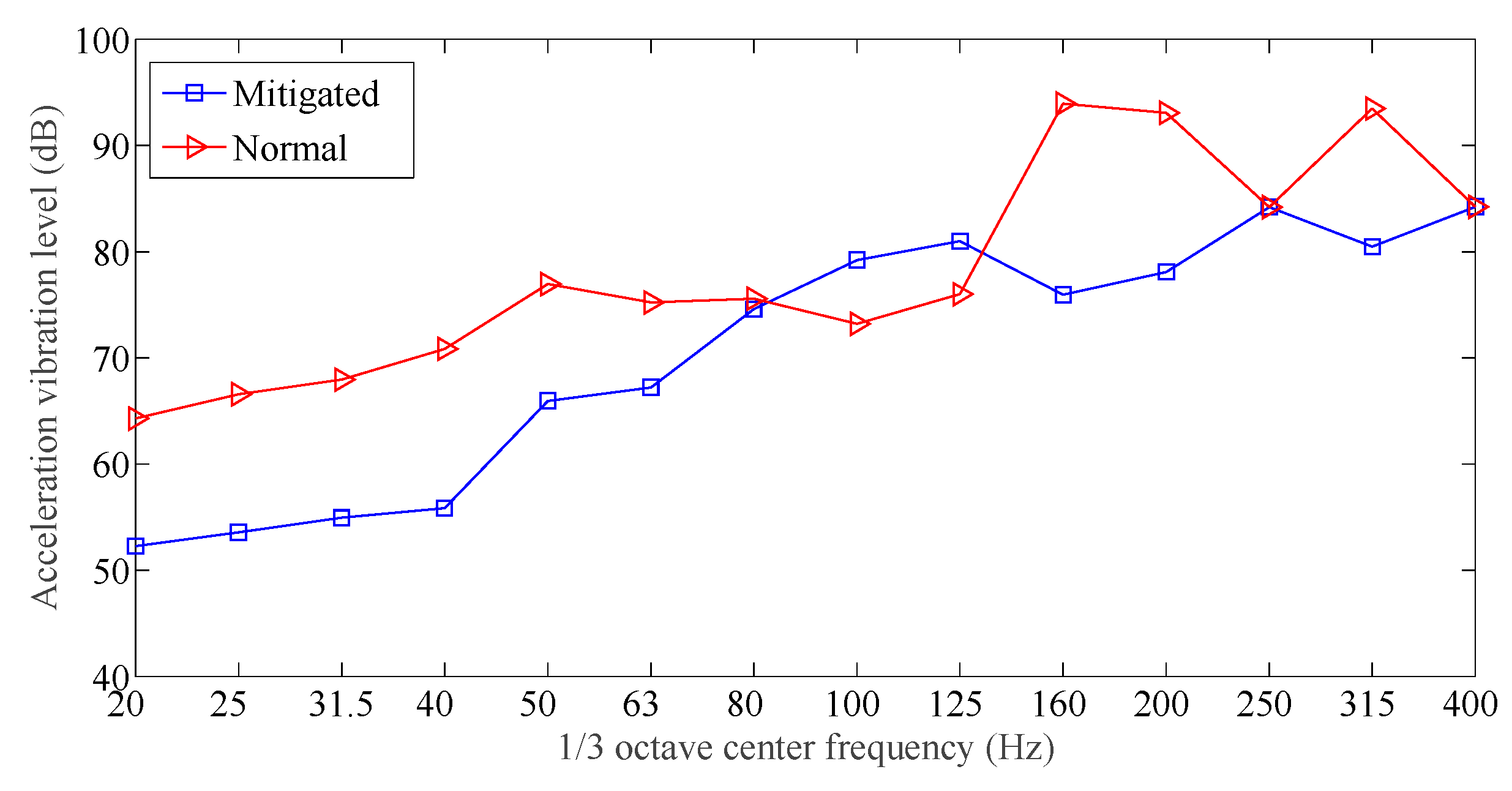
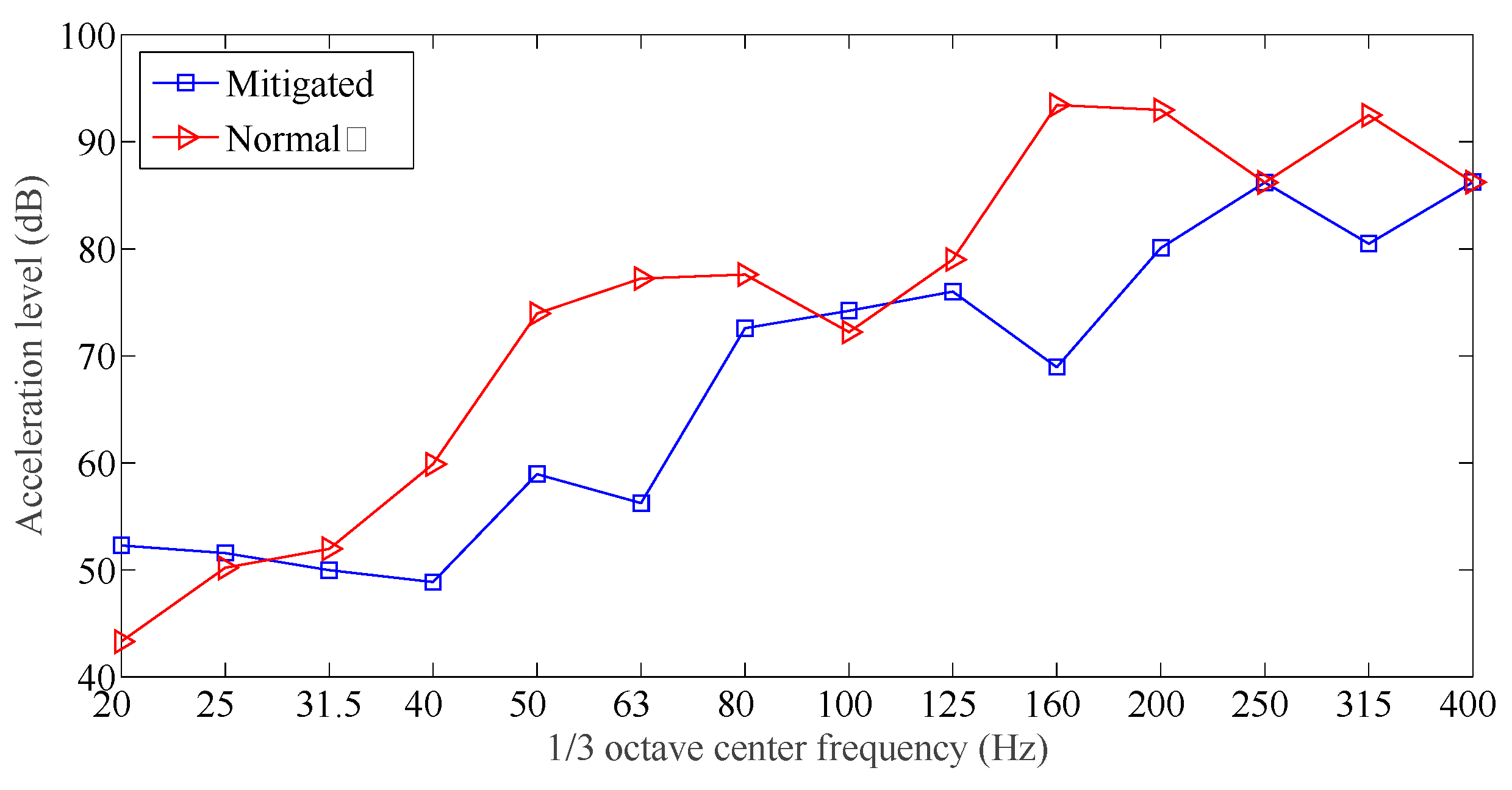
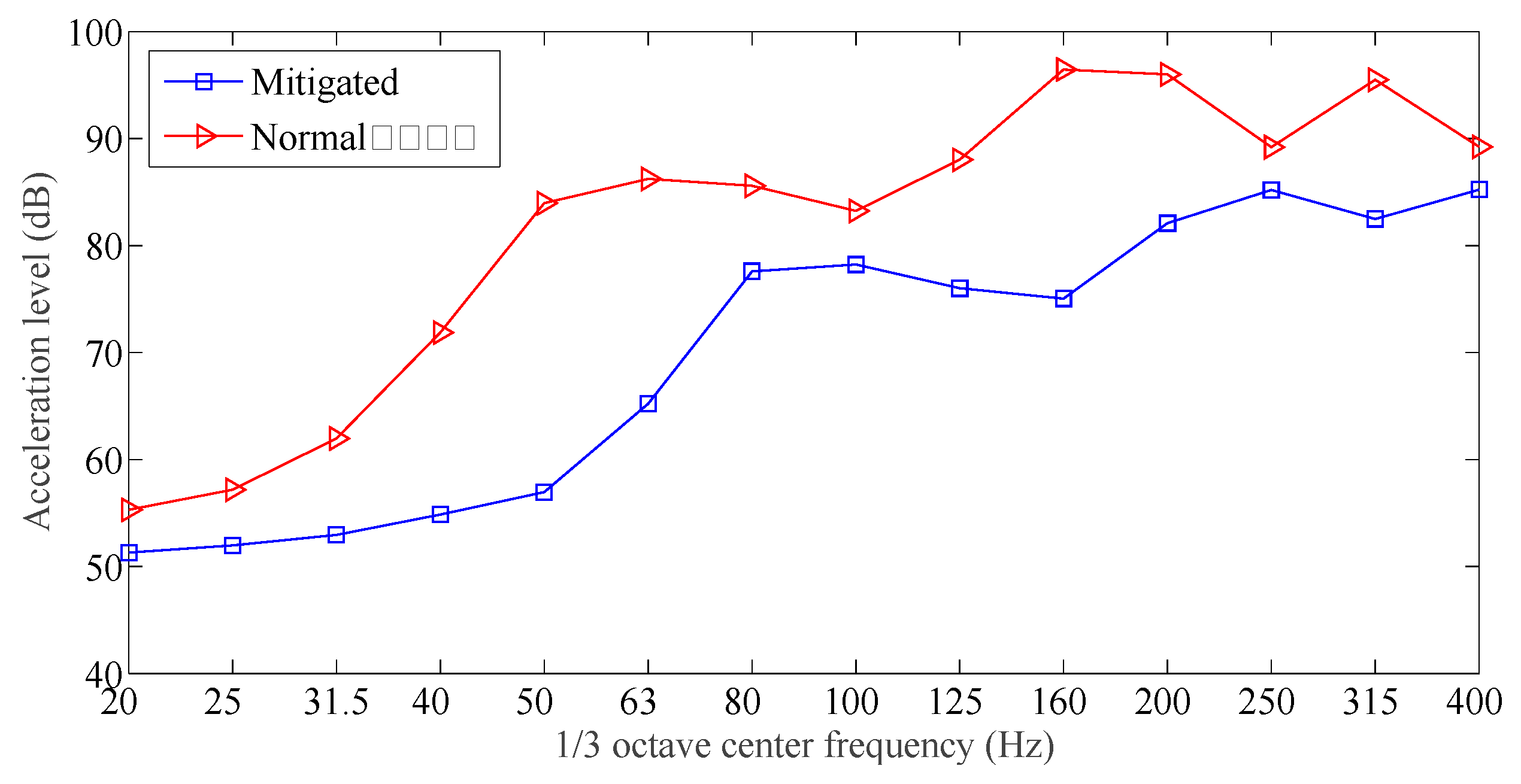
| Measuring Points | Designed Damping Slab (dB) | Normal Track Slab (dB) | Average Difference | ||
|---|---|---|---|---|---|
| Maximum | Average | Maximum | Average | ||
| 1 | 85 | 70.5 | 93 | 77.9 | 7.4 |
| 2 | 86 | 66.5 | 92 | 73.5 | 7.0 |
| 3 | 84 | 58.6 | 96 | 70.8 | 12.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Wang, X.; Zhou, Y.-L.; Qin, J. Vibration Mitigation Effect Investigation of a New Slab Track Plate Design. Sensors 2019, 19, 168. https://doi.org/10.3390/s19010168
Liu L, Wang X, Zhou Y-L, Qin J. Vibration Mitigation Effect Investigation of a New Slab Track Plate Design. Sensors. 2019; 19(1):168. https://doi.org/10.3390/s19010168
Chicago/Turabian StyleLiu, Linya, Xuan Wang, Yun-Lai Zhou, and Jialiang Qin. 2019. "Vibration Mitigation Effect Investigation of a New Slab Track Plate Design" Sensors 19, no. 1: 168. https://doi.org/10.3390/s19010168
APA StyleLiu, L., Wang, X., Zhou, Y.-L., & Qin, J. (2019). Vibration Mitigation Effect Investigation of a New Slab Track Plate Design. Sensors, 19(1), 168. https://doi.org/10.3390/s19010168





