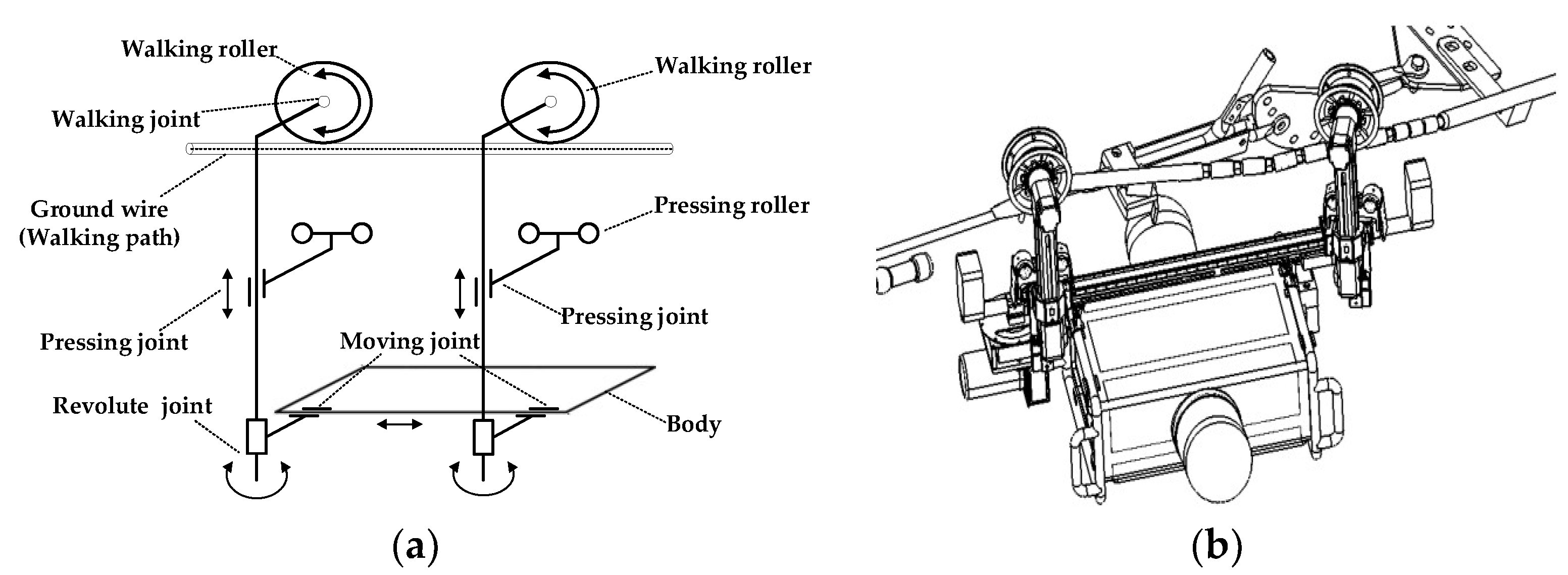
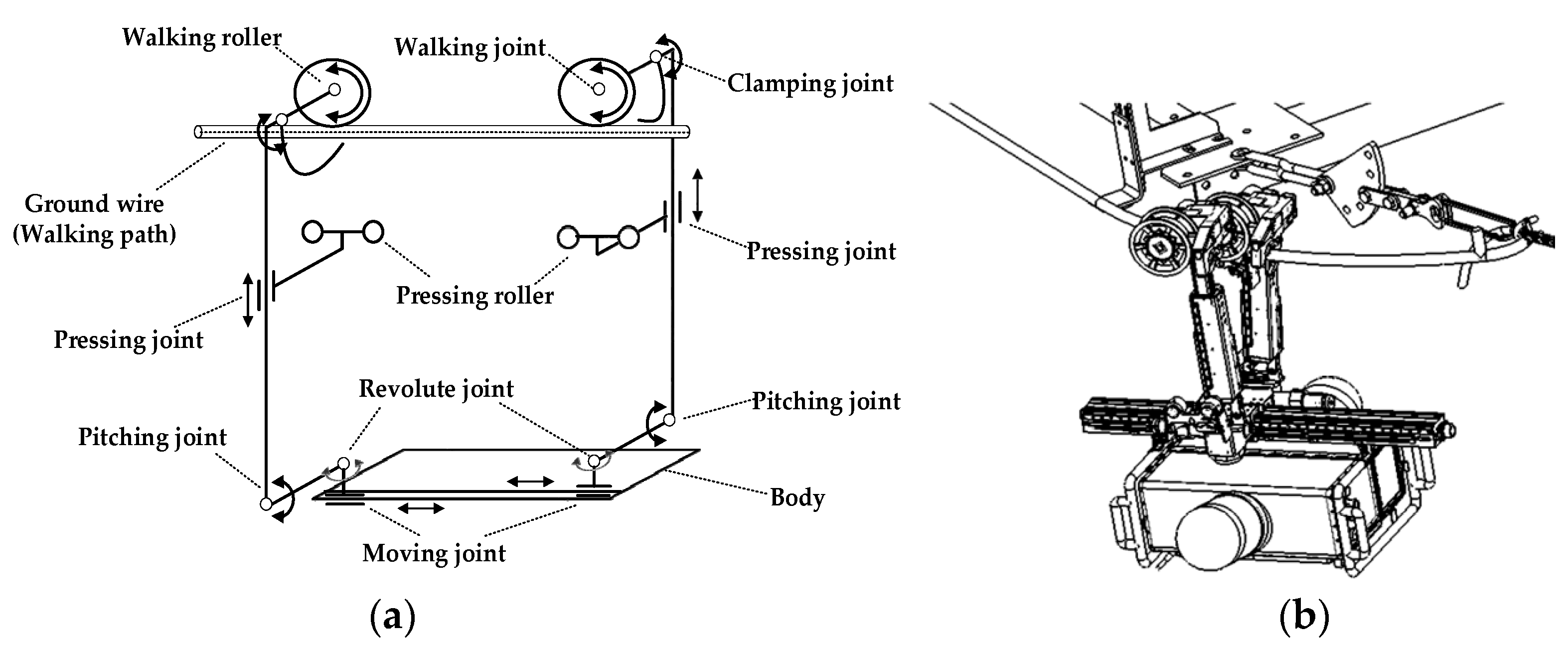
5.1. Modeling and Simulation of the MRCPS
The MRCPS should autonomously and periodically cover transmission lines to monitor environmental variables. This paper initiates a task-based multi-robot team model for the maintenance and monitoring of transmission lines. The system composition plan is changeable for different tasks.
The inspection and communication capabilities of a multi-robot team should meet the objective task demand, and their values can be obtained by previous experience. In this paper, the inspection time
t is used to describe the efficiency of robot inspection. The mathematical expectation of the robot team’s objective task demand in different inspection tasks satisfies Equation (15). The working ability of each independent robot is expected to satisfy Equation (16), and the variance of working ability can be obtained by previous experience.
In Equation (15), no denotes the number of targets for inspection tasks, L denotes the mileage of inspection routes, to denotes the required inspection time, and |Rx| = N denotes the number of robots in the team. Equation (15) is a function that takes the duration of inspection t as an independent variable. It can alter the objective demand of the task by changing the value of parameters. In Equation (16), v denotes the motion rate of a robot, tw denotes the nu-refueled inspection time, and τ denotes the average inspection time length for a single target. The communication efficiency between robots is obtained by Equation (17) where Ce denotes the communication efficiency, Cs denotes the communication control semaphore, and Ct denotes the total amount of communication.
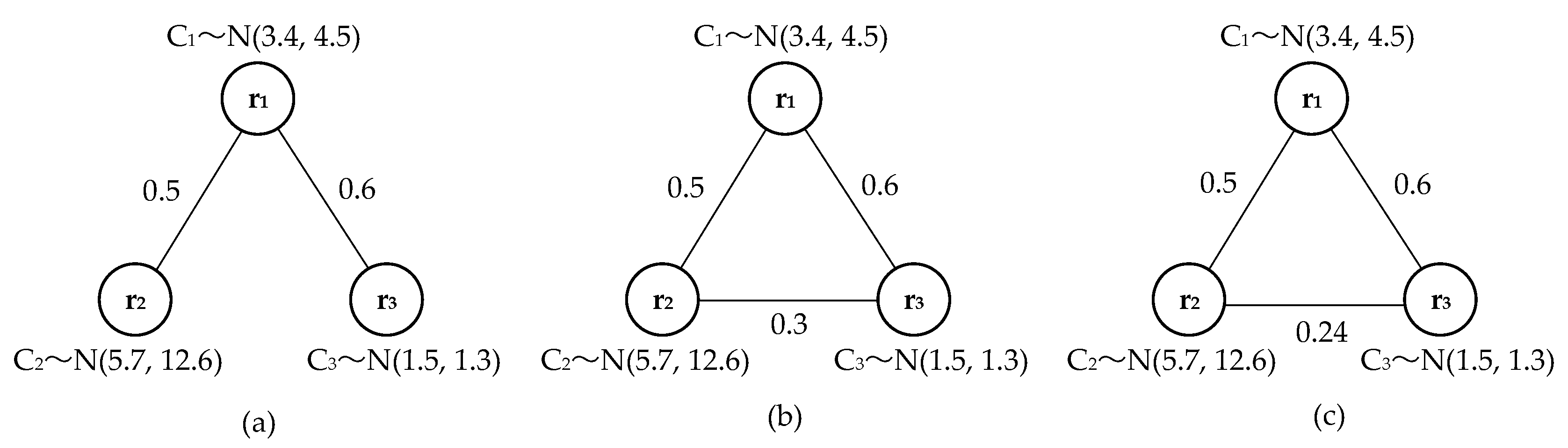
A task-based multi-robot team model aims at different task demands. The optimal team is formed on the basis of the weighted synergy graph and the algorithm of forming a robot team. The team performs real-time or delay tolerant communication with other wireless nodes in the inspection task. The uniform distribution of the motion model is used for the inspection of transmission lines. The specific steps for forming a multi-robot team are as follows.
Step 1: Analyze and determine the objective demand of the robot inspection task of transmission lines.
Step 2: Calculate the robots’ working ability and communication efficiency, and establish a weighted synergy graph of the multi-robot team based on the task.
Step 3: Use the Multi-Robot Team Formation Algorithm (MTFA) to find the best team for an objective task demand.
Step 4: Establish an inspect task database and assign the inspection task of each robot inspection task in the team.
Step 5: Form a wireless dynamic sensor network with the heterogeneous multi-robot team and the static nodes for the transmission line monitoring.
Step 6: The robots adopt a uniformly-distributed motion model BMI, and the transmission line inspection by multi-robot team is conducted.
Equation (18) is used to calculate the effectiveness of forming the multi-robot team.
where
ρ* is the objective task risk factor,
Rmin is the robot team with the minimum risk factor obtained under the objective task demand, and
Rx is the select robot team.
Then, the robot team formation effectiveness is a value from 0 to 1, where 1 is the target team and 0 is the worst performance team. We use the team formation effectiveness to measure the difference in task performance between the robot team and the target team to further evaluate the practical role of the weighted synergy graph model.
Two experiments are designed to verify the effectiveness of the weighted synergy graph model and Multi-robot Team Formation Algorithm (MTFA). In the first experiment, a comparison is performed on the effect of the weighted synergy graph model and the unweighted synergy graph model on the robot team. The second experiment compares the performance of the MTFA with that of the original SA. The total number of robots in the robot set is N. For each N, the robot sets are tested 100 times. The MTFA parameters are configured as follows: complexity of initial robot set λ0 = N, attenuation factor α = 0.95, adaptive strength κ = 1, and adaptive strength ε = 0.1.
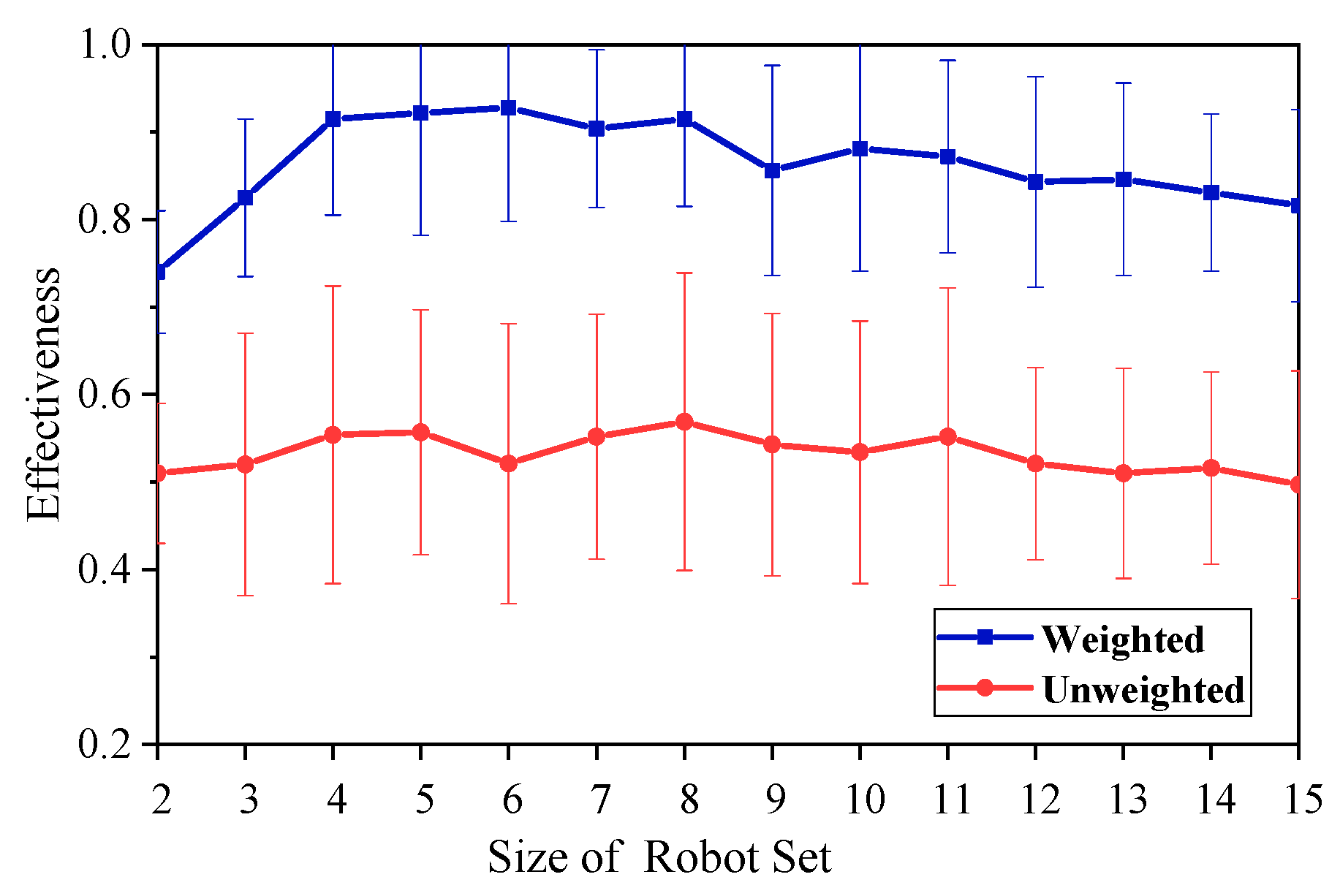
Figure 12 and
Figure 13 show the effectiveness of the team found in the weighted and unweighted synergy graph, where
Figure 12 uses 1000 iterations and
Figure 13 uses 2000 iterations.
As can be seen from
Figure 12, the performance of the weighted graph model is superior to that of the unweighted graph model. In addition, with the growth of the initial size of the robots’ set, the two models tend to exhibit similar properties, which are described below. As the growth of the robot set increased, the effectiveness of the two methods is firstly improved rapidly (in the range of the size of robots from two to four), and then relatively stabilized with a slight downward trend.
As shown in
Figure 13, the performance of a 2000 iteration is better than that of a 1000 iteration, whether using the weighted graph model or the unweighted graph model. Furthermore, under different conditions, the curves of effectiveness show a similar trend, i.e., first increasing rapidly and then declining gently.
While the size of the robots set is small, especially from two to four, the optimal solution and the target have a large error, although the two methods can quickly find the optimal team, and the error of the solution decreases gradually with the set increasing. Therefore, when the size of the robots set is from two to four, the effectiveness of the two models increases rapidly with the increase of the set.
As the size of the set increases further, the difficulty of calculating the optimal solution is gradually increasing, and it is more and more constrained by the computational time and the number of iterations. Therefore, the effectiveness curve shows a slow downward trend, and the group with more iterations obviously perform better.
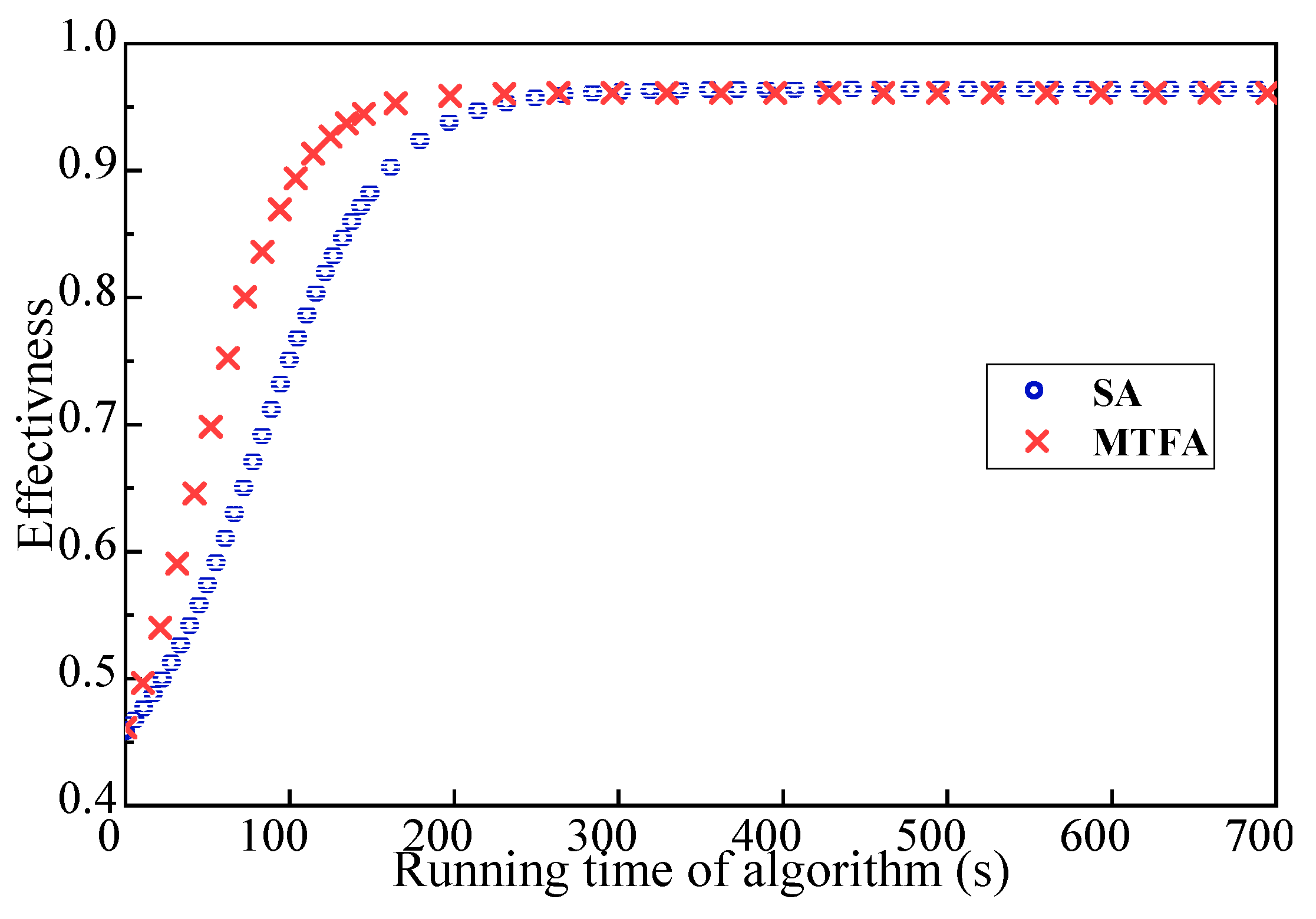
Figure 14 and
Figure 15 show the relationship between the operation time and the effectiveness of the robot team. The size of the initial robot set is 15 and 35, respectively. In
Figure 14 and
Figure 15, the convergence rate of the MTFA’s optimal solution is much better than that of the original SA. Furthermore, the larger the size of the robot set, the more obvious the advantage of MTFA. In addition, the results of a larger robot set can be improved after removing the restriction of the computation time and the number of iterations.
5.2. Result of Field Experiments
These experiments were conducted at the test site of Wuhan University to verify the effectiveness of the MRCPS for sensing the environmental variables of a transmission line. This test site is used to simulate the working environment of the inspection robot.
In order to simulate the open terrain around the overhead transmission line, a testing site with 50-m length and 30-m width is located on the top floor of the building. In addition, the analog line uses a more complex distribution than the actual power line. The transmission line of the test site integrates an adjustable number of on-line devices to cause spatial variations in environmental variables.
Figure 16 shows an image of a field experiment.
In this work, both effects were fully validated: the effectiveness of collaborative work of the multi-robot in MRCPS, and the balance performance of the economy and collaboration capability of the multi-robot team in the multiple scenarios.
Firstly, the inspection robot carries the laser scanner and the Inertial Measurement Unit
(IMU) equipment to measure the space parameters. The basic spatial data of the test site is obtained, such as the number of transmission lines, the length of each line, the type, number, and location of devices on the line, and the vegetation distance. With obtained spatial data, a multi-robot system inspection map and inspection database are then constructed. The obtained point cloud data and map are shown in
Figure 17 (these data are cited from our previous articles [
24,
25,
26], which have described the acquisition process and results in detail), in which
Figure 17a is the point cloud data collected by the robot, and
Figure 17b is the constructed inspection map.
Subsequently, scenario 1 was designed for verifying the effectiveness of the multi-robot team of the MRCPS.
Table 5 shows the default experimental parameters of scenario 1.
Table 6,
Table 7,
Table 8 and
Table 9 shows the variation rules of the sub-scenarios 1.1–1.4. In the multiple scenarios, different objective task demands are proposed by changing the inspection distance, the number of inspection objectives, and the required inspection time.
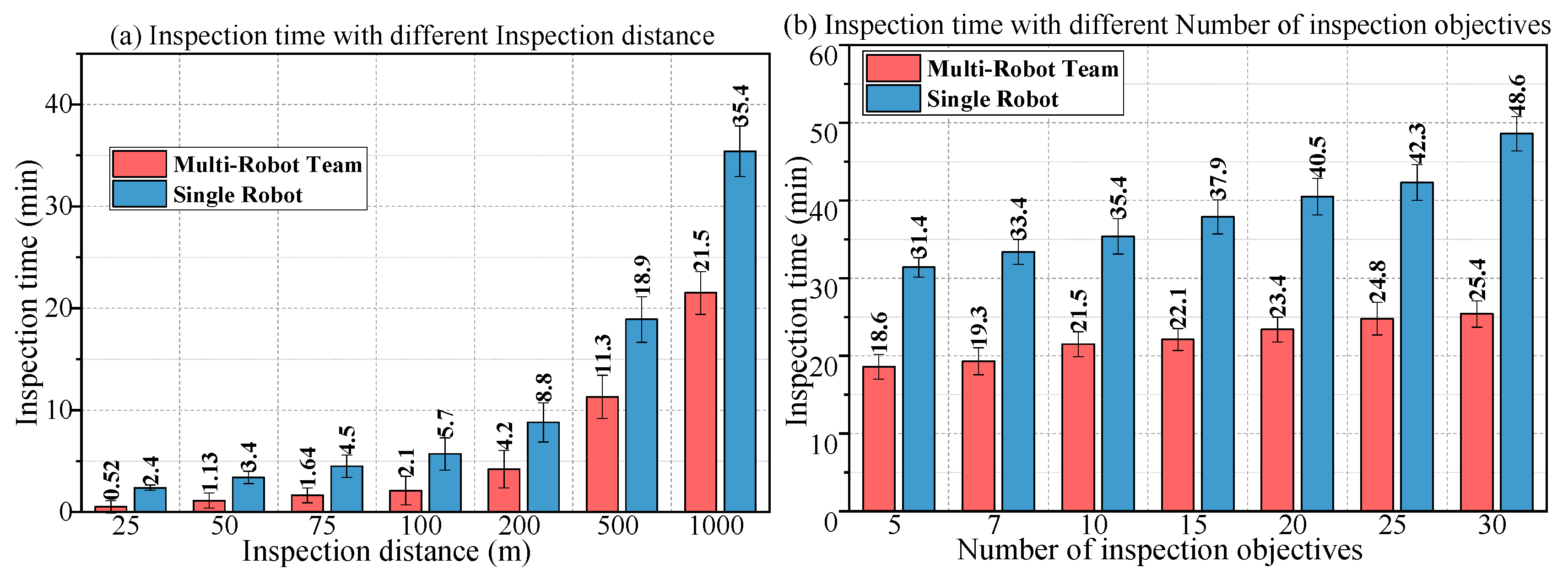
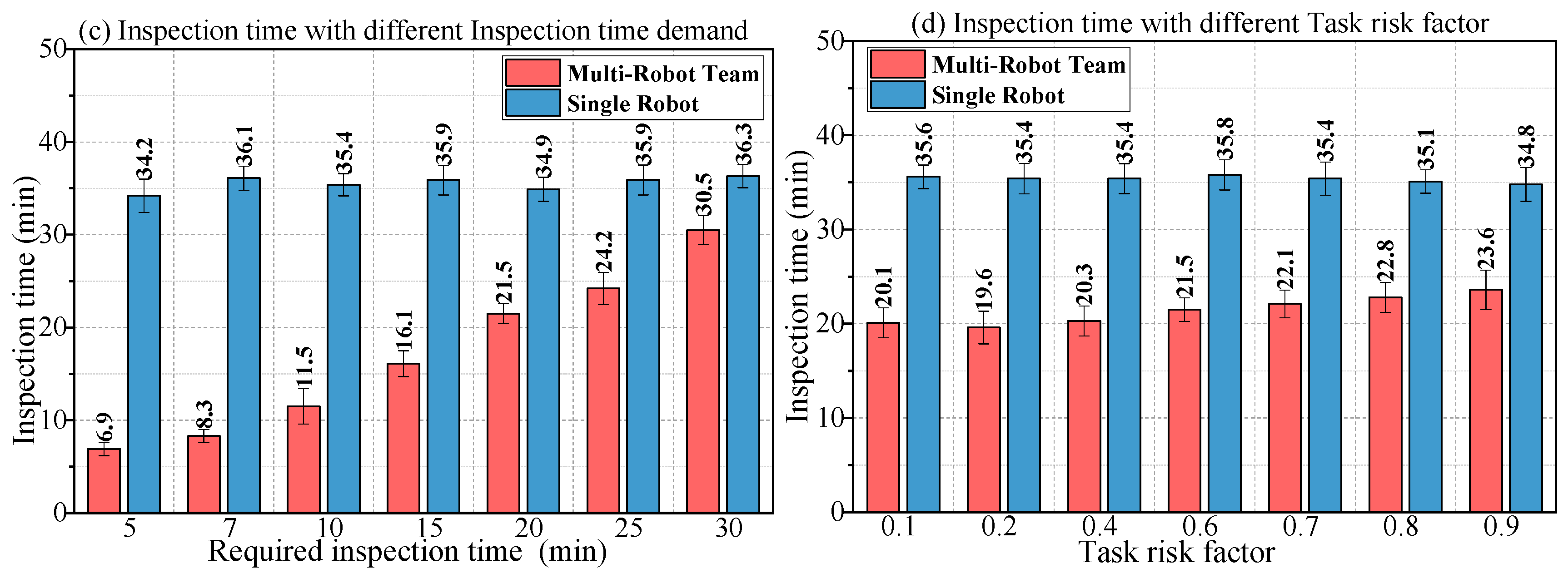
Figure 18 shows the comparison of the inspection results of the multi-robot team with those of the individual robot in Scenario 1. In
Figure 18a–d, the objective task demand and the task risk factor are adjusted to obtain the duration of the multi-robot team and the individual robot under different conditions.
The comparison between the robot team and the individual robot is shown in
Figure 13. The following properties are summarized.
Under the same conditions, the multi-robot team completed the inspection task in a much shorter time than the single robot.
The inspection time of the multi-robot team was most affected by required inspection time to and inspection distance L. The inspection time of the single robot was most affected by inspection distance L and the number of inspection objectives no.
The higher the required inspection time to, the harder it was for the robot team to achieve the goal.
First of all, the collaborative inspection of MRCPS greatly reduces the time required for completing the task. Secondly, to directly restricts the inspection time of the robot team and has the greatest impact on the results. In the test of the L change, the collaborative inspection rate is constant, and to is changed indirectly, which makes the actual inspection time change obviously. However, the single robot is affected only by the difficulty of the inspection task (L, no). Finally, due to the limitation of the initial size of the robot set, the team capability is constrained, i.e., the higher the requirement, the worse the performance will be.
Finally, the default experimental parameters for scenario 2 are shown in
Table 10. The performance of cost and collaboration capability of the multi-robot team in MRCPS is adjusted by changing the objective task demand and the task risk factor.
Table 11 and
Table 12 shows the range of variation of the experimental parameters for sub-scenarios 2.1 and 2.2.
Similar to the effectiveness of the team formation, the effectiveness of the multi-robot team in collaboration capability is calculated by the relationship between the actual inspection time and the required inspection time. The effectiveness of the multi-robot team in practical work is shown in Equation (19).
where
to is the required inspection time, and
tRx is the actual inspection time of the multi-robot team.
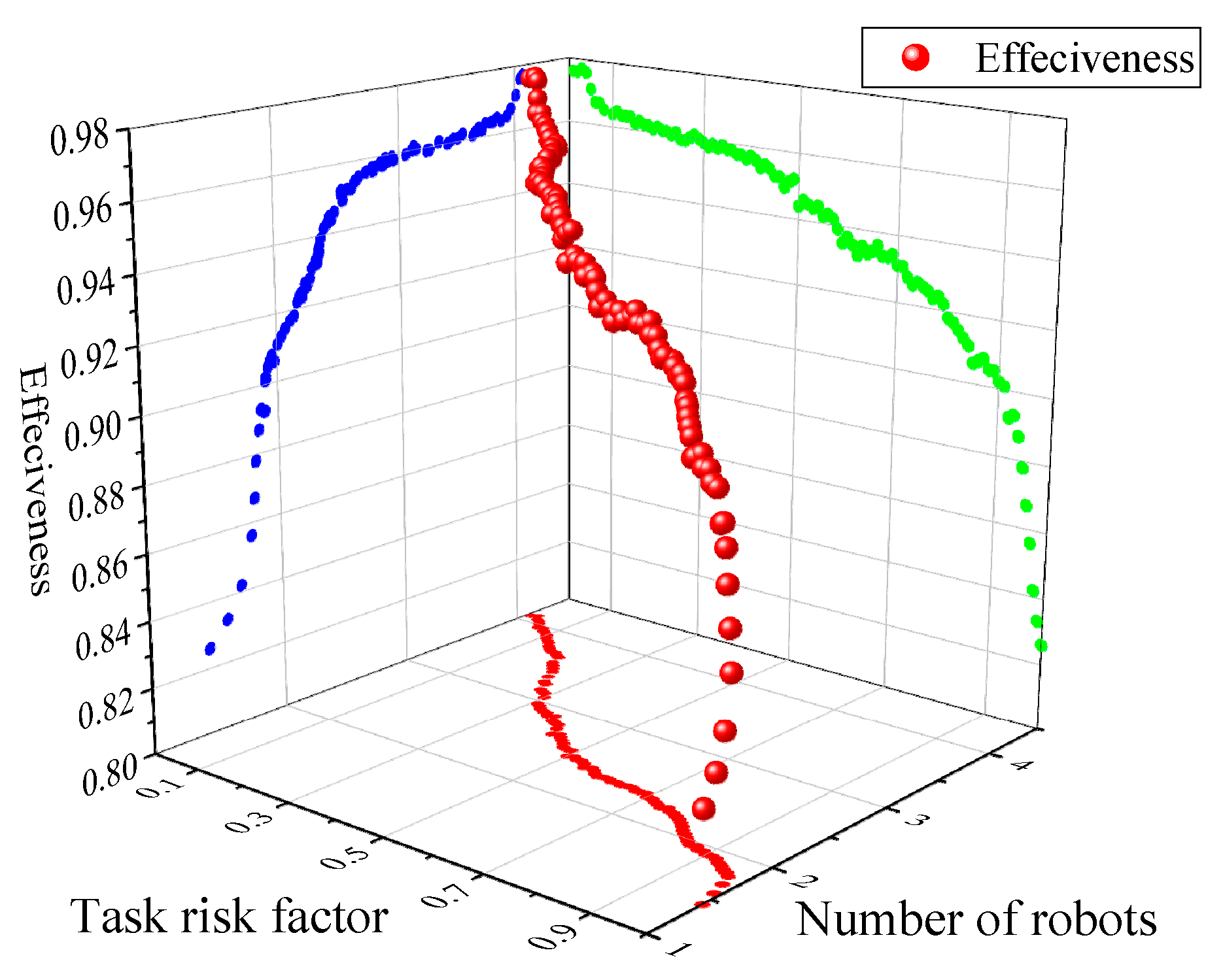
Figure 19 shows the effectiveness of multi-robot team with different objective task demands, and the effectiveness of different task risk factors is shown in
Figure 20.
It is seen from
Figure 19 that the effectiveness of the robot team is negatively related to the objective task demand
μo; corresponding to the specified set of robots, especially the task demand is too low or too high, the variation of the working efficiency of the robot team is more obvious. For the moderate value of
μo, little change is observed in the effectiveness of the multi-robot team, and it can maintain a high efficiency (0.89–0.93). In addition, with the difficulty of the target task increasing, the number of robots is gradually increasing, that is, the economic efficiency declines the execution of the robot team.
The changing of the effectiveness of the MRCPS is more obvious under the influence of task risk factor
ρ (as shown in
Figure 20). The effectiveness of robot team is also negatively related to the task risk factors. There is no stable phase in the efficiency curve, and the change rate is large compared with the result in
Figure 19. With the increase of task risk factor, the number of robots has steadily declined, and the economic efficiency has been gradually enhanced. That is, the higher the risk, the greater the return; the lower the risk, the greater the cost.