Entropy Correlation and Its Impacts on Data Aggregation in a Wireless Sensor Network
Abstract
1. Introduction
2. Joint Entropy Estimation
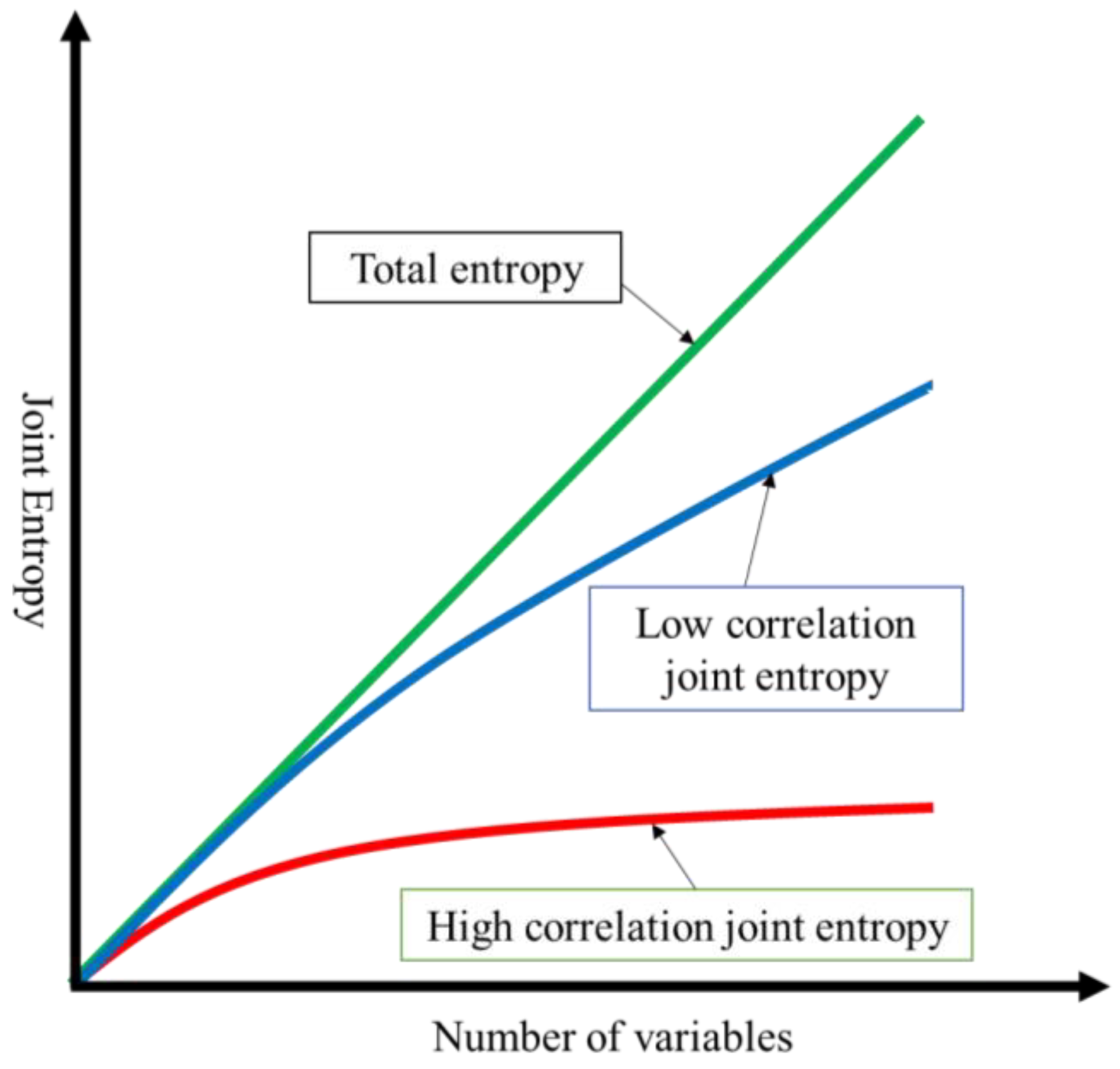
2.1. Entropy Concept
2.2. Joint Entropy Estimation
2.2.1. Joint Entropy Upper Bound
2.2.2. Joint Entropy Lower Bound
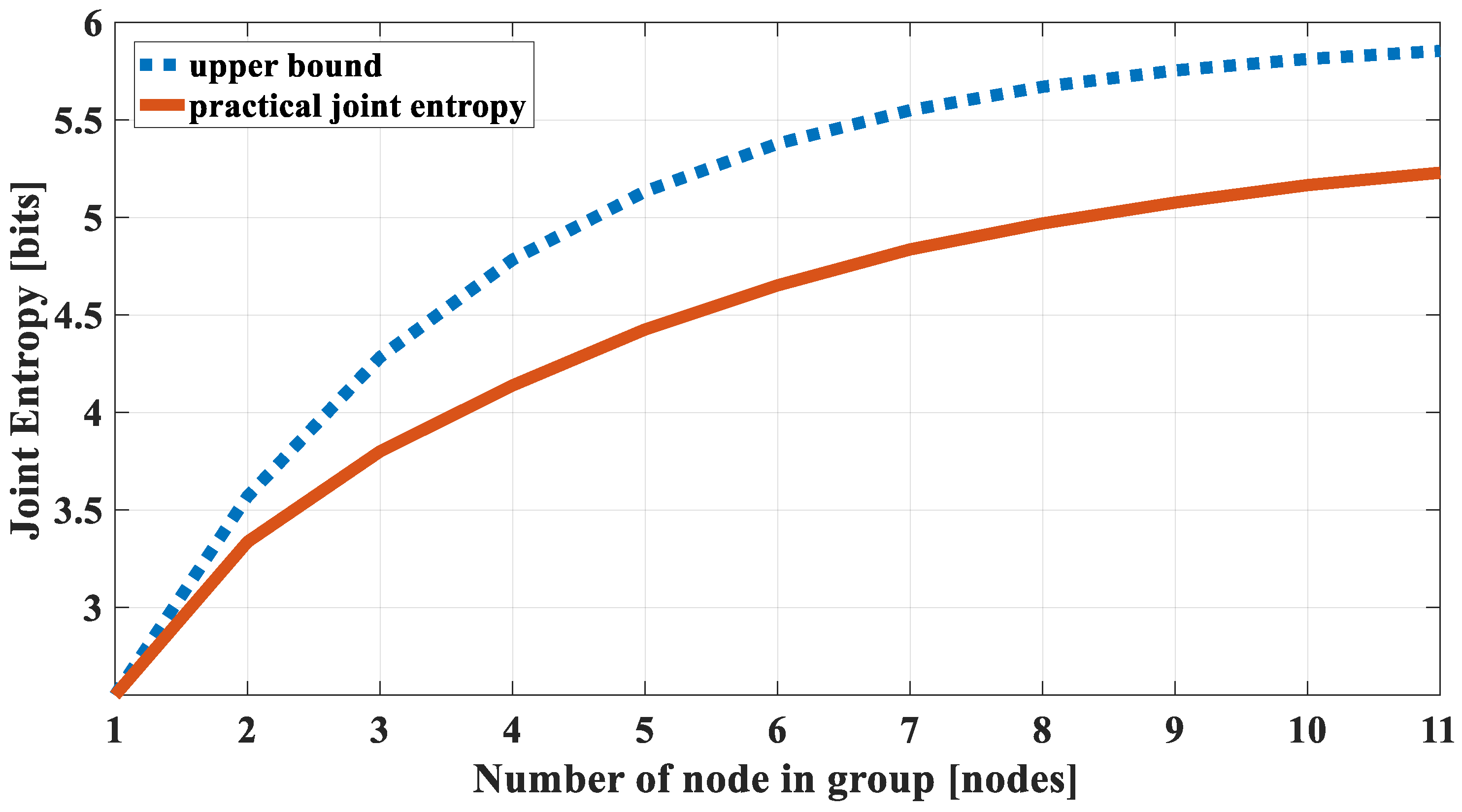
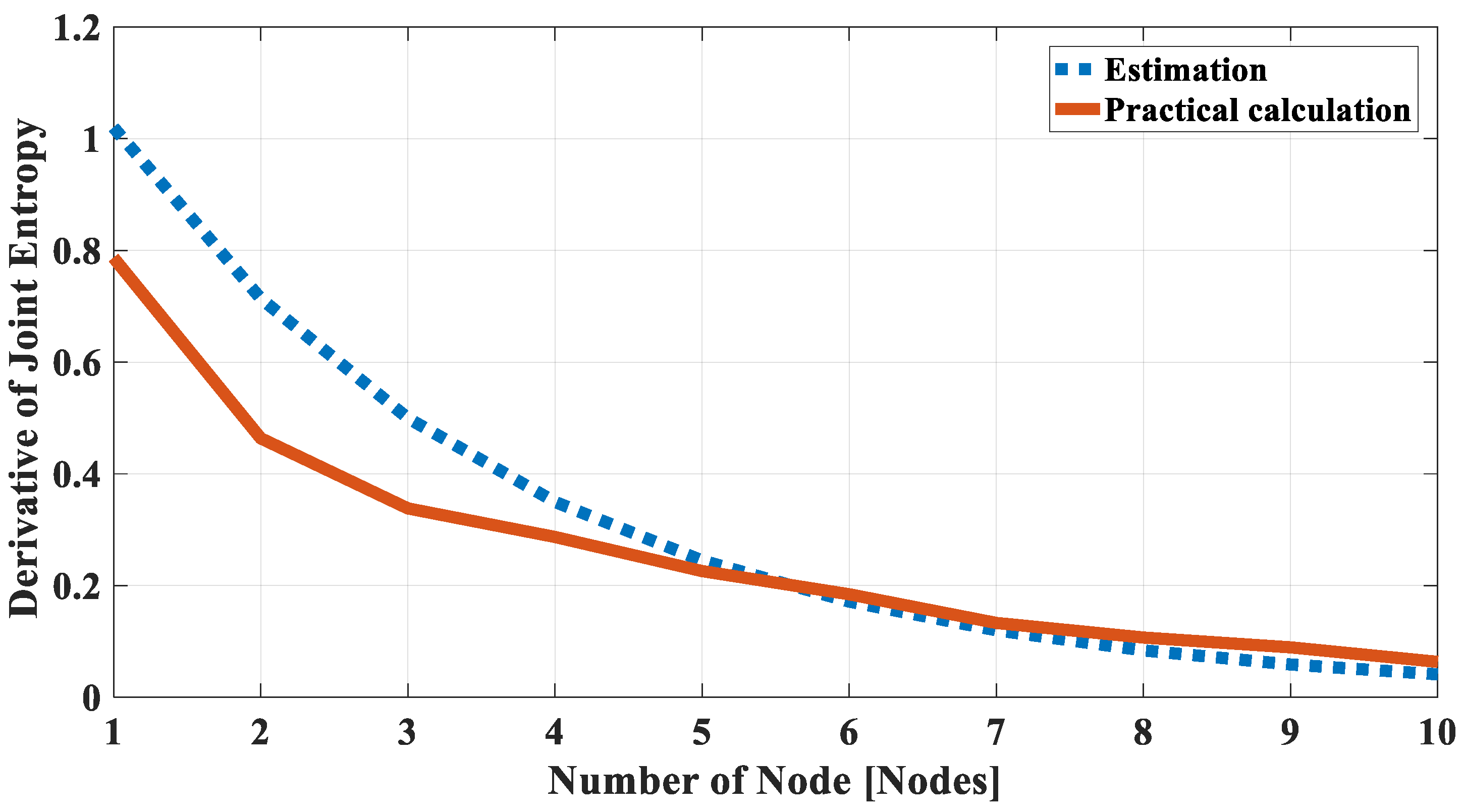
2.2.3. Validation of Joint Entropy Estimation
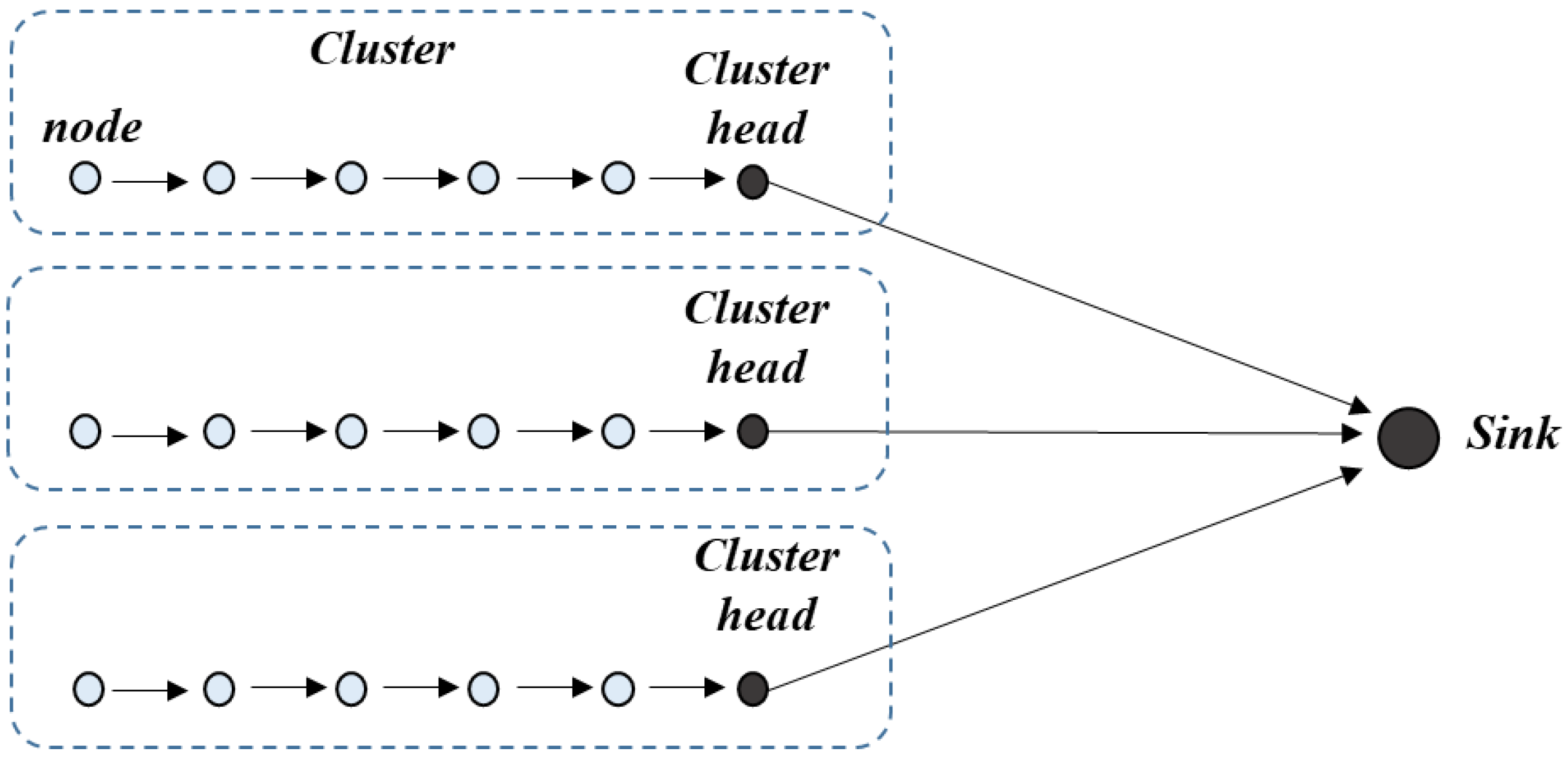
3. Correlated Region and Correlation Clustering Algorithm
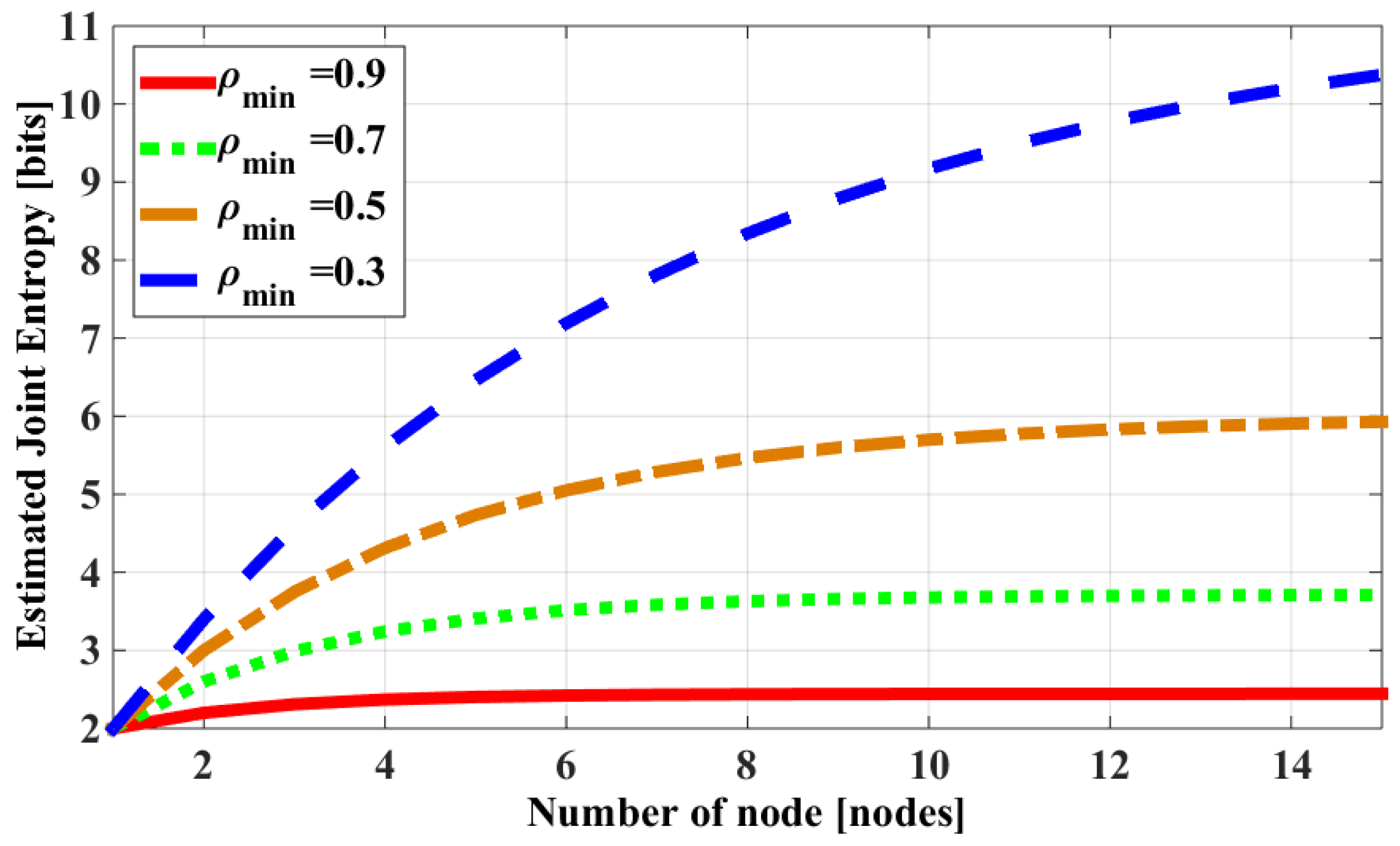
3.1. Estimated Joint Entropy and Correlation
- It is acceptable to use a lower/upper bound function to estimate the joint entropy of a correlation group because they have similar characteristics of going to a “saturation” state when the number of nodes in the group increases.
- The entropy correlation coefficient of all pairs in the group can be represented by a correlation’s level of the group.
3.2. Correlated Region Definition
3.3. Correlation Clustering Algorithm
| Algorithm 1: Correlation-based Clustering Algorithm |
| 1. BEGIN 2. FOR each node Xi in the network 3. Calculate entropy H(Xi) 4. ENDFOR 5. FOR each node Xi in the network 6. FOR each node Xj in the network and Xj ≠ Xi 7. Calculate 8. ENDFOR 9. ENDFOR 10. REPEAT 11. Choose H0, ρ0, ΔH; (*) 12. Initialize new group G = Φ. 13. FOR each node Xi in the network and not belonging to any group 14. IF 15. Add Xi into G 16. ENDIF 17. ENDFOR 18. FOR each node Xi in G 19. Calculate B(Xi) = number of nodes Xj that 20. ENDFOR 21. X0 = argmax{B(Xj), Xj∈G} 22. FOR each node Xi in G 23. IF 24. Remove Xi from G 25. ENDIF 26. ENDFOR 27. REPEAT 28. FOR each node Xi in G 29. Calculate C(Xi) = number of nodes Xj that 30. ENDFOR 31. FOR each node Xi in G 32. IF 0 < C(Xi) = max{C(Xj), Xj∈G} 33. Remove Xi from G (**) 34. ENDIF 35. ENDFOR 36. UNTIL max{C(Xj), Xj∈G}=0 37. UNTIL all nodes are grouped 38. END |
3.4. Validation
4. Data Aggregations Using Entropy Correlation
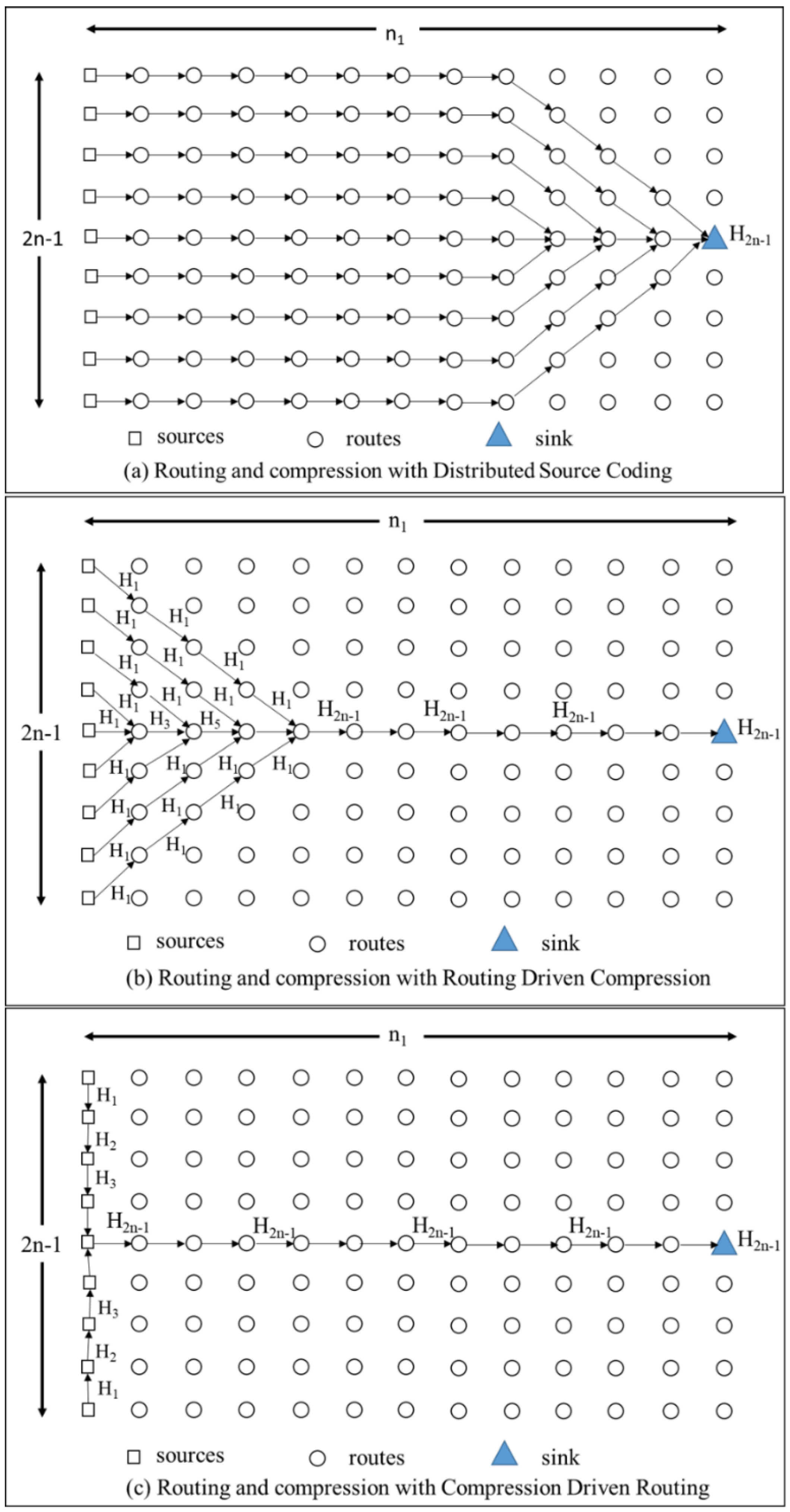
4.1. Compression Aggregation
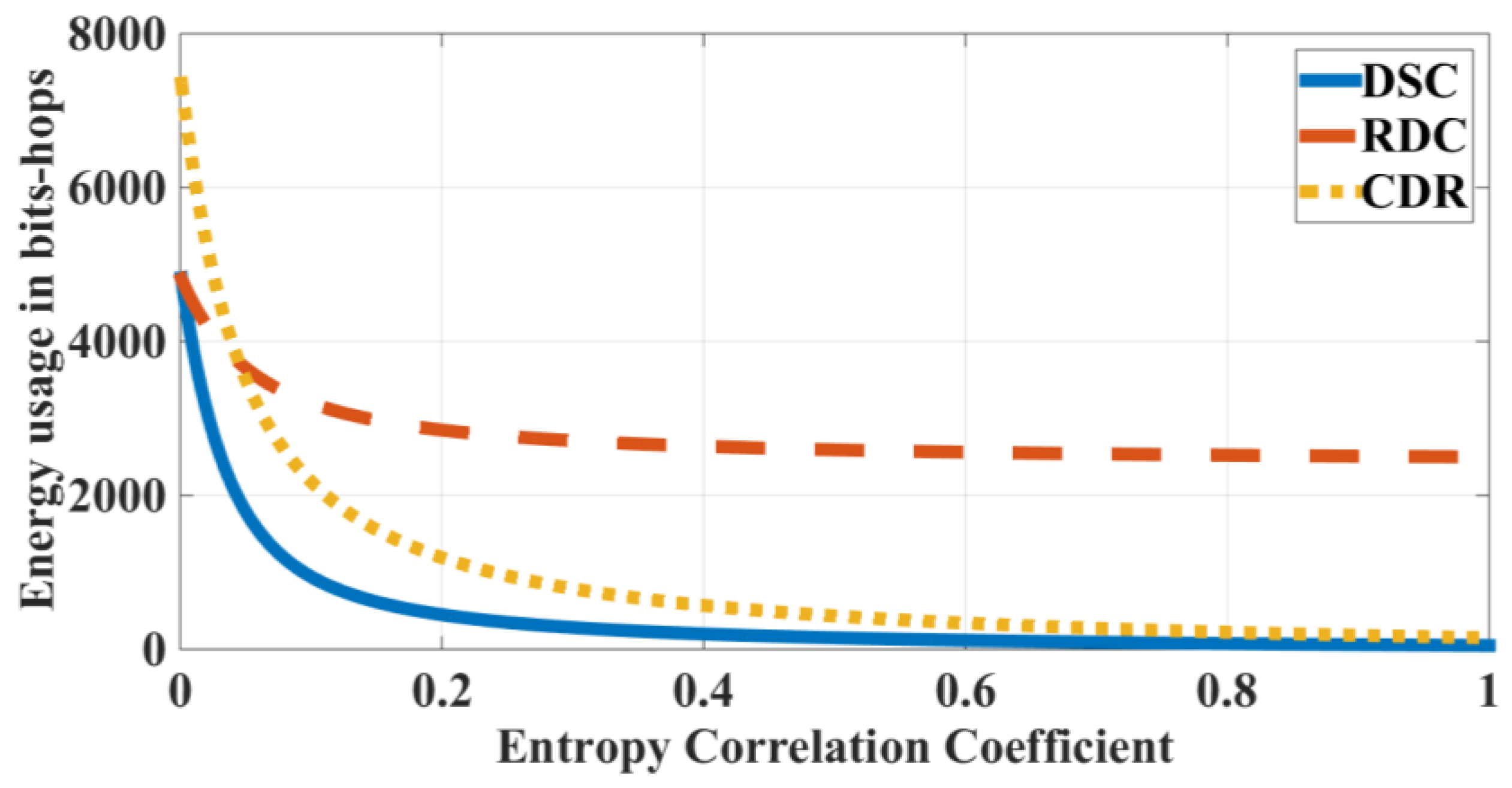
4.1.1. Comparison of Compression Schemes
4.1.2. Compression Based Routing Scheme in a Correlated Region
4.1.3. 1-D Analysis
4.1.4. 2-D Analysis
4.1.5. General Topology Model Analysis
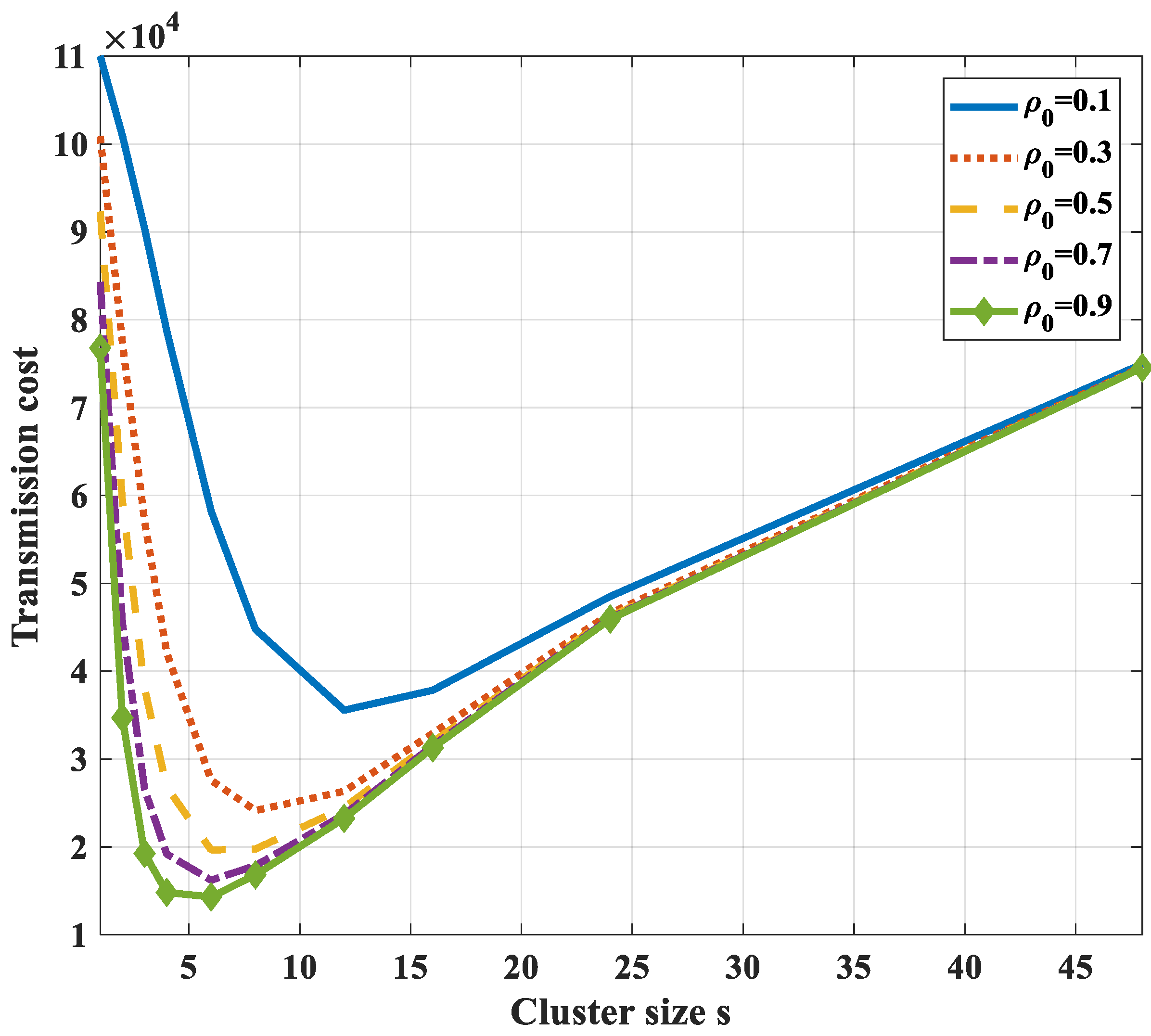
4.1.6. Optimal Routing Schemes in Correlation Networks
- -
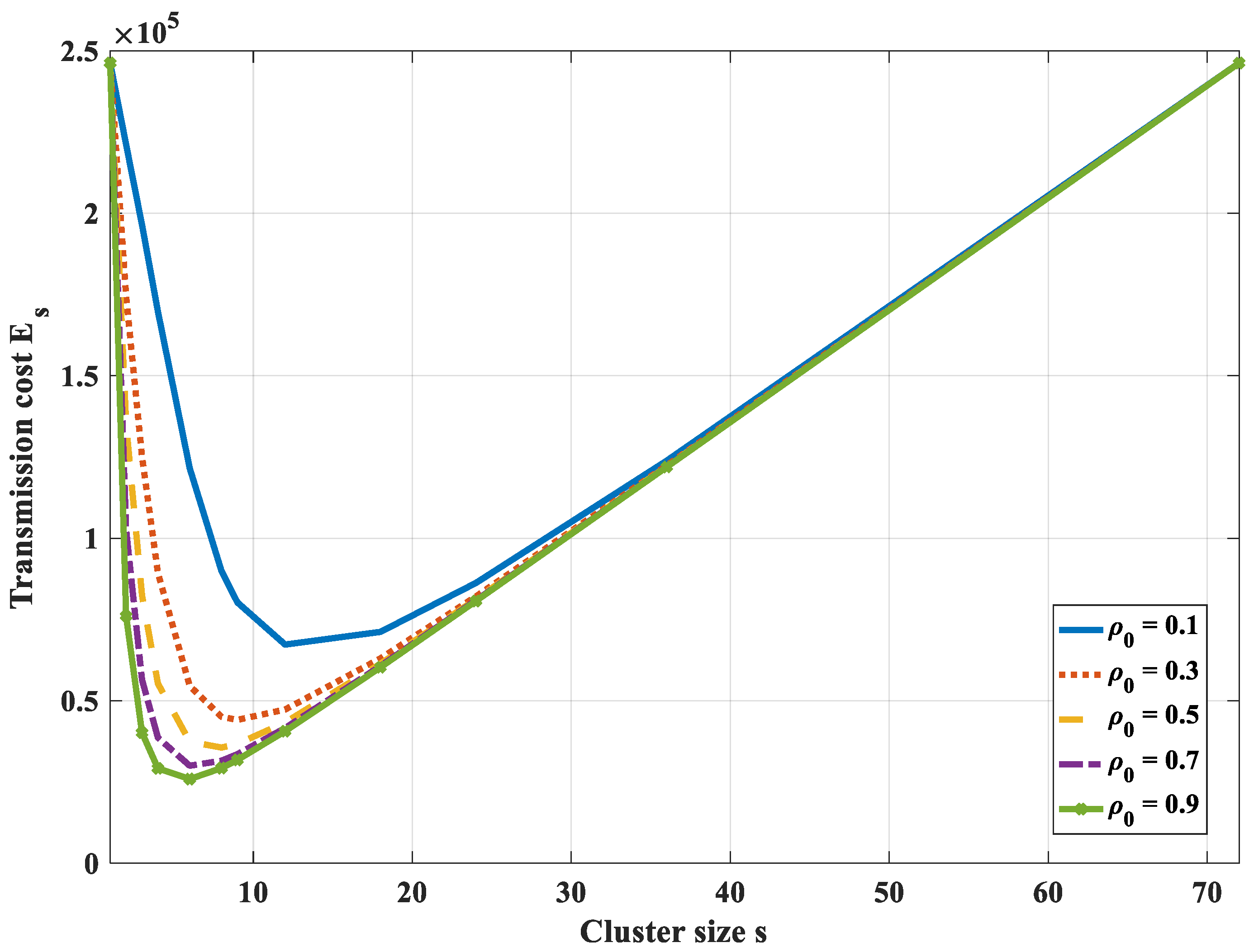
- In case compression along the transmission path to the cluster head is used, it is not necessary to divide a correlated region into smaller clusters to optimize the transmission cost. Instead, each correlated region becomes a cluster and the optimal routing path in each cluster is the shortest path from nodes to their cluster head.
- -
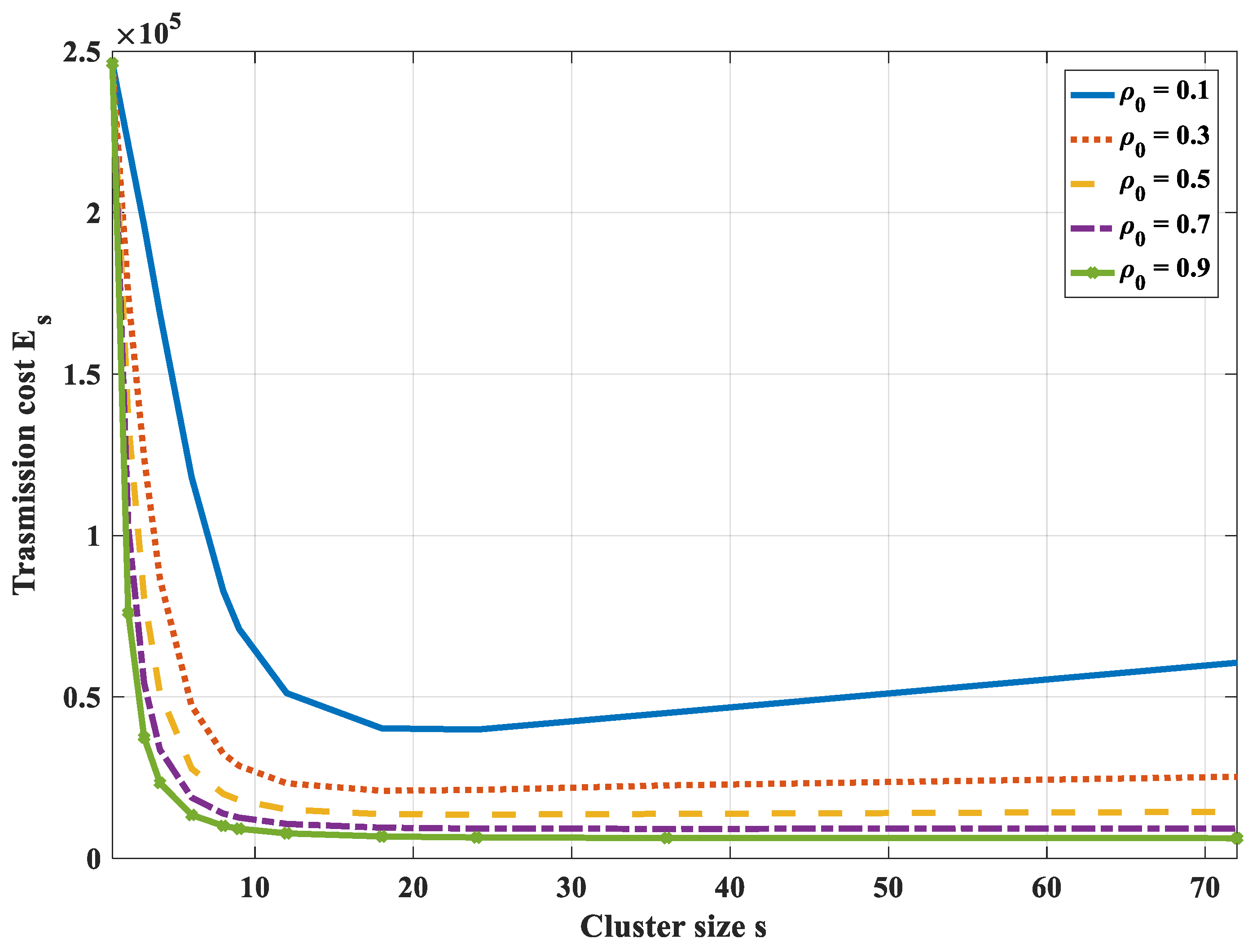
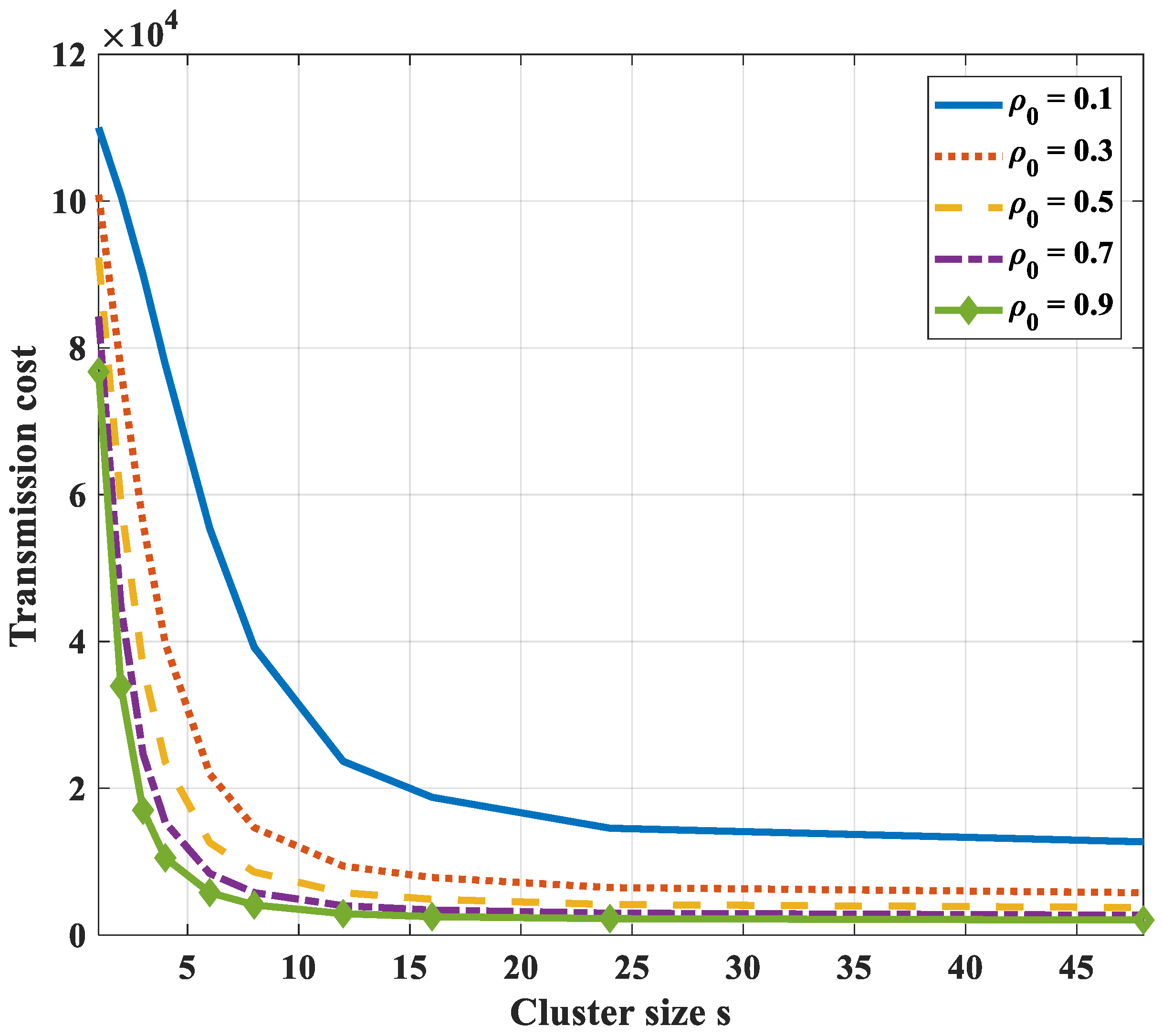
- In the case of compression at the cluster head only and not at intermediate nodes, the transmission path is the shortest path to the cluster head. To get the optimal transmission cost, it is necessary to divide a correlated region into some smaller clusters. It is difficult to get the analytical solution of the optimal cluster size. Yet, we can draw the total transmission cost curves and find the nearly optimal value with a specified correlation coefficient and the number of network nodes.
4.2. Representative Aggregation
4.2.1. Distortion Function
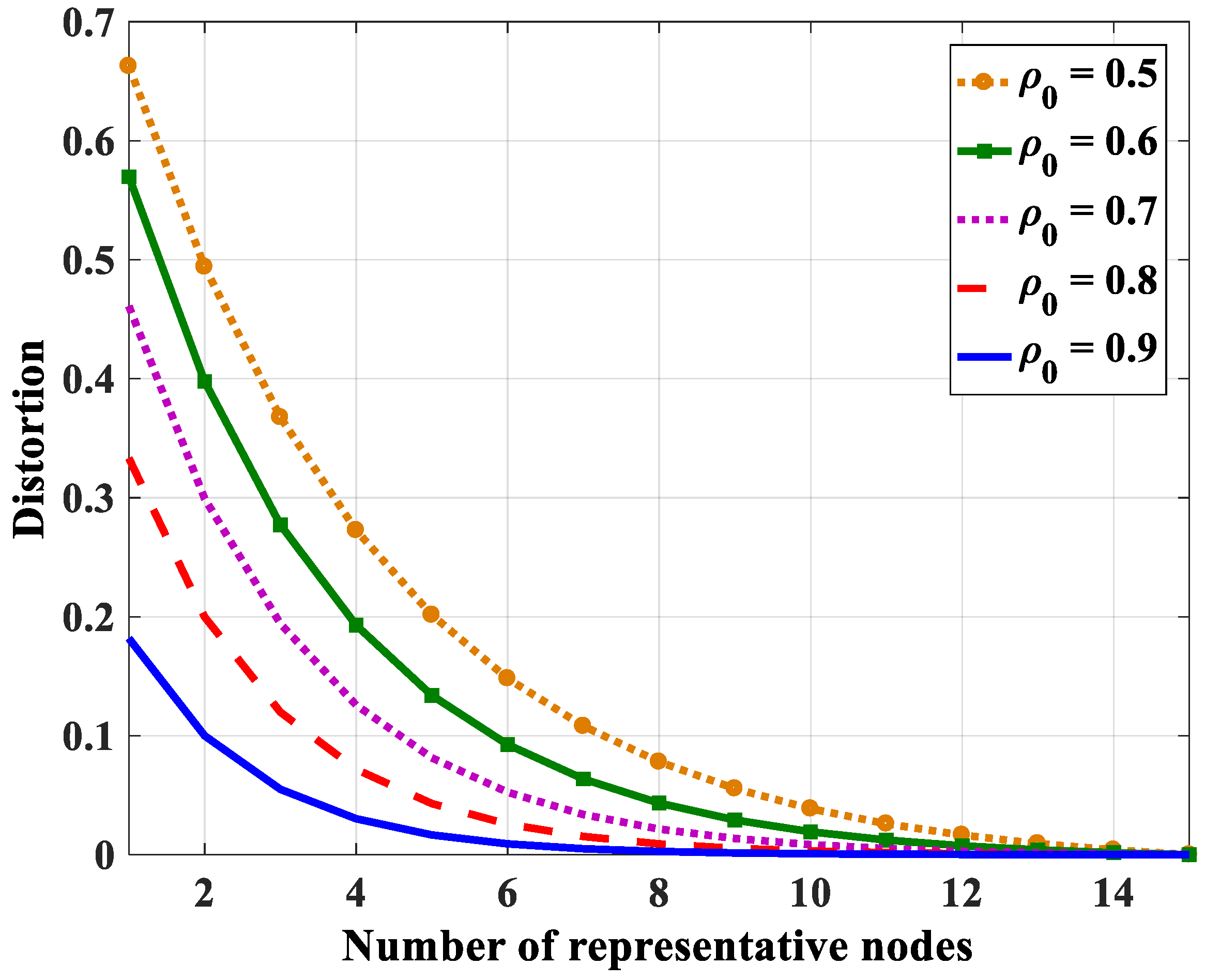
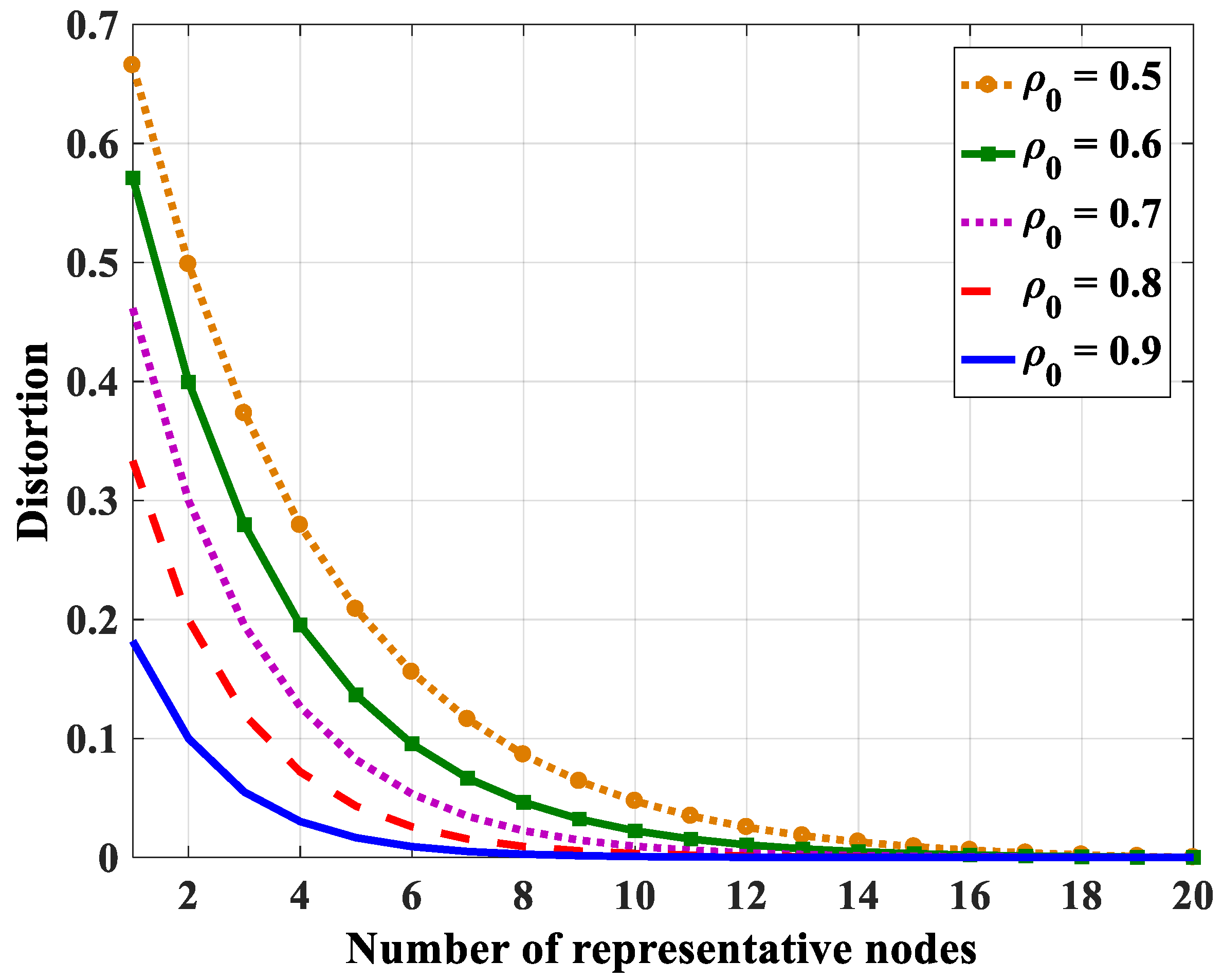
4.2.2. Number of Representative Nodes
4.2.3. Representative Node Selection
| Algorithm 2: Maximizing the Obtained Information-Based Representative Node Selection Algorithm |
| 1. BEGIN 2. C = {X1, X2, …, XN};//correlation node set 3. Initialize new group R = Φ//representative set 4. FOR Xi, Xj ∈ C 5. Calculate ; 6. Calculate ; 7. ENDFOR 8. FOR k = 1 to iM 9. Find ; 10. Add Xi to R; 11. Remove Xi from C; 12. ENDFOR 13. END |
4.2.4. Practical Validation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Proof that
Appendix A.2. Proof of Equation (38)
Appendix A.3. Proof of Equation (40)
Appendix A.4. Proof of Equation (42)
Appendix A.5. Proof of Equation (46)
References
- Akyildiz, I.F.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw. 2002, 38, 393–422. [Google Scholar] [CrossRef]
- Srisooksai, T.; Keamarungsi, K.; Lamsrichan, P.; Araki, K. Practical data compression in wireless sensor networks: A survey. J. Netw. Comput. Appl. 2012, 35, 37–59. [Google Scholar] [CrossRef]
- Razzaque, M.A.; Bleakley, C.; Dobson, S. Compression in wireless sensor networks: A survey and comparative evaluation. ACM Trans. Sens. Netw. 2013, 10. [Google Scholar] [CrossRef]
- Gaeta, M.; Loia, V.; Tomasiello, S. Multisignal 1-D compression by F-transform for wireless sensor networks applications. Appl. Soft Comput. J. 2015, 30, 329–340. [Google Scholar] [CrossRef]
- Vuran, M.C.; Akan, Ö.B.; Akyildiz, I.F. Spatio-temporal correlation: Theory and applications for wireless sensor networks. Comput. Netw. 2004, 45, 245–259. [Google Scholar] [CrossRef]
- Nikolov, M.; Haas, Z.J. Encoded Sensing for Energy Efficient Wireless Sensor Networks. IEEE Sens. 2010, 18, 875–889. [Google Scholar] [CrossRef]
- Bhuiyan, M.Z.A.; Wang, G.; Wu, J.; Cao, J.; Liu, X.; Wang, T. Dependable Structural Health Monitoring Using Wireless Sensor Networks. IEEE Trans. Dependable Secur. Comput. 2017, 14, 363–376. [Google Scholar] [CrossRef]
- Dabirmoghaddam, A.; Ghaderi, M.; Williamson, C. Cluster-Based Correlated Data Gathering in Wireless Sensor Networks. In Proceedings of the 2010 IEEE International Symposium on Modeling, Analysis and Simulation of Computer and Telecommunication Systems, Miami Beach, FL, USA, 17–19 August 2010; pp. 163–171. [Google Scholar]
- Von Rickenbach, P.; Wattenhofer, R. Gathering correlated data in sensor networks. In Proceedings of the 2004 Joint Workshop on Foundations of Mobile Computing—DIALM-POMC’04, Philadelphia, PA, USA, 1 October 2004; p. 60. [Google Scholar]
- Shakya, R.K.; Singh, Y.N.; Verma, N.K. Generic correlation model for wireless sensor network applications. IET Wirel. Sens. Syst. 2013, 3, 266–276. [Google Scholar] [CrossRef]
- Liu, C.; Wu, K.; Pei, J. An Energy-Efficient Data Collection Framework for Wireless Sensor Networks by Exploiting Spatiotemporal Correlation. IEEE Trans. Parallel Distrib. Syst. 2007, 18, 1010–1023. [Google Scholar] [CrossRef]
- Peng, C.H.W.; Tsai, Y.S.; Lee, W. Exploiting Spatial and Data Correlations for Approximate Data Collection in Wireless Sensor Networks. In Proceedings of the Second ACM International Workshop on Knowledge Discovery from Sensor Data (In conjunction with ACM SIGKDD), Las Vegas, NV, USA, 24 August 2008; pp. 111–118. [Google Scholar]
- Liu, Z.; Xing, W.; Zeng, B.; Wang, Y.; Lu, D. Distributed spatial correlation-based clustering for approximate data collection in WSNs. In Proceedings of the 2013 IEEE 27th International Conference on Advanced Information Networking and Applications (AINA), Barcelona, Spain, 25–28 March 2013; pp. 56–63. [Google Scholar]
- Gupta, H.; Navda, V.; Das, S.; Chowdhary, V. Efficient gathering of correlated data in sensor networks. ACM Trans. Sens. Netw. 2008, 4, 1–31. [Google Scholar] [CrossRef]
- Ma, Y.; Guo, Y.; Tian, X.; Ghanem, M. Distributed clustering-based aggregation algorithm for spatial correlated sensor networks. IEEE Sens. J. 2011, 11, 641–648. [Google Scholar] [CrossRef]
- Yuan, F.; Zhan, Y.; Wang, Y. Data density correlation degree clustering method for data aggregation in WSN. IEEE Sens. J. 2014, 14, 1089–1098. [Google Scholar] [CrossRef]
- Pattem, S.; Krishnamachari, B.; Govindan, R. The Impact of Spatial Correlation on Routing with Compression in Wireless Sensor Networks. ACM Trans. Sens. Netw. 2008, V, 1–31. [Google Scholar] [CrossRef]
- Long, H.L.H.; Liu, Y.L.Y.; Fan, X.F.X.; Dick, R.P.P.; Yang, H.Y.H. Energy-efficient spatially-adaptive clustering and routing in wireless sensor networks. In Proceedings of the 2009 Design, Automation & Test in Europe Conference & Exhibition, Nice, France, 20–24 April 2009; pp. 1267–1272. [Google Scholar]
- Dai, R.; Akyildiz, I.F. A spatial correlation model for visual information in wireless multimedia sensor networks. IEEE Trans. Multimed. 2009, 11, 1148–1159. [Google Scholar] [CrossRef]
- Dang, T.; Bulusu, N.; Feng, W.C. RIDA: A Robust Information-Driven Data Compression Architecture for Irregular Wireless. IEEE Sens. J. 2007, 16, 5471–5480. [Google Scholar]
- Intel Berkeley Research Lab. Available online: http://db.csail.mit.edu/labdata/labdata.html (accessed on 25 February 2017).
- Wang, F.; Wu, S.; Wang, K.; Hu, X. Energy-Efficient Clustering Using Correlation and Random Update Based on Data Change Rate for Wireless Sensor Networks. IEEE Sens. J. 2016, 16, 5471–5480. [Google Scholar] [CrossRef]
- Maeda, D.; Uehara, H.; Yokoyama, M. Efficient Clustering Scheme Considering Non-Uniform Correlation Distribution for Ubiquitous Sensor Networks. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2007, E90-A, 1344–1352. [Google Scholar] [CrossRef]
- Nga, N.T.T.; Khanh, N.K.; Hong, S.N. Entropy-based Correlation Clustering for Wireless Sensor Networks in Multi-Correlated Regional Environments. In Proceedings of the 15th International Conference on Electronics, Information and Communication (ICEIC 2016), Da Nang, Vietnam, 27–30 January 2016; Volume 5. [Google Scholar]
- Nga, N.T.T.; Khanh, N.K.; Hong, S.N. Entropy correlation and its impact on routing with compression in wireless sensor network. In Proceedings of the Seventh Symposium on Information and Communication Technology—SoICT’16, Ho Chi Minh City, Vietnam, 8–9 December 2016; pp. 235–242. [Google Scholar]
- Cover, T.M.; Thomas, J.A.; Bellamy, J.; Freeman, R.L.; Liebowitz, J. Elements of Information Theory Wiley Series in Expert System Applications to Telecommunications; John Wiley & Sons, Inc.: New York, NY, USA, 1991. [Google Scholar]
- Cahill, N.D. Normalized Measures of Mutual Information With General Definitions of Entropy for Multimodal Image Registration in Biomedical Image Registration; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6204, pp. 258–268. [Google Scholar]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Pradhan, S.S.; Ramchandran, K. Distributed source coding using syndromes (DISCUS): Design and construction. IEEE Trans. Inf. Theory 2003, 49, 626–643. [Google Scholar] [CrossRef]
- Intanagonwiwat, C.; Estrin, D.; Govindan, R.; Heidemann, J. Impact of network density on data aggregation in wireless sensor networks. In Proceedings of the 22nd International Conference on Distributed Computing Systems 2002, Vienna, Austria, 2–5 July 2002; pp. 457–458. [Google Scholar]
- Krishnamachari, L.; Estrin, D.; Wicker, S. The impact of data aggregation in wireless sensor networks. In Proceedings of the 22nd International Conference on Distributed Computing Systems Workshops, Vienna, Austria, 2–5 July 2002; pp. 575–578. [Google Scholar]
- Scaglione, A.; Servetto, S. On the Interdependence of Congestion and Contention in Wireless Sensor Networks. Wirel. Netw. 2002, 11, 149–160. [Google Scholar] [CrossRef]
- Heinzelman, W.B.; Chandrakasan, A.P.; Balakrishnan, H. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]

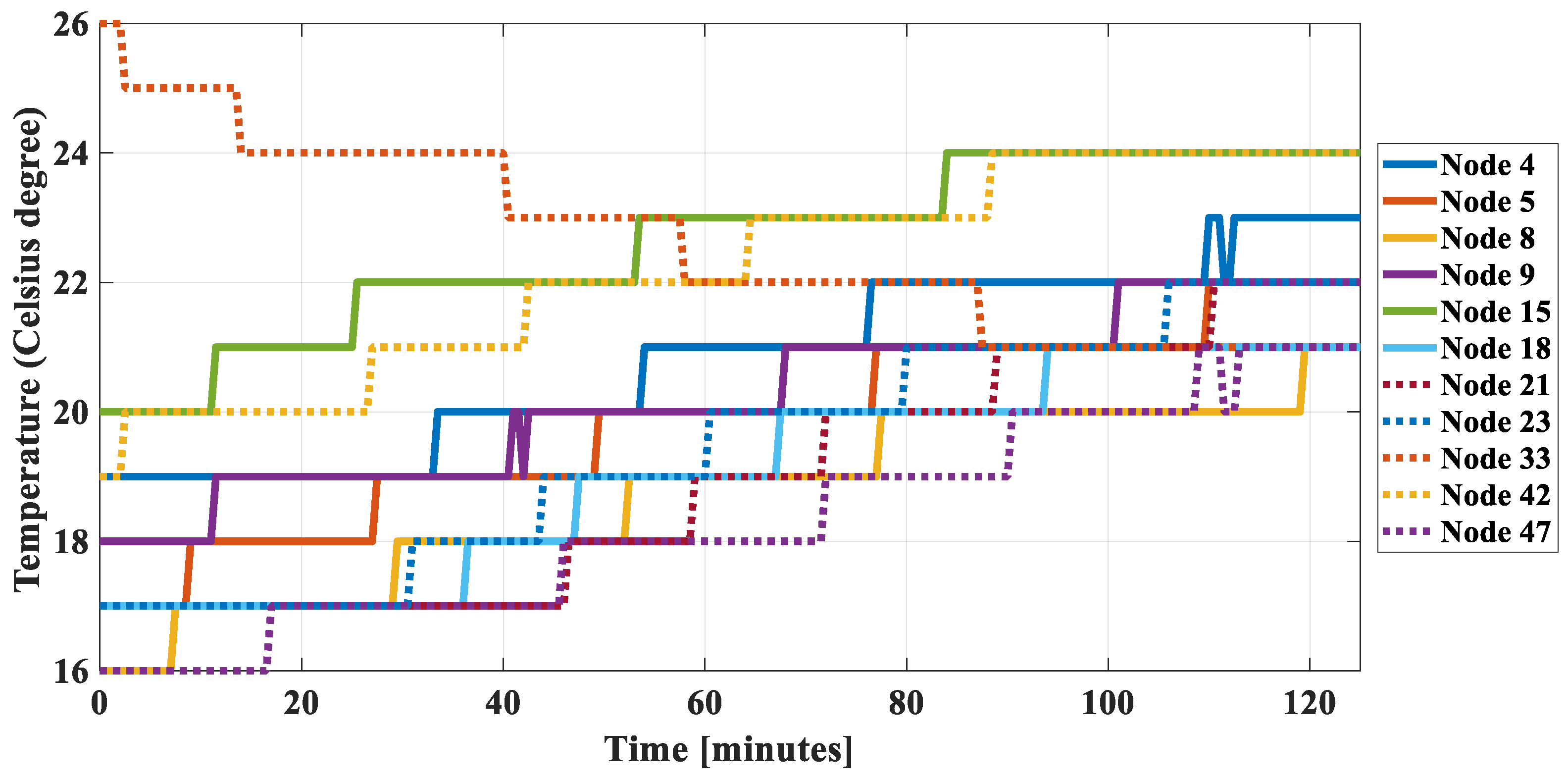



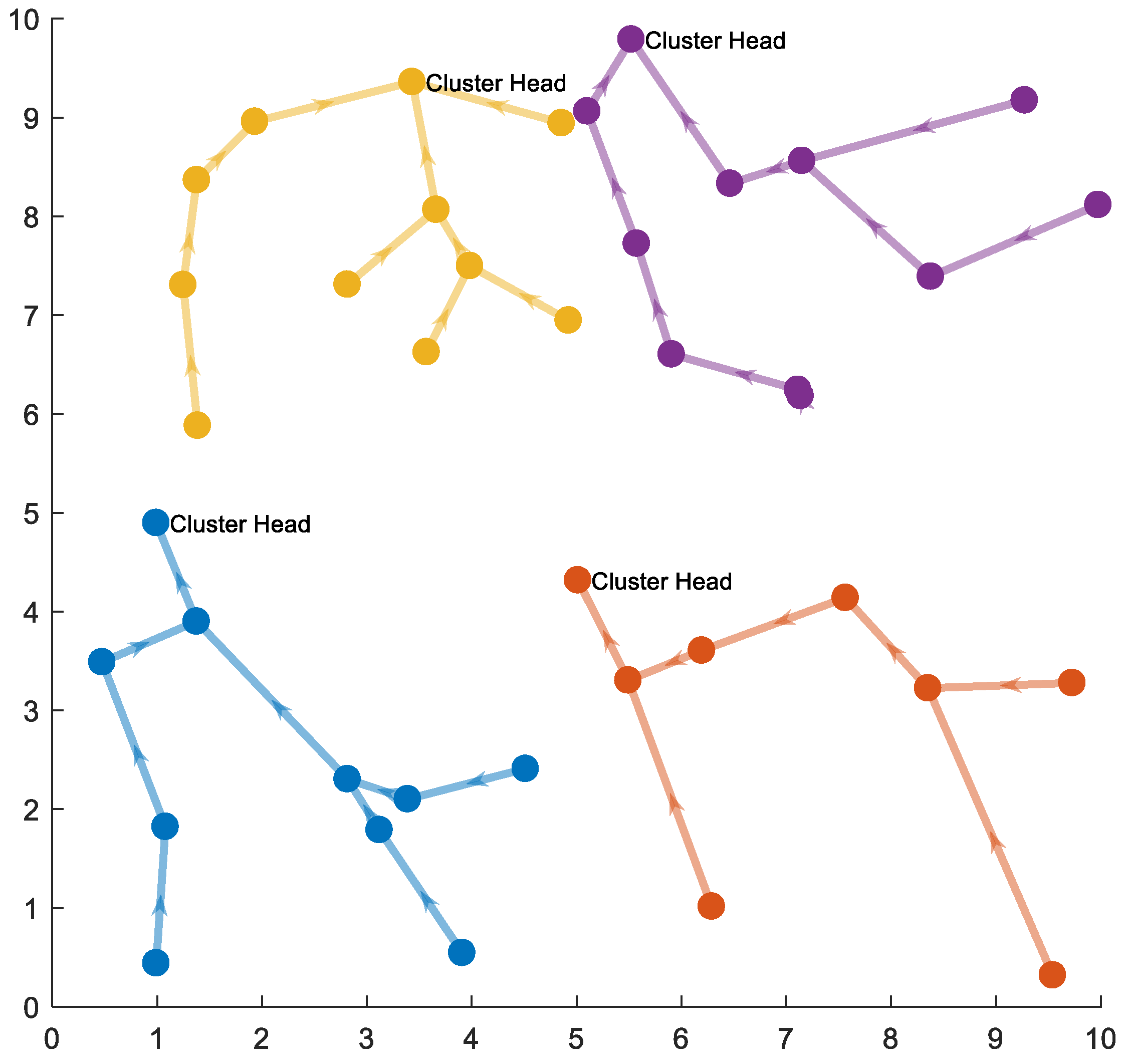

| Node | 4 | 5 | 8 | 9 | 15 | 18 | 21 | 23 | 33 | 42 | 47 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Entropy [bit] | 2.27 | 2.49 | 2.39 | 2.25 | 2.16 | 2.22 | 2.40 | 2.53 | 2.30 | 2.35 | 2.55 |
| Node | 4 | 5 | 8 | 9 | 15 | 18 | 21 | 23 | 33 | 42 | 47 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 1 | 0.80 | 0.77 | 0.64 | 0.69 | 0.69 | 0.72 | 0.76 | 0.64 | 0.64 | 0.70 |
| 5 | 0.80 | 1 | 0.81 | 0.67 | 0.73 | 0.65 | 0.70 | 0.73 | 0.64 | 0.68 | 0.71 |
| 8 | 0.77 | 0.81 | 1 | 0.62 | 0.74 | 0.63 | 0.62 | 0.71 | 0.65 | 0.66 | 0.64 |
| 9 | 0.64 | 0.67 | 0.62 | 1 | 0.66 | 0.75 | 0.66 | 0.69 | 0.72 | 0.71 | 0.71 |
| 15 | 0.69 | 0.73 | 0.74 | 0.66 | 1 | 0.63 | 0.61 | 0.66 | 0.74 | 0.72 | 0.65 |
| 18 | 0.69 | 0.65 | 0.63 | 0.75 | 0.63 | 1 | 0.73 | 0.71 | 0.69 | 0.74 | 0.72 |
| 21 | 0.72 | 0.70 | 0.62 | 0.66 | 0.61 | 0.73 | 1 | 0.73 | 0.69 | 0.70 | 0.81 |
| 23 | 0.76 | 0.73 | 0.71 | 0.69 | 0.66 | 0.71 | 0.73 | 1 | 0.68 | 0.73 | 0.70 |
| 33 | 0.64 | 0.64 | 0.65 | 0.72 | 0.74 | 0.69 | 0.69 | 0.68 | 1 | 0.79 | 0.69 |
| 42 | 0.64 | 0.68 | 0.66 | 0.71 | 0.72 | 0.74 | 0.70 | 0.73 | 0.79 | 1 | 0.70 |
| 47 | 0.70 | 0.71 | 0.64 | 0.71 | 0.65 | 0.72 | 0.81 | 0.70 | 0.69 | 0.70 | 1 |
| Nodes in Subset | Hmin [bit] | Hmax [bit] | ρmin | ρmax | Practical JE [bit] | Upper Bound JE [bit] | Lower Bound JE [bit] |
|---|---|---|---|---|---|---|---|
| 4, 5 | 2.27 | 2.49 | 0.80 | 0.80 | 2.84 | 2.99 | 2.72 |
| 4, 5, 8 | 2.27 | 2.49 | 0.77 | 0.81 | 3.13 | 3.41 | 2.96 |
| 4, 5, 8, 9 | 2.25 | 2.49 | 0.62 | 0.81 | 3.72 | 4.54 | 3.08 |
| 4, 5, 8, 9, 15 | 2.16 | 2.49 | 0.62 | 0.81 | 3.95 | 4.85 | 3.05 |
| 4, 5, 8, 9, 15, 18 | 2.16 | 2.49 | 0.62 | 0.81 | 4.22 | 5.06 | 3.10 |
| 4, 5, 8, 9, 15, 18, 21 | 2.16 | 2.49 | 0.61 | 0.81 | 4.51 | 5.21 | 3.13 |
| 4, 5, 8, 9, 15, 18, 21, 23 | 2.16 | 2.53 | 0.61 | 0.81 | 4.75 | 5.40 | 3.15 |
| 4, 5, 8, 9, 15, 18, 21, 23, 33 | 2.16 | 2.53 | 0.61 | 0.81 | 4.96 | 5.47 | 3.16 |
| 4, 5, 8, 9, 15, 18, 21, 23, 33, 42 | 2.16 | 2.53 | 0.61 | 0.81 | 5.06 | 5.52 | 3.16 |
| 4, 5, 8, 9, 15, 18, 21, 23, 33, 42, 47 | 2.16 | 2.55 | 0.61 | 0.81 | 5.23 | 5.60 | 3.17 |
| Group | Node Number | Entropy Range [bit] | ρ0 |
|---|---|---|---|
| 1 | 4, 5, 8, 9, 15, 18, 21, 23, 33, 42, 47 | 2.16–2.55 | 0.6 |
| 2 | 22, 24, 30, 31, 40, 41 | 2.64–3.09 | 0.6 |
| 3 | 1, 10, 11, 28, 35, 37, 39, 44, 46 | 1.83–2.17 | 0.5 |
| 4 | 2, 3, 6, 7, 12, 13, 14, 16, 17, 19, 20, 25, 26, 27, 29, 32, 34, 36, 38, 43, 45, 48 | 0.60–3.09 | 0.03 |
| ρ0 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|
| N = 10 | 8 | 7 | 6 | 5 | 4 |
| N = 15 | 10 | 8 | 7 | 5 | 4 |
| N = 20 | 10 | 8 | 7 | 5 | 4 |
| ρ0 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|
| N = 10 | 7 | 6 | 5 | 4 | 2 |
| N = 15 | 8 | 6 | 5 | 4 | 2 |
| N = 20 | 8 | 6 | 5 | 4 | 2 |
| ρ0 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|
| N = 10 | 6 | 5 | 4 | 3 | 2 |
| N = 15 | 6 | 5 | 4 | 3 | 2 |
| N = 20 | 7 | 5 | 4 | 3 | 2 |
| Desired Distortion | 0.05 | 0.1 | 0.15 |
|---|---|---|---|
| Number of representative nodes | 8 | 6 | 5 |
| Selected nodes | 4, 8, 9, 15, 18, 21, 33, 47 | 8, 9, 15, 18, 21, 33 | 8, 9, 15, 18, 33 |
| Actual distortion | 0.08 | 0.15 | 0.20 |
| Desired Distortion | 0.05 | 0.1 | 0.15 |
|---|---|---|---|
| Number of Representative Nodes | 9 | 7 | 6 |
| Selected Nodes | 4, 8, 9, 15, 18, 21, 33, 42, 47 | 8, 9, 15, 18, 21, 33, 47 | 8, 9, 15, 18, 21, 33 |
| Actual Distortion | 0.05 | 0.10 | 0.15 |
| Node Number | 5 | 21 | 24 | 31 | 33 | 40 | 41 | 42 | 46 | 47 |
|---|---|---|---|---|---|---|---|---|---|---|
| Entropy [bits] | 2.79 | 2.74 | 2.64 | 2.84 | 2.80 | 2.81 | 2.68 | 2.62 | 2.81 | 2.82 |
| Desired Distortion | 0.05 | 0.1 | 0.15 |
|---|---|---|---|
| Number of Representative Nodes | 7 | 6 | 5 |
| Selected Nodes | 5, 24, 33, 40, 41, 42, 46 | 5, 33, 40, 41, 42, 46 | 5, 40, 41, 42, 46 |
| Actual Distortion | 0.068 | 0.100 | 0.135 |
| Desired Distortion | 0.05 | 0.1 | 0.15 |
|---|---|---|---|
| Number of Representative Nodes | 8 | 7 | 6 |
| Selected Nodes | 5, 24, 31, 33, 40, 41, 42, 46 | 5, 24, 33, 40, 41, 42, 46 | 5, 33, 40, 41, 42, 46 |
| Actual Distortion | 0.045 | 0.068 | 0.100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen Thi Thanh, N.; Nguyen Kim, K.; Ngo Hong, S.; Ngo Lam, T. Entropy Correlation and Its Impacts on Data Aggregation in a Wireless Sensor Network. Sensors 2018, 18, 3118. https://doi.org/10.3390/s18093118
Nguyen Thi Thanh N, Nguyen Kim K, Ngo Hong S, Ngo Lam T. Entropy Correlation and Its Impacts on Data Aggregation in a Wireless Sensor Network. Sensors. 2018; 18(9):3118. https://doi.org/10.3390/s18093118
Chicago/Turabian StyleNguyen Thi Thanh, Nga, Khanh Nguyen Kim, Son Ngo Hong, and Trung Ngo Lam. 2018. "Entropy Correlation and Its Impacts on Data Aggregation in a Wireless Sensor Network" Sensors 18, no. 9: 3118. https://doi.org/10.3390/s18093118
APA StyleNguyen Thi Thanh, N., Nguyen Kim, K., Ngo Hong, S., & Ngo Lam, T. (2018). Entropy Correlation and Its Impacts on Data Aggregation in a Wireless Sensor Network. Sensors, 18(9), 3118. https://doi.org/10.3390/s18093118





