Integrated Longitudinal and Lateral Networked Control System Design for Vehicle Platooning
Abstract
:1. Introduction
- local control strategy (LCS): based on a local context, the convoy is controlled from near-approach.
- global control strategy (GCS): based on the global context, the convoy is ordered by reference to the leader.
- mixed control strategy (MCS): taking into account the complementarities of the two LCS and GCS methods, a mixed approach can be developed.
- We investigate the impact of the car group on the circulation flow by using a local architecture for platoon. Compared to the mixed structure adopted in [11], this one just employs data from neighboring vehicles and the car is entirely autonomous—hence it doesn’t need sophisticated sensors.
- The robustness of the proposed control law is considered regarding the communication delays. In addition, the comfort of the passenger by saturating actuators (e.g.,the maximum deceleration and the maximum jerk (The acceleration’s time derivative is the best way to exhibit a human comfort criteria.)) is taken into account. This strategy is compared to [26] in order to show its advantages with respect to communication delay in design.
- The integrated longitudinal and lateral autonomous is considered in order to cover lane change maneuver. Using TS fuzzy modeling to represent the lateral vehicle dynamic as in [18], the proposed lateral controller can handle a large variation range of vehicle speed. This approach reduces the design conservatism.
2. Longitudinal Controller Design
2.1. Longitudinal Vehicle Dynamics Modelling and Feedback Linearisation
2.2. Problem Formulation
2.2.1. Miscellaneous Information Feedback
2.2.2. Impact of Communication Limitations
2.2.3. Saturation Effect of Actuator
2.2.4. The Aim
- Individual vehicle stability: the global closed-loop platoon system is asymptotically stable with respect to the communication delay and saturation effects.
- The vehicle platoon mets the following performance index:
- String stability: the swings are not magnifying with a vehicle index due to any handling of the head vehicle [10], namely, for any , where ; or in the same way, the impulse response corresponding to is larger than zero for all t.
2.3. Single Vehicle Stabilisation
Guaranteed Cost Controller Design
2.4. String Stability
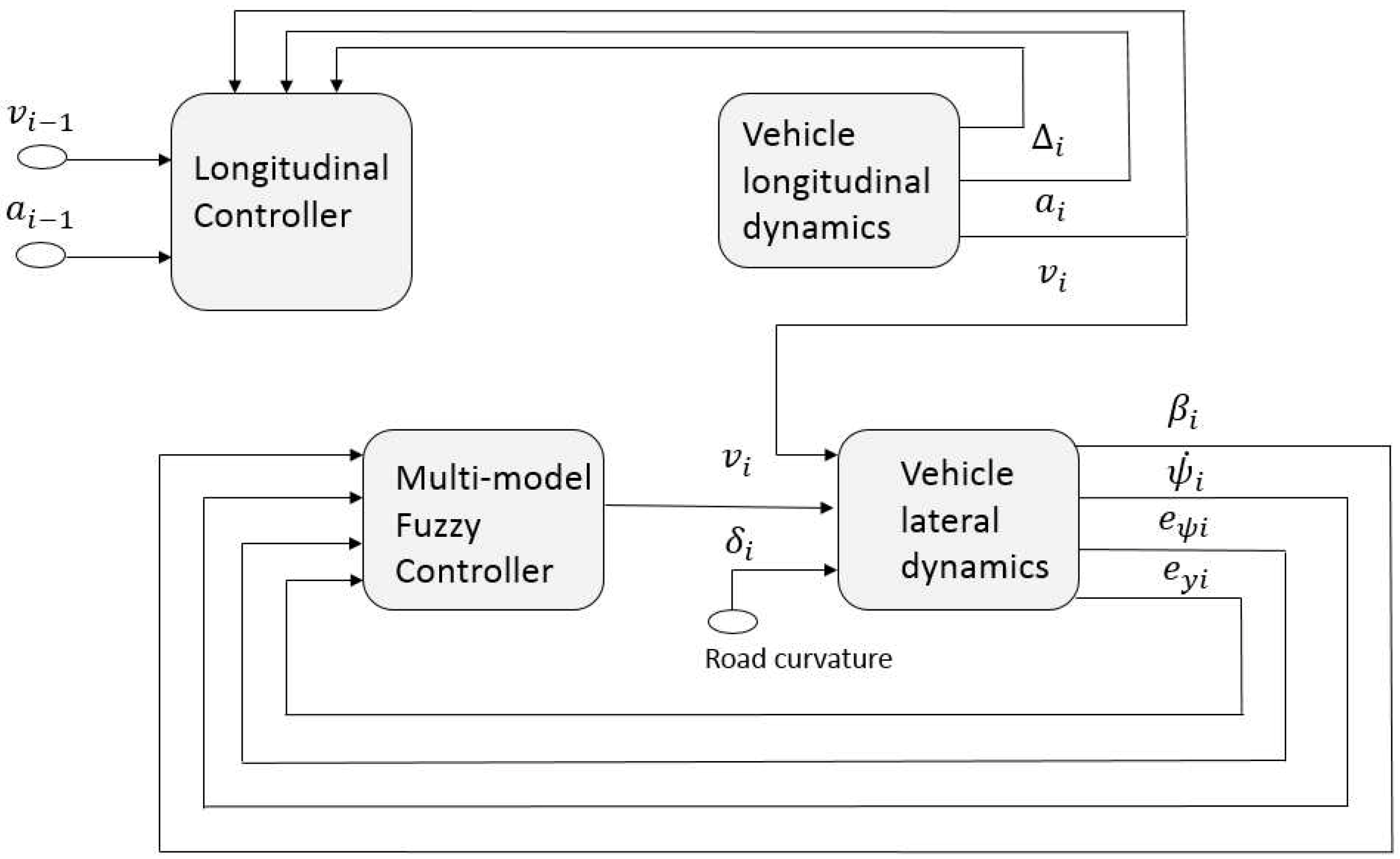
3. Lateral Controller Design
3.1. Bicycle Model
3.2. TS Design Conditions
3.3. Coupling Dynamics
4. Simulation Results
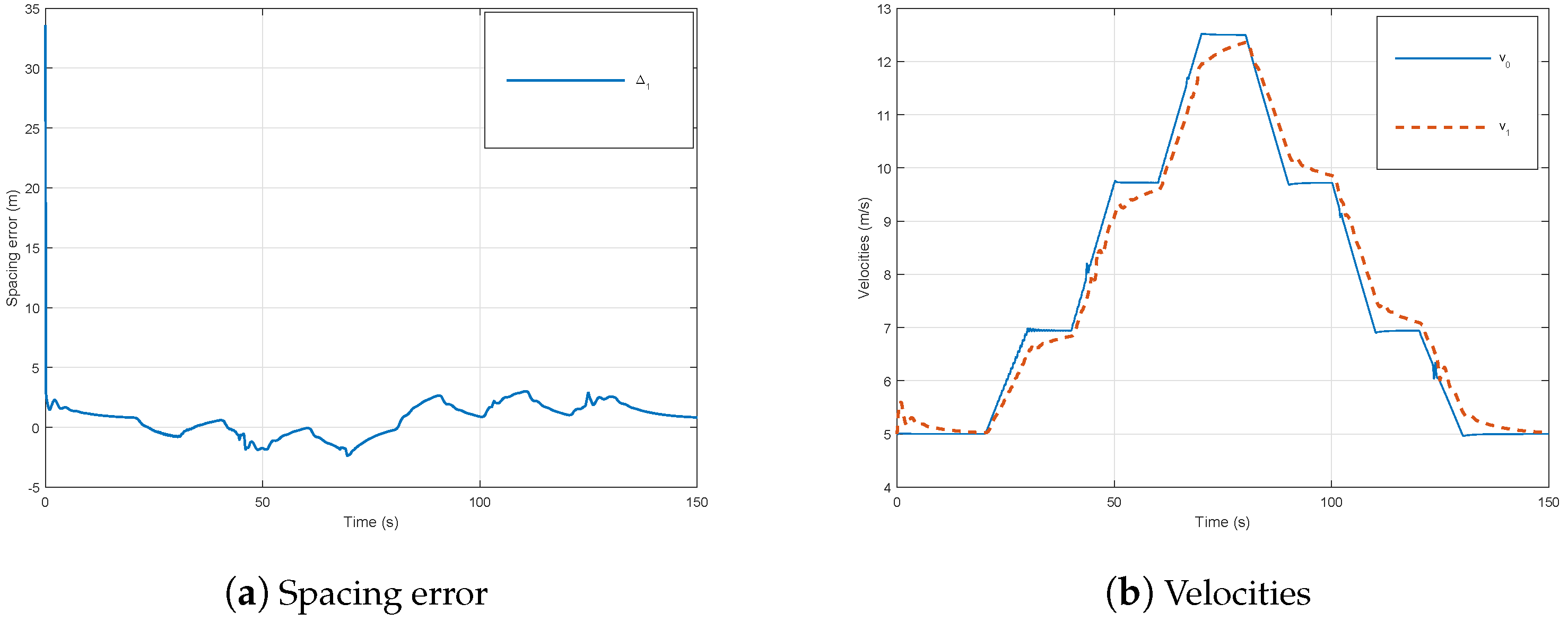
4.1. Longitudinal Tracking Performance and String Stability
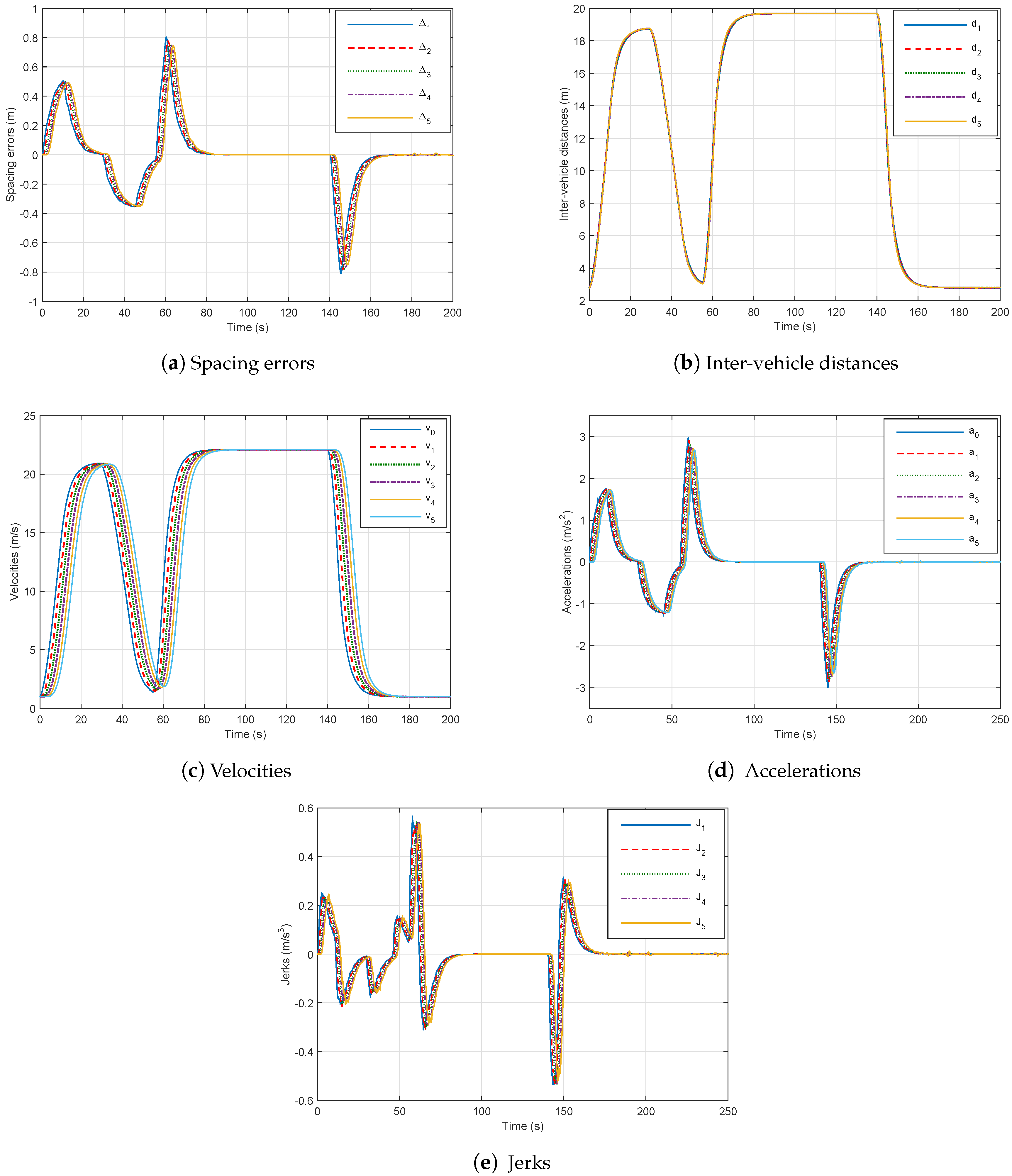
- The following parameters are used in the simulation process: the delay lower bound = 60 ms, upper bound = 680 ms, = 0.8, = 0.1, R = 1 and . According to Theorems 1 and 2, we get these controller gains:
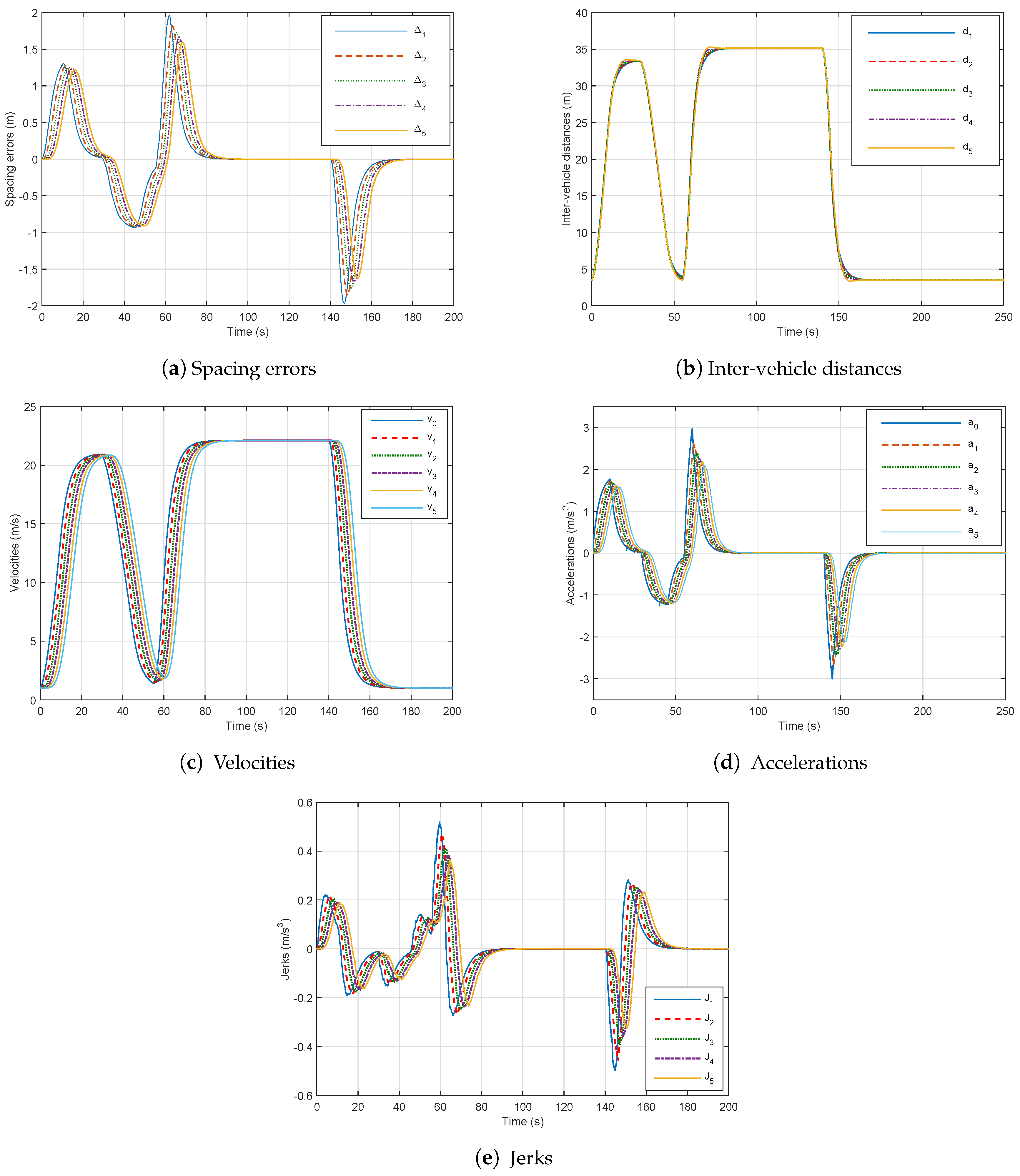
- If we choose , = 60 ms and upper bound ms, we obtain the following controller gains:
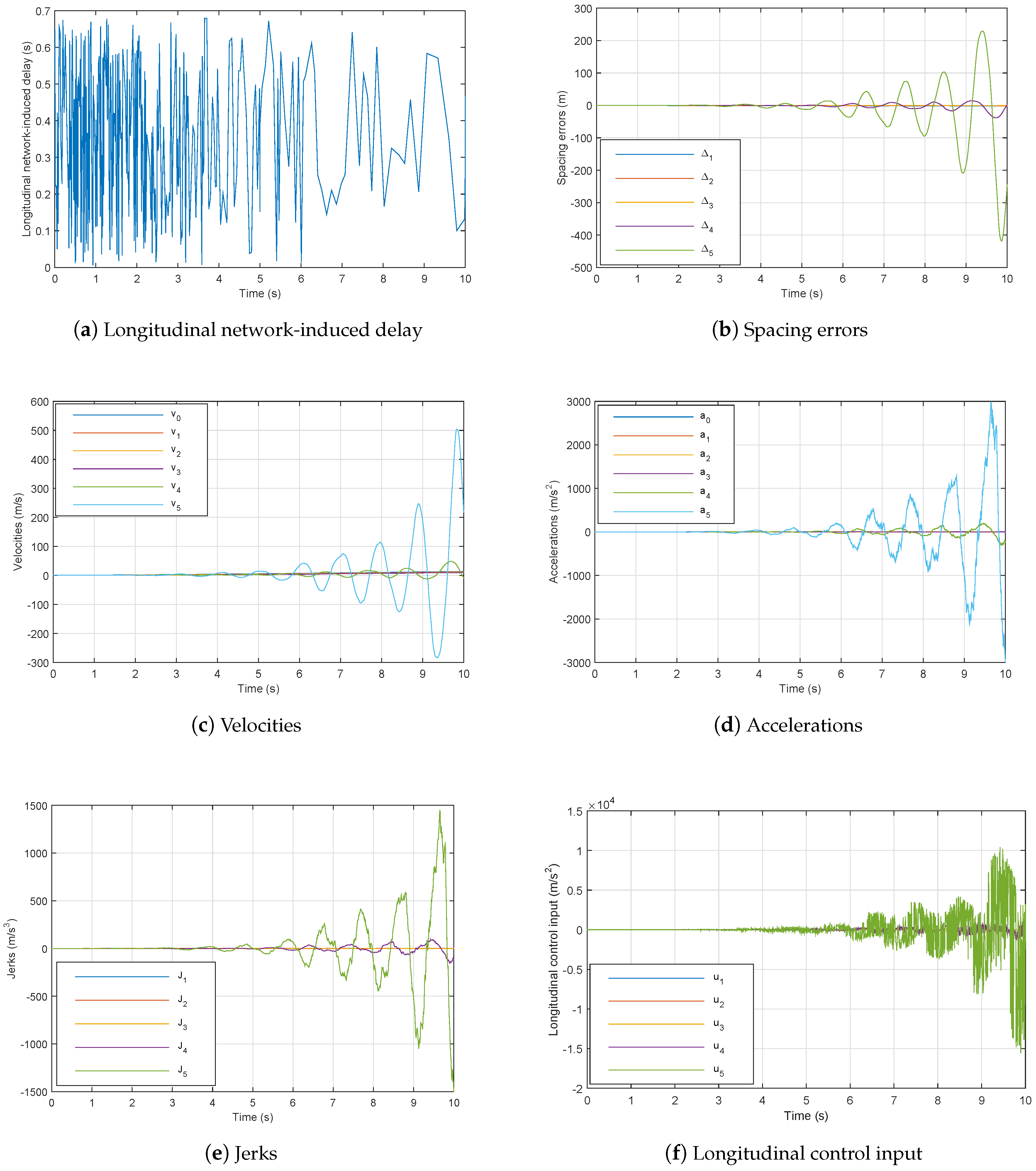
- However, if we neglect transmission delay in design, by Lemma 2 in [26], we can find the following controller gains:
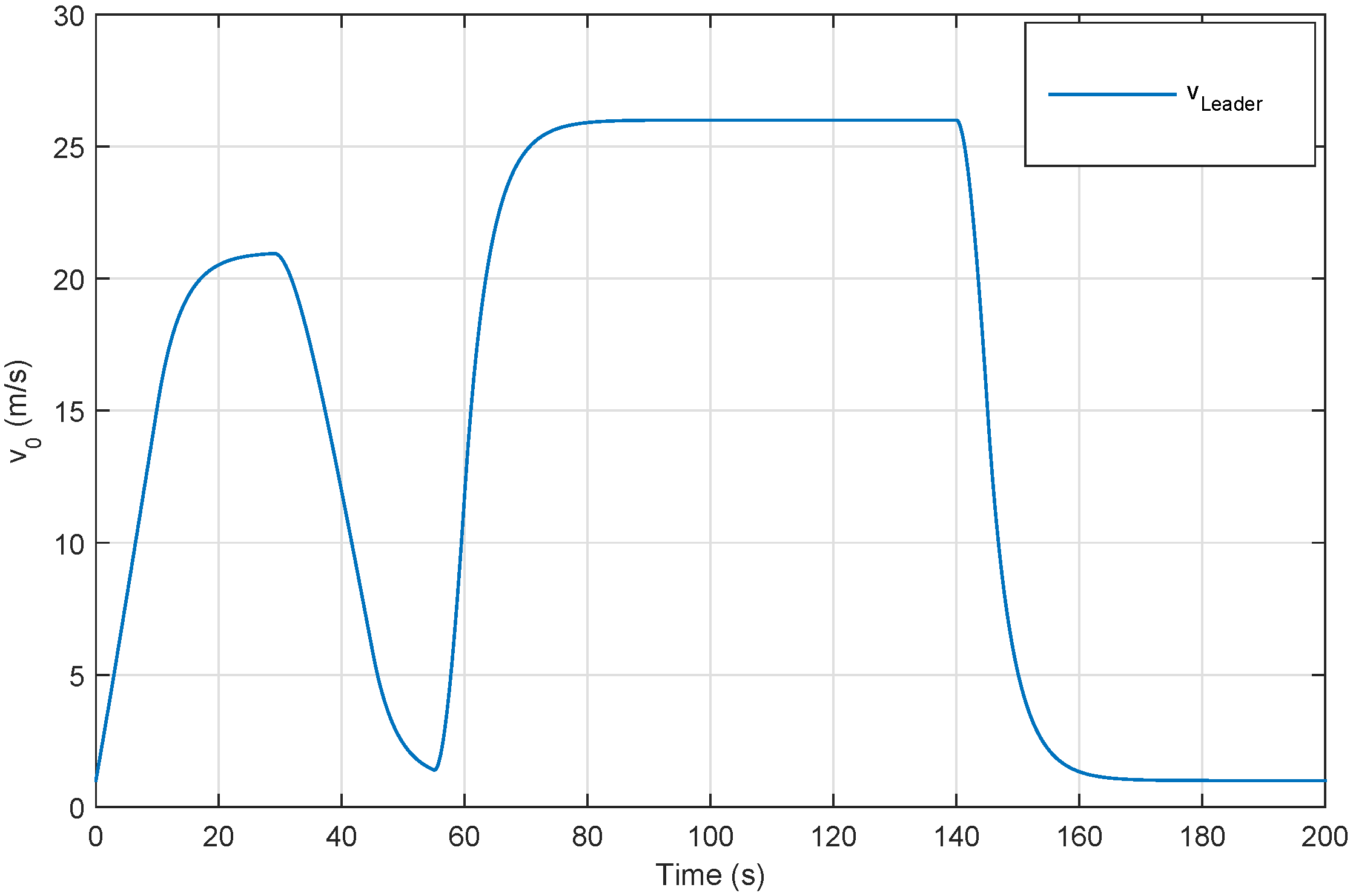
- Changing the speed of the platoon (from 2 m/s to 20 m/s) at 0 s to verify string stability.
- Performing an emergency braking at 30 s to satisfy the driver longitudinal ride comfort.
- Thereafter, the lead vehicle is accelerated and decelerated (hard braking-and-go) to check safety.
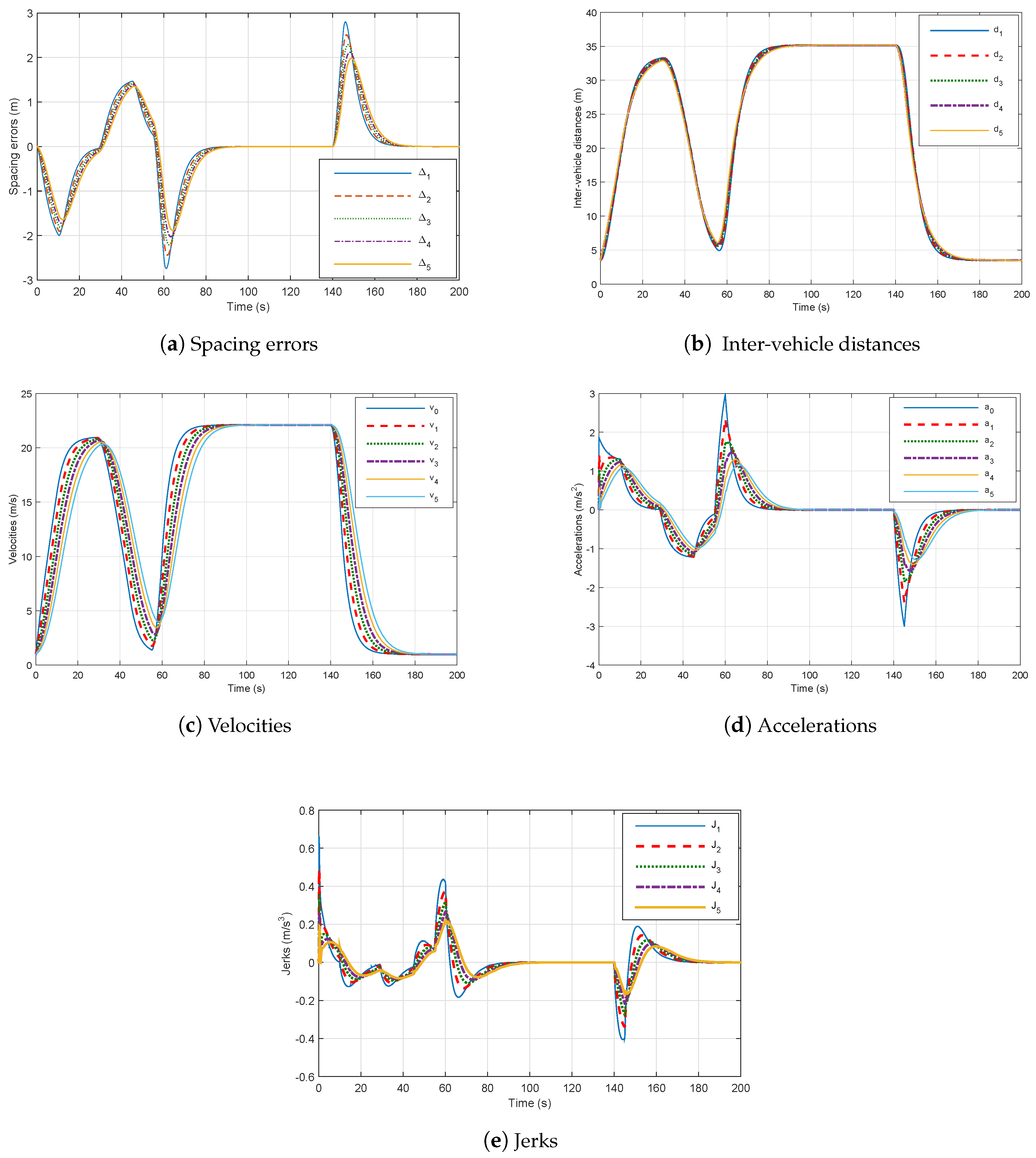
- The spacing errors decrease which guarantee string stability as shown in Figure 8a,
- The inter-distances magnitude in the presence of networked communication is positive and smaller than those without delay, which prove the good performance of our controller (48) as in Figure 8b.
- The speed tracking performances are good as well in dynamics as in statics as depicted in Figure 8c.
- The platoon maintains its stability, safety and good performance with controller (47) despite constraints of communication networks.
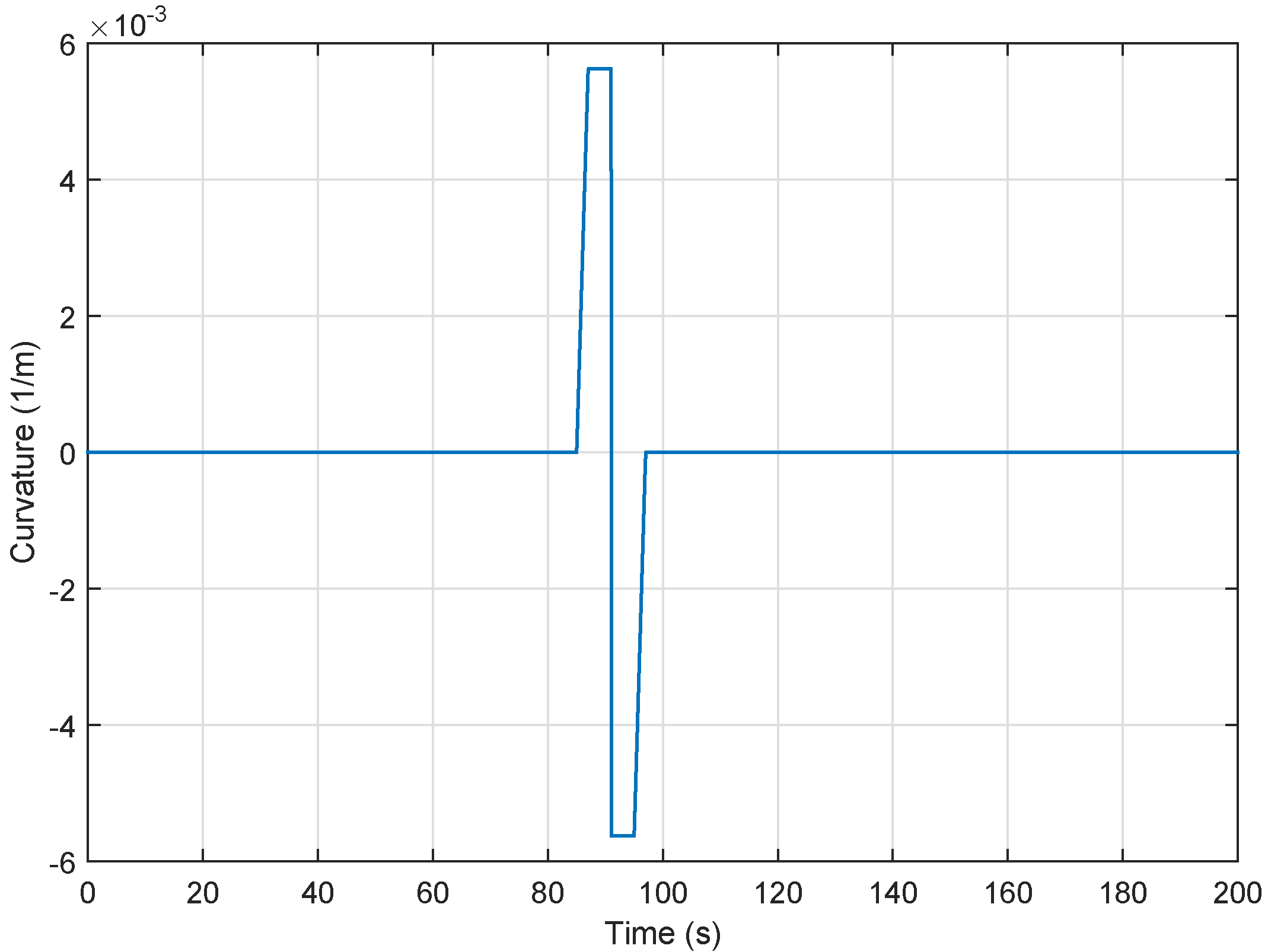
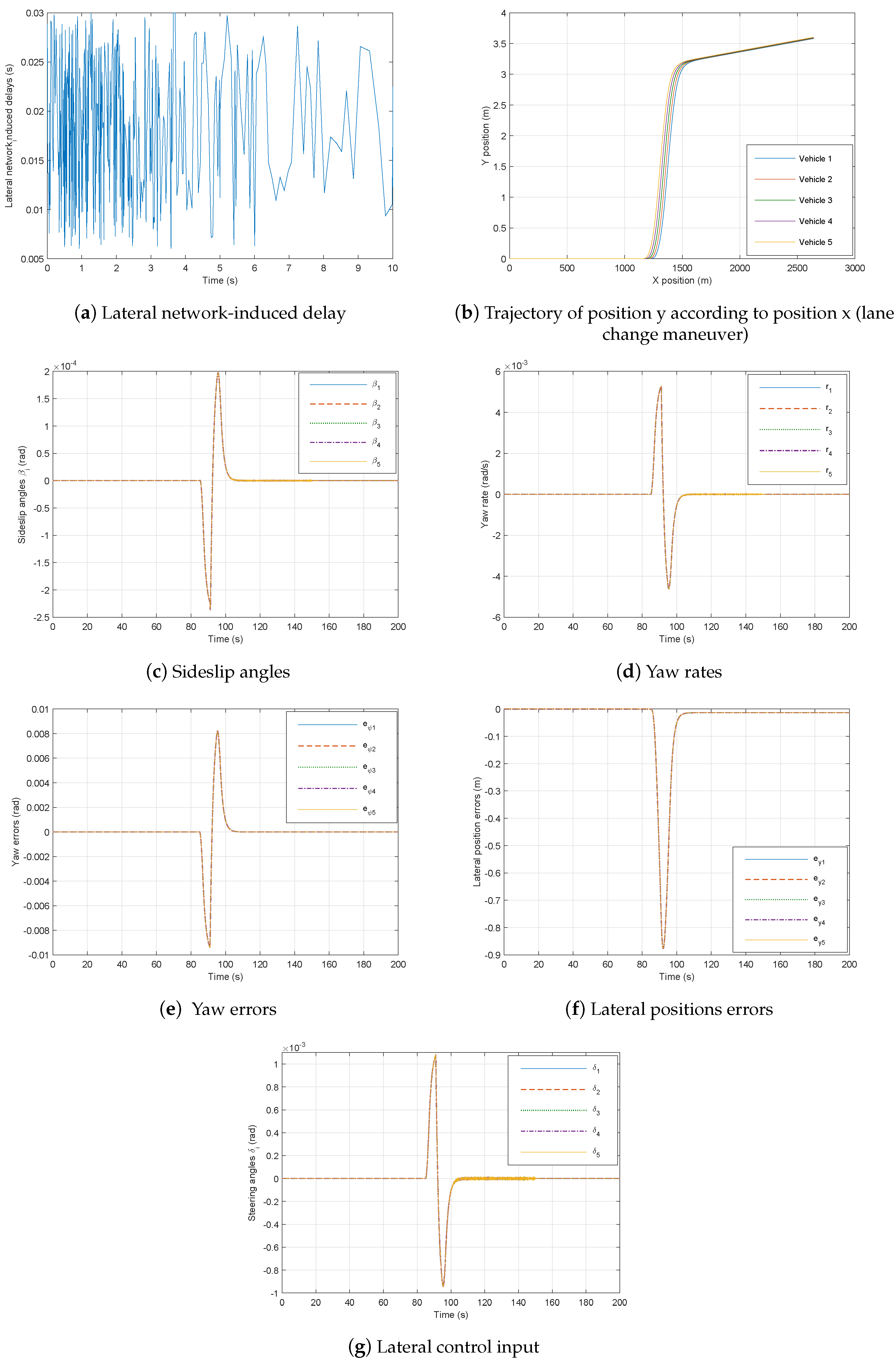
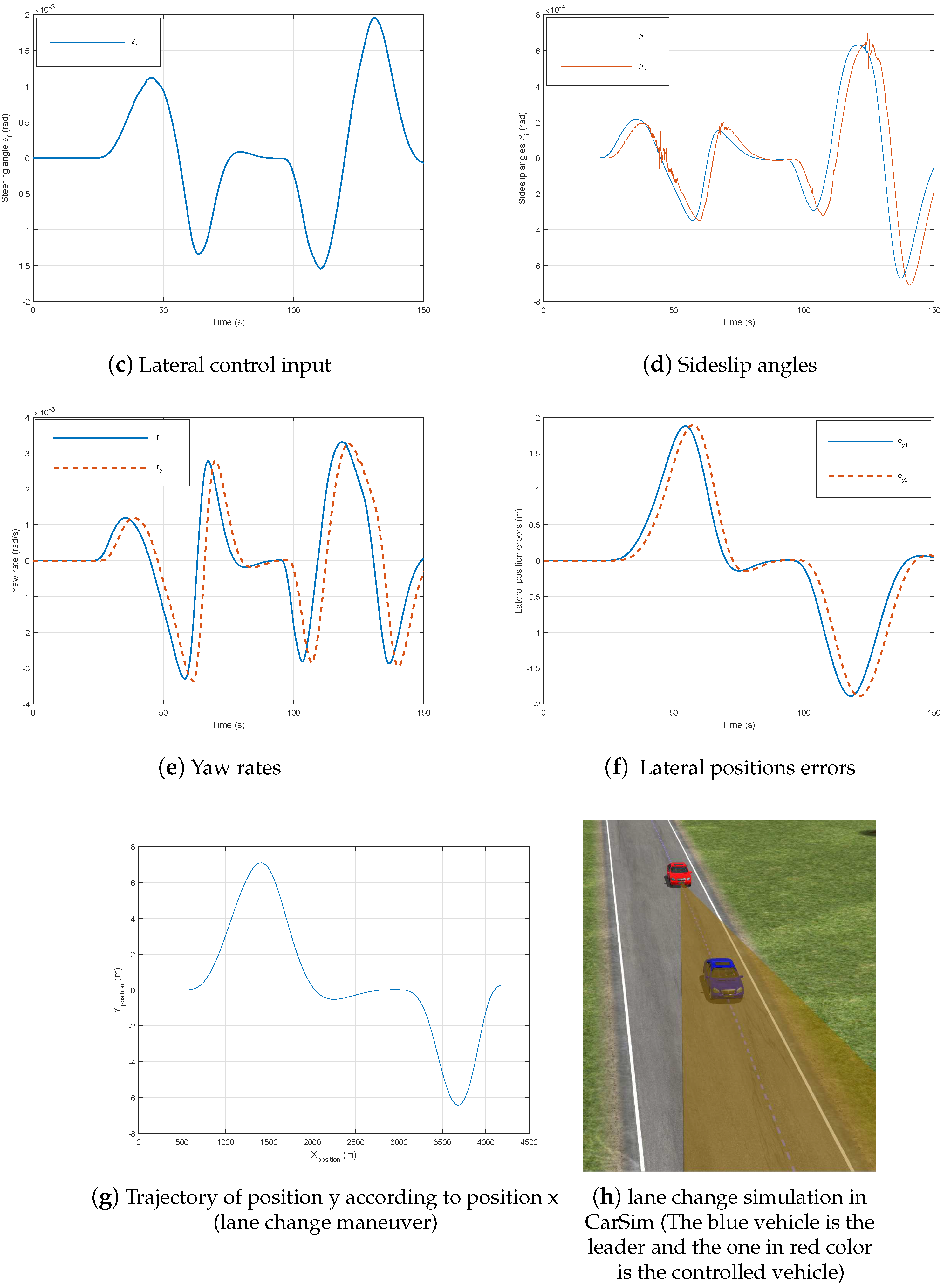
4.2. Lateral Control Performance
4.3. CarSim Software Validation
- Vehicle Parameters: This block is used to define several physical parameters of the vehicle (dimensions, engine, tires, bodywork and mathematical models that represent the tire/ground contact forces and suspension forces exerted on the vehicle, etc.).
- Test conditions: In this block, we can create our own test circuit, choose the maneuver, the state of the road and the aerodynamic forces.
- Code Generator: This block is used to generate a block diagram that can be used in various mathematical calculation tools Matlab/Simulink, labVIEW, dSPACE.
- Animation: once the program has been compiled, this block allows for visualizing the maneuver on a 3D video.
- Visualization: For each test, this block allows you to record and plot variables and measures chosen by the user.
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| NCS | Networked Control System |
| TS | Takagi Sugeno |
| LMI | Linear Matrix Inequality |
| BMI | Bilinear Matrix Inequality |
| SOF | Static Output Feedback |
| SSP | Safety Spacing Policy |
| VANET | Vehicular Ad-hoc NETworks |
| COG | Center Of Gravity |
References
- Kianfar, R.; Ali, M.; Falcone, P.; Fredriksson, J. Combined longitudinal and lateral control design for string stable vehicle platooning within a designated lane. In Proceedings of the IEEE 17th International Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 1003–1008. [Google Scholar]
- Zhao, J.; Elkamel, A. Integrated Longitudinal and Lateral Control System Design for Autonomous Vehicles. IFAC Proc. Vol. 2009, 42, 496–501. [Google Scholar] [CrossRef]
- Kianfar, R.; Falcone, P.; Fredriksson, J. A control matching model predictive control approach to string stable vehicle platooning. Control Eng. Pract. 2015, 45, 163–173. [Google Scholar] [CrossRef]
- Rahmana, M.; Abdel-Atyb, M. Longitudinal safety evaluation of connected vehicles platooning on expressways. Accid. Anal. Prev. 2017, 117, 381–391. [Google Scholar] [CrossRef] [PubMed]
- Tuchner, A.; Haddad, J. Vehicle platoon formation using interpolating control: A laboratory experimental analysis. Trans. Res. Part C 2017, 84, 21–47. [Google Scholar] [CrossRef]
- Ghasemi, A.; Rouhi, S. Stability Analysis of a Predecessor-Following Platoon of Vehicles With Two Time Delays. Sci. J. Traff. Trans. Res. 2015, 27, 35–46. [Google Scholar] [CrossRef] [Green Version]
- Xiao, L.; Gang, F. Effects of information delay on string stability of platoon of automated vehicles under typical information frameworks. J. Cent. South Univ. Technol. 2010, 17, 1271–1278. [Google Scholar] [CrossRef]
- Bom, J.; Thuilot, B.; Marmoiton, F.; Martinet, P. A Global Control Strategy for Urban Vehicles Platooning relying on Nonlinear Decoupling Laws. IEEE/RSJ Int. Conf. Intell. Robots Syst. 2005, 1999–2000. [Google Scholar] [CrossRef]
- Abou Harfouch, Y.; Yuan, S.; Baldi, S. An Adaptive Switched Control Approach to Heterogeneous Platooning with Inter-Vehicle Communication Losses. IEEE Trans. Control Netw. Syst. 2017, 1–10. [Google Scholar] [CrossRef]
- Oncu, S.; Ploeg, J.; Van de Wouw, N.; Nijmeijer, H. Cooperative Adaptative Cruise Control: Network-Aware Analysis of String Stability. IEEE Trans. Intell. Trans. Syst. 2014, 15, 1527–1537. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, L.; Ge, G. Event-triggered platoon control of vehicles with time-varying delay and probabilistic faults. Mech. Syst. Signal Process. 2017, 87, 96–117. [Google Scholar] [CrossRef]
- Ioannou, P.; Chien, C. Autonomous intelligent cruise control. IEEE Trans. Veh. Technol. 1993, 42, 657–672. [Google Scholar] [CrossRef]
- Wen, S.; Guo, G.; Chen, B.; Gao, X. Event-triggered cooperative control of vehicle platoons in vehicular ad hoc networks. Inf. Sci. 2018, 459, 341–353. [Google Scholar] [CrossRef]
- Kamali, M.; Dennis, L.; McAree, O.; Fisher, M.; Veres, S. Formal verification of autonomous vehicle platooning. Sci. Comput. Program. 2017, 148, 88–106. [Google Scholar] [CrossRef]
- Baek, J.; Park, M. Fuzzy bilinear state feedback control design based on TS fuzzy bilinear model for DC-DC converters. Electr. Power Energy Syst. 2012, 42, 710–720. [Google Scholar] [CrossRef]
- Lendek, Z.; Nagy, Z.; Lauber, J. Local stabilization of discrete-time TS descriptor systems. Eng. Appl. Artif. Intell. 2018, 67, 409–418. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, M. Finite time non-fragile dissipative control for uncertain TS fuzzy system with time-varying delay. Neurocomputing 2016, 177, 509–514. [Google Scholar] [CrossRef]
- Nguyen, A.; Sentouh, C.; Popieul, J. Fuzzy Steering Control for Autonomous Vehicles under Actuator Saturation: Design and Experiments. J. Frankl. Inst. 2017, 1–27. [Google Scholar] [CrossRef]
- Gong, J.; Zhao, Y.; Lu, Z. Sampled-data vehicular platoon control with communication delay. J. Syst. Control Eng. 2018, 232, 1–11. [Google Scholar] [CrossRef]
- Peters, A.; Middleton, R.; Mason, O. Leader tracking in homogeneous vehicle platoons with broadcast delays. Automatica 2014, 50, 64–74. [Google Scholar] [CrossRef] [Green Version]
- Guo, G.; Yue, W. Hierarchical platoon control with heterogeneous information feedback. IET Control Theory Appl. 2011, 5, 1766–1781. [Google Scholar] [CrossRef]
- Xing, H.; Ploeg, J.; Nijmeijer, H. Padé Approximation of Delays in Cooperative ACC Based on String Stability Requirements. IEEE Trans. Intell. Veh. 2016, 1, 277–286. [Google Scholar] [CrossRef]
- Behera, A.; Chalanga, A.; Bandyopadhyay, B. A new geometric proof of super-twisting control with actuator saturation. Automatica 2018, 87, 437–441. [Google Scholar] [CrossRef]
- Wu, F.; Lian, J. A parametric multiple Lyapunov equations approach to switched systems with actuator saturation. Nonlinear Anal. Hybrid Syst. 2018, 29, 121–132. [Google Scholar] [CrossRef]
- Wei, Y.; Liyuan, W. Robust Exponential H∞ Control for Autonomous Platoon against Actuator Saturation ans Time-varying Delay. Int. J. Control Autom. Syst. 2017, 15, 1–11. [Google Scholar]
- Wang, G.; Chen, C.; Yu, S. Optimization and static output-feedback control for half-car active suspensions with constrained information. J. Sound Vib. 2016, 378, 1–13. [Google Scholar] [CrossRef]
- Latrech, C.; Kchaou, M.; Guéguen, H. Networked Non-fragile H∞ Static Output Feedback Control Design for Vehicle Dynamics Stability: A descriptor approach. Eur. J. Control 2018, 40, 13–26. [Google Scholar] [CrossRef]
- Li, H.; Liu, H.; Gao, H.; Shi, P. Reliable Fuzzy Control for Active Suspension Systems with Actuator Delay and Fault. IEEE Trans. Fuzzy Syst. 2012, 20, 242–257. [Google Scholar] [CrossRef] [Green Version]
- Swaroop, D.; Hedrick, J. String Stability of Interconnected Systems. IEEE Trans. Autom. Control 1996, 41, 348–357. [Google Scholar] [CrossRef]
- Liang, C.; Peng, H. Optimal Adaptive Cruise Control with Guaranteed String Stability. Int. J. Veh. Mech. Mob. 2010, 32, 313–330. [Google Scholar] [CrossRef]
- Mondek, M.; Hromcik, M. Linear analysis of lateral vehicle dynamics. In Proceedings of the 21st International Conference on Process Control (PC), Strbske Pleso, Slovakia, 6–9 June 2017; pp. 240–246. [Google Scholar]
- Latrach, C.; Kchaou, M.; Rabhi, A.; Elhajjaji, A. Decentralized networked control system design using (TS) fuzzy approach. Int. J. Autom. Comput. (IJAC) 2015, 12, 125–133. [Google Scholar] [CrossRef]
- Martinez, J.; Canudas-de-Wit, C. A Safe Longitudinal Control for Adaptative Cruise Control and Stop-and-Go Scenarios. IEEE Trans. Control Syst. Technol. 2007, 15, 246–258. [Google Scholar] [CrossRef]


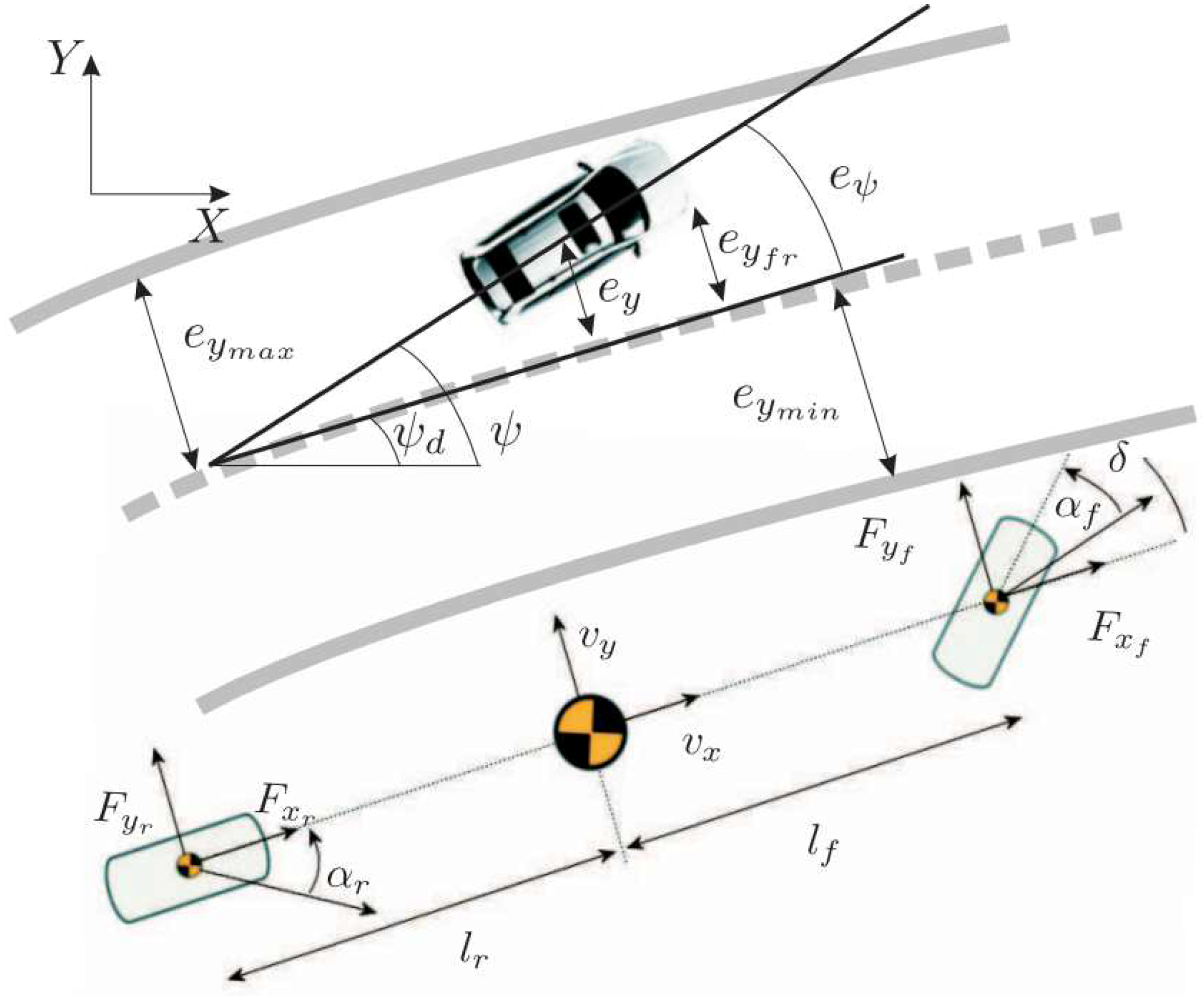
| Symbols | Value | Units | Meaning |
|---|---|---|---|
| 2000 | Kg m2 | Yaw moment of inertia | |
| m | 1500 | Kg | Vehicle mass |
| 1.3 | m | Distance from COG to front wheel center | |
| 1.7 | m | Distance from COG to rear wheel center | |
| 100,000 | N/rad | Nominal cornering stiffness of front tire | |
| 120,000 | N/rad | Nominal cornering stiffness of rear tire | |
| - | N | Front tyre cornering force | |
| - | N | Rear tyre cornering force | |
| - | rad | Front tyre slip angle | |
| - | rad | Rear tyre slip angle |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Latrech, C.; Chaibet, A.; Boukhnifer, M.; Glaser, S. Integrated Longitudinal and Lateral Networked Control System Design for Vehicle Platooning. Sensors 2018, 18, 3085. https://doi.org/10.3390/s18093085
Latrech C, Chaibet A, Boukhnifer M, Glaser S. Integrated Longitudinal and Lateral Networked Control System Design for Vehicle Platooning. Sensors. 2018; 18(9):3085. https://doi.org/10.3390/s18093085
Chicago/Turabian StyleLatrech, Chedia, Ahmed Chaibet, Moussa Boukhnifer, and Sébastien Glaser. 2018. "Integrated Longitudinal and Lateral Networked Control System Design for Vehicle Platooning" Sensors 18, no. 9: 3085. https://doi.org/10.3390/s18093085
APA StyleLatrech, C., Chaibet, A., Boukhnifer, M., & Glaser, S. (2018). Integrated Longitudinal and Lateral Networked Control System Design for Vehicle Platooning. Sensors, 18(9), 3085. https://doi.org/10.3390/s18093085






