1. Introduction
Assistive autonomous robots that help humans in day-to-day tasks are becoming increasingly popular in domestic and industrial applications. Indoor cleaning robots [
1,
2], surveillance robots [
3], lawn mowing and maintenance robots [
4,
5] and indoor personal assistant vehicles for the disabled [
6] are but a few applications of autonomous assistive robots on the horizon. In the near future, one of the most popular consumer applications of mobile robots will be in the form of self-driving passenger/cargo vehicles [
7]. While several major automobile manufacturers have set targets to launch commercially available fully autonomous driverless vehicles by 2020, vehicles that are adequately capable to roam without the need for human intervention, are still a distant reality that requires extensive research effort for realization [
8].
A typical autonomous mobile robot/vehicle is composed of three major technological components: a mapping system that is responsible for sensing and understanding the objects in the surrounding environment; a localization system with which the robot comes to know its current location at any given time, and the third component responsible for the driving policy. The driving policy refers to the decision-making capability of the autonomous robot when faced with various situations, such as negotiating with human agents and other robots. Effective environment mapping is crucial accurate localization and driving decision making of the mobile robot. Throughout the paper, we will use the term autonomous mobile robots and autonomous vehicles interchangeably.
Current prototypes of autonomous mobile robots (also widely referred in the literature as autonomous vehicles) [
9] utilise multiple different sensors, such as Light Imaging Detection and Ranging (LiDAR), radars, imaging and ultrasound sensors to map and understand their surroundings. Radar is used for long-range sensing, while ultrasound sensors are effective at very short ranges. Imaging sensors are often used to detect objects, traffic signals, lane markings and surrounding pedestrians and vehicles. Often, these prototypes rely on LiDAR sensors or stereo cameras to map the surrounding environment in 3-dimensions (3D). Data generated from each sensor need to be interpreted accurately for satisfactory operation of autonomous vehicles. The precision of operation of an autonomous vehicle is, thus, limited by the reliability of the associated sensors. Each type of sensor has its own limitations, for example, LiDAR sensor readings are often affected by weather phenomena such as rain, fog or snow [
10]. Furthermore, the resolution of a typical LiDAR sensor is quite limited as compared to RGB-cameras. In comparison, stereo camera-based dense depth estimation is limited by its baseline distance [
11]. Therefore, for accurate operation an autonomous mobile robot typically relies on more than one type of sensor.
The diversity offered by multiple sensors can positively contribute to the perception of the sensed data. The effective alignment (either spatially, geometrically or temporally) of multiple heterogeneous sensor streams, and utilization of the diversity offered by multimodal sensing is referred to as sensor data fusion [
12]. Sensor data fusion is not only relevant to autonomous vehicles [
13], but also applicable in different applications such as surveillance [
14], smart guiding glasses [
15] and hand gesture recognition [
16]. Overcoming heterogeneity of different sensors through effective utilization of redundancy across the sensors is the key to fusing different sensor streams.
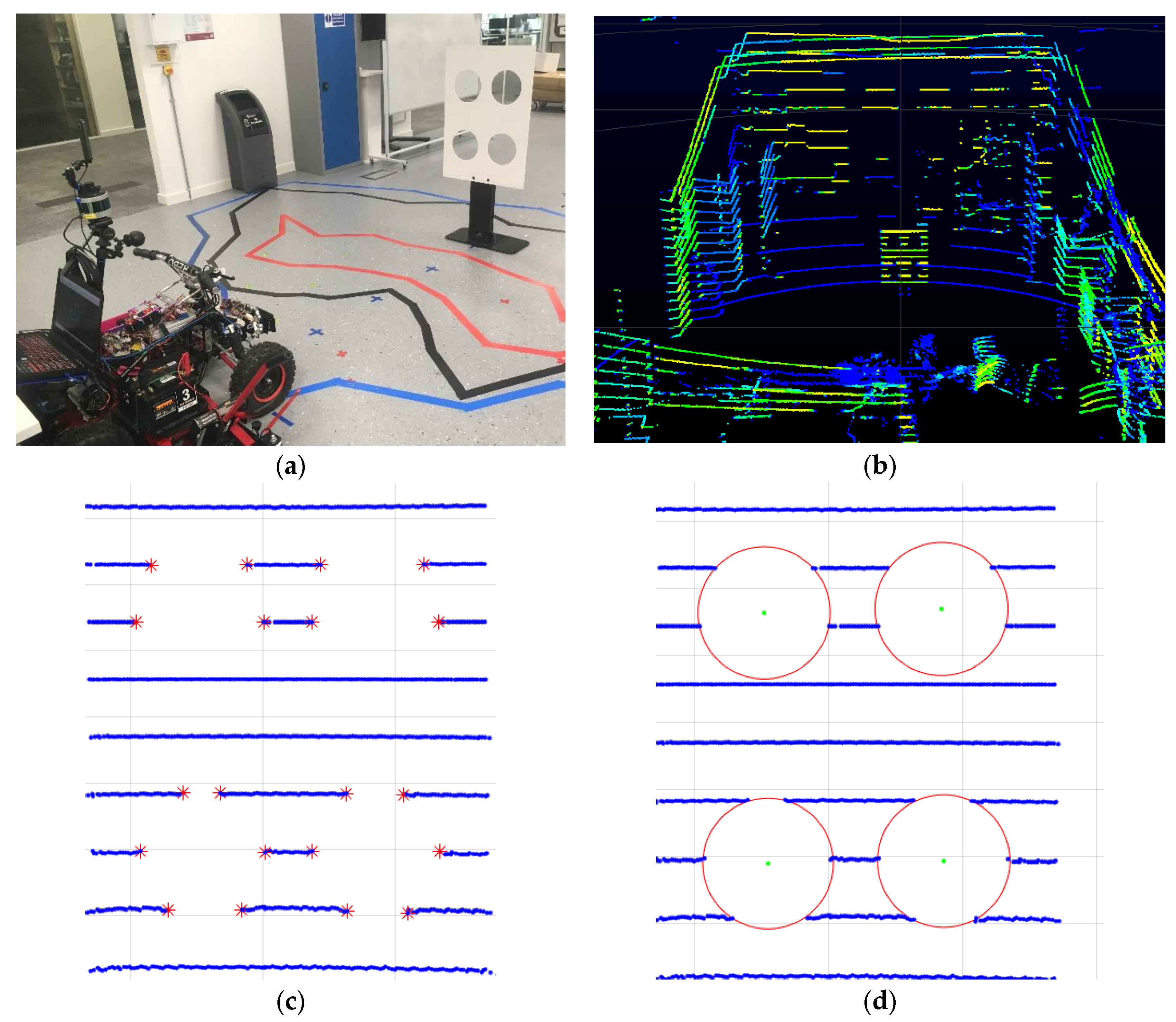
Wide-angle cameras are increasingly becoming popular in different applications. Unlike standard cameras, wide angle cameras provide the capability to capture a broad area of the world with as few sensors as possible. This is advantageous from a cost perspective as well as from a system complexity perspective. If wide-angle cameras can be utilized effectively in mobile robots it will pave way for more compact and cost-effective robots. In this paper, we investigate indoor mobile robot navigation by fusing distance data gathered by a LiDAR sensor, with the luminance data from a wide-angle imaging sensor. The data from the LiDAR comes in the form of a 3D point cloud, whereas wide-angle camera captures the scene from a larger visual angle (typically > 180°). Recently, LiDAR data and wide-angle visual data were fused for odometry and mapping of indoor environments [
17]. Most work that involves camera and LiDAR fusion often focuses on extrinsic calibration of the two sensors to align the data [
18,
19]. However, data fusion goes beyond extrinsic calibration and involves resolution matching, handling missing data and accounting for variable uncertainties in different data sources. The objective of this paper is to address the issues of resolution mismatch and uncertainty in data sources while fusing wide angle camera and LiDAR data.
LiDAR and stereo camera fusion is often tackled through utilization of the common dimension of depth in the two modalities. In comparison, fusing LiDAR with wide-angle luminance data is non-trivial as there is no common dimension of depth, as there is no way to capture depth in a wide-angle camera. To overcome above challenges, in this paper we try to address the problem of fusing LiDAR data with wide-angle camera. Furthermore, the technique goes beyond a simple geometric calibration by developing a robust fusion algorithm, which enable the robot to make decisions under uncertainty. We illustrate the effectiveness of our approach with a free space detection algorithm, which utilizes the fused data to understand areas in the world that the robot can navigate to without colliding with any obstacle.
The rest of this paper is organised as follows:
Section 2 provides an overview of the related work and associated challenges. The framework for fusion of LiDAR and Imaging sensor data are presented in
Section 3.
Section 4 describes the experimental framework and discussion of the free space detection results. Finally, we conclude the paper in
Section 5, with some references to possible future work.
2. Sensor Data Fusion for Computer Vision
A review of the literature relevant to the contributions of this paper is presented in this section, followed by the positioning of the current contribution. This section is organized in three sections: the need for data fusion and challenges it poses, relevant work in LiDAR and camera data fusion and finally on challenges addressed by the current work within the scope of driverless vehicles.
2.1. Challenges in Multimodal Data Fusion
Information about a system can be obtained from different types of instruments, measurement techniques and sensors. Sensing a system using heterogeneous acquisition mechanisms is referred to as multimodal sensing [
20]. Multimodal sensing is necessary, because a single modality cannot usually capture complete knowledge of a rich natural phenomena. Data fusion is the process by which multimodal data streams are jointly analysed to capture knowledge of a certain system.
Lahat et al. [
20], identified several challenges that are imposed by multimodal data. These challenges can be broadly categorized into two segments: challenges at the acquisition level and challenges due to uncertainty in the data sources. Challenges due to data acquisition level problems include: differences in physical units of measurement (non-commensurability), differences in sampling resolutions, and differences in spatio-temporal alignment. The uncertainty in data sources also pose challenges that include: noise such as calibration errors, quantization errors or precision losses, differences in reliability of data sources, inconsistent data and missing values.
The above challenges discussed by Lahat et al. [
20], were identified by considering a multitude of applications. In the next subsection, we will discuss specific challenges associated with fusing LiDAR and imaging data.
2.2. Fusion of LiDAR and Different Types of Imaging Data
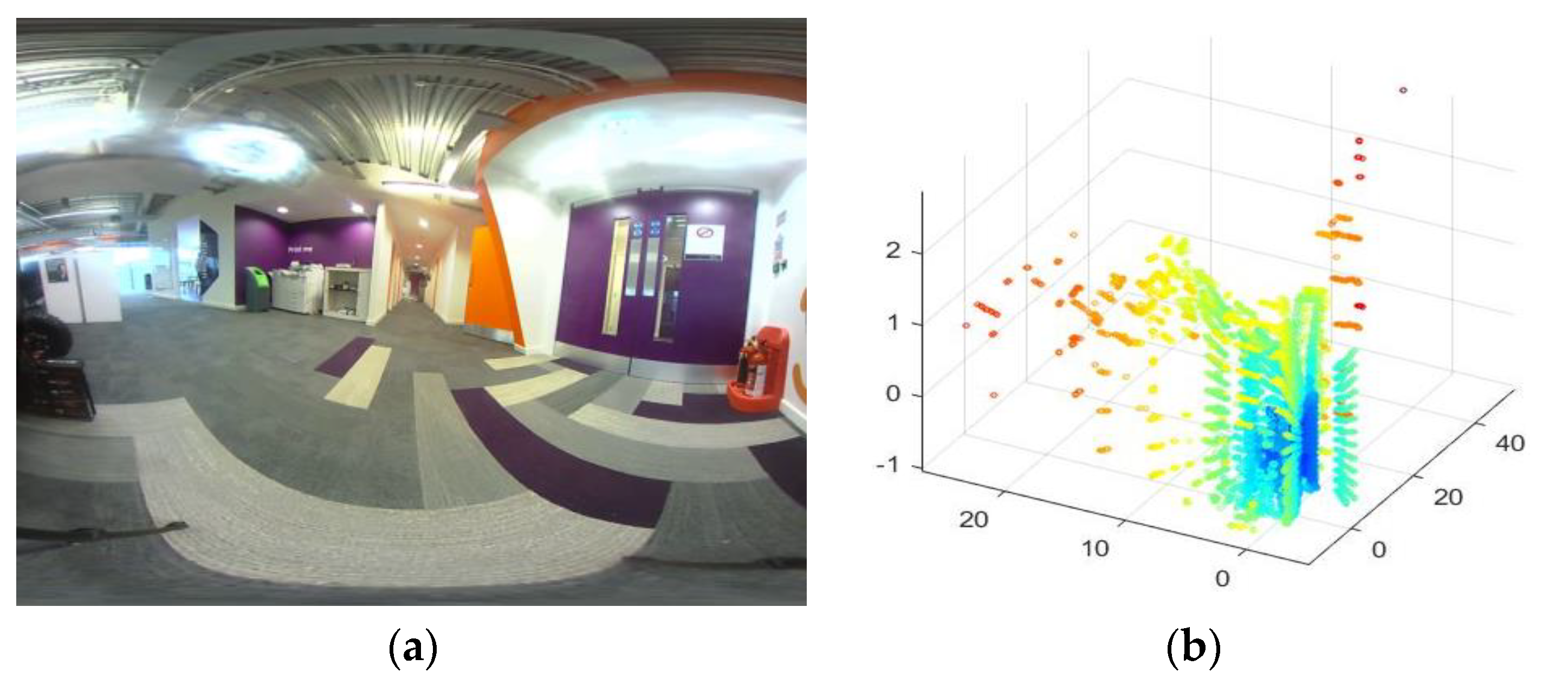
LiDAR data can be fused with different types of imaging sensor data to cater for a range of applications. An example of two types of data, i.e., from wide angle camera and the LiDAR are illustrated in
Figure 1. Terrain mapping is a popular application of LiDAR data that uses an aerial borne LiDAR scanner to identify various ground objects such as buildings or vehicles. The independent use of LiDAR scanner proves challenging in such applications due to obstructions and occlusions caused by vegetation. Therefore, while LiDAR exhibits good height measurement accuracy, it lacks in horizontal segmentation capability to delineate the building boundaries. A graph based data driven method of fusing LiDAR data and multi-spectral imagery was proposed in. Authors in [
21] propose, a connected component analysis and clustering of the components to come up with a more accurate segmentation algorithm.
In a substantial body of literature, LiDAR and image data fusion is considered as an extrinsic calibration process. Here fusion is regarded as the process of rigid body transformation between the two sensors’ coordinate systems [
18]. For the purpose of extrinsic calibration, an external object, such as a trihedral calibration rig [
22,
23], a circle [
24], a board pattern [
25,
26] or a checkerboard pattern [
27,
28,
29], is used as a target to match the correspondences between the two sensors. Li et al. proposes a calibration technique to estimate the transformation matrix that can then be used to fuse a motorized 2D laser scanner with a monocular image [
19]. While such methods, yield accurate alignment, they do not address the issues related to uncertainty of sensor readings.
The problem of LiDAR and imaging data fusion can be approached as a camera pose estimation problem, where the relationship between 3D LIDAR coordinates and 2D image coordinates is characterised by camera parameters such as position, orientation, and focal length. In [
30], the authors propose an information-theoretic similarity measure to automatically register 2D-Optical imagery with 3D LiDAR scans by searching for a suitable camera transformation matrix. LiDAR and optical image fusion is used in [
30] for creating 3D virtual reality models of urban scenes.
The fusion of 3D-LiDAR data with stereoscopic images is addressed in [
31]. The advantage of stereoscopic depth estimation is its capability to produce dense depth maps of the surroundings by utilising stereo matching techniques. However, the dense stereo depth estimation is computationally quite complex. This is due to the requirement of matching corresponding points in the stereo images. Furthermore, dense depth estimation using stereo images suffer from the limited dynamic range of the image sensors, for instance, due to the saturation of pixel values in bright regions [
32].
Another, drawback of stereo based depth estimation is the limited range of depth sensing. LiDAR scanning on the other hand provides a utility to measure depth at high accuracies, albeit at lower point resolutions compared with imaging sensors. The authors of [
31] proposed a probabilistic framework to fuse sparse LiDAR data with stereoscopic images, which is aimed at real-time 3D perception of environments for mobile robots and autonomous vehicles. An important attribute of probabilistic methods, such as in [
31] is that it represents the uncertainty of estimated depth values.
2.3. Challenges in Data Fusion Addressed in this Paper
In this paper, we consider LiDAR and imaging sensor data fusion in the context of autonomous vehicles. Autonomous vehicles as an application pose significant challenges for data driven decision making due to the associated safety requirements. For reliable operation, decisions in autonomous vehicles need to be made by considering all the multimodal sensor data they acquire. Furthermore, the decisions must be made in the light of the uncertainties associated with both data acquisition methods, and the utilized pre-processing algorithms.
This paper addresses two fundamental issues surrounding sensor data fusion, namely the resolution difference in heterogeneous sensors and making sense of heterogeneous sensor data streams while accounting for varying uncertainties in the data sources. Apart from being different from previous contributions in the type of sensors used for data fusion, our motivations for this paper are two-fold: Firstly, we are interested in developing a more robust approach for data fusion, which accounts for uncertainty in the fusion algorithm. This will enable the subsequent perception tasks in an autonomous vehicle to operate more reliably. Secondly, we envisage situations in the future, where autonomous vehicles will be exchanging useful sensor data between each other. In such situations it would be impractical for extrinsic calibration methods to work, because there are inevitable per-unit variations that exist between sensors due to manufacturing variations. Based on the above premises, we propose a robust framework for data fusion with minimal calibration.
3. The Proposed Algorithm for LiDAR and Wide-Angle Camera Fusion
To address the challenges presented above, in this section we propose a framework for data fusion. This section describes the proposed algorithm for fusion of LiDAR data with a wide-angle imaging sensor. The organization of the section is as follows: in
Section 3.1 the geometric model for alignment of the two sensor types are presented, followed by Gaussian process-based matching of resolutions of the two sensors, in
Section 3.2.
3.1. Geometric Alignment of LiDAR and Camera Data
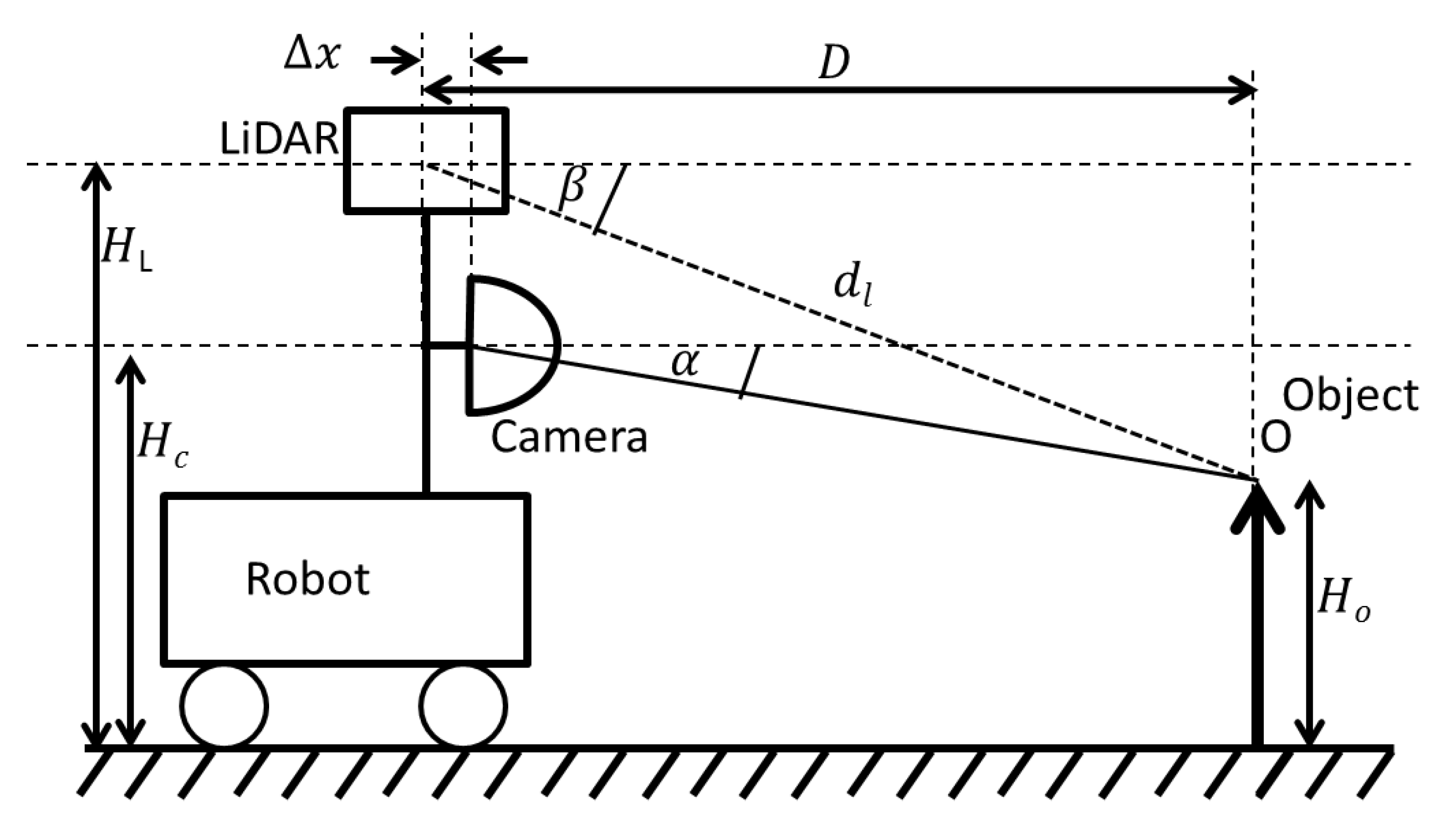
The first step of the data fusion algorithm is to geometrically align the data points of the LiDAR output and the 360° camera. The purpose of the geometric alignment is to find the corresponding pixel in the camera output for each data point output by the LiDAR sensor. For the purpose of this derivation, consider an object
of height
at distance
from the robot. The sensor setup is graphically illustrated in
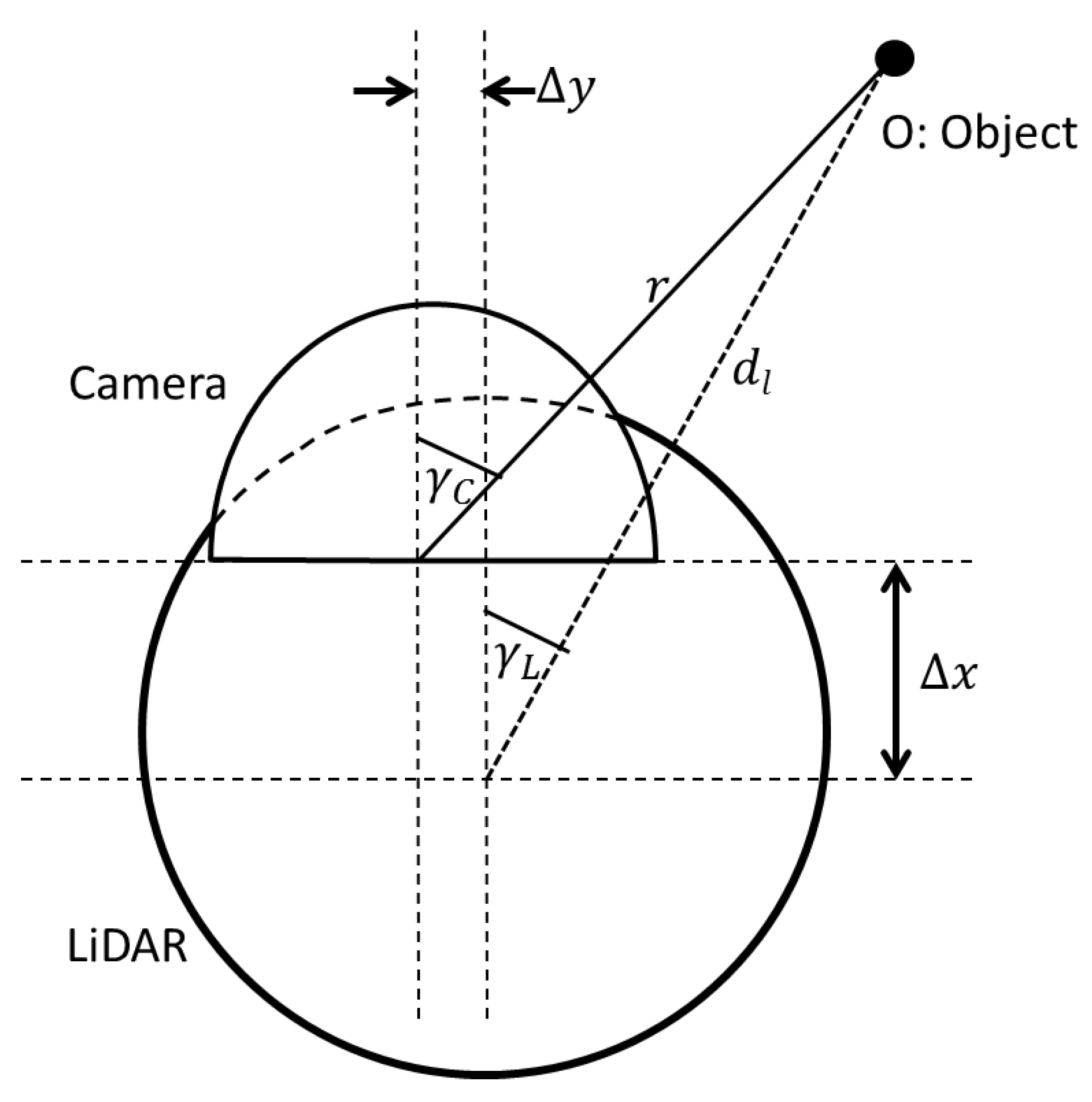
Figure 2 and the horizontal alignment of the sensors are depicted in
Figure 3.
= Frontal displacement of the centres of LiDAR and camera sensor. = horizontal displacement of the centres of LiDAR and camera sensor. = distance to the object O sensed by LiDAR. = latitude and longitude of object O as measured by the LiDAR, respectively. = height of the camera from the ground. = vertical height of the LiDAR, and = latitude and longitude of object O as measured by the camera, respectively.
The values
are the outputs of the LiDAR sensor. The purpose of this alignment is to find the corresponding pixel in the camera output for each data point output by the LiDAR sensor. Here we assume that the main axis of the camera and the LiDAR are aligned with each other. Considering the distance to object
O, we have:
Considering the vertical height of the object
O, we have:
From (1) and (2), we can calculate corresponding latitude
of the camera as follows:
Considering the horizontal displacement from the setup in
Figure 3, we have:
From (1) and (4), we can calculate corresponding longitude
of the camera as follows:
The Equations (3) and (5) pave the way to align the data points of the LiDAR and the camera. The purpose of the calibration process is to find the parameters , , , .
Although posing minimalistic needs for calibration, the above geometric alignment process cannot be fully relied upon as a robust mechanism, because errors in calibration measurements, imperfections in sensor assembly, and per-unit variations derived from the manufacturing processes may introduce factors that deviate from the ideal sensor geometry. For example, the curvature of the 360° camera might not be uniform across its surface. Therefore, to be robust enough for such discrepancies, the geometrically aligned data ideally must undergo another level of adjustment. This is accomplished in the next stage of the framework by utilizing the spatial correlations that exist in image data.
Another problem that arises when fusing data from different sources is the difference in data resolution. For the case addressed in this paper, the resolution of LiDAR output is considerably lower than the images from the camera. Therefore, the next stage of the data fusion algorithm is designed to match the resolutions of LiDAR data and imaging data through an adaptive scaling operation.
3.2. Resolution Matching Based on Gaussian Process Regression
In this section we describe the proposed mechanism to match the resolutions of LiDAR data and the imaging data. In
Section 3.1, through geometric alignment, we matched the LiDAR data points with the corresponding pixels in the image. However, the image resolution is far greater than the LiDAR output. The objective of this step is to find an appropriate distance value for the image pixels for which there is no corresponding distance value. Furthermore, another requirement of this stage is to compensate for discrepancies or errors in the geometric alignment step.
We formulate this problem as a regression based missing value prediction, where the relationship between the measured data points (available distance values) is utilized to interpolate the missing values. For this purpose we use Gaussian Process Regression (GPR) [
20], which is a non-linear regression technique. GPR allows to define the covariance of the data in any suitable way. In this step, we derive the covariance from of the image data, and thereby adjusting to account for discrepancies in the geometric alignment stage. A Gaussian Process (GP) is defined as a Gaussian distribution over functions [
20]:
where,
, and
.
The power of GPs lies in the fact that we can define any covariance function as relevant to the problem at hand.
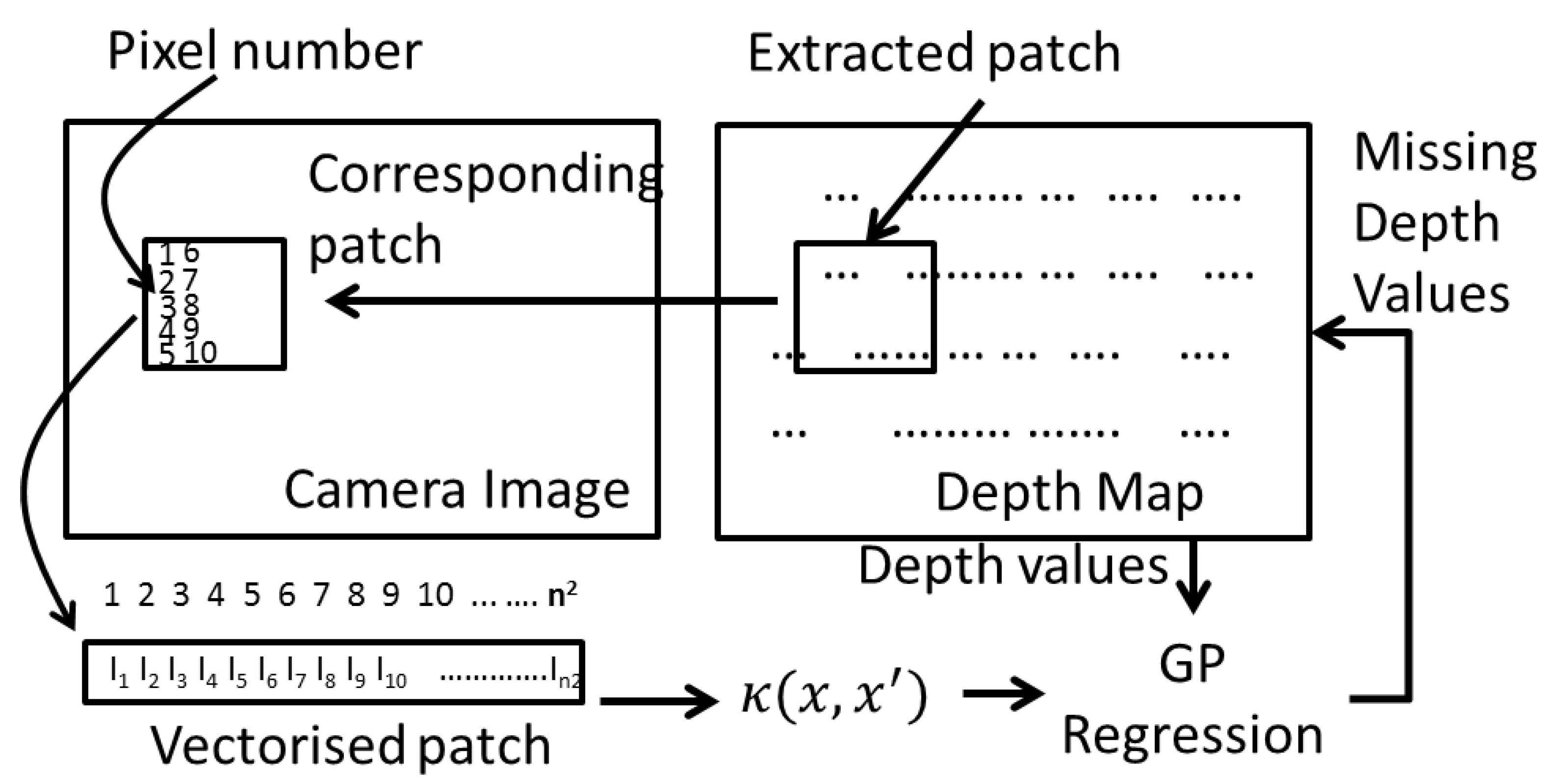
Let’s denote a patch of size extracted from the depth map D, as yi. Pixels in an extracted patch is numbered from 1 to n2—increasing along the rows and columns. Some pixels of this patch have a distance value associated with it (geometric alignment stage). The objective of this regression step is to fill the rest of the pixels with an appropriate depth value.
The pixels with a depth associated to it will act as the training set
, where
N is the number of pixels that has a depth associated with it, and
xi is the pixel number. Let
,
, and
{
}, is the set of pixel numbers for which the depth map is empty. The resolution matching problem then becomes to find
, the depth of the pixels corresponding to
. By definition of the GP, the joint distribution between
and
has the following form:
where,
,
, and
, are the covariance matrices defined utilising the covariance function
,
and
is the corresponding mean vectors for
and
. The solution to
is given as the posterior predictive density as follows [
33]:
where:
and:
A suitable covariance function
has to be defined to meet the objective of filling the missing values in the depth map D. So how do we define a suitable covariance function? To do so, we make the assumption that similar pixels of the colour image will have the same depth value. Similarity of the pixels is defined based on the Euclidian distance between the pixels and the grey-level of the pixel. As such we define the covariance function as,
, where the covariance between any two pixels
,
is the multiplication of two factors:
: closeness between the two pixels in terms of spatial Euclidian distance and
: similarity between the two pixels in terms of its grey-level value, defined as follows:
where
denotes the grey-level value of the camera image at pixel position
.
Kp and
KI controls the width of the respective kernels. The missing depth value of a pixel
, is taken to be the mean value
at
x given by Equation (9), and the corresponding uncertainty of the calculated pixel value is taken to be the variance at
given by Equation (10). To summarize, the GP based regression to fill the missing depth values is illustrated in
Figure 4.
5. Conclusions and Future Work
This paper addresses the problem of fusing the outputs of a LiDAR scanner and a wide-angle monocular image sensor. The first part of the proposed framework spatially aligns the two sensor data streams with a geometric model. The resolutions of the two sensors are quite different, with the image sensor having a much denser spatial resolution. The two resolutions matched, in the second stage of the proposed framework, by utilizing a Gaussian Process regression algorithm that derives the spatial covariance from the image sensor data. The output of the GP regression not only provides an estimation of the corresponding distance value of all the pixels in the image, but also indicates the uncertainty of the estimation by way of standard deviation. The advantages of the proposed data fusion framework is illustrated through performance analysis of a free space detection algorithm. It was demonstrated that perception tasks in autonomous vehicles/mobile robots can be significantly improved by multimodal data fusion approaches, as compared to single sensor-based perception capability. As compared to extrinsic calibration methods, the main novelty of the proposed approach is the ability to fuse multimodal sensor data by accounting for different forms of uncertainty associated with different sensor data streams (resolution mismatches, missing data, and blind spots). The future work planned, includes extension of the sensor fusion framework to include multiple cameras, radar scanners and ultra sound scanners. Furthermore, we will research methods for robust free space detection based on the data fusion framework. Advanced forms of uncertainty quantification techniques will be utilized to capitalize on the diversity offered by multimodal sensors.