Spatial Extension of Road Traffic Sensor Data with Artificial Neural Networks
Abstract
1. Introduction
2. Background
2.1. Road Traffic Monitoring Systems and Technologies
2.2. ANNs and Their Application to Traffic Flow Forecasting
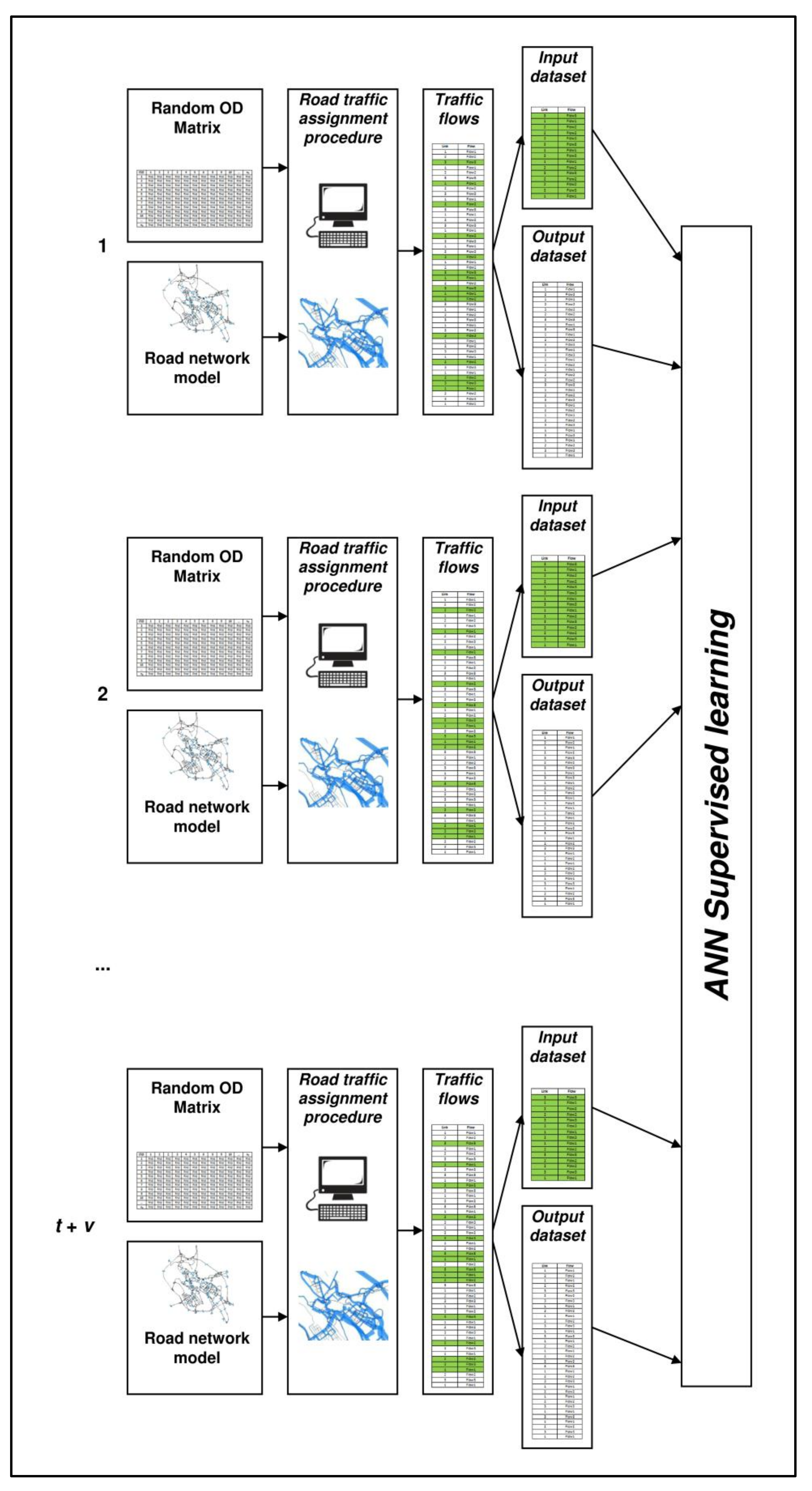
3. Proposed Approach
- we build a road network model of the case study, as detailed as possible;
- we identify on this network the monitored links, ml, and the unmonitored links, ul;
- we randomly generate several origin-destination (OD) matrices, di with i = 1, ..., n;
- we assign each matrix, di, to the road network model, so as to generate the corresponding traffic flows on monitored links, fiml, and on unmonitored links, fiul with i = 1, ..., n; we assume that they are the real flows on the network and constitute the datasets for training, validating, and testing the ANN; specifically, input datasets contain fiml and output datasets contain fiul; and
- we divide the datasets into three groups: training sets (i = 1, ..., t), validation sets (i = t + 1, ..., t + v), and testing sets (i = t + v + 1, ..., t + v + p; t + v + p = n); first, two groups are used in the training procedure while the third group is used for evaluating the forecast capacity of trained ANNs.
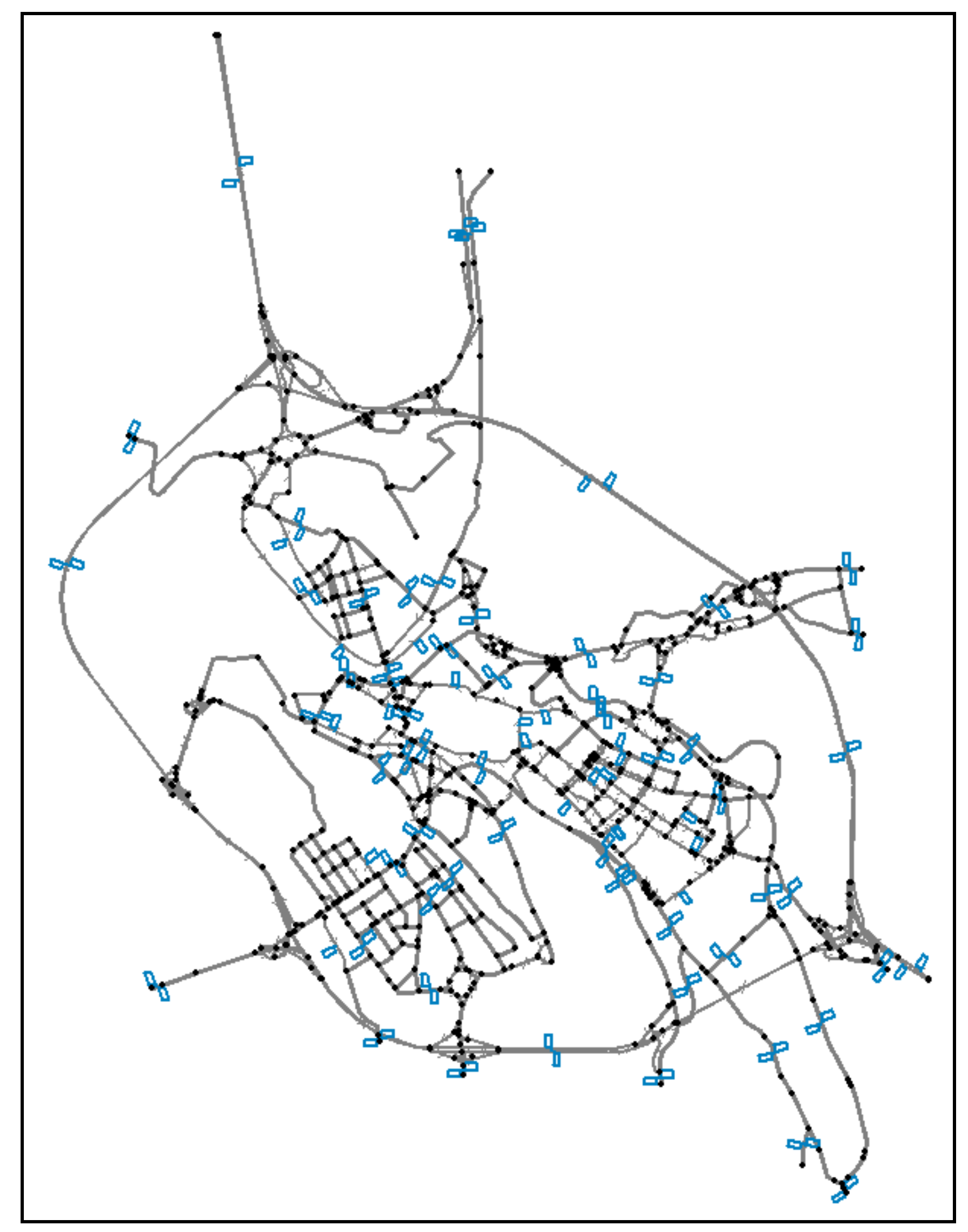
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gallo, M.; Simonelli, F.; De Luca, G.; Della Porta, C. An Artificial Neural Network approach for spatially extending road traffic monitoring measures. In Proceedings of the 2016 IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems (EESMS 2016), Bari, Italy, 13–14 June 2016; pp. 209–213. [Google Scholar] [CrossRef]
- FHWA. Traffic Detector Handbook: Third Edition—Volume I; Report No. FHWA-HRT-06-108; U.S. Department of Transportation: Washington, DC, USA, 2006.
- FHWA. Traffic Detector Handbook: Third Edition—Volume II; Report No. FHWA-HRT-06-139; U.S. Department of Transportation: Washington, DC, USA, 2006.
- Bennet, C.R.; de Solminihac, S.; Chamorro, A. Data Collection Technologies for Road Management; Transport Notes No. 30; The World Bank: Washington, DC, USA, 2006; pp. 1–8. [Google Scholar]
- Leduc, G. Road Traffic Data: Collection Methods and Applications; Working Papers on Energy; Transport and Climate Change, JRC 47967: Luxembourg, 2008. [Google Scholar]
- Salvo, G.; Caruso, L.; Scordo, A. Urban Traffic Analysis through an UAV. Procedia Soc. Behav. Sci. 2014, 111, 1083–1091. [Google Scholar] [CrossRef]
- Li, M.; Zhen, L.; Wang, S.; Lv, W.; Qu, X. Unmanned aerial vehicle scheduling problem for traffic monitoring. Comput. Ind. Eng. 2018, 122, 15–23. [Google Scholar] [CrossRef]
- Chong, C.-Y.; Kumar, S.P. Sensor Networks: Evolution, Opportunities, and Challenges. Proc. IEEE 2003, 91, 1247–1256. [Google Scholar] [CrossRef]
- Tubaishat, M.; Zhuang, P.; Qi, Q.; Shang, Y. Wireless sensor networks in intelligent transportation systems. Wirel. Commun. Mob. Comput. 2009, 9, 287–302. [Google Scholar] [CrossRef]
- Guitton, A.; Skordylis, A.; Trigoni, N. Utilizing Correlations to Compress Time-Series in Traffic Monitoring Sensor Networks. In Proceedings of the 2007 IEEE Wireless Communications and Networking Conference, Kowloon, China, 11–15 March 2007. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Karlaftis, M.G.; Golias, J.C. Short-term traffic forecasting: Where we are and where we’re going. Transp. Res. C 2014, 43, 3–19. [Google Scholar] [CrossRef]
- Oh, S.; Byon, Y.J.; Jang, K.; Yeo, H. Short-term travel-time prediction on highway: A review of the data-driven approach. Transp. Rev. 2015, 35, 4–32. [Google Scholar] [CrossRef]
- Sharma, A.; Chaki, R.; Bhattacharya, U. Applications of wireless sensor network in Intelligent Traffic System: A review. In Proceedings of the 3rd International Conference on Electronics Computer Technology, Kanyakumari, India, 8–10 April 2011; pp. 53–57. [Google Scholar] [CrossRef]
- Shojafar, M.; Cordeschi, N.; Amendola, D.; Baccarelli, E. Energy-saving adaptive computing and traffic engineering for real-time-service data centers. In Proceedings of the 2015 IEEE International Conference on Communication Workshop (ICCW), London, UK, 8–12 June 2015; pp. 1800–1806. [Google Scholar] [CrossRef]
- Cordeschi, N.; Amendola, D.; Baccarelli, E. Reliable adaptive resource management for cognitive cloud vehicular networks. IEEE Trans. Veh. Technol. 2015, 64, 2528–2537. [Google Scholar] [CrossRef]
- Baccarelli, E.; Cordeschi, N.; Mei, A.; Panella, M.; Shojafar, M.; Stefa, J. Energy-efficient dynamic traffic offloading and reconfiguration of networked data centers for big data stream mobile computing: Review, challenges, and a case study. IEEE Netw. 2016, 30, 54–61. [Google Scholar] [CrossRef]
- Sun, Z.; Bebis, G.; Miller, R. On-road vehicle detection using optical sensors: A review. In Proceedings of the 7th IEEE Conference on Intelligent Transportation Systems, Washington, WA, USA, 3–6 October 2004; pp. 585–590. [Google Scholar] [CrossRef]
- D’Acierno, L.; Cartenì, A.; Montella, B. Estimation of urban traffic conditions using an Automatic Vehicle Location (AVL) System. Eur. J. Oper. Res. 2009, 196, 719–736. [Google Scholar] [CrossRef]
- Klunder, G.A.; Taale, H.; Kester, L.; Hoogendoorn, S. Improvement of network performance by in-vehicle routing using floating car data. J. Adv. Transp. 2017, 2017, 16. [Google Scholar] [CrossRef]
- Yang, X.; Lu, Y.; Hao, W. Origin-destination estimation using probe vehicle trajectory and link counts. J. Adv. Transp. 2017, 2017, 18. [Google Scholar] [CrossRef]
- McCullocg, W.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Hebb, D.O. The Organization of Behaviour. A Neuropsychological Theory; Wiley: New York, NY, USA, 1949. [Google Scholar]
- Rosenblatt, F. Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms; Cornell Aeronautical Laboratory, Inc.: Buffalo, NY, USA, 1961. [Google Scholar]
- Minsky, M.; Papert, S. An Introduction to Computational Geometry; M.I.T. Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Grossberg, S. Neural Networks and Natural Intelligence; The Mit Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Minsky, M.L. Theory of Neural—Analog Reinforcement System and Its Application to the Brain—Model Problem. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1954. [Google Scholar]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Judd, J.S. Neural Network Modeling and Connectionism. Neural Network Design and the Complexity of Learning; MIT Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Haykin, S. Neural Networks—A Comprehensive Foundation; McMaster University: Hamilton, ON, Canada, 1994. [Google Scholar]
- Miller, W.T.; Werbos, P.J.; Sutton, R.S. Neural Networks for Control; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Rojas, R. Neural Networks. A Systematic Introduction; Springer: Berlin, Germany, 1996. [Google Scholar]
- Haykin, S.S. Kalman Filtering and Neural Networks; Wiley Online Library: Hoboken, NJ, USA, 2001. [Google Scholar]
- Aggarwal, C.C. Neural Networks and Deep Learning; Springer: Berlin, Germany, 2018. [Google Scholar]
- Baptista, D.; Morgado-Dias, F. A survey of artificial neural network training tools. Neural Comput. Appl. 2013, 23, 609–615. [Google Scholar] [CrossRef]
- Scarselli, F.; Tsoi, A.C. Universal approximation using feedforward neural networks: A survey of some existing methods, and some new results. Neural Netw. 1998, 11, 15–37. [Google Scholar] [CrossRef]
- Timotheou, S. The random neural network: A survey. Comput. J. 2010, 53, 251–267. [Google Scholar] [CrossRef]
- Huang, G.; Huang, G.-B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Yao, X. A review of evolutionary artificial neural networks. Int. J. Intell. Syst. 1993, 8, 539–567. [Google Scholar] [CrossRef]
- Dougherty, M. A review of neural networks applied to transport. Trans. Res. C 1995, 3, 247–260. [Google Scholar] [CrossRef]
- De Luca, G.; Gallo, M. Artificial Neural Networks for forecasting user flows in transportation networks: Literature review, limits, potentialities and open challenges. In Proceedings of the 2017 5th IEEE International Conference on Models and Technologies for Intelligent Transportation Systems, Naples, Italy, 26–28 June 2017; pp. 919–923. [Google Scholar] [CrossRef]
- Ciresan, D.; Meier, U.; Masci, J.; Schmidhuber, J. Multi-column deep neural network for traffic sign classification. Neural Netw. 2012, 32, 333–338. [Google Scholar] [CrossRef] [PubMed]
- Arcos-Garcia, A.; Alvares-Garcia, J.A.; Soria-Morillo, L.M. Deep neural network for traffic sign recognition systems: An analysis of spatial transformers and stochastic optimisation methods. Neural Netw. 2018, 99, 158–165. [Google Scholar] [CrossRef] [PubMed]
- Sang, Y.; Lv, J.; Qu, H.; Yi, Z. Shortest path computation using pulse-coupled neural networks with restricted autowave. Knowl.-Based Syst. 2016, 114, 1–11. [Google Scholar] [CrossRef]
- Huang, W.; Yan, C.; Wang, J.; Wang, W. A time-delay neural network for solving time-dependent shortest path problem. Neural Netw. 2017, 90, 21–28. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, D.; Sharma, V.; Toh, K.A. Reduced multivariate polynomial-based neural network for automated traffic incident detection. Neural Netw. 2008, 21, 484–492. [Google Scholar] [CrossRef] [PubMed]
- Tanprasert, T.; Saiprasert, C.; Thajchayapong, S. Combining unsupervised anomaly detection and neural networks for driver identification. J. Adv. Transp. 2017, 2017, 13. [Google Scholar] [CrossRef]
- Kirby, H.R.; Watson, S.M.; Dougherty, S. Should we use neural networks or statistical models for short-term motorway traffic forecasting? Int. J. Forecast. 1997, 13, 43–50. [Google Scholar] [CrossRef]
- Zhang, H.J.; Ritchie, S.G.; Lo, Z.P. Macroscopic modeling of freeway traffic using an artificial neural network. Trans. Res. Rec. 1997, 1588, 110–119. [Google Scholar] [CrossRef]
- Dougherty, M.S.; Kirby, H.C. The use of neural networks to recognize and predict traffic congestion. Traffic Eng. Control 1998, 346, 311–314. [Google Scholar]
- Park, B.; Messer, C.; Urbanik, T. Short-term freeway traffic volume forecasting using radial basis function neural network. Trans. Res. Rec. 1998, 1651, 39–46. [Google Scholar] [CrossRef]
- Zheng, W.; Lee, D.-H.; Shi, Q. Short-term freeway traffic prediction: Bayesan combined neural network approach. J. Transp. Eng. 2006, 132, 114–121. [Google Scholar] [CrossRef]
- Kumar, K.; Parida, M.; Katiyar, V.K. Short term traffic flow prediction for a non urban highway using Artificial Neural Network. Procedia Soc. Behav. Sci. 2013, 104, 755–764. [Google Scholar] [CrossRef]
- Park, D.; Rilett, L.R. Forecasting Freeway Link Travel Times with a Multilayer Feedforward Neural Network. Comput.-Aided Civ. Infrastruct. Eng. 1999, 14, 357–367. [Google Scholar] [CrossRef]
- Yasdi, R. Prediction of road traffic using a neural network approach. Neural Comput. Appl. 1999, 8, 135–142. [Google Scholar] [CrossRef]
- Goves, C. Short term traffic prediction on the UK motorway network using neural networks. In Proceedings of the European Transport Conference, Frankfurt, Germany, 28–30 September 2015. [Google Scholar]
- Florio, L.; Mussone, L. Neural network models for classification and forecasting of freeway traffic flow stability. In Transportation Systems: Theory and Application of Advanced Technology; Liu, B., Blosseville, J.M., Eds.; Pergamon Press: Oxford, NY, USA, 1995; pp. 773–784. [Google Scholar]
- Hodge, V.; Austin, J.; Krishnan, R.; Polak, J.; Jackson, T. Short-term traffic prediction using a binary neural network. UTSG 2011. [Google Scholar] [CrossRef]
- Zheng, F.; Van Zuylen, H. Urban link travel time estimation based on sparse probe vehicle data. Trans. Res. C 2013, 31, 145–157. [Google Scholar] [CrossRef]
- Csikos, A.; Viharos, Z.J.; Kisk, B.; Tettamanti, T.; Varga, I. Traffic speed prediction method for urban networks an ANN approach. In Proceedings of the Models and Technologies for Intelligent Trasportation Systems (MT-ITS), Budapest, Hungary, 3–5 June 2015. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, S. Multi-link traffic flow forecasting using neural networks. In Proceedings of the 2010 Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010; pp. 398–401. [Google Scholar] [CrossRef]
- Gao, J.; Leng, Z.; Qin, Y.; Ma, Z.; Liu, X. Short-term traffic flow forecasting model based on wavelet neural network. In Proceedings of the 25th Chinese Control and Decision Conference, Guiyang, China, 25–27 May 2013; pp. 5081–5084. [Google Scholar] [CrossRef]
- Ledoux, C. An urban traffic flow model integrating neural networks. Trans. Res. C 1997, 5, 287–300. [Google Scholar] [CrossRef]
- Li, R.; Lu, H. Combined neural network approach for short-term urban freeway traffic flow prediction. Lect. Notes Comput. Sci. 2009, 5553, 1017–1025. [Google Scholar] [CrossRef]
- Lin, S.; Xi, Y.; Yang, Y. Short-Term Traffic Flow Forecasting Using Macroscopic Urban Traffic Network Model. In Proceedings of the 11th International IEEE Conference on Intelligent Transportation Systems, ITSC, Beijing, China, 12–15 October 2008. [Google Scholar] [CrossRef]
- Zheng Zhu, J.; Xin Cao, J.; Zhu, Y. Traffic volume forecasting based on radial basis function neural network with the consideration of traffic flows at the adjacent intersections. Trans. Res. C 2014, 47, 139–154. [Google Scholar] [CrossRef]
- Kikuchi, S.; Nanda, R.; Perincherry, V. A method to estimate trip O-D patterns using neural network approach. Transp. Plan. Technol. 1993, 17, 51–65. [Google Scholar] [CrossRef]
- Yang, H.; Akiyama, T.; Sasaki, T. A neural network approach to the identification of real time origin-destination flows from traffic counts. In Proceedings of the International Conference on Artificial Intelligence Applications in Transportation Engineering, San Buenaventura, CA, USA, 20–24 June 1992; pp. 253–269. [Google Scholar]
- Gong, Z. Estimating the urban OD matrix: A neural network approach. Eur. J. Oper. Res. 1998, 106, 108–115. [Google Scholar] [CrossRef]
- Mussone, L.; Grant-Muller, S.; Chen, H. A Neural Network Approach to Motorway OD Matrix Estimation from Loop Counts. J. Transp. Syst. Eng. Inf. Technol. 2010, 10, 88–98. [Google Scholar] [CrossRef]
- Remya, K.P.; Samson, M. OD Matrix Estimation from Link Counts Using Artificial Neural Network. Int. J. Sci. Eng. Res. 2013, 4, 293–296. [Google Scholar]
- Bell, M.G.H. The estimation of origin–destination matrix from traffic counts. Trans. Sci. 1983, 10, 198–217. [Google Scholar] [CrossRef]
- Cascetta, E. Estimation of trip matrices from traffic counts and survey data: A generalized least squares estimator. Trans. Res. B 1984, 18, 289–299. [Google Scholar] [CrossRef]
- Marzano, V.; Papola, A.; Simonelli, F. Limits and perspectives of effective O–D matrix correction using traffic counts. Trans. Res. C 2009, 17, 120–132. [Google Scholar] [CrossRef]
- Philipp, G.; Carbonell, J.G. Nonparametric neural networks. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
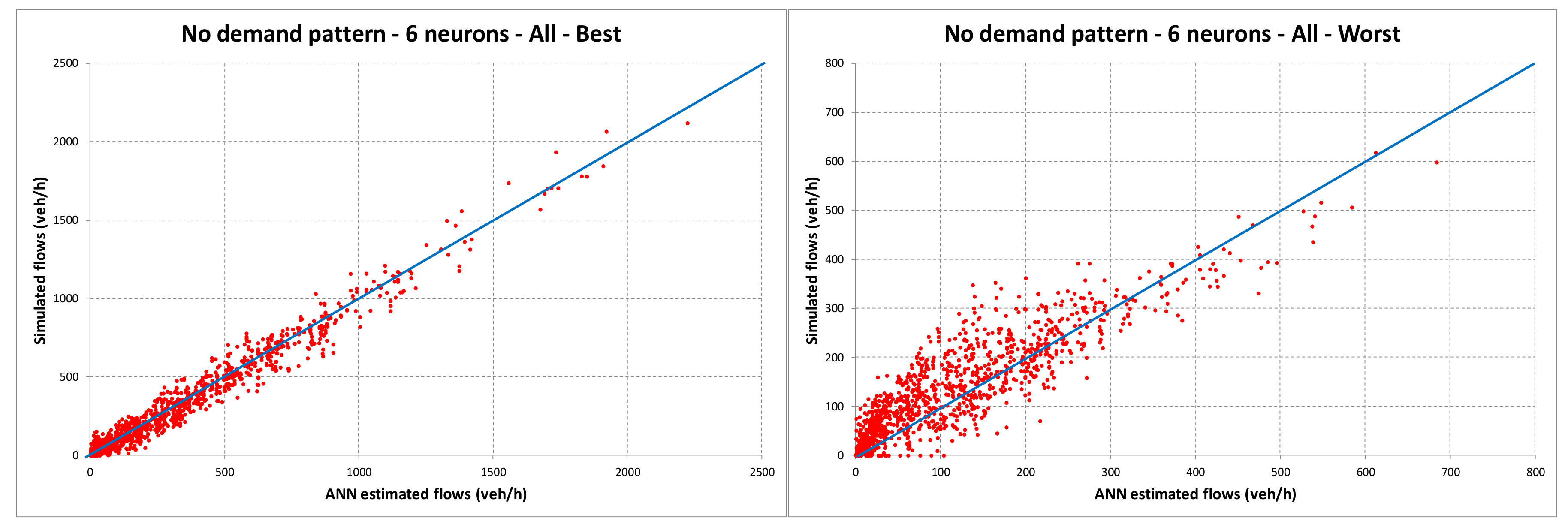

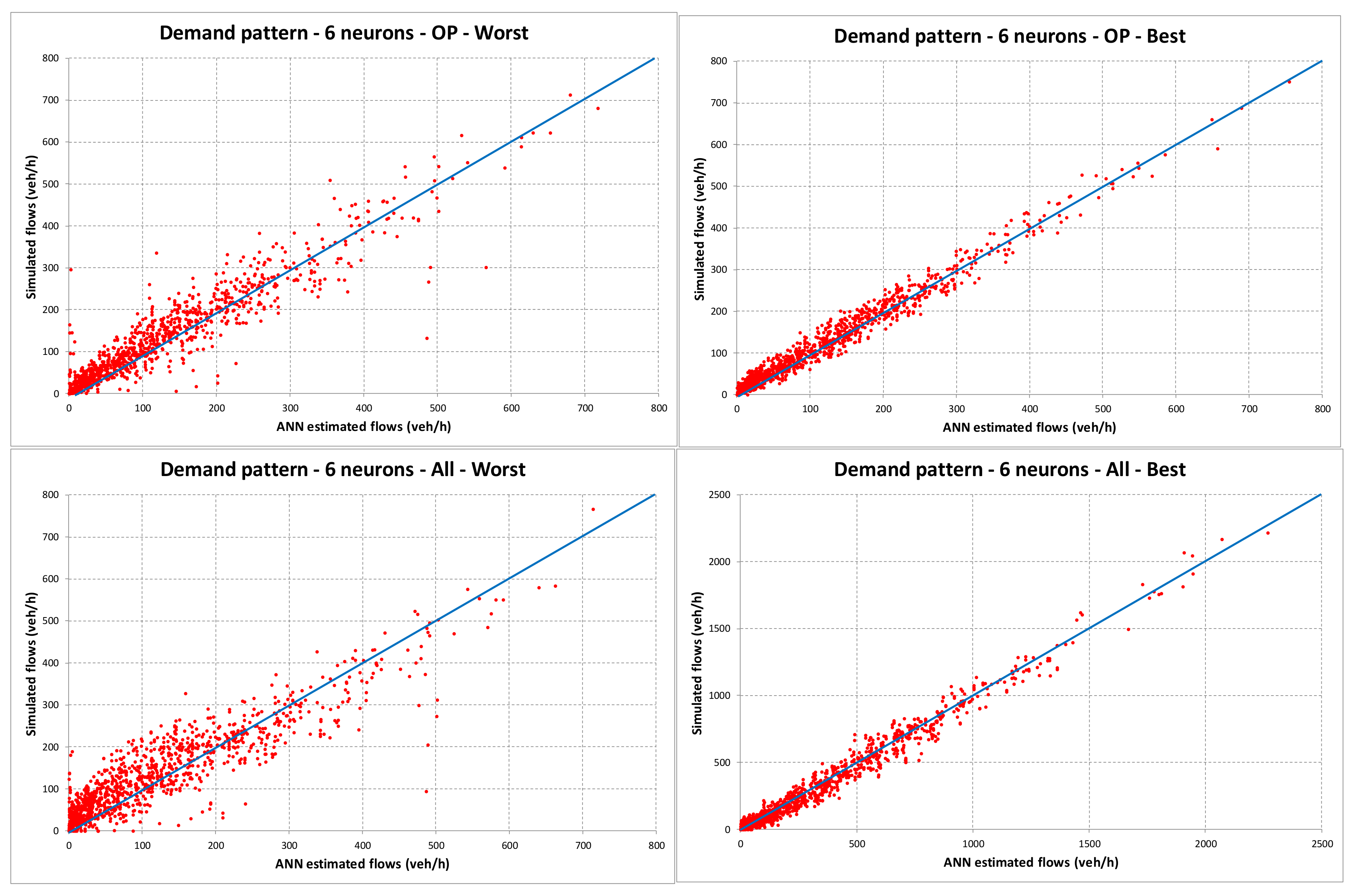
| Demand Pattern | Period | Neurons |
|---|---|---|
| No | All | 6 |
| 10 | ||
| 20 | ||
| 50 | ||
| Yes | MP | 6 |
| 10 | ||
| 20 | ||
| 50 | ||
| AP | 6 | |
| 10 | ||
| 20 | ||
| 50 | ||
| OP | 6 | |
| 10 | ||
| 20 | ||
| 50 | ||
| All | 6 | |
| 10 | ||
| 20 | ||
| 50 |
| Neurons | 6 | 10 | 20 | 50 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Best Case | Worst Case | Best Case | Worst Case | Best Case | Worst Case | Best Case | Worst Case | ||
| MSE | |||||||||
| Without demand pattern | All periods | 4068.57 | 2940.26 | 5750.85 | 8618.68 | 8398.84 | 4395.26 | 10,902.83 | 3817.52 |
| With demand pattern | MP | 2745.55 | 12,187.61 | 2711.22 | 13,885.76 | 2794.76 | 12,428.60 | 3125.40 | 13,403.28 |
| AP | 1837.69 | 6275.93 | 1788.36 | 8857.49 | 2253.55 | 8686.23 | 2723.28 | 8990.26 | |
| OP | 352.64 | 1577.61 | 319.70 | 1606.36 | 312.06 | 1436.70 | 487.15 | 2332.71 | |
| All periods | 3273.54 | 2638.57 | 2487.71 | 1855.52 | 3073.77 | 2360.71 | 2842.60 | 1961.30 | |
| RMSE | |||||||||
| Without demand pattern | All periods | 63.79 | 54.22 | 92.84 | 75.83 | 91.65 | 66.30 | 104.42 | 61.79 |
| With demand pattern | MP | 52.40 | 110.40 | 52.07 | 117.84 | 52.87 | 111.48 | 55.91 | 115.77 |
| AP | 42.87 | 79.22 | 42.29 | 94.11 | 47.47 | 93.20 | 52.19 | 94.82 | |
| OP | 18.78 | 39.72 | 17.88 | 40.08 | 17.67 | 37.90 | 22.07 | 48.30 | |
| All periods | 57.21 | 51.37 | 49.88 | 43.08 | 55.44 | 48.59 | 53.32 | 44.29 | |
| RMSE% | |||||||||
| Without demand pattern | All periods | 0.00016 | 0.00034 | 0.00022 | 0.00044 | 0.00023 | 0.00040 | 0.00027 | 0.00038 |
| With demand pattern | MP | 0.00013 | 0.00027 | 0.00013 | 0.00029 | 0.00013 | 0.00028 | 0.00014 | 0.00029 |
| AP | 0.00014 | 0.00025 | 0.00014 | 0.00030 | 0.00015 | 0.00030 | 0.00017 | 0.00031 | |
| OP | 0.00013 | 0.00027 | 0.00013 | 0.00028 | 0.00013 | 0.00027 | 0.00016 | 0.00034 | |
| All periods | 0.00014 | 0.00033 | 0.00013 | 0.00029 | 0.00013 | 0.00032 | 0.00013 | 0.00030 | |
| R2 | |||||||||
| Without demand pattern | All periods | 0.966 | 0.786 | 0.946 | 0.668 | 0.931 | 0.702 | 0.912 | 0.762 |
| With demand pattern | MP | 0.978 | 0.908 | 0.978 | 0.895 | 0.977 | 0.897 | 0.973 | 0.890 |
| AP | 0.975 | 0.925 | 0.976 | 0.895 | 0.971 | 0.893 | 0.963 | 0.906 | |
| OP | 0.975 | 0.894 | 0.976 | 0.889 | 0.976 | 0.902 | 0.966 | 0.846 | |
| All periods | 0.975 | 0.831 | 0.979 | 0.877 | 0.977 | 0.847 | 0.978 | 0.871 | |
| Neurons | 6 | 10 | 20 | 50 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Epochs | Time | Epochs | Time | Epochs | Time | Epochs | Time | ||
| MSE | |||||||||
| Without demand pattern | All periods | 447 | 16′′ | 465 | 17′′ | 544 | 22′′ | 489 | 26′′ |
| With demand pattern | MP | 406 | 17′′ | 196 | 8′′ | 322 | 14′′ | 387 | 21′′ |
| AP | 185 | 8′′ | 146 | 6′′ | 201 | 9′′ | 216 | 16′′ | |
| OP | 197 | 8′′ | 300 | 13′′ | 583 | 25′′ | 596 | 30′′ | |
| All periods | 1000 | 1′11′′ | 1000 | 1′13′′ | 1000 | 1′16′′ | 1000 | 1′37′′ | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallo, M.; De Luca, G. Spatial Extension of Road Traffic Sensor Data with Artificial Neural Networks. Sensors 2018, 18, 2640. https://doi.org/10.3390/s18082640
Gallo M, De Luca G. Spatial Extension of Road Traffic Sensor Data with Artificial Neural Networks. Sensors. 2018; 18(8):2640. https://doi.org/10.3390/s18082640
Chicago/Turabian StyleGallo, Mariano, and Giuseppina De Luca. 2018. "Spatial Extension of Road Traffic Sensor Data with Artificial Neural Networks" Sensors 18, no. 8: 2640. https://doi.org/10.3390/s18082640
APA StyleGallo, M., & De Luca, G. (2018). Spatial Extension of Road Traffic Sensor Data with Artificial Neural Networks. Sensors, 18(8), 2640. https://doi.org/10.3390/s18082640




