Infrared Image Super Resolution by Combining Compressive Sensing and Deep Learning
Abstract
1. Introduction
2. Super-Resolution Framework
2.1. Super-Resolution with Compressive Sensing Theory
| Algorithm 1. IRLS Method for Super-Resolution |
| Parameters: = 1, use DCT basis as , down-sampling matrix , N/M = 2 or 3, . |
| Step 1: Initialize the size of output image and the formation of sparsity basis. |
| Step 2: Do the inner loop: |
| 2.1 Initialize , and = O. |
| 2.2 Update using (5). |
| 2.3 Compute using (4). |
| 2.4 If (6) is satisfied, go to step 3; otherwise, let and go to step 2.2. |
| Step 3: Update the regularization parameter, . |
| Step 4: If , finish; else, go to Step 2. |
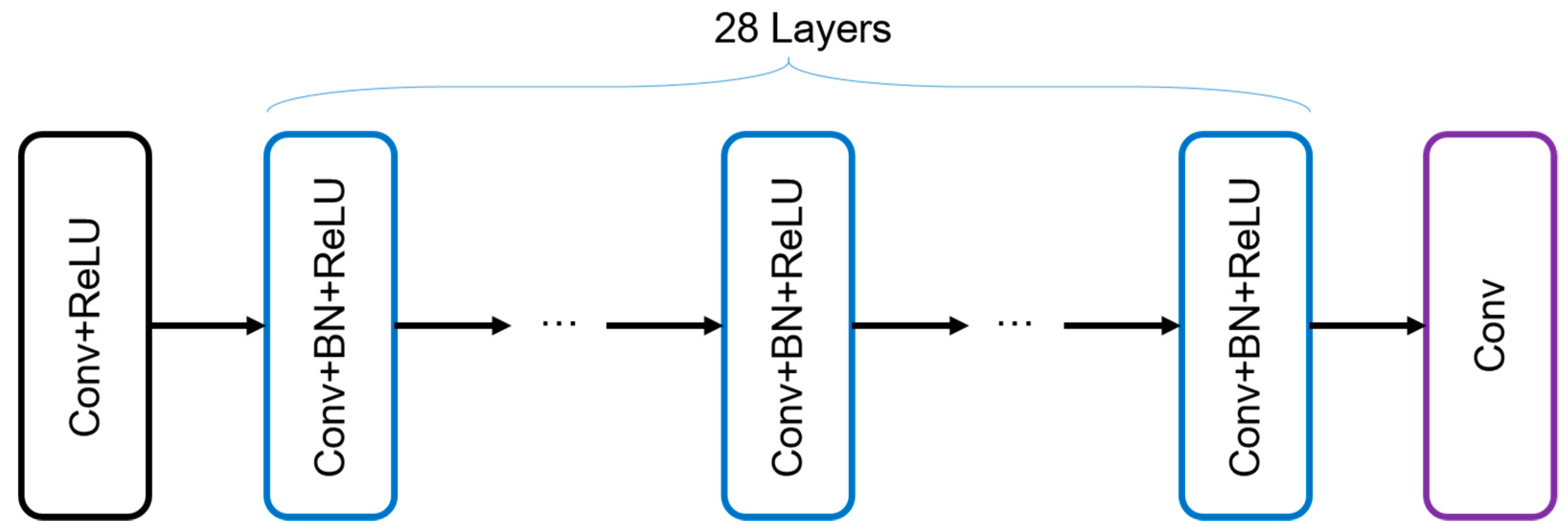
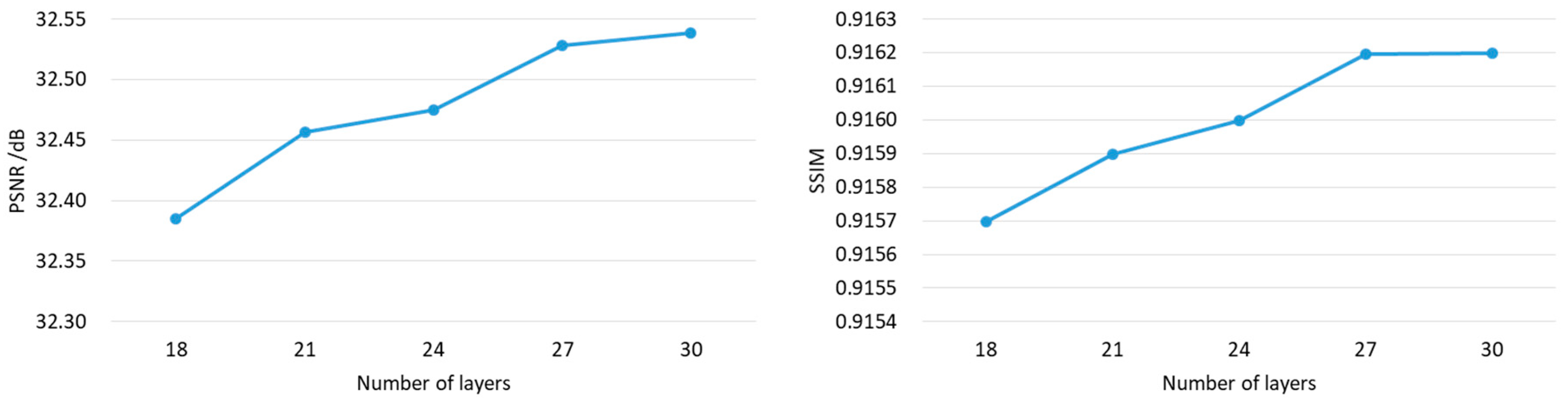
2.2. Image Denoising and Reconstruction with Deep Learning
| Algorithm 2. Adam Method for Optimization |
| Parameters: is the stepsize; are the exponential decay rates for the moment estimates; is the loss function with parameter . |
| Step 1: Initialize the parameters as , , , . |
| Step 2: Initialize the vectors. |
| is the initial first moment vector. |
| is the initial second moment vector. |
| is the initial timestep. |
| Step 3: Do the inner loop: |
| 3.1. Update the timestep. |
| 3.2. Decay the first moment running average coefficient. |
| 3.3. Get gradients corresponding to loss function at timestep t. |
| 3.4. Update biased first moment estimate. |
| 3.5. Update biased second raw moment estimate. |
| 3.6. Compute bias-corrected first moment estimate. |
| 3.7. Compute bias-corrected second raw moment estimate. |
| 3.8 Update parameters, where is for preventing the denominator to be zero. |
| 3.9 if is converged, go to step 4; otherwise go to step 3.1. |
| Step 4: Return . |
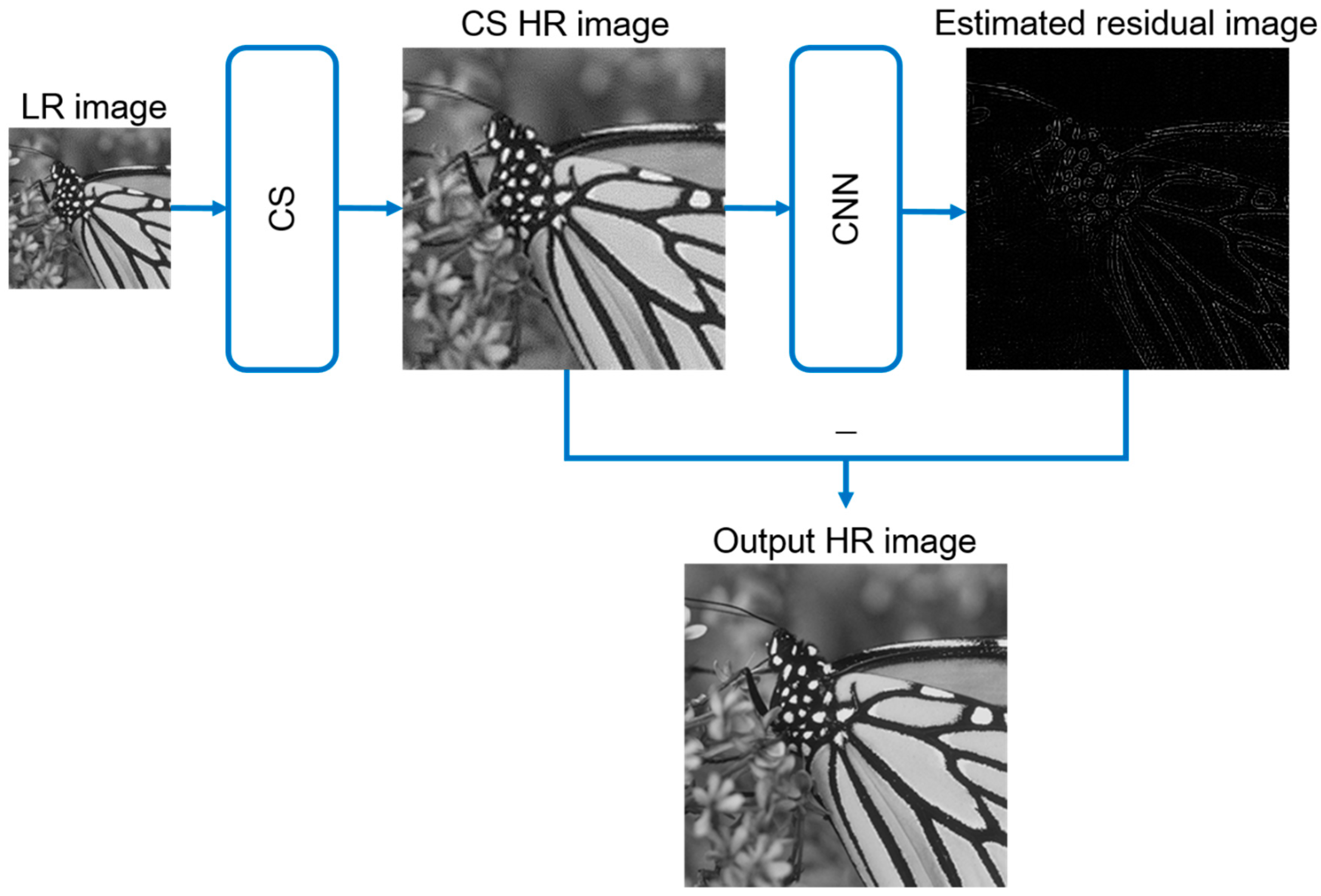
2.3. The Whole Super-Resolution Algorithm Architecture
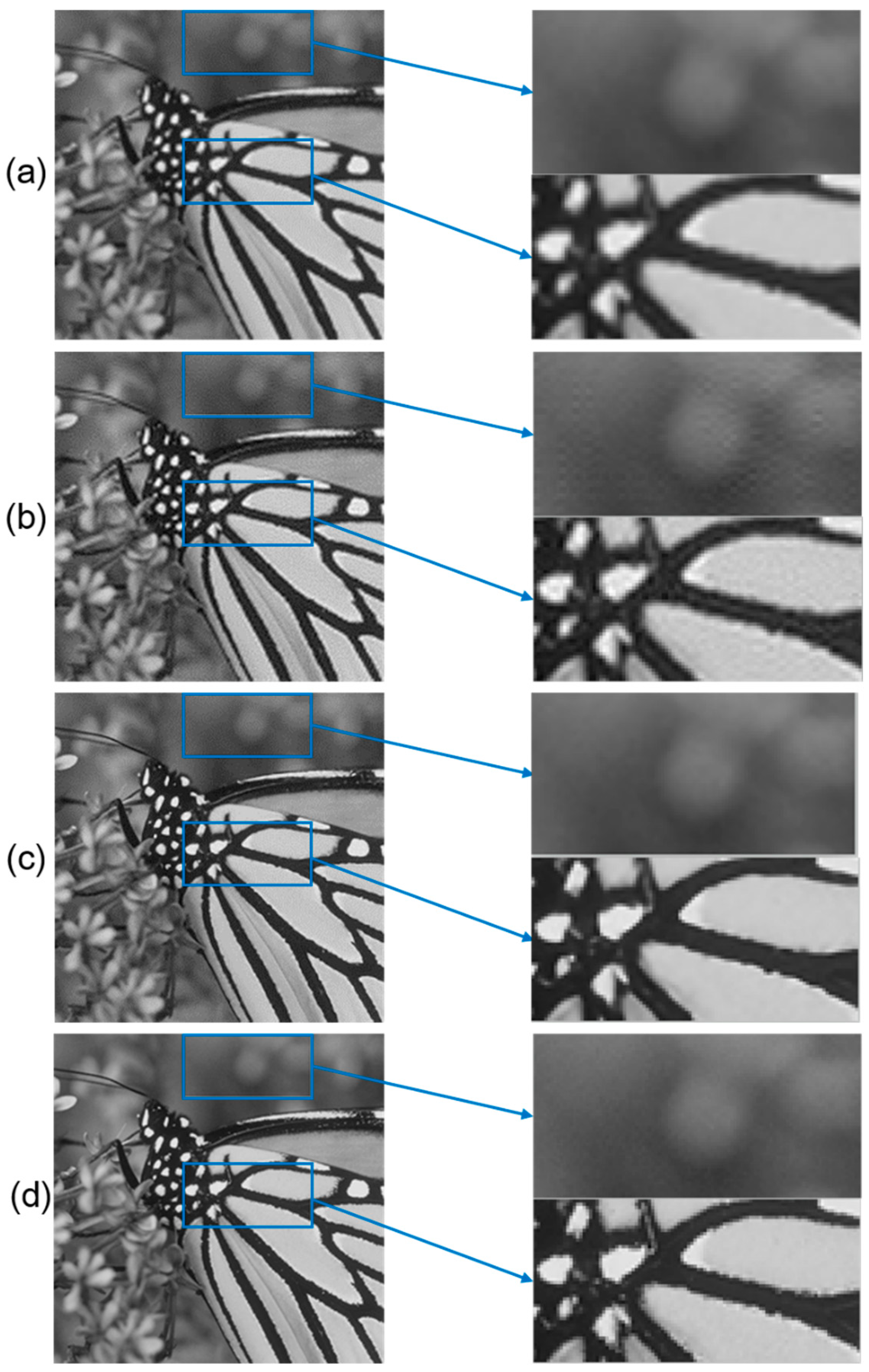
3. Simulation Results
4. Imaging Experiments
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shi, W.; Caballero, J.; Huszar, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar] [CrossRef]
- Liu, F.; Han, P.; Wang, Y.; Li, X.; Bai, L.; Shao, X. Super resolution reconstruction of infrared images based on classified dictionary learning. Infrared Phys. Technol. 2018, 90, 146–155. [Google Scholar] [CrossRef]
- Greenspan, H. Super-Resolution in Medical Imaging. Comput. J. 2009, 52, 43–63. [Google Scholar] [CrossRef]
- Shen, H.; Ng, M.K.; Li, P.; Zhang, L. Super-resolution reconstruction algorithm to modis remote sensing images. Comput. J. 2008, 52, 90–100. [Google Scholar] [CrossRef]
- Gunturk, B.K.; Batur, A.U.; Altunbasak, Y.; Rd, H.M.; Mersereau, R.M. Eigenface-domain super-resolution for face recognition. IEEE Trans. Image Process. 2003, 12, 597. [Google Scholar] [CrossRef] [PubMed]
- Quan, T.; Li, P.; Long, F.; Zeng, S.; Luo, Q.; Hedde, P.N.; Nienhaus, G.U.; Huang, Z. Ultra-fast, high-precision image analysis for localization-based super resolution microscopy. Opt. Express 2010, 18, 11867–11876. [Google Scholar] [CrossRef] [PubMed]
- Nasrollahi, K.; Moeslund, T.B. Super-resolution: A comprehensive survey. Mach. Vis. Appl. 2014, 25, 1423–1468. [Google Scholar] [CrossRef]
- Li, X.; Hu, Y.; Gao, X.; Tao, D.; Ning, B. A multi-frame image super-resolution method. Signal Process. 2010, 90, 405–414. [Google Scholar] [CrossRef]
- Kim, K.I.; Kwon, Y. Single-image super-resolution using sparse regression and natural image prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1127–1133. [Google Scholar] [CrossRef] [PubMed]
- Sreeja, S.J.; Wilscy, M. Single image super-resolution based on compressive sensing and TV minimization sparse recovery for remote sensing images. In Proceedings of the 2013 IEEE Recent Advances in Intelligent Computational Systems, Trivandrum, India, 19–21 December 2013; pp. 215–220. [Google Scholar] [CrossRef]
- Kulkarni, N.; Nagesh, P.; Gowda, R.; Li, B. Understanding compressive sensing and sparse representation-based super-resolution. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 778–789. [Google Scholar] [CrossRef]
- Sen, P.; Darabi, S. Compressive image super-resolution. In Proceedings of the 2009 Conference Record of the Forty-Third Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–4 November 2009; pp. 1235–1242. [Google Scholar] [CrossRef]
- Yang, S.; Wang, M.; Sun, Y.; Sun, F.; Jiao, L. Compressive sampling based single-image super-resolution reconstruction by dual-sparsity and non-local similarity regularizer. Pattern Recognit. Lett. 2012, 33, 1049–1059. [Google Scholar] [CrossRef]
- Bertocco, M.; Frigo, G.; Narduzzi, C.; Tramarin, F. Resolution enhancement in harmonic analysis by compressive sensing. In Proceedings of the IEEE International Workshop on Applied Measurements for Power Systems, Aachen, Germany, 25–27 September 2013; pp. 40–45. [Google Scholar] [CrossRef]
- Baraniuk, R.; Foucart, S.; Needell, D.; Plan, Y.; Wootters, M. One-bit compressive sensing of dictionary-sparse signals. Inf. Inference A J. IMA 2018, 7, 83–104. [Google Scholar] [CrossRef]
- Chartrand, R.; Yin, W. Iteratively reweighted algorithms for compressive sensing. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 3869–3872. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar] [CrossRef]
- Li, D.; Wang, Z. Video superresolution via motion compensation and deep residual learning. IEEE Trans. Comput. Imaging 2017, 3, 749–762. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; Shi, W. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar] [CrossRef]
- Dong, C.; Chen, C.L.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the EVVC 2014—European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- Duan, G.; Hu, W.; Wang, J. Research on the natural image super-resolution reconstruction algorithm based on compressive perception theory and deep learning model. Neurocomputing 2016, 208, 117–126. [Google Scholar] [CrossRef]
- Bora, A.; Jalal, A.; Price, E.; Dimakis, A.G. Compressed sensing using generative models. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 537–546. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Li, X.; Lu, X.; Yuan, H.; Yan, P.; Yuan, Y. Geometry constrained sparse coding for single image super-resolution. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 1648–1655. [Google Scholar] [CrossRef]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Boufounos, D.; Liu, D.; Boufounos, P.T. A lecture on compressive sensing. IEEE Signal Process. Mag. 2007, 24, 1–9. [Google Scholar]
- Nasibov, H.; Kholmatov, A.; Akselli, B.; Nasibov, A.; Baytaroglu, S. Performance analysis of the CCD pixel binning option in particle-image velocimetry measurements. IEEE/ASME Trans. Mechatron. 2010, 15, 527–540. [Google Scholar] [CrossRef]
- Lu, F.; Au, O.C. Novel 2-D MMSE subpixel-based image down-sampling for matrix displays. In Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 986–989. [Google Scholar] [CrossRef]
- Fan, N. Super-resolution using regularized orthogonal matching pursuit based on compressed sensing theory in the wavelet domain. In Proceedings of the International Conference on Computer Graphics, Tianjin, China, 11–14 August 2009; pp. 349–354. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, Y.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Dai, W.; Milenkovic, O. Subspace Pursuit for Compressive Sensing Signal Reconstruction. IEEE Trans. Inf. Theory 2009, 55, 2230–2249. [Google Scholar] [CrossRef]
- He, L.; Carin, L. Exploiting structure in wavelet-based Bayesian compressive sensing. IEEE Trans. Signal Process. 2009, 57, 3488–3497. [Google Scholar] [CrossRef]
- Miosso, C.J.; Borries, R.V.; Argaez, M.; Velazquez, L.; Quintero, C.; Potes, C.M. Compressive sensing reconstruction with prior information by iteratively reweighted least-squares. IEEE Trans. Signal Process. 2009, 57, 2424–2431. [Google Scholar] [CrossRef]
- Al-Najjar, Y. Comparison of image quality assessment: PSNR, HVS, SSIM, UIQI. Int. J. Sci. Eng. Res. 2012, 3, 1. [Google Scholar]
- Megha, G.; Yashpal, L.; Vivek, L. Analytical relation & comparison of PSNR and SSIM on babbon image and human eye perception using matlab. Int. J. Adv. Res. Eng. Appl. Sci. 2015, 4, 108–119. [Google Scholar]
- Satya, K.; JayaChandra, T. Deep learning approach for image denoising and image demosaicing. Int. J. Comput. Appl. 2017, 168, 18–26. [Google Scholar] [CrossRef]
- Rivenson, Y.; Zhang, Y.; Günaydın, H.; Teng, D.; Ozcan, A. Phase recovery and holographic image reconstruction using deep learning in neural networks. Light Sci. Appl. 2018, 7, 17141. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the 19th International Conference on Computational Statistics, Paris, France, 22–27 August 2010; pp. 177–186. [Google Scholar] [CrossRef]
- OTCBVS Benchmark Dataset Collection. Available online: http://vcipl-okstate.org/pbvs/bench/ (accessed on 12 June 2018).







| Image | SRCNN | ScSR | Proposed Method | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | Time/s | PSNR | SSIM | Time/s | PSNR | SSIM | Time/s | |
| 1 | 33.03 | 0.9529 | 2.5 | 33.29 | 0.9662 | 17.6 | 34.78 | 0.9629 | 9.6 |
| 2 | 36.78 | 0.9633 | 1.6 | 36.34 | 0.9685 | 17.7 | 38.08 | 0.9689 | 12.1 |
| 3 | 34.42 | 0.9700 | 1.7 | 34.26 | 0.9718 | 21.1 | 34.65 | 0.9702 | 15.2 |
| 4 | 40.59 | 0.9769 | 1.6 | 41.36 | 0.9793 | 20.9 | 41.53 | 0.9786 | 15.4 |
| 5 | 35.34 | 0.9652 | 1.7 | 35.93 | 0.9691 | 20.9 | 36.10 | 0.9678 | 15.2 |
| 6 | 30.63 | 0.8118 | 1.8 | 30.34 | 0.8141 | 24.4 | 31.08 | 0.8154 | 14.1 |
| 7 | 28.20 | 0.9005 | 1.5 | 27.56 | 0.8940 | 17.7 | 29.48 | 0.9111 | 14.5 |
| 8 | 32.66 | 0.9398 | 1.4 | 31.75 | 0.9333 | 17.3 | 33.72 | 0.9464 | 53.0 |
| 9 | 32.51 | 0.9618 | 1.5 | 30.84 | 0.9520 | 16.7 | 34.18 | 0.9719 | 57.6 |
| 10 | 28.55 | 0.9180 | 1.5 | 28.41 | 0.9169 | 17.9 | 29.59 | 0.9254 | 57.2 |
| 11 | 36.19 | 0.9381 | 9.8 | 35.84 | 0.9353 | 70.1 | 36.74 | 0.9380 | 56.8 |
| 12 | 32.98 | 0.9201 | 10.2 | 32.44 | 0.9147 | 69.3 | 33.55 | 0.9265 | 54.0 |
| Image | SRCNN | ScSR | Proposed Method | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | Time/s | PSNR | SSIM | Time/s | PSNR | SSIM | Time/s | |
| 1 | 28.22 | 0.8666 | 1.8 | 27.42 | 0.8851 | 47.6 | 28.73 | 0.9001 | 5.0 |
| 2 | 32.06 | 0.9222 | 1.4 | 31.50 | 0.9194 | 51.3 | 32.42 | 0.9259 | 4.2 |
| 3 | 29.47 | 0.9045 | 1.5 | 28.36 | 0.9070 | 52.2 | 29.27 | 0.9117 | 4.2 |
| 4 | 36.59 | 0.9452 | 1.4 | 35.61 | 0.9542 | 53.5 | 37.30 | 0.9528 | 4.0 |
| 5 | 30.93 | 0.9011 | 1.5 | 30.89 | 0.9096 | 52.5 | 30.57 | 0.9045 | 4.8 |
| 6 | 28.48 | 0.7134 | 1.6 | 27.97 | 0.7127 | 60.5 | 28.72 | 0.7216 | 5.1 |
| 7 | 26.53 | 0.8427 | 1.3 | 26.11 | 0.8342 | 45.2 | 27.24 | 0.8596 | 5.1 |
| 8 | 30.44 | 0.9117 | 1.2 | 28.69 | 0.8977 | 43.0 | 31.18 | 0.9269 | 18.7 |
| 9 | 29.04 | 0.9105 | 1.3 | 26.94 | 0.8835 | 44.8 | 30.27 | 0.9334 | 22.3 |
| 10 | 26.12 | 0.8693 | 1.3 | 25.75 | 0.8640 | 46.0 | 27.08 | 0.8838 | 22.4 |
| 11 | 33.40 | 0.9097 | 9.2 | 32.66 | 0.9041 | 183.3 | 33.48 | 0.9124 | 22.7 |
| 12 | 30.79 | 0.8636 | 9.8 | 30.14 | 0.8543 | 186.7 | 31.17 | 0.8731 | 22.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Li, C.; Meng, Q.; Liu, S.; Zhang, Y.; Wang, J. Infrared Image Super Resolution by Combining Compressive Sensing and Deep Learning. Sensors 2018, 18, 2587. https://doi.org/10.3390/s18082587
Zhang X, Li C, Meng Q, Liu S, Zhang Y, Wang J. Infrared Image Super Resolution by Combining Compressive Sensing and Deep Learning. Sensors. 2018; 18(8):2587. https://doi.org/10.3390/s18082587
Chicago/Turabian StyleZhang, Xudong, Chunlai Li, Qingpeng Meng, Shijie Liu, Yue Zhang, and Jianyu Wang. 2018. "Infrared Image Super Resolution by Combining Compressive Sensing and Deep Learning" Sensors 18, no. 8: 2587. https://doi.org/10.3390/s18082587
APA StyleZhang, X., Li, C., Meng, Q., Liu, S., Zhang, Y., & Wang, J. (2018). Infrared Image Super Resolution by Combining Compressive Sensing and Deep Learning. Sensors, 18(8), 2587. https://doi.org/10.3390/s18082587





