1. Introduction
Lighting accounts for approximately 19% of the electricity consumed all over the world [
1], but there are great possibilities of achieving savings by replacing inefficient lighting sources [
2,
3]. Indeed, over the past decade, the worldwide demand for artificial lighting increased at an average rate of 2.4% per year [
1]. In buildings, artificial lighting is a significant contributor to energy consumption and costs, consuming the highest electrical energy, approximately one-third of the electricity used [
3,
4,
5]. Therefore, the knowledge of the real lighting inventory and conditions and the adequate management of lighting systems are crucial when addressing energy conservation measures (ECMs) [
5]. Not only does this knowledge allow us to reduce energy consumption, but it can also save money for the building’s owners [
3]. Consequently, the building lighting must be accurately known and then reliably integrated into the building information modelling (BIM).
BIM is a technology widely recognized and increasingly investigated in the architecture, engineering and construction (AEC) industry [
6,
7,
8]. BIM can be defined as “a set of interacting policies, processes and technologies producing a methodology to manage essential building design and project data in digital format throughout the building’s lifecycle” [
9]. It represents the digital model of the building as an integrated and coordinated database that enables sharing and transferring information about the whole building [
8]. BIM tools are designed mainly for the analysis of multiple performance criteria, including lighting as a main issue [
7,
8,
10]. Typically, BIM software implements internally a lighting condition analysis, differentiating between the natural and artificial lighting [
7]. However, the main obstacle is the lack of accurate information [
7]. The work presented in this article tries to solve this issue by looking for new methods that allow the accurate identification and state of lamps. Although research on the building lighting related to BIM has been deeply addressed by many authors [
8,
11,
12,
13], the integration of computer vision is relatively new [
14].
Computer vision is a technology of obtaining and evaluating a digital image to acquire a certain type of information and can be widely applied [
15]. Moreover, computer vision is helpful to shorten the time-consuming inspection process [
15,
16]. Computer vision systems (CVSs) have progressed and currently focus on depth data besides edge-based image algorithms. Nevertheless, edge-based image algorithms still lead to better outcomes for object detection and location in many cases [
17]. Methods for object detection, location and 3D pose estimation have been comprehensively explained in a previous article [
14], classifying them into image-based [
18] and model-based techniques [
19] suitable for textureless object detection. Matching is a key problem in the digital image analysis, and edges are perhaps the most important low-level image feature [
20]. Chamfer matching algorithms are high-performance solutions to the shape-based object detection, which calculate distances between edges, and the chamfer distance transform has been effectively used in model-based methods for the edge-based matching [
14]. State-of-the-art and different chamfer distance transform algorithms are gathered and explained in depth [
14]. The new procedure proposed in this work outperforms other methods in different aspects. The new procedure is an improved version of our previous work, which enhances the candidate and model selection while leveraging the fast directional chamfer matching (FDCM) [
21] and the pose refinement and scoring of the direct directional chamfer optimization (D
CO) [
17].
Image registration is a process of overlapping two or more images of the same scene taken at different times, from different perspectives, and by different sensors [
22]. Typically, image registration is required in remote sensing, medicine, cartography and computer vision [
22]. Several authors have applied this to detect lighting and lamps. Elvidge et al. [
23] investigated the optimal spectral bands for the identification of lighting types and estimated four major indices to measure the efficiency of lighting, which lead to good results with minimal spectral overlap. Liu et al. [
24] proposed an imaging sensor-based light emitting diode (LED) lighting system that implemented a finer perception of the environmental lighting, resulting in a more precise lighting control. Ng et al. [
15] presented an integrated approach combining a CVS and real-time management system (RTMS) to solve quality control problems in the manufacturing of lighting products.
This work proposes a complete and novel methodology based on computer vision to detect, identify and locate all types of lamps independently of the shape of their light surface. We describe the design and the development of new algorithms that enhance current methods in the literature using computer vision and imaging processing tools. The results from the whole system, which is suitable for any type of lamp shape, are integrated into a BIM with the aim of solving problems related to time-consuming operations and human errors. The main contribution of this work lies in the generalization of the shape and pose estimation techniques to allow the identification of a much wider range of lamp shapes and the improvements in the localization system and the BIM integration step. This work applies a novel technology in a fast and practical way, therefore innovating the building lighting. However, the applications can be extended to other sectors given the cross-sectional nature of the method. In addition, the method can be widely used in the continuous and automatic scanning of lamps, the precise knowledge of the state of a lamp, the establishment of a lamp stock, the electrical facility maintenance, the energy audit and the setting of conformable indoor conditions for the occupants.
2. Materials and Methods
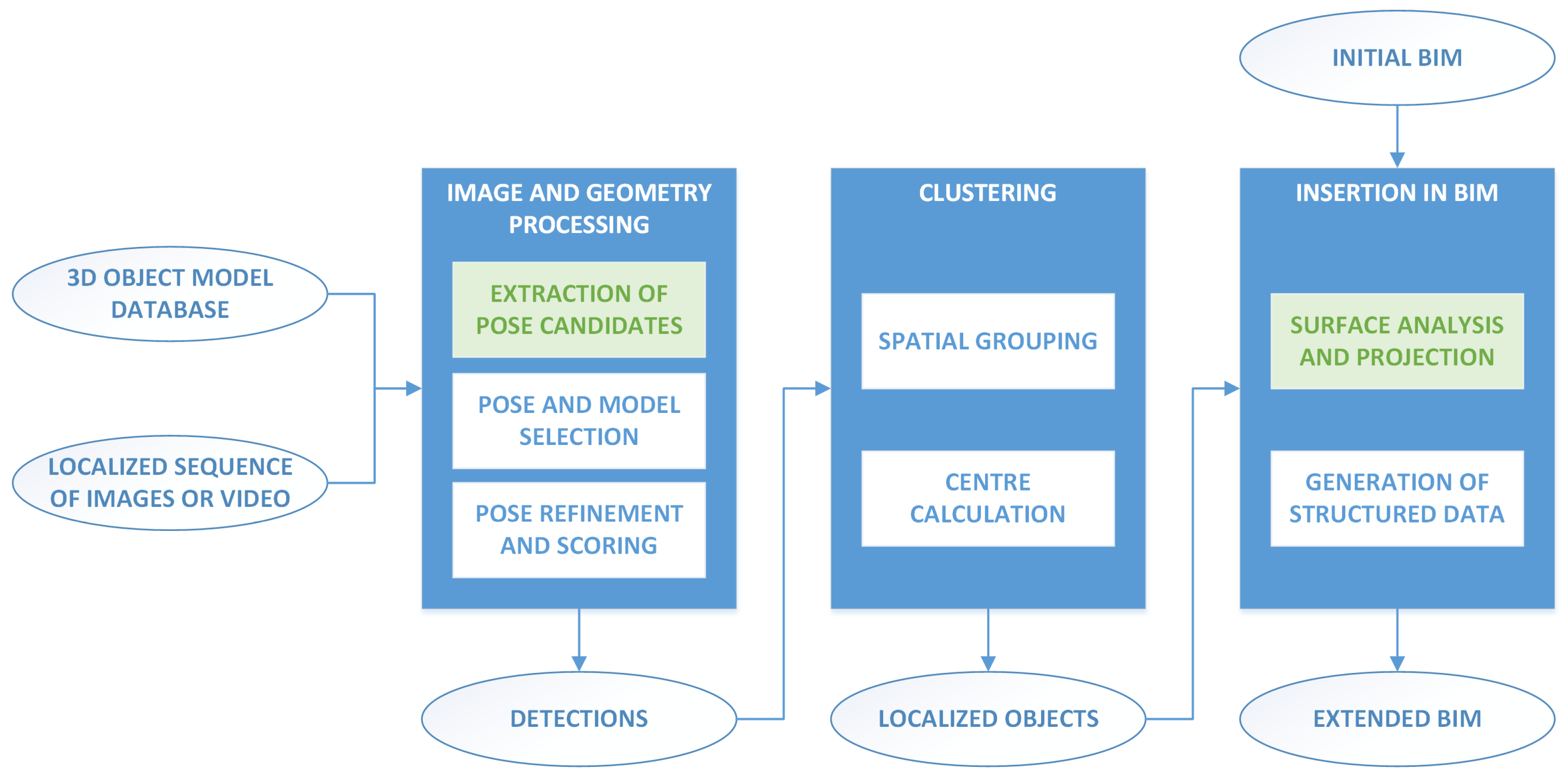
The methodology proposed in this work is based on three main steps: image and geometry processing, clustering, and insertion in the BIM.
Figure 1 shows a general diagram of this whole process. In the first step, the input images are analysed to obtain initial pose candidates based on the detected shapes. Then, for each detection, a lamp model is selected leveraging the FDCM [
21] based on the available edge information of the image extracted using the line segment detector (LSD) [
25]. Lastly, the pose is refined using the D
CO [
17]. In the second step, a clustering operation is performed on the set of individual detections, and a centre is calculated for each of the resulting clusters, leading to a collection of localized objects. In the last step, the information from the detected objects is inserted into the BIM model of the building, assigning the detections to the corresponding space.
We introduce the following major enhancements to our previous work [
14]: (i) the generalization of the shape and pose estimation to automatically detect polygonal shapes with different numbers of sides and elliptical shapes; and (ii) the use of the available BIM information in the final insertion step by means of a surface projection method. These improvements yield more refined results and provide a wider range of application.
The complete system and each of the custom algorithms presented in this work have been developed in C++, with the help of the following supporting software libraries: OpenCV [
26] for general artificial vision algorithms, OpenMesh [
27] to read and process the 3D geometric information of object models, Ceres Solver [
28] to solve the different optimization problems involved in the method, and OpenGL [
29] to obtain the occlusion information on the 3D projections.
2.1. Generalized Shape and Pose Estimation
In our previous work [
14], we introduced an algorithm to obtain the shape and the pose of objects projecting a quadrilateral on the image. Here, we generalize the shape estimation to automatically detect the number of sides of the final polygon, with the possibility of also detecting elliptical shapes, and introduce the necessary changes to the pose estimation to be compatible with either polygonal or elliptical shapes. We use the term
pose to denote a rigid transformation of an object, composed of a vector in
that determines the translation and a vector in
—the Lie algebra associated with the special orthogonal group
—that determines the orientation.
2.1.1. Polygon Estimation
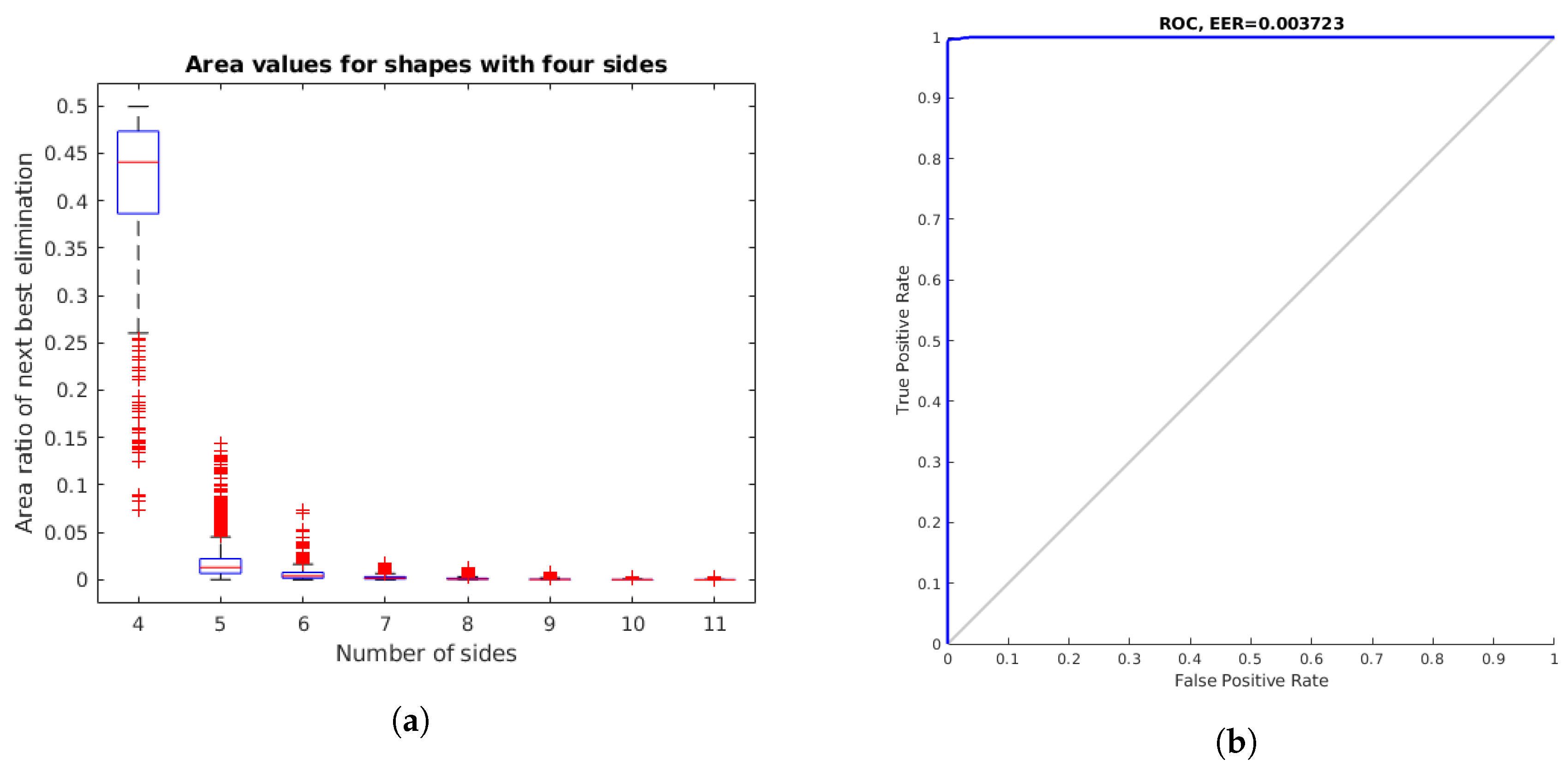
The method presented in [
14] aims to obtain an estimation of the shape of a polygon with a fixed number of sides
k based on an initial contour with
sides. The method is an extension of the work of Visvalingam et al. [
30] for strictly inner, strictly outer, or general polygons, based on a predefined score function. Here, we use an area-based score function to detect polygons with an arbitrary number of sides based on a threshold
as the termination criterion. This method is presented in Algorithm 1 with the additional functions in Algorithm 2. We use the method of Sklansky [
31] to make the initial contour convex. The method stops when the next best area relative to the original contour area is greater than
. This method is based on the fact that the reduction of the area should be relatively small until the final number of sides is reached, at which point there should be a noticeable increase in the area reduction.
| Algorithm 1 Fit polygon. |
Require:Ensure:- 1:
functionFitPolygon(, ) - 2:
ConvexHull( P) ▹ From [ 31] - 3:
Area() - 4:
; ; - 5:
for do - 6:
InnerScore(, k) ▹ Algorithm 2 - 7:
OuterScore(, k) ▹ Algorithm 2 - 8:
end for - 9:
while true do - 10:
; - 11:
- 12:
if then - 13:
break - 14:
end if - 15:
- 16:
RemoveElement(R, l); RemoveElement(S, l); RemoveElement(, l) - 17:
if then - 18:
- 19:
end if - 20:
RemoveElement(, l) - 21:
InnerScore(, ); InnerScore(, l) ▹ Algorithm 2 - 22:
OuterScore(, ); OuterScore(, l) ▹ Algorithm 2 - 23:
if then - 24:
InnerScore(, ) ▹ Algorithm 2 - 25:
else - 26:
OuterScore(, ) ▹ Algorithm 2 - 27:
end if - 28:
end while - 29:
return - 30:
end function
|
| Algorithm 2 Score functions. |
- 1:
functionInnerScore(, k) - 2:
return Area(, , ) - 3:
end function - 4:
- 5:
functionOuterScore(, k) - 6:
if then - 7:
Intersection(, , , ) - 8:
Area(, , ) - 9:
else - 10:
; - 11:
end if - 12:
return a, - 13:
end function
|
2.1.2. Shape Estimation
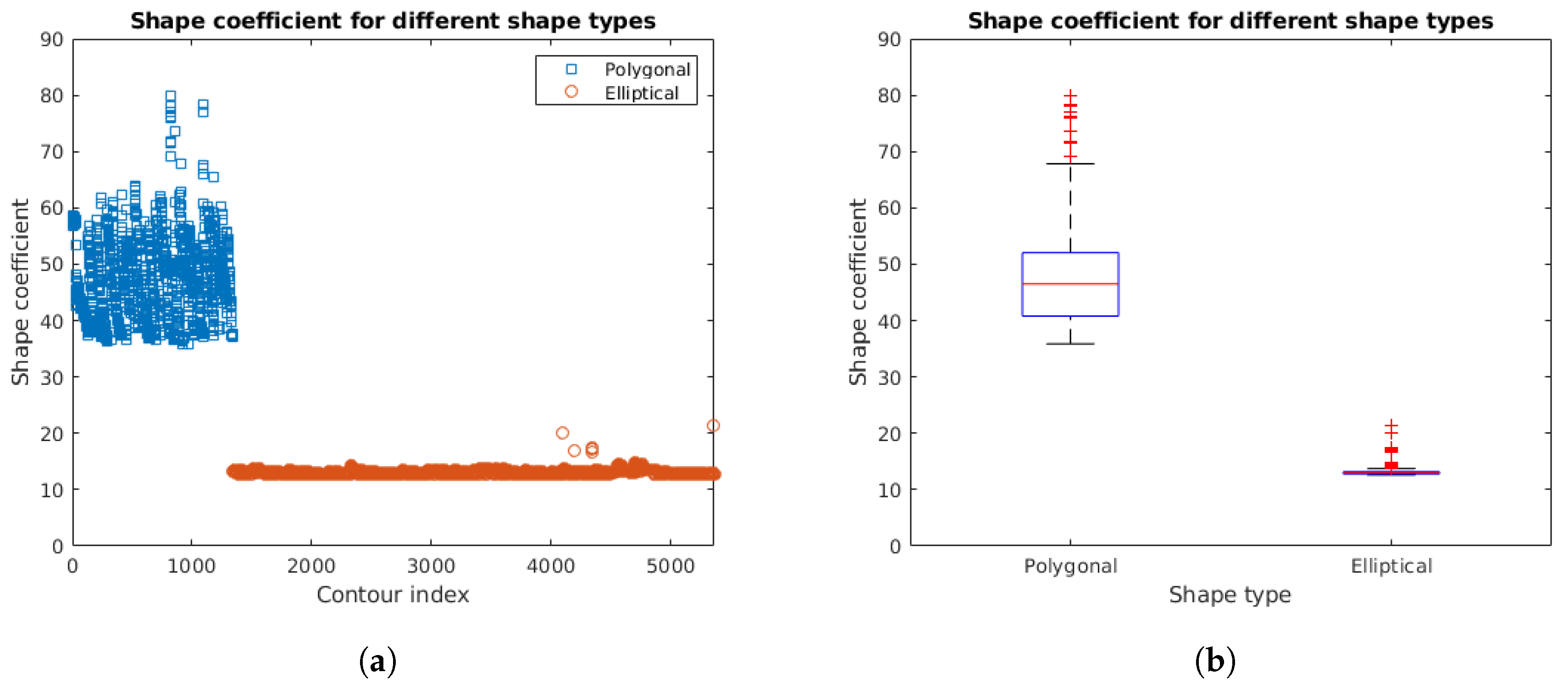
The polygon estimation method is included in a more general shape and pose estimation technique presented in Algorithm 3. First, we obtain a coefficient to determine if the shape is polygonal or elliptical based on a predefined threshold
. In the first case, we estimate the polygon using Algorithm 1; in the second case, we use the method introduced by Fitzgibbon and Fisher [
32] to obtain the final shape parameters.
| Algorithm 3 Fit shape. |
Require: is a sequence of n points is the area threshold to stop removing sides is the maximum number of sides for the shape to be considered a polygon is a set of object models are the parameters of the camera model
Ensure:- 1:
functionFitShape(, ) - 2:
- 3:
FitPolygon() ▹ Algorithm 1 - 4:
for all do - 5:
if has a non-circular shape then - 6:
SolvePnp(, C, ) - 7:
end if - 8:
end for - 9:
else - 10:
FitEllipse( ) ▹ From [ 32] - 11:
for all do - 12:
if has a circular shape then - 13:
- 14:
end if - 15:
end for - 16:
end if - 17:
return , - 18:
end function
|
The shape coefficient
s is obtained based on the circularity [
33] of the shape as follows:
being
p the shape perimeter and
a its area.
The aim is to obtain higher values for polygons compared to those for ellipses.
2.1.3. Pose Estimation
We use two different methods to estimate the pose based on the image shape. In the case of a polygon, we solve a PnP (
Perspective-n-Point) problem using an iterative method based on the Levenberg–Marquardt optimization [
34,
35] as described in [
14]. However, if the shape is elliptical, we do not have a direct correspondence between points in 2D and in 3D. We could use the four axis points from the projected ellipse, but Luhmann [
36] showed that the eccentricity in the projection of circular target centres should not be ignored in real applications. Therefore, we have to modify the classic PnP problem to account for the absence of a direct correspondence. Using the contour points from the image, we formulate a minimization problem based on the distance of the projected image points on the circle plane to its circumference.
Let
be an ellipse with a centre
, a semi-major axis of length
a and a semi-minor axis of length
b, rotated by an angle
. Let
be a circle for which
E is a projection on the image plane, with a centre
and a radius
, included in the plane
with a unit normal vector
. Let
be the matrix of the intrinsic parameters of the camera:
with focal lengths
and
, and principal point offsets
and
.
For each point
on the contour of the ellipse, we can obtain its corresponding position
in the camera coordinate system on the plane
as
Let
be the projection line from the camera origin to the point
. The intersection point
between this line and the circle plane is given by their corresponding equations:
Then, for each point, we try to minimize the distance from its projection to the circumference:
As for the classic PnP problem, we solve the minimization using an iterative method based on the Levenberg–Marquardt optimization [
34,
35]. The constraint on the unit normal vector is taken into account by performing a local parameterization of
in the tangent space of the unit sphere.
To improve the convergence of the method, we adopt the following initial guess of
and
:
being
the corresponding position of
in the camera coordinate system on the plane
and
a unit vector along the direction of the minor axis of the projected ellipse.
Lastly, we obtain the rotation vector from the resulting unit normal vector of the plane as follows:
2.2. Surface Projection in the BIM Integration
The BIM model of the building represents an additional source of information that can be used to improve the accuracy of the detections. Apart from the insertion of the new data exemplified in [
14], we can also use the geometric information from the BIM model to extract a list of surfaces with spatial information and use them to adjust the positions of the detections. Assuming gbXML [
37]—an open schema created to facilitate the transference of building data stored in BIM to engineering analysis tools—as the supporting format for the BIM information, we can obtain the required data by accessing the elements with path “gbXML/Campus/Surface/PlanarGeometry” in the XML tree.
Given that the detected lamps are embedded in the ceilings of the building, we can perform a projection in the 3D space of each of the detections to the nearest building surface. Let
be the set of the surfaces of a building model, each one with a unit normal vector
and a point
included in the plane defined by the surface. Then, the surface in the model that is the closest to a point
is given by
Then, the projected location
of a detection positioned at
, with the nearest model surface
at a distance
and with a unit normal vector
, is
With this method, we can improve the location of the detections and, at the same time, assign the detections to the corresponding space in the building model based on the nearest surface. This is a more effective and simpler approach compared to the point-in-polyhedron test used in [
14].
3. Description of the Experimental System
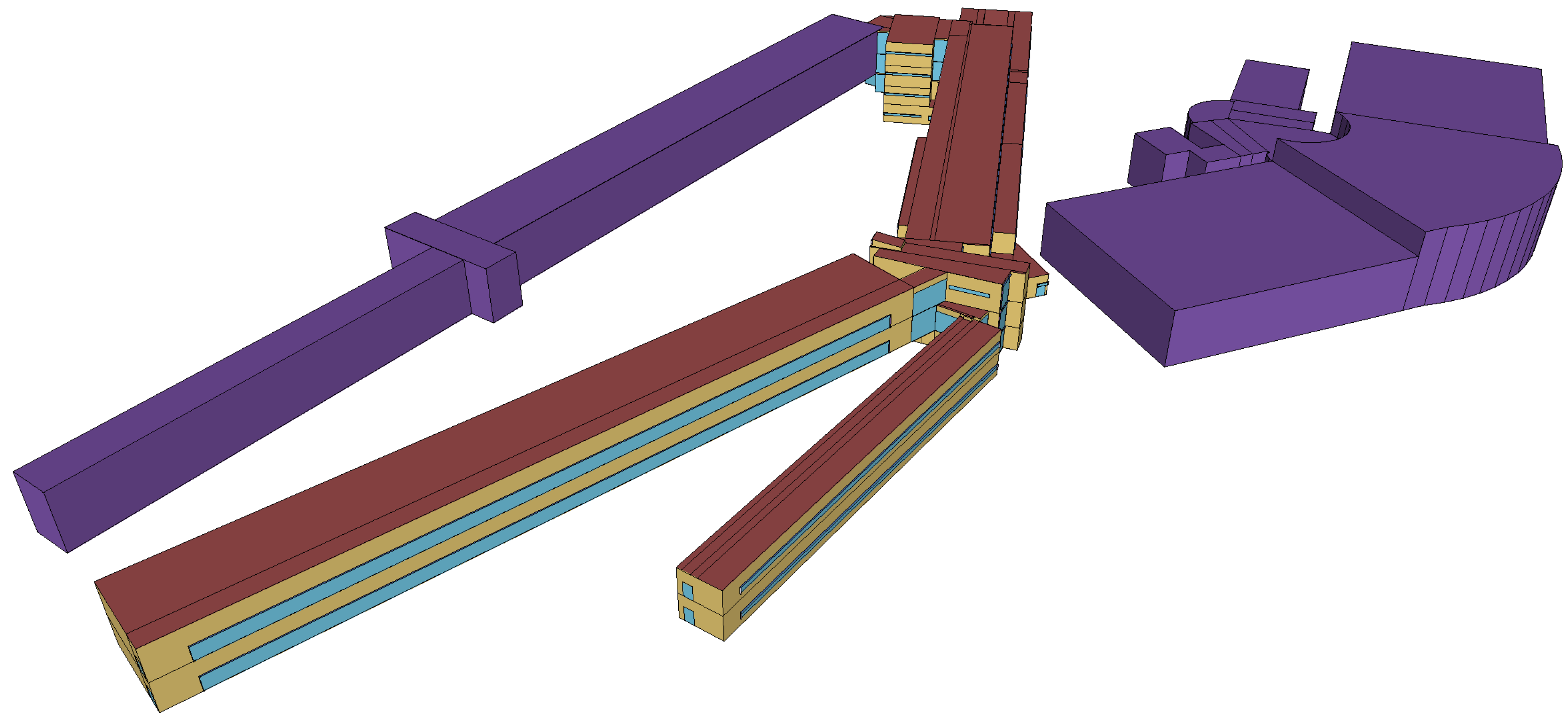
The acquisition of the experimental data took place in two locations at the Mining and Energy Engineering School of the University of Vigo in Spain.
Figure 2 shows the geometry of the BIM model of this building. The two locations used for our tests are displayed in
Figure 3. The first one consists of a corridor of a classroom area with rectangular lamps, while the second one is a hall with circular lamps. Both lamp types are embedded in the ceiling.
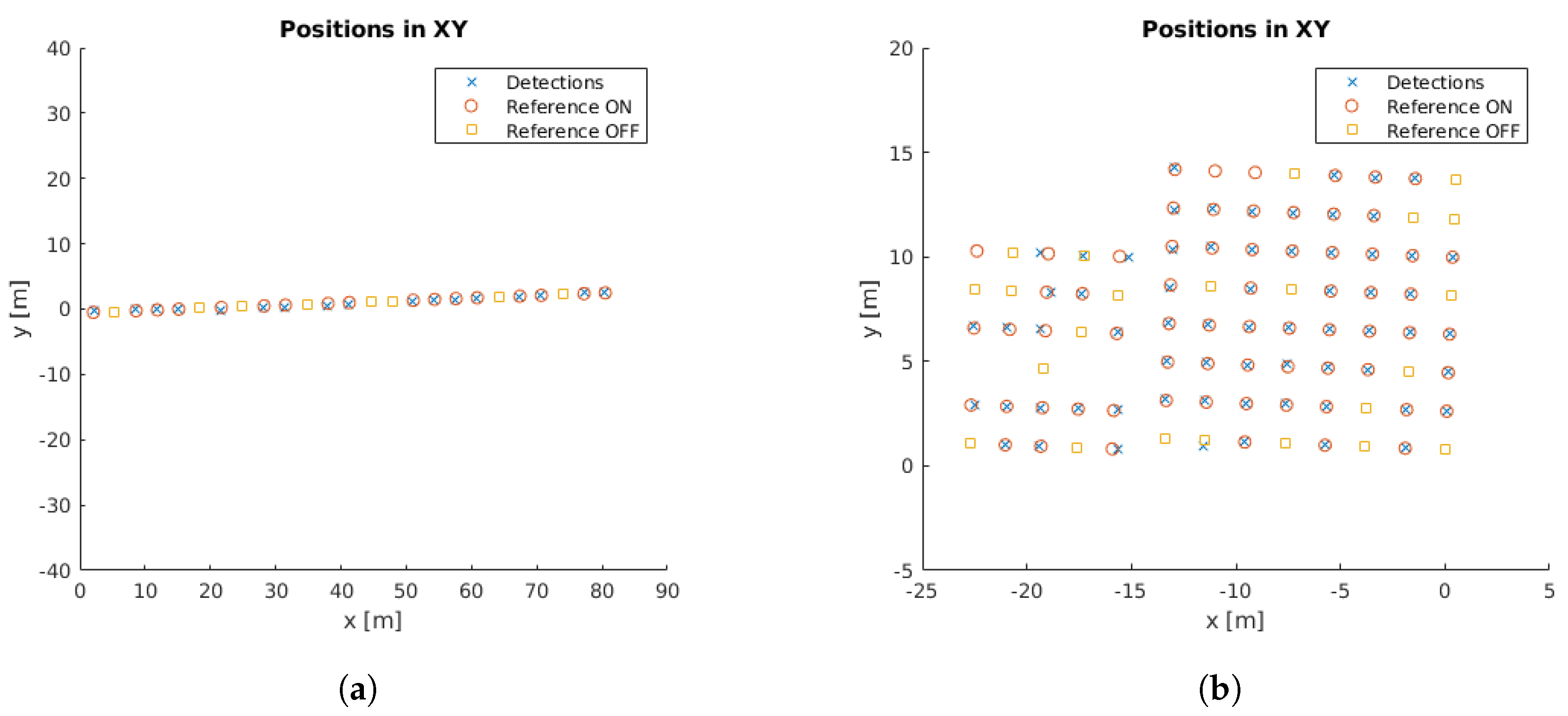
We used point clouds extracted with high-accuracy sensors as the ground truth for our experiments for the position of the lamps. These clouds are shown in
Figure 4. The cloud in
Figure 4a was obtained using a backpack-based inspection system based on LiDAR sensors and inertial measurement unit (IMU), whose data were processed with simultaneous localization and mapping (SLAM) techniques [
38,
39]. The second cloud, in
Figure 4b, was captured with a FARO Focus3D X 330 Laser Scanner from FARO Technologies Inc. (Lake Mary, FL, USA). The technical characteristics of both systems are presented in
Table 1.
We obtained the greyscale images and the location data for the two places using a Lenovo Phab 2 Pro with Google Tango [
40]. The images were extracted at an approximate rate of 30 frames per second and had an original resolution of 1920 × 1080 but were later downscaled to 960 × 540 before the processing to improve the speed of the method. The location data were obtained from the information provided by the IMU of the device combined with the visual features of the environment using advanced computer vision and image processing techniques to improve the accuracy of the motion tracking information [
40]. Some statistics of the complete dataset of images and the two locations used in the experiments are displayed in
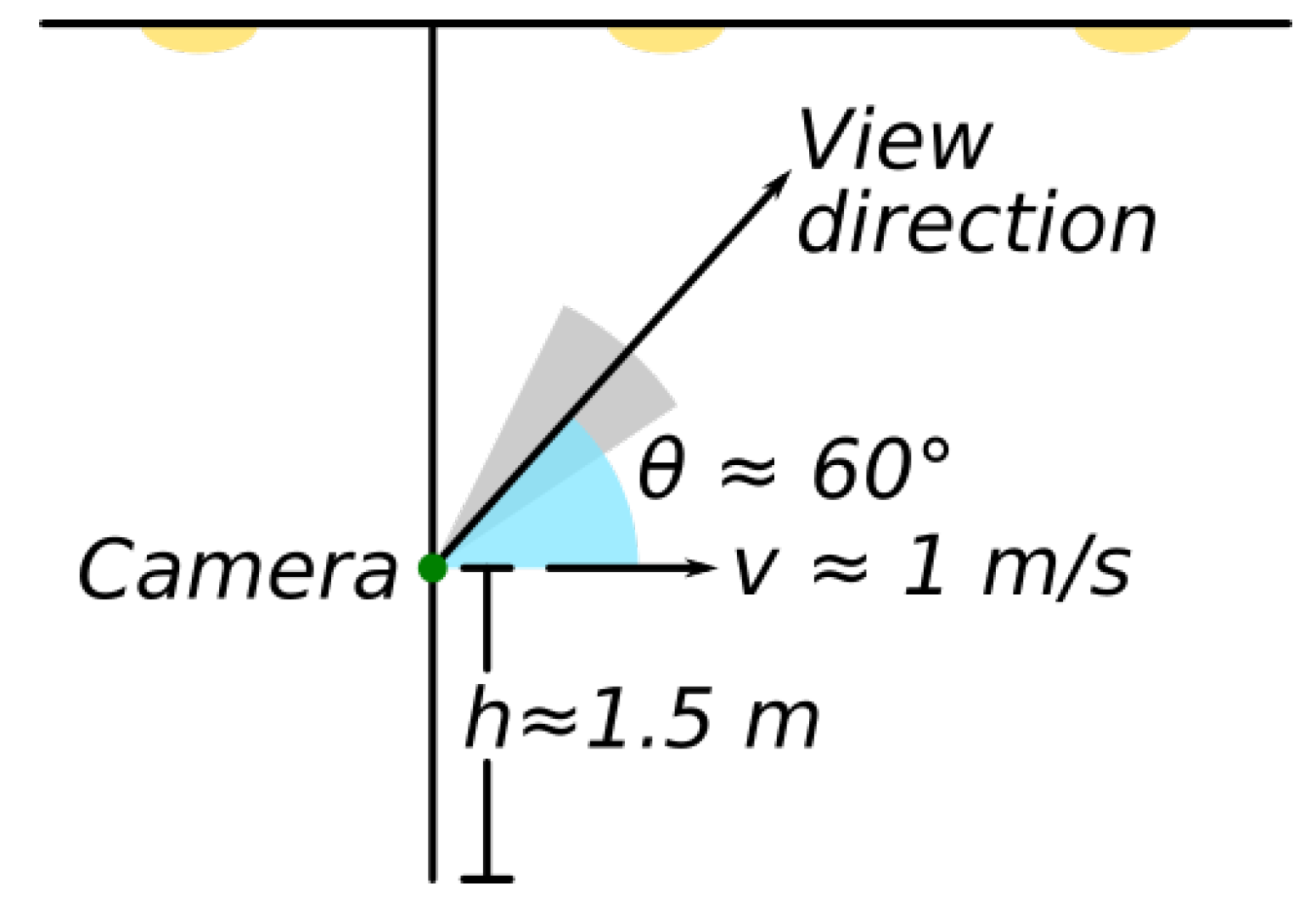
Table 2. The acquisition process, depicted in
Figure 5, was done at a walking speed of ≈1 m/s, positioning the camera at 1.5 m from the floor with a pitch of ≈60
with respect to the horizontal plane.
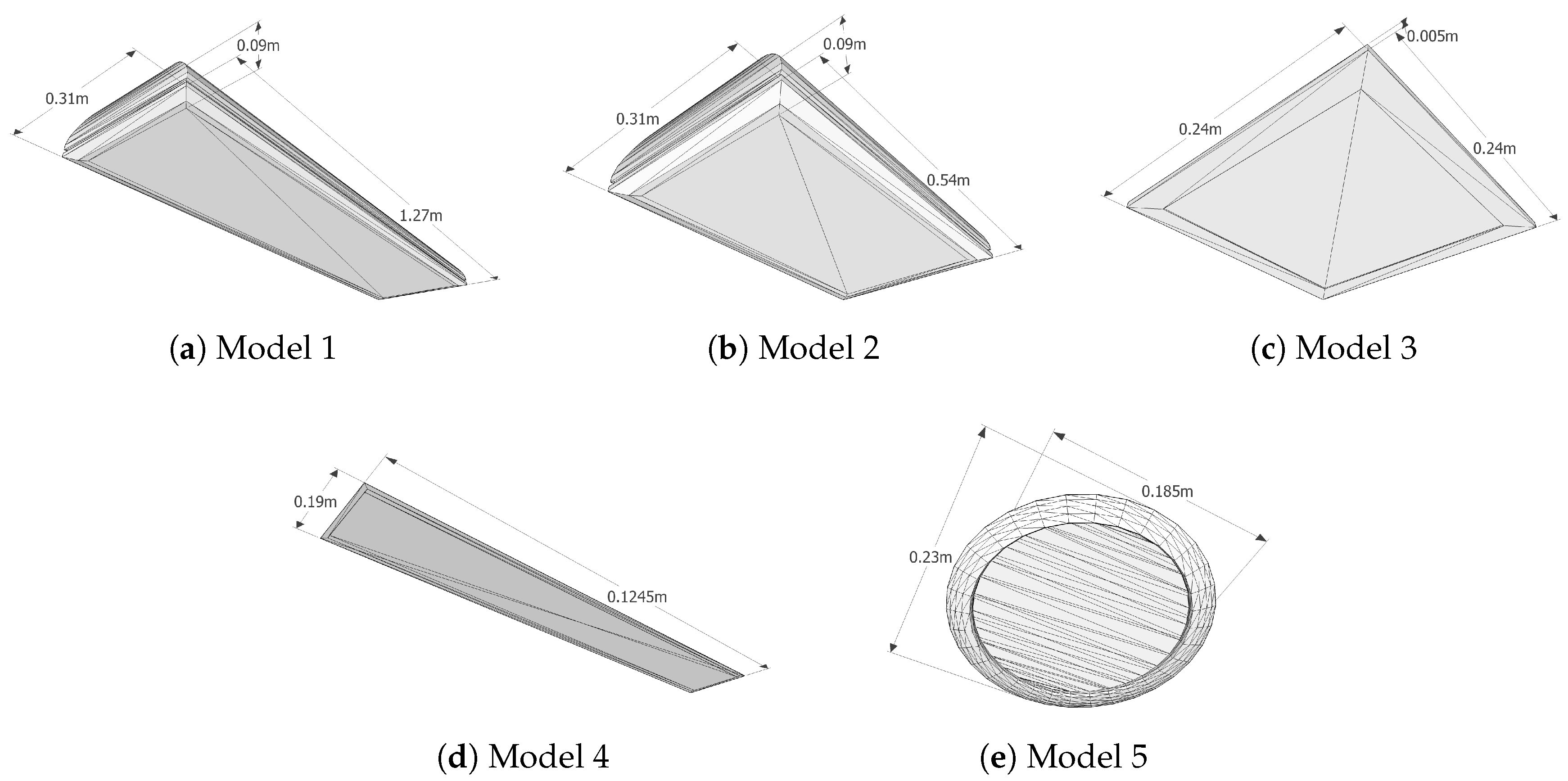
Regarding the 3D models, we added two new items to the ones presented in [
14], corresponding to the lamps found in the locations of the experiments. With this addition, the geometric characteristics of all the elements in the database used for the experiments are shown in
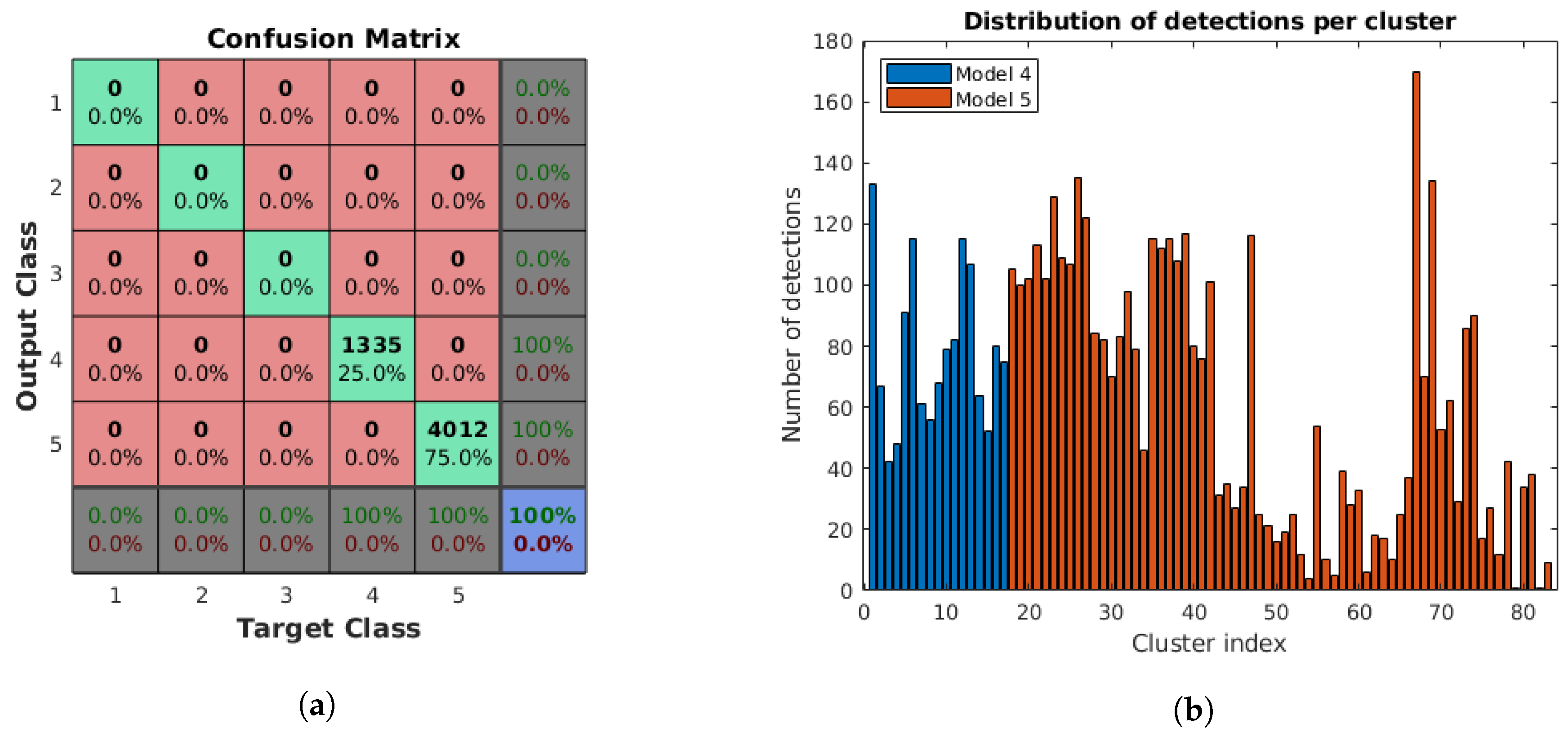
Figure 6, including the two new lamp models (Models 4 and 5). We keep the original three lamps to assess the identification capability of our system with additional models of similar geometries. The specifications of the lamp bulbs for each model are shown in
Table 3.
5. Conclusions
We have presented a complete method for the automatic detection, identification and localization of the lamps to be directly integrated into the BIM of the building. The method is based on our previous work, extending its applicability to a much wider type of lamps and improving the integration method in the BIM. We have applied this method to a completely new case study with different lamp models to assess the performance benefits and the enhanced versatility accomplished with the introduction of the novel contributions.
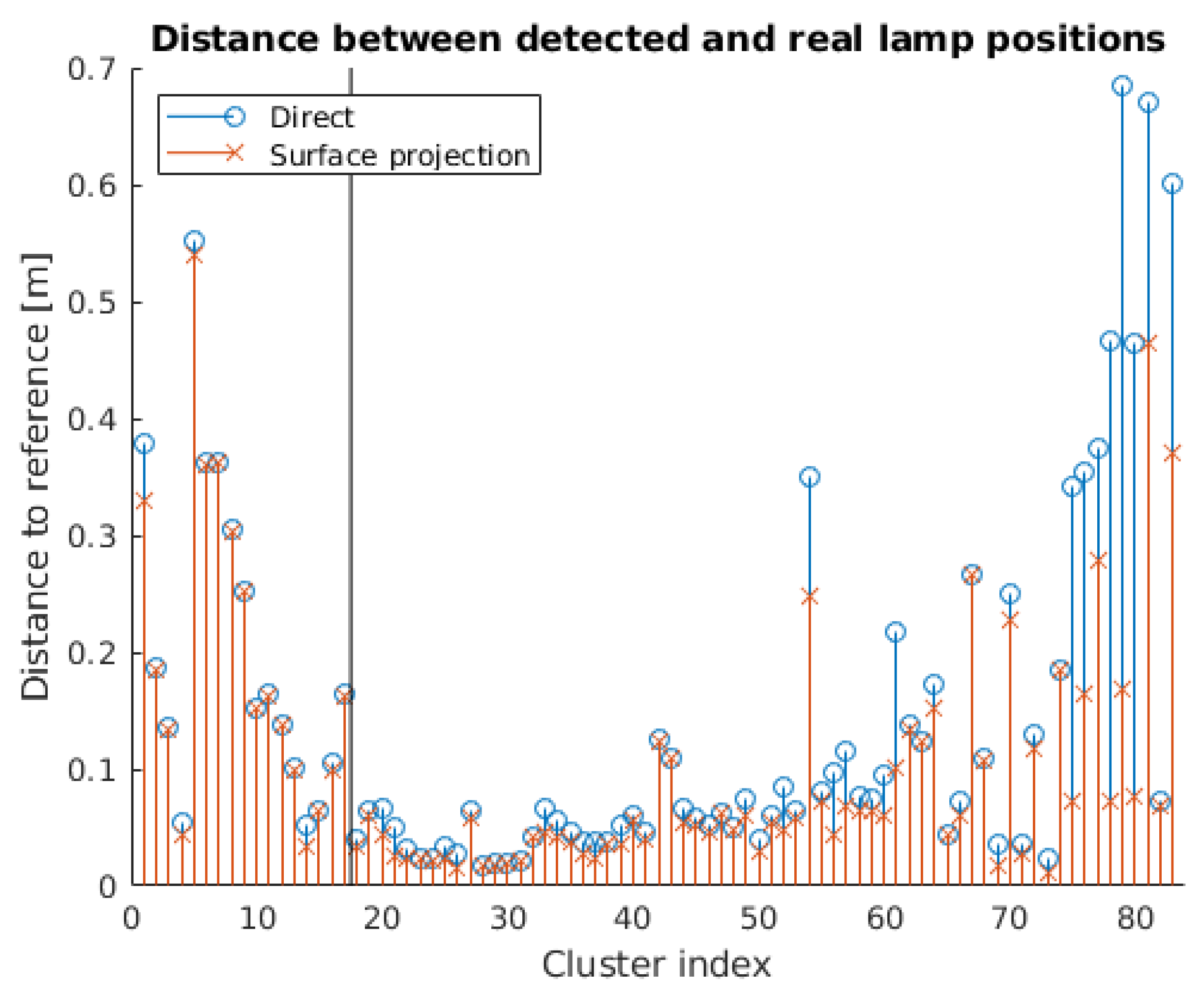
The results show that there is a high percentage of polygonal shapes correctly identified as quadrilaterals, with an EER of 0.003723. Moreover, all 5363 light surface contours in the dataset are accurately classified as either polygonal or elliptical. Finally, the identification of 5347 detections has a 100% success rate, even when three additional models are kept in the database. With respect to the lamp state, there is a high percentage of correct classification, with 95.7% of the lamps assigned to the appropriate state. Additionally, the distance between the detected and actual lamp positions in the building is 14.54 cm on average and is reduced to 10.71 cm if the surface projection step is included, which results in a 26.3% decrease in the location error. Considering all the results obtained in the experiments, we have verified that the method can be applied to the intended use cases and that the new additions lead to better results in terms of the identification and the localization.
Our method relies only on single-image information; thus, a procedure to distinguish lamps with the same shape and different size does not exist. We are working on extensions to our methodology to overcome this limitation by leveraging the combined information of the same detection from different camera views and to also use the available depth information provided by the Tango platform. Moreover, if the BIM information is known beforehand, which can be used in prior steps of the methodology. Therefore, we are working on methods to utilize this information earlier to better adjust the data to the specific model for each of the individual detections and improve the overall accuracy of the results.