Strategy for Determining the Stochastic Distance Characteristics of the 2D Laser Scanner Z + F Profiler 9012A with Special Focus on the Close Range
Abstract
1. Introduction
- This study proposes a new general approach for determining intensity-based stochastic models for 2D laser scanners. This is vital for our investigations because previous research [24,25,26] only addressed 3D laser scanners. Based on the static scanning of surfaces with different backscatter, our approach is beneficial because the 2D laser scanner is operated in its normal measurement mode, no model assumptions for the scanned surface are made and no sophisticated equipment is required. Therefore, the approach can also be applied by end users.
- The approach is used to derive three intensity-based stochastic models for the three scan rates of the Z + F Profiler 9012A. These models describe the precision of the sensor in general. Moreover, the approach is used for investigating the sensor’s behavior in the range of up to 20 m. In this context, the performance of the hardware-based close range optimization of the Z + F Profiler 9012A is analyzed. As a result, an increased noise in the range below 5 m is verified caused by a decreased intensity but not contradicting the general stochastic models. The sensor’s close range optimization partially compensates for this performing best at about 2 m.
2. Methodologies for Quality Assessment of Laser Scanners
3. Characteristics of the 2D Laser Scanner Z + F Profiler 9012A
3.1. Construction of the Z + F Profiler 9012A
3.2. Specifications for the Distance Measurements of the Z + F Profiler 9012A
3.3. Close Range Optimization of the Z + F Profiler 9012A
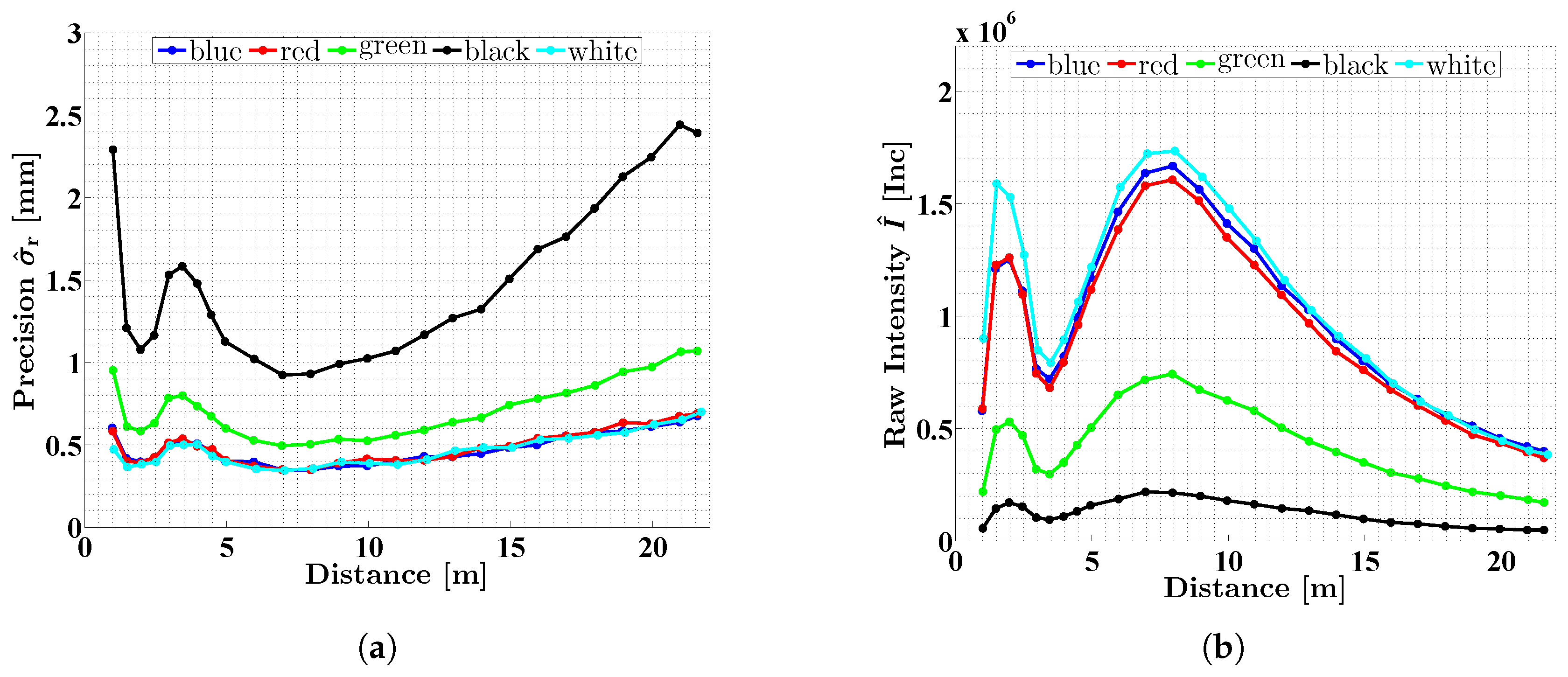
- The focus of the optical receiving unit of the laser scanner is set to infinity, i.e., at medium and larger distances, parallel incident laser light leads to a good optical efficiency resulting in a sufficient signal input power. In contrast, in the close range, divergent incident laser light leads to a defocusing of the received laser spot on the avalanche photodiode (APD). This means that not all of the light received by the optics actually falls on the APD and, thus, is converted into an electrical signal. The intensity maximum at about 8 m arises from the fact that for distances smaller than 8 m more light is lost by the defocusing than is collected by the optical aperture due to the increase by the squared distance.
- The optical receiving unit is constructed as a coaxial system. The received laser beam is coaxially guided around the emitted laser beam. Thus, the aperture for the emitted laser beam is located exactly in the center of the received laser beam. This aperture is like a shadow in the cross section of the received laser beam as seen from the APD. At short distances, this shadow grows larger and at some point covers the APD completely. In Figure 2a, this is indicated by the abrupt drop of the intensity curve for distances smaller than 4.5 m.
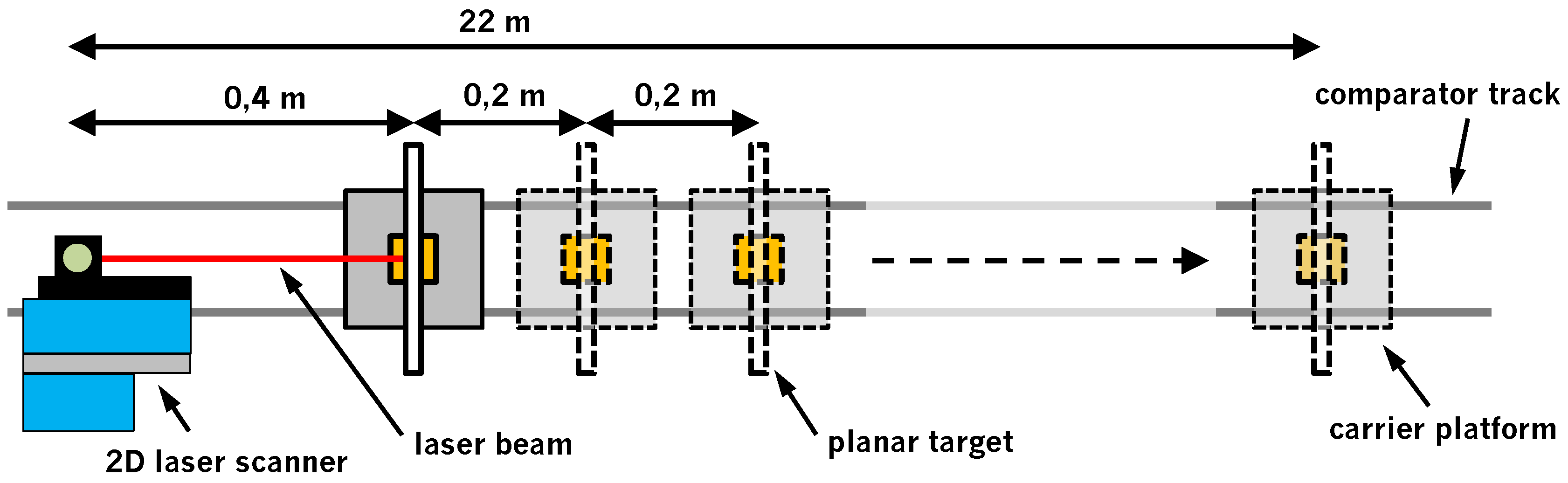
4. Measurement Concept
4.1. Experiments
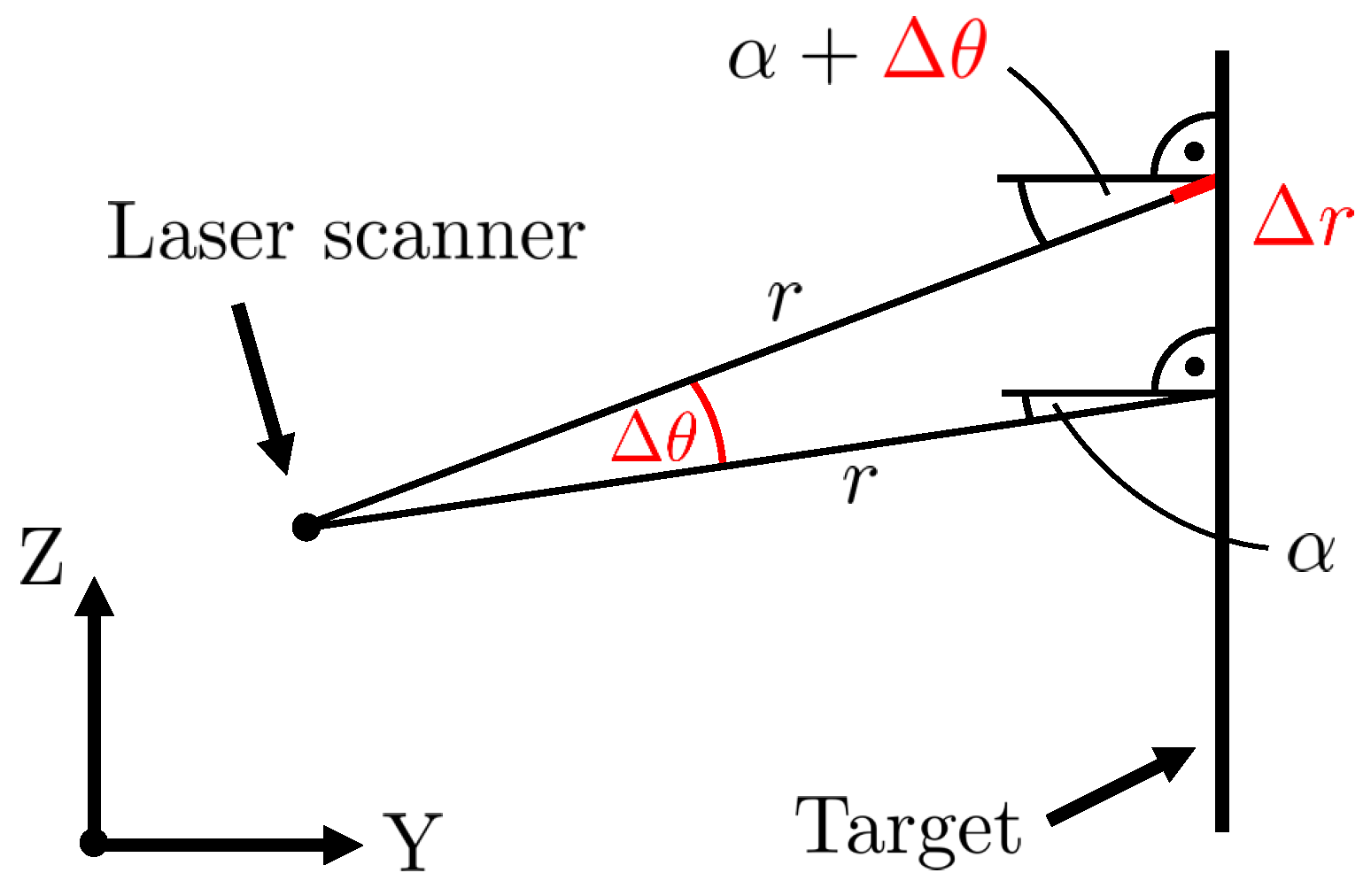
4.2. Impact of Angular Errors on the Experiments
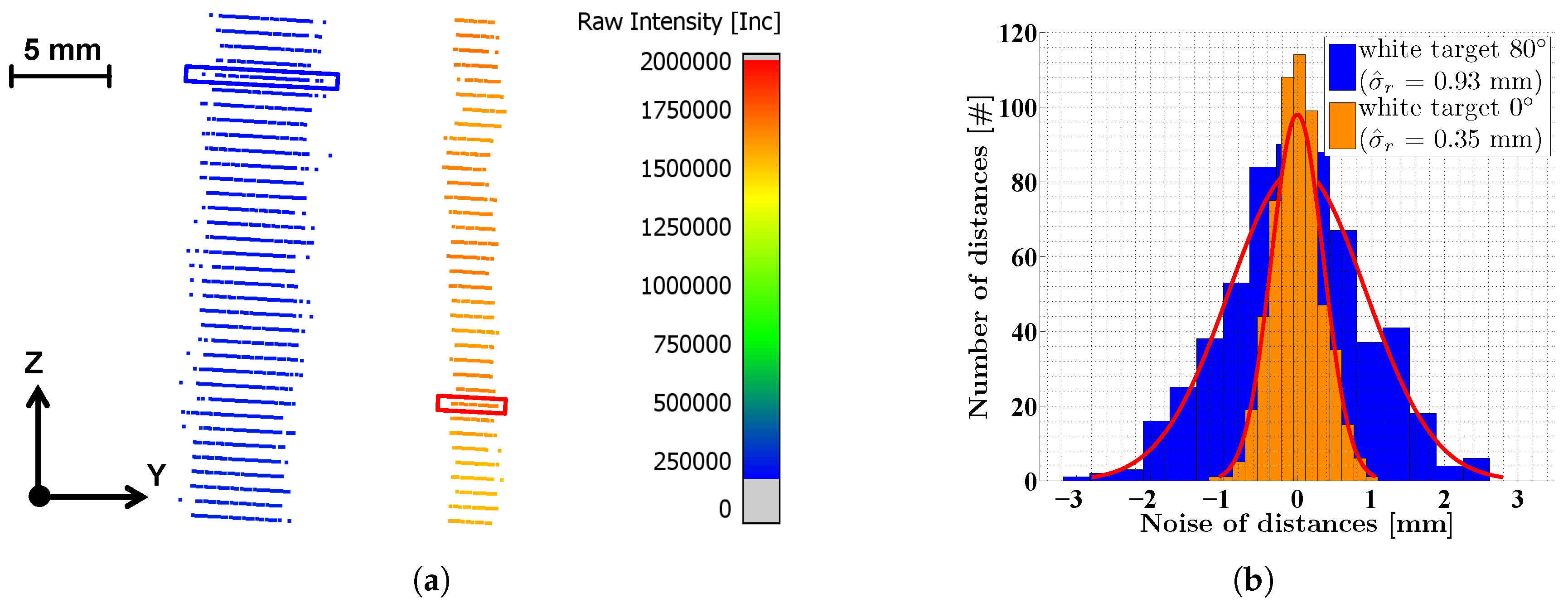
5. Data Analysis
6. Results and Discussion
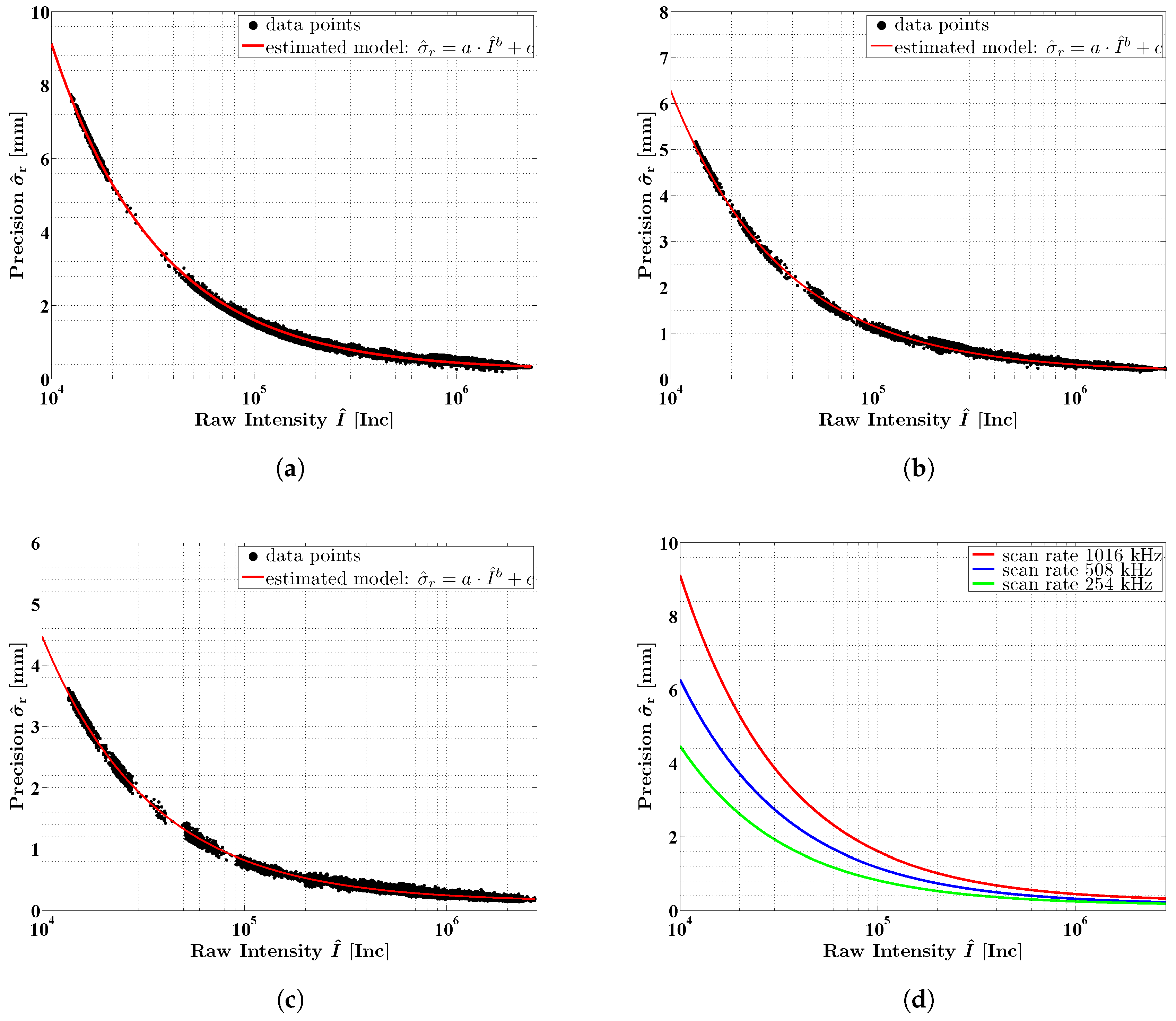
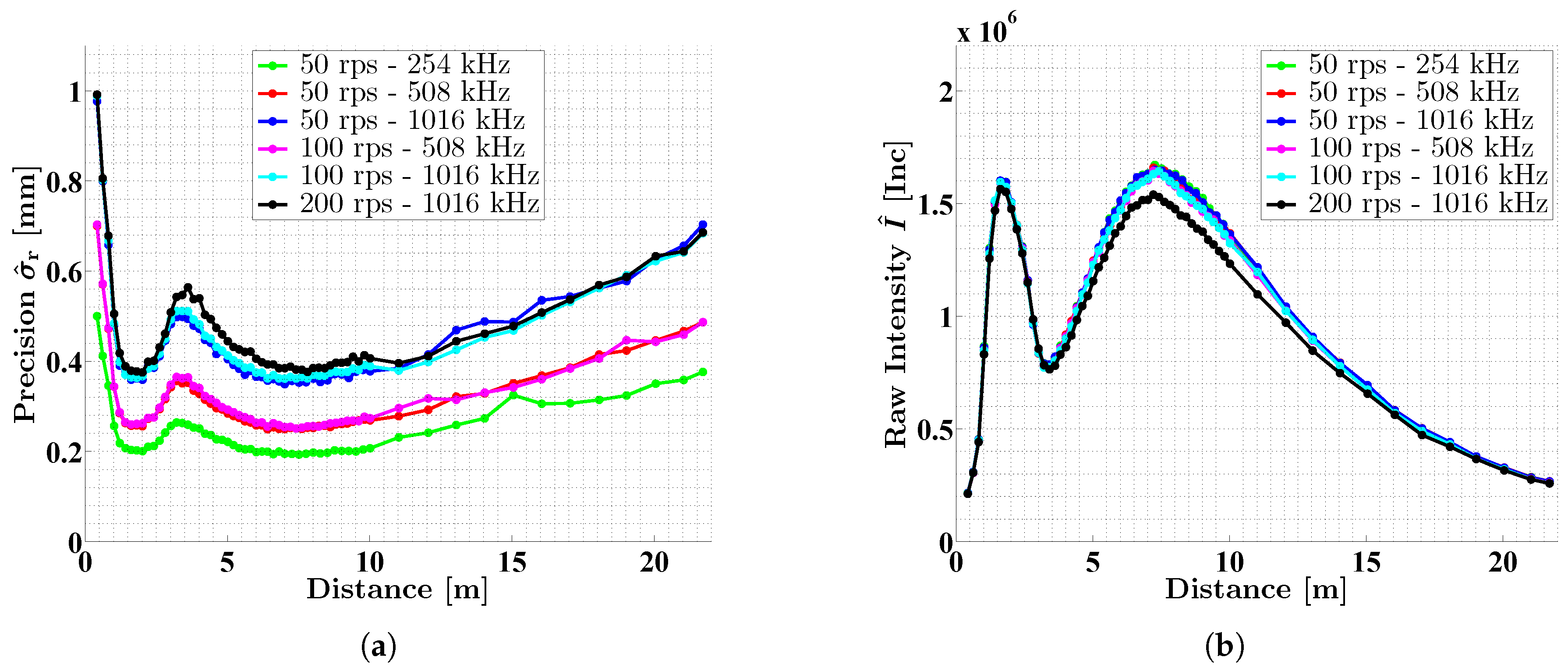
6.1. Determination of Intensity-Based Stochastic Models
6.2. Investigation of the Close Range Optimization
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| APD | Avalanche Photo Diode |
| GNSS | Global Navigation Satellite System |
| IMU | Inertial Measurement Unit |
| kHz | kilohertz |
| rps | rotations per second |
| RTK | Real-Time Kinematic |
| Z + F | Zoller + Fröhlich |
References
- Vosselman, G.; Maas, H.-G. Airborne and Terrestrial Laser Scanning; CRC Press: Boca Raton, FL, USA; Whittles Publishing: Dunbeath, UK, 2010. [Google Scholar]
- Mettenleiter, M.; Härtl, F.; Kresser, S.; Fröhlich, C. Laserscanning—Phasenbasierte Lasermesstechnik für die hochpräzise und schnelle dreidimensionale Umgebungserfassung; Die Bibliothek der Technik, Band 371; Süddeutscher Verlag onpact GmbH: Munich, Germany, 2015. [Google Scholar]
- Kuhlmann, H.; Holst, C. Flächenhafte Abtastung mit Laserscanning: Messtechnik, flächenhafte Modellierungen und aktuelle Entwicklungen im Bereich des terrestrischen Laserscannings. In Handbuch der Geodäsie; Freeden, W., Rummel, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–46. [Google Scholar]
- Riveiro, B.; González-Jorge, H.; Conde, B.; Puente, I. Laser Scanning Technology: Fundamentals, Principles and Applications in Infrastructure. In Non-Destructive Techniques for the Evaluation of Structures and Infrastructure; Riveiro, B., Solla, M., Eds.; CRC Press: Leiden, The Netherlands, 2016; pp. 7–34. [Google Scholar]
- Puente, I.; González-Jorge, H.; Martínez-Sánchez, J.; Arias, P. Review of mobile mapping and surveying technologies. Measurement 2013, 46, 2127–2145. [Google Scholar] [CrossRef]
- Olsen, M.J.; Roe, G.V.; Glennie, C.; Persi, F.; Reedy, M.; Hurwitz, D.; Williams, K.; Tuss, H.; Squellati, A.; Knodler, M. Guidelines for the Use of Mobile LIDAR in Transportation Applications; Technical Report, National Cooperative Highway Research Program (NCHRP) Report 748; National Academy of Sciences: Washington, DC, USA, 2013. [Google Scholar]
- Kuhlmann, H.; Klingbeil, L. Mobile Multisensorsysteme. In Handbuch der Geodäsie; Freeden, W., Rummel, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–36. [Google Scholar]
- Williams, K.; Olsen, M.J.; Gene, V.R.; Glennie, C. Synthesis of Transportation Applications of Mobile LIDAR. Remote Sens. 2013, 5, 4652–4692. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Cao, S.; Yu, Y. Use of mobile LiDAR in road information inventory. Int. J. Image Data Fusion 2016, 7, 219–242. [Google Scholar] [CrossRef]
- Sairam, N.; Nagarajan, S.; Ornitz, S. Development of Mobile Mapping System for 3D Road Asset Inventory. Sensors 2016, 16, 367. [Google Scholar] [CrossRef] [PubMed]
- Haala, N.; Peter, M.; Kremer, J.; Hunter, G. Mobile LIDAR mapping for 3D point cloud collection in urban areas—A performance test. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1119–1127. [Google Scholar]
- Reiterer, A.; Dambacher, M.; Maindorfer, I.; Höfler, H.; Ebersbach, D.; Frey, C.; Scheller, S.; Klose, D. Straßentzustandsüberwachung in Submillimeter. In Photogrammetrie Laserscanning Optische 3D-Messtechnik, Beiträge der Oldenburger 3D-Tage; Luhmann, T., Müller, C., Eds.; Wichmann Verlag: Berlin, Germany; Offenbach, Germany, 2013; pp. 78–85. [Google Scholar]
- Gräfe, G. High precision kinematic surveying with laser scanners. J. Appl. Geod. 2007, 1, 185–199. [Google Scholar] [CrossRef]
- Hesse, C.; Weltzien, K.; Stromhardt, A. Hochpräzises Mobile Mapping im Ingenieur- und Verkehrswegebau. In Schriftenreihe des DVW e.V., Band 85, Terrestrisches Laserscanning 2016 (TLS 2016); Wißner Verlag: Augsburg, Germany, 2016; pp. 131–143. [Google Scholar]
- Kremer, J.; Grimm, A. A Dedicated Mobile LIDAR Mapping System For Railway Networks. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, XXII ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012; Volume XXXIX-B5. [Google Scholar]
- Mikrut, S.; Kohut, P.; Pyka, K.; Tokarczyk, R.; Barszcz, T.; Uhl, T. Mobile Laser Scanning Systems for Measuring the Clearance Gauge of Railways: State of Play, Testing and Outlook. Sensors 2016, 16, 683. [Google Scholar] [CrossRef] [PubMed]
- Schauer, J.; Nüchter, A. Efficient Point Cloud Collision Detection and Analysis in a Tunnel Environment Using Kinematic Laser Scanning and k-D Tree Search. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, ISPRS Technical Commission III Symposium, Zurich, Switzerland, 5–7 September 2014; Volume XL-3. [Google Scholar]
- Keller, F.; Sternberg, H. Multi-Sensor Platform for Indoor Mobile Mapping: System Calibration and Using a Total Station for Indoor Applications. Remote Sens. 2013, 5, 5805–5824. [Google Scholar] [CrossRef]
- Hartmann, J.; Paffenholz, J.-A.; Strübing, T.; Neumann, I. Determination of Position and Orientation of LiDAR Sensors on Multisensor Platforms. J. Surv. Eng. 2017, 143, 04017012. [Google Scholar] [CrossRef]
- Nüchter, A.; Borrmann, D.; Elseberg, J.; Redondo, D. A Backpack-mounted 3D Mobile Scanning System. Allg. Vermess.-Nachr. (AVN) 2015, 122, 301–307. [Google Scholar]
- Lehtola, V.V.; Kaartinen, H.; Nüchter, A.; Kaijaluoto, R.; Kukko, A.; Litkey, P.; Honkavaara, E.; Rosnell, T.; Vaaja, M.T.; Virtanen, J.-P.; et al. Comparison of the Selected State-Of-The-Art 3D Indoor Scanning and Point Cloud Generation Methods. Remote Sens. 2017, 9, 796. [Google Scholar] [CrossRef]
- Klingbeil, L.; Lottes, P.; Kuhlmann, H. Laserscanning-Technologie auf sich bewegenden Plattformen. In Schriftenreihe des DVW e.V., Band 78, Terrestrisches Laserscanning 2014 (TLS 2014); Wißner Verlag: Augsburg, Germany, 2014; pp. 19–29. [Google Scholar]
- Pfeifer, N.; Höfle, B.; Briese, C.; Rutzinger, M.; Haring, A. Analysis of the Backscattered Energy in Terrestrial Laser Scanning Data. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences (Part B5), Beijing, China, 3–11 July 2008; Volume XXXVII, pp. 1045–1052. [Google Scholar]
- Wujanz, D.; Burger, M.; Mettenleiter, M.; Neitzel, F. An intensity-based stochastic model for terrestrial laser scanners. ISPRS J. Photogramm. Remote Sens. 2017, 125, 146–155. [Google Scholar] [CrossRef]
- Wujanz, D.; Burger, M.; Tschirschwitz, F.; Nietzschmann, T.; Neitzel, F.; Kersten, T. Bestimmung von intensitätsbasierten stochastischen Modellen für terrestrische Laserscanner basierend auf 3D-Punktwolken. In Photogrammetrie Laserscanning Optische 3D-Messtechnik—Beiträge der Oldenburger 3D-Tage; Luhmann, T., Schumacher, C., Eds.; Wichmann Verlag: Berlin, Germany; Offenbach, Germany, 2018; pp. 155–166. [Google Scholar]
- Lambertus, T.; Belton, D.; Helmholz, P. Empirical Investigation of a Stochastic Model Based on Intensity Values for Terrestrial Laser Scanning. Allg. Vermess.-Nachr. (AVN) 2018, 125, 43–52. [Google Scholar]
- Zoller & Fröhlich GmbH. Z + F Profiler 9012A, 2D Laser Scanner. 2018. Available online: http://www.zf-laser.com (accessed on 26 February 2018).
- Soudarissanane, S.; Lindenbergh, R.; Menenti, M.; Teunissen, P. Scanning geometry: Influencing factor on the quality of terrestrial laser scanning points. ISPRS J. Photogramm. Remote Sens. 2011, 66, 389–399. [Google Scholar] [CrossRef]
- Soudarissanane, S. The Geometry of Terrestrial Laser Scanning—Identification of Errors, Modeling and Mitigation of Scanning Geometry. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Holst, C.; Neuner, H.; Wieser, A.; Wunderlich, T.; Kuhlmann, H. Calibration of Terrestrial Laser Scanners. Allg. Vermess.-Nachr. (AVN) 2016, 123, 147–157. [Google Scholar]
- Böhler, W.; Bordas, M.; Marbs, A. Investigating Laser Scanner Accuracy. In Proceedings of the XIXth CIPA Symposium, Antalya, Turkey, 30 September–4 October 2003. [Google Scholar]
- Zámečníková, M.; Wieser, A.; Woschitz, H.; Ressl, C. Influence of surface reflectivity on reflectorless electronic distance measurements and terrestrial laser scanning. J. Appl. Geod. 2014, 8, 311–325. [Google Scholar] [CrossRef]
- Lindstaedt, M.; Kersten, T.; Mechelke, K.; Graeger, T. Prüfverfahren für terrestrische Laserscanner—Gemeinsame geometrische Genauigkeitsuntersuchungen verschiedener Laserscanner an der HCU Hamburg. In Photogrammetrie Laserscanning Optische 3D-Messtechnik—Beiträge der Oldenburger 3D-Tage; Luhmann, T., Müller, C., Eds.; Wichmann Verlag: Berlin, Germany; Offenbach, Germany, 2012; pp. 264–275. [Google Scholar]
- Zámečníková, M.; Neuner, H.; Pegritz, S.; Sonnleiter, R. Investigation on the influence of the incidence angle on the reflectorless distance measurement of a terrestrial laser scanner. Österr. Z. Vermess. Geoinf. (VGI) 2015, 103, 208–218. [Google Scholar]
- Wunderlich, T.; Wasmeier, P.; Ohlmann-Lauber, J.; Schäfer, T.; Reidl, F. Objective Specifications of Terrestrial Laserscanners—A Contribution of the Geodetic Laboratory at the Technische Universität München; Technical Report; Blue Series Books at the Chair of Geodesy; Technische Universität München: Munich, Germany, 2013; Volume 21. [Google Scholar]
- Neitzel, F.; Gordon, B.; Wujanz, D. Verfahren zur standardisierten Überprüfung von terrestrischen Laserscannern. Technical Report, DVW-Merkblatt 7-2014. 2014. Available online: www.dvw.de/merkblatt (accessed on 2 March 2018).
- Rivera-Castillo, J.; Flores-Fuentes, W.; Rivas-López, M.; Sergiyenko, O.; Gonzalez-Navarro, F.F.; Rodríguez-Quiñonez, J.C.; Hernández-Balbuena, D.; Lindner, L.; Básaca-Preciado, L.C. Experimental image and range scanner datasets fusion in SHM for displacement detection. Struct. Control Health Monit. 2017, 24, e1967. [Google Scholar] [CrossRef]
- Stenz, U.; Hartmann, J.; Paffenholz, J.-A.; Neumann, I. A Framework Based on Reference Data with Superordinate Accuracy for the Quality Analysis of Terrestrial Laser Scanning-Based Multi-Sensor-Systems. Sensors 2017, 17, 1886. [Google Scholar] [CrossRef] [PubMed]
- Voegtle, T.; Schwab, I.; Landes, T. Influences of Different Materials on the Measurements of a Terrestrial Laser Scanner (TLS). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1061–1066. [Google Scholar]
- Bolkas, D.; Martinez, A. Effect of target color and scanning geometry on terrestrial LiDAR point-cloud noise and plane fitting. J. Appl. Geod. 2018, 12, 109–127. [Google Scholar] [CrossRef]
- Kurz, S.; Blersch, D.; Held, C.; Mettenleiter, M.; Fröhlich, C. Neues profilgebendes 360∘-Laserscansystem von Z + F für Mobile Mapping Trägerplattformen. In Photogrammetrie Laserscanning Optische 3D-Messtechnik—Beiträge der Oldenburger 3D-Tage; Luhmann, T., Müller, C., Eds.; Wichmann Verlag: Berlin, Germany; Offenbach, Germany, 2013; pp. 194–205. [Google Scholar]
- Rodríguez-Quiñonez, J.C.; Sergiyenko, O.Y.; Básaca-Preciado, L.C.; Tyrsa, V.V.; Gurko, A.G.; Podrygalo, M.A.; Rivas-López, M.; Hernández-Balbuena, D. Optical monitoring of scoliosis by 3D medical laser scanner. Opt. Lasers Eng. 2014, 54, 175–186. [Google Scholar] [CrossRef]
- Heinz, E.; Eling, C.; Wieland, M.; Klingbeil, L.; Kuhlmann, H. Development, Calibration and Evaluation of a Portable and Direct Georeferenced Laser Scanning System for Kinematic 3D Mapping. J. Appl. Geod. 2015, 9, 227–243. [Google Scholar] [CrossRef]
- Mandlburger, G. Interaction of Laser Pulses with the Water Surface—Theoretical Aspects and Experimental Results. Allg. Vermess.-Nachr. (AVN) 2017, 124, 343–352. [Google Scholar]
- Heinz, E.; Eling, C.; Wieland, M.; Klingbeil, L.; Kuhlmann, H. Analysis of different reference plane setups for the calibration of a mobile laser scanning system. In Ingenieurvermessung 17, Beiträge zum 18. Internationalen Ingenieurvermessungskurs, Graz, Austria; Lienhart, W., Ed.; Wichmann Verlag: Berlin, Germany, 2017; pp. 131–145. [Google Scholar]
- IMAR Navigation GmbH. Inertial Navigation System iNAV-FJI-LSURV. 2016. Available online: http://www.imar.de/index.php/en/products/by-product-names (accessed on 23 December 2016).
- Förstner, W.; Wrobel, B. Photogrammetric Computer Vision—Statistics, Geometry, Orientation and Reconstruction; Springer: Berlin, Germany, 2016. [Google Scholar]
- Mikhail, E.M.; Ackermann, F.E. Observations and Least Squares; Dun-Donnelley Pub: New York, NY, USA, 1976. [Google Scholar]
- Niemeier, W. Ausgleichungsrechnung—Statistische Auswertemethoden (2. Auflage); de Gruyter Verlag: Berlin, Germany; New York, NY, USA, 2008. [Google Scholar]
- Schabenberger, O.; Gotway, C.A. Statistical Methods for Spatial Data Analysis; Chapman & Hall/CRC: Boca Raton, FL, USA; London, UK; New York, NY, USA; Washington, DC, USA, 2005. [Google Scholar]




| Mirror Speed | 200 rps | 100 rps | 50 rps |
|---|---|---|---|
| Points/360 | Scan rate/Noise factor | Scan rate/Noise factor | Scan rate/Noise factor |
| 20,480 | — | — | 1016 kHz/× 2.8 |
| 10,240 | — | 1016 kHz/× 2.8 | 508 kHz/× 2.0 |
| 5120 | 1016 kHz/× 2.8 | 508 kHz/× 2.0 | 254 kHz/× 1.4 |
| Distance Noise | Z + F Profiler 9012 | 9012A | Z + F Profiler 9012 | 9012A | Z + F Profiler 9012 | 9012A |
|---|---|---|---|
| Target Distance | White (80 %) | Grey (37 %) | Black (14 %) |
| 1 @ 0.5 m | 0.5 mm | 0.5 mm | 0.8 mm | 0.8 mm | 1.3 mm | 1.3 mm |
| 1 @ 1 m | 0.5 mm | 0.3 mm | 0.6 mm | 0.4 mm | 1.0 mm | 0.8 mm |
| 1 @ 2 m | 0.3 mm | 0.2 mm | 0.5 mm | 0.3 mm | 0.8 mm | 0.4 mm |
| 1 @ 5 m | 0.3 mm | 0.2 mm | 0.4 mm | 0.3 mm | 0.6 mm | 0.5 mm |
| 1 @ 10 m | 0.2 mm | 0.2 mm | 0.3 mm | 0.3 mm | 0.5 mm | 0.5 mm |
| 1 @ 25 m | 0.4 mm | 0.4 mm | 0.6 mm | 0.6 mm | 1.1 mm | 1.1 mm |
| 1 @ 50 m | 0.9 mm | 0.9 mm | 1.4 mm | 1.4 mm | 3.1 mm | 3.1 mm |
| Scan Rate | Mirror Speed | Experiments | Pairs / |
|---|---|---|---|
| 254 kHz (= 254,000 points/s) | 50 rps | 1, 4 | # 47969 |
| 508 kHz (= 508,000 points/s) | 50 rps, 100 rps | 1, 4 | # 81484 |
| 1016 kHz (= 1,016,000 points/s) | 50 rps, 100 rps, 200 rps | 1, 2, 3 | # 141858 |
| Scan Rate | ||||||
|---|---|---|---|---|---|---|
| 254 kHz | 7.09896 | 0.03902736 | −0.80377 | 0.00055374 | 0.00014 | 0.00000030 |
| 508 kHz | 8.21610 | 0.02611121 | −0.78192 | 0.00031518 | 0.00015 | 0.00000026 |
| 1016 kHz | 15.67256 | 0.03579010 | −0.81170 | 0.00022396 | 0.00024 | 0.00000024 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heinz, E.; Mettenleiter, M.; Kuhlmann, H.; Holst, C. Strategy for Determining the Stochastic Distance Characteristics of the 2D Laser Scanner Z + F Profiler 9012A with Special Focus on the Close Range. Sensors 2018, 18, 2253. https://doi.org/10.3390/s18072253
Heinz E, Mettenleiter M, Kuhlmann H, Holst C. Strategy for Determining the Stochastic Distance Characteristics of the 2D Laser Scanner Z + F Profiler 9012A with Special Focus on the Close Range. Sensors. 2018; 18(7):2253. https://doi.org/10.3390/s18072253
Chicago/Turabian StyleHeinz, Erik, Markus Mettenleiter, Heiner Kuhlmann, and Christoph Holst. 2018. "Strategy for Determining the Stochastic Distance Characteristics of the 2D Laser Scanner Z + F Profiler 9012A with Special Focus on the Close Range" Sensors 18, no. 7: 2253. https://doi.org/10.3390/s18072253
APA StyleHeinz, E., Mettenleiter, M., Kuhlmann, H., & Holst, C. (2018). Strategy for Determining the Stochastic Distance Characteristics of the 2D Laser Scanner Z + F Profiler 9012A with Special Focus on the Close Range. Sensors, 18(7), 2253. https://doi.org/10.3390/s18072253






