Wide-Band Color Imagery Restoration for RGB-NIR Single Sensor Images
Abstract
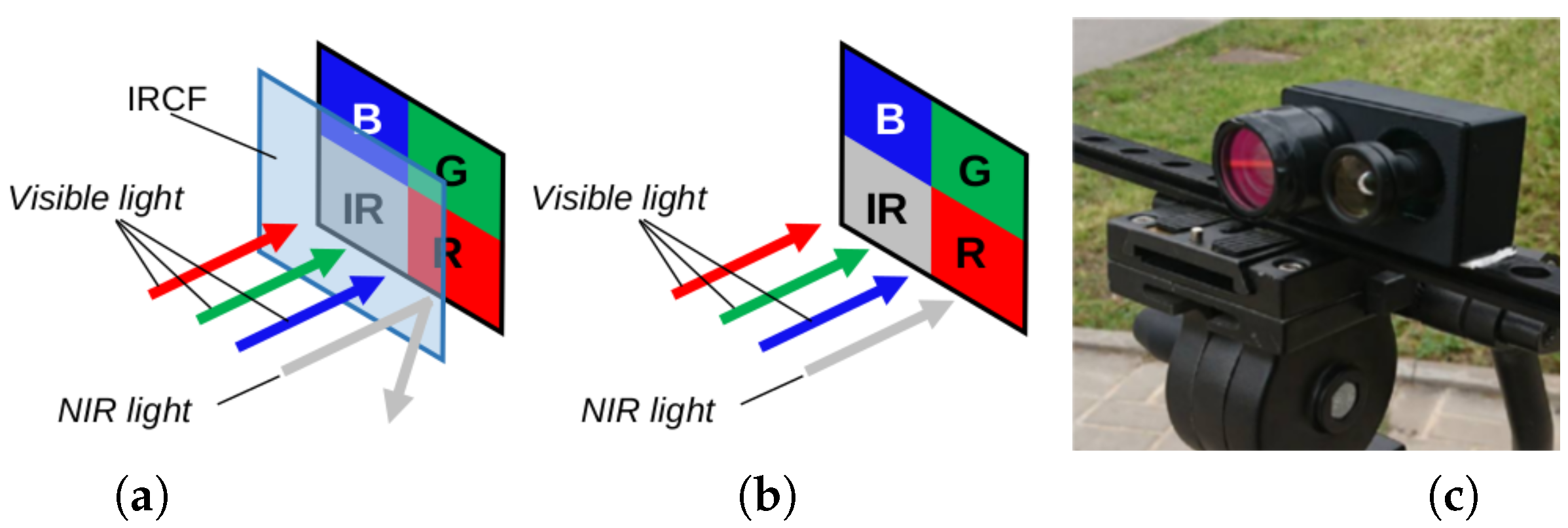
1. Introduction
- To propose two custom CNN architectures to generate RGB images from their corresponding RGB+N data. The codes of these fully trained networks are available through https://github.com/xavysp/color_restorer.
2. Related Works
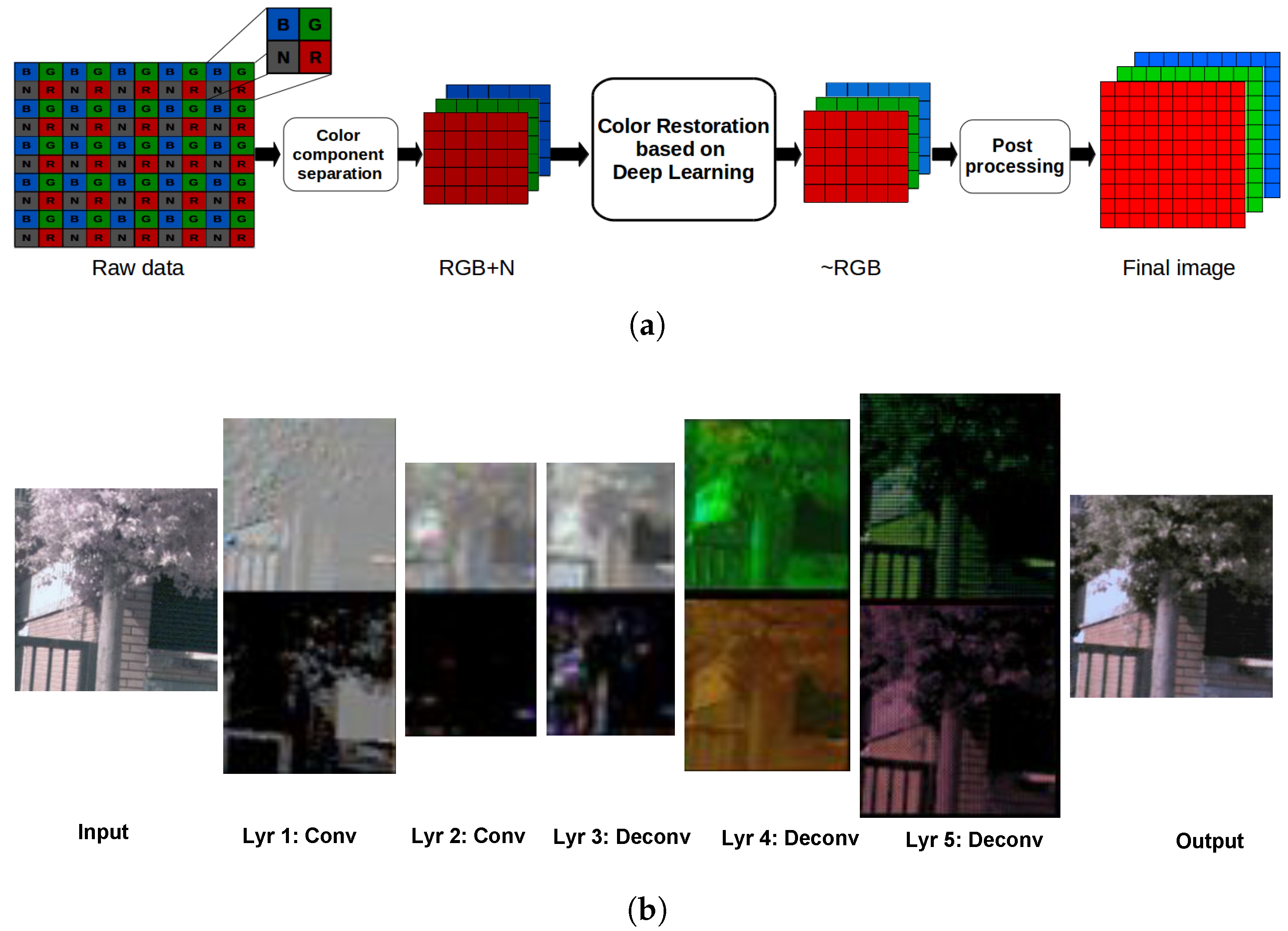
3. Proposed Approach
3.1. Convolutional Neural Networks
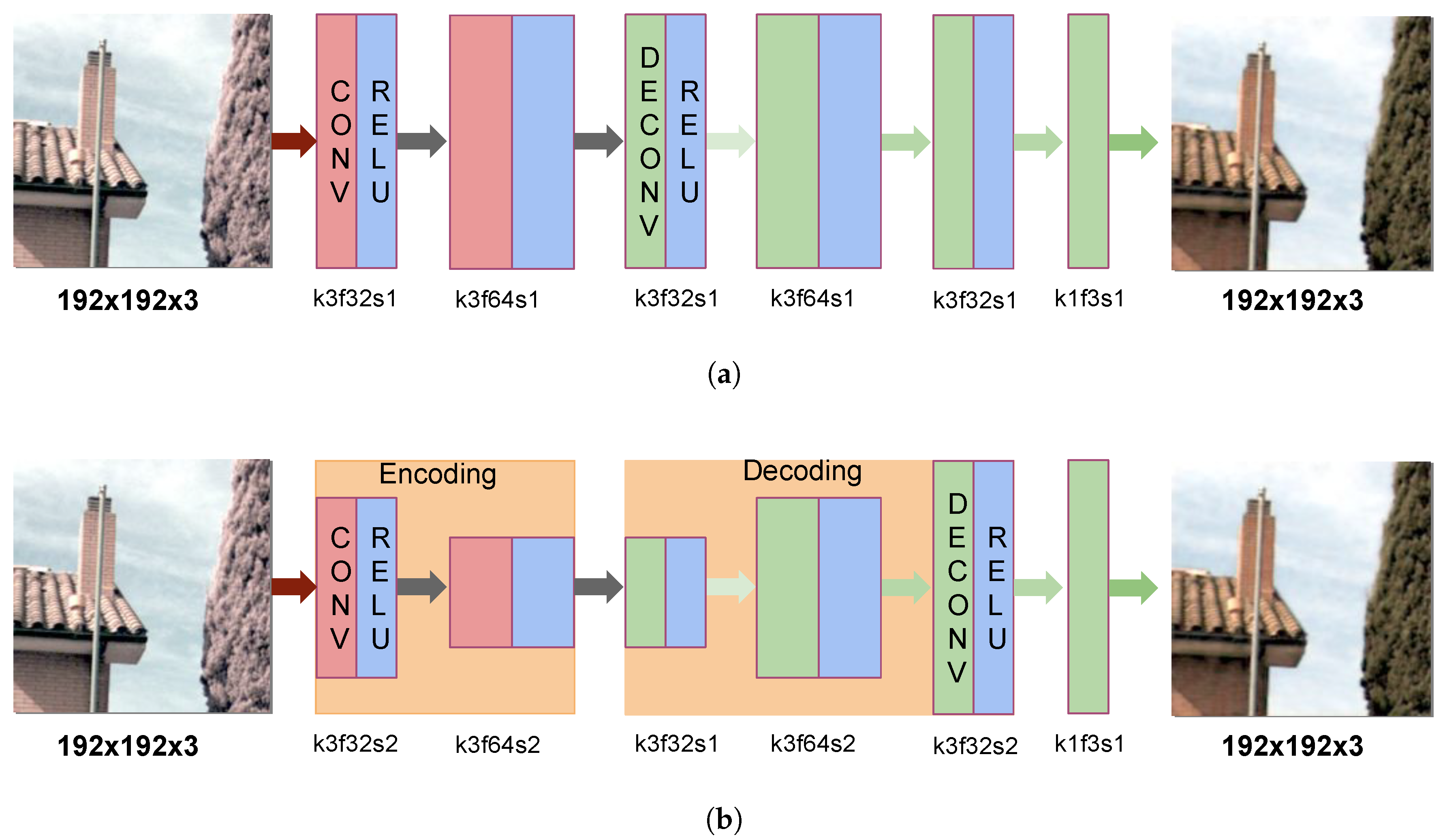
3.2. Proposed Restoration Architectures
4. Experimental Results
4.1. System Setup
4.2. Image Similarity Quantitative Evaluation
4.3. Results and Comparisons
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Moeslund, T.B. Introduction to Video and Image Processing: Building Real Systems and Applications; Springer: Berlin, Germany, 2012; pp. 7–21. [Google Scholar]
- Monno, Y.; Kiku, D.; Kikuchi, S.; Tanaka, M.; Okutomi, M. Multispectral Demosaicking with Novel Guide Image Generation and Residual Interpolation. In Proceedings of the IEEE International Conference on Image Processing, Paris, France, 27–30 October 2014; pp. 645–649. [Google Scholar]
- Dahl, R.; Norouzi, M.; Shlens, J. Pixel Recursive Super Resolution. arXiv, 2017; arXiv:1702.00783. [Google Scholar]
- Sadeghipoor, Z.; Thomas, J.B.; Süsstrunk, S. Demultiplexing Visible and Near-infrared Information in Single-sensor Multispectral Imaging. In Proceedings of the Color and Imaging Conference, San Diego, CA, USA, 7–11 November 2016; pp. 76–81. [Google Scholar]
- Salamati, N.; Fredembach, C.; Süsstrunk, S. Material Classification Using Color and NIR Images. In Proceedings of the Color and Imaging Conference, Albuquerque, NM, USA, 9–13 November 2009; pp. 216–222. [Google Scholar]
- Ricaurte, P.; Chilán, C.; Aguilera-Carrasco, C.A.; Vintimilla, B.X.; Sappa, A.D. Feature Point Descriptors: Infrared and Visible Spectra. Sensors 2014, 14, 3690–3701. [Google Scholar] [CrossRef] [PubMed]
- Barrera, F.; Lumbreras, F.; Sappa, A.D. Evaluation of Similarity Functions in Multimodal Stereo. In Proceedings of the International Conference Image Analysis and Recognition, Aveiro, Portugal, 25–27 June 2012; pp. 320–329. [Google Scholar]
- Mouats, T.; Aouf, N.; Sappa, A.D.; Aguilera, C.; Toledo, R. Multispectral Stereo Odometry. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1210–1224. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support Vector Machines in Remote Sensing: A Review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Rugege, D. Multispectral and Hyperspectral Remote Sensing for Identification and Mapping of Wetland Vegetation: A Review. Wetl. Ecol. Manag. 2010, 18, 281–296. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Liang, R. RGB-NIR Multispectral Camera. Opt. Express 2014, 22, 4985–4994. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zhu, N.; Pacheco, S.; Wang, X.; Liang, R. Single Camera Imaging System for Color and Near-Infrared Fluorescence Image Guided Surgery. Biomed. Opt. Express 2014, 5, 2791–2797. [Google Scholar] [CrossRef] [PubMed]
- Martinello, M.; Wajs, A.; Quan, S.; Lee, H.; Lim, C.; Woo, T.; Lee, W.; Kim, S.S.; Lee, D. Dual Aperture Photography: Image and Depth from a Mobile Camera. In Proceedings of the IEEE International Conference on Computational Photography, Houston, TX, USA, 24–26 April 2015; pp. 1–10. [Google Scholar]
- Tang, H.; Zhang, X.; Zhuo, S.; Chen, F.; Kutulakos, K.N.; Shen, L. High Resolution Photography with an RGB-Infrared Camera. In Proceedings of the IEEE International Conference on Computational Photography (ICCP), Houston, TX, USA, 24–26 April 2015; pp. 1–10. [Google Scholar]
- Aguilera, C.; Soria, X.; Sappa, A.D.; Toledo, R. RGBN Multispectral Images: A Novel Color Restoration Approach. In Proceedings of the Trends in Cyber-Physical Multi-Agent Systems. The PAAMS Collection 15th International Conference, Porto, Portugal, 21–23 June 2017; De la Prieta, F., Vale, Z., Antunes, L., Pinto, T., Campbell, A.T., Julián, V., Neves, A.J., Moreno, M.N., Eds.; Springer International Publishing: Cham, The Netherland, 2017; pp. 155–163. [Google Scholar]
- Soria, X.; Sappa, A.D.; Akbarinia, A. Multispectral Single-Sensor RGB-NIR Imaging: New Challenges and Opportunities. In Proceedings of the IEEE Seventh International Conference on Image Processing Theory, Tools and Applications, Montreal, QC, Canada, 28 November–1 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Park, C.; Kang, M.G. Color Restoration of RGBN Multispectral Filter Array Sensor Images Based on Spectral Decomposition. Sensors 2016, 16, 719. [Google Scholar] [CrossRef] [PubMed]
- Park, C.H.; Oh, H.M.; Kang, M.G. Color Restoration for Infrared Cutoff Filter Removed RGBN. In Proceedings of the Multispectral Filter Array Image Sensor, Berlin, Germany, 11–14 March 2015; pp. 30–37. [Google Scholar]
- Hu, X.; Heide, F.; Dai, Q.; Wetzstein, G. Convolutional Sparse Coding for RGB + NIR Imaging. IEEE Trans. Image Process. 2018, 27, 1611–1625. [Google Scholar] [CrossRef] [PubMed]
- Monno, Y.; Tanaka, M.; Okutomi, M. N-to-sRGB Mapping for Single-Sensor Multispectral Imaging. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Santiago, Chile, 7–13 December 2015; pp. 33–40. [Google Scholar]
- Teranaka, H.; Monno, Y.; Tanaka, M.; Ok, M. Single-Sensor RGB and NIR Image Acquisition: Toward Optimal Performance by Taking Account of CFA Pattern, Demosaicking, and Color Correction. Electron. Imaging 2016, 2016, 1–6. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Hayat, K. Super-Resolution via Deep Learning. arXiv, 2017; arXiv:1706.09077. [Google Scholar]
- Dong, W.; Wang, P.; Yin, W.; Shi, G.; Wu, F.; Lu, X. Denoising Prior Driven Deep Neural Network for Image Restoration. arXiv, 2018; arXiv:1801.06756. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Burger, H.C.; Schuler, C.J.; Harmeling, S. Image Denoising: Can Plain Neural Networks Compete with BM3D? In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2392–2399. [Google Scholar]
- Jain, V.; Seung, S. Natural Image Denoising with Convolutional Networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–10 December 2008; pp. 769–776. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. arXiv, 2016; arXiv:1609.04802. [Google Scholar]
- Hore, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 20th international conference on Pattern recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Klette, R. Concise Computer Vision; Springer: Berlin, Germany, 2014. [Google Scholar]
- Bhardwaj, S.; Mittal, A. A Survey on Various Edge Detector Techniques. Proc. Technol. 2012, 4, 220–226. [Google Scholar] [CrossRef]
- Tuytelaars, T.; Mikolajczyk, K. Local Invariant Feature Detectors: a Survey. Found. Trends Compu. Gr. Vis. 2008, 3, 177–280. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Krishnan, D.; Taylor, G.W.; Fergus, R. Deconvolutional Networks. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2528–2535. [Google Scholar] [CrossRef]
- Murugan, P.; Durairaj, S. Regularization and Optimization Strategies in Deep Convolutional Neural Network. arXiv Preprint, 2017; arXiv:1712.04711. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv Preprint, 2014; arXiv:1412.6980. [Google Scholar]
- Evangelidis, G. IAT: A Matlab Toolbox for Image Alignment; MathWorks: Natick, MA, USA, 2013. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale Structural Similarity for Image Quality Assessment. In Proceedings of the IEEE Conference Record of the Thirty-Seventh Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar]
- Luo, M.R.; Cui, G.; Rigg, B. The Development of the CIE 2000 Colour-Difference Formula: CIEDE2000. Color Res. Appl. 2001, 26, 340–350. [Google Scholar] [CrossRef]
- Sharma, G.; Wu, W.; Dalal, E.N. The CIEDE2000 Color-Difference Formula: Implementation Notes, Supplementary Test Data, and Mathematical Observations. Color Res. Appl. 2005, 30, 21–30. [Google Scholar] [CrossRef]
- Hong, G.; Luo, M.R.; Rhodes, P.A. A Study of Digital Camera Colorimetric Characterisation Based on Polynomial Modelling. Color Res. Appl. 2001, 26, 76–84. [Google Scholar] [CrossRef]



| Methods | PSNR | SSIM | AE | |||||
|---|---|---|---|---|---|---|---|---|
| Average | Median | Average | Median | Average | Median | Average | Median | |
| X | 17.626 | 16.367 | 0.610 | 0.635 | 6.322 | 5.417 | 53.454 | 56.452 |
| [20] | 20.768 | 21.306 | 0.590 | 0.606 | 5.490 | 5.366 | 66.027 | 73.711 |
| [21] | 16.921 | 17.391 | 0.315 | 0.332 | 6.137 | 5.501 | 45.929 | 47.808 |
| SRCNN [31] | 18.056 | 17.847 | 0.528 | 0.521 | 7.705 | 6.938 | 50.499 | 51.094 |
| ENDENet | 22.544 | 22.894 | 0.690 | 0.691 | 5.338 | 4.484 | 77.154 | 86.700 |
| CDNet | 22.874 | 22.999 | 0.704 | 0.725 | 5.237 | 4.593 | 76.005 | 85.264 |
| Image # | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | PSNR | #t | ||||||||||||||
| X | 26.16 | 11.50 | 25.15 | 16.29 | 16.49 | 13.41 | 15.20 | 18.23 | 12.66 | 15.32 | 16.29 | 16.34 | 25.80 | 17.24 | 15.41 | - |
| [20] | 24.99 | 21.38 | 27.04 | 18.76 | 20.89 | 19.84 | 19.76 | 22.18 | 18.81 | 19.77 | 15.31 | 17.86 | 22.07 | 24.63 | 17.30 | 5 |
| [21] | 18.70 | 12.68 | 22.70 | 15.17 | 12.69 | 13.50 | 15.88 | 16.60 | 12.64 | 18.90 | 16.57 | 17.78 | 19.24 | 13.87 | 14.06 | 0 |
| SRCNN [30] | 28.04 | 22.82 | 19.88 | 14.85 | 16.14 | 18.01 | 15.48 | 18.43 | 17.33 | 18.57 | 17.79 | 18.42 | 22.92 | 19.80 | 12.93 | 0 |
| ENDENet | 33.51 | 17.96 | 26.07 | 20.31 | 23.10 | 18.28 | 21.59 | 23.27 | 21.10 | 19.55 | 18.84 | 19.24 | 26.79 | 26.28 | 15.48 | 5 |
| CDNet | 34.44 | 15.19 | 26.00 | 20.04 | 23.00 | 18.09 | 22.25 | 23.39 | 21.74 | 19.62 | 18.63 | 17.88 | 27.20 | 26.13 | 15.32 | 5 |
| Method | SSIM | |||||||||||||||
| X | 0.91 | 0.45 | 0.59 | 0.60 | 0.70 | 0.35 | 0.62 | 0.59 | 0.53 | 0.41 | 0.49 | 0.42 | 0.87 | 0.74 | 0.64 | - |
| [20] | 0.79 | 0.70 | 0.69 | 0.49 | 0.63 | 0.51 | 0.49 | 0.59 | 0.52 | 0.65 | 0.56 | 0.54 | 0.79 | 0.80 | 0.64 | 4 |
| [21] | 0.36 | 0.24 | 0.36 | 0.34 | 0.19 | 0.22 | 0.36 | 0.31 | 0.17 | 0.39 | 0.20 | 0.24 | 0.36 | 0.34 | 0.31 | 0 |
| SRCNN [30] | 0.87 | 0.67 | 0.52 | 0.36 | 0.49 | 0.45 | 0.37 | 0.50 | 0.54 | 0.60 | 0.58 | 0.44 | 0.72 | 0.70 | 0.48 | 0 |
| ENDENet | 0.96 | 0.69 | 0.62 | 0.60 | 0.71 | 0.49 | 0.67 | 0.73 | 0.58 | 0.62 | 0.70 | 0.55 | 0.85 | 0.84 | 0.65 | 4 |
| CDNet | 0.96 | 0.63 | 0.61 | 0.63 | 0.73 | 0.39 | 0.69 | 0.73 | 0.63 | 0.59 | 0.68 | 0.52 | 0.87 | 0.85 | 0.67 | 9 |
| Method | AE | |||||||||||||||
| X | 1.40 | 5.06 | 8.82 | 3.37 | 3.25 | 9.55 | 6.27 | 8.78 | 4.77 | 5.54 | 4.80 | 7.81 | 1.68 | 4.07 | 4.28 | - |
| [20] | 3.55 | 5.28 | 8.12 | 4.24 | 3.45 | 6.22 | 8.50 | 8.30 | 7.63 | 3.45 | 4.02 | 5.89 | 2.72 | 3.09 | 3.83 | 2 |
| [21] | 1.54 | 5.51 | 9.18 | 3.69 | 3.63 | 5.49 | 7.95 | 7.79 | 7.96 | 3.96 | 4.50 | 6.67 | 2.74 | 4.34 | 3.71 | 1 |
| SRCNN [30] | 1.37 | 4.91 | 12.51 | 5.47 | 5.41 | 6.15 | 9.31 | 11.61 | 5.52 | 3.63 | 3.47 | 5.81 | 3.13 | 5.63 | 6.74 | 2 |
| ENDENet | 0.76 | 3.76 | 8.79 | 3.66 | 3.38 | 6.80 | 5.80 | 6.04 | 9.32 | 3.46 | 3.03 | 5.89 | 2.05 | 2.53 | 4.16 | 6 |
| CDNet | 0.75 | 4.13 | 9.14 | 4.02 | 3.76 | 8.07 | 5.43 | 6.30 | 6.56 | 4.08 | 3.56 | 6.19 | 2.02 | 2.71 | 3.78 | 4 |
| Method | ||||||||||||||||
| X | 84.52 | 7.70 | 95.34 | 26.44 | 26.64 | 13.38 | 43.92 | 64.98 | 48.51 | 26.85 | 26.40 | 18.52 | 91.64 | 72.96 | 31.71 | - |
| [20] | 99.43 | 90.37 | 93.14 | 37.54 | 60.69 | 65.58 | 71.02 | 80.80 | 75.99 | 48.36 | 15.87 | 16.70 | 58.91 | 88.38 | 31.72 | 3 |
| [21] | 30.06 | 11.40 | 90.91 | 23.70 | 14.29 | 21.18 | 53.74 | 59.02 | 22.99 | 37.30 | 11.39 | 16.70 | 46.96 | 28.02 | 26.37 | 0 |
| SRCNN [30] | 95.10 | 93.30 | 97.52 | 8.82 | 13.20 | 55.92 | 29.71 | 58.47 | 62.46 | 45.82 | 22.11 | 16.87 | 82.20 | 71.33 | 22.61 | 0 |
| ENDENet | 99.65 | 61.14 | 93.31 | 42.56 | 70.24 | 61.78 | 81.76 | 90.36 | 77.89 | 56.63 | 52.88 | 27.27 | 92.48 | 91.84 | 26.40 | 6 |
| CDNet | 99.76 | 36.32 | 92.99 | 43.71 | 68.14 | 46.65 | 84.46 | 87.82 | 85.41 | 50.55 | 37.81 | 19.27 | 93.72 | 92.11 | 26.56 | 6 |
| Method | HEP | |||||||||||||||
| SAME | 32 | 8 | 5 | 9 | 15 | 8 | 22 | 16 | 11 | 13 | 5 | 6 | 28 | 29 | 16 | 3 |
| ENDENet | 13 | 36 | 40 | 22 | 5 | 10 | 4 | 15 | 4 | 4 | 37 | 12 | 11 | 4 | 12 | 4 |
| CDNet | 5 | 6 | 5 | 19 | 30 | 32 | 24 | 19 | 35 | 33 | 8 | 32 | 11 | 17 | 22 | 8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soria, X.; Sappa, A.D.; Hammoud, R.I. Wide-Band Color Imagery Restoration for RGB-NIR Single Sensor Images. Sensors 2018, 18, 2059. https://doi.org/10.3390/s18072059
Soria X, Sappa AD, Hammoud RI. Wide-Band Color Imagery Restoration for RGB-NIR Single Sensor Images. Sensors. 2018; 18(7):2059. https://doi.org/10.3390/s18072059
Chicago/Turabian StyleSoria, Xavier, Angel D. Sappa, and Riad I. Hammoud. 2018. "Wide-Band Color Imagery Restoration for RGB-NIR Single Sensor Images" Sensors 18, no. 7: 2059. https://doi.org/10.3390/s18072059
APA StyleSoria, X., Sappa, A. D., & Hammoud, R. I. (2018). Wide-Band Color Imagery Restoration for RGB-NIR Single Sensor Images. Sensors, 18(7), 2059. https://doi.org/10.3390/s18072059





