Abstract
This paper proposes two novel, event-triggered fault-tolerant control strategies for a class of stochastic systems with state delays. The plant is disturbed by a Gaussian process, actuator faults, and unknown disturbances. First, a special case about fault signals that are coupled to the unknown disturbances is discussed, and then a fault-tolerant strategy is designed based on an event condition on system states. Subsequently, a send-on-delta transmission framework is established to deal with the problem of fault-tolerant control strategy against fault signals separated from the external disturbances. Two criteria are provided to design feedback controllers in order to guarantee that the systems are exponentially mean-square stable, and the corresponding -norm disturbance attenuation levels are achieved. Two theorems were obtained by synthesizing the feedback control gains and the desired event conditions in terms of linear matrix inequalities (LMIs). Finally, two numerical examples are provided to illustrate the effectiveness of the proposed theoretical results.
1. Introduction
Network control systems have been widely used in many applications such as video surveillance, satellite clusters, offshore platforms, and mobile robotics, among others, because of their advantages of wireless connectivity, efficiency, and flexibility [1,2,3,4]. However, introducing a network into a control loop can cause some problems, especially when the communication bandwidth is limited. It is indicated that only a few system components can obtain communication resources for data exchange simultaneously, which may affect the system performance and even cause system instability. Furthermore, the main constraint of wireless sensor networks is the limited battery life. Normally, it is impractical to replace batteries so the lifetime of the network control systems is equal to its battery life. The best option to lengthen the battery life is to reduce the wireless communication, which is a major source of energy consumption. The disadvantage of traditional periodic communication and control is that even when the output fluctuation is sufficiently small to change the output signal, the measurement value is also transmitted, resulting in a waste of communication and energy resources of battery-based devices [5,6,7].
The propositions of “replacing periodic control with event-triggered control” have been known since 1950s [8,9]. In addition, the interest on event-triggered control was initiated by the paper [10]. The basic idea of event-triggered control is that communication data based on the measured signals (states or outputs) are sent only when the designed conditions of the event-triggered strategy are satisfied, which can reduce unnecessary calculation and transmission, lower the requirement of a communication network system, and achieve a better balance between the control performance and traffic load [11]. This is particularly important when multiple systems use a shared network to communicate. Compared with time-triggered systems, shared networks can support more event-triggered systems [12]. The event-triggered control scheme can save energy resources of battery-based devices, computation resources, and limited network resources as well [13].
In the last decade, event-triggered control has become a hot research topic and significant contributions have been made [14,15,16,17,18,19,20,21,22,23,24,25,26]. The event-triggered data sampling strategies based on send-on-delta have been investigated in [19,20]. Recent discussions of event-triggered control for stochastic systems could be found in [21,22]. Literature [23,24] studied the event-triggered strategy of uncertain systems, and some of them are applicable to nonlinear systems. In addition, the event-triggered strategy for transmission time-delayed systems was studied in literature [25,26]. However, the reliability of the sensors cannot always be guaranteed because of actuator faults and unknown disturbances, the problem of fault-tolerant control has been actively investigated [27,28,29]. Notably, event-triggered fault-tolerant control for stochastic systems with state delays has not been adequately addressed. Thus, the main contributions of this paper can be summarized as follows: two novel event-triggered fault-tolerant control strategies are proposed based on a state and a send-on-delta event generators for a stochastic system with state delays. The closed-loop networked control system is exponentially mean-square stable, and the prescribed disturbance attenuation performance is also achieved. A simple algorithm is developed to deal with the addressed problem, which can be easily implemented using an efficient linear matrix inequalitie (LMI) toolbox.
This paper is organized as follows. Section 2 formulates the problem and some important lemmas are presented. Our main results are described in Section 3, the state-based event-triggered controls are presented in Section 3.1. Section 3.2 describes the send-on-delta strategy. Two numerical examples are presented in Section 4 to illustrate the results. Section 5 concludes this paper.
Notations: The superscript “T” stands for matrices transport. and denote n dimensional Euclidean space and set of all matrices, respectively. For a square matrix S, means that this matrix is positive definite (negative definite). In symmetric block matrices, “*” is used as an ellipsis for terms induced by symmetry. I denotes an identity matrix with appropriate dimensions. Let be a complete probability space, where is the sample space, is the -algebra of subsets of the sample space, and is the probability measure on . Furthermore, denotes the mathematical expectation of a matrix. stands for standard Euclidean norm in .
2. Problem Statement
Consider the following discrete-time linear stochastic system with state delays defined in a probability space :
where k is a discrete-time index, is the state vector, denotes the control vector, and is the initial state. correspond to the controlled output variables. The stochastic variable is a scalar Wiener process defined on a complete space with , and (). Moreover, the fault signals and disturbance signals are assumed to be signals (), where d is a delay coefficient. The matrices A, , , D, F and Z are known constant matrices with appropriate dimensions.
This paper assumes controllers and sensors to be collocated or hard-wired. The architecture of the event-triggered network control system used in this study is shown in Figure 1, which is similar to literature [7]. The event-triggered mechanism is composed of two units: a feedback controller and a trigger mechanism (event strategy, conditions, or algorithm). The trigger mechanism determines whether the control input should be sent to the actuator via the network. In this event-triggered mechanism, the event condition based on the current controlled output is monitored continuously. Once the condition is satisfied, an event is triggered.
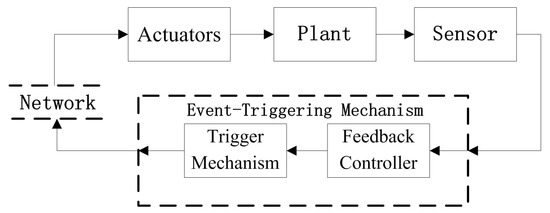
Figure 1.
Architecture of the event-triggered network control system.
The plant is assumed to be time-driven, whereas the actuator is event-triggered. The actuator is triggered only when a new control vector is received. Further, is defined as an event-triggered decision variable that determines whether to send the control vector at each sampling time: when , can be calculated and sent out; when , cannot be allowed to update. In this study, the event-triggered mechanism and feedback controller are co-designed. The objective is to use the minimum trigger time to maintain the control performance.
Remark 1.
The design of the event-triggered strategy must specify the minimum trigger time to avoid the zeno phenomenon, i.e., an infinite number of trigger times in finite time [7]. The system event generator used in this study is time-driven and sampled at a constant frequency; thus, the minimum trigger time of an event-triggered strategy is the sampling time, and hence, no zeno phenomenon can occur.
Before proceeding further, it is necessary to introduce the definition of mean-square stability.
Definition 1.
[30] A discrete stochastic process is said to be exponentially mean-square stable, if there exist constants and such that
where is the set of positive integers and d is a constant.
With the help of Definition 1, this paper focuses on the co-design of the feedback controller and the event-triggered mechanism such that the discrete-time linear stochastic system (1) satisfies the following requirements simultaneously.
- 1:
- When , the system is exponentially mean-square stable.
- 2:
- Under the zero-initial conditionfor all nonzero , where , and a is prescribed scalar.
Some lemmas are presented, which will play an important role in the proof of our main theorems in Section 3.
Lemma 1.
[31] Suppose , and is a Gaussian random vector satisfying , . Let η be the random variable
then .
Lemma 2.
(S-procedure [32], Lemma 3) Let and be two arbitrary quadratic forms over . Then
satisfying if and only if there exist a scalar such that for .
Lemma 3.
[33] Let the matrix be of full-column rank with singular value decomposition following the structure
if there exist positive–definite matrices satisfying
then there exists an invertible matrix such that , where .
3. Main Results
In this section, two event-triggered fault-tolerant control strategies are studied based on a state information and a send-on-delta strategy, respectively.
3.1. Event-Triggered Control Based on State Information
In this subsection, we intend to design the following event-triggered state feedback controller:
where K represents gain matrices with appropriate dimensions to be determined. Thus, the corresponding closed-loop systems are given by
Remark 2.
Notably, the fault signals are discussed together with the external disturbance, because they have no influence on the main results; if separated, they will increase the complexity of the following stability analysis.
To design an event-triggered fault-tolerant control strategy and the gain matrices of the controller, the following theorem will be provided to guarantee mean-square stability and the -norm disturbance attenuation level of the closed-loop stochastic system (7).
Theorem 1.
For a given scalar , if there exist real matrices and satisfying the following matrix inequality:
where .
Under the following event-triggering condition:
where and . Then there exists a state-feedback controller K such that the system (7) is exponentially mean-square stable when . The -norm constraint is achieved when .
Proof.
Consider the following Lyapunov–Krasovskii function:
let , thus, we have
As , it follows that
By applying Lemma 1, one can obtain
Combining (11), (12) and (13), it follows that
when and , one can obtain
The condition (8) implies that for
Let
Thus, we have for satisfying . According to Lemma 2, it can be demonstrated that there exists a scalar such that:
Thus, it follows that
Subsequently, by following the proof of Lemma 1 in [30], it can be demonstrated that the system (7) is exponentially mean-square stable when and .
When and , we have . Thus, (14) can be rewritten as
with the event-triggering condition (9), there are some satisfying the following inequality, which indicates that when :
Considering (19), one can obtain
Similar to the proof of the case of above, when one can obtain:
Thus, the system (7) is exponentially mean-square stable when and .
When and , let . Considering (14), one can obtain
The condition (8) implies that
Summing up (24) from to results in
By the definition of the Lyapunov—Krasovskii function and the zero initial condition, it can be shown that and . Thus
which implies that
Hence, the -norm constraint (3) is achieved when and . Similar to the proof of the case that , it can be shown that the -norm constraint (3) is achieved when and .
This completes the proof. ☐
Let , , according to the Schur complement, (8) is equivalent to the following LMI
However, equations such as cannot be calculated using LMI toolbox of MATLAB. Algorithm 1 based on the Lemma 3 is proposed for obtaining the parameters of (28).
| Algorithm 1 Design procedure for solving the problem of Theorem 1 |
3.2. Event-Triggered Control Based on Send-on-Delta Strategy
Notably, the fault signals are discussed together with the external disturbance in Section 3.1, which is a special case. In this subsection, a send-on-delta strategy is proposed to deal with the fault signals separated from the external disturbance. We are interested in finding the following event-triggered state feedback controller:
where K represents gain matrices with appropriate dimensions to be determined, and the variable represents the latest control input sent to the remote actuator. The control inputs are not periodically sent to the remote actuator owing to the event-triggered data-transmission.
Denoting , the stochastic system (1) via the event-triggered controller (29) can be rewritten as the following close-loop form:
where and K represent gain matrices with appropriate dimensions to be designed.
Let us design the feedback gain and the event-triggered control strategy such that the resulting close-loop system (30) is exponentially mean-square stable when . The -norm constraint (3) is achieved when .
Theorem 2.
For a given scalar and , if there exist the real matrices , , , , satisfying the following matrix inequality:
where . Under the following event-triggering condition:
Then there exists a state-feedback controller K such that the resulting close-loop system (30) is exponentially mean-square stable when . The -norm constraint is achieved when .
Proof.
Consider the following Lyapunov–Krasovskii function:
Similar to the proof of Theorem 1 above, it can be shown that the system (30) is exponentially mean-square stable when and .
When and , considering , it follows that
where
The condition (31) implies that , thus
Similar to the proof of Theorem 1 above, it can be shown that the -norm constraint that of system (30) is achieved when .
Different from Algorithm 1, here we apply the Schur complement for the condition (31) directly. It follows that
where . Then, the unknown parameters can be easily calculated with the efficient LMI toolbox of MATLAB.
This completes the proof. ☐
Remark 3.
It is observed that the system (30) is reduced to the following form when : , i.e., , and hence, the proof of stability analysis for the case of is omitted.
4. Results and Discussion
In this section, two academic examples are presented to illustrate the properties of the proposed control strategies.
4.1. Example 1
Consider system (7) with:
which is taken from [34]. By applying the proposed method in Theorem 1 and using the steps of Algorithm 1, the parameters are calculated as follows:
Assuming the initial condition to be for . In addition, the unknown disturbance was selected as , the fault signal is selected as . Then, the states’ responses of the system (7) are given in Figure 2 and Figure 3 while the values of are given in Figure 4.
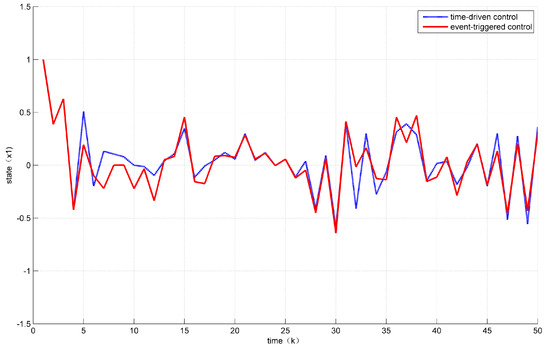
Figure 2.
Evolution of state x1.
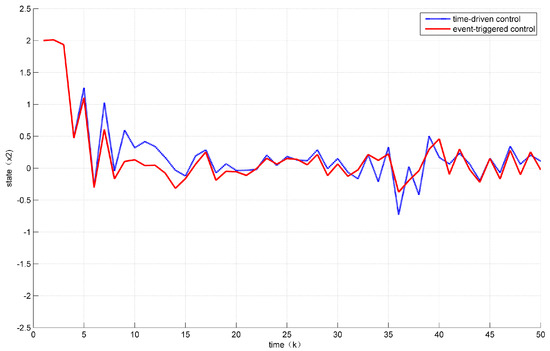
Figure 3.
Evolution of state x2.
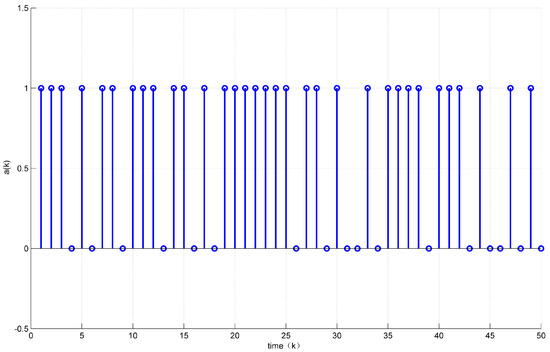
Figure 4.
Evolution of a(k).
Figure 4 shows that the control vector was sent 33 times, i.e., 34% of the network resources were saved.
At the same time, it can be seen from Figure 2 and Figure 3 that the control performance was not much loss compared with the time-driven control.
The effect of different time delays on system data transmission and control performance is described below. Figure 5 shows the trajectory of the state corresponding to different time delays. Table 1 shows the number of event triggers corresponding to different time delays.
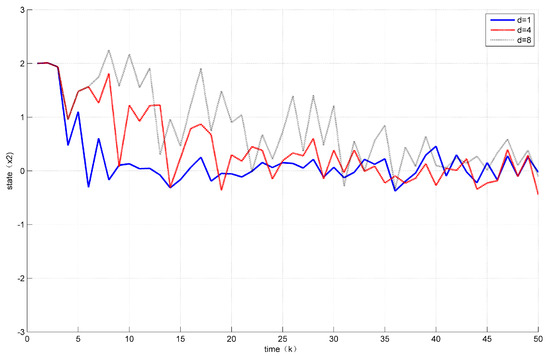
Figure 5.
The trajectory of state x2 corresponding to different time delays a(k).

Table 1.
The number of event triggers corresponding to different time delays.
As can be seen from Figure 5 and Table 1, with the increase of time delay, the convergence speed of the system gradually slows down, the number of event-driven triggers gradually increases, and the system performance gradually deteriorates. When the delay is excessively large for periodic control to guarantee system performance, the event will not be triggered.
4.2. Example 2
Consider system (30) with:
which is taken from [35]. By applying the proposed method in Theorem 2 and using the LMI toolbox of MATLAB, the parameters were calculated as follows:
Assume the initial condition to be for . In addition, the unknown disturbance was selected as , the fault signal was selected as . The states response of the system (30) are shown in Figure 6 while the values of are shown in Figure 7.
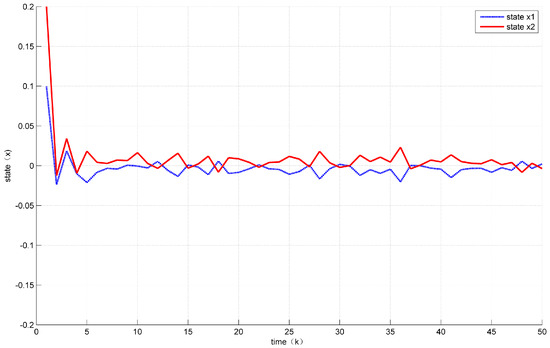
Figure 6.
The state trajectories under Theorem 2.
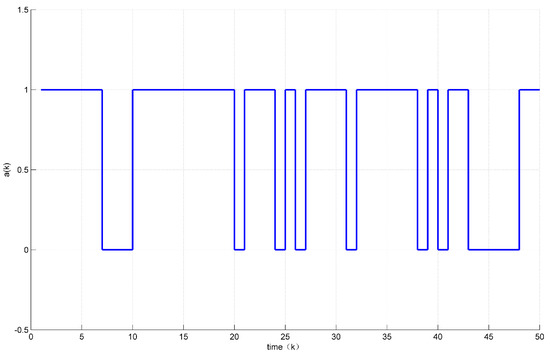
Figure 7.
Evolution of a(k).
From the Figures above, we can observe that, compared with time-driven systems, the proposed event-triggered control strategy reduced the unnecessary transmission effectively and found a better balance between the control performance and traffic load.
5. Conclusions
In this article, event-triggered fault-tolerant control strategies were investigated for stochastic systems subject to unknown disturbances and state time-delays. To reduce unnecessary calculation and transmission, two novel, event-triggered fault-tolerant control strategies were proposed according to which the systems were exponentially mean-square stable, and the prescribed -norm disturbance attenuation level was achieved. Finally, two academic examples were presented according to which we can conclude that, compared with time-triggered systems, the proposed event-triggered control strategy achieves a better balance between the control performance and traffic load.
Author Contributions
Conceptualization, Y.G.; Funding acquisition, L.P.; Software, Y.G.; Supervision, Y.L.; Validation, L.P.; Writing—original draft, Y.G.; Writing—review & editing, L.P. and J.L.
Funding
This research was partial supported by Natural Science Foundation of the Jiangsu Higher Education Institutions (Grant No.16KJB510044); Education Ministry and China Mobile Science Research Foundation: Video Big Data Analysis and c Interaction Technology Research (MCM20170204); Jiangsu province “Application of IOT technology based on block chain and intelligent information” technology innovation team (Jiangsu Provincial Department of Finance and Education [2017] No. 153), respectively.
Acknowledgments
The authors would like to thank the reviewers for their helpful comments and suggestions which have helped improve the presentation of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LD | linear dichroism |
| IOT | Internet of things |
| LMIs | linear matrix inequalities |
References
- Zhang, X.M.; Han, Q.L. Network-based H∞ filtering using a logic jumping-like trigger. Automatica 2013, 49, 1428–1435. [Google Scholar] [CrossRef]
- Zhang, B.L.; Han, Q.L.; Zhang, X.M. Recent advances in vibration control of offshore platforms. Nonlinear Dyn. 2017, 89, 755–771. [Google Scholar] [CrossRef]
- Zhao, G.; Guo, J.; Qiang, H. Research on SFLA-based bidirectional coordinated control strategy for EV battery swapping station. Comput. Mater. Contin. 2017, 53, 343–356. [Google Scholar]
- Cao, Z.Z.; Du, F.; Xu, P. Control mechanism of surface subsidence and overburden movement in backfilling mining based on laminated plate theory. Comput. Mater. Contin. 2017, 53, 175–186. [Google Scholar]
- Li, Y.J.; Wu, Q.E.; Peng, L. Simultaneous Event-Triggered Fault Detection and Estimation for Stochastic Systems Subject to Deception Attacks. Sensors 2018, 18, 321. [Google Scholar] [CrossRef] [PubMed]
- Selivanov, A.; Fridman, E. Event-triggered H∞ control: A switching approach. IEEE Trans. Autom. Control 2016, 61, 3221–3226. [Google Scholar] [CrossRef]
- Khashooei, B.A.; Antunes, D.J.; Heemels, W.P.M.H. Output-based event-triggered control with performance guarantees. IEEE Trans. Autom. Control 2017, 62, 3646–3652. [Google Scholar] [CrossRef]
- Jury, E.I.; Mullin, F.J. The analysis of sampled-data control systems with a periodically time-varying sampling rate. IRE Trans. Autom. Control 1959, 4, 15–21. [Google Scholar] [CrossRef]
- Miskowicz, M. Event-Based Control and Signal Processing; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Åström, K.J.; Bernhardsson, B. Comparison of periodic and event based sampling for first-order stochastic systems. In Proceedings of the 14th IFAC World Congress, Cape Town, South Africa, 24–29 August 1999; pp. 301–306. [Google Scholar]
- Donkers, M.C.F.; Heemels, W.P.M.H. Output-based event-triggered control with guaranteed L∞-gain and improved and decentralized event-triggering. IEEE Trans. Autom. Control 2012, 57, 1362–1376. [Google Scholar] [CrossRef]
- Ramesh, C.; Sandberg, H.; Johansson, K.H. Performance analysis of a network of event-based systems. IEEE Trans. Autom. Control 2016, 61, 3568–3573. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Zhang, B.L. An Overview and Deep Investigation on Sampled-Data-Based Event-Triggered Control and Filtering for Networked Systems. IEEE Trans. Ind. Inf. 2017, 13, 4–16. [Google Scholar] [CrossRef]
- Acho, L. Event-Driven Observer-Based Smart-Sensors for Output Feedback Control of Linear Systems. Sensors 2017, 17, 2028. [Google Scholar] [CrossRef] [PubMed]
- Socas, R.; Dormido, S.; Dormido, R.; Fabregas, E. Event-based control strategy for mobile robots in wireless environments. Sensors 2015, 15, 30076–30092. [Google Scholar] [CrossRef] [PubMed]
- Putra, I.P.E.S.; Brusey, J.; Gaura, E.; Vesilo, R. An Event-Triggered Machine Learning Approach for Accelerometer-Based Fall Detection. Sensors 2018, 18, 20. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.Z.; Liu, G.L.; Yan, H.T.; Cheng, B.; Lin, F.L. Trail-Based Search for Efficient Event Report to Mobile Actors in Wireless Sensor and Actor Networks. Sensors 2017, 17, 2468. [Google Scholar] [CrossRef] [PubMed]
- Santos, C.; Martinez-Rey, M.; Espinosa, F.; Gardel, A.; Santiso, E. Event-Based Sensing and Control for Remote Robot Guidance: An Experimental Case. Sensors 2017, 17, 2034. [Google Scholar] [CrossRef] [PubMed]
- Miskowicz, M. Send-on-delta concept: An event-based data reporting strategy. Sensors 2006, 6, 49–63. [Google Scholar] [CrossRef]
- Diaz-Cacho, M.; Delgado, E.; Barreiro, A.; Falcon, P. Basic Send-on-Delta Sampling for Signal Tracking-Error Reduction. Sensors 2017, 17, 312. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.C.; Meng, X.Y.; Chen, T.W. Event based pulse-modulated control of linear stochastic systems. IEEE Trans. Autom. Control 2014, 59, 2144–2150. [Google Scholar] [CrossRef]
- Wu, L.G.; Gao, Y.B.; Liu, J.X.; Liu, H.Y. Event-triggered sliding mode control of stochastic systems via output feedback. Automatical 2017, 82, 79–92. [Google Scholar] [CrossRef]
- Albattat, A.; Gruenwald, B.C.; Yucelen, T. On Event-Triggered Adaptive Architectures for Decentralized and Distributed Control of Large-Scale Modular Systems. Sensors 2016, 16, 1297. [Google Scholar] [CrossRef] [PubMed]
- Li, H.P.; Shi, Y. Event-triggered robust model predictive control of continuous-time nonlinear systems. Automatical 2014, 50, 1507–1513. [Google Scholar] [CrossRef]
- Wang, X.F.; Lemmon, M.D. Event-triggering in distributed networked control systems. IEEE Trans. Autom. Control 2011, 56, 586–601. [Google Scholar] [CrossRef]
- Hu, S.; Yin, X.; Zhang, Y.; Tian, E.G. Event-triggered guaranteed cost control for uncertain discrete-time networked control systems with time-varying transmission delays. IET Control Theory Appl. 2012, 6, 2793–2804. [Google Scholar] [CrossRef]
- Guo, X.F.; Ren, X.M.; Li, Z.J.; Han, C.W. Fault detection and fault-tolerant control over signal-to-noise ratio constrained channels. Int. J. Robust Nonlinear Control 2018, 28, 2806–2827. [Google Scholar] [CrossRef]
- Zeng, Y.L.; Xu, L.; Chen, Z.D. Fault-Tolerant Algorithms for Connectivity Restoration in Wireless Sensor Networks. Sensors 2016, 16, 3. [Google Scholar] [CrossRef] [PubMed]
- Xiahou, K.S.; Wu, Q.H. Fault-tolerant control of doubly-fed induction generators under voltage and current sensor faults. Int. J. Electr. Power Energy Syst. 2018, 98, 48–61. [Google Scholar] [CrossRef]
- Wang, Z.D.; Yang, F.W.; Ho, W.D.C.; Liu, X.H. H∞ robust filtering for stochastic time-Delay systems with missing measurements. IEEE Trans. Signal Process. 2006, 54, 2579–2587. [Google Scholar] [CrossRef]
- Cogill, R.; Lall, S.; Hespanha, J.P. A constant factor approximation algorithm for event-based sampling. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 11–13 July 2007; pp. 305–311. [Google Scholar]
- Oya, H.; Hagino, K.; Kayo, S. Adaptive robust control based on piecewise Lyapunov functions for a class of uncertain linear systems. In Proceedings of the European Control Conference 2007, Kos, Greece, 2–5 July 2007; pp. 810–815. [Google Scholar]
- Yang, F.W.; Wang, Z.D.; Hung, Y.S.; Gani, M. H∞ control for networked systems with random communication delays. IEEE Trans. Autom. Control 2006, 53, 511–518. [Google Scholar] [CrossRef]
- Gao, H.; Lam, J.; Wang, C.; Wang, Y. Delay-dependent output-feedback stabilisation of discrete-time systems with time-varying state delay. IEE Proc.-Control Theory Appl. 2004, 151, 691–698. [Google Scholar] [CrossRef]
- Shi, D.W.; Chen, T.W.; Shi, L. Event-triggered maximum likelihood state estimation. Automatica 2014, 50, 247–254. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).