Experimental Demonstration of Low-Uncertainty Calibration Methods for Bragg Grating Interrogators
Abstract
1. Introduction
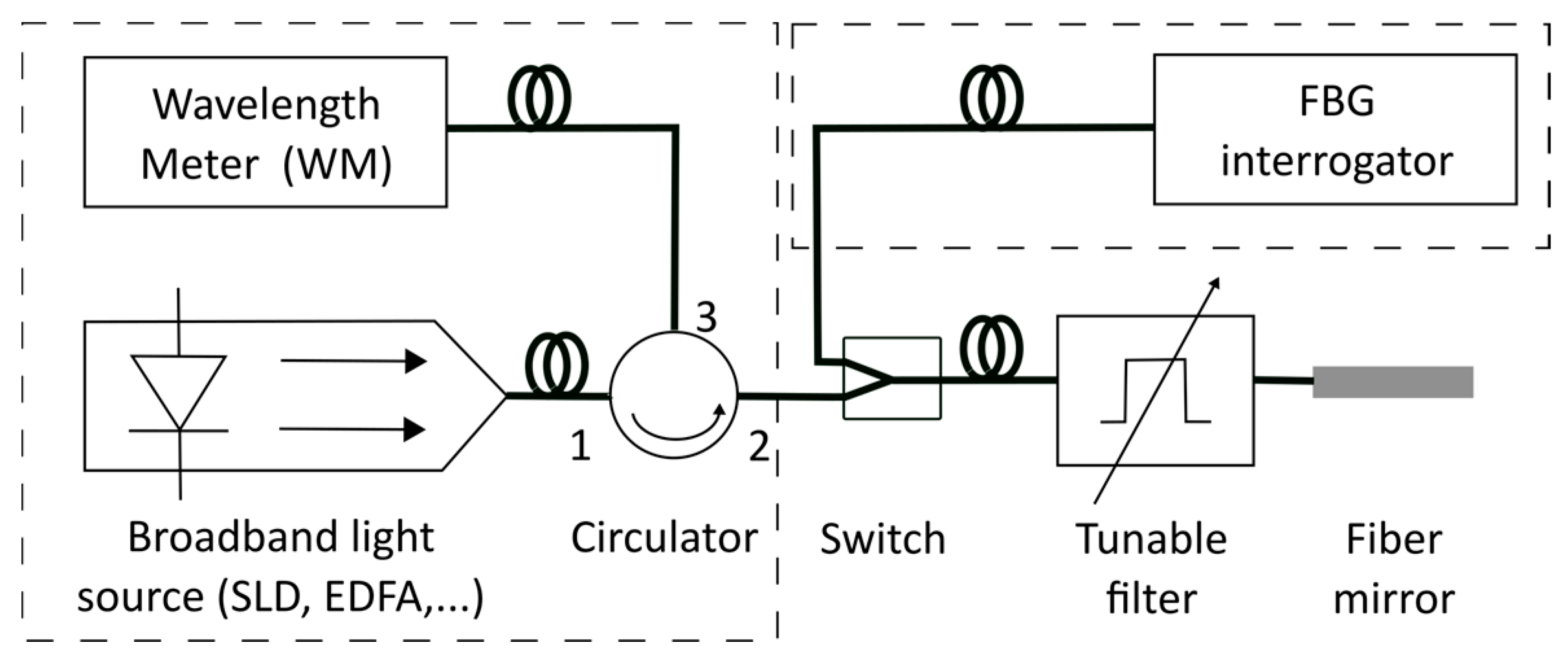
2. Materials and Methods
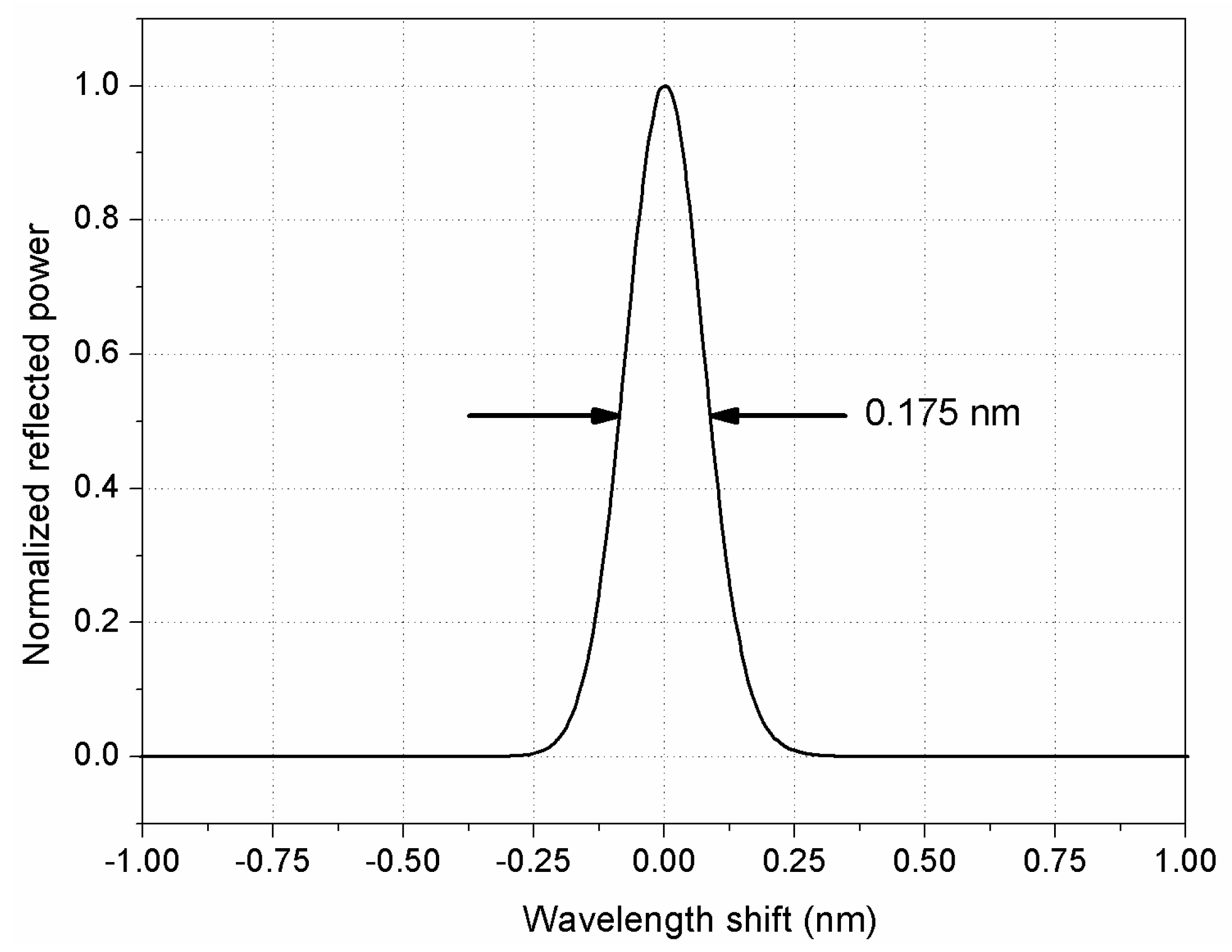
2.1. First Method: Simulated Tunable Bragg Grating
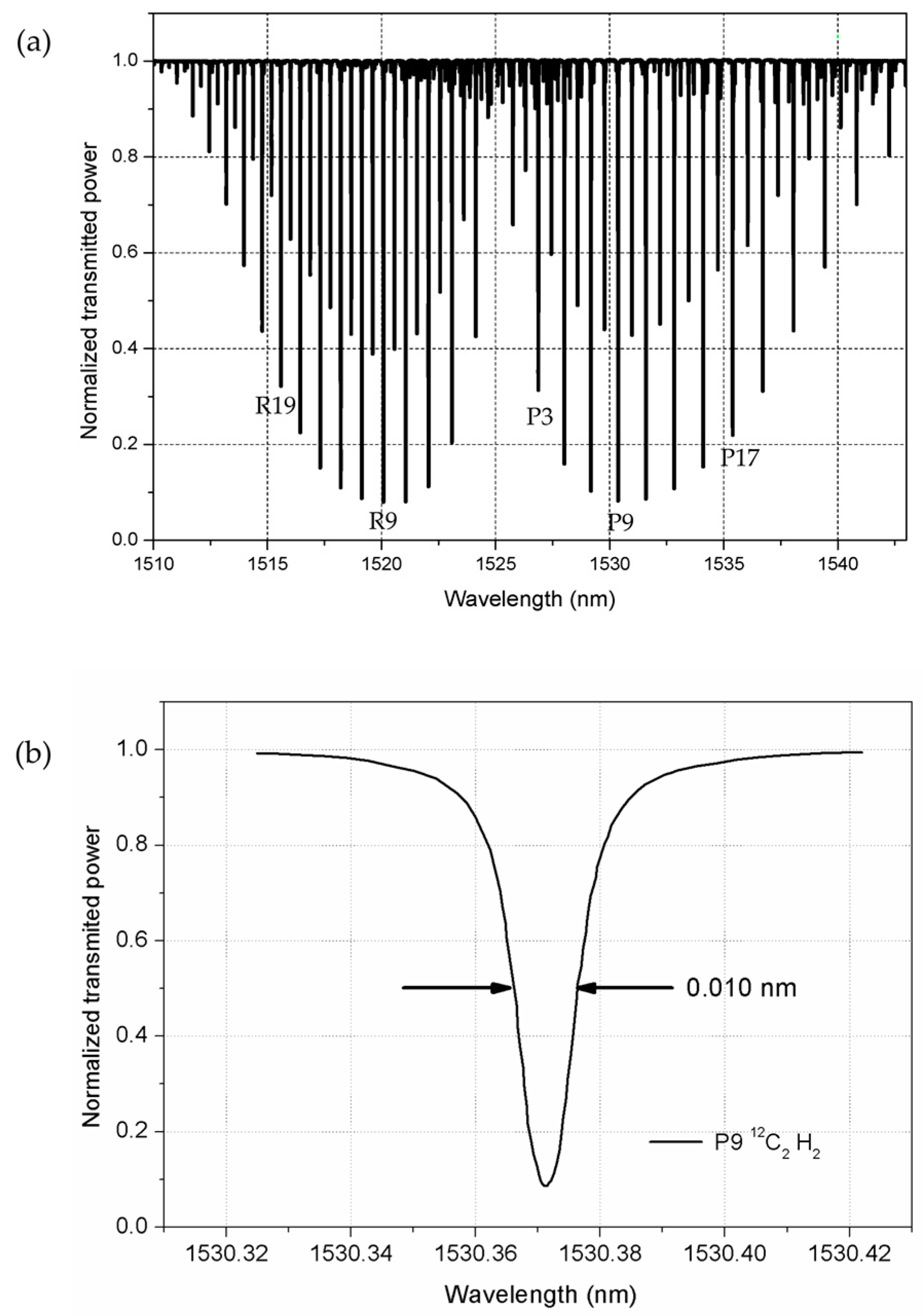
2.2. Second Method: Gas Absorption Cell
3. Results
3.1. Devices Under Test
3.2. First Method: Simulated Bragg Grating
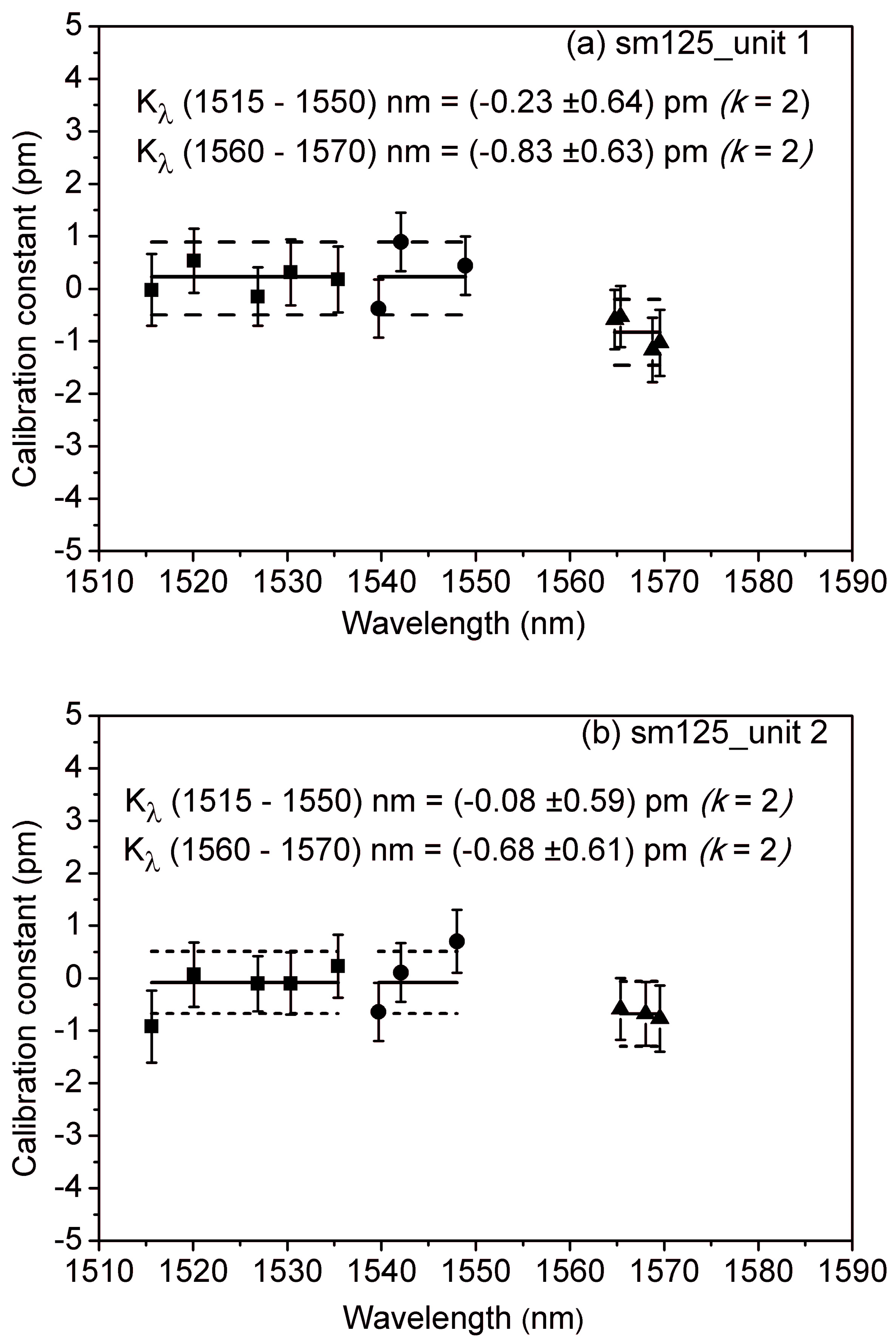
3.3. Second Method: Gas Absorption Cell
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kashyap, R. Fiber Bragg Gratings, 2nd ed.; Academic Press: Burlington, VT, USA, 2009; ISBN 978-0-12-372579-0. [Google Scholar]
- Krohn, D.A.; MacDougall, T.; Mâendez, A. Fiber Optic Sensors: Fundamentals and Applications, 4th ed.; SPIE: Bellingham, WA, USA, 2014; p. 63. ISBN 9781628411812. [Google Scholar]
- Technology Focus: Optical-fibre sensors. Nat. Photonics 2008, 2.
- Poeggel, S.; Tosi, D.; Duraibabu, D.; Leen, G.; McGrath, D.; Lewis, E. Optical fibre pressure sensors in medical applications. Sensors 2015, 15, 17115–17148. [Google Scholar] [CrossRef] [PubMed]
- Giraldo, C.M.; Zúñiga Sagredo, J.; Sánchez Gómez, J.; Corredera, P. Demonstration and methodology of structural monitoring of stringer runs out composite areas by embedded optical fiber sensors and connectors integrated during production in a composite plant. Sensors 2017, 17, 1683. [Google Scholar] [CrossRef] [PubMed]
- Murayama, H.; Wada, D.; Igawa, H. Structural health monitoring by using fiber-optic distributed strain sensors with high spatial resolution. Photonic Sens. 2013, 3, 355–376. [Google Scholar] [CrossRef]
- Kinet, D.; Mégret, P.; Goossen, K.W.; Qiu, L.; Heider, D.; Caucheteur, C. Fiber bragg grating sensors toward structural health monitoring in composite Materials: Challenges and solutions. Sensors 2014, 14, 7394–7419. [Google Scholar] [CrossRef] [PubMed]
- Sante, R.D. Fibre optic sensors for structural health monitoring of aircraft composite structures: recent advances and applications. Sensors 2015, 15, 18666–18713. [Google Scholar] [CrossRef] [PubMed]
- Ferraro, P.; De Natale, G. On the possible use of optical fiber Bragg gratings as strain sensors for geodynamical monitoring. Opt. Lasers Eng. 2002, 37, 115–130. [Google Scholar] [CrossRef]
- Tosi, D. Review and analysis of peak tracking techniques for fiber bragg grating sensors. Sensors 2017, 17, 2368. [Google Scholar] [CrossRef] [PubMed]
- IEC 61757-1-1:2016. Fibre Optic Sensors-Part 1-1: Strain Measurement-Strain Sensors Based on Fibre Bragg Gratings. Available online: http://www.iec.ch/ (accessed on 7 May 2018).
- Taylor, B.N.; Kuyatt, C.E. Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results, 1994 ed.; NIST Technical Note 1297; US Department of Commerce, Technology Administration, National Institute of Standards and Technology: Gaithersburg, MD, USA, 1994.
- Ibrahim, S.K.; Farnan, M.; Karabacak, D.M.; Singer, J.M. Enabling technologies for fiber optic sensing. Proc. SPIE 2016, 9899. [Google Scholar] [CrossRef]
- JCGM/WG 1. JCGM 100:2008 Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement, 1st ed.; BIPM: Pavillon de Breteuil, France, 2008; Corrected Edition, 2010.
- Dyer, S.D.; Williams, P.A.; Espejo, R.J.; Kofler, J.D.; Etzel, S.M. Fundamental limits in fiber Bragg grating peak wavelength measurements. In Proceedings of the 17th International Conference on Optical Fibre Sensors Volume 5855, Bruges, Belgium, 23–27 May 2005; Voet, M., Willsch, R., Ecke, W., Jones, J., Culshaw, B., Eds.; SPIE: Bellingham, WA, USA, 2005. Invited Paper, 88. [Google Scholar]
- Galindo-Santos, J.; Velasco, A.V.; Corredera, P. Fibre optics wavemeters calibration using a self-referenced optical frequency comb. Rev. Sci. Instrum. 2015, 86, 013104. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, S.L.; Swann, W.C.; Wang, C.M. Hydrogen cyanide H13C14N absorption reference for 1530 nm to 1565 nm wavelength Calibration–SRM 2519a. NIST Spec. Publ. 2005, 260, 137. [Google Scholar]
- Salgado, P.; Martín López, S.; Carrasco-Sanz, A.; Corredera, P. Método de calibración para interrogadores de redes de Bragg en fibra óptica. Opt. Pura Apl. 2012, 45, 361–368. [Google Scholar] [CrossRef]
- Gornal, W.S. U.S. Interferometer Apparatus for the Direct Measurement of Wavelength and Frequency. Patent Number 4,319,843, 16 March 1982. [Google Scholar]
- Gornal, W.S.; Houk, M.T. Laser Wavelength Meter. U.S. Patent 6,842,252, 11 January 2005. [Google Scholar]
- Demtröder, W. Laser Spectroscopy 1: Basic Principles, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2014; p. 196. ISBN 978-3-642-53859-9. [Google Scholar]
- Castell, R.; Demtröder, W.; Fischer, A.; Kullmer, R.; Weickenmeier, H.; Wickert, K. The accuracy of laser wavelength meters. Appl. Phys. B 1985, 38, 1–10. [Google Scholar] [CrossRef]
- Gilbert, S.L.; Swann, W.C. Acetylene 12C2H2 Absorption Reference for 1510–1540 nm Wavelength Calibration—SRM 2517; Special Publication (NIST SP) 260-133; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2001.
- Edwards, C.S.; Margolis, H.S.; Barwood, G.P.; Lea, S.N.; Gill, P.; Rowley, W.R.C. High-accuracy frequency atlas of 13C2H2 in the 1.5 μm region. Appl. Phys. B 2005, 80, 977–983. [Google Scholar] [CrossRef]
- Sasada, H.; Yamada, K. Calibration lines of HCN in the 1.5-μm región. Appl. Optics 1990, 29, 3535–3547. [Google Scholar] [CrossRef] [PubMed]
- Swann, W.C.; Gilbert, S.L. Pressure-induced shift and broadening of 1560–1630 nm carbon monoxide wavelength-calibration lines. J. Opt. Soc. Am. B 2002, 19, 2461–2467. [Google Scholar] [CrossRef]
- Swann, W.C.; Gilbert, S.L. Pressure-induced shift and broadening of 1510–1540 nm acetylene wavelength calibration lines. J. Opt. Soc. Am. B 2000, 17, 1263–1270. [Google Scholar] [CrossRef]
- Swann, W.C.; Gilbert, S. L line centers, pressure shift, and pressure broadening of 1530–1560 nm hydrogen cyanide wavelength calibration lines. J. Opt. Soc. Am. B 2005, 22, 1749–1756. [Google Scholar] [CrossRef]
- Bao, Y.; Daugherty, D.; Hsu, K.; Li, T.Q.Y.; Miller, C.M.; Miller, J.W.Y. Calibrated Swept-Wavelength Laser and Interrogator System for Testing Wavelength-Division Multiplexing System. U.S. Patent 6,449,047, 10 September 2002. [Google Scholar]
- Garcia-Benadí, A.; del Río Fernandez, J.; Nogueres-Cervera, M.; Pulido de Torres, C.; García Izquierdo, C.; del Campo, D.; Hernandez, S.; Corredera, P. Traceable sea temperature vertical profile measured by optical fibers. In Proceedings of the OCEANS 2017, Aberdeen, UK, 19–22 June 2017. [Google Scholar] [CrossRef]


| Parameter | Micron Optics sm125-500 | Micron Optics sm130-700 | Micron Optics si155 Standard | HBM FS22—Industrial BraggMETER (Static) | HBM FS22—Industrial BraggMETER | HBM FS42—Portable BraggMETER | Smart Fibers SmartScope FBG Interrogator | Smart Fibers SmartScan FBG Interrogator | FAZT I4G Interrogator | Optilab FSI-RM-18 | BaySpec WaveCapture® Turn-key FBG Sensing | Ibsen I-MON 256 (512) OEM Monitors |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Operating principle | Swept laser | Spectrometer | ||||||||||
| Stability (*) (Reproducibility) (pm) | ±1 | ±2 typically, ±5 max | ±1 | ±1 | ±5 | ±2.5 | 3 | <5 | <±1 | ±2.5 | ||
| Repeatability (pm) | ±0.5 at 1 Hz; ±0.2 at 0.1 Hz | ±1 | ±1 | <±0.5 | <±0.5 | ±1.0 | <±2 | <±1 | ±0.05 | ±1 | ± 2 (±5 without internal reference) | ±3 (±5 max) |
| Wavelength range (nm) | 1510–1590 | 1510–1590 | 1460–1620 | 1500–1600 | 1500–1600 | 1500–1600 | 1528–1568 | 1528–1568 | 1529–1568 | Up to 60 | 1525–1565 (1510–1590) | 1525–1570 (1510–1595) |
| Sampling rate (Hz) | 2 | 1000 | 1000 | 1 | Up to 1000 | 1 | 5 | 2500 | 16 | 10–100 | 5 (Fast: ~5000) | |
| Number of optical channels | 4 | 4 (up to 16) | 1 or 4 | 1, 4, or 8 | 1, 4, or 8 | 1, 2, or 4 | 1, 2, or 4 | 4 | 18 | 1 or 4 | ||
| Maximum sensors | 60–120 | 160 × 16 | 125–1000 | 125–1000 | 24–96 | 24–96 | 120 | |||||
| Dynamic range (dB) | 50 | 25 | 25 peak/40 FS | >50 | >25 | >50 | 38 | 38 | >30 | 30 | ||
| Internal wavelength reference | Yes | No | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Option | |
| Wavelength Standard Reference Material | Wavelength Range (nm) |
|---|---|
| 12C2H2 [23] | 1510–1540 |
| 13C2H2 [24] | 1520–1550 |
| H12C14N | 1520–1555 |
| H13C14N [25] | 1530–1565 |
| 12C16O [26] | 1560–1595 |
| 13C16O [26] | 1595–1630 |
| Magnitude | Component of Uncertainty | Value (pm) | Type | Uncertainty Contribution (pm) |
|---|---|---|---|---|
| Wavelength meter (WM) calibration | 9.4 × 10−2 | B | 4.7 × 10−2 | |
| Linewidth of FBG | 1.4 × 100 | B | 3.9 × 10−1 | |
| Repeatability of reference | 4.0 × 10−1 | B (*) | 2.3 × 10−1 | |
| Optical resolution | 8.0 × 10−1 | B | 2.3 × 10−1 | |
| Display resolution | 1.0 × 10−2 | B | 2.9 × 10−3 | |
| On-off repeatability | 2.0 × 10−1 | B (*) | 1.2 × 10−1 | |
| Expanded uncertainty (U) (k = 2) | ±1.1 × 100 | |||
| Magnitude | Component of Uncertainty | Value (pm) | Type | Uncertainty Contribution (pm) |
|---|---|---|---|---|
| Absorption line value | 3.5 × 10−1 | B | 1.8 × 10−1 | |
| λFBGI | Measurement stability | 6.0 × 10−4 | A | 1.3 × 10−5 |
| Optical resolution | 8.0 × 10−1 | B | 2.3 × 10−1 | |
| Display resolution | 1.0 × 10−2 | B | 2.9 × 10−3 | |
| On-off repeatability | 2.0 × 10−1 | B (*) | 1.2 × 10−1 | |
| Expanded uncertainty (U) (k = 2) | ±6.3 × 10−1 | |||
| Commercial System | Method 1 | Method 2 | |||
|---|---|---|---|---|---|
| Kλ (pm) | U (k = 2) (pm) | Kλ (pm) | U (k = 2) (pm) | ||
| sm125_unit 1 | −0.9 | ±1.1 | −0.23 (*) | ±0.64 (*) | |
| −0.83 (**) | ±0.63 (**) | ||||
| sm125_unit 2 | −0.08 (*) | ±0.59 (*) | |||
| −0.68 (**) | ±0.61 (**) | ||||
| FS42 | −0.6 | ±1.1 | |||
| sm130 | 16.4 | ±1.1 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Miguel, J.L.; Galindo-Santos, J.; Pulido de Torres, C.; Salgado, P.; Velasco, A.V.; Corredera, P. Experimental Demonstration of Low-Uncertainty Calibration Methods for Bragg Grating Interrogators. Sensors 2018, 18, 1895. https://doi.org/10.3390/s18061895
De Miguel JL, Galindo-Santos J, Pulido de Torres C, Salgado P, Velasco AV, Corredera P. Experimental Demonstration of Low-Uncertainty Calibration Methods for Bragg Grating Interrogators. Sensors. 2018; 18(6):1895. https://doi.org/10.3390/s18061895
Chicago/Turabian StyleDe Miguel, José Luis, Juan Galindo-Santos, Concepción Pulido de Torres, Pedro Salgado, Aitor V. Velasco, and Pedro Corredera. 2018. "Experimental Demonstration of Low-Uncertainty Calibration Methods for Bragg Grating Interrogators" Sensors 18, no. 6: 1895. https://doi.org/10.3390/s18061895
APA StyleDe Miguel, J. L., Galindo-Santos, J., Pulido de Torres, C., Salgado, P., Velasco, A. V., & Corredera, P. (2018). Experimental Demonstration of Low-Uncertainty Calibration Methods for Bragg Grating Interrogators. Sensors, 18(6), 1895. https://doi.org/10.3390/s18061895





