Improved Cross-Ratio Invariant-Based Intrinsic Calibration of A Hyperspectral Line-Scan Camera
Abstract
1. Introduction
2. Related Work
3. Calibration Method
3.1. The Camera Model for a Line-Scan Camera
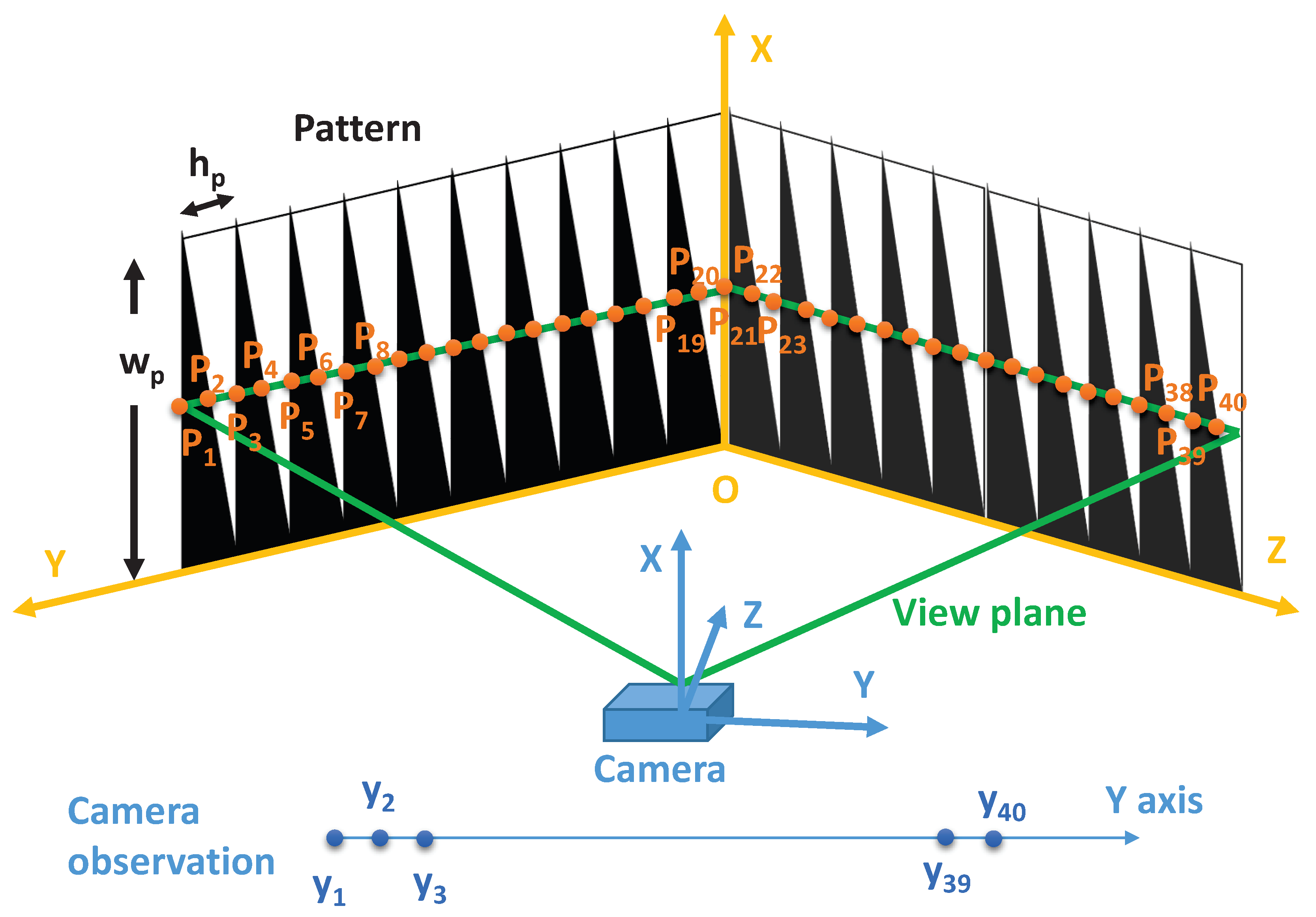
3.2. Calibration Target
3.3. Signal Processing
3.4. Direct Linear Solution
3.5. Nonlinear Optimization for Each Camera Pose
3.6. Joint Nonlinear Optimization for Multi Camera Poses
4. Validation
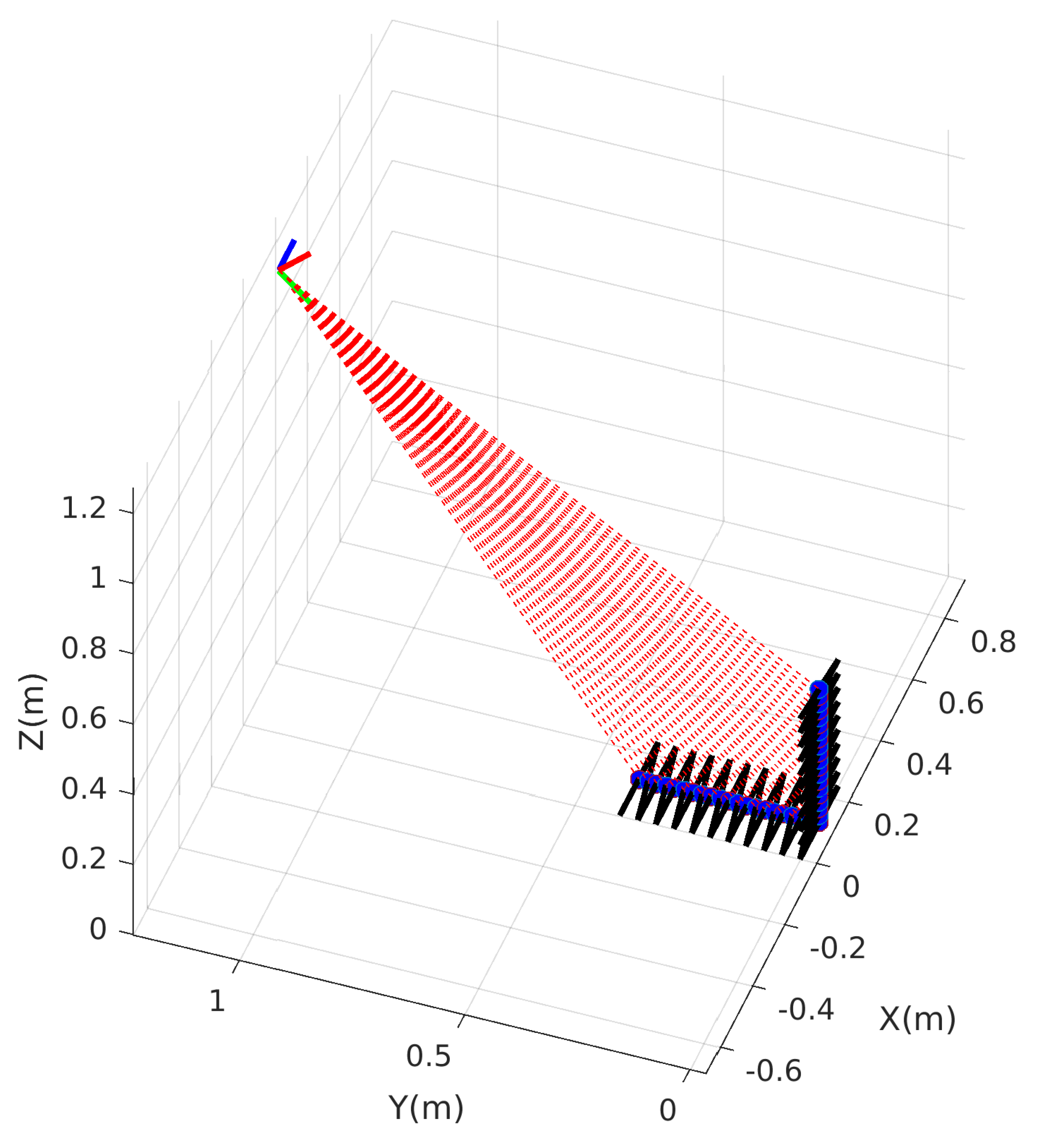
4.1. Simulation
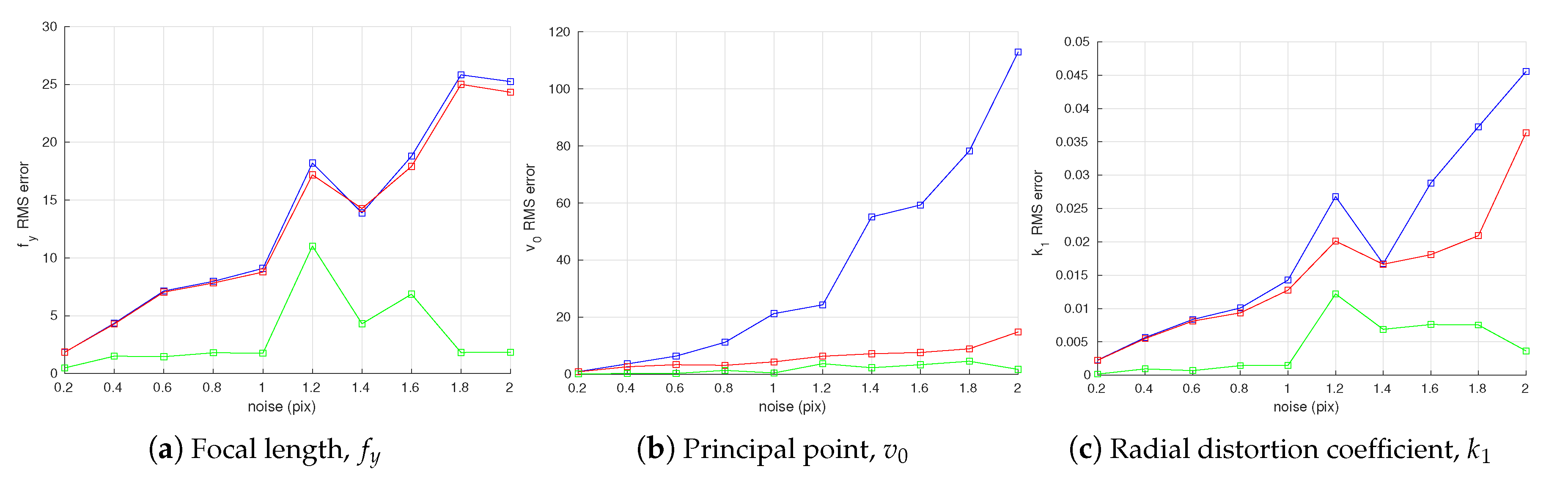
4.1.1. Noisy Camera Observations
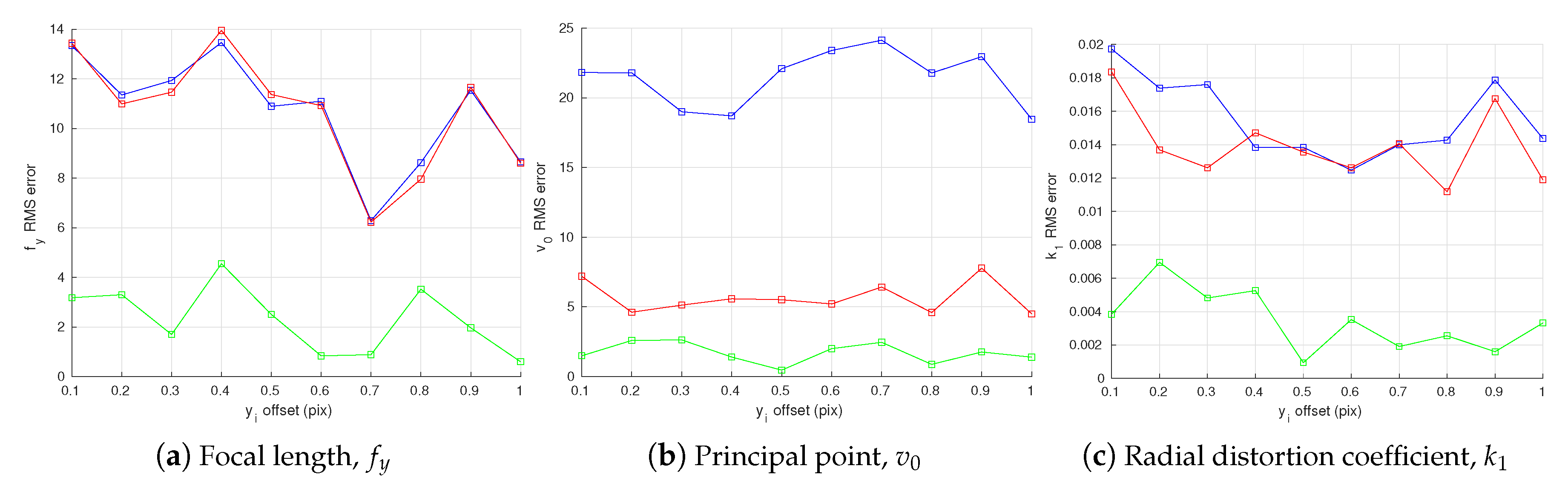
4.1.2. Noisy Camera Observations with Bias
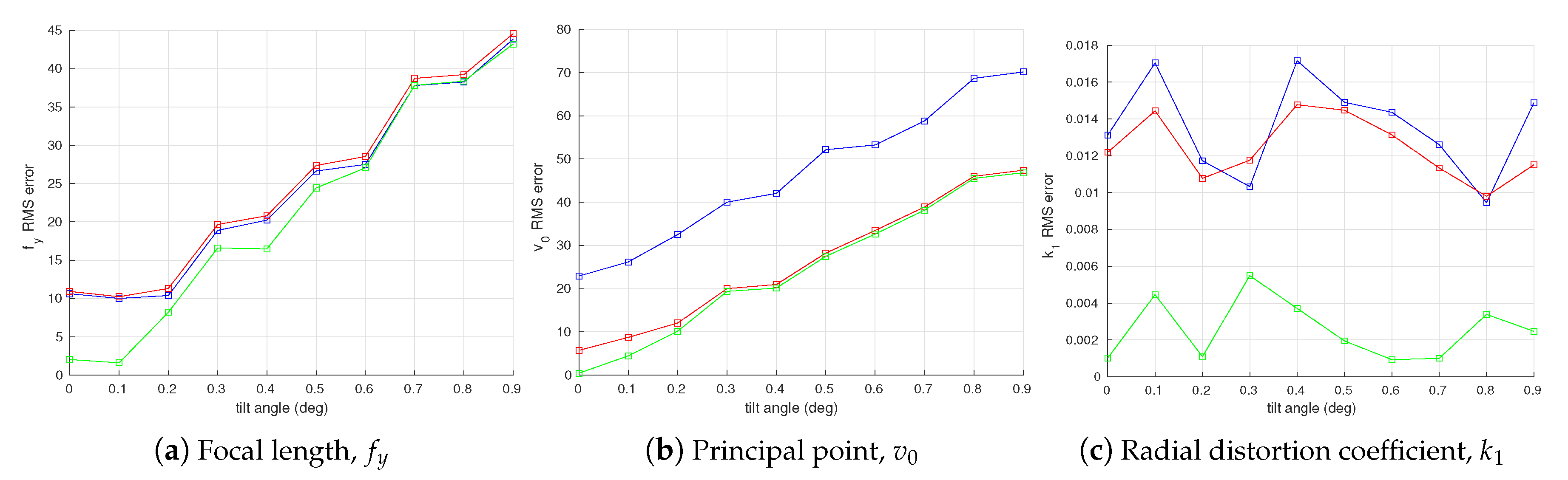
4.1.3. Calibration Target Error
4.2. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Okamoto, H.; Lee, W.S. Green citrus detection using hyperspectral imaging. Comput. Electron. Agric. 2009, 66, 201–208. [Google Scholar] [CrossRef]
- Okamoto, H.; Murata, T.; Kataoka, T.; HATA, S. Plant classification for weed detection using hyperspectral imaging with wavelet analysis. Weed Biol. Manag. 2007, 7, 31–37. [Google Scholar] [CrossRef]
- Okamoto, H.; Murata, T.; Kataoka, T.; Hata, S. Weed detection using hyperspectral imaging. In Proceedings of the 2004 Conference of Automation Technology for Off-Road Equipment, Kyoto, Japan, 7–8 October 2004. [Google Scholar]
- Suzuki, Y.; Okamoto, H.; Kataoka, T. Image segmentation between crop and weed using hyperspectral imaging for weed detection in soybean field. Environ. Control Biol. 2008, 46, 163–173. [Google Scholar] [CrossRef]
- Suzuki, Y.; Okamoto, H.; Tanaka, K.; Kato, W.; Kataoka, T. Estimation of chemical composition of grass in meadows using hyperspectral imaging. Environ. Control Biol. 2008, 46, 129–137. [Google Scholar] [CrossRef]
- Vanegas, F.; Bratanov, D.; Powell, K.; Weiss, J.; Gonzalez, F. A Novel Methodology for Improving Plant Pest Surveillance in Vineyards and Crops Using UAV-Based Hyperspectral and Spatial Data. Sensors 2018, 18, 260. [Google Scholar] [CrossRef] [PubMed]
- Mo, C.; Kim, G.; Lim, J.; Kim, M.S.; Cho, H.; Cho, B.K. Detection of lettuce discoloration using hyperspectral reflectance imaging. Sensors 2015, 15, 29511–29534. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Kim, M.S.; Jeong, D.; Delwiche, S.R.; Chao, K.; Cho, B.K. Detection of cracks on tomatoes using a hyperspectral near-infrared reflectance imaging system. Sensors 2014, 14, 18837–18850. [Google Scholar] [CrossRef] [PubMed]
- Alchanatis, V.; Safren, O.; Levi, O.; Ostrovsky, V.; Stafford, J.V. Apple yield mapping using hyperspectral machine vision. In Proceedings of the 2007 6th European Conference on Precision Agriculture, Skiathos, Greece, 3–6 June 2007; pp. 555–562. [Google Scholar]
- Cetin, M.; Musaoglu, N. Merging hyperspectral and panchromatic image data: Qualitative and quantitative analysis. Int. J. Remote Sens. 2009, 30, 1779–1804. [Google Scholar] [CrossRef]
- Lucas, R.; Rowlands, A.; Niemann, O.; Merton, R. Hyperspectral Sensors and Applications; Springer: New York, NY, USA, 2004; pp. 11–49. [Google Scholar]
- Tsai, R. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE J. Robot. Autom. 1987, 3, 323–344. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Gupta, R.; Hartley, R.I. Linear pushbroom cameras. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 963–975. [Google Scholar] [CrossRef]
- Yao, M.; Zhao, Z.; Xu, B. Geometric calibration of line-scan camera using a planar pattern. J. Electron. Imaging 2014, 23, 013028. [Google Scholar] [CrossRef]
- Horaud, R.; Mohr, R.; Lorecki, B. On single-scanline camera calibration. IEEE Trans. Robot. Autom. 1993, 9, 71–75. [Google Scholar] [CrossRef]
- Mohr, R.; Morin, L. Relative positioning from geometric invariants. In Proceedings of the 1991 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 1991), Maui, HI, USA, 3–6 June 1991; pp. 139–144. [Google Scholar]
- Luna, C.A.; Mazo, M.; Lazaro, J.L.; Vazquez, J.F. Calibration of line-scan cameras. IEEE Trans. Instrum. Meas. 2010, 59, 2185–2190. [Google Scholar] [CrossRef]
- Li, D.; Wen, G.; Hui, B.W.; Qiu, S.; Wang, W. Cross-ratio invariant based line scan camera geometric calibration with static linear data. Opt. Lasers Eng. 2014, 62, 119–125. [Google Scholar] [CrossRef]
- Drareni, J.; Roy, S.; Sturm, P. Plane-based calibration for linear cameras. Int. J. Comput. Vis. 2011, 91, 146–156. [Google Scholar] [CrossRef]
- Hui, B.; Wen, G.; Zhao, Z.; Li, D. Line-scan camera calibration in close-range photogrammetry. Opt. Eng. 2012, 51, 053602. [Google Scholar] [CrossRef]
- Behmann, J.; Mahlein, A.K.; Paulus, S.; Kuhlmann, H.; Oerke, E.C.; Plumer, L. Calibration of hyperspectral close-range pushbroom cameras for plant phenotyping. ISPRS J. Photogramm. Remote Sens. 2015, 106, 172–182. [Google Scholar] [CrossRef]
- Li, D.; Wen, G.; Qiu, S. Cross-ratio-based line scan camera calibration using a planar pattern. Opt. Eng. 2016, 55, 014104. [Google Scholar] [CrossRef]
- Hui, B.; Wen, G.; Zhang, P.; Li, D. A novel line scan camera calibration technique with an auxiliary frame camera. IEEE Trans. Instrum. Meas. 2013, 62, 2567–2575. [Google Scholar] [CrossRef]
- Weng, J.; Cohen, P.; Herniou, M. Camera calibration with distortion models and accuracy evaluation. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 965–980. [Google Scholar] [CrossRef]
- Boor, C.D. A Practical Guide to Splines; Springer: New York, NY, USA, 1978. [Google Scholar]
- More, J.J. The Levenberg–Marquardt algorithm: Implementation and theory. Numer. Anal. 1978, 630, 105–116. [Google Scholar]
- Underwood, J.; Wendel, A.; Schofield, B.; McMurray, L.; Kimber, R. Efficient in-field plant phenomics for row-crops with an autonomous ground vehicle. J. Field Robot. 2017, 34, 1061–1083. [Google Scholar] [CrossRef]
- Underwood, J.P.; Calleija, M.; Taylor, Z.; Hung, C.; Nieto, J.; Fitch, R.; Sukkarieh, S. Real-time target detection and steerable spray for vegetable crops. In Proceedings of the 2015 International Conference on Robotics and Automation: Robotics in Agriculture Workshop, Seattle, WA, USA, 26–30 May 2015; pp. 26–30. [Google Scholar]
- Wendel, A.; Underwood, J. Illumination compensation in ground based hyperspectral imaging. ISPRS J. Photogramm. Remote Sens. 2017, 129, 162–178. [Google Scholar] [CrossRef]
- Wendel, A.; Underwood, J. Self-supervised weed detection in vegetable crops using ground based hyperspectral imaging. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA 2016), Stockholm, Sweden, 16–21 May 2016; pp. 5128–5135. [Google Scholar]
- Wendel, A.; Underwood, J. Extrinsic Parameter Calibration for Line Scanning Cameras on Ground Vehicles with Navigation Systems Using a Calibration Pattern. Sensors 2017, 17, 2491. [Google Scholar] [CrossRef] [PubMed]







| Parameters | Values |
|---|---|
| Width of the triangle in the target () | 0.24 m |
| Height of the triangle in the target () | 0.04 m |
| Ground truth value of the focal length () | 5000 pix |
| Ground truth value of the principal point () | 1024 pix |
| Number of pixels in spatial dimension | 2048 |
| Rotation (R) of camera in axis angle | (−163.6, 0.095, 8.203) |
| Translation (T) of camera | (−0.071, 0.115, 1.671) m |
| Calibration images for each camera view angle | 100 |
| Number of camera view angles | 15 |
| Least square optimiser | Levenberg–Marquardt |
| No. | Focal Length | Principal Point | Radial Distortion | Max Re-Proj. Error | Re-Proj. RMSE |
|---|---|---|---|---|---|
| 1 | 3922.7 | 989.0 | −0.0110 | 1.7648 | 0.3782 |
| 2 | 3925.5 | 988.6 | −0.0078 | 1.7684 | 0.3776 |
| 3 | 3926.4 | 988.3 | −0.0062 | 1.7693 | 0.3764 |
| 4 | 3920.6 | 990.1 | −0.0134 | 1.7640 | 0.3794 |
| 5 | 3910.8 | 990.1 | −0.0239 | 1.7466 | 0.3804 |
| 6 | 3914.5 | 998.4 | −0.0221 | 1.7762 | 0.3766 |
| 7 | 3914.3 | 998.4 | −0.0234 | 1.7756 | 0.3756 |
| 8 | 3911.2 | 999.0 | −0.0281 | 1.7708 | 0.3748 |
| 9 | 3919.0 | 995.6 | −0.0149 | 1.7771 | 0.3783 |
| 10 | 3922.1 | 992.7 | −0.0111 | 1.7062 | 0.3799 |
| 11 | 3918.9 | 990.0 | −0.0144 | 1.7610 | 0.3764 |
| 12 | 3918.4 | 990.3 | −0.0143 | 1.7609 | 0.3756 |
| 13 | 3916.2 | 992.1 | −0.0165 | 1.7623 | 0.3743 |
| 14 | 3916.1 | 990.5 | −0.0178 | 1.7574 | 0.3768 |
| 15 | 3915.5 | 991.3 | −0.0189 | 1.7584 | 0.3782 |
| Mean | 3918.1 | 992.3425 | −0.0163 | 1.7613 | 0.3772 |
| STD | 4.7088 | 3.7250 | 0.0062 | 0.0173 | 0.0018 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, D.; Bender, A.; Sukkarieh, S. Improved Cross-Ratio Invariant-Based Intrinsic Calibration of A Hyperspectral Line-Scan Camera. Sensors 2018, 18, 1885. https://doi.org/10.3390/s18061885
Su D, Bender A, Sukkarieh S. Improved Cross-Ratio Invariant-Based Intrinsic Calibration of A Hyperspectral Line-Scan Camera. Sensors. 2018; 18(6):1885. https://doi.org/10.3390/s18061885
Chicago/Turabian StyleSu, Daobilige, Asher Bender, and Salah Sukkarieh. 2018. "Improved Cross-Ratio Invariant-Based Intrinsic Calibration of A Hyperspectral Line-Scan Camera" Sensors 18, no. 6: 1885. https://doi.org/10.3390/s18061885
APA StyleSu, D., Bender, A., & Sukkarieh, S. (2018). Improved Cross-Ratio Invariant-Based Intrinsic Calibration of A Hyperspectral Line-Scan Camera. Sensors, 18(6), 1885. https://doi.org/10.3390/s18061885





