A User-Adaptive Algorithm for Activity Recognition Based on K-Means Clustering, Local Outlier Factor, and Multivariate Gaussian Distribution
Abstract
1. Introduction
2. Related Works
2.1. Physical Activity Intensity Recognition
2.2. Fall Detection
2.3. User-Adaptive Recognition Model without Manual Interruption
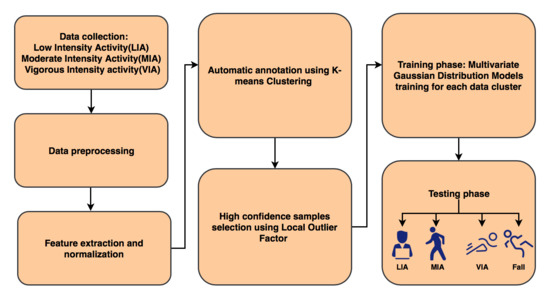
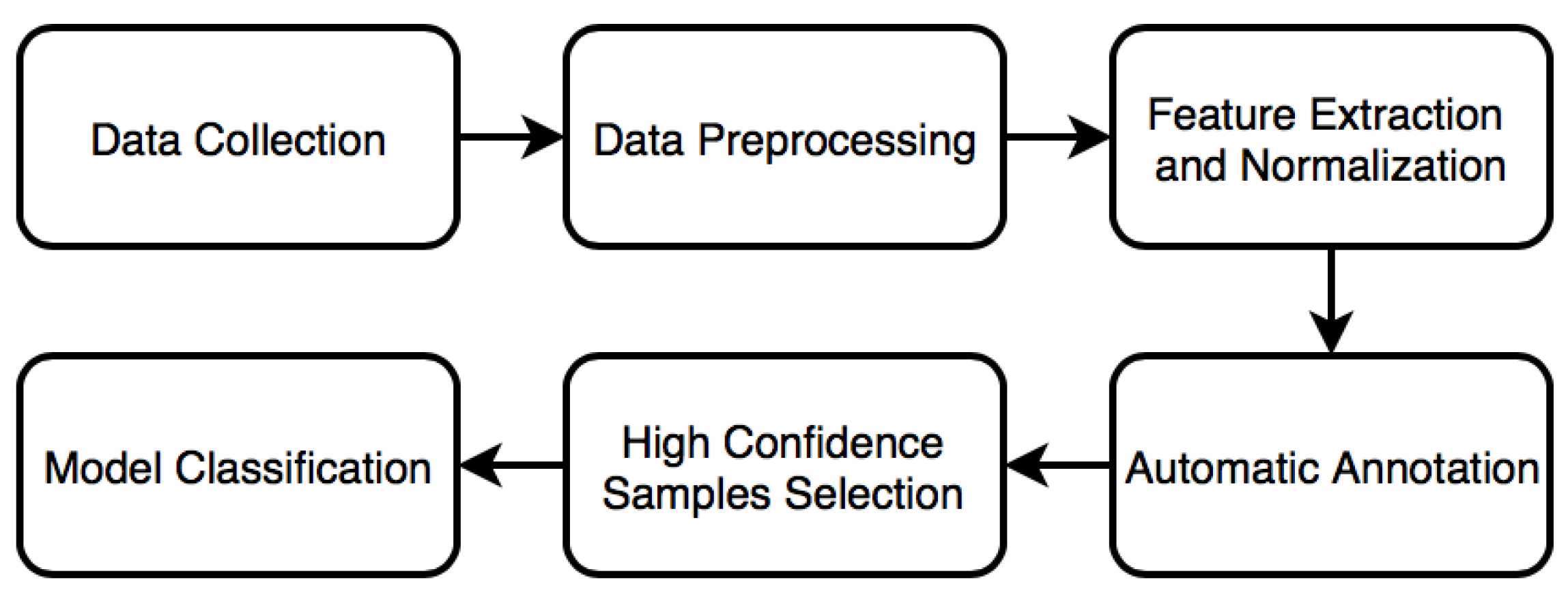
3. User-Adaptive Algorithm for Activity Recognition
3.1. Data Preprocessing and Feature Extraction
3.2. Automatic Annotation Using K-Means Algorithm
- (1)
- Initialization step: Calculate the centers as:where is the number of samples in the kth cluster of a pre-collected dataset.
- (2)
- Assignment step: Determine the category of the patterns in one of the K clusters whose mean has the least squared Euclidean distance.where each is assigned to exactly one .
- (3)
- Update step: Calculate the new as:is the number of samples in the kth cluster of the unclustered dataset.
- (4)
- Repeat steps 2 and 3 until there is no change in the assignment step.
3.3. High Confidence Samples Selection
3.4. Training Phase
| Algorithm 1 Training phase |
| Input: raw dataset without annotation , prelabeled dataset , max iterations T, nearest neighbor number k, outlier threshold |
Output: personalized MGD models
|
3.5. Testing Phase
| Algorithm 2 Classifier |
| Input: real-time data A |
Output: human activity category
|
4. Experimental Section
4.1. Experiment Protocol
4.2. Classification Performance of Our Proposed Method
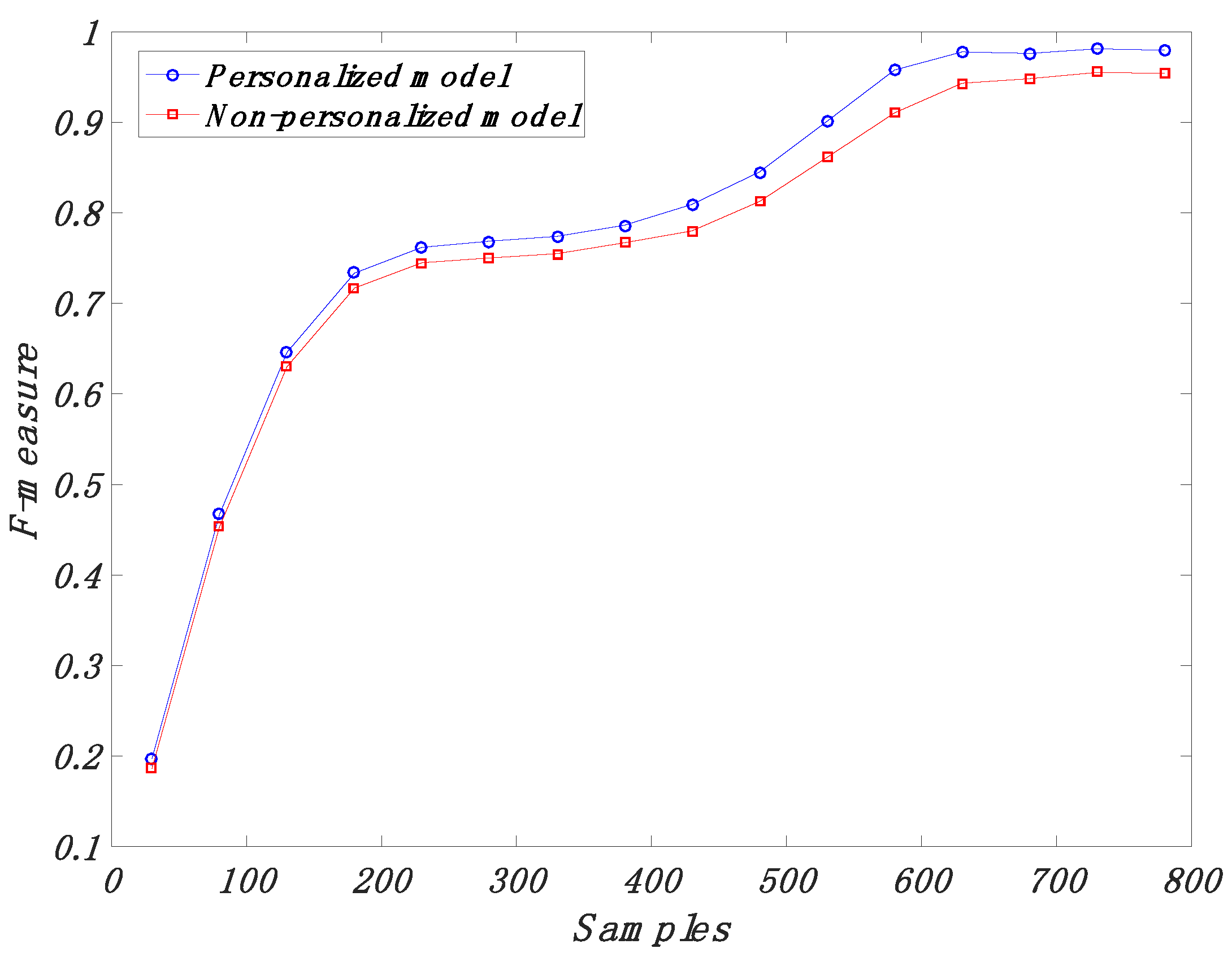
4.3. Comparison of the Proposed Algorithm with Previous Studies
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Davila, J.C.; Cretu, A.M.; Zaremba, M. Wearable Sensor Data Classification for Human Activity Recognition Based on an Iterative Learning Framework. Sensors 2017, 17, 1287. [Google Scholar] [CrossRef] [PubMed]
- Crispim-Junior, C.F.; Gómez Uría, A.; Strumia, C.; Koperski, M.; König, A.; Negin, F.; Cosar, S.; Nghiem, A.T.; Chau, D.P.; Charpiat, G.; et al. Online Recognition of Daily Activities by Color-Depth Sensing and Knowledge Models. Sensors 2017, 17, 1528. [Google Scholar] [CrossRef] [PubMed]
- Janidarmian, M.; Roshan Fekr, A.; Radecka, K.; Zilic, Z. A Comprehensive Analysis on Wearable Acceleration Sensors in Human Activity Recognition. Sensors 2017, 17, 529. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Tian, Y.L. Super normal vector for human activity recognition with depth cameras. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1028–1039. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wong, Y.; Liu, A.A.; Li, Y.; Su, Y.T.; Kankanhalli, M. Multi-camera action dataset for cross-camera action recognition benchmarking. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 187–196. [Google Scholar]
- Chen, C.; Jafari, R.; Kehtarnavaz, N. A survey of depth and inertial sensor fusion for human action recognition. Multimedia Tools Appl. 2017, 76, 4405–4425. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, G. A review on radio based activity recognition. Digital Commun. Netw. 2015, 1, 20–29. [Google Scholar] [CrossRef]
- Medrano, C.; Plaza, I.; Igual, R.; Sánchez, Á.; Castro, M. The effect of personalization on smartphone-based fall detectors. Sensors 2016, 16, 117. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Xue, Y. A deep learning approach to human activity recognition based on single accelerometer. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Kowloon, China, 9–12 October 2015; pp. 1488–1492. [Google Scholar]
- Preece, S.J.; Goulermas, J.Y.; Kenney, L.P.; Howard, D.; Meijer, K.; Crompton, R. Activity identification using body-mounted sensors—A review of classification techniques. Physiol. Meas. 2009, 30, R1. [Google Scholar] [CrossRef] [PubMed]
- Safi, K.; Attal, F.; Mohammed, S.; Khalil, M.; Amirat, Y. Physical activity recognition using inertial wearable sensors—A review of supervised classification algorithms. In Proceedings of the International Conference on Advances in Biomedical Engineering (ICABME), Beirut, Lebanon, 16–18 September 2015; pp. 313–316. [Google Scholar]
- Weiss, G.M.; Lockhart, J.W. The Impact of Personalization on Smartphone-Based Activity Recognition; American Association for Artificial Intelligence: Palo Alto, CA, USA, 2012; pp. 98–104. [Google Scholar]
- Ling, B.; Intille, S.S. Activity recognition from user-annotated acceleration data. Proc. Pervasive 2004, 3001, 1–17. [Google Scholar]
- Saez, Y.; Baldominos, A.; Isasi, P. A Comparison Study of Classifier Algorithms for Cross-Person Physical Activity Recognition. Sensors 2017, 17, 66. [Google Scholar] [CrossRef] [PubMed]
- Okeyo, G.O.; Chen, L.; Wang, H.; Sterritt, R. Time handling for real-time progressive activity recognition. In Proceedings of the 2011 International Workshop on Situation Activity & Goal Awareness, Beijing, China, 18 September 2011; pp. 37–44. [Google Scholar]
- Pärkkä, J.; Cluitmans, L.; Ermes, M. Personalization algorithm for real-time activity recognition using PDA, wireless motion bands, and binary decision tree. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 1211–1215. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.T.; Chan, C.T. A Fuzzy Logic Prompting Mechanism Based on Pattern Recognition and Accumulated Activity Effective Index Using a Smartphone Embedded Sensor. Sensors 2016, 16, 1322. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Gao, R.X.; John, D.; Staudenmayer, J.W.; Freedson, P.S. Multisensor data fusion for physical activity assessment. IEEE Trans. Biomed. Eng. 2012, 59, 687–696. [Google Scholar] [PubMed]
- Jung, Y.; Yoon, Y.I. Multi-level assessment model for wellness service based on human mental stress level. Multimed. Tools Appl. 2017, 76, 11305–11317. [Google Scholar] [CrossRef]
- Fahim, M.; Khattak, A.M.; Chow, F.; Shah, B. Tracking the sedentary lifestyle using smartphone: A pilot study. In Proceedings of the International Conference on Advanced Communication Technology, Pyeongchang, Korea, 31 January–3 February 2016; pp. 296–299. [Google Scholar]
- Ma, C.; Li, W.; Gravina, R.; Cao, J.; Li, Q.; Fortino, G. Activity level assessment using a smart cushion for people with a sedentary lifestyle. Sensors 2017, 17, 2269. [Google Scholar] [CrossRef] [PubMed]
- Tong, L.; Song, Q.; Ge, Y.; Liu, M. Hmm-based human fall detection and prediction method using tri-axial accelerometer. IEEE Sens. J. 2013, 13, 1849–1856. [Google Scholar] [CrossRef]
- Bourke, A.K.; Lyons, G.M. A threshold-based fall-detection algorithm using a bi-axial gyroscope sensor. Med. Eng. Phys. 2008, 30, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Sucerquia, A.; López, J.D.; Vargas-Bonilla, J.F. Real-Life/Real-Time Elderly Fall Detection with a Triaxial Accelerometer. Sensors 2018, 18, 1101. [Google Scholar] [CrossRef] [PubMed]
- Aziz, O.; Musngi, M.; Park, E.J.; Mori, G.; Robinovitch, S.N. A comparison of accuracy of fall detection algorithms (threshold-based vs. Machine learning) using waist-mounted tri-axial accelerometer signals from a comprehensive set of falls and non-fall trials. Med. Biol. Eng. Comput. 2017, 55, 45–55. [Google Scholar] [CrossRef] [PubMed]
- Mao, A.; Ma, X.; He, Y.; Luo, J. Highly Portable, Sensor-Based System for Human Fall Monitoring. Sensors 2017, 17, 2096. [Google Scholar] [CrossRef] [PubMed]
- Shi, G.; Zhang, J.; Dong, C.; Han, P.; Jin, Y.; Wang, J. Fall detection system based on inertial mems sensors: Analysis design and realization. In Proceedings of the IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems, Shenyang, China, 8–12 June 2015; pp. 1834–1839. [Google Scholar]
- Zhao, S.; Li, W.; Niu, W.; Gravina, R.; Fortino, G. Recognition of human fall events based on single tri-axial gyroscope. In Proceedings of the 15th IEEE International Conference on Networking, Sensing and Control, Zhuhai, China, 26–29 March 2018; pp. 1–6. [Google Scholar]
- Viet, V.Q.; Thang, H.M.; Choi, D. Personalization in Mobile Activity Recognition System Using K-Medoids Clustering Algorithm. Int. J. Distrib. Sens. Netw. 2013, 9, 797–800. [Google Scholar]
- Zhao, Z.; Chen, Y.; Liu, J.; Shen, Z.; Liu, M. Cross-people mobile-phone based activity recognition. In Proceedings of the International Joint Conference on Artificial Intelligence, Barcelona, Spain, 19–22 July 2011; pp. 2545–2550. [Google Scholar]
- Deng, W.Y.; Zheng, Q.H.; Wang, Z.M. Cross-person activity recognition using reduced kernel extreme learning machine. Neural Netw. 2014, 53, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.; Wang, Z. Sensor-based adaptive activity recognition with dynamically available sensors. Neurocomputing 2016, 218, 307–317. [Google Scholar] [CrossRef]
- Fallahzadeh, R.; Ghasemzadeh, H. Personalization without user interruption: Boosting activity recognition in new subjects using unlabeled data. In Proceedings of the 8th International Conference on Cyber-Physical Systems, Pittsburgh, PA, USA, 18–20 April 2017; pp. 293–302. [Google Scholar]
- Siirtola, P.; Koskimäki, H.; Röning, J. Personalizing human activity recognition models using incremental learning. In Proceedings of the 26th European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN 2018), Brugge, Belgium, 25–27 April 2018; pp. 627–632. [Google Scholar]
- Greene, B.R.; Doheny, E.P.; Kenny, R.A.; Caulfield, B. Classification of frailty and falls history using a combination of sensor-based mobility assessments. Physiol. Meas. 2014, 35, 2053–2066. [Google Scholar] [CrossRef] [PubMed]
- Pereira, F. Developments and trends on video coding: Is there a xVC virus? In Proceedings of the 2nd International Conference on Ubiquitous Information Management and Communication, Suwon, Korea, 31 January–1 February 2008; pp. 384–389. [Google Scholar]
- Giansanti, D.; Maccioni, G.; Cesinaro, S.; Benvenuti, F.; Macellari, V. Assessment of fall-risk by means of a neural network based on parameters assessed by a wearable device during posturography. Med. Eng. Phys. 2008, 30, 367–372. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.L.; Chung, C.Y. A real-time model-based human motion tracking and analysis for human-computer interface systems. Eurasip J. Adv. Sign. Proces. 2004, 2004, 1–15. [Google Scholar] [CrossRef]
- Peters, G. Some refinements of rough K-Means. Pattern Recognit. 2006, 39, 1481–1491. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. Lof: Identifying density-based local outliers. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 93–104. [Google Scholar]
- Khan, S.S.; Hoey, J. Review of fall detection techniques: A data availability perspective. Med. Eng. Phys. 2017, 39, 12–22. [Google Scholar] [CrossRef] [PubMed]
- Kangas, M.; Vikman, I.; Nyberg, L.; Korpelainen, R.; Lindblom, J.; Jämsä, T. Comparison of real-life accidental falls in older people with experimental falls in middle-aged test subjects. Gait Posture 2012, 35, 500–505. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar]
- De la Cal, E.; Villar, J.; Vergara, P.; Sedano, J.; Herrero, A. A smote extension for balancing multivariate epilepsy-related time series datasets. In Proceedings of the 12th International Conference on Soft Computing Models in Industrial and Environmental Applications, León, Spain, 6–8 September 2017; pp. 439–448. [Google Scholar]
- Metabolic Equivalent Website. Available online: https://en.wikipedia.org/wiki/Metabolic_equivalent (accessed on 10 September 2017).
- Alshurafa, N.; Xu, W.; Liu, J.J.; Huang, M.C.; Mortazavi, B.; Roberts, C.K.; Sarrafzadeh, M. Designing a robust activity recognition framework for health and exergaming using wearable sensors. IEEE J. Biomed. Health Inf. 2014, 18, 1636. [Google Scholar] [CrossRef] [PubMed]
- Hess, A.S.; Hess, J.R. Understanding tests of the association of categorical variables: The pearson chi-square test and fisher's exact test. Transfusion 2017, 57, 877–879. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Lin, C.J. Libsvm: A library for support vector machines. ACM Trans. Intel. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Gravina, R.; Alinia, P.; Ghasemzadeh, H.; Fortino, G. Multi-Sensor Fusion in Body Sensor Networks: State-of-the-art and research challenges. Inf. Fusion 2017, 35, 68–80. [Google Scholar] [CrossRef]
- Cao, J.; Li, W.; Ma, C.; Tao, Z.; Cao, J.; Li, W. Optimizing multi-sensor deployment via ensemble pruning for wearable activity recognition. Inf. Fusion 2017, 41, 68–79. [Google Scholar] [CrossRef]
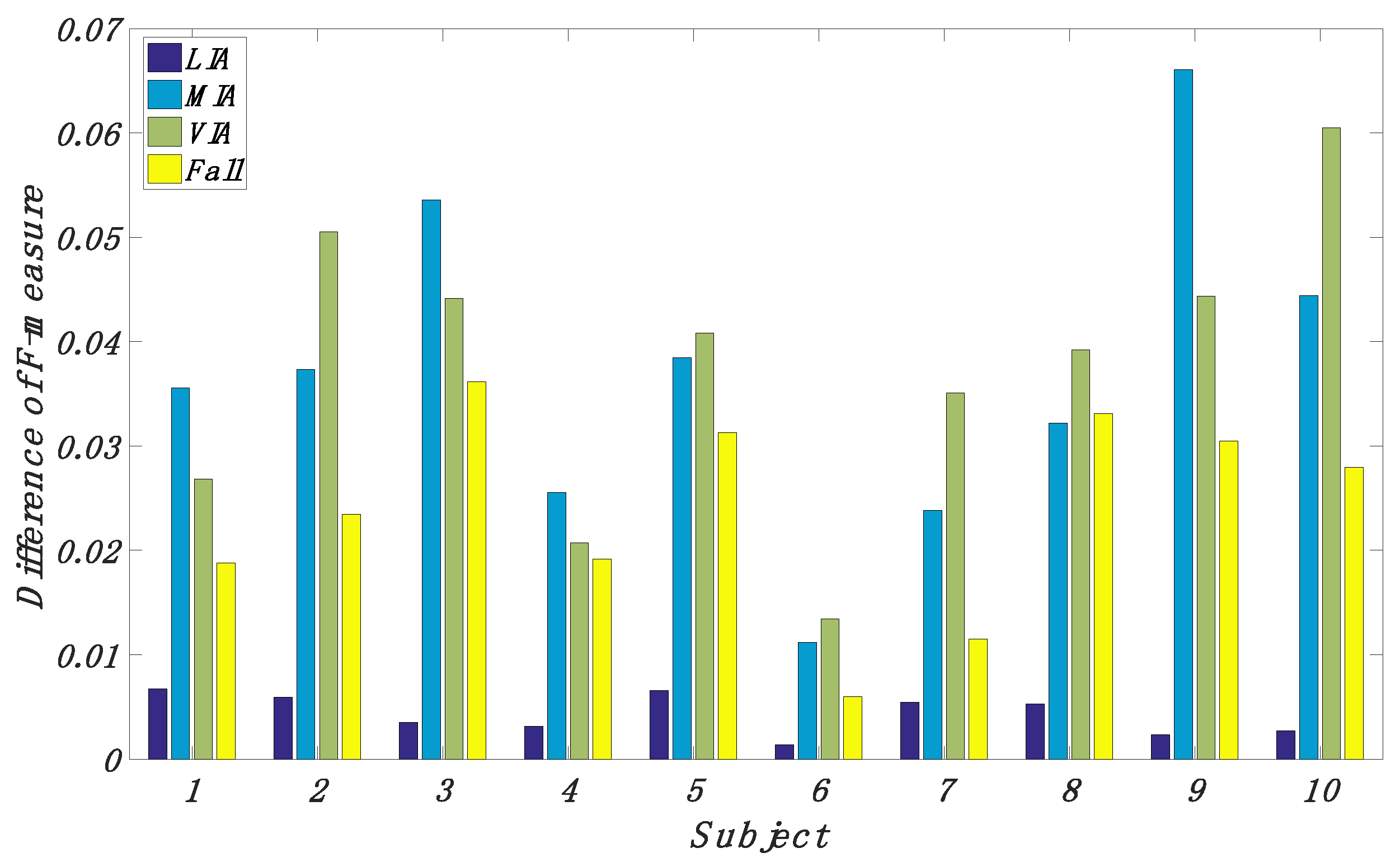
| Activity Category | Description | Activities |
|---|---|---|
| Light intensity activity (LIA) | Users perform common daily life activities in light movement condition. | Working at a desk, reading a book, having a conversation |
| Moderate intensity activity (MIA) | Users perform common daily life activities in moderate movement condition. | Walking, walking downstairs, walking upstairs |
| vigorous intensity activity (VIA) | Users perform vigorous activities to keep fit. | Running, rope jumping |
| Fall | Users accidentally falls to the ground in a short time. | Forward falling, backward falling, left-lateral falling, right-lateral falling |
| Description | Underweight | Normal | Overweight and Obese |
|---|---|---|---|
| BMI | <18.5 | (18.5, 25) | 25 |
| Number of subjects | 3 | 5 | 2 |
| Users | LIA | MIA | VIA | Fall |
|---|---|---|---|---|
| 1 | 0.9822 | 0.9766 | 0.9765 | 0.9709 |
| 2 | 0.9985 | 0.9821 | 0.9673 | 0.9635 |
| 3 | 0.9963 | 0.9782 | 0.9775 | 0.9836 |
| 4 | 0.9822 | 0.9673 | 0.9661 | 0.9750 |
| 5 | 0.9866 | 0.9687 | 0.9642 | 0.9809 |
| 6 | 0.9782 | 0.9821 | 0.9739 | 0.9774 |
| 7 | 0.9865 | 0.9680 | 0.9641 | 0.9887 |
| 8 | 0.9733 | 0.9753 | 0.9661 | 0.9850 |
| 9 | 0.9978 | 0.9653 | 0.9523 | 0.9711 |
| 10 | 0.9931 | 0.9651 | 0.9839 | 0.9723 |
| Mean | 0.9875 | 0.9729 | 0.9692 | 0.9766 |
| Normal | Abnormal | Row total | |
|---|---|---|---|
| SS | 1 | 5 | 6 |
| IS | 4 | 0 | 4 |
| Column total | 5 | 5 | 10 |
| Author | Algorithm | Parameter Setting |
|---|---|---|
| Viet et al. [29] | K-Medoids, SVM | |
| Deng et al. [31] | TransRKELM | |
| Tong et al. [22] | HMM | |
| Shi et al. [27] | J48 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Li, W.; Cao, J. A User-Adaptive Algorithm for Activity Recognition Based on K-Means Clustering, Local Outlier Factor, and Multivariate Gaussian Distribution. Sensors 2018, 18, 1850. https://doi.org/10.3390/s18061850
Zhao S, Li W, Cao J. A User-Adaptive Algorithm for Activity Recognition Based on K-Means Clustering, Local Outlier Factor, and Multivariate Gaussian Distribution. Sensors. 2018; 18(6):1850. https://doi.org/10.3390/s18061850
Chicago/Turabian StyleZhao, Shizhen, Wenfeng Li, and Jingjing Cao. 2018. "A User-Adaptive Algorithm for Activity Recognition Based on K-Means Clustering, Local Outlier Factor, and Multivariate Gaussian Distribution" Sensors 18, no. 6: 1850. https://doi.org/10.3390/s18061850
APA StyleZhao, S., Li, W., & Cao, J. (2018). A User-Adaptive Algorithm for Activity Recognition Based on K-Means Clustering, Local Outlier Factor, and Multivariate Gaussian Distribution. Sensors, 18(6), 1850. https://doi.org/10.3390/s18061850